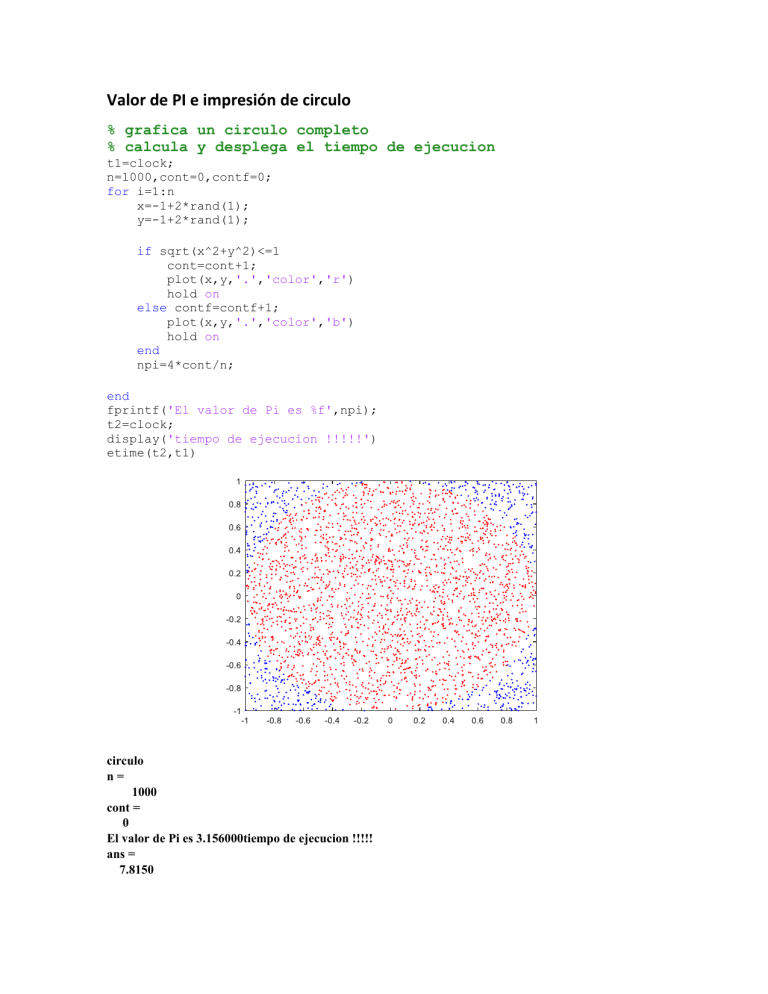
Valor de PI e impresión de circulo
% grafica un circulo completo
% calcula y desplega el tiempo de ejecucion
t1=clock;
n=1000,cont=0,contf=0;
for i=1:n
x=-1+2*rand(1);
y=-1+2*rand(1);
if sqrt(x^2+y^2)<=1
cont=cont+1;
plot(x,y,'.','color','r')
hold on
else contf=contf+1;
plot(x,y,'.','color','b')
hold on
end
npi=4*cont/n;
end
fprintf('El valor de Pi es %f',npi);
t2=clock;
display('tiempo de ejecucion !!!!!')
etime(t2,t1)
circulo
n=
1000
cont =
0
El valor de Pi es 3.156000tiempo de ejecucion !!!!!
ans =
7.8150
tic, toc
Measure performance using stopwatch timer
Syntax
tic
any statements
toc
t = toc
Description
tic starts a stopwatch timer.
toc prints the elapsed time since tic was used.
t = toc returns the elapsed time in t.
Remarks
The tic and toc functions work together to measure elapsed time. tic saves the current time that toc uses later
to measure the elapsed time. The sequence of commands
tic
operations
toc
measures the amount of time MATLAB takes to complete one or more operations, and displays the time in
seconds.
Examples
This example measures how the time required to solve a linear system varies with the order of a matrix.
for n = 1:100
A = rand(n,n);
b = rand(n,1);
tic
x = A\b;
t(n) = toc;
end
plot(t)
% grafica un circulo completo
% calcula y desplega el tiempo de ejecución con TIC TOC
%t1=clock;
n=1000,cont=0,contf=0;
for i=1:n
x=-1+2*rand(1);
y=-1+2*rand(1);
tic
if sqrt(x^2+y^2)<=1
cont=cont+1;
plot(x,y,'.','color','r')
hold on
else contf=contf+1;
plot(x,y,'.','color','b')
hold on
t(n)=toc;
end
npi=4*cont/n;
end
fprintf('El valor de Pi es %f',npi);
%t2=clock;
display('tiempo de ejecucion !!!!!')
etime(t2,t1)
fopen
Abra un archivo u obtenga información sobre archivos abiertos
Sintaxis
fid = fopen (nombre de archivo)
fid = fopen (nombre de archivo, permiso)
[fid, mensaje] = fopen (nombre de archivo, permiso, formato de
máquina)
fids = fopen ('todos')
[nombre de archivo, permiso, machineormat] = fopen (fid)
Descripción
abre el archivo filenamepara acceso de lectura. (En las
PC, fopenabre archivos para acceso de lectura binario).
fid = fopen(filename)
fides
un entero MATLAB escalar, llamado identificador de archivo. Utiliza
el fidcomo primer argumento para otras rutinas de entrada / salida de
archivo. Si fopenno puede abrir el archivo, vuelve -1. Dos identificadores de
archivo están disponibles automáticamente y no necesitan
abrirse. Son fid=1(salida estándar) y fid=2(error estándar).
abre el archivo filenameen el modo
especificado por permission. permissionpuede ser:
fid = fopen(filename,permission)
'r'
Abrir archivo para leer (predeterminado).
'w'
Abrir un archivo o crear un nuevo archivo para escribir; descarte los contenidos
existentes, si los hay.
'a'
Abrir un archivo o crear un nuevo archivo para escribir; agregar datos al final del
archivo.
'r+'
Abrir archivo para leer y escribir.
'w+'
Abrir un archivo o crear un nuevo archivo para leer y escribir; descarte los
contenidos existentes, si los hay.
'a+'
Abrir un archivo o crear un nuevo archivo para leer y escribir; agregar datos al
final del archivo.
'A'
Añadir sin enjuague automático; usado con unidades de cinta
'W'
Escribir sin enjuague automático; usado con unidades de cinta
filenamepuede
ser un MATLABPATHnombre de ruta parcial relativo si el archivo se
abre solo para lectura. Siempre se busca primero una ruta relativa con respecto al
directorio actual. Si no se encuentra y solo se especifica o implica la lectura,
entonces fopen realiza una búsqueda adicional deMATLABPATH
Los archivos se pueden abrir en modo binario (predeterminado) o en modo
texto. En modo binario, no se seleccionan caracteres para un tratamiento
especial. En el modo de texto en la PC, el carácter de retorno de carro que
precede a un carácter de nueva línea se elimina en la entrada y se agrega antes del
carácter de nueva línea en la salida. Para abrir en modo texto, agregue "t" a la
cadena de permisos, por ejemplo 'rt'y 'wt+'. (En Unix, el texto y el modo
binario son los mismos, por lo que esto no tiene ningún efecto. Pero en los
sistemas de PC es crítico).
Nota Si se abre el archivo en modo de actualización ( '+'), un comando de
entrada como fread, fscanf, fgets, o fgetlno puede ser seguida
inmediatamente por un comando de salida como fwrite o fprintf sin una
intervención fseek o frewind. Lo contrario también es cierto. Es decir, un
comando de salida como fwrite o fprintf no puede ser seguida
inmediatamente por un comando de entrada como fread, fscanf, fgets, o fgetl
sin una intervención fseek o frewind.
abre un archivo como el
anterior. Si no puede abrir el archivo, fides igual -1y messagecontiene un
mensaje de error dependiente del sistema. Si fopenabre un archivo con éxito, el
valor de messageestá vacío.
[fid,message] = fopen(filename,permission)
[fid,message] = fopen(filename,permission,machineformat)abre
el archivo
especificado con el especificado permissiony trata los datos leídos usando freado
los datos escritos usando fwriteun formato dado
por machineformat. machineformates una de las siguientes cadenas:
'cray' o 'c'
Punto flotante Cray con orden de bytes big-endian
'ieee-be'
o 'b'
Punto flotante IEEE con orden de bytes big-endian
'ieee-le'
o 'l'
Punto flotante IEEE con ordenación de bytes little-endian
'ieeebe.l64'
o 's'
Punto flotante IEEE con orden de bytes big-endian y tipo de datos
largo de 64 bits
'ieeele.l64'
o 'a'
Punto flotante IEEE con ordenación de bytes little endian y tipo de
datos largo de 64 bits
'native' o 'n'
Formato numérico de la máquina en la que se ejecuta MATLAB (el
valor predeterminado).
'vaxd' o 'd'
VAX D punto flotante y pedido VAX
'vaxg' o 'g'
VAX G coma flotante y pedido VAX
devuelve un vector de fila que contiene los identificadores
de todos los archivos abiertos, sin incluir 1y 2(salida estándar y error
estándar). El número de elementos en el vector es igual al número de archivos
abiertos.
fids = fopen('all')
devuelve
el filename, permissioncuerda y machineformatcadena asociada con el archivo
especificado. Un inválido fiddevuelve cadenas vacías para todos los argumentos
de salida.
[filename,permission,machineformat] = fopen(fid)
Los permisos 'W'y 'A'están diseñados para su uso con unidades de cinta y no
realizan automáticamente una descarga del búfer de salida actual después de las
operaciones de salida. Por ejemplo, abra una cinta de cartucho de 1/4 "en una
estación SPARCstation para escribir sin enjuague automático:
fid = fopen ('/ dev / rst0', 'W')
Ejemplos
El ejemplo se utiliza fopenpara abrir un archivo y luego pasa fid, devuelto
por fopen, a otras funciones de E / S de archivo para leer datos del archivo y
luego cerrar el archivo.
fid = fopen ('fgetl.m');
mientras que 1
tline = fgetl (fid);
if ~ ischar (tline), break, end
disp (tline)
fin
fclose (fid);
MÉTODO DE NEWTON-RAPHSON (ITERACIONES)
Ejemplo:
Figura: Muestra el método de Newton -Raphson aplicado a una función para encontrar su raíz
PROGRAMA MÉTODO DE NEWTON-RAPHSON (ITERACIONES)
x=.
f[x_]:=(x^3)+(4*x^2)-10;
tol=0.001;
a=0.0;
b=2.0;
n=1;
x=(a+b)/2;
iter=20;
While[Abs[f[x]]>=tol,
if[f[a]*f[x]<=0,b=x,a=x];
x=(a+b)/2;
Print["por metodo de Newton iteracion",n,"f(x)=", N[f[x]],"Raíz =",x]
n++;
otra forma:
Newton-Raphson
(*función y gráfica para determinar el punto inicial*)
f[x_]:=x^3+4*x^2-10;
Plot[f[x],{x,-5,5},PlotStyle-> Magenta]
(*Vaor inicial*)
x0=1;
(*numero maximo de iteraciones y tolerancia*)
maxIter=20;
ϵ=0.001;
(*algoritmo*)
xa=x0; (*Estimado anterior de la raiz*)
For[i=1,i<=maxIter,i++,
(*aproximación de la raiz*)
xn=Round[xa-f[xa]/f'[xa],0.0001];
(*calculo del error y condición de parada del metodo*)
ea=N[Abs[xn-xa]];
Print[i," ",xn," ",ea];
If[ea<=ϵ,Break[],xa=xn];
];
Print["La raiz de f(x) es: ",N[xn],"y se obtuvo con ",i,"iteraciones."]
Newton-Raphson
150
100
50
4
1
2
3
4
1.4545
1.3689
1.3652
1.3652
2
2
0.4545
0.0856
0.0037
0.
La raiz de f(x) es: 1.3652 y se obtuvo con 4 iteraciones.
NOTAS ADICIONALES
Derivando la función: 𝑓 (𝑥) = 𝑋3 -𝑋 − 1 = 0
𝑓 ′(𝑥) = 3𝑋2 – 1
Aplicando el Método de Newton-Raphson
Primera iteración para:
X1=1
𝑓 (𝑥1)
𝑓 (𝑥1)
(3)
1 −1−1
𝑋2 =X1– 𝑓′(𝑥1) = 1– 𝑓′(𝑥1)=1– 3(1
(2) )−1 = 𝟏. 𝟓
Segunda iteración para:
X2=1.5
𝑋3 =X2–
𝑓 (𝑥2)
𝑓′(𝑥2)
(3)
−1.5−1
= 1.5– 1.5
= 𝟏. 𝟑𝟒𝟕𝟖𝟐
3(1.5(2) )−1
Tercera iteración para:
X3= 𝟏. 𝟑𝟒𝟕𝟖𝟐
𝑋4 =X3–
𝑓 (𝑥3)
𝑓′(𝑥3)
(3)
−1.34782−1
= 1.34782– 1.34782
= 𝟏. 𝟑𝟐𝟓𝟐𝟎
3(1.34782(2) )−1
Cuarta iteración para:
X4= 𝟏. 𝟑𝟐𝟓𝟐𝟎
𝑋5 =X4–
𝑓 (𝑥4)
𝑓′(𝑥4)
(3)
−1.32520−1
= 1.32520– 1.32520
= 𝟏. 𝟑𝟐𝟒𝟕
3(1.32520(2) )−1
4
MÉTODO DE LA REGLA FALSA (ITERACIONES)
REGLA FALSA
(*función y gráfica para determinar el punto inicial*)
f[x_]:=x^3+4*x^2-10;
a=-2;
b=3;
Plot[f[x],{x,a,b},PlotStyle-> Magenta]
(*numero maximo de iteraciones y tolerancia*)
maxIter=20;
ϵ=0.1;
(*algoritmo*)
xma=a; (*Estimado anterior de la raiz para el calculo del error*)
For[i=1,i<=maxIter,i++,
(*aproximación del punto medio*)
xm=Round[b-(f[b]*(b-a))/(f[b]-f[a]),0.001];
(*calculo del error y condición de parada del metodo*)
ea=N[Abs[xm-xma]];
Print[i," ",xm," ",ea];
If[N[ea]<=ϵ,Break[];
(*determinación del nuevo intervalo*)
If[f[a]*f[xm]<0,b=xm,a=xm,Break[]];
];
(*Actualización de la aproximación anterior de la raíz*)
xma=xm;
];
Print["La raiz de f(x) es: ",Round[xm,0.001],"y se obtuvo con ",i,"iteraciones."]
FALSA REGLA
50
40
30
20
10
2
1
1
2
3
10
1 -1.818 0.182
2 -1.818 0.
La raiz de f(x) es: -1.818 y se obtuvo con 2 iteraciones.
Método del Punto Fijo
Este método, al igual que los descritos anteriormente, tiene como fin de resolver ecuaciones no lineales F(x)=0
basándose, valga la redundancia, en la idea de punto fijo de una función que se logra dando la forma que
no es única
F(x)=x-G(x)=0
lo que es equivalente a resolver
x=G(x)
Este es un método iterativo, es decir, un proceso que se repite hasta encontrar un resultado
xk+1=G(xk)
que se puede ser cuando:
1) alcance un error absoluto o relativo deseado.
2) las iteraciones se repita una cantidad predeterminada de veces.
Ahora queda la duda si al realizar el método la sucesión de puntos generados converge a un valor o diverge,
pues se determina la convergencia analizando la derivada de la función G:
si |G'(x)|<1, entonces el método converge.
si |G'(x)|>1, entonces el método diverge.
PUNTO FIJO
(*función y gráfica para determinar el punto inicial*)
f[x_]:=x^3+4*x^2-10;
Plot[f[x],{x,-6,6},PlotStyle-> Magenta]
g[x_]:=f[x]+x;
(*valor inicial*)
x0=1;
(*numero maximo de iteraciones y tolerancia*)
maxIter=20;
ϵ=0.1;
(*algoritmo*)
xa=x0; (*Estimado anterior de la raiz para el calculo del error*)
(*aproximación de la raiz*)
xn=Round[g[xa],0.001];
(*calculo del error y condición de parada del metodo*)
ea=N[Abs[xn-xa]];
Print[1," ",xn," ",ea];
If[N[ea]<=ϵ,Break[],xa=xn];
Print["La raiz de f(x) es: ",N[xn],"y se obtuvo con ",1,"iteraciones."]
FIJO PUNTO
200
150
100
50
6
4
2
2
4
50
1 -4. 5.
La raiz de f(x) es: -4. y se obtuvo con 1 iteraciones.
6