17

Capítulo
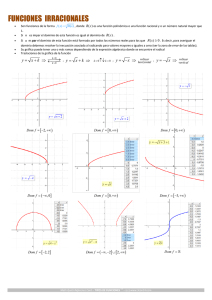
500 000
450 000
100 000
350 000
300 000
250 000'
200 000
a 150 000
j
.........'"i
|........
10 15 20 25 30 35 40 45 años
Funciones
C a p ít u l o IV
F u n c io n es
Objetivos
• Conocer los conceptos básicos sobre relaciones y funciones.
• Identificar una función real de variable real y calcular su dominio y su rango.
• Efectuar operaciones con funciones reales de variable real.
• Graficar funciones reales no elementales, aplicando algunas propiedades geométricas
propias de las funciones.
• Calcular la función inversa de una función biyectiva.
Introducción
El concepto de función no solo es uno de los pilares de la matemática moderna, sino de la ciencia en
su conjunto. Sin él no se podría concebir la construcción del conocimiento científico com o se hace
hoy en día. La ciencia que hoy conocem os no sería imaginable sin el concepto de función, una formi­
dable herramienta matemática que nos permite expresar muchas leyes de la naturaleza y solucionar
muchos problemas prácticos en los diversos campos de las ciencias.
Este concepto se utiliza para describir relaciones entre elementos de dos conjuntos A y B. A los ele­
mentos se les llama variables, pues al describir la relación entre ellos, se considera que se les puede ir
variando o tomando uno primero y otro después.
El término función tiene una historia larga y su significado se ha ido modificando para describir cosas
cada vez más generales. Fue introducido por primera vez en 1637 por el matemático francés René Des­
cartes, quien lo usó para designar la potencia n de una variable x. lo que hoy en día escribimos com o x n,
solo que en aquel entonces esta notación no era usual. Años más tarde, en 1694, el matemático alemán
Gottfried W. Leibniz usó el término función para referirse a distintos aspectos de una curva. No fue sino
hasta el siglo xix, concretamente en 1829, que otro matemático alemán, Peter Dirichlet, introdujo los con­
ceptos de variable dependiente e independiente de una función entre dos conjuntos numéricos A y B.
En el curso del siglo xix e inicios del xx, después de la introducción de la teoría de conjuntos, se vio
que resultaba conveniente definir el concepto de función en una forma que no solo tenga en cuenta a
funciones numéricas, sino a relaciones mucho más generales.
215
Lumbreras Editores
Una razón muy importante de que las reglas de correspondencia vengan dadas a menudo en forma
numérica es que la ciencia trata de describir todo no solo cualitativamente sino también cuantitativa­
mente; un evento se considera explícito si se le pueden asociar cifras y, mejor aún, si se puede predecir
los valores de las variables involucradas. Por ejemplo, en la meteorología nos interesa saber los valores
de temperatura, humedad, velocidad de viento, etc., que predominarán en una cierta región en los
días venideros. En la econom ía nos interesaría saber cóm o van a variar los precios de bienes y servicios
para invertir en la opción más conveniente. En la química se desea saber cuánto de tal o cual sustancia
y a qué temperatura, presión, etc., generará tal cantidad de otra sustancia.
La utilidad de las funciones es muy amplia y variada. Imaginemos, por ejemplo, que se desea saber
la concentración de un contaminante en el lecho de un río, por ejemplo, de plomo. Para ello se rea­
lizan una cierta cantidad de mediciones a intervalos de tiempo conocidos y se miden algunas otras
variables com o son: temperatura, densidad, volumen de agua que fluye, etc. Al analizar los datos se
da uno cuenta de que las cantidades parecen cumplir una cierta regla, la cual se puede expresar en
términos de una función. Con algunas pruebas estadísticas se puede saber si la función que se cree
que describe la relación entre las variables ajusta bien a los puntos obtenidos en la medición. Si así
fuera el caso, se supone que la función será entonces útil para obtener valores de las concentraciones
de plomo, incluso para rangos de valores diferentes a los que se midieron. Por ejemplo, se podría llegar
a conocer qué concentraciones hubo entre dos instantes de tiempo en los que sí hubo mediciones. A
dicho proceso se le conoce com o interpolación. Si se deseara saber qué valores de la concentración
de plomo se tendrán para valores más allá del periodo de tiempo en el que se midió, el proceso se
llama extrapolación.
En la historia de las matemáticas se le da crédito al matemático Leonard Euler por precisar el concepto
de función, así com o por realizar un estudio sistemático de todas las funciones elementales, inclu­
yendo sus derivadas e integrales; fue Euler, en el año 1740, el primero en usar la notación de f(xy Hoy
sabemos que
216
es la regla de correspondencia de la función /'.
CAPÍTULO IV
► C o njunto s
NOCIÓN DE CONJUNTO
Funciones
Los conjuntos pueden ser finitos o infinitos, de­
pendiendo de la cantidad finita o infinita de ele­
mentos; en particular, si tiene un solo elemento
El concepto de conjunto dado por Cantor, com o
se llama “conjunto unitario”.
“una agrupación de un todo de objetos muy
distintos de nuestra intuición o de nuestro pen­
Subconjuntos y superconjuntos
samiento”, es para las matemáticas actuales de­
Se dice que un conjunto A es subconjunto de B
masiado vago e insuficiente. Un conjunto es una
o un conjunto B es superconjunto de A denotado
lista o colección de objetos bien definidos, es
por:
decir, de ciertas características comunes.
Un conjunto está formado por elementos sus­
A<zB : A está contenido en B.
B^A: B contiene a A.
ceptibles a poseer ciertas características (pro­
piedades) y de tener, entre ellos o con elem en­
tos de otros conjuntos, ciertas relaciones.
Ejemplo
En los conjuntos dados
A = { 2; 4; 6; 8}
B = { 1; 2; 3; 4; 5; 6; 7; 8; 9}
Ejemplos
• El
conjunto formado por todas las vocales.
• El
conjunto de todos los peces marinos.
vemos que todo elemento de A es elemento de
B, entonces se denota A c B o se dice también
que A es un subconjunto de B.
• El conjunto formado por todos los números
que son múltiplos de 5, mayores que 19 y m e­
nores que 47.
•
El conjunto de todos los números primos.
/*""*......
n™,n””™T ....... ..."V
Propiedades
Sean A ,B y C conjuntos cualesquiera,
luego se cumple:
Notación de un conjunto
Un conjunto se denota con una letra mayúscula
y los objetos que lo forman se llaman elementos.
I. A cA
II. Sí A q B a B c A -» A=B
III.S iA c ñ
a
B
c
C
-> A q C
Por ejemplo, el conjunto A = {a; b ; c; d; e ) está
formado por las letras a; £>; c; d; e. La letra a es
Igualdad de conjuntos
un elemento de A, que matemáticamente se ex­
Dos conjuntos son iguales, denotado por A=B,
presa o e A y se lee «a pertenece a A».
si constan de los mismos elementos, esto es, si
Los conjuntos se denotan por comprensión
todo elemento de A es elemento de B y todo ele­
(mediante alguna característica) o por extensión
mento de B es elemento de A.
(mencionando cada uno de sus elementos). Por
ejemplo:
• Por comprensión: A = {x /x es un número en­
•
La negación de A = B esA *B .
Dos conjuntos A y B son iguales si y solo s i 4 c B
y B q A.
tero par, menor de 17}
Cuando A q B
Por extensión: A = {2; 4; 6; 8; 10; 12; 14; 16}
conjunto propio de B.
a
B*A, se dice que A es un sub­
217
Lumbreras Editores
Formalmente definimos
Conjunto vacío
Es aquel conjunto que no contiene ningún ele­
(a; £>)= {{a}; { a ; b } }
mento y se representa por $ o { }.
donde a es la primera componente y b, la se­
gunda.
Ejemplo
4 = { x e R/x 2+ 1 6 < 0 } es un conjunto vacío, pues
Ejemplos
no existe número real alguno que verifique:
•
(3; 5) = { { 3 } ; {3; 5 }}
•
(V2 ; - 1)={{V 2 }; {V 2 ; - 1}}
•
C r ;* - 2) = { { x } ; { * ; x - 2 } }
•
(x; /(x)) = { { * } ; {x; f(x)}}
x 2+ 1 6 < 0 .
Conjunto universo
Es el conjunto referencial donde se definen otros
subconjuntos.
Igualdad de pares ordenados
Ejemplo
<-»a = c a b = d
-................. ..... .J
(a ;b )= (c ;d )
^ ; i - ■' ■.■■■' ■..Ihk: j:1
A = {1; 2; 3; 4}
B = {2 ; 4}
Ejemplo
C = {1 ; 3}
Si se cumple que (x -3 ; y )= ( 6-y ; 5) calcule el
valor de xy.
El conjunto A es el universo de B y C. Al conjunto
Resolución
(x -3 ;y ) = ( 6-y ; 5)
universo se le denota por U.
<-»jr - 3 = 6 - y
x -3 = l
Los diagramas de este género llevan el nombre
de diagramas de Venn. Veamos otro diagrama,
<-> x= 4
dados los conjuntos M, N, U.
Ejemplo
a y=5
a
y=5
a y=5
xy = 4-5= 20.
U
x e M tz N —> x e N
x e N c í/ —> x e í/
►
►Tenga en cuenta
(a; tí) * (f>; a )
En efecto
(o; b)={{a}; {a; b}}
(.bt a ) = m - { b - ,a }}
En consecuencia
Par ordenado
(a; b)=(b; a)
a= b
Es un conjunto formado por dos elementos: a y
b bajo un criterio de ordenación que establece
Cardinal de un conjunto
cuál es la primera y la segunda componente. Se
El cardinal de un conjunto A se define como el nú­
denota por (a; b) y se lee “par ordenado de com ­
mero de elementos de dicho conjunto A. Si el con­
ponentes a y b".
junto es vacío, su cardinal es cero.
218
CAPÍTULO IV
Ejemplos
1.
3.
Dados los conjuntos
El conjunto A = {3; 5; 7; 9; 17} tiene cinco ele­
A = { 3; 4; 7}
mentos, entonces su cardinal es 5 y se deno­
B = { 1 ;3 ; 5; 7; 15}
ta por CardC4)=5 o nG4)=5
2.
Funciones
-> A u B = { l; 3; 4; 5; 7; 15}
El conjunto fí={(|)} tiene un elemento, en­
tonces su cardinal es 1 y se denota por
Intersección
Card(B) = l o n ( B ) = l.
La intersección de dos conjuntos A y B, deno­
El conjunto vacío S= { } o S = <|)tiene cardinal
tado por A n B , es el conjunto de los elementos
cero, entonces Card(,S)=0 o n (S )= 0
com unes a A y fí; de no tener elementos com u­
nes, la intersección será el conjunto vacío. Estos
OPERACIONES ENTRE CONJUNTOS
conjuntos, con esta última condición, son llama­
Unión de conjuntos
dos disjuntos.
La unión de dos conjuntos A y B, denotado por
A u B , es el conjunto de todos los elementos que
Ar\B={x € U /x e A
a
x
e B}
pertenecen al conjunto A o al conjunto B, o a
ambos. Es decir:
Ejemplo
A\j B = { x e U / x eA v x e B }
Diagrama d e A u B
A = { 2; 3; 5; 7}
B = { 0 ;2 ;4 }
-> A n B = {2 }
|
Ejemplo
►
►Tenga en cuenta
Si A n S=(|), entonces Ay B son
disjuntos.
A
B
219
Lumbreras Editores
Complemento de A
Diferencia
La diferencia d e A y B, denotado por A -B y lla­
El complemento del conjunto A, denotado por
mado también el complemento de B respecto al
Ac , es el conjunto de los elementos que perte­
conjunto A, es el conjunto de los elementos de A
necen a cierto universo, pero no pertenecen al
que no pertenecen a B. Es decir:
conjunto A. Es decir:
/—------ ---------------------------------------------- |---------- -------------j-------------\
A -B = {x e U / x e A
a
x tB )
v,... ........................................
Ac = {x e U / x t A}
.....
V,.........................................................
J
U
Diagrama
Ejemplo
Sea A = {x e R/ x > 1}. Hallaremos su com ple­
Ejemplo
mento Ac .
U
Resolución
Como A = {x e R/ x > 1} = [ 1; + °°) entonces
—
.4 = {3; 5; 7; 15; 24}
oo
1
+°°
Luego: Ac = R - J4=<-°°; 1)
B = {1 ; 2; 3; 8; 15; 23}
A -B = {5 ; 7; 24}
Nótese q u e A u A c = U = R
B -A = { 1; 2; 8; 23}
Cuando se trabaja con intervalos el conjunto
universal es R.
Diferencia sim étrica
A n (B-A)=<|>
A n (A -B )= A -B
220
La diferencia simétrica de A y B, denotada por
A A S, se define así: A A B = (A -B )
vj (B -A ).
CAPÍTULO IV
Funciones
Ejemplo
Ejemplos
U
^
U={ 1; 2; 3 ;...; 8}; A = {1; 2; 3}
B
2)
1
S
\9
/)
\
12 s 7 j
4
j 3 5
1. Sean
B = {3 ; 4; 5; 7}; C = { 3 ;5 ;8 }
Halle
6
a. Ac
c. B -C
b. (/tnC)c
d. (A u fi)c
Resolución
A = {2; 3; 5; 7; 9; 12}
a. A = {1; 2; 3} —> Ac = {4 ; 5; 6; 7; 8}
B = {1 ; 2; 4; 6; 7; 10}
b. 4 n C = { 3 } -» G4nC)c = { l ; 2; 4; 5; 6; 7; 8}
A -B = { 3; 5; 9; 12}
c. B - C = { 4 ; 7}
B-A={\\ 4; 6; 10}
d. í4 u B = { 1 ;2 ;3 ;4 ;5 ;7 } -» 0 4 u B )c = { 6 ;8 }
.4 A B = {1 ; 3; 4; 5; 6; 9; 10; 12}
2. Demuestre que {A-B)c\B=§.
Propiedades
Los conjuntos verifican las siguientes
leyes enunciadas:
Resolución
Leyes de idem potencia
Sea x e (A -B )n B
A uA =A
Por definición
Ar\A=A
o
x e 04- B )
(x e .4
Leyes asociativ as
a
xeB
a
x tB )
xeB
a
(/ Iu 8 ) u C=A u ( B u C )
(jf e ,4 a x 6 B c)
(A n B ) r¡ C=A n (B n C)
x e /l a x e (flc n fi)
Leyes conm utativas
x eB
a
<-> ie / 1 A*e<j>
A u B = B yjA
<-> X £ (v4 Pl 0) = (j)
A n B = B n/l
Leyes distributivas
A yj (S n C)=C4 u f i ) n ( / l u C )
A n ( B u C)=(A n B) u (4 n C)
Leyes de identidad
4u<M
A vU =U
A n ÍM 4
A n $= 0
3.
Demuestre que B -A = B n,4c.
Resolución
Por igualdad de conjuntos
B~A =BnA c <-> B - A c f i n / a B n A c c B - A
•
—> x e B
Leyes de com plem ento
•
<|f= U
Leyes de De Morgan
04 u B ) c =Ac n B c
{A n f i ) c =Ac u f i c
a
x eA c —> x e B n,4c
- * (B -/ l)c B n A c
A kjA c =U A n A c =0
U C) C=A
Sea x e ( B -A ) -» x e B a i M
(a)
Sea x e B nAc —> x e B
—> x e B
a
x íA
a
x eA c
—> x e (B -A )
-> B n A c c ( B - 4 )
(P)
De (a ) y (P) se concluye
B -A = B n A c
221
Lumbreras Editores
PRODUCTO CARTESIANO
Diagrama cartesiano o plano cartesiano
Dados dos conjuntos A y B, se llama conjunto
René Descartes (1596-1650) fue el creador de
producto o producto cartesiano de A y B, deno­
la geometría analítica, para lo cual estableció el
tado por AxB , al conjunto de todos los pares or­
sistema de coordenadas ortogonales (conocido
denados (a, b ), donde a e A y b e B.
en la actualidad com o el sistema cartesiano),
formado por dos rectas que se cortan perpendi­
A x B = {(a ; b) / a e A
a
b e B}
cularmente en un punto denominado origen: O.
Representamos los conjuntos en el plano carte­
El conjunto producto de un conjunto A por sí
mismo, es decir AxA, se denota por A2.
siano. Así:
B
(5 ;n)
Ejemplo
A = {5; 6; 7}; B = {m ,n }
A x B = {(5 ;m ), (5 ;n ), ( 6;m ), ( 6;n ), (7 ;m ), (7 ;n )}
0<m<n
m
(5; m)
(6; n)
(6 ;m )
(7 ;n )
(7; rri)
B y.A ={(m ; 5), (m; 6), (m; 7), (n; 5), (n; 6), (n; 7)}
Como (a; £>)*(£>; a), se observa A xB^BxA .
El producto se puede realizar de diferentes mane­
ras, las más importantes son:
Luego
A x B = {(5 ;m ), (5;n), ( 6;m ), (6;n), (7 ;m ), (7;n )}
Diagrama de Venn-Euler
Diagrama del árbol
Los diagramas de Venn tienen el nombre de su
Un diagrama de árbol es la representación grá­
creador, John Venn, matemático y filósofo britá­
fica que ilustra las diferentes formas en que se
nico. Venn introdujo en julio de 1880 el sistema
agrupan elementos de dos o más conjuntos,
de representación que hoy conocem os, con la
desde puntos de partida (raíz), es decir, elem en­
publicación de su trabajo titulado De la represen­
tos de un conjunto de partida.
tación m ecánica y diagram ática de proposicio­
Realizamos todas las correspondencias posibles
n es y razonamientos.
entre los elementos de A con los elementos de
Los conjuntos A - {5; 6; 7} y B={m\ n} se repre­
B. Así:
sentan mediante una región plana y cerrada. Así:
Luego
AxB={(5\m ), (5;n), ( 6;m ), (6;n), (7;m ), (7;n )}
222
Luego
A x B = {(5 ;m ),(5 ;n ), ( 6;m ), (6;n), (7;m ), (7;n )}
CAPITULO IV
Funciones
Nótese que el cardinal de A x B es 6.
Resolución
En general, dados los conjuntos A y B de m y n
a.
A x B = {(a ; b ) / - 3 < a < 3
0< £> < 2}
a
elementos, respectivamente. Entonces A xB y
B
BxA tienen el mismo cardinal rnn.
Luego:
Si /4= { 3 ; 4 ; 2 }
a
B = {1 ; 4; 0; 3}, entonces AxB
-3
tendrá 3 x 4 = 1 2 elementos, es decir, 12 pares or­
|
A
3
denados.
Nótese que
Si uno de los conjuntos o ambos tienen infinitos
(- 3 ; 0) M
elementos, su cardinal es infinito.
(3; 0) fi A x B
x B
(3; 2) é -4 x B
Ejemplos
b. B x A = {{ b \ á ) /ü < b < 2
1. Sean los conjuntos
A = {x e R/ 1 < x < 3 } ;
a
-3 < a < 3 }
A\
B = {x e R /x = 2 }.
Halle A xB.
Resolución
Hallamos el producto cartesiano.
A x B = { ( a ; 6 )/ 1 < o < 3
a
-3
£>=2}
Usamos el diagrama cartesiano
Nótese que
(0; - 3 ) é B x A
B
(0; 3) <É B x A
(2; 3) é B x A
c.
Tenemos y l- B = [-3 ; 3 }-(0 ; 2]
-> A - B = [ - 3 ; 0] u <2; 3)
Luego
2.
(A -B ) x B = {(o; £>)/
Sean los conjuntos
/ (-3 < o < 0
A = {a e R / - 3 < a < 3 };
B = { b e R / 0 < fc < 2 }.
v
2<a<3)
a
0
< ¿> < 2 }
B
Halle los siguientes conjuntos
a. A xB
b. BxA
c.
(A -B )x B
-3
A -B
223
Lumbreras Editores
R
► R e l a c io n e s
DEFINICIÓN
Una relación R, del conjunto A al conjunto B, es
todo subconjunto del producto cartesiano A xB ;
es decir, R es una relación d e / l a f i n R a A x B .
Se denota por R: A —> B o A
conjunto
de partida
B
conjunto
de llegada
/ ?= {(*:y )/ * ¿A a y e B }
Es decir
Si R: A —» B es una relación
►
►Tenga en cuenta
-> R c A x B
O; y) e R «-» xRy
Donde
AxB={{x\y')/x e A Ay e B}
Ejemplos
1.
Ejemplos
1.
Sean los conjuntos
A ={2; 3; 4; 5; 7}; B = {1 ; 2; 3; 4}.
Se tiene una relación R de A a B, tal que:
Sean los conjuntos
R
A = { 3; 2; 5; 7} y B = { 1 ;2 ;5 ; 15}
Algunas relaciones de A a B son
/?, = {(3 ; 1), (2; 2), (5; 15)}
R2= i& , 5), (7; 1), (7; 5), (7; 15)}
/?3= {(3 ; 1), (3; 5), (3; 15), (5; 1), (5; 2)}
« 4= U 5; 1), (5; 5)}
-»
2.
mar s i A = {3; 5; 7; 15}
a
B={a\b\cY!
Resolución
2. Sean los conjuntos
A = {x e Z /x es un múltiplo de 5};
B = {x e J J x es un número par}.
Si un conjunto A tiene n elementos, entonces
Se tendrá una relación de A a B , tal que
fl= {(0 ; 0), (5; 2), (10; 8), (15; 4), (20; 2)}
existen 2" subconjuntos contenidos en A.
Luego
Como A tiene 4 elementos y B tiene 3 ele­
mentos, entonces A xB tiene 4 x 3, es decir 12
elementos; en consecuencia, A xB tendrá 212
subconjuntos o relaciones.
En una relación R del conjunto A al conjunto
B ,R :A —> B, el conjunto A se llama conjun­
to de partida y el conjunto B, de llegada.
224
R = {& , 2), (4; 1), (5; 2), (3; 1)}
¿Cuántas relaciones de A a B se pueden for­
A
B
CAPÍTULO IV
Funciones
RELACIÓN BINARIA
Los elementos del dominio son 1; 2; 7 y los ele­
Dados A y B conjuntos no vacíos, una relación R
mentos del rango son -1 ; 5; 21. Luego, definimos
es cualquier subconjunto de A xB que, de m ane­
el dominio y el rango de una relación:
ra particular, si A=B luego R se llama “relación
binaria en A".
Sean A y B conjuntos no vacíos y RczAxB una
relación del conjunto A al conjunto B.
R = { ( a ;b ) / a eA
Ejemplo
beB }
a
R -.A ^ A tal que
Dominio de una relación
El dominio de una relación R: A —> B es el con­
junto formado por todas las primeras com po­
nentes de los pares ordenados que definen a la
relación, y de denota por Dom(7?) o Dom/?.
Es decir:
R = {{ 1; 2), (2; 1), (1; 3), (2; 3)}
es una relación binaria en A.
DOMINIO Y RANGO DE UNA RELACIÓN
Sean los conjuntos
Dom(fi) = {o € A / (a; b) e R} c A
En el ejemplo anterior, para la relación R :A —>B
se tiene que
A = {1; 2; 3; 4; 5; 7; 15; 20}; B= {-1 ; 3; 5; 7; 21; 40}.
Dom(7?) = { l ; 2; 7}
a
Ran(/?) = { - l ; 5; 21}
Definimos una relación R: A —>B como
/?={( 1 ;-1 ) , (2; 5), (7; 21), (7; 5)}
y lo representamos en el diagrama de Venn. Así:
Rango de una relación
El rango de la relación R: A —> B, llamado tam­
bién imagen del dominio o conjunto de imáge­
R
nes de los elementos del dominio, es el conjunto
de las segundas com ponentes de los pares orde­
nados que definen la relación, y se denota por
Ran(7?) o RariR.
Es decir:
—
.
—-
Ran(/?) = {b e B / (a; b) e R} c B
v________
J
A los elementos del primer conjunto que definen
a la relación R, se les llama elementos del domi­
nio, y a los elementos del segundo conjunto que
definen la relación R, se les llama elementos del
rango.
Ejemplo
Sean los conjuntos
A ={ 1; 2; 3; 4; 5; 6}; B = { 1; 4; 9; 16; 25; 36; 49};
y la relación R={(x\ y) eA x B /y = (2 x + \ )2}.
Halle su dominio y su rango.
225
Lumbreras Editores
Resolución
Ejemplo
Como (x;y) e A xB tal que x e A a
> '= ( 2 x +
l )2 6 B
Dada la relación R -.X ^ Y tal que
R = {{- 2; 3), (1; 2), (0; -1), (3; 5), (3; - 2 ) } ,
Entonces, si:
esboce su gráfica.
Resolución
Representamos cada par ordenado en el plano
cartesiano.
R aX xY
x = 1 -> y= 9 e B
x = 2 —> y=25 e B
x = 3 -> y=49 e B
x = 4 -> y=81 « B
x = 5 -> y= 121 e B
x =6 —> y = 1 6 9 g B
Luego
La gráfica de R: X —>Y está formada por los cinco
puntos ubicados en el plano.
Dom(7?) = { l ; 2; 3}
Ran(/?) = {9; 25; 49}
Luego
GRÁFICA DE UNA RELACIÓN
Dom(/?) = { - 2 ; 1; 0; 3}
Sea R '.X ^ /Y una relación. La gráfica de R es la
Ran(/?) = {3; 2; -1 ; 5; - 2 }
representación geométrica de los pares ordena­
dos (x ; y) que definen a la relación en el plano AY.
REGLA DE CORRESPONDENCIA
Es decir, si R: X -> Y es la relación
Es una representación algebraica que define la
relación existente entre los elementos del domi­
R = {(x; y ) / x e X ;y e Y } ,
nio y el rango de una relación.
entonces su gráfica se denota por:
Graf(7?) = {(x ;y ) sR /x R y }
R
Y‘
y0
(0; 0)
226
o; ^o)
X
CAPÍTULO IV
Funciones
Luego, decimos que:
Resolución
y es una relación de x, o y es una dependencia
Como y=R(x)=2x+ 1, las imágenes se calculan
de x, o y es la imagen de x.
así:
Se denota por y=7?(x) y se lee: “y es igual a 7? de
7?(_ i ) = 2 ( - l ) + l = -1
7?(o)= 2(0) + l = 1
7?(2)= 2(2) + l= 5
7?(3)=2(3) + l =7
Ejemplo
En la relación R.X ^>Y tal que:
7?
Escribimos la relación 7? por extensión
/?={(—1; —1), (0; 1), (2; 5), (3; 7)}
Se dirá
y= RM
En el plano cartesiano
2 =7?,
0)
Y
/ (3; 7)
5=7?,(2)
10=7?,(3)
/ (2; 5)
17=7?,(4)
(0; 1)
Buscamos una representación generalizada que
relacione a los elementos del dominio y los ele­
mentos del rango.
X
t—l; —13
/?(])=2 = 1 2H
+1
7?(2)= 5= 2■>2 _l+1
7?(3)=10=332h
+1
2.
Grafique la relación 7?.
7 ? = {(jr;y )/ y = 2 x -l, x e [-2 ; 3)}.
7?(4)= 17= 4a2+1
Resolución
RM~X +1
7?(x) =x2+1 se llama regla de correspondencia de 7?.
Luego, la relación se define como
7?= {(x ;y )/ y = x 2+ l }
Es una relación cuyo dominio es [-2; 3), y su
rango puede hallarse a partir de su dominio, así
- 2 < x < 3 —> - 4 < 2 x < 6 —> -5 < 2 x r-l < 5
.-. Ran(7?) = [-5 ; 5)
Tabulando una cantidad significativa de pun­
tos veremos que su gráfica es una línea recta.
Ejemplos
Tomamos algunos puntos
1. Grafique la relación 7?.
1
1
y
co
A = { - 1 ; 0; 2; 3}.
-2 - 1 0
1
X
Cn
R = {(x; y ) /y = 2 x + 1, x sA}\
1
2
3
3
5
227
Lumbreras Editores
En el plano cartesiano tenemos:
En el plano cartesiano
rt
-*---- 1---- 1----H
X
Como el dominio de R es finito, entonces R es
El rango se calcula observando la variación en el
una relación discreta y la gráfica está formada
eje Y. En el ejemplo, note que
por los puntos que se indican.
Ran(/?)=[-5; 5)
RELACIÓN INVERSA
3.
Grafique la relación R.
Sea R una relación del conjunto A al conjunto B,
/?={(x;y)/y2+x2=16},Jí'E {—4; —3 ;—2; —1; 0; 1}
definida por
R={(x\y) / x eA
Resolución
a
y e 5}
La relación inversa de R, denotado por R~\ se
Calculamos las imágenes
define
x = -4
—>y2= 0
-> y = 0
x = -3
—» y2=7
—>y=\¡7 v y = -V 7
x= -2
—>y2= 12 —> y = 2^3 v y = - 2^3
x= -1
—> y2= 15 —> y=>/T5 v y = -V Í5
x=0
—>y2= 16 -> y = 4 v
x=l
—>y2= 15 —> y=V Í5 v y = -V Í5
y = -4
/?“' = {(y ;x )/ (x ;y ) e R }
Ejemplos
1. Sea R la relación definida por
/?={(—1; 0), (0; 1), (1; 3), ( 2 ;- 5 ) } .
Su relación inversa R~] es
Luego
/? = { ( - 4; 0), (-3; V7), (-3; - V7), (-2; 2V3 ),
(-2; -2 V 3 ), (-1; V Í5), (-1; - V l5), (0; 4), (0; -4 ),
/?"' = {(0; -1), (1; 0), (3; 1), (-5 ; 2)}.
Observamos que R~l se obtiene con solo in­
vertir el orden de los elementos de los pares
(l;VT5),(l;-VT5)}
228
ordenados de R.
CAPÍTULO IV
Funciones
R
El plano cartesiano se tiene:
Yk
/
y= x
log2x
R-
-r-
Nótese que, la recta y=x es el eje de simetría
para y= 2* y la inversa y = log2x
Nótese que:
Dom(/?"')=Ran(/?)
Ran(/?“')=Dom(/?)
a
COMPOSICIÓN DE RELACIONES
A partir de las relaciones RczAxB y SczBxC, es
2.
Si /?={(*; 2*)} entonces R~] = {(2X\x )}
posible definir una relación entre A y C llamada la
Si hacem os: 2x=y -» x= log 2y ; y > 0
composición entre R y S, denotada por S °R m e­
Llamemos y=x (por ser variable muda)
-> /?“' = {(x; log2x )}
Para esbozar la gráfica de R y R~' tabulamos
diante
S oR = {(x;z) e A x C / 3 y e B
a
(x ; y ) e / ?
a
a
( y ;z ) e S >
algunos valores.
2X
-1
1/2
0
1
2
4
3
8
X
lo g V
1/2
-1
1
0
4
2
8
3
En el esquema
Es decir,
(x-, z) e S o R <-> 3 y e B /(x; y) e R a (y; z) e S
229
Lumbreras Editores
b. Similarmente, para hallar R ° S se parte
►
►Tenga en cuenta
de M —
S o R existe si y solo si
N y luego N —
P.
Ran(7?) n Dom(S);*<|>. Esto nos indica
que debemos calcular los elementos y,
tal que:
y e Ran(/?)
a
y s Dom(5); es decir,
y e Ran(fl) n Dom(S). Luego calcule los
| pares (x; z).
Ejemplos
1. Sean las relaciones
/ ?= {(!; 2), (3; 4), (2; 5), (1; 3), (2; 0 )};
S = { ( - 1 ;2 ) , (2; 3), (5; 1), (0; 7)}.
-> R o S = {{- 1; 5), (-1; 0), (2; 4),(5; 2), (5; 3)}
Halle las relaciones compuestas
a. S o R
Algebraicamente, se define la composición
b. R o S
de relaciones RoS así:
Resolución
I. Dom(/?oS)={xe Dom(5) a 5 w e Dom(/?)}
R
a. Para hallar S » ff, se parte de A ------ >B y
II. (/?oS)M =/?(Sw )
luego B —— » C.
R
S
2.
Sean las relaciones
R ~ {ix \ y )Iy = x 2~\, x e {1; 2; 3; 4 }} ;
5 = {( x ;y )/ y = 2 x + l, x e (1; 2; 3; 4 }}.
Halle
a. SoR
b. RoS
Resolución
Escribimos los conjuntos por extensión:
• /?={(1; 0), (2; 3), (3; 8), (4; 15)}
S . / ?= {(!; 3), (2; 1), (2; 7)}
230
• 5 = {( 1 ; 3), (2; 5), (3; 7), (4; 9 )}
Funciones
CAPÍTULO IV
a.
DEFINICIONES
Hallemos S ° R
(S<-R)(l)=S^R(¡)'j=S(tí) No existe
Relación reflexiva
(5 o/?)(2) =5(/?(2)) =5(3) = 7
Una relación R: A —>A se dirá reflexiva si y solo si
(5o/?)(3)= S (fi(3))= S (8) No existe
(5o/?)(4)=5(/?(4)) = 5 (]5) No existe
S °R = {(2; 7)}
(o; a) g R ,V a eA .
Ejemplos
1. / ?= {(!; 1). (1; 2), (2; 2), (3; 3), (3; 1)}
b. Hallemos R ° S
Relación de A -> A, con A = {1; 2; 3}.
/?oS (, 5=/?(5(1))=/?(3)=8
2 . Sea/ ?= {(1; 2), ( 2 ; 3), ( 3 ; 5), ( 1 ; 1 ), ( 2 ; 2)}
R°S( 2)=R(S(2'))=R(5) No existe
No es reflexiva por la falta de (3; 3) y (5; 5).
/?o5 (3)=/?(5 (:3))=/?(7) No existe
=/?(S(4))=í?(9) No existe
RoS = {( 1; 8) }
3.
Relación sim étrica
Una relación R: A —> A es simétrica si y solo si
V(a; b) e R se tiene que ( b\ a) e R.
Sean U, V las relaciones en R definidas por
U = {(x-,y)/x2+ y2= l } ;
Ejemplos
1. fl= {(2 ; 3), (5; 1), (1; 5), (3; 2), (1; 1)}
Es simétrica en/i, donde A = {1; 2; 3; 5}.
V = { ( y ;z ) / y + z = - 2 }.
Halle V°U.
2. /?={(4; 1), (3; 2), (2; 3), (7; 7)}
No es simétrica ya que existe (4; 1) y no (1; 4).
Resolución
La relación V°U, composición de las rela­
ciones U y V, puede obtenerse de las dos
ecuaciones
Relación transitiva
Una relación R: A —> A es transitiva si y solo si
V [(a; b ) e R
Jx 2 +y 2 = l
(a)
1 y + z= -2
(p)
(b; c) e /?] se tiene que (a; c) e R.
a
Ejemplos
1. /?={(1; 2), (2; 3), (1; 3), (5; 4 )}
mediante la eliminación de y en estas dos
Es transitiva ya que
ecuaciones para relacionar x con z.
(1; 2 ) e R a (2; 3 ) e R -> (1; 3) e R .
De (P) obtenem os: y = - z - 2
2. R={{2\ 3), (3; 5), (5; 1), (2; 5), (2; 4 )}
Reemplazamos en (a)
x 2+ ( - z - 2) 2= l
-> x2 + (z + 2) 2= l
V o U = {(x ;z )/x 2+ (z+ 2)2=\j
No es transitiva puesto que
(3 ;5 ) e R
a
No i m p l i c a
(5; 1) e R .
que
(3; 1)
e
R.
231
Lumbreras Editores
Relación de equivalencia
La representación de un par ordenado (o, b ) de
Una relación R: A -> A es de equivalencia si y
componentes reales en el plano cartesiano es
solo si R es reflexiva, simétrica y transitiva.
com o se muestra.
Es decir, R: A —>A es de equivalencia si se cum­
ple que:
R,
(o; o)
II.
(a; b) e R —> (£>; a) g R
III.
(o; b) e R
e
> ; b)
V a eA
I.
a
(£>; c) £ /? —> (a; c) e /?
x
Si la relación R: A —>/l no cumple almenos una
de las tres condiciones, entonces no es de equi­
valencia.
Ejemplo
La gráfica de la ecuación y = —J — se construye
x +\
Ejemplo
Sea R= {x; y }/x -y = k para algún k e Z fijo}
X
y
-3
1/5
-2
2/5
-1
1
0
2
—> /? es simétrica
1
1
III. (a ; b ) e R —> a - b = k
2
2/5
(6 ; c) £ /? —> b - c = k
3
1/5
Demuestre que n es una relación de equivalencia.
Resolución
I.
a - a = 0 = k —> (o ;a )£ / ?
—> R es reflexiva
II. (a ; b ) e R
a -b = k
( b ; a ) e R —> b - a = - ( a - b ) = - k = k
Sumamos: ( a - b ) + ( b - c ) = k
—> a - c = k —> (a ;c )e / ?
—> /? es transitiva
Por lo tanto, /? es una relación de equivalencia.
GRÁFICAS DE ECUACIONES NOTABLES
La representación geométrica de todos los pa­
res ordenados (x , y) que verifican una ecuación
y = fM de incógnitas x e y, en el plano cartesiano,
se llama gráfica de dicha ecuación.
232
CAPITULO IV
Se establece una correspondencia biunívoca en­
Funciones
Se tiene
tre algunos puntos del plano cartesiano R 2 y los
yi~y\ _ y\-y
pares ordenados (x; y) que verifican la ecuación.
x2-x ¡
x ¡-x
A continuación veremos las gráficas de algunas
y.
ecuaciones notables.
f t - y i L i y\x2~x \y2
* 2 '* 1
(a)
{ X2 ~ X\J
La ecuación de la recta
Todo polinomio lineal o de primer grado es co­
Llamemos
rrespondido por los puntos de una recta; en tal
A b=n * 2 - m
caso, serán necesarios solo dos puntos de paso
* 2~*1
x2~xi
para determinar dicha recta.
Luego, si queremos hallar la ecuación de la recta
Luego en (a)
que pasa por los puntos P x= (x\, y]) y P 2=(x2', y2)
y= m x + b es la ecuación de la recta r£ .
procederemos así:
Donde m es la pendiente de la recta.
Ejemplos
1.
Halle la ecuación de la recta que pasa por los
puntos (-2 ; - 1 ) y (3; 5).
Resolución
Sea y = m x + b la ecuación y los puntos
P \= (*i> y0 = C~2 ;- 1 ) ; P 2= (x 2;y 2) = (3; 5).
Tomamos arbitrariamente un punto P=(x; y) de
la recta 3/.
Luego: m=
Por sem ejanza de triángulos
5 —(—1) _ 6
3 -(-2 )_ 5
com o (3; 5) pertenece a la recta
^
5 = —(3)+í»
5
b=l
5
6
7
Por lo tanto, y = - x + - es la recta buscada.
5
5
233
Lumbreras Editores
2.
Halle la ecuación de la recta que pase por el
punto (1; 2) y sea de pendiente 3.
Por el teorema de Pitágoras en el triángulo ACB
d 2= (x 2- x , ) 2+(y 2- y ,)2
Resolución
d=^/(x2 - x 1)2 +(y 2 - y ,)2
La propiedad es para dos puntos arbitrarios.
Además, d también se puede calcular así:
d=A
/(x1 - x 2)2 + (y ,-y 2)2
pues la distancia de A a B es igual a la distancia
de B a A.
Sea (x; y) un punto en la recta.
Hallamos la pendiente y lo igualamos a 3
y- 2
x -1
3 -> y = 3 x - l
Ejemplo
Halle la distancia entre los puntos
A= (3; 2), B = (5 ; 1).
Por lo tanto, la ecuación de la recta es
y = 3 x - l.
Resolución
D istan cia e n tre d os puntos
Sean los puntos A =(x^ y j , ñ = (x 2; y2). La distan­
cia entre ellos está dada por
d='J(x2- x lf+ ( y 2- y lf
V...................................................................J
Dem ostración
d = V (3 -5 ) 2 + (2 - l )2 -> d = J 5
La ecuación de la circunferencia
Una circunferencia de radio r y centro (h; k) tie­
ne la siguiente ecuación:
: ( x - h ) 2+ ( y - k ) i =rl
234
1 .
Funciones
CAPÍTULO IV
Es decir:
Dem ostración
Una circunferencia se define como un lugar
geométrico donde cada punto de ella equidista de
su centro.
2.
Halle la ecuación de la circunferencia que
pasa por los puntos (0; 3), (-1; 0) y (2; 3).
Resolución
Tomemos un punto P=(x; y). En la circunferen­
Graficamos aproximadamente la circunfe­
cia, cualquier punto P equidista con el centro,
rencia ubicando los puntos mencionados.
y a la distancia entre estos puntos se le llama
radio. Tenemos la distancia entre ( h ; k ) y (x; y).
r = •jix-ti)2 + ( y - k f , de donde se tiene
(x -h ) 2+ ( y - k ) 2= r2 ; C=Oí; k )
Ejemplos
1.
Grafique la relación
R = { ( x ;y ) /x 2+y2= 2 (2 * -y )}.
Resolución
Nótese que |>4C|representa la distancia de A a
De la ecuación x 2+y 2=2(2 x -y )
tenemos
x 2-4 x + y 2+2y=0
Sabemos que \AC\2= |Z?C|2= \BC\2= r2
C.
De la gráfica se tiene el sistema
-> x 2-4 x + 4 + y 2+ 2 y + l= 5
^
( x - 2 ) 2+ ( y + l ) 2=5
Esta es la ecuación de la circunferencia de
radio V5 y centro en ( 2 ; - 1 ).
W
(h+l)2+k2= r2
(«)
h 2+ (k-3 )2= r2
(P)
(h -2 )2+ (k-3 )2 = r2
(y)
235
Lumbreras Editores
De ((3) y (y)
Graficamos las rectas
/¡2+(/?-3) 2=(/7-2) 2+(/e-3 )2 -> h = 1
De (a ) y (P)
22+ k 2= \ + ( k - 3 f
->
* = 1
De (P)
1 + 22= r 2 -» ^ = 5
Luego, la ecuación de la circunferencia es
<&: ( x - l ) 2+ ( y - l ) 2=5
3.
Halle la ecuación de una circunferencia de
radio r= 1 y de centro en el primer cuadrante
que sea tangente a las rectas
J2?,: 3 x -4 y = 0 y ,0 2: 4 x -3 y = 0 .
Resolución
Para el problema, la distancia de C a Stx y SP2
es la misma e igual a 1 .
14/ 1-3*1
,( p . r ,
Sabemos que la distancia del punto (x,; y,) a
la recta SU: A x+By+C= 0 está dado por
d\Pi,C)= , _
;■= !
2 +3 2
4/7-3/?=5
d{P2, c ) =
(a )
13/7-4*1
V i2 + 3 2
-» -3/?+4/?=5
(P)
De (a ) y (P)
4/7-3/ü = -3/? + 4*
h=k
En (a ) se tiene
4/?-3/? = 5
|Ax, +Sy] +C|
V.42 + B 2
236
/? = 5
Luego k = 5
Entonces, la ecuación de la circunferencia es
«
( x - 5 ) 2+ ( y - 5 ) 2= 1
CAPÍTULO IV
Funciones
De la definición:
La ecuación de la parábola
La parábola se define com o un conjunto de pun­
tos que equidistan de un punto fijo llamado foco
|d(P;P)|2 =|d(P; Q) | 2
x2+ { y - p ) 2 = ( x -x )2+ (y + p )2
y de una recta fija llamada directriz.
De donde: x2 = 4px
Parábola en el e je X, con vértice en (0; 0)
Nótese que, el eje focal y la recta directriz
son perpendiculares.
Definición
--------------------De la definición:
d(P; Q )=d(P; F)
K______________
|£/(P; Q)|2=|d(P;P ) | 2
F: foco
-> (x + p ) 2+ (y -y ) 2= ( x - p ) 2+y 2
V\ vértice
De donde: y2=4 px
Parábola en el e je Y, con vértice en (0 ; 0)
Parábola con el vértice en (h ; k )
Y
eje focal
fp fr y )
\ \
directriz
F
(o\ p y
\
v
:
Q(x; -p )
y
P
237
Lumbreras Editores
Ejemplos
Además, el punto (0; - 5 ) satisface la ecua­
1.
ción de la parábola.
En el gráfico, calcule el área de la región
sombreada si m<(POO)=90°, M/V=3 y PQ= 8.
Considere al eje X como la directriz.
-» (0 + 2 ) 2= 4 p (-5 + 3 ) -4 p = - |
Por lo tanto, la ecuación de la parábola es
(x + 2 ) 2= -2 (y + 3 ).
La ecuación de la elipse
Dados dos puntos fijos F¡ y F2 distintos llamados
focos, separados por una distancia 2c, y dada
una constante a tal que a > c > 0.
Se define una elipse E, com o un conjunto de pun­
tos P{x\ y) de R 2, tales que la suma de las distan­
cias de P a los focos Fh F.¡ es igual a «2a» (a es
radio mayor de la elipse).
Resolución
Vemos que POQ forma un triángulo rectán­
Es decir: d(P ; F ])+d(P; F2)= 2 a
gulo isósceles con 90° en O.
Gráficamente
C om oPQ =8 —> OQ=4\¡2.
Asimismo, OF= 4 por definición de parábola;
entonces FA=FO -AO =4-3= 1.
Luego MFA es un triángulo rectángulo, en­
tonces:
AÍ4=V3 2 -1 2 -» MA=2s¡2
El área pedida: '3 ( 2 V 2 ) + ^ — =7^2.
2. Determine la ecuación de la parábola de vér­
tice en VX-2; -3 ) , cuyo eje focal es paralelo al
eje Y\ además, pasa por el punto .1-7(0; -5 ).
Resolución
238
C: centro de la elipse
X : eje focal
a
V,; V2: vértices
Y': eje normal
a
F¡; F2: focos
[V,; V2]: eje mayor de longitud 2o
Como el vértice es (- 2 ; - 3 ) y el eje focal es
[S ,; B2]\ eje mayor de longitud 2b
paralelo al eje Y, la ecuación de la parábola
| F ,_C | = C = | F 2-C|
es (x + 2 ) 2=4p(y+3).
Relación pitagórica: a 2 = b 2 + c 2
CAPÍTULO IV
Funciones
Eje focal paralelo al e je X
o
(a 2- c 2) ( x - h ) 2 + a 2c2 + a 2( y - k ) 2 = a 4
b 2{ x - h ) 2 + a \ y - k ) 2 = a 2(a 2- c 2)
b \ x - h j1 + a \ y - k ) 2 = a 2b 2
b 2 (x -h ) 2 |( y - k f a 2 ,
a 2b 2
a 2b 2
•
,
o2
(y - fe)2 =1, a> 6
b2
Eje focal paralelo al e je Y
Por definición: d(F{, P) +d(F¿ P }=2a
x - h + c ) 2+ ( y - k f + yj(x-h~c)2+ ( y - k f =2 a
<J(x-h+c)2 + ( y - k f = 2 a -y ¡(x -h -c )2+ ( y - k f (*)
Además: a 2 = b 2 + c2.
Veamos el desarrollo de (*). Elevamos al cua­
drado
(x -h + c)2+
= 4o 2 -4 a y J(x -h -c )2 + {y-k)2 +
Por definición, se probará que de b 2- a 2+ c2 se
obtiene la ecuación
+ (x -h -cf +
b> a
<-> (x -h + c)2- ( x - h - c ) 2 =
= 4a2- 4 a ^ j( x - h -c ) 2 + ( y - k f
Ejemplos
^
,4 (x -h )c = ,4 a 2- jía y J ( x - h - c ) 2+ (y -k )2
■o
a y j(x -h -c )2 + ( y - k f = a 2- ( x - h ) c
1.
Del gráfico
elipse
<-> a 2[ ( x - h - c ) 2+ ( y - k f ) - a A- 2 ( x - h ) c a 2 +
+ (x - h ) 2c2
<h> a 2[(x -h )2- 2 (x - h )c + c2+ ( y - k ) 2]= a 4- 2 ( x - h ) c a 2 + c2( x -h ) 2
demuestre que a 2= b 2+ c2.
239
Lumbreras Editores
En la elipse se tiene:
Resolución
Como se conoce el centro (h; k ), se pueden
conocer los focos F h F2y el punto P.
P(h; k+ b )
F^(h-c-,k)
Por definición:
(h\k)
F2(h+c\ k)
Jf-------- 2a -------- i
P )+ d (P ; F2)= 2a
y](h-h+c)2 + {k + b -k )2 +
+ \ ¡(h-h -c)2 + (k + b -k )2 =2 a
La ecuación de la elipse es de la forma
-> \lc2+ b2 +\lc2+ b2 =2a
( x - 4 )2 (y+2 )2
c2+ b 2= a 2
2.
a2
Una elipse de eje focal paralelo al eje X pasa
b2
pero a = 5, pues el radio de la circunferencia
es 5.
por ( 6; 0) y tiene sus vértices en la circun­
ferencia de ecuación
x 2+ y2- 8x + 4y- 5 = 0 .
Halle la ecuación de la elipse.
Luego
( x - 4 )2 (y - (-2 ))2
Resolución
52
Graficamos la circunferencia y la elipse.
x 2-8 x + 1 6 + y 2+4y+ 4 = 5 + 4 + 1 6
b2
( x - 4 )2 (y+2 )2
25
b2
( x - 4 ) 2+ (y + 2 ) 2= 5 2 - * C = (4; - 2 ) , r= 5
Por dato, (6; 0) satisface la ecuación de la
elipse.
( 6 - 4 )2 (0+2 )2
25 + b 2
h? J M
^
21
Por lo tanto, la ecuación de la elipse es
( x - 4 )2 (y+2 )2
25
100
circunferencia
240
21
CAPÍTULO IV
Funciones
La ecuación de la hipérbola
Dados dos puntos fijos F t y F2 distintos, tales que su distancia sea 2c, es decir, Fj ~F2 j =2c y dada una
constante a tal que 0 < a < c, se define una hipérbola H com o el conjunto de todos los puntos P tal que
el valor absoluto de la diferencia entre las distancias de P, F} y F2 es igual a "2a".
Es decir: |\P-Ft \- \P-F2 \\= 2 a
Gráficamente
C: centro de la hipérbola
V¡; V2: vértices
a
X': eje focal
Y'\ eje normal
a
F ¡; F2: focos
[V^; V2\: eje transverso de longitud 2b
circunferencia con centro C y ra­
dio C que pasa por los dos focos.
|F2-C | = c = | F ,-C |
\V2-C\=a=\V ]~C\
Relación pitagórica: c2 = a 2 + b 2
Cuando el e je focal es paralelo al e je X.
De la definición: |d[P\ F2)-d [P ; F]) |= 2 a < 2c
\ \ J (x - h -c f+ ( y -k f - ^ {x -h + c)2+ (y -kf\ = 2 a
Además, c2= a 2+ b 2
De donde se obtiene la ecuación
(x -h i)2
(y -k f
241
Lumbreras Editores
Cuando el e je focal es paralelo al e je Y.
X
1
Como la asíntota y = — tiene pendiente
los
3
3
catetos están en la relación de 1 a 3.
En el triángulo O/VM, aplicamos el teorema
de Pitágoras
(3o)2 + a 2 =8 2
2 64
2 576
—> a = — a 9 a = ----10
10
Por lo tanto, la ecuación de la hipérbola es
2
*
576
10
es decir,
(y -k )
t x-ti)
,
La ecuación es: -— tt- ---------,— =1
a2
b
2.
y
2
,
64
’
10
\0x2 10y2
576
64
Halle las ecuaciones de las asíntotas a la hi­
pérbola y2- x 2- 6y + 6x - l = 0.
Ejemplos
1.
Los focos de una hipérbola son F , = ( - 8; 0)
y F2= {8 ; 0), y la ecuación de sus asíntotas
X
X
son y = —, y = — . Halle la ecuación de la
7 3
3
Resolución
Agrupamos convenientemente
(y 2- 6 y + 9 ) - ( x 2- 6 x + 9 ) - l = 0
(y- 3 )
hipérbola.
Resolución
Gráficamente
Vemos que el centro de la hipérbola es en el
origen de coordenadas.
242
Graficando
( x - 3 )2
=1
CAPITULO IV
Funciones
Por pendiente
1= ^
x -3
GRÁFICAS DE INECUACIONES
-» x= y ->
Para graficar las inecuaciones en el plano car­
3 /x\y=x
tesiano es necesario graficar previamente las
-1 = — | —> y - 3 = -x + 3 —> & ¿ :y = -x + 6
3.
Halle la ecuación de la hipérbola cuyas
asíntotas tienen por ecuaciones x - y + 1 =0 y
x + y -3 = 0 ; adem ás, uno de los vértices de la
ecuaciones y luego les damos el sentido, que­
dando el plano dividido en dos regiones.
Es decir, si queremos graficar lo siguiente:
a. y = fM b. y > f(x)
c. y < f {x)
d. y> f{x) e. y< f{x)
hipérbola es ^ = (4; 2).
procedemos así:
Resolución
Graficamos las asíntotas y el vértice V de la
hipérbola.
I.
Supongamos que la gráfica de y=f(x) no es
una gráfica cerrada.
3 /x: y = -x + 3
Si
£B>¿. y = x + l
a.
Y
Entonces
•
Hallamos
el
punto A igualando
las
ecuaciones de las asíntotas.
••"7
|
X
y = x + \ = -x + 3 -> at= 1 ,y=2
•
El punto M: en
Para x =4 —> y = 5
Luego, la hipérbola es de centro: (1; 2) y su
ecuación es
( * - } ) _ _ ( y - 2)
3
3
v x2_y2_2x+4y_\2=0
243
Lumbreras Editores
II. Supongamos que la gráfica de }'=f(x) es una
gráfica cerrada.
y > 2jf —1
Entonces
.
c.
b.
Y
Yt
y>f
J
k
2.
Dadas las relaciones
/?={(>; y )/ * 2+y2< 16}
d.
e.
S = {(x; y) /y< |x|}.
Halle R n S gráficamente.
Resolución
Graficamos cada relación
• R: x2+y2< 16 es la parte interior y fronte­
ra de la circunferencia de centro ( 0; 0) y
radio 4.
Ejemplos
1. Grafique las inecuaciones
a. y > 2x - l
b. y < 2x - l
c. y > 2jc —1
d. y < 2x - l
Resolución
En todos los casos, primero se graficará la
igualdad y luego se le da el sentido, confor­
m e indican los gráficos anteriores.
244
CAPÍTULO IV
• S: y< |x|
Primero graficaremos la igualdad
Funciones
El concepto de función fue utilizado por prime­
ra vez por René Descartes para indicar la rela­
ción entre dos o más cantidades, pero su uso en
el contexto de las matemáticas se remonta a los
estudios realizados por G. Leibniz para referirse a
varios aspectos de una curva, como su pendiente.
Su aplicabilidad en matemáticas se le atribuye a
Jean Bernoulli (1667-1748).
La idea de función constituye uno de los con­
ceptos más útiles y necesarios en la matemática,
y siempre vemos sus aplicaciones en otras cien­
cias y en la cotidianidad. Mediante las funciones
podemos describir el tiempo que tardamos en ir
de nuestra casa a la universidad, calcular el área
del terreno de nuestra vivienda, la velocidad de
Luego, R r¡S es
un automóvil que se desplaza por la autopista,
el crecim iento de una bacteria en un tiempo
determinado, el crecimiento de la población, la
inflación, el ingreso y el egreso de una familia,
y otros.
DEFINICIÓN
Una relación binaria f: A —>B se llama función del
conjunto A al conjunto B, si para todo elemento
x de A existe un único elemento y en B , llamado
su imagen.
Es decir, f : A —>B es función,
si \/x eA 3 !y e B / Qc;y) e AxB.
►F u n c io n e s
En el diagrama de Venn
INTRODUCCIÓN
f
Frecuentemente, resulta interesante estudiar la
relación existente entre los elementos de dos
conjuntos. Por ejemplo, la edad de un niño pe­
queño y su peso; la posición de un cuerpo móvil
en diversos instantes; el volumen de una esfera
con su radio, son conjuntos cuyos elementos es­
tán relacionados. Una función es, precisamente,
la descripción de la relación que existe entre los
elementos de dos conjuntos.
conjunto
de partida
O;
conjunto
de llegada
y)
e f
<->
y = f (x)
245 ,
Lumbreras Editores
Una función f de A en B se denota por:
8
3,1
f:A ^>B
.
x ~>y=f w
Donde y=f(X) es la regla de correspondencia de f.
/
\ ____
/ 1
/ 2—
De la definición se desprende que una relación
V
B
/Ia
\ b
\ c
\ d
es una función si cumple las siguientes condi­
ciones:
I.
g es una función, pues para cada elemento
Todo el conjunto A (conjunto de partida) es
de A existe un único elemento en B.
el dominio.
II. No existen dos pares distintos con la misma
primera componente; es decir, si (x ; y) e f
a
(x ;
z)
e
4.
h
f, siendo f una función, entonces
y=z.
Ejemplos
h no es función, pues 2 eA tiene dos imáge­
nes en B.
^
/ = {(!; 5), (2; 5), (3; 4 )}
es una función
G no es función, pues 5eA, no tiene imagen
FUNCIÓN REAL EN VARIABLE REAL
Una función f: A -> B es una función real en va­
-> F = {(1 ; 4), (2; 7), (3; 7)},
246
riable real si y solo si A y B son subconjuntos de
es una función. Además, í ’(|)=4;
R, es decir, el dominio y el rango son subconjun­
Fm = 7’ F(3)=7
tos del conjunto de los números reales: R.
CAPÍTULO IV
Funciones
Ejemplos
1.
Resolución
La función f: [3; 2) —> R + cuya regla de co­
Como del dominio es Dom f = { - j 2; 2),
rrespondencia es f(x) = X+ , es una función
calculamos el rango así:
real de variable real.
—> -% ¡2< x< 2
En efecto, vemos que [3; 2) c R y asimismo
->
R +c R.
2.
,
0 > - x2 > - 4
—> 5 > 5 - x 2 >1
Halle el dominio de la función f.
0 <x2 < 4
—> 1 < V 5 - x 2 <>/5
—> -1 > -\J5 - x 2 > -V 5
4 x -l
-> 2 > 3 - ^ 5 - x 2 > 3 -V 5
'J5 ^ x '
~
—> 3 —V5 <
j<2
Resolución
.-. R a n (0 = [3 -V 5 ; 2)
Cuando se pide el dominio, se pregunta
equivalentemente para qué valores reales
de la variable x está definida la función
GRÁFICA DE UNA FUNCIÓN
Así, f(x) está definida en R si 5 - x > 0 , luego
Si /: .4 —>S es una función real de variable real, su
x<5
gráfica denotada por Graf(/) está dada por
Dom(/0=<-°°; 5)
3.
Halle el rango de la función f.
/M = 2x + 5;
----------------------------------- Graf(/)={(x; y) e R 2 /y=/'w ; x e Dom(/)}
............ .„.y.-vv,,..... ,.... .......... ----..V
V............
x e (-4 ; 2]
Resolución
Aquí el dominio es Dom f= (-4 ; 2].
Para hallar su rango, habrá que hallar la varia­
ción de f(xy Así:
-4 <x<2
Ejemplos
1.
Grafique la función f.
fM=x2- 2x+2; x e {1; 2; 3; 4}.
Resolución
Si /'m = x 2- 2 x + 2 = ( x - 1 ) 2+1,
<-> - 8 < 2x<4
tabulamos los valores de x para hallar su
<-> - 3 < 2 x + 5 < 9
imágenes.
<-> -3 < A (x)<9
X
R a n (0 = < -3 ;9 ]
4.
Halle el rango de la función real f.
fM= 3 - V 5 - X 2; x e (-V 2 ; 2)
1
2
3
4
1
2
5
10
Luego
M ( l ; 1), (2; 2), (3; 5), (4; 10)}
247
Lumbreras Editores
Gráficamente
Proposición
Si f e s una función de A en B, entonces
Y
Gmí(f) c Dom(/') x Ran(/) <zAxB
10
D em ostración
Si P 6 Graf(7) -> P = {a;{fM)), pero a e A mien­
tras que f (a) e Ran(/) y Ran(/) c B .
Por tanto, ha) 6 B
—>
cada P e Graf(/") es un
elemento de Dom(/)x RanCO y como
1 2
X
34
DomCO xRan(Z') cA x S , entonces P e A xB.
2. Grafique la función f.
Ejemplo
f^ = x + 2; x e (-3 ; 2],
Grafique la función f cuya regla de correspon­
Resolución
dencia es f(Y\=rr—w M +l
Tabulamos algunos valores de x para hallar
Resolución
las imágenes.
Tabulamos algunos valores de x s Dom f= R, para
- 1
-2
-1
0
1
0
2
1
2
...
3
4
...
hallar las imágenes.
X
-3
-2
-1
f (x)
-1
-1
-1
1
ro |
f w>
-3
O
X
-1
" I
2
3
Gráficamente
i
°
Graficamente
Luego
Dom (Y)=<-3;2]
248
a
Ran(/r) = ( - l ;
D om (/)=xeR
a
Ran (/")= [—1 ; 1)
1
1
3
2
...
CAPÍTULO IV
Funciones
Proposición
Ejemplos
Una Graf(/') en R 2 representa a la gráfica de una
1.
función, si toda recta paralela al eje Y corta a la
¿Cuál de los siguientes gráficos representa a
una función?
gráfica en un solo punto.
Dem ostración
Se presentan dos casos
Caso I
g no es función
Que la recta vertical (paralela al eje Y) corte a la
gráfica de f e n un solo punto.
2.
Así, /={(*„; y0), (* ,; y,), (x2; y2) , ...}
cumple todas las condiciones para ser función.
S c a y = f(xj tal que x 2+y 2-2 y = 3 .
¿Es f una función?
Resolución
De la condición
Caso II
Que la recta vertical corte a la gráfica de f e n más
de un punto.
x 2+y 2-2 y = 3
<-> x 2+y 2- 2 y + l = 4
<-> x 2+ ( y - l ) 2= 22
Como sabemos, esta ecuación es la circun­
ferencia de centro ( 0; 1) y radio 2 .
Así, /={(x 0;y 0), (x 0;y ,), (x 0;y 2), •••}
Como (x0; y0) e f
a
(x0; y,) <=f, con y0*y „
entonces f(x^no es /unción.
La recta vertical A co rta a W en más de un
punto, con lo cual / no es una función.
249
Lumbreras Editores
3.
Sea y=f(¿) tal que 4x 2-12xy+9y 2-4 x + 6 y + l =0.
Resolución
¿Es f una función? En caso afirmativo, grafí-
Recordemos que si (a; b) e f
quela.
siendo f una función, entonces b= c.
a
( o ; c)
e f,
En el diagrama sagital
Resolución
Buscaremos despejar y.
f
A
-------
4 x 2 -12xy + 9y 2 -4 x + 6 y + l= 0
(2 x -3 y ) 2-2 (2 x -3 y ) + l= 0
/
x
r— *2+1
\\
2x
( 2 x - 3 y - l ) 2= 0 <-» 2 x - 3 y - l = 0
\
2z
rV z2+
1/
-2 z /
Nótese que para que f sea función se tiene
que cumplir
Vemos que fíx) es una
Entonces,
x 2+ l = 2 x
función.
—> ( x - l ) 2 = 0
Tabulamos algunos valores para x :
X
-l
a
0
1
3
3
2
5
1
3
1
f (x)
—> x = l
Gráficamente
a
Entonces,
z
a
2+ 1 = - 2
( z + l ) 2= 0
z = -l
/ = { ( 1 ; 2 ), ( - 2 ; 2 ) }
Dom(/') = { l ; - 2 }
a
Ran(g) = { 2 }
.-. Dom(/')uRan(/') = { - 2 ;
5.
z
1; 2 }
Dada la función
,
(x)
_ (x + 2 )(x 2 + 6 x -1 6 )(x -6 )
(x -2 )(x 2-4 x -1 2 )
’
halle la suma de los valores de x, para los
cuales no está definida la función.
Resolución
Como f es una función racional, el denomi­
nador debe ser diferente de cero, entonces
veamos la restricción correspondiente. Para
ello, igualemos a cero el denominador y lue­
go retiramos dichos valores de x. Es decir:
4.
Halle Ran(/') u Dom(/) si
/={(x;
1 ), (x; 2x ) ,( 2z ;z 2+ l), (2 z; - 2z)}
es una función.
250
( x - 2 ) ( x 2- 4
x
-1 2 )= 0
( x - 2) ( x - 6)( x + 2)=0
x =2 v x =6 v x = - 2
Funciones
CAPITULO IV
En seguida, el dominio de í e s el conjunto
8. Si/'w = 2 x + l ; -1 < x < 6,
D o m (/ )= R -{2 ; 6; - 2 }
calcule el rango de f.
Por lo tanto, la suma de valores donde f no
Resolución
está definida es 6.
Como el dominio de f es [-1 ; 6], entonces
partimos de - 1 < x <6 para formar f(xy
6. S e a f(r*,= ']7 -x sen x + —^—.
y>
x -2
En efecto
Halle Dom(/).
- 1 < x <6
Resolución
<-> - l < 2 x + l < 1 3
Como/'w e R, entonces %/7-x e R
—> 7 -x > 0
x<7
a x
-2 ^ 0
Luego -1 </■(*)< 13
x -2 *0
a
...
x *2
a
Dom(/)=<-»; 7 ] - { 2 }
7.
- 2 < 2x <12
9.
Si el dominio maximal de f con regla funcio­
nal
R a n (0 = [-1 ; 13]
Sea f con regla funcional
_ *+1
w “ 2x + r
Halle Ran(/).
, \¡2-x2 t a nx
2 ,n ,
íírl=——,---- + -------- 163x + 9 x - l
KX>
|xl-l
x
Resolución
es el conjunto
£2 = [a; b ) u (b; c) u (c; d) u (d; - a ] , con
Vemos que x ^ — , entonces
2
a < b < c < d , La qué sera igual a 2+ b 2+ c2+ d2l
Resolución
Para calcular el rango despejamos x de
Como f(x) e R, entonces
\l 2 - x 2 e
2 - x 2> 0
x 2< 2
a
R
a
a
I x l^ l
x *± l
-V2<x<V2
|x|-l*0
a
a
x*0,
a x *0
x +1
2x + l
Así
2x y + y = x + l o x ( 2y - l ) = - y + l
a x *0
x*-l
y=
a
x*l
a
x^O
«
- y +1
2y —1
x= -
Luego el dominio de f es
Q = [-V 2 ; - l ) u ( - l ; 0 )u (0 ; l)u (l; V2]
Como el denominador 2 y - 1 ^0,
de donde
a=-\Í2; b = - 1 ; c = 0; d = l
a 2+í>2+ c 2+ d 2= 2 + l + 0 + l = 4
Luego el R a n (/ )= R -j251
Lumbreras Editores
10. Sea f,(x)~
x +1
; -4 < x < -l.
2x + l
—> —8 < 2jc < —1 v - l < 2x < 2
-7 < 2 x + l< 0
Halle Ran(/).
1
1
1
2 x + l< 7
Resolución
v 0 < 2 x + l< 3
V 2x + l
1
>3
Como Dom(/')=[-4; -1 ), entonces formare­
2x+ l
mos f(x).
Para ello, es conveniente descomponer f(x)
2
así:
f( x ) ~
x+\ 1 2x+2
= - í i + — !—
2x + 1 2 2x+\
21 2x+\
Luego partimos de: - 4 < x < - l
-> - 8 < 2 x < - 2
-> - 1 < — -—
2x + l
0<
-
2
1+
1+
7
2x+l
-
2x+ l.
1+
3
2
>2 x +1. 3
-
3
2
Entonces: f(x)< - v f(x)> -
Ran(/)=(-°°; - u ( - ; +oo
-» - 7 < 2 x + l < - 1
0 < 1+ — !— < -
7
2x+l
-
2x + l A
-* o<fM4
7
12. Si el conjunto A = {x e R / |x| < 1} es el dominio de fw
ftx)=xl
r - 2 x - 1. Halle el Ran(/).
Resolución
Como |x| <1 <-> - 1<x<1, entoncesj4=[—1; 1]
Luego tenemos la función
Ran(/)=(0; -
f(x) = x ¿ - 2 x - 1; - 1 < X < 1
/■m = ( x - 1 ) 2- 2 ; - 1 < x < 1
x +1
11. Sea f(r)= ------- ; - 4 < x < 1; x * —
U) 2x + l
í
Partimos de - 1 < x< 1 para formar f(xy.
- 2 < x - l <0
- 1 < x <1
Calcule Ran(/).
-> 0 < ( x - 1 ) 2<4
-» - 2 < ( x - l ) 2- 2<2
Resolución
C o m o -4 < x < l
x *--
a
-> - 2 < ^ , < 2
2
.-. R an (/ )= [-2; 2]
—> - 4 < x < —1 v —1 < x < l
2
además kx)~
2
13. Si/(x)= | x| -x 2+ 2 ; - l < x < 2 ,
halle Ran(/).
i+-
2x + l.
Resolución
En seguida tenemos:
fx; x >0
-4 < x < —
2
252
v — <x<l
2
-x ; x <0
CAPÍTULO IV
Funciones
entonces redefmimos la función, así:
De (a ) y ((3) tenemos que
| - x - x 2+2;
x—
ro 9 i
91
Ran(/O=(0;
0; - u 2; - =(0; 4 \ 4.
\ 4.
-
w
4
Construimos por partes
x 2- x + l
Halle Ran(/).
+ - ; -l< x < 0
2)
l f
14. Sea f(x) = í L t í i l _
4
X + -
1
-1 < x < 0
+ -; 0<x<2
2)
L
L
x - x +2; 0 < x < 2
r( x ) z
Resolución
(x)
Como x 2- x + 1 > 0 V x e R,
9
entonces Dom(/) = R.
y= T ~ 2 j + 4 ; ° - X < 2
1
1
3
2
2
2
Luego, para calcular el Ran(7) hacem os
C om o0<x<2 —> — < x — <—
-
-
0
, - ^
1
x 2+ x + l
y = — -------X - x +1
<-» yx2-y x + y = x 2+ x + l
_
h -(i-lU ° > 0
4
l
2) 4
-,
7 > y >o
S
4
<-» ( y - l ) x 2- ( y + l ) x + ( y - l ) = 0
Como x s R, entonces A > 0
-» 0 < y < ^
(a)
-> A = ( - ( y + l) ) 2- 4 ( y - l ) C y - l ) > 0
-» ( y + l ) 2- 4 ( y - l ) 2 > 0
• y = - ^ x + ^ j+ ^ ; - l < x <0
-» y2 + 2y+ l-4 (y 2-2 y + 1) > 0
—>
C o m o -l< x < 0
-
2
< x + -< 2
2
-¥ -3 y 2 + 10y-3 > 0
-> 3y2-10y + 3 < 0
os("lTsi
-> ( 3 y - l) ( y - 3 ) < 0
- * -< y < 3
3 7
Ran(/) =
- , —> - f x + —Y + —>2
4
v
2/
4
x
.3
3-3
x
3
.
2-
x
+3
15. Sea f(r)= -----=------------- una función racional.
{>
x -4 x + 3
(P )
Indique su rango.
253
Lumbreras Editores
Resolución
Factorizamos el numeradory el denominador
_ (x + \ )ix ^ ix ^ )
ix)
w
w
Su gráfica es una recta paralela al eje X , conse­
guido a través de la tabulación.
x * 1 a x *3
’
f^=x+\\ x*\\ x * 3
Como x *\ , entonces f{x) * 2
Como x * 3 , entonces f(x¡*4
Luego fM 6 R —{2; 4}
.-.
R a n (/ )= R -{2 ; 4}
FUNCIONES ELEMENTALES O SIMPLES
Son aquellas funciones especiales que nos servi­
Función lineal
Función polinomial de primer grado; definida
por
f= {(x\ y)/y= ax+ b\ a * 0 } , con dominio: R
rán de apoyo para el estudio de otras funciones.
Gráficamente, representa una línea recta que
Las más importantes son:
corta al eje y en & y al eje X en -b /a . Es decir:
Funciones polinomiales
Sea /'(x) un polinomio de coeficientes reales, cu­
yos casos particulares son:
Función constante
Es una función cuyo dominio es R y su rango es
la constante real c.
Es decir: f= {(x ; y) /y=c, c es constante}
Dom(/)=R
a
R an(/)={c}
Veamos el diagrama sagital
f \R —» R es una función constante.
En ambos casos:
Dom (/)=R
254
a
Ran(/) = R
CAPÍTULO IV
Funciones
2.
►
►Tenga en cuenta
Grafique la función f : f^x\=x.
En la función lineal y=ax+b el coeficiente
Resolución
principal es llamado pendiente de la recta
Graf(/) pues: a=tana
Este es un caso particular de la función li­
neal, cuando su pendiente es 1 (a = 4 5 °) e
intersecta al eje Y en 0. Esta función recibe
Ejemplos
1.
también el nombre de función identidad.
Grafique la función,
a. fM=3x-\
b- g(x)= ~2x+3
Resolución
Se sabe que sus gráficas serán rectas, para
ello solo se necesitan dos puntos de paso.
X
0
i
...
f(x)
-i
2
...
D om (0 = R a Ran(/)=R
3.
Grafique la función/7: f{x)=-x.
Resolución
Esta es una función lineal de pendiente -1 y
corta al eje Y en y = 0.
X
0
1
...
S(x)
3
1
...
Dom(/) = R
a
Ran(/) = R
255
Lumbreras Editores
Proposición
Sean f y g
dos
funciones lineales
cuyas
ecuaciones son
Como tan[ — | no está definido, en tal caso
\+m2-m }=0
m xm 2=-
M C * ; y)/ y = m ,x+ f?]}
g={(.x ; y ) /y = m 2x + b 2}
Por lo tanto, dos rectas son perpendiculares
cuando el producto de sus pendientes es igual
Si 0 es el ángulo formado por sus gráficas (rec­
tas), entonces:
tan 0 =
m2 - m ]
1+ m^m2
a - 1.
Gráficamente
Y
Dem ostración
y = m lx + b ]
Graficamos ambas rectas
\
/
\
X
y = m 2x + b 2\
Donde: m ^tanoc
a
m 2=tanP
Del gráfico se observa que: a+ 0= (3 —> 0=p~oc
Tomamos tangente: tan 0= ta n (P -a )
En consecuencia, las funciones:
f( x) = x
a
S ( x ]=
- x cuyas gráficas se muestran
tan^ -tana
Como ta n (P -a )=
1+tanatanP
Corolario
Si 0 = —; es decir, si las rectas son perpendicula­
con pendientes respectivas, m fym gl cumplen que
res, tenemos:
m f-mg= - 1 .
256
CAPÍTULO IV
Funciones
Ejemplos
1.
Su gráfica es:
Halle la ecuación de una función lineal cuya
gráfica es perpendicular a la gráfica de la rec­
ta 9?\ 3 x - y - l = 0 y pase por el punto (1; 2).
Resolución
Graficamos
y = 3 x -1
Además, sea fM= ax + b la función buscada.
Función c u a d rá tic a
Es una función polinomial de segundo grado cuya
regla de correspondencia es f(xj= ax 2+bx+ c;
<2 * 0, y con dominio: R.
Su gráfica es una parábola con eje focal paralelo
al eje Y. Así:
o> 0
a< 0
f —> 3 a = - l —> a = —
Si
3
Luego: f(x)= -^ x + b
Como (1; 2) e f —> /(1)=2
1
7
-> — + b = 2 -> b = 3
3
f
_
1
7
3 * +3
2.
Grafique la función /': f{x)= \x \.
►
►Recuerde
La ecuación cuadrática de coeficientes rea­
les: fM=ax2+bx+c; a * 0
tiene raíces: x u x2 tal que:
Resolución
Redefmimos la función f, así:
r(x) =
1
\x s i x >0
con A=b2-4ac\ discriminante
\x s i x <0
donde
Son dos funciones lineales en un cierto do­
minio y su rango es R q (función valor abso­
luto).
-b+J~K
- b —fK
2a
' 2 2a
X , = ------------- ■ X n = ------------
• SiA>0 —» jfi;x 26R
a
x ¡*x 2
• SiA=0
—>
a
x t=x2
• Si A<0
—»
a
x¡=x2
257
Lumbreras Editores
Observe las gráficas de las fundones cuadráticas más sencillas.
Análisis de la gráfica de la función cuadrática
Sabemos que la gráfica de fM= ax2+bx+c\ A *0 es una parábola que abre hacia arriba o hacia abajo,
dependiendo del primer coeficiente de
A>0
A= 0
Y
Y
f(x)
1
a>0
A i
a <0
com o se observa en los diferentes casos.
x
^
* 1=*2
Y
Y
h
X\=X2
* 2\ X
n
A<0
Y
J
x
X
Y‘
'
í
Nótese que
si A > 0, la parábola corta al eje X en dos puntos.
si A = 0, la parábola es tangente al eje X. Esto sucede porque sus dos raíces son iguales.
si A < 0, la parábola no corta al eje X ya que sus raíces son com plejas imaginarias y conjugadas.
258
Funciones
CAPÍTULO IV
3.
Ejemplos
1.
Grafique la función g: g M = x 2-4 x + 5 .
Grafique la función/: f^ = x 2- 2 x -3 .
Resolución
Resolución
Nótese que g (x)=x2-4 x + 5 tiene discriminante
Hallamos las raíces de f^xy f (xj=0
negativo:
A = (-4 ) 2- 4 ( l ) ( 5 ) = - 4 < 0,
f(x)=x¿- 2 x -3 = 0
—> ( x - 3 ) ( x + l ) = 0 —» jcj = —1;
x 2=3
entonces g M > 0; Vx e R.
Adem ásgM = ( x - 2 ) 2+ l c o n g (0)= 5
a
Su gráfica es una parábola que abre hacia
arriba y corta al eje X en x = - 1 y en x = 3.
g (2í = l.
Su gráfica es:
Graficamos
Teorem a
Toda función cuadrática de coeficientes rea­
2.
Grafique la funcióng: g (x)= - 2 x + 5 x -3 .
les f(x)= ax 2+ bx+ c se puede escribir com o
f(x1 = a ( x - h ) 2+k.
Resolución
Hallamos las raíces de g^xy g(x)= 0
g(x) = - 2x 2+ 5 x -3 = 0
3
—> x, = l ; x 2= -
-> ( - 2 x + 3 ) ( x - l) = 0
Su gráfica es una parábola que abre hacia
El par (h; k) es el vértice de la parábola.
Dem ostración
Sea f^ = a x 2+ bx+ c, a * 0
Completamos cuadrados. Así:
abajo (primer coeficiente negativo) y corta al
eje X en x = 1 y en x =
3
f( x ) ~ a
b_¿
2 .
b¿
x + b x + — 5 + c4a
4a 2
Se tiene
Graficamos
f(x)=a x + -2a
2 A a c-b 2
4a
En este caso, el vértice se da en el punto
b
A ac-b
2
a'
=(/i; k)
4a
Como se observa
b _X ]+X 2
4ac-¿>
2a
2
A
4a
_J
b
i. 2a
259
Lumbreras Editores
Entonces, la gráfica dé f{x]= ax¿+ bx+ c, con a*(),
Su gráfica es una parábola que abre hacia
a ; b ; c e R, es
abajo, con vértice en V = (l; -2 ) .
Ejemplos
3.
1. Grafique la función f\ flx)=x¿-6x+ 5.
Halle el rango de la función f, tal que:
f(j¿)=4 + 2 x -x 2; x
[-2 ; 3}
e
Resolución
Resolución
Hallamos las raíces de f(xy f (x-¡= 0
Prim er m étodo (algebraico)
A partir de su dominio, hallamos su rango.
/(x) = x 2 - 6 x + 5 = ( x - 1 ) C x - 5 ) = 0
Como x e [-2 ; 3) —> - 2 < x < 3
—> jcj = 1; x 2=5,
-> - 3 < x - l <
y su vértice (h ; k) se obtiene así:
->
.
h - x'+xz - 1+5- 3
2
2
-»
V =(3; - 4 )
• k = fm = fm = 3 2- 6 ( 3 ) + 5 = - 4
1> 2 x - x 2 > -8
->
-4 < 4 + 2 x -x 2< 5
R an (0 = t - 4 ;
0 < (x -l)2< 9
-»
0 < x 2- 2 x + 1 < 9
->
Su grafica es una parábola que abre hacia
arriba con vértice en V=(3; -4).
-»
2
-1
< x2- 2 x < 8
—> 5 > 4 + 2 x - x 2 > - 4
-*
- 4 < f (x) < 5
5]
Segundo m étodo (gráfico)
Completamos cuadrados:
/M = - ( x 2- 2 * + l ) + 4 + l = - ( x - l ) 2+5
La gráfica de f es una parábola que abre ha­
cia abajo con vértice en V = (l; 5) y ^_2) = - 4.
2.
Grafique la función/': fM= -2 x 2+ 4x-4.
Resolución
Completamos cuadrados
fM= - 2 ( x 2 - 2 x +
1)-2
-» fM= - 2 ( * - l ) 2- 2 -> V = ( l ;- 2 )
.-.
R an(/ )=[-4; 5]
CAPÍTULO IV
Funciones
Función cúbica
Es una función polinomial de grado tres,con regla de correspondencia
f(x)= a x 3+ b x 2+ cx + d , a ± 0, y cuyo dominio es el conjunto R.
Si hacem os x = t - ~ - podemos transformar f M = a x 3 + b x 2 + ex + d en f^ = a\ t3+ p t+ q ], donde p y q
dependen de o; b ; c y d.
La naturaleza de sus raíces depende de la expresión
j + j^ j .
Así
s iA <0
t i , t 2, t 3 e R
a
t\ ± t2 * t z
• siA = 0 —» f|;f2; f 3 € R
a
t2= t3
•
• si A > 0
—>
—> /, e R
a
í z; f 3 í R
Análisis de la gráfica de la función cúbica
La gráfica de la función cúbica f^ = a [ t 3+ p t+ q ) depende del primer coeficiente y de la expresión
O
II
<
A< 0
%
i
r rJ
Y
a> 0
r
Y
t2 \ _ y t3
1
t2~t3
/■
Y
a <0
A >0
Y
Y
1
,
{/ \J
t
t
(\
Y
t2~t3
‘
M
'
261
Lumbreras Editores
Función poiinomial general
Ejemplos
1.
Esboce la gráfica de la función f:
f{x)= ^ -3x-2.
Sea el polinomio de grado n y coeficientes reales
fM= a 0xn+ a ]xn~] +d'2xn~2+ ...+ an; a 0* 0.
Resolución
La geometría de estas funciones depende del
Factorizamos el polinomio: f(x)= (x + l) 2(x -2 ) y
obtenemos las raíces:
x ,= x 2= - l ; x 3 = 2 .
tipo de raíces que posee, aunque puede decirse
que estas funciones tienen un comportamiento
ondulatorio.
Graficamos
I.
Si todas las raíces son reales y sim ples, la
función será escrita com o
fw = ao{x-X \ ){x-x2){x -x ¿ )..{x -x n)
y su gráfica será cualquiera de las siguientes:
• a > 0 ,n impar
La intersección con el eje X representa a una
El número de cortes de la gráfica de la
raíz real.
función poiinomial con el eje A-, depende
El punto de tangencia implica, por lo menos,
del número de raíces reales de fM.
dos raíces reales e ¡guales.
2. Esboce la gráfica la función f: /(x)= x 3-7 x + 6 .
Resolución
Resolvemos la ecuación
0 para hallar las
raíces.
jc3- 7 x + 6 = 0 —> ( x - l ) ( x - 2 ) ( jf + 3) = 0
Cuando n es impar y el coeficiente prin­
x ,= - 3 ; x2=\\ x3= 2: son raíces reales y dis­
cipal es positivo, el extremo derecho es
tintas.
+ °° y el izquierdo, -<».
Gráficamente
262
• a < 0 ,n impar
La función f tiene tres raíces reales, por ello
corta al eje X en tres puntos tal com o se
Similarmente, si el primer coeficiente es
muestra en la gráfica.
izquierdo, +°°.
negativo, el extremo derecho es -<» y el
CAPÍTULO IV
Funciones
• a > 0 ,n par
Ejemplos
1.
Esboce las gráficas de las siguientes funcio­
nes
a. /(x)= 3 0 t- l)(x + 5 )(x -4 )(x + 2 )
b. g M = 5 (x -2 )( x - 5 )(x + 2 )(x + l) x
c. h w = - ( x - 4 ) ( x - 3 ) ( x + 2 ) ( x + l)
Cuando n es par y el coeficiente principal
es positivo, los extremos de la gráfica
son + 00.
•
d- ./(x) = - V 2 ( x + 3 ) ( x + ^ ) ( x + l ) ( x - l ) ( x - 3 )
Resolución
a < 0, n par
Son funciones polinomiales de raíces reales
y simples.
•
a. y b.
Las raíces de
Las raíces de f>(xy 2; 5; - 2 ; -1 ; 0
Si el coeficiente principal es negativo, los
extremos de la gráfica son -<*>.
II. En raíces reales con multiplicidad,
1; - 5 ; 4; - 2
Sus gráficas son
tie­
ne un factor de la forma ( x - x 0)*, donde k es
la multiplicidad; k e Z +; k>2.
•
Si k es par, no hay corte con el eje X.
•
Si k es impar, si hay corte con el eje X.
•
c. y d.
Las raíces de h (xy 4; 3; -2 ; -1
Las raíces de j^xy. - 3 ; -V 2 ; -1 ; 1; 3
263
Lumbreras Editores
Sus gráficas son
Función potencial
Es aquella función polinomial de grado n >2.
La función potencial es de la forma f^=kxP,
cuyo dominio es el conjunto R.
Su gráfica es cualquiera de las siguientes:
Si n es par
2.
k> 0
k=\
k< 0
k = -\
Esboce las gráficas de las siguientes funcio­
nes
a. /M =2C v+3)(x+2) 40 - 3 )5
b. fr(x) = - 5 0 f + l) jf 2( jf-2 ) 4( x - 4 )5
Resolución
Tengamos en cuenta que:
•
Multiplicidad par genera punto de tan­
gencia.
•
Multiplicidad impar genera corte y punto
de tangencia con el eje X.
Si n es impar
k> 0
k=\
íx5
y
264
-
1*3
Funciones
CAPÍTULO IV
*< 0
Equivalentemente
* = -1
1;
s i x >0
sgn(x) 0;
s i x =0
- 1;
V
si jc <0
D om (0 = R
Ran(/') = { - l ; 0; 1}
a
Su gráfica es la unión de tres funciones cons­
tantes.
Y
-X5
1
Función escalón unitario
Es una función denotada por í/aM; a es fijo y
está definida por
1, s ix > a
f( x ) ~ U a U ) |
10, s ix < a
Ran(/)={1; 0}
Dom(Y)=R a
Ejemplos
1.
Esboce la gráfica de la función f :
x-\
^M—sSn i 2
V X
Su gráfica es la unión de dos funciones constan­
tes.
,
+X + 1
Resolución
x
Nótese que f<x\=—¿-------x +x+l
Y
está definida V x e R,
1
pues x ^ + x + ^ O ; V x e R
Entonces, Dom(/) = R
Luego
Nótese que, para a = 0 , se tiene:
1; x >0
U0(x) = U(x)=
0; x <0
f( x )~
1;
x - l >0
0;
x - l =0
- 1 ; x - l <0
Función signo
f(x )~
1;
si x > l
0;
si x = l
- 1 ; si x < l
Gráfica
Es una función denotada por sgn(x) y se define
-,
si
sgn(x)
X
0,
s i x =0
265
Lumbreras Editores
2.
Esboce la gráfica de la función f:
f{x)=sgn
III. Graficamos la función.
'( jc+1)0 c+4)"
^6- x -x
-3
Resolución
I. Hallamos su dominio
6 - x - x 2> 0
-» x 2+ x - 6 < 0
—> (x + 3 )0 f-2 ) < 0
-> - 3 < x < 2
—> x e (-3 ; 2)
Función máximo entero
Es la función denotada por /(X) = M , cuyo do­
El dominio de f e s (-3, 2).
minio es el conjunto de los números reales. Se
Luego, respecto al dominio se analiza
(x+ l)(x+4) .
define:
M es el mayor entero no mayor que x, esto es
sÍ6- x - x
M < a:; x g R.
pero V6 - x - x 2 es positivo, entonces
De la definición
basta analizar (jc+ l)(x + 4) sobre (- 3 ; 2).
lx}= n <-> n< x <n+\, n e Z
II. De la definición
Ejemplos
si O + l)(> r+ 4)> 0
fU)~ 0;
si (x + l)O + 4 )= 0
-1 ;
Como
si (jf+ l)(jc + 4 )< 0
x g
{-3;2>
1.
p ,4 7 J= 3 porque 3 < 3 ,4 7 < 4
2.
|[-4,51J=-5 porque - 5 < 4 ,5 1 < - 4
3.
Si x e Z, entonces |[x ] =x. Luego tenemos
—> x + 4 > 0
1;
si x + l> 0
a
-3 < x < 2
0;
si x + l= 0
a
-3 < x < 2
-1 ;
si x + l< 0
a
-3 < x < 2
1;
—1 <j\:<2
[ 21 = 2 ; [ 01=0
[ —3 J = —3; I —11 = —1
4.
\x)~- 0;
-1 ;
x=-\
Resuelva la ecuación [5 x -4 1 = 1.
Resolución
Usamos la definición
[5 x -4 1 = l <-> 1 < 5 x -4 < 2
-3 < x < -l
x<5x<6
1;
■■ f<
\x)~- 0;
si x e ( - l ; 2)
-1 ; si x e (-3 ; -1)
266
6
si x=-\
.-. CS= [ 1; 6/5}
Funciones
CAPÍTULO IV
De (II)
Propiedades b ásicas
1.
2 x -3
<3 <-> (2 x -3 ) < (3 x -3 )
x -1
[x ]e Z, V x e R
2. M < x < M + l , V í e R
4x2- 1 2 x + 9 < 9 x - 1 8 x + 9 «
3. 0 < x - M < l
4.
[x+m]|=|[x]+rr¡, V m e Z
5.
VnsZ:
6.
V n s Z: ([x] < n <-> x < n)
7.
VneZ:
([x j< n <-> x < n + l )
8.
VneZ:
([x ]> n
x (5 x - 6 )> 0
x < 0
v
5 x - 6x > 0
x > -
( jx j > n <-> x > n + l )
<-> x e ( - ~ ; 0) u ( - ; +°
x>n)
(P )
De (a ) n (P)
Ejemplos
1.
2 x -3
Resuelva la ecuación
=
x -1
2.
°
1 6
5
5
4
+ oo
Resolución
/
n\
/6 5
►
►Recuerde
[xJ=nsZ
<-> n < x < n + l
2.
Resuelva la ecuación |— jJ = x
Usamos la definición
2 x -3
x -1
=2 <-> 2 <
2 x -3
Resolución
<3
Como |— - J = x entonces x e Z.
Nótese que los únicos enteros que verifican
la ecuación son: - 1 y 2
De (I)
C S = { - 1 ,2}
4 ^ (2 x -3 )_ ^
( x - 1)2
(2x - 3)2 >( 2x - 2)2 a x * l
GRÁFICA DE LA FUNCIÓN MÁXIMO ENTERO
Para graficar la función f : AM =|[xJ, hay que re-
<-> 4 x 2 - 1 2
«-» x < -
4
a
x
+ 9> 4
x*l
x
2- 8
x
+4
<-> 4 x < 5
a x
*1
(a)
definir la función, sobre todo si se sabe que su
dominio es R y su rango es Z. Para ello, hay que
recordar que:
[x]| = n h n < x < / i + l ;/ ¡e Z
267
Lumbreras Editores
Luego, escribimos
Ejemplos
1.
3 «
3<x<4
2 <-» 2 < x < 3
1o
l< x < 2
Esboce la gráfica de la función f: fM = \\2x-1 J
Resolución
I.
Dominio de f: Dom/= R
II. Rango de f : Ran/= Z
III. Redefinimos la función
/rw = M = 0 <-> 0 < x < l
-1 <-> - l < x < 0
- 2 *-> -2 < x < -\
f(x )~
- 3 <-> - 3 < x < - 2
-3 ;
-3 < 2 x -l< -2
- 2;
- 2 < 2x - l < - l
- 1;
- l < 2x - l <0
0;
0 < 2x - l < l
1;
l< 2x - l <2
2;
2 < 2 * - l< 3
Vemos que queda definida com o la unión de
funciones constantes, cuya gráfica es
Equivalentemente
-3;
- 2;
- 1;
-3
-2
-1
- l< x < —
2
-<x<0
0<x<-
2
0;
-< x < l
2
1;
l< x < -
2
-<x<2
268
Funciones
CAPÍTULO IV
IV. Graficamos la función f.
r
2
1
-
1
-1
2
1
1
2
-1
2
3
2
-2
-3
2.
Esboce la gráfica de la función f:
III. Graficamos la función f.
Y
2 -----------------
Resolución
I.
v 3 ----------------- —
Dominio de f
f{x)
^
\!'¿
eR
—
M >0
<-> x >0
1
2
-I----- 1----- 13 4 5 X
II. Redefinimos la función
3.
Esboce la gráfica de f : ^ )-| '/ 2 -3 x J.
0 <-> xe[0; l)
1o
xe[l; 2)
Resolución
I.
V2 <-> xe[2; 3}
f(x)~
V3 <-> xe[3; 4)
2 <-> xe[4 ; 5>
Su dominio
íy e R
<-> 2 - 3 x > 0
II. Como [V 2 -3 x ]= n
<-> n < V 2 -3 x < n + 1
pues V2 - 3 x > 0.
269
Lumbreras Editores
Redefinimos la función
A continuación indicamos algunas propiedades
complementarias del máximo entero.
f( x ) -
0
0 < V 2 -3 x < l
1
l< V 2 -3 x < 2
2
2<\l2-3x <3
3
3 < j2 - 3 x < 4
4
4 < V 2 -3 x < 5
Resolviendo las desigualdades, tenemos:
0
xe
3’ 3
2
3
1
; 3
x e { - 7- ; - 2' 3
3.
o
/ 14
7
3 * e ----- —
' 3 3
4
|[xl+[y]+l
2.
I-x l =
■[xl,
si x e¿
• lxl-1, si xeZ
3.
[l-x ] = l+
4.
Si [x l - [y] = 1 -» 0 < x - y < 2
5.
[2 x l= [x ]+ | x + -
6.
[3x]=Ixl+||x+-||+ x + 3
7.
| 4x]=[xl+ x + —
4
I-x ]
2]
l\
xg( —
2
)ILxJI+[yJ
1 . [x + y ]=
/ 23
14
x e ( ----- ; -----3
3
2
" Irr!
Función potencial general
Es aquella función definida en R + y cuya regla
de correspondencia es
f^x'j =xn; x > 0, donde n e R.
Su gráfica depende del valor de n.
III. Graficamos la función f.
— i—
-23
3
-14
3
-7
3
y=xn, x > 0
270
a
ne R
Funciones
CAPÍTULO IV
FUNCIONES ESPECIALES
Funciones acotadas
En una función f creciente en
Una función es acotada cuando el valor absoluto
[a; b\, el rango es [ha)’ hti]-
de la función es menor que cierto número real
fijo, para cualquier valor de la variable. Es decir,
f es acotada si existe un número real M > 0 tal
que |/(x)| <M Vx e Domf/). M se llama cota de
la función.
Funciones decrecientes
Una función/es decreciente en [a; b ] si para todo
x ,, x 2 6 [a; £>], con x, < x 2, se cumple
> f^ y
Gráficamente
Gráficamente
Corolario
Equivalentemente:
f es acotada si existen c; d e R tal que
En una función /'decreciente en
V x e Dom f:c < f{x) < d.
[a; b\, el rango es [/’(í)); Z^].
Funciones crecientes
Una función f es creciente en [a; b] si para todo
Funciones periódicas
x h x2 e La; £>], con x, < x 2, se cumple
Se dice que una función f, con dominio Dom(/),
Gráficamente
< f^ y
es periódica si existe un número 7V 0, tal que
para todo x 6 Üom(/) —> {T+x) e Dom(/) se
cumple f(x+T)~hx)' v x e Dom(Y).
Al menor valor real positivo de T se le llama pe­
riodo de la función f.
Gráficamente
V x ,;x 2e [ a ; b ] : x j < x 2 -> ^ 1) < /'(x2)
271
Lumbreras Editores
Función par
Función univalente
Una función f es univalente, inyectiva o uno a
Una función f es par
si V x e Domt/), - x e Dom(/) y f(_x)=f(x)
La gráfica de f e s simétrica con respecto al eje Y.
uno, si para todo par de elementos distintos del
dominio, sus imágenes son distintas.
Es d e c ir le s inyectiva si:
V x ,x 2 e Dom(/>. x , * x 2
Equivalentemente
X
V x ,x 2 e DomC/): f(x])=f(x¿ - * x ,= x 2
Ejemplo
f (x]= 2 1x |+x2 es una función par.
Ejemplos
1. Analice si la función /(r)= 3 x - 1 es inyectiva.
En efecto:
Dom/=R; por lo tanto, si x e Dom/-
Resolución
entonces - x e DomA
SeanX], x 2 e Dom (A)
Si
También:
f ( - x ) = 2 1- x | + ( - x ) 2 = 2 | x |
+x2= f(x)
De esto se concluye que, f e s una función par.
3 x , - 1 = 3 x 2- 1
f {xx) = f {x2)
—^ 3X] = 3xj —^ X] —%2
Por lo tanto, f es inyectiva.
2. Analice si la función g w = x 2+ x - l inyectiva
Función im par
Una función es impar
Resolución
si x, - x e Dom(7) y f{ - x ) = - fíx) V x e DomC/).
Sean x b x 2 e Dom(/)
Ejemplo
Si
f ^ = 5 +[ |es una func'ón impar
—>
% l)
x
,2 -
% 2)
x
| = x 2-
x
,
-» (xj + x 2) ( x j—x 2) + (xj —x 2) =0
En efecto:
—> (x 1- x 2)(x ] + x 2+ l )=0
Dom /= R; por lo tanto,
si x
Dom/' entonces - x
e
6
Dom/'.
Por lo tanto, g no es inyectiva.
También:
r
=
~x
(- x) 5+|-x|
= ___í _ = _ f
5+|x|
w
De esto se concluye q u e d e s una función impar.
272
— > X ] = X 2 v X j + X 2= - 1
Nótese además que, la función f>M= x + x - l no
es inyectiva, pues
i ) = - l . Luego, hay dos
elementos en el dominio con la misma imagen.
CAPÍTULO IV
3.
Funciones
Pruebe que
vte4
f(x)~ <
c x+
^ ; ad ^ b c es inyectiva
!
Prueba
En f(r\=- X-+~ , fíjese que la condición a d * b c
cx+ d
f es inyectiva
es fundamental para analizar la inyectividad
de f.
Sean x x,x 2 e Dom(/'), entonces
t
W
_t
(*2) ^
ax\+b ax2+b
~ ^ d~ 7^ d
—> apxpc^ + adxx+bcx2 + b d =
= a£xpo¿ +bcxi +adx2 + bd
Función suryectiva
Es llamada también función suprayectiva, sobreyectiva o epiyectiva.
f . A ^ B e s suryectiva si el rango coincide con el
conjunto de llegada.
Es decir, Vy e B existe x e /t(Dom(/))
tal que y=f(xy
—» (ad-bc')xl + ( b c -a d )x 2=0
—> ( a d - b c )( x ] - x 2) = 0; com o a d * b c
—» x ]- x 2=0 —> x ,= x 2
Por lo tanto, f es inyectiva
INTERPRETACIÓN GEOMÉTRICA
Gráficamente, se dice que una función f es in­
yectiva si toda recta paralela al eje X corta a la
gráfica de la función en un solo punto.
Ejemplos
1.
S e a [0; 1 ] —> [-1; 0] tal que/'M = x2- l
¿ fe s suryectiva?
Resolución
Como 0 < x < l
—> 0 < jc2< 1
-4 -1 <x2- l <0
-> - 1</M<0
Luego el rango de f e s [-1; 0] y coincide con
el conjunto de llegada.
g no es inyectiva
.-. f es suryectiva.
273
Lumbreras Editores
2. S e a / :R
'W
Se observa fácilmente que f es inyectiva,
—» R, tal que:
2x
pues las reglas de correspondencia son li­
x 2+\
neales y adem ás f es suryectiva. Como la
¿podemos afirmar que f e s suryectiva?
primera regla de correspondencia /¡(n)=^
Resolución
genera a los Z+ y la segunda regla de corres­
Como Dom/= R, entonces y=
2x
x 2+ \
xe R
-> yx2-2x+ y= 0; x e R
tenemos una ecuación cuadrática con
pondencia /*>(n)=—
genera a los Z0, luego
el rango de f es Z.
.-. f es biyectiva.
raíces reales.
—> A = 4 -4 y 2>0
-»
y2< l
|y |< 1 -> - l < y < l
Luego el rango de f es [-1; 1] y no coincide
con el conjunto de llegada
.-. f no es suryectiva.
FUNCIONES TRIGONOMÉTRICAS
Son llamadas también funciones no algebraicas
o trascendentes del tipo trigonométrico.
Las funciones trigonométricas se definen de la
siguiente manera:
Considere una circunferencia de radio r con
centro en el origen
Función biyectiva
Una función f : A —>B es biyectiva si es inyectiva
y suryectiva a la vez.
Ejemplos
1.
Sea/: A —>B tal que:
x y x y Y
y las razones —; —; —; —;
r
f es suryectiva e inyectiva, por lo tanto f es
biyectiva.
2. Sea /: N —>Z tal que:
n
2
f(n)=
274
1-/7
~2~
; npar
; n impar
r
y x
y
Y
, donde x e y
x
son las coordenadas de un punto P sobre la cir­
cunferencia.
A medida que el punto P recorre la circunferen­
cia, el ángulo 0 (medido en radianes y formado
por el radio de la circunferencia y el eje X), varía.
Se puede asociar a cada valor del ángulo un va­
lor para cada uno de las razones mencionadas.
Estas relaciones son las funciones circulares o
trigonométricas.
CAPITULO IV
Funciones
y
• se n 0 = —: seno del ángulo 0
r
co s 0 = — : coseno del ángulo I
►
►Recuerde
sen 20+cos 20=l
En efecto:
r
tan 0 = —: tangente del ángulo I
de
x
• c o t 0 = —: cotangente del ángulo 0
se tiene a2+ b2=c2
f
Como
r
a= —
a a co s a
b
sen 0
0= —
c
c
• s e c 0 = —: secante del ángulo 0
x
• c s c 0 = —: cosecante del ángulo 0
y
—> sen 0 + eos 0 = ^ r+ —5<r c¿
2
2q a 2+b2 c 2
sen 0 + eos 0 = — — = - 5-= 1
Observe que cuando el punto P ha recorrido
cl
toda la circunferencia, se llega a una situación
idéntica a la inicial.
c
También
Si consideramos el radio 1, a la circunferencia se
l+ cot 20= csc 20
le llama circunferencia trigonométrica.
l+tan 20=sec 20
Como
y
sen 0= — —> y = sen 0
1
x
COS0 = — —> X=COS0
Función seno
Es una función denotada por sen, cuyo dominio
es el conjunto R y su regla de correspondencia es
y=/'M=senx.
En el plano cartesiano se tiene
Luego
/= {(*; y)/y=senx, x e R }
Dom(/) = R
a
R a n (/ )= [-l; 1]
Algunos valores particulares de la función seno
son
AB = sen0; DC = tan0; OC= sec0
X
0
seruc
0
OA = cos0; EF = cot0; OF= csc0
Estudiaremos el comportamiento geométrico de
cada una de estas funciones.
71
6
1
2
71
4
71
71
3
2
V2
V3
2
2
1
275
Lumbreras Editores
Su gráfica es:
Su gráfica es:
Observamos que después de que x ha recorrido
2n, se repiten las características. En este caso,
se dirá que el seno es una función periódica de
periodo 2n, es decir:
senx=sen(x+27t)=sen(x+4ji)=... =sen(x+2*7t)
La función coseno es una función periódica de
periodo 2n.
Observe que el dominio de f es R, el rango de
f [ - 1 ; 1 ], y la gráfica no pasa por el origen, pues
cosO =l.
Luego decimos que:
Función tangente
El dominio de f es el conjunto de los números
Es una función denotada por tan, cuyo do­
reales: R, el rango de f e s [-1; 1], y la gráfica pasa
minio es el conjunto R “m enos” el conjunto
por el origen.
j(2 6 + l)^ ,
fcezj. Su regla de correspondencia
es /'(x)=tanx.
Función coseno
Es una función denotada por eos, cuyo dominio
es el conjunto R y su regla de correspondencia es
Luego
/-*------------ l—
y=f(x)=cosx.
V
^={(x; y) /y=tanx, x e D o m (0 }
______________ J
/7= {(x ;y )/ y = co sx , x e R }
con Dom(/,)=R-|(2/?+l)^ j £ e z j.
Luego
Su gráfica es:
D o m (0 = R
Ran(/) = [ - l; 1]
a
Algunos valores particulares de la función cose­
no son
71
X
cosx
276
0
6
1 T
71
4
n
\Í2
1
2
2
3
n
2
...
0
...
CAPÍTULO IV
Funciones
La función tangente es una función periódica de
periodo 71.
Observe que la tangente no está definida en los
puntos
71 371 571
2’T ’T ’
71
371
571
T ~ T ’~T’
Función secante
Es una función denotada por sec, cuyo do­
minio es el conjunto R “m enos” el conjunto
(2/e+l)^ ^/fcezj- Su regla de correspondencia
es f^ = se c x .
Luego
Función cotangente
Es una función denotada por cot, cuyo dominio
f={{x\y) / y = secx, x e Dom/}
es el conjunto R “m enos” el conjunto {kn; k e Z } .
Su regla de correspondencia es fU) =cotx.
Luego
con D o m / = R -U 2 £ + l)“ j k e Z
f = { O; y) /y=cotx, x g Dom/}
con Dom/7= R - { * t i / k e l}\ además
cotx=
1
tanx^O.
tanx
además s e c x = cosx^O.
eos x
De la definición vemos que la secante no está
definida en los puntos
71 371 571
2’T ’T
Su gráfica es
71
371
571
Su gráfica es
La función cotangente es una función periódica
de periodo n.
Observe que el dominio e s R - { k n , k e Z},
es decir, no está definido en los puntos
y su rango es
-1 ] u [ 1; +°°).
0, 71, 271, 371, ...
La función secante es una función periódica de
—71, -271, -371, ...
periodo 2tl
277
Lumbreras Editores
Función cosecante
3.
1+ cot x = c s c x
Es una función denotada por ese, cuyo dominio
4.
s e n x c s c x = l, x e R - { n n } ; n e Z
5.
c o s x -s e c x = l, x e R -(2 n + l ) —; n e i
6.
ta n x c o tx = l, x e R - ^ n ; n e Z
7.
sen(x ± y )= serixeosy ± cosxseny
8.
eos (x ± y) = cosxcosy T senxse nv
9.
sen2x=2senxcosx
Luego
/ = {(x ;y )/ y = cscx , x e Dom/}
71
con Dom f=R -{ttn /keZ }-,
10. cos2x= cos2x - s e n 2x
adem ás cscx=
11. c o sx -co sy = -2 s e n
senx^O.
•
0, n, 2n, 3n, 4n , ...
•
- 7 1 ,- 2 7 1 ,- 3 7 1 ,...
Su gráfica es
13. senx+seny = 2sen
14. tan(x+y) =
eos
l 2 J
eos
2 J1
2
1
12. cosx+cosy = 2cos
ción no está definida en los puntos
( x -y
" M
X
De la definición de cosecante, vemos que la fun­
x+ y'^1
~~2
\
^
Su regla de correspondencia es /M = cscx:
*
1
lv-
es el conjunto R “m enos” el conjunto {kn /keZ }.
V 2 J
tanx+tany
-ta n xta n y
Ejemplos
1.
Halle el rango de la función
f(x) =sen 3x+cos3x.
Resolución
Partimos de la identidad: sen23x + co s23x= 1
Sumamos m.a.m. 2sen3xcos3x
sen23x+ 2sen3xcos3x+ cos23x=
= 1 +2sen3xcos3x
—> (sen3x+ cos3x)2= l+ s e n 6 x
y su rango es (-°°; -1 ] u [ 1; +<»).
La función cosecante es una función periódica
Sabemos que: -l< s e n 6 x < l
de periodo 2 ti.
—> 0 < l+ s e n 6 x < 2
Identidades trigonom étricas
A continuación mencionamos algunas identida­
des trigonométricas.
—> 0 < (sen 3x+ co s3x)2<2
—> -V 2 < se n 3 x + c o s3 x < V 2
- * -y ¡2< f{x)< 42
1.
sen2x + c o s 2x = l
R an(/)=[-V 2; V2 ]
278
CAPÍTULO IV
2.
Funciones
¿Es periódica la función /?M=5cos7xsen7x+9?
Ejemplo
En caso afirmativo, ¿cuál es su periodo?
Esboce la gráfica de las funciones siguientes:
Resolución
a.
Por definición de función periódica,
es
periódica si existe un T e R tal que f(x+T)=f(xy
Si Aí(x)=5cos7xsen7x+9
b- S (x )= x '
+4x+4
c- ftw = ^ i
h (x+T) = 5cos(7x+ 771sen (7x+ 77}+ 9
Resolución
Luego
a.
5cos(7x+ 77*)sen(7x+770+ 9=
=5cos7xsen7x+9
0)
Si
Si /(x)=V x
S(x)=^ x - =
Luego
x = 0 —> cos77’sen77’=0
—» 2cos77sen77'=0
-> sen l47’=0 ^
\ 4 T = k n ;k e Z +
n n 3n
-> T=14 7
14
El menor valor de T que verifica (I) es
Por lo tanto, su periodo es
Nótese que la gráfica se desplazó cinco uni­
dades hacia la derecha.
PROPIEDADES SOBRE GRAFICAS DE
FUNCIONES
b. g (x)= (x + 2 )2
Existen algunos criterios para obtener de m ane­
ra fácil y rápida las gráficas de algunas funciones
relacionadas con una función elemental dada
Note que si/'M = x 2 —> g(x)=/:(x+2j= ( x + 2 )2
Luego
y = f(x). Veamos algunos criterios.
Desplazamientos
D esp lazam ien to horizontal
Se utiliza para graficar f(x±k) partiendo de f(xj, así
k >0
(x+ k)
'(.x)
\ x -k)
Nótese que la gráfica se desplazó dos unida­
-k
des hacia la izquierda.
279
Lumbreras Editores
c. h M =
Ejemplo
x+\
Esboce la gráfica de las funciones siguientes:
Note que si fix) =
h.íx ) “
'(*+ !)
x+1
a. / ^ = 3a-+2
b. g w = x 2- 3
Luego
c- h M = \ x \ - j 2
Resolución
a. f(xi=3x+2
Graficamos y=3x y luego lo desplazamos
dos unidades hacia arriba.
Luego
►
►Conclusión
f
nos indica el desplazamiento de la grá­
fica de /hacia la derecha en tres unidades y
f(x+S) nos indica el desplazamiento de la grá­
fica de /hacia la izquierda en tres unidades.
Desplazamiento vertical
£>> 0
Y
'(x)
1 *
'u r
Lb
í
280
X
b-
S ( x ) = *
~3
Graficamos y=x2 y luego lo desplazamos ha­
cia abajo 3 unidades.
Luego
Funciones
CAPÍTULO IV
Resolución
c. h w =\x\-y¡2
Graficamos y=|x| y luego lo desplazamos
a. fM= - J 2 x - l
Graficamos y=sl 2 x - l y luego se refleja con
hacia abajo en V2.
respecto al eje X.
Luego
Luego
b- £ ( ,) = - 1*-1|
Graficamosy= |x-l |y luego se traza lo sim é­
trico con respecto al eje X.
Reflejos
Reflejo en el eje X
Para graficar ~f(x) a partir de
la gráfica de f lo
reflejamos con respecto al eje X; es decir, el eje
X tiene el comportamiento de un espejo.
Reflejo en el eje Y
Para graficar f{_x) a partir de f(xp la gráfica de f lo
reflejamos con respecto al eje Y; es decir, el eje
Y tiene el comportamiento de un espejo.
Nótese que, las gráficas de
y
son simétri­
cas con respecto al eje X.
Ejemplo
Esboce la gráfica de las siguientes funciones.
a-
Nótese que las gráficas de
b- g M =-|JC-l|
cos con respecto al eje Y.
y
son simétri­
281
Lumbreras Editores
Ejemplo
Resolución
Esboce la gráfica de las siguientes funciones.
a. fM= 5 (x -1 )2
a. f(x)= ~ 2x + l
Primero se grafica y = ( x - l ) 2 y luego la
b. g M = V -J c+2
gráfica de
= 5 ( x - l ) 2 se comprime ha­
cia el eje Y.
Resolución
el.
Luego
f( x ) = —2-^ “í" 1
b. g M= s F x + 2
b - SM= ^ yfx + 2
Primero se grafica y=\¡x + 2 y luego la
gráfica de g(x)=^%/x+2 se comprime
hacia el eje X
Luego
Dilatación ■Compresión
1.
Grafique a -f^ a partir de
o £ R +. Tene­
mos dos casos:
•
Si o > 1 se dilata verticalmente.
•
Si 0 < o < 1 se comprime verticalmente.
Ejemplo
Esboce las gráficas de las siguientes funcio­
nes.
a. fM= 5 ( x - l ) 2
b- g (x)= ^ V í+ 2
282
2.
Grafique /(ax) a partir de f(x>. Tenemos dos
casos:
•
Si a > 1 se comprime horizontalmente.
•
Si O< a < 1 se dilata horizontalmente.
Funciones
CAPÍTULO IV
Ejemplo
Ejemplo
Esboce las gráficas de las siguientes funciones.
Esboce la gráfica de la función /(x)= 15 x -2 \.
a.
5x + l
Resolución
b. g w = s e n |
Resolución
a. /’(X)=5x+1
Para graficar /(jx|) a partir de /(x).
Tenemos en cuenta lo siguiente:
Como/(|_x|)=/(jx|), se ve que /qx|) es una fun­
ción par, por lo cual solo se requiere la gráfica
parax>() ya que p arax< () será solo un reflejo
de f(x¡ en el eje Y.
b. g(x)= sen —
f(x) ~ \
k-x»; x < °
Ejemplo
Sea /(x)= ( x - l ) ( x - 2 ) ( x - 3 ) , esboce la gráfica
de/'(|x|).
Resolución
Para la función /Cx)= ( x - l ) ( x - 2 ) ( x - 3 ) , basta
graflcarla para x > 0 y luego se refleja en la
Valor absoluto
1.
Para graficar |f(x) | a partir de
reflejamos
parte negativa del eje Y.
la parte negativa de la gráfica de /'con respec­
to al eje X.
283
Lumbreras Editores
►A l g e b r a
UNION DE FUNCIONES
d e f u n c io n e s
Es el conjunto de relaciones u operaciones entre
Una función f: Dom/ —> R se puede considerar
dos o más funciones bien definidas.
como una unión de funciones: f h f2, f 3, ..., fn cuan­
do está definida por tramos.
IGUALDAD DE FUNCIONES
Dos funciones fy g son iguales si tienen el mismo
Es decir:
dominio y la misma regla de correspondencia, es
decir
\x )
xeD om (/¡)
h {xy xeDom(/2)
I.
f=g<^>
Dom(/')=DomCg)
H- f(x)=S(x)
v
f(x)~
%cY x e D o m (fi)
.................
Ejemplos
fnixy x e D o m (fn
X
1. Analice si las funciones f,r) = — ; x e R - { 0 } y
w |x|
g M=sgn(x); x^O son iguales:
Donde:
Resolución
de dominios f¡ dos a dos son disjuntos.
La unión de dominios f¡ es Dom/y la intersección
Redefinimos cada una de las funciones
Gráficamente
x>0
1;
-> f,(x)-
k x )~
; x<0
gw =sgn(x)=
fl;
x>0
x>0
1; x < 0
; x *0
[-1; x < 0
Como D om (0=D om (g)
f (x)=g(x)
a
Se concluye que f=g
2. Analice si las funciones f(x)='¡~¡? y S(x)=x
Ran(/) = Ran(/',) u R a n ^ ) u Ran(f3) u R a n ^ )
son iguales:
Resolución
Por ejemplo, la función f está definida por tra­
Note que:
mos
/(;c)=lxl=
[x;
x>0
!
a
g w =x;
(-x ; x < 0
—> Dom/=R
a
D om g = R
Pero fM* g M -> f* g .
284
Dom(/')=Dom(/1) u D om ^ ) u Dom(/3) u Dorn^,)
x g R
l+ se n x
k x )~ 2 x - l
x 2- 4 x
; x<0
; 0<x<5
; x>5
Funciones
CAPÍTULO IV
Resolución
Ejemplos
1.
Graficando cada una de las funciones en sus
Grafique la función f.
respectivos dominios
- 2 x + l;
x e ( - l ; 2>
n/x
- 2;
x e [2 ; 3)
x 2 - l 1;
x s [ 3 ; 4)
S im = x + 1 ; - 2 < x < -i
g 2 M = i- * 2; - i < * < o
g 3 M = ' ñ -x ; o < x < i
S 4 M = *3- 5 ; 1 < x < 2
Resolución
Graficando cada una de las funciones en sus
respectivos dominios.
fi(x) = ~ 2 x + 1; -1 < x < 2
/2(x) =V x - 2; 2 < x < 3
-11; 3 < x < 4
rm =
ADICIÓN DE FUNCIONES
Dadas las funciones f y g con sus respectivos do­
minios, la función suma f+ g se define así:
I.
Dom(/'+g)=Dom(/r)riDom(g)^(|
II. (^+g)fa)=^(x)+g(x)
2.
Grafique la función g.
x + 1 ; x e ( -2 ; -1]
1 - x 2; x e ( - l ; 0)
De la definición se deduce que: f+ g = g + f
Ejemplos
1.
Dadas las funciones
H ( 3 ; 4 ) , (2; 1), (-3 ; 7 ) ,( 1 ;0 ) }
Vi—x ; xe[0; 1)
x
3-5 ;
x e (l; 2]
g = {(3; 2), (5; 1), (0; 3), (2; 4)}
halle la función f+ g .
285
Lumbreras Editores
Resolución
Sean
Sabemos que los dominios respectivos son
Dom(/)={3; 2; -3 ; 1} a Dom(g)={3; 5; 0; 2}
í/lw = 3x+ l; x e (-2; 1)
f(x)~
—> Dom(/'+g)=Dom(/') n DomCg) = {3; 2}
|^2W = V x -2 x + 5 ; x e[l; 4)
3\(r\
= x 2 +5x; x e ( -7 ; 0]
'( x ) ‘
Sus imágenes:
S(x) =
;
g2(x) = 7
( / + 5 ) (3)= ■^(3) + 5 ( 3 ) = 4 + 2 = 6
x e
(0 ; 3)
^+5)(2)= ^(2)+5(2)= 1 + 4 = 5
f + g = {(3 ; 6), (2; 5)}
►
►Tenga en cuenta
(f¡ + g¡)(lí) está definido si y solo si
2.
Dadas las funciones
Dom(Q n DomQj,) * <j>
f(x)=x3- 5 x + l; i e { - 4 ; 2 ]
5(x)=3^+7; x e (0; 7),
Luego
halle la función f+ g .
/i ( x ) + g l (x) : x e ( ~ 2 ’
Resolución
•
A(x)+ s2(x); x e <-2; i>^(0; 3)
Dom(/'+g)=Dom(/') n Dom(g)
(f+s\x)=
f2(x)+ S ] (x) '
Dom(/7+g)= <-4; 2 ]n (0 ; 7>=<0; 2]
*
°í
X e f1: 4'>n ( '~ 7’ °1
h (x)+ S 2W ; xe[\; 4>n(0; 3)
(f +5)(x)= ^(x)+5(x)= (-!í:3_5 x + i) + (3a'+7)
(f+ g )M=x3-2x+ 8, x e (0; 2]
3.
^+í)(x) -
Dadas las funciones
\3x+\
; x e (-2 ; 1)
|\/x-2x+5
;x
(3x+l)+7
;x e (-2 ; l)n(0; 3)
( a/x - 2
;xe[l;
4 ) n ( - 7 ; 0]
;xe[l;
4 )n (0 ;
x 2+5x
|7
;
x e
; xe(0; 3)
(f+ s\xr
x
('+ «)(*) =
xe
(-2; 0]
xe
(0; 1}
X 2 + 3 x +%/x + 5 ; XE<)) —> n o s e toma
en cuenta
\ / x -2 x + 1 2 ;
Antes de resolver el ejercicio, veamos el es­
quema que nos ayudará a resolver este tipo
2 + 8 x +1;
3x+8;
( - 7 ; 0]
Resolución
286
3)
; x e[l; 4)
halle la función f+ g .
de problemas.
+ 5 ) + x 2+ 5 x
V x-2x+5+7
x
S(x)~
x
s
{-2 ;
l)n{-7; 0]
( 3 x + 1 )+ (x 2 + 5 x )
2 + 8x +1;
x e
[1; 3 )
x e ( - 2 ; 0]
3x+8;
x e
( 0 ; 1)
%/x-2x+12;
x e
[1;
3)
Funciones
CAPÍTULO IV
Graficamos f u f2 y f.
La gráfica de la función suma
Sean f y g dos funciones con sus respectivos do­
minios.
De la definición de la adición de funciones: f+ g
1. Dom(/'+g)=Dom(/')nDom(g)
II- (.f+S\x')=k x )+S(_x')
Vemos que f+g está definido solo si:
D om (0 n Dom(g) * 0
Si conocem os los gráficos de f y g, entonces se
puede graficar f+g\ para ello se suman las imá­
Como se observa, el rango de /=/, +f2 es (2; 6].
genes respectivas.
2.
Halle el rango de la función
Graficando se tiene
= \l2x-\ + sl5-2x.
Resolución
Sean
f,
=yj2x-\\ 2 x - l >0
f2 =n/5-2x; 5 -2 x > 0
(x)
Graficamos cada una de las funciones
f u =n/2*-1; x>1/2
*(-*•)
fn = s l5 -2 x ; x<5/2
to
Ejemplos
1. Grafique la función
f^ = x+ \ íx, con x e ( l ; 4 ] .
Resolución
Si f {x)= f\ {x )+ f 2(xy c o n x e < l ; 4 ]
Lumbreras Editores
SUSTRACCIÓN DE FUNCIONES
como:
Dadas las funciones f y g con sus respectivos do­
[x 2 - 3
minios, se define la función diferencia f - g , así:
f(x ) —
D om (/-g)= Dom(/) n DomCg)
I.
x
x e ( -5 ;
+ 1;
•Jx+2+x; x e [ - l;
-1 )
3)
-1; x< 0
H- V - 8 )(x)=f(*)- 8 (x)
g (x )~
0;
x= 0
1;
x>0
Ejemplos
(x 2 - 3
1. Sean las funciones
/'(x)= x3-5 x + 7 ; x e (-4 ; 2]
x
+ 1 )-(-1 );
x e ( -5 ;
-1 )
( V x + 2 + x j- ( - l ) ; x e ( - l ; 0)
g(x)= 2x2+ 7 x -9 ; x e ( - 3 ;jx ]
(f ~ g \ x ) =
Halle la función {f-g ).
V x + 2 + x -0 ;
x=0
V x + 2 + x - l;
x e (0 ;
3)
Resolución
1.
D om (/-g)=Dom (/)nDorn(ij)
Por lo tanto:
D om (/-g)=x e (-4 ; 2] n ( - 3 ; jt]
x
2-3
x
+2;
x e (-5 ;
-1 )
—> D om (/-g)=x e (-3 ; 2]
^ ■ ^ f~ g \ x )
(f -8)<x) =
h x ) ~ g (x)
V x + 2 + x + l; x e ( - l ; 0)
V 2; x = 0
(f - g )M = (x3- 5x+ 7) - (2x2+ 7x - 9)
\ / x+ 2 + x -l; x e (0 ;
-> ( f-g ) M=x 3 - 2 x 2 -\ 2 x + \ 6
(/:- g ) M = x 3-2 x 2-1 2 x + 1 6 ; x e ( - 3 ; 2 ]
3)
MULTIPLICACION-DIVISION DE FUNCIONES
Dadas las funciones f y g con sus respectivos do­
2.
Dadas las funciones
lx 2-3 x + l; x e ( -5 ; -1)
minios, se definen las funciones producto y co ­
ciente, respectivamente, f-g] f/g , así
[V x+ 2+x; x e [ - l; 3)
gM =sgn(x),
halle la función {f-g ).
I. Dom(/-g)=Dom(/)nDom(g)
f-g-
Resolución
Recuerde que
(f-g ) está definido si:
Dom(y) n Dom(g) *<j
288
H. ( f -g)(x)= f(x)'g[x)
I. Dom(/7g)=Dom(0i~iDom(g)AgM* 0
f/g:
-1
S J(x )
_ f{x)
&(x)
CAPÍTULO IV
Funciones
Ejemplos
Resolución
1.
•
Dadas las funciones
A={(3; 5), (-2; 3), (7; 0), (4; 3), (0; 5)}
Hallamos la función f-g
Dom(/-ij) = Dom(/) n Dom (g)=x e (-2 ; 3)
á?= {(-5; 3), (- 2 ; 1), (2; 9), (4; 0), (0; 7)},
(jc2 —5)(jc2 —3)(j«r+1); x e (-2 ; 1)
halle
a. f-g
b. f/g
(fs\x)=
(x+ 7)(x2 -3 ) (x + l); j<re[l; 3)
Resolución
a.
•
Hallamos la función —
8
Dom(/-g)=Dom(/') n Dom(t>) = { - 2 ; 4; 0}
{ f ' S)(_a = k-2) ’S(-2) = 3 ’1= 3
D o m í^ j = D om (0 n (Domfe) A g íO )
f g = < ( f - g \ 4)=f(4)-8(4)=3 0 = °
(^ g)(o) =^(o) S(o) =5-7=35
Nótese que:
g M = 0 <-> (x2- 3 ) ( * + 1) = 0
f g = { (- 2 ; 3), (4; 0), (0; 35)}
<-» x = y¡3 v x = —1n/3 v X = —1
b. Dom(//g)=Dom(/')i^Dom(g) AgM * 0 ) =
D o m í^ j = (-2; 3 )- {V 3 ;- V 3 ;- l}
= { - 2; 0}
8
A- 2) 8 (- 2 )
(x 2-3)( x +1)
S kx)
-)
- ^(0) - 5
8 J(o) 8 (0) 7
r P 3X(0;f
2.
Dadas las funciones
x + 7 ; x e[l; 3)
g(x)=(Jf2- 3 ) ( x + l ) ; x e R,
[i; 3 > - { V 3 }
POTENCIACION DE FUNCIONES
Sea f una función bien definida, f n indica la ené­
sima potencia de f, y se define así:
x 2- 5 ; x e ( - 2 ; 1)
k x )~
x+7
(x 2-3)( x +1)
x e <-2; —1)—{—1; —J í }
kx)<
si n= 1
p w ]";
s in ^ 2
fn =
(x)
En cualquier caso:
halle las funciones f-g y
Dom(/") = Dom(0.
289
Lumbreras Editores
Ejemplos
1.
3.
Sean fy g funciones reales tales que
Dada la función
fM=2x + 1 y g = {(-1 ; 2), (3; 6), (2; -4 ), (0; 7)}
/= { C1; 2), (2; 3), (3; -2 ) , (-2 ; 1)} se tiene:
calcule:
Dom(/7) = { l ; 2; 3; - 2 } , entonces
a.
^(i)= ^(i)'^(i)= 2 '2 = 4 —> ( l ; 4 ) e / '2
b- (2g2-0 (o )
f(W (2 )'f(2 )= 3 -3 = 9
(2; 9) e f 2
Z7(3) ( 3)" ^(3)= C—2) - (—2) = 4 —> (3; 4) e f l
( f 2 + 3g)(_|)
Resolución
a.
(/f 2 + 3g)(_|) = f\_i) + 3g(_,)
^(-2)= ^(-2)'^(-2) = 0 ) ' Cl) = 1 —> (-2 ; 1) 6 f 2
Luego: f 2={(\\ 4), (2; 9), (3; 4), (- 2 ; 1)}
2.
= (-1 )2 + 3(2) = 7
b.
(2 g 2 - f \ 0) = 2 g
= 2• (7)2- 1 = 97
Dadas las funciones
f= {(3; 5), (-2; 3), (7; 0), (4; 3), (0; 5)}
g = { ( - 5 ; 3), (-2; 1 ),( 2 ;9 ),(4 ; 0), (0; 7)}
halle: f 2 - g 2.
COMPOSICIÓN DE FUNCIONES
Si f y g son dos funciones en sus dominios res­
pectivos, se define la composición de funciones,
denotada por f°g, y leída com o “f compuesta
con g ”, así:
Resolución
•
Dominio
1.
Dom(/2- g 2) = Dom(/2) n Dom(g2)
Dom/°g={x/xe Dom(g)Agw e Dom(/')}
11
—> Dom(/2- g 2) =Dom(/') n Dom(g)
-> Dom(/2- g 2) = {-2 ; 4; 0}
•
Cálculo de imágenes
Dadas las funciones reales f, g.
f
8
( f 2 ~8 2)(-2) = rf- 2) S ( - 2) = 32- 1 2 = 8
= f (4)~8 (4) = 32- 0 2 = 9
( f 2 _g2)(o)= ^(0) _Sco)= 52- 72 = - 24
A2- g 2= {( -2 ; 8), (4; 9), (0; -2 4 ) }
►
►Tenga en cuenta
Si a e R entonces la función a f se
define así:
a/'=|(x; af(x))/x e Dom/}
290
Si existe un elemento en el dominio de
g (x e Dom(g)) con la característica de que
g (x) e Dom(f), la cantidad
^ existe.
CAPÍTULO IV
Funciones
Reunimos todos los valores x con la propiedad
En (a)
Ran(g) n Dom(/) *
—> Dom(/°g)=[l;
4 )n
i;
i;
II. (/Fog)(x)=/(gw)= ( 5 - 3 x ) 2- 2 ( 5 - 3 x ) + 3
-» (/°g)(x)=9x2-2 4 x + 1 8
V °S)od= 9x2-2 4 x + 1 8 ; x e 1; |
b. Hallamos g °f\
I.
Podemos construir una nueva función h, tal que:
h:D om g —> Ran/, co n ftM =/'p( ^
Dom(g o f)= {x e Dom(/) a
a/w e Dom(g)}
x6
( - 3 ; 2]
a
(p)
1 < x 2- 2 x + 3 < 4
Como vemos
1 <x2- 2 x + 3 < 4 -> - 1 < x 2- 2 x +1 < 2
-> ( x - 1 ) 2 < 2 -> -\Í2 < x-\ < \ ¡ 2
Dom(/¡)={x/íE Dom(g)Agw e Dom(/)}
—> 1 -V 2 < x< l+ V 2
Entonces a h se le denomina composición de f
En (p):
con g.
DomCgo/-)=(-3; 2 ]n (i-V 2 ; I+V 2 )
Ejemplos
-> DomCgo/')=(l-%/2; 2 ¡
1. Sean las funciones
f^ = x 2 - 2x+ 3; x e { - 3 ;2 | ;
H- (S 0 ^) (x ) =S (/(x))= 5 - 3 (x2- 2x+ 3)
g (x)= 5 -3 x ; x e [ 1; 4>.
—> (g ° 0 (x)= - 3 x 2+ 6 x -4
halle las funciones
.-.
a. fo g
b. g o f
En general:
f° g * g ° f
Resolución
a. Hallamos f° g:
1.
(g°/)(x)= - 3x 2+ 6 x -4 ; x e (l—V2; 2]
2.
D o m (y °g )= {x e Dom(g)
a
x e [ l;4 )
a
a
g M e DomCO}
(5 -3 x ) e (-3 ; 2]
(a)
co m o :- 3 < 5 -3 x < 2 —> - 8 < - 3 x < - 3
8
-> 3 < 3 x < 8 -> 1 < x < —
Sean las funciones
/M = I * I + 2; x e (-1; 0);
I
g M= senx; x e [ - - ; - j .
n
n\
Halle las funciones
a. fo g
b. g o f
291
Lumbreras Editores
Dem ostración
Para que se cumpla esta propiedad, tenemos
que demostrar que ( f° g ) ° h y f° ( g o h ) tienen
Resolución
a. Hallamos f °g:
I.
Dom(/ oíj) = { x e Dom(g) a
a g M e Dom(/)}
x e (-^ ;
a
- l< s e n x < 0
la misma regla de correspondencia y que sus
dominios son iguales.
(a)
I.
Dom[(y
= {xeDom (/?) a
Como: - l< s e n x < 0 —> — < x < 0
h {x)
= {xeD o m (/ í) a
2
e Dom(/°g)}
e Domfe) a
A > « ) e Dom^ ) }
En (a )
= {x e Dom(g°/0 a
D o m (^ o g )= x 6 ( - | ;
0
g { h {x])
e D o m (0}
= {x e Dom(g°f?) a
e D o m (0}
= D o m [/ '» ( g o h ) |
Dom(/°g) = x e \~^> 0
II. [(*>S)°/i]M =(f<>g)(#,w)
«■ ^ 05)w=/'(*M)=|senx|+2
(/ °s)w =|sen*|+2; x e \ - 2 ’ 0
2.
b. Hallamos g °f:
1.
->
Dom(g°/0 = {x e Dom(/) a
a fM e Dom(g)}
x e (-1; 0) a -^<|x|+2<^
3.
[ ( . f ° g ) ° h ] M = { f ° ( g ° h ) \ x)
Distributividad f, g, h
a.
( f+ g ) o h = f° h + g ° h
b.
(f g ) ° h = [f° h ) ( g ° h )
Para toda función f existe la función identi­
dad I tal que
Como: -^<|x|+2<^
—» = - ——2 < Ixl < —- 2 < 0
_ 2 ____
2
¡Absurdo!
fo ¡= f= ¡o f
4.
Nunca se verifica
•
h ° ( f+ g ) = h o f + h ° g
• h o (f-g ) = (h ° f){h ° g)
—> xe<¡)
Ejemplo
3g°f
Propiedades
1.
292
Dadas las funciones
/: R —> R
g: R
X —»X 2
(f o g )o h = f o(goh)t es decir, la composición
Halle las funciones
de funciones es asociativa.
a. h o g o f
R h: R - { 0 } - > R
X —> X — 1
b. g o f° h
X
X—
CAPÍTULO IV
Funciones
Resolución
De la definición vemos que:
Note que:
I.
Dom(/*)=Ran(/)
f{JC) = x ¿ ; x e R
II. Ran(/*)=Dom(/)
gM = x - l ; x e R
III. y= fM <r>x=f*M
= \/x
; x e R -{0 }
►
►Recuerde
a.
Hallamos h °g °f:
Una función es biyectiva si es inyectiva y
I.
suryectiva a la vez. Si la función /está definida
Dom (ft°g°/)=Dom ((/í°g)°/)
solo por su dominio y regla de corresponden­
II. {h og of),x)=(h oS) { fix))= {h cg)(x2)
cia, entonces f es obviamente suryectiva. En
consecuencia para que /sea biyectiva bastará
que / sea inyectiva y, por lo tanto, existirá /*
solo con esta condición.
=/j (x2- o =^2
CALCULO DE LA FUNCION INVERSA
.-. (/7ogo/)(x)= - y —; x e R - { 1 ; - 1 }
Si / es una función biyectiva, y =/(*)•
I.
b. Hallamos g °/=/?:
I.
Se despeja x en función de y.
II. Se reemplaza y por x, y a la función y se le
Dom(go/o/j) = Dom[(go/)oA?]
llama inversa de / y se denota por /*.
II. (go/o/i) M = (g o / )(^ )) = (go/)|-
Ejemplos
=íB n ?r? "'
” °
.-. (g°/o/?)M = - l —1; x e R - { 0 }
x
►I n v e r s a
d e u n a f u n c ió n
1.
Si existe, halle la función inversa de /.
x+3
'(*)- x + 2 , x e R - { - 2 } .
Resolución
I.
Veamos la inyectividad
x ,= x 2?
Dada un función /= {(x; /(x)) / x e Dom(/)} biyec­
Xj+3
Xj+2
tiva, se define la función inversa de / denotado
por/* a la función /* = {(/M, x)/x e Dom(/)}.
->
Por ejemplo, si tenemos:
1+ -
X2+3
X2+2
1
X j+2
=1+x2 +2
/= {(-1 ; 2), (2; 0), ( 3 ;- 2 ) , (4; 3 ) ,( 1 ;6 ) }
-> /* = {(2; -1 ), (0; 2), (-2 ; 3), (3; 4), (6; 1)}
-> /es inyectiva
293
Lumbreras Editores
II. Sea fM=y -> y=
III. Cálculo de la inversa.
x+ 3
x+2
Como la función f es inyectiva, entonces
existe su inversa.
Despejamos x: xy+ 2y= x+ 3
^
x =fl
'W
x+3
x+ 2
Sea/M=y=
- * x ( y - l) = 3 - 2 y
x+ 3
x+ 2
y -1
Intercambiamos y por x:
-> y = 1 + -----7
x+ 2
,*
3 -2 x
-> f {x) ------- —; x± 1
x -1
2
_L
y “ 1 _ x+ 2
2.
Halle, si existe, la inversa de la función
x+2 =
x+3
/(x) V x + 2 ’
1
y2 - l
-> x = ^ )= - 2 + ,
y -i
Resolución
Intercambiamos y por x:
I.
D o m (/ )H x eR / r>£^ | > 0
f?Y) = - 2+ -^ !— ; x e R +- { 1 }
—>
x
e
—3]
Además y> 0
a
u
(—2;
Propiedades
y * l.
En efecto, si y = l entonces
—» x + 3 = x + 2
x —1
+ °°)
x+3
x+2
—> 3=2,
lo cual es absurdo.
1.
Dom(/*)=Ran(/)
a
Rari(/*)=Dom(/')
2. f * e s biyectiva, luego: (/ *)* = ^
3.
Característica geométrica del gráfico de f*
Luego el rango de f e s :
Ran(/) = R +- { 1 }
II. Recordemos que:
Ran(/*)=D om (/)=(-°°;-3] u ( - 2 ; +°°)
Dom(/*)=Ran(/) = [0; +°°)
Tenga en cuenta que, cuando la función
no muestra el conjunto de llegada, se
294
define únicamente por su dominio y su
Nótese que, la gráfica de la función inversa
regla de correspondencia. Al ser f inyec-
es simétrica de la gráfica de f(xj, respecto a la
tiva entonces existe f*.
recta de la función identidad y=x.
Funciones
CAPÍTULO IV
4.
Para toda función / se cumple:
a.
( f°f*)(y)=y sobre Dom(/*)=Ran(/)
En efecto:
I.
Dom(/°/*) = {x e Dom(/*) a
= {x e Ran(/)
a
/ *
e
Dom(/)}
/* e Ran(/*)}
= Ran(/)= Dom(/ *)
II. Regla de correspondencia
(f°0*y)=f (f*y))= f(x)=y'' y 6 Dom(/*)
Vemos que la función es inyectiva, entonces
tiene inversa.
b. Análogamente se cumple que:
I.
(/'*o/r) (x)= x sobre Dom(/)
Sea/]M= - 5 - V x + 4 ; x e (-4 ; 0)
Hallamos su rango
- 4 < x < 0 -> 0 < x + 4 < 4
Prueba de (2)
-> 0 < sfx+4 < 2
Como f={{x\ f(x))/x e Dom(/)}
-> 0 > -yfx+4 > -2
r * = { { rW’ x) / x e Dom(/)}
—> - 5 > - 5 - V x + 4 > - 7
/ **= |(x; /(x)) ¡ x e Dom(/)}
R an(/,)=(-7; - 5 )
/•** = /
(/*)*=/Como Ran(/1)=Dorri(/'|*)={-7; -5>
Ejemplos
1.
Halle, si existe la función inversa para la fun­
Hallamos la inversa de
ción:
y,=-5-% /x+4;
- 5 - n/x +4; x e ( - 4 ; 0)
k x )~
|x 2- 2 x ;
x e (l; 3)
x e < -4;0)
y, + 5 = -V x + 4
—> x + 4 = (y + 5 )2
x = -4 + (y + 5 )2
Resolución
/:i*(x)= - 4 + ( x + 5 ) 2
Como la función f es fácil de graficar, enton­
ces la graficamos para ver su inyectividad.
.-. /,*m = (x + 5 )2- 4 ; x e { - 7 ; - 5 )
295
Lumbreras Editores
II.
Sea f 2 {x=xl -2x\ x e (1; 3)
/2Cx)=Cjc-1)2- 1 ;
b. ( g o f)o (f* o g * )= g o (fo (f* o g *))
= g o ((fo f*)c g *)
e <1;3>
= goIog *= g og *= IB
Hallamos su rango
De a. y b.
1< x < 3 -> 0 < x - l < 2
-> 0 < ( x - l ) 2 < 4
(,fo g ) * = g * o f*
-» -1 < ( x - l ) 2- l < 3
-> Ran(/'2) = ( - l ;3 )
FUNCIONES TRIGONOMÉTRICAS INVERSAS
Como Ran(/2)=Dom(/'2 * ) = ( - l ; 3)
Hallamos la inversa de f2.
Resulta conveniente definir, explícitamente, las
funciones inversas de las funciones trigonomé­
tricas.
Sean f2(x) =y2= (x -1 f - 1 -> y2+1 = (x -1 ) 2
Recuerde que
-> x-\=±Jy^+\
-» x= \ ± Jy2+\
Función
Dominio
^2 %)= ^+s/x+\; x e (-1 ; 3)
y=senx
n
. 2 ’ 2_
Rango
[-1 ; 1]
Finalmente
y=cosx
[0; ti]
[-1 ; i]
1+vGc+T; x e (-1; 3)
y=tanx
/ n n\
Y 2 ’ 2/
R
Sean las funciones biyectivas
y=cotx
<0; n)
R
(x + 5 )2- 4 ; x e {-7; - 5 )
f(x)=\
2.
f:A ^ > B y g :B —>C
Demuestre que ( g ° f)* : C —>A existe y ade­
y=secx
i» « ]-{|
R -< -l; i)
más ([g °f)*= f*o g *.
y= cscx
Resolución
L 2
-1 -Í0 }
2]
R - < - i; i>
Por la propiedad 4, se prueba que
I.
(f * ° g * ) ° ( g ° 0 = I A
►
►Nota
II. ( g ° f ) ° ( f * ° g * ) = I B
a.
= f * o [ g * o(go/-))
= f* o (g * o g ) o f = f* o I o f
= f*°f= IA
296
La función trigonométrica inversa está
denotada por
F.T.(0)=/V -» 0=arc F.T.(A0
o 0=F.Tr'(AO
Funciones
CAPÍTULO IV
Función arco tangente
Función arco seno
/■={(x;y)/y=arctanx; i e R }
f= {(x ',y ) /y=arcsenx; x e [-1 ; 1]}
De y=tanx —> x=arctany.
D ey=senx, x e
n
n
'2 ' 2
. Despejando x se obtuvo
x= arcsen y ; luego, intercambiando x por y tene­
Luego y = arctanx; x e R.
Gráfica
mos y=arcsenx.
Gráfica
Función arco cotangente
/ = {(x;y )/ y = arcco tx; x e R }
Función arco coseno
De y= cotx —> x=arccoty.
Luegoy=arccotx; x e R
Gráfica
/ = {(x;y)/ y = arcco sx; x e [-1 ; 1]}
D ey= cosx —> x=arccosy. Intercambiando x por
y tenemos y = arccosx.
Gráfica
Función arco secante
/ = {(x ;y )/ y = arcsecx; x e R - ( - l ; 1)}
D ey = se cx —> x=arcsecy.
Luego y = arcsecx; x e ( - « ; - l ] u [ l ; + » ) .
297
Lumbreras Editores
Gráfica
Propiedades
I.
a rc s e n (-x )= -a rc se n x ;
xe[-1;1]
a rcco s(-x )= 7 i-a rcco sx ; x e [-1; 1]
a rcta n (-x )= -a rcta n x ; x e IR
a rcse c (-x )= 7 t-a rc se c x ; x s R - ( - l ; l )
arcco t(-x )= 7 t-a rcco tx ;
x e R
a rc c s c (-x )= -a rc c s c x ; x e R —<—1; 1)
n —
n\) u ( —;
n n
Ran(/) = 0;
2/
\2
II. arcsen x+ arccosx= —: x e [-1;11
2
.
arctan x+arccotx=—;
2
Función arco cosecante
x6 ¡
a rcsecx+ a rccscx = —; x e R - ( - 1 ; 1 )
2
/ = {(x ;y )/ y = arccscx ; x e R - ( - 1 ; 1 ) }
D ey = cscx —> x=arccscy.
L uegoy=arccscx; x e R —<—1; 1).
III. arctanx+arctany=arcta:
{% )
+nk
Si xy < 1 —> k= 0
Gráfica
S ix y > l,x > 0
—> k=\
Si xy > 1, x < 0
—> * = - 1
►
►Tenga en cuenta
t ¡ S + í ] 571
arctan —¡=— = —
V 3 -lJ
12
Ejemplos
Ran(/) =
1. M = a rc ta n ^ j + arctan^ ^ ] = arctan
n —1—n
3 2
►
►Recuerde
III.
(/*o/)M=x; x e D o m (0
Ejemplos
• sen(arcsenx)=x;
• sec(arcsecx )= x ;
[ - 1 ;1 ]
x e R-(-1;1)
• arccos(cosx)=x;
• arccot(cotx) =x;
x e [ 0 ;7 t]
x e (0 ;7 t)
298
3
( f °f*Xy)=y\ y e Ran(0
x e
—> A/= arctanl = —
4
2+4
1-2-4 ,
2. S = arctan2+ arctan4= arctanl , „ , I+ n
—» S = arctanl- - Ì +7t= 7i-arctan7J
7
2
)
Funciones
CAPÍTULO IV
De (I) y (II) se tiene:
3. /? = arctan(-l)+arctan(-\/3)
D om (0=<-°°; - 4 ] u (0; +°°)
(-l)+(-V3)
l-(-l)(-V 3 )
Ran(/)=
71 7n
2
’ ~2
-{2?t}
* = arctan
, í—
^¡=—
+1l - t i
R
5.
57t
de
variables
7 ji
R = ----- n = -----12
Demuestre que mediante los cambios
x= x'co s0-y 'sen 0, y=x'sen0+y'cos0
12
se elimina el término x'y' de la ecuación
Halle el dominio y el rango de la función.
/,(jr)=3arcsec| 4 + 1 1+-?1
1
( B
si 0 = -a rcta n -------
Resolución
Resolución
Sabemos que
Reemplazando los cambios se tiene
Si
2
U -C
4 (x'cos0 -y'sen0)2+ B (x'cos0 -y'sen0)
= arcsec u, entonces
(x'sen0 +y'cos0)+ C(x'sen0 +y'cos0)2+
u < - 1 v u> 1 a F m e [0; n ]-
•
+D(YcosO -y'sen0) +£,(x'sen0+y'cos0) + F = 0
Luego, para u = —+1 se tiene:
Desarrollando e igualando a cero el término
x'y’ se tiene
- + 1 < - 1 v -+ 1> 1
2
x'y'(24cos0sen0+ñ(sen20 -c o s 0 2) -
2
-2C sen0cos0)=O
—» x < - 4 v x > 0
—> x’y'[(4-C ) •2sen0 •cos0-ñ(cos20-sen 20) ] =0
Además: F (u) = arcsec u e [0; 71]
De donde:
arcseq —+1 j e [0;
(A - C)sen20 - 5 c o s 2 0 =0
sen 20 _ B
cos20 A -C
—> 3arcsec| —+ 1 1 e [0; 37t]
1
•
(I)
J.3
1
1?=1
4.
Ax2 +Bxy+ Cy2 +Dx+Ey+F= 0,
( 3 a r c s e c í—+ ll+ —]e
l
12 J 2 ) L2
f(,x)e
f; a
u
.
2J
- { 2 ti}
(II)
—> tan 20
B
A -C
1 r c t a n ------B
0„ = -a
2
A -C
299
B
iografía
David Hilbert
Nació el 23 de enero de 1862 en Königsberg, Prusia Oriental (hoy
Kaliningrado, Rusia), y murió el 14 de febrero de 1943 en Gotinga,
Alemania. Fue uno de los matemáticos más influyentes del siglo xix
y principios del xx gracias a su aporte en la configuración de los
métodos axiomáticos actuales, sus profundos resultados en álge­
bra, la teoría de números, la geometría y teoría de funciones, los
23 problemas matemáticos de 1900 y sus intentos por resolver la
cuestión de los fundamentos de las matemáticas.
Descendiente de una larga tradición de jueces, Hilbert vivió en su
ciudad natal hasta que cumplió 33 años. Estudió en las universida­
des de Heidelberg y de Berlín, y en la de Königsberg (la Albertina).
Hilbert recibió clases de Heinrich Weber, quien le enseñó sobre
funciones elípticas, teoría de números y teoría de invariantes. La influencia de Weber, y a través de él la
tradición de Gauss, Riemann y Dedekind, sería decisiva para Hilbert. Pero más decisiva fue la amistad
que mantuvo con Adolf Hurwitz, su profesor asistente (Privatdozent), y Hermann Minkowski, que coinci­
dió con Hilbert en los estudios y llegaron a ser muy buenos amigos.
En 1885 Hilbert obtuvo su doctorado. El tema de su tesis había sido propuesto por su asesor Ferdinand
Lindemann, quien demostró dos años antes qué es un número trascendente, y trataba de los invariantes
algebraicos. Posteriormente, viajó a Leipzing para asistir a las clases de Felix Klein, y a París, donde
conoció a Henry Poincaré, Camille Jordan y Charles Hermite.
Un año más tarde, de regreso a Königsberg, Hilbert se convirtió en Privatdozent y se dedicó a publicar
en el campo de la teoría de invariantes. En 1892 fue nombrado profesor extraordinario como sucesor de
Hurwitz, quien se encontraba en Zúrich, y al año siguiente obtuvo el puesto de Professor (equivalente a
lo que hoy conocemos como catedrático). Pero en 1895 Hilbert abandonó su ciudad natal cuando Felix
Klein logró que fuera nombrado catedrático en la Universidad de Gotinga, donde permanecería el resto
de su vida.
En 1897 publicó Zahlbericht, que es una síntesis de los trabajos de Kummer, Kronecker y Dedekind, con
ideas propias de Hilbert sobre teoría de números. Los primeros trabajos que realizó Hilbert fueron sobre
invariantes algebraicos. Anteriormente, en 1868, Paul Gordan había establecido que existe una base finita
para los invariantes y covariantes de las formas binarias, con la demostración de su teorema de la finitud
de generadores y usando un complejo enfoque computacional. Veinte años después, Hilbert enfocó
la cuestión de manera abstracta y se dio cuenta de que era necesario seguir un camino diferente. Con
su teorema de la base, Hilbert logró mostrar la existencia de un conjunto finito de generadores para las
300
invariantes de cuánticas en cualquier número de variables, pero de forma abstracta. Esto es, demostró
la existencia de dicho conjunto, pero no de forma algorítmica sino mediante un teorema de existencia.
Cuando Hilbert envió sus resultados a la Mathematische Annalen, Gordan, el experto en teoría de in­
variantes de la revista, no fue capaz de apreciar la naturaleza revolucionaria del teorema de Hilbert y
rechazó el artículo. Klein, por otro lado, reconoció la importancia del trabajo y publicó al artículo sin
alteraciones. Animado por Klein, Hilbert extendió su método a un segundo artículo, proporcionando
estimaciones sobre el grado máximo del conjunto mínimo de generadores, y lo envió una vez más a los
Annalen. Tras leer el manuscrito, Klein le escribió diciendo: “Sin duda, este es el trabajo más importante
en álgebra general que los Annalen han publicado nunca” .
En 1899, su obra Fundamentos de la geometría reemplazó eficazmente la geometría euclídea con un
conjunto de 21 axiomas mucho más completos y abstractos, que tratan sobre puntos, líneas y planos y
seis tipos de relaciones entre ellos.
Para 1900, Hilbert preparó una conferencia sobre “ Problemas matemáticos” , en el Segundo Congreso In­
ternacional de Matemáticos de París, donde recopiló 23 problemas que no habían sido resueltos todavía,
de los cuales solo alcanzó a discutir diez. Hilbert creía que el futuro de la matemática estaría vinculado a
la resolución de estas cuestiones; sin embargo, actualmente se ha llegado a la conclusión de que unos
pocos son irrelevantes o imposibles de cerrar y otros continúan siendo un reto para los matemáticos.
A partir de 1904, Hilbert desarrolló un programa para dotar de una base axiomática a la lógica, la arit­
mética y la teoría de conjuntos, con el propósito de axiomatízar toda la matemática. Adicionalmente,
dedicó su atención a problemas relacionados con el átomo y la relatividad; es conocida la competencia
amistosa que entabló con Albert Einstein en 1915 sobre la teoría de la gravitación relativista, donde el
intercambio de ideas llevó a la forma final de las ecuaciones de campo a la relatividad general.
En 1930, a la edad de 68 años, Hilbert dejó de enseñar en la universidad. Esta última etapa de su vida es­
tuvo oscurecida por la tragedia que trajo consigo el régimen nazi a muchos de sus colegas y estudiantes.
Dos años después, Adolfo Hitler fue nombrado canciller de Alemania, y aprobó una ley que prohibía a los
judíos Impartir clases. Fueron varios los profesores expulsados de la universidad de Gotinga, entre ellos
se encontraban Hermann Weyl, que había ocupado la cátedra de Hilbert tras su retiro, Emmy Noether,
a quien Hilbert propuso como Privatdozent cuando los otros miembros no la aceptaban por ser mujer, y
Edmund Landau.
Al año siguiente, en un banquete, el nuevo ministro de Educación le preguntó a Hilbert: “ ¿Y cómo es la
matemática en Gotinga ahora que ha sido liberada de la influencia judía?”. A lo que Hilbert respondió:
“¿La matemática en Gotinga? Ya no queda nada de eso” .
Una caída que sufrió en 1941 durante un paseo por Gotinga tuvo consecuencias en su salud que le llevó
a la muerte el 14 de febrero de 1943. Al funeral asistieron menos de una docena de personas, solo dos
de los cuales eran colegas suyos. En su tumba se puede leer este epitafio recogido de una conferencia
pronunciada por Hilbert: “Debemos saber, sabremos” .
Fuente:
h ttp ://es.w ik ip ed ia.o rg /w ik i/D avid _ H ilb ert
http ://divu lgam at.ehu .es/w eb orriak/historia/m ateospetsuak/H ilb ert.asp
http://w w w .biografiasyvidas.eom /biografia/h/hilbert.htm
► B io g r a f í a
Problemas
RESUELTOS
b. En (a) se ha demostrado que
Problema 1
Demuestre que
(M u i V ) n P = ( M n P ) u ( J V n B )
a.
C 4 u B )n C = C 4 n C )u (B n C )
b.
(A n fl)u C = (iu C )n (B u C )
Tomamos com plemento en ambos m iem­
bros
[(Ai u AO n P ]c = [(M n P) u (/Vn P) jc
Resolución
Aplicamos las leyes de De Morgan
{M u N)c k j P° ={M n P)° n (N n P)c
►
►Recuerde
A=B
Ac.B
-> [m c n Nc) u P c = [_MCu P c) n (n c u Pc)
Bc/t
a
Aquí hacem os M °=A ;N C= B; P0 = C
-» ( A n B ) u C = ( A u C ) n ( B u C )
a.
Se demostrará por doble inclusión
I.
d S e a x e (A v B )n C
-»
X
£ (A u B ) A
X
con lo cual queda concluida la demostra­
ción.
6C
—» (x e -4 v x e B) a x e C
Problema 2
—> ( x e / 4 A x e C ) v ( x e B A X e C )
Halle el equivalente del conjunto
—> x e ( A n C ) v x e ( B n C )
M = ( 0 4 - B ) u ( B c - 4 c )) C
—» x e (A n C )u (B n C )
Resolución
—> C 4 u B )n C c C 4 n C )v j(B n C )
En la resolución aplicaremos A-B=Ar^Bc .
II. 3 l S e a x e (A n C )u (B n C )
M = ((A -B )uÍB c - AC))C
—> x e (í4nC ) v x e {B n C )
= ( U n B c )u (B c n U c )C))
-> ( x e i A x e C ) v (x e B a x e C)
—> ( x e ^ l v x e B ) A x e C
= ( U n B c )u (B c nA ))C
—> x e (A u B )n C
= U n B c )C
—> (A n C ) u (B n C )c (A u B ) n C
Con I y II queda demostrado.
302
=AC u ÍB c )C
M =AC u B
Funciones
CAPÍTULO IV
Problema 3
Demuestre que A x (B n C)={AxB) n (AxC).
Resolución
La demostración igualdad de conjuntos se hará
por doble inclusión.
I.
d Sea (x; y) e A x (B n C)
A1uA2 u ...u A „ = ljA ; = l jA í , /={1; 2;...; n}
i=l
te/
A1nA2 n ...n A n = P )A ,= p A í , / = {l;2 ;...;n }
i=l
te/
De la ley de De Morgan
\ Cc
x e A a y e (B n C)
UA;
V ' =fÍA ,C
¡el
iel
te/ J
x e i a [y e B a y e C ]
De donde
—> (x e A /\ y e B ) a ( x e A A y e C )
nC
íi A,- = U A f
./€/ y /€/
halle los siguientes conjuntos.
—> ( x ;y ) e A x B a (x ;y )e A x C
—> (x; y) e (A x B ) n (A x C)
a.
U [/—1; i)
Í=1
-> A x (B n C) c (A x B ) n (A x C)
b-
n
-4 ; 4
í=i\ i
i
II. al Sea (x; y) e (A x B)n(A x C)
—> (x; y) e A x B a (x; y) e A x C
'■ a(o;)
—» x e A A x e B A X e A A y e C
—> x e A a ^ e B Ay e C )
Resolución
a.
-> x e A Ay e B n C
|J[/-1; /)=[0; l)u[l; 2}u[2; 3)...=[0; +°°)
1=1
—> (x; y) g A x (B n C)
—> (A x B )
(A xC )
A x (B n C )
De 1y II queda concluida la demostración.
Problema 4
Sea {A,; A2; ...; A„} un conjunto finito de conjun­
tos; en este caso, se puede hallar la unión y la
intersección de estos conjuntos.
i
303
Lumbreras Editores
C.
III. Dom(7?) = { l ; 2; 3; 4}
n (0 ; j) .( 0 ; , ) ^ 0 ; - ^ 0 ; j
« - ' = {(3; 1), (5; 1), (3; 2), (5; 2), (5; 3), (5; 4 )}
Dom(/?-l) = {3; 5}
IV. a. RoR~'
Problema 5
Sea R la relación menor entre A = {1; 2; 3; 4 } y
£ = { 1 ; 3; 5}, es decir (a; b) e R <-> a < b .
I.
Exprese R com o un conjunto de pares orde­
nados.
II. Represente R en un diagrama cartesiano de
AxB.
III. Halle el dominio de R yR~x.
R°R~l = {(3\ 3), (3; 5), (5; 3), (5; 5)}
IV. Halle
a. R o R -]
b. R-'oR
b. R-'oR
Resolución
I.
R = {(a ;b )/a < b }
Sabem os que a e A y b e B .
R= {(1; 3), (1; 5), (2; 3), (2; 5), (3; 5), (4; 5)}
II.
---4
R~'°R={ (1; 1), (1; 2), (1; 3). (1; 4), (2; 1),
(2; 2), (2; 3), (2; 4), (3; 1), (3; 2), (3; 3),
3
304
4
D
(3; 4), (4; 1), (4; 2), (4; 3), (4; 4)}
CAPÍTULO IV
Funciones
IV. Sea (a; b) e R, entonces
Problema 6
Sea R una relación en A, es decir, R c A x A , de­
R °R = {(a;c) eR , 3 b e A / ( a ; b ) e R , (b ; c) e/?}
muestre que
Ahora bien (a; b) e R y com o /? es reflexiva
I.
(6; b) e /?, así (a; b) e
R es reflexiva si y solo si A0 c R.
es decir/? c R°R.
Además, Aa c R c R ° R —> R°R es reflexiva.
Aa= {(o ; a ) / a e Á )
V
II. R es simétrica si y solo si R=R~\
R°R~] = {(a; c) 3 beA/{a\ b) 6 /T1a (b; c) e/?}
por la simetría de
III. R es transitiva si y solo si R°R c R.
y R~l se tiene
/?=/?“' = {(a; c) 3 b e Afta; b ) e R
IV. Si R es reflexiva -^ R oR ziR y R R e s reflexiva.
a
(b; c) e /?"'}
RoR-' = R~'°R
V. SiR es simétrica -^>R°R~'=R~l °R.
Problema 7
Resolución
I.
es una relación en X definida
Si AT= {1; 2; 3} y
El conjunto Aa= {(o ; a) / a 6/4} se llama dia­
gonal.
por /?= {(1; 1), (2; 3), (3; 2 )}, indique el valor de
verdad de las siguientes proposiciones:
I.
Además, R es reflexiva si y solo si
R es reflexiva.
II. R es simétrica.
Va s A, (a; a) e R, es decir, si Aa c R.
III. R es transitiva.
IV. R es una relación de equivalencia.
II. De la definición de simétrica e inversa, tene­
mos:
Resolución
/?={(a; b ) / (a; b) e A x B }
I.
Falsa
Vemos que (2; 2) g R —> R no es reflexiva.
R~l= {(b ; a) / (a; b) e R}
II. Verdadera
Si R es simétrica.
P a ra (l; 1), 3 (1 ; 1) e R
(ia \ b ) e R a (b ; a ) e R —> R c R ~ ]
(b; a ) e R~] a (a; b) e /? —> /?“' c /?
Para (2; 3), 3 (3; 2) e R
—> R es simétrica
De otra forma:
De donde R=R~'
Se observa R=R~] —>R, es simétrica.
III. Sea (a;c) s R°R —>3 b e A/( a ; b ) e R a (b; c) e
Por transitividad (a; c) e R —> R-^R rzR
Por otra parte, supongamos que /?o/? c ü
si (a; b), (b; c) e /? —> (a; c) e
Por lo tanto, /? es transitiva.
c /?
III. Falsa
(2; 3 ) e R
a
(3; 2) e R, pero (2; 2) g R
—> R no es transitiva
IV. Falsa
Si no es reflexiva ni transitiva, entonces no es
una relación de equivalencia.
305
Lumbreras Editores
Un ejemplo que representa la descripción alge­
Problema 8
Conteste las siguientes preguntas.
a.
Sea A un conjunto no vacío y R una relación
en A. ¿Cuándo se dice que R no es reflexiva?
braica de la función cuadrática es
Ax2 +üx+Ef{x,+/•'=0, donde f(x)=y se escribe
com o Ax2 +Dx+Ey+F=0, cuyo dominio es R.
Un tipo muy importante de funciones son las
b. Sea A un conjunto cualquiera no vacío y sea D
funciones cónicas, que se encuentran al estudiar
la diagonal de/lx/l, es decir, D={(a; á )/a eA }.
la relación de R en R, tal que asocia a cada x e R
¿Qué condición existe entre todas las rela­
los valores de y e R que satisfacen la ecuación:
ciones reflexivas R (en A) y DI
Axí +Bxy+Cy¿+Dx+Ey+F= 0, con A, B o C no nulo.
La forma de la cónica depende del discriminante:
Resolución
a. R es relación reflexiva si V o eA , (o; o) e R.
A=B 2 -4AC.
R no es reflexiva si ~(v a e A, (o; a) e R)
Así:
~(\/a e A, (a; a ) e r ) = 3 a e A/(a\ a ) <£R
I.
Si B 2 -4AC > 0, la gráfica de la relación se lla­
ma hipérbola.
Luego, R no es reflexiva.
II. Si S 2-4 4 C = 0 , la gráfica de la relación se lla­
ma parábola.
►
►Nota
Si 3 o e A / ( a ; a) e R
III. Si B 2 -4AC < 0, la gráfica de la relación se lla­
ma elipse.
Indique el tipo de función cónica que representa
cada ecuación.
b. S i>4^c[>,£>={(a; á ) / a e .4 } —> D c A x A
Si R es reflexiva en A —> V a e A: (a; a ) e R
-> D ^ R
a. x2+3xy+2y2+ 5 x -3 y + 2 = 0
b. x 2+4xy+5y2- x + 2 y - l =0
c.
4x2+4xy+y2-3 x + 2 y -5 = 0
(a; a) e D, a e A —> (o; a) e R
-> D a R
R es reflexiva en A
Resolución
Dc R
Sabemos que el tipo de función cónica depende
solo del discriminante, así:
Problema 9
a.
hipérbola.
Forma implícita de una función
En muchos casos, resulta conveniente, o incluso
b. 42- 4 ( 5 ) = - 4 < 0, entonces, su gráfica será
una elipse.
necesario, representar una función mediante una
expresión algebraica en forma de ecuación, en la
cual no aparece despejada ninguna variable.
306
32- 4 ( 2 ) = l > 0, entonces, su gráfica será una
c.
42-4 (4 )= 0 , entonces, su gráfica será una pa­
rábola.
CAPÍTULO IV
Funciones
Problema 10
Resolución
Demuestre q u eg (x-)= 5+ V 9-x es una función es­
Hallamos la relación C.
trictamente decreciente en 0< x<9.
|x-l| = |y-l|
•o x - l = y - l v x - l = l - y
o
Resolución
I.
El dominio de la función es 9 - x > 0 —» x< 9.
II. S e a n x ,;x 2 e Dom(g), tal q u e *] < x 2
Luego: -x ¡ > -x 2 —> 9 - x , >
C o m o X ];x 2e
y = x v y = 2 -x
la relación C está formada por la unión de ambas
rectas.
Graficamos dichas rectas
9 -x 2
(-■*>; 9] —> 9 - x , >
0
a
9 - x 2> 0
-> p - x ¡ > j 9 - x 2
—> 5+^/9-x, > 5+ yj9-x 2
S{X])> S {X2y V x ,;x 2 e ( - ° ° ; 9 ]
Por lo tanto, g es decreciente.
Problema 11
Grafique la siguiente relación.
Problema 13
R = {(x ;y ) e R x R / x - y e R +}
Dados los productos cartesianos
A x B = { ( l ;3 ) , (1; 5), (2; 3), (2; 5)}
Resolución
fix C = {(3 ; 2), (3; 3), (3; 5), (5; 2), (5; 3), (5; 5)},
Si x - y e R + <-» x - y > 0 <-» y < x
halle el conjunto C4 u B )-C .
Gráfica
Resolución
Y
Por definición de producto cartesiano.
A x B = {(a ; b) /a eA
/
y<x
a
beB}
Luego, de A x B = {( 1; 3), (1; 5), (2; 3), (2; 5)} se
tiene
A = { 1; 2}, ñ = {3 ; 5}
/'
D e B x C = {(3 ; 2), (3; 3), (3; 5), (5; 2), (5; 3), (5; 5)}
se tiene C = {2; 3; 5}.
Como 04 u S ) - C = { x £ 4 v x e f i
a
xíC}
Problema 12
y además/l u B = { l ; 2; 3; 5}, C = { 2 ;3 ;5 }
Grafique la siguiente relación.
-» (A u B ) - C = { l ; 2; 3; 5 }- {2 ; 3; 5}
C = {(x ;y ) e R x R / |jt- 1 |= [y -1 1 >
.-. ( A u S ) - C = ( l (
307
Lumbreras Editores
Problema 14
B: 3 <
Dada la función f:
x
2< 4
-> x e [-2 ; -V 3 )u (V 3 ; 2]
-> S = { - 2 ; 2}
x - > x 2-2 x + 1 8
Luego, A xB tendrá 4 x 2 = 8 elementos.
Entonces, la proposición es falsa.
y los conjuntos
9
1
II. A: x y - 9 y - l = 0 -> y = —ñ—
x -9
¿ = { * e Z / / r(x+3)= 33}
B = {x e Z //qc_3)= 21},
x 2- 9 * 0 —> x * 3
halle <4xB.
a
x *-3
-> D o m G 4 )= R -{-3 ;3 }
Entonces, la proposición es verdadera.
Resolución
III. f¡x)=x
Sea la función
/■(x)= x 2- 2 x + 1 8 = ( x - l ) 2+17
4 : /(x+3)= (x + 3-1 )2+ 17=33 -» (x + 2 )2=16
—> x + 2 = 4 v x + 2 = - 4 —> x = 2 v x = - 6
Si ffá > 0
a
x > 0 —> f ^ —y[x
—> f e s función
Entonces, la proposición es verdadera.
-» A = {2; -6 }
ñ: /(x_3)=( x - 3 - 1 ) 2+ 17=21 -> ( x - 4 ) 2=4
—> x - 4 = 2 v x - 4 = - 2 —> x = 6 v x = 2
- * S = { 6; 2}
Problema 16
Dada la siguiente relación
/ ? = {(x ;y )e R 2/ (2 -y )2= 9 - x 2},
halle Dom(7?) n Ran(/f).
Como A = { 2 ; - 6 } ; S = {6; 2} entonces
A x£ ¡= {(2; 6), (2; 2), (-6 ; 6), (-6 ; 2)}
Problema 15
Dé el valor de verdad de las siguientes afirma­
ciones
I.
Resolución
Hallamos la relación R.
La relación dada: x 2+ ( y - 2 ) 2= 3 2, es la ecuación
de la circunferencia de centro en (0; 2) y radio 3.
Si i = { x £ Z / - l < x + 2 < 4},
B = {x e Z / 3 < x 2 < 4},
entonces el cardinal de A xB es 3.
II. Si A = {(x ;y ) e R 2/x2y - 9 y - l = 0 } ,
entonces DomC4) = R - { - 3 ; 3}.
III. f 2x)= x es función si Ran(/) = [0; +°°).
Resolución
Analizando las proposiciones:
I.
A: -1 < x + 2 < 4
-3 < x < 2
- * A = { - 2 ;- 1 ; 0; 1}
308
Dom(7?) = [-3 ; 3]
R an(/?)=[-l; 5]
.-. Dom(7?) n Ran(7?) = [-1 ; 3]
CAPÍTULO IV
Funciones
Problema 17
En el problema
Dada la fundón f - . A ^ B definida por
A = (-6 y )2-4 y ( 1 0 y -2 )> 0
,
-> 36y2-4 0 y 2+8y > 0 -» 4y2- 8 y < 0
>/2x-l
halle su dominio.
[1 -x ]
'(y)=-iT,—
a
y *0
-> 4 y (y - 2 )< 0 -> y ( y - 2 ) < 0
—> 0 < y < 2
Resolución
Para que la función esté bien definida, es n ece­
sario que 2 x - l> 0 a |[l-x]]*0.
y *0
a
Luego
y e
[0 ; 2 ]
y * 0
a
-»
y e (0 ;2 ]
Entonces, y puede tomar (valores enteros)
•
2 x - l > 0 —> x > ^
•
l l - x ] ] * 0 —> 1 - x g [0; 1) -> - x t [-1 ; 0)
x e (0; 1] - 4 * 6
(a )
0] u <1; +°°)
y, = l, y2=2
yi+y 2
CP)
" 2
2
2
Problema 19
De (a ) y ((3): Dom(A)=(l; +=o)
Halle el área determinada por el conjunto A.
A ={(x; y) e R 2/ |x| + |y |<8
Problema 18
Halle la semisuma del mayor y el menor valor
entero que puede tomar la función
f
2
{x) x 2-6 x + 1 0
I.
a
[Nótese que |x|=x
x2 -6x+ ]0^ 0 - * (x -3 )2+1^0
..
y> x}
y>x>0
L u e g o :x + y < 8
(x -3 )2* - l
a
Resolución
Calculamos su dominio.
Vemos que x puede ser cualquier número
real
x>0
Para hallar el conjunto A hay que resolver el sis­
tema
|x| + |y| <8 a x > 0 a y > x
<-> |x| + |y| <8
Resolución
a
a
a
|y|=y]
y>x >0
Graficamos las desigualdades
x+y<8
a
y > x> 0
Dom(/) = R
II. Sea y= fM -» y=-® — ------w
x -6 x + 1 0
-> yx2-6 y x + 1 0 y -2 = 0 ;y > 0
Esta ecuación, respecto a x, es de segundo
grado y de soluciones reales.
►
►Recuerde
Ax2+Bx +C=0,,4*0 tiene soluciones reales
si y solo si A= B2-4AC > 0 (discriminante)
Sea Área (A) = 5 ->
5 = ------= 16u 2
2
309
Lumbreras Editores
Además
Problema 20
Determine el rango de la función f.
f(x)='í 4 x 2- 4 x + l - x .
1 < x < 2 —> 1x1 = 1
Luego se tiene
n
n
k=\
k=\ k=\
n
I (1+6)= 1 1+ £ k = n+
Resolución
n ( n + 1)
2
Redefinimos la función
f(x)=\J(2 x -\ ? - x = \ 2 x -\ \ -x
( 2 x - l - x ; 2 x - l> 0
f(x)~
- ( 2 x - l ) - x ; 2 x - l< 0
Problema 22
Halle la longitud de la cuerda común de
jc—1;
x>-
F(xj = 2xl —22
2
a
G(x^——x^+5.
k x )~
-3x+l; x<
Resolución
Para hallar los puntos extremos de la cuerda co ­
mún igualamos las funciones: F(xí = CM.
Gráfica
-y 2x2- 2 2 = - x 2+5 -> 3x 2=27
—> x = 3 v x = - 3
Graficamos las funciones F y G.
Ran (f)= — ; +oo
2
Problema 21
n
Si 1 < x < 2 , calcule X [* + £ j.
k=\
Resolución
Propiedad
|x+A:l=[[xl+fc, si k e Z
310
la longitud de la cuerda común MN es
ImvI = 3 - ( - 3 ) = 6 u
CAPÍTULO IV
Funciones
Problema 23
Problema 24
Halle Dom(/) u Ran(/) si
Dada la gráfica de la función f^ = a x 3 + b, calcule
el producto ab.
f{x)= x 2 sgn
H 3+l
"
Vxsgn
x + x + l.
x 2 +\
, x *0
Resolución
Dom(/') = {x > 0; x / 0 }= (0 ; +°°)
•
|x|3+ l > 0
sgn
a
lx|3+l
kx +x+\j
x2 + x + \ > 0 , V x e R
= 1,
VxeR
Resolución
I.
x 2 > 0 -> x 2+ l > 1
( 0 ; a ) E f —> f(o)=a —> a - 0 + b = a —> a - b
II. (1 ;2 )e / ' -> f0)=2 -> a + b = 2
0 <
o , < 1» x*Q
x ¿+ \
De I. y II. se tiene: a = l , b = l
.-. o 6 = l
x 2+ l
=0
Problema 25
s8n i
2 i
=
X +1
0
Dadas las rectas 3}x y
I.
3tx pasa por puntos (1; 5) y (-2 ; 3)
II. S/^2 - 2 a x -(a + 3 )y = 5
—> f(x)=x + 0, x > 0
Si 5?, es perpendicular a í£«b calcule el valor de a .
Gradeamos la función f.
Resolución
Graficamos las rectas en el plano.
Dom(/) = R - { 0 }
a
R an (0 = R +
Dom(/') u Ran(/) = R - {0 }
311
Lumbreras Editores
Tenemos
Luego
2a 'i
2a
5
M-
y = l a + 3 j X _ o + 3 COn P e n d ,e n t e m * = ^ 3
^
91a2 - 5 b 4
91a2 -5 (4 a )2
1la£>
1 la (4a)
1
¡By. y = m ]x+ b . Calculamos la pendiente m ,,
Problema 27
así:
3 -5
-2 -1
Construya la gráfica de la función
2
2
3
m' = 3
f
w
M zl
w +r
Como ^ 1 ~> m\m 2 = -\
Resolución
Luego:
Como |jc| +1 > 0 , V x e R,
entonces el dominio de f e s R.
4 a = -3 (a + 3 )
Nótese que V i e R : f{x) = f ^
9
7
a =—
—> f es una función par.
Para dibular su gráfica, basta analizarla para jí> 0
y luego hacem os un reflejo respecto al eje Y.
Problema 26
Si f^ = a x 2 +bx+c, a > 0, /¿o)=2 y Ran(/)=[1; +°°),
91a2-5fc4
Entonces
ab¿
11
Resolución
Como fM= ax 2 + bx+ c —> fm = c= 2 —> c = 2
Completamos cuadrados:
^(x)=a
2
bx
+2
X +—
+2
k x )= a
/w = °
x+ -
2a
+
2-
—
4a
Como Ran(/0= [ 1; + °°)
b2
,
—> /(X)S1 —» 2 —— =1 —» b = 4 a
4a
312
,
x -l
,
2
Tenemos f M = — -= 1------ w x+1
x+\
calcule el valor de
M=
Luego dibujamos la gráfica de f para x> 0.
Funciones
CAPÍTULO IV
Problema 28
Problema 30
Grafique la siguiente función
Dadas las funciones
f
_ “I
kx )~
-x + 1 ; x<-\
Resolución
I.
x>l
x
Observamos f(-x)=f(x), entonces f es par.
Luego, la gráfica solo será necesaria para
x > 0 ya que será simétrica respecto al eje Y.
x<0
x;
S(x)~
x — ; x>\
x
II. Tabulando algunos puntos
X
0
1
2
3
f (x)
-1
-1/2
-1/5
-1/10
Resolución
...
Hallamos f +g .
III. Graficamos la función f.
—+ x ; x e [l,+ °°)n (-~ ; 0)*(|>
—+ x 2 - — ; x e fl; +°°)n(l; +°°)
x
(Í + S \ X) = x
- x + l + x ; xe(-~>; -l)n ( -° ° ; 0)
-x + l+ x 2 — ;x e (-° ° ; -l) n ( l; +=»)=
x
Problema 29
Recuerde que f +g está definida si
Bosqueje la gráfica de f ^ = 4|x| - x 2, x e (-4 ; 4).
Dom(/) n Dom(g)*<]>
Resolución
I.
x 2; x e (l; +<=°}
Se observa /"(_*)=A » entonces f es par.
II. Para x > 0
fw = 4 x -x 2= 4 - ( x - 2 ) 2
Cf + 8 \ x ) =
1;
x e (-°°; -1)
III. Graficamos para x > 0 y recordando que es
una función par, hay simetría con respecto al
Graficamos f +g .
eje Y.
313
Lumbreras Editores
II.
Problema 31
Intercepto con el eje Y
Grafique la función f ^ —gws |senx|
f
- 20-b
(o)“ - y =
ÍO; 0<x<7t
si S(x)=<
[1; n<x<4n
Resolución
I.
o
Redefinimos fíx)
90
1R
a -3 £ > + /? = --3 (-2 )-— = - — + 6=0
3
3
3
0 ■Isenx!; x e (0 ; n)
/« = «(x>lsen*l = , .
.
.
.
(Msenxl; xe{n\ 4n)
Problema 33
10; x e (0 ; ti)
Si ffjQ=5x+k a g(A)= 3 x -k, halle el valor de k si se
f(x) = \
|Isenjcl; xe{n\ 4jc)
cumple {fo g )M+4=(g
II. Graficamos la función f.
Resolución
I.
Como f y g son funciones polinomiales, el
dominio para ambas es R.
II.
•
(f° g )(x )
= 5 (3 x -k )+ k = \ 5 x -4 k
{fo g \ x)= I5 x -4 k
*
Problema 32
■>
f e ° 0 ( x ) = g ( f ( x ) ) - g ( 5 x + k)
20
La gráfica de la función f^ = a x + b x —— inter-
= 3 (5 x + k )-k = \5x + 2k
secta al eje X en los puntos (-2 ; 0) y (5; 0); al eje
- * [g °f)(x)=\'óx + 2 k
Y, en el punto (0; k). Halle el valor de a - 3 b + k .
*
Resolución
1. Intercepto con el eje X
-g(x)=( 5 x + k )-(3 x -k )
( f-g \ x)= 2 x + 2 k
20
f( 2)=o -> 4 a - 2 b —^-=0
20
f ls¡= 0 -» 25o+5£>—— = 0
—> (í-g )^ = 2 k + 2 k = 4 k
(a )
En el dato:
((3)
l
De (a ) y CP): a = | , b = - 2
314
( f - g ) (X) = f( x )
->
Sx - 4 k + 4 = I S í + 2 k - 0
2 k = 4 -> k = 2
Funciones
CAPÍTULO IV
Luego en el conjunto F, se cumple:
Problema 34
Dada la función f(x\=— —,
m x -5
- 1=/'(5 )= /'(2x-y) -» 2 x -y = 5
halle /(5xj en términos de f(x).
2
” ^(-3) =f(y-x)
(a)
y~x = - 3(p)
De (a ) y ((3): x = 2 , y = -l
Resolución
I.
x 2+y2= 22+ ( - l ) 2=5
2x
De
Xhx)~^kx)~^x
$kx)
X~ J
x (^(x)- 2 ) - 5^(x)
(x )~ 2
Problema 36
Sea la función f: [5; b } —> [a; 5], cuya regla de
correspondencia es fM = x -8 x + 7 .
„ .. ,
2x
IL S ,/ w _ ^ 5
^
>
_ 2(5x)
“5^5
Calcule el valor de (a+ b ) para que f sea biyectiva.
2x
->
f(5x)
Resolución
x
Si f e s biyectiva, será inyectiva y suryectiva a la vez.
--(y-)
5/f
III. Reemplazando x = —
en f((5x)
f(x) ~ 2
% )
Suryectividad
/■(x ) =
%■)
x
2- 8
x
+ 1 6 - 9 = ( x - 4 ) 2- 9
Graficamos la función
'W - 2
<5A>
•
10/(x)
]
5 f ( x ) ~ f( x ) + 2
kx )-*
ksx)-~
5Í(x)
Problema 35
Halle el valor de x 2+y2 sabiendo que
/■={(5; -1 ) , (-3 ; 2), (2x-y; -1 ), (y -x ; 2), ( x ^ + y 2)}
es una función inyectiva.
tonces:
f(b)= 5 -> ( b - 4 ) 2- 9 = 5 h> (¿>-4)2=14
-> b = 4+V Í4.
Resolución
Recordando, f e s inyectiva si Vx,, x 2 e DornA:
^ l ) = ^2) ^
Como es creciente (inyectiva) y suryectiva, en­
Xl=X2
Además a = f ^ = - 8
o + & = -8 + 4 + V Í4 = -4 + V T 4
315
Lumbreras Editores
II. Verdadero
Problema 37
Dé el valor de verdad de cada una de las siguien­
tes proposiciones.
= 2 + 4 x -x 2 = - (x2 - 4x + 4 )+ 6
0)
- x 2;
I.
Si f,(*)-
1
Graficamos
g (x)= - ( * - 2 ) 2+6; x e [2; +oo)
;
x g
(0 ;
+ °°)
4~x
entonces f admite inversa.
II. La función g(x) = 2 + 4 x - x 2 es inyectiva para
x e [2; +<»).
' f'
III. El dominio de [ — |es (0; 6], donde
r(x)
, x e (0 ; 6]
-4 x
- 4
S(x) -\l-x2 +7x+\8
Resolución
Notamos que g es monótona decreciente.
I.
Por lo tanto, g es inyectiva.
Verdadero
Tabulamos algunos valores
X
1
1
16
4
1
9
3
l
4
2
III. Verdadero
1
4
9
...
1
1
2
1
3
-
Dom(/)=(0; 6]
Dom(g): - x 2+ 7 x + 1 8 > 0
* 2- 7 x - 1 8 < 0
Graficamos f
(x -9 )(x + 2 )< 0
—> x e [-2; 9]
Asimismo
Dom|—j =D om (/)nD om (g)
a
g ( x) * 0
Dom í^J=<0; 6] n [-2; 9 ] -{ -2 ; 9}
Función inyectiva y suryectiva.
Por lo tanto, f tiene inversa.
316
.-. D o m ^ J= < 0 ;6 ]
CAPÍTULO IV
Problema 38
Funciones
III. Falso
Sumando las funciones (gráficamente)
Respecto a la función f\ [0; 6] —> [-4 ; 4], cuya
gráfica se muestra a continuación.
Vemos que f+\f\ no es inyectiva.
Por lo tanto, 3 no existe la inversa de f+ 1/1.
Dé el valor de verdad de cada una de las siguien­
tes proposiciones.
Problema 39
I.
f es biyectiva.
Sean las funciones
II.
|f |no es biyectiva.
fM= J x + 3
III. Existe g* donde gM= fM+\fM \.
Resolución
I.
g(x)=|x|.
a
Halle la gráfica de [f og) {xy
Resolución
Verdadero
►
►Recuerde
Del gráfico, f e s inyectiva y suryectiva, enton­
Para fog se tiene
ces es biyectiva.
I. Dom (/° g)=jx/x e Dom (g) a
6 Dom (/)j.
Por lo tanto, f es biyectiva.
" • « * ) >=k>)
II. Verdadero
Graficamos |/¡
I.
x e Dom(g)
x e
R
a
a
|at| e
,-------
g(x) e Dom(/)
[-3 ; +°°)
—> x e
R
[Vx>3 ; x > 0
(v -x + 3 ; x <0
III. Graficamos f°g(xy
Se observa que ¡/I no es inyectiva.
Por lo tanto, |/"| no es biyectiva.
317
Lumbreras Editores
II. Graficando
Problema 40
Si /■=j(x ; y )e R x R // y = ^ | J , halle
(f*
es la inversa de
f*
f).
Resolución
i
c
x + 1 -2
2
.
y w=_i+r= x+1 esmyectiva
—> existe
f* .
x —1
II. De y = ----- —> x y + y = x x+1
,*
Problema 42
Dadas las funciones reales
,
y+1
x + [x V ¡x i-l]x + 3 ; xe[2; 3}
x = \ y )\ --y 'y * x
¡x+ a; x s ( i ; 1)
.
••
r(x) ~- x1 + l ’• v i i
w
|_x
Q(x) -
¡2-[x'/\/x2 - l ] x ; x e[l; 7)
|x+c; x e{8 ;
Problema 41
donde {o; £>; c;
Grafique la siguiente función.
d}
d)
cR .
Grafique la función (P + Q).
f(x ) = -v/jf+C—J f l + X W
Resolución
Resolución
Redefinimos la función
I.
Como: 2 < x < 3 —> |x|=x; \[x2 =x
Hallando su dominio
x + [ - x l> 0 -> [-x]| > (-x)
Cot)
Por teoría se sabe que para todos (- x ) £ R;
Luego
| x + [x V x -l]x + 3 ; xe[2; 3)
P( x ) ~
luego se cumple
[-x l< (-x )
(ß)
De (a ) y (ß)
[- x j= - x ; - x e Z
—> x + [ - x ] = 0
hx r
318
a
x [x l= x 2
|x+o; x e (b ; 1)
Í 2 - [ x V x - l] x ; x e[l; 7)
Q(x) -
x + c; x s (8 ;
d)
Para sumar, recordemos que:
Dom (P + Q)= x e Dom (P) n Dom (Q)
(P+Q \x)=p(x)+Q(x)
CAPÍTULO IV
Funciones
Entonces
Por definición
x+ [xV x^I]x+3+2-[xV x-l]x; x g
[2;
3)
x+[xV x-lJx+3+x+c; xe<|>
[1;
f(x) ~ I
10;
si x es V
si x es F
(p + Q)u)=
(x + a )+ 2 -[x V x -l] x;
(x+a)+(x+c);
x g
(|)
xe<|)
—> (P + 0)(x )= -x'+5; x e [2; 3), cuya gráfica es
/■(V a V)=/(V) = 1 = 1-1 =/(V) -f(V)
/(V a F) =/(F)= 0= 1 •0=f(V)-f(F)
/(F
/ (
Y\
A
V)=/(F) = 0 = 0 - 1 =/(F) -/(V)
F A F )= / (F)= 0= 0-0= / (F)-/ (F)
•• hp ^q'>~hpYhq)
II. Verdadero
P
~P
V
F
V
F
/"(—F)=/"(V) = 1—0= 1—/"(F)
/ ( - V) =/(F)= 0 = 1 -1 = 1 -/XV)
Problema 43
Sea <(>={x/x es una proposición}.
Se define la función:
/: i
[1, si x es V
R por f(x)=
k~p)= x ~hp)
III. Falsa
p q
[0, s ix es F
V
V
F
F
Indique cuáles de las siguientes afirmaciones
son verdaderas.
*• fípr.q)= f{p)'f(q)
h~p)~^~hp)
V
F
V
F
p^ q
V
F
V
V
p^q=~pv q
/(V -> V) =/(V) = 1 = 1 -1 +1 = 1-/(V)+/(V)
Resolución
f ( y -> F )= / (F )= 0= 1-1 + 0= 1 -/(V)+/(F)
Usamos la tabla de verdad
/(F -> V)=/(V)= 1= 1- 0 + 0 = 1-/(F)+/(F) (*)
I.
Verdadera
/•(F -» F)=/(V)=1 = 1 -0 + 0 = 1 -/(F)+/(F)
p q
V
V
F
F
V
F
V
F
pA q
V
F
F
F
Luego, no es cierto que:
f(p ->q) ~
I ~ h p )Jrhq)
Nótese que falla en (*)
319
Lumbreras Editores
Problema 44
Problema 45
Grafique la función f ^ = x - \senx |.
Grafique la función
x se n ^ —J; s ix > 0
Resolución
Si f ]M=x; x e R
a
^ x ) - - |senx|; x e R
f( x ) ~
0; s ix = 0
Vemos que
+ (-% ))
Luego, graficamos f x; f.¿ y f.
Resolución
Vemos que la función f¡x) es una función acotada
entre x; - x dado que
1
x s e n — <|xl —> - l x l< x s e n — <1x1
x
x
Es decir
1
-x < x sen — < x para x > 0
x
Luego, su gráfica
f
n si•—=mn
1
r(x)=
0,
x
1
—> X = —
mn
►
►Nota
x > s e n x ;x > 0 —> x -se ru o O
320
1.
El dominio de
= \J8 - x 2 + eo s 8 x
A) R -{V 8 }
6,
La gráfica d ey = |jc|- 2 ; - 1 < x< 4 es
B)
C) [ 2V2 ; + ~ )
D) [-V 2 ; n/2]
2.
E)
[-2V 2; 2V2 ]
El rango d e y = x 2- l ; - l < x < 2 es
A) [2; 3]
B) [-1; 4]
D) [-1; 3]
C) [-1 ; 1]
E) [I; 3]
, si x es primo
3.
Sea fix) =
D)
Y
E)
Y
, si x no es primo
Halle /p)+/(4)- ^(7i) _ ^(43)A) -5 8
B) 47
D) 110
4.
C) 200
E) -110
Si a e R tal que h {xj=x 2 ~ x - a 2, entonces
7.
Esboce la gráfica de y = sgn (\lx- 1).
A)
B)
Y
1
1
A) la función h intersecta al eje X en dos
puntos.
y
X
1
X
B) la intersección con el eje A" depende de a.
C) la intersección de h con el eje X no depen­
de de a.
C)
1
D) existe a e R tal que h no corta al eje X.
E) A v C
5.
y
Dadas las funciones f = { (2; 0), (3; 5), ( 1 ;- 3 ) ,
(4; 0 )} y g = {(2 ; 1), (1; 8), (6; 0 )}, calcule la
D)
E)
Y
Y
suma de los elementos del rango de f/g.
A) -1
D) 3/8
B) 1/8
C) -3/8
X
X
E) 0
321
Lumbreras Editores
8.
El rango de /'={(x; V x -l)/ x > 5 } es
A) (-V 2; V2)
10. El rango de la inversa de y = - — - es
B) [ - 7 2 ; -Jí] C) [-2 ; 2]
D) ( - 0=; 2]
A) R
E) [2; +=0)
B) R -{2/ 3}
C) R -{3/ 2}
9.
Grafique y=\¡2-x.
D) R - {4/3}
E) R - { 2 }
B)
A)
V2
11. Si f(x ) =x + — es una función tal que
x
-2
X
Ran(/0=<-=»; a] u [- a ; +=°), entonces
A) a=y¡ 2
C)
y
B) a = W 2
D) o= 2
-V 2
C) a = l
E) o = - 2
12. Sean las funciones reales f^ = \ íx - 1; x > 1 y
g(x)= x 2+ 1; entonces A°g es
A
A) (Aog)w = V W -l; *> 1 v x<-\
D) Y
E)
B) (/:°g)w =|x|; x e R
C) (f°g )M=x; x e R
X
d)
(f°g )M= *; x ¿ 0
E) (f°g )M= -x ; x < 0
—
H / F
12 / D
322
*
H / a
iA /T
C laves — — —
Ia / c
Lz / b *
l §_/ A
lA / E
Ii ^ b '
B
Iü / e '
112/ B
Problemas
PROPUESTOS
Nivel I
1.
4.
Halle el rango la función h co n regla funcional
„2 ,
h W = ~ r+ x -
Si la relació n
/?={(!; 2a), (2; 7), (5; 1), (1; 3 a -5 ) , (7; 9)}
+°°)
A)
2. 2
4 ’ 4.
B)
e s u n a función, ca lcu le la su m a d e los e le ­
m e n to s del ran go d e d ich a función.
A) 22
D) 27
2.
B) 16
5.
B)
b -a
D) { b - a f
E) a 2 + b 2
II.
V l-H
'-1 0 x .
2x + l
B) (-1;
C) [1; +°°>
D)
6.
E) [-1 ; 1]
2x+l
Si el rango de f ^ =
3 x -l
es R a n / = R -{a },
,2
ca lcu le el valor d e 9a +1
Dada la función f cuya regla de correspon­
dencia es f(x)=x¿- 2 x + a, indique lo correcto
respecto a los gráficos adjuntos.
1.
E)
~4.
A) <-00; - i ]
C) (b - a ) b 2
4
Halle el d om inio d e la función
f (x) —
f\ [a ; b] —> R, tal q u e f (,)= ? . C alcule el
m e n o r valor d e k tal q u e |f^ { b - a ) |<k p ara
tod o t, sien d o a \b \> 0.
Sea
A) b 2 - a 2
3.
C) 15
E) 10
D)
C)
A) 5
D) 8
7.
B) 6
C) 7
E) 4
Sea //w = V(x - 5) (x +6) (x -1) (x +2)+196.
Halle la regla funcional de la función
R=^H(x)+ 16,25.
A) 2x+l
B) x+2
D) 2 x - l
O -y
E)
2x+ l
f:R
R yg: R - { 0 } —> R dos fu n cion es
tales q u e
=mx+12, m * 0, S (x )= ~ - ¿P ara
S ean
q u é v alo res d e
2
m las fu n cio n es f y g ad m iten
d os pun tos d e in tersecció n ?
A) El g ráfico I o c u rre c u a n d o a > 1.
B) El g rá fico II o c u rre c u a n d o a < 1.
C) El g rá fico III o c u rre c u a n d o a = l .
D) El g rá fico I o c u rre c u a n d o
E)
El g ráfico II o c u rre c u a n d o
a < 1.
a > 1.
A) <-2;+~>
B) (-18; 0> u (0; +<=°)
C) ( - 00; - 1 8 )
D) (—°°; + °°)
E) (-18; 18)
323
Lumbreras Editores
9.
L a gráfica ad ju nta re p re s e n ta a y = f(xy
A) 10
B) 8
C) 28
D) 26
E) 17
12. Dadas las funciones
/={(1; 4), (-1; 0), (6; 2), (8; V¿)} y
g = {(-l; 2), (6; 5), (1; 8), (4; 9), (V3; -8 )},
¿Cuál de las siguientes gráficas representa a
y=W
halle el rango de f+g.
A) {2; 7; 12}
B) {2; 7; 10}
C) {2; 7}
D) {2; 5; 8; 9}
E) {2; 5; 8; 9 ; - 8 }
13. Indique cuál es la gráfica del conjunto
A = {(*; y ) / ^ y < * 2}u{(l0; 0)}.
A)
Y
y
/ - 2
E)
Y
—i1 ^ ^ C x
C)
J
/w = 4 - x 2, g (x)=0. Halle el número de pares
pertenecen a la región R. Considere la fron­
tera en dicha región.
A) 15
D) 12
B) 10
C) 8
E) 18
11. Si p ara m e (a; b) la función flx)=m x 2 +rnx + 1
no intersecta al eje X, calcule el valor de
a 2+ 6 2+ l.
324
)
Y
10. Sea R la región formada por las funciones
ordenados de com ponentes enteros que
B)
Y
( X (
f
X
Y
í
D)
Y
X
J
X
CAPÍTULO IV
Funciones
/U ) = ^ - 4
Vx
g (x) =
a
-1
halle el ran g o d e f g.
A) <2; 4)
D) (0; +°°)
Y“
D)
14. D adas las fu n cion es
B) (2; +°°)
CD<-«»;-2)
E) <-4;-2)
Y
E)
/
\
15. L a in versa d e la siguiente función
f(x) = 'l 5 - x (b c-5 1 + l+ x ) e s tá d a d a p or
B,
\
\\x
-2
h
17. S ean f, g : [1; + °°) —> R fu n cion es definidas
p o r f ^ = x 2-\x\ V g(x)=\f~x. Dibuje, a p ro xim a­
d a m e n te , la gráfica d e la función co m p o si­
r'» X2 - 2 0
°
n
- ¿ T ;x > 0
ció n g o f.
E)
36-x2
180
16. L a gráfica d e frx-¡= | x + l |+
|x-l | e s
D) ^ ; * , 0
36
B) Y
Y
1
1
/
/\
X
X
Y
A)
; 2
-1
B)
/
T
c)
x>0
Y
2/
/
1 X
/
X
y
2
18. Halle el ran g o d e
A) R"
D) R
w
= 5^ 7 ( x 2 - 2 x ) .
\x\
B) [—1; 1]—{0} C) R+
E) R0+
325
Lumbreras Editores
19. E sb o ce la g ráfica d e la re lació n x2+y2 > 3.
Y
A)
21
a. A c <t> —> ,4=<t>
.
V3V
K,
B)
Nivel II
r
- v3
,Á/5 a:
V3 *
b. (A - B )= A - (A n B )= ( A u B ) -B
c.
G 4 u B )-C = G 4 -C )u (S -C )
d. ( A n B ) - C = ( A - C ) n ( B - C )
e.
(A -B ) -C = A -( B v j C)
f.
A -(B -C )= (A -B ) u ( A u C )
g.
(A -B )-C < z A -(B -C )
h. A u ( B - C ) = ( / l u S ) - ( C - / l)
22. Sean los conjuntos
A = {x e Z/ |x| < 3}
E)
B = { x e Z / x2< 7}
¿cuántos de los siguientes conjuntos son nulos?
•
AnB
•4uB
•
A -S
• B-A
•
(A -B ) u (B-A )
• 0 4 -B )n ( S - ,4 )
20. Grafique la relación definida por |y| + |x|<2.
A) 2
B) 3
C) 4
E) 6
D) 5
23. Demuestre que
a. A={A n B) u (A n Bc )
b. B c A <-» (A -B ) u B=A
c.
Si (A -B) u (B-A)=<\> <-» A=B
d. SÍ/4xB = (|> <r-> 4=(t) v ñ=(|)
e.
(A -B )x C = (A x C )-(B x C )
f.
Si/4 nñ=(|)
a
A u B = C —» A = C -B
24. Se define la diferencia simétrica entre A y S.
A A B=(A -B) u (ñ -A ), demuestre que
E)
Y
a. AAB=BAA
b. (AAB)AC=AA(BAC)
c. A A B = (A < jB )-(A n B )
d. SiAAB=AAC -> B=C
e.
(4 iB )n C = (A n C )A (B n C )
CAPÍTULO IV
Funciones
25. Indique el valor de verdad de las siguientes
proposiciones.
I.
S e a n A = {l; 2; 3; 4 } yR una relación en A.
/ ?= {(!; D ; 0 ; 3 ) ; (2; 2); (3; 3); (4; 4 )} es
reflexiva.
II. La relación
II. Si R y S son relaciones transitivas
—> R n 5 es transitiva.
III. Si R es transitiva —> R~l es transitiva.
A) VVV
D) FVV
B) VFV
C) VFF
E) FFV
R={(x-y)/x, y son triángulos sem ejantes}
29. Dados los conjuntos
es de equivalencia.
III. S e a n A = {l; 2; 3; 4 } y R una relación enA.
/?={( 1; 2); (3; 4); (2; 1); (3; 3)} es simétrica.
A = {xe
R/|UI - 1| < W}
fí={xeR/|U2 -l|-Jc|=x},
halle el cardinal de A n B.
A) VVV
D) VFV
B) VVF
C) FFV
E) FFF
A) 2
D) 5
B) 3
C) 4
E) infinito
26. ¿Cuáles de las siguientes relaciones son de
equivalencia?
I.
30. Halle el dominio y el rango de la función
R = {(a; b )/a e s p aralela a b }
^M= s g n (jf+ l)-s g n (jf-1).
II. R={(A;B)/A<zB ; A, B conjuntos no v acío s}
III. R = {(a; b ) / a - b = n ; a , b e Z }
A) solo I
D) I y III
B) solo II
C) solo III
E) I, II y III
27. D eterm ine el valor d e verd ad d e las siguien­
te s p ro p o sicio n es.
I.
D o m (0 = R +; Ran(7)={0; 1; 2}
C)
Dom(/)=R~; R an(O ={0;
D)
Dom(/)=R; R a n (0 = {-1 ; 0; 1}
1; 2}
E) Dom(/0=R“; R a n (f)= {-1 ; 0; 1}
31. Si
G<>Fm = x +2 a F (x)= x 3+ 6x2+ 1 2 *+ 8 ,
halle G(jr).
Sean,4 = { l ; 2; 3; 4} y R una relación en A.
R={(x\ y)/x=y v x + y = 3 }
a)
es de equivalencia.
B) CM=Vx
II. Una relación f i e n R tal que
/?={(*; y ) / | * - i | = | y - i | }
III. Sea R una relación, R u /?“' es simétrica.
A) VVV
D) FVF
B) VFV
C) Gíx)= í ?
D) C(x)= V x+ 2
es de equivalencia.
C) VFF
E) FVV
28. Determine el valor de verdad de las siguien­
tes proposiciones.
I.
A) Dom(/0=R; Ran(/7)= {0 ; 1; 2}
B)
( ñ : m últiplo d e n )
Sea A = [ -l; 1] y la relación/? en A.
R = { ( x ;y ) lx 2 =y2} es de equivalencia.
E) G(x)= 4 ?
b } y la
función/':A ->Stalque/?= { ( l;a ) ,( 2 ;o ) ,( l;y ) ,
32. Dados los conjuntos A={1; 2; 3}, B={a\
(2; z), O; a )}.
(x+y+zf
Si — - — - — =7 calcule el valor de a.
2a+3
A) 2
D) 4
B) 1
C) 3
E) 5
327
Lumbreras Editores
33.
A) 4
Halle todos los polinomios kx) lineales que
. ^_X
verifican ( / ' ° / ' ) í i ) = ----- , x * 0 y calcule la
suma de todos los términos independientes
38.
S (x ) =
°>!
S -I
D)
Ln
B)
tc+2
Ln
ji +9
L
„
C)
indique el valor de verdad de las siguientes
I. f e s par.
II. g es impar.
III. f y g son pares.
A) VVV
D) VFV
71+ 4
39.
C) FFF
E) FFV
Determine por extensión el conjunto
A = {x e Z / V 3 x -2 -V x + 3 < l}.
A) {1; 2; 3;... 10}
Respecto a la gráfica de la función
B) (1; 2; 3;... 11}
x2
F, .. =— — , indique la proposición falsa.
1 x ¿-\
A)
B)
C)
D)
E)
B) FVF
4L
71
E)
71 + 4
71+ 4
Ixl+— , D om (g)=[-l; 1],
proposiciones.
Un alambre de longitud L ha de ser cortado
en dos partes, una de las cuales servirá para
formar una circunferencia y la otra para for­
mar un cuadrado. ¿Dónde se ha de cortar
para que la suma de las áreas del círculo y
del cuadrado formados sea la menor posible?
A
35.
x + - l , Dom(/')=[-l; 1]
B)
a> 4
„
C) 9
E) 27
Dadas las funciones
de las funciones obtenidas.
34.
B) 8
D) 13
Existen asíntotas verticales en -1 y en 1.
Existe asíntota horizontal en 1.
Es creciente en (-1; 0).
Es creciente en (1; +~).
Es decreciente en (0; 1).
C) {1; 2; 3; 4; 5; 6}
D) {1; 2; 3;... 8}
E) {1; 2; 3;... 9}
40.
Si x e (0; 1), calcule el valor de A+B.
4 = [x + [x + Ix ll]
B= sgn (x+ sgn(x+ sgn (x)))
36.
El valor mínimo de la función
f (x) = V x2 +X + 1
es a y el valor máximo de la función
A) 0
a
b
o
* > T
B ,|
D) 2
37.
41.
C)
E)
B) 1
D) 3
goo=-3A: + 6 x - l es b. Calcule —.
V3
3
Dada la relación definida por
C) 2
E) 4
Sea f\ R —> R una función definida por
[sg n (-9 ); 0 < x < l
f( x ) ~
{ [ x j; l< x < 2
Determine el rango de la función.
5 = { ( x ;y ) e R x R / |y| < |x|; |x| < 3},
328
halle el número de elementos del conjunto
A) {-1; 1; 2}
P = { ( x ; y ) c S / x , y e Z}.
D) [-1; 1)
B) [-1; 2]
C) {-1 ; 0; 2}
E) (1; °°)
CAPÍTULO IV
Funciones
42. Halle el dominio de la función
f(x)= *Jx 2 sgn(|x|+l)-l
f.
A)
-
+% 4-x
3 ab
4
ab
B) (0 I;
ab
—
4
C) (0; a)
A) < - o c ;- l > u < l;4 ]
D) (0; b)
B) <-«•;-1)
C) <1; 4)
D) [4;+oc)
E)
3a b
~
46. Halle el rango de la función
E) (1; +<*>)
ab
4~ ' T
f.
/(x)= \x-2\ + | x-l |+1; x e (1; 3]
43. Halle el dominio de la función
f.
A) [2; 4]
D) [4; +°o>
B) (2; 4)
47. Halle el rango de la función
A) (-4 ; 5}
-
B) (-4 ; 5]
C) [V 3-1; 7]
f.
/=-!(x; - ^ y ^ i x 2 - 4)>0
E) 4
D) [-4; 5)
44. Halle el rango de la función
C) (2; 4]
E) <2; + “ >
f.
f2jc—1; x e (l; 2]
[jc2 +1; x e(2 ; 7)
A) (1; 3] u (5; 50)
B) <1; 3]
C) [3; 5)
D) (5; 50}
A) (_oo; -1> u <1;
B) (—°°; -1] u < l;
C) (_oo; -1)
D)
-1] u < l;
E)
- l> u [1;
+ “>
+ °°)
{0}
+ °o)
+ =o)
48. Dadas las funciones
o
fM =x-~ 5 *+ 5
5
g M= - 2 x + - ,
a
halle el dominio de H,M-
E) [1; 3] u [5; 50)
fW +3g(x)
45. Si el área de un rectángulo está definida
com o el área de la superficie rectangular ins­
crita en el primer cuadrante bajo el segm en­
to ab, com o se indica en el gráfico, halle el
rango de la función área.
A) R -{1 }
B) R.—{10}
D) R —{—1; - 2 }
C) R - { l ; 2}
E) R -{1 ; 10}
49. Halle Dorn(A+g) n Ran(/+g) si
jg w ; x e ( - l; 2 )
|x2 +2; xe[2; +■»)
J f t (x); x e ( - o o ; - 1 )
S (x ) =
|2x-l; x e (2 ; + « )
A) <2; +«.)
D) R
B) (9; +°°)
C) [9; +<*>).
E) <t>
329
Lumbreras Editores
50. D adas las fu n cion es
j( x - 5 ) 2; x e (l; 4}
O
/r0 0=jc2- l ; x e <6; 13);
Sm =
x 2-
6
x
(f°3 \ x) =
|Vx+5; x e(5 ; 11)
xe^4; y ) ,
+6;
|(x+5)2; x e (l; 4)
halle el complemento del dominio de (f°g\ xy
°)
( f° s \ x) =
E)
(í o 4 ) =
A ) <-«>; 6 ]
/
f ( x - 5 ) 2; x e (l; 4)
13
|V x-5; x e(5 ; 11)
B)
fto =ax 2 + a x + 1, indique el
intervalo de valores para a que hace que una
raíz sea mayor que 1 y la otra menor que 1.
53. Dada la función
O (e; f
D)
6;
13
A)
13
E) (-= ; 6]u — ; +°°
2
B)
51. Indique el valor de verdad de cada una de
[0 5 )
f
C) <0 4 )
las siguientes proposiciones respecto a la
función
D) <4 + oo)
f(x) = V -x 2- 8 x - 1 2 + V -x 2 - 4x.
E)
I. Existe f*.
II. f tendrá inversa para x e ( - 3 ; - 2 ) .
III. f es inyectiva si x e (-4 ; -3 ).
A) FVF
D) V W
l^ x + 5 ; xe(5\ 11)
B) VFV
[8 + oo]
54. Sea '(x)
/(x)= x+sgn(x4+ 2). ¿Cuál de las gráficas
representa a y=f.U+DB)
C) FFV
E) F W
52. Dadas las funciones reales
jx 2; xe[5; 9)
g (x)= x + 5 ; x e [1; 12],
Y
C)
|n/x ; xe[lO; 16)
halle
/
[(x + 5)2; x e [l; 4)
a)
E)
Y
D)
(f° g \ x r
X
2
Y
[\/x+5; x e(5 ; 11)
\/
|(x+5)2; x e [l; 4)
B)
(fo g )^
|%/x+5; xe[5; 11)
330
/
/
-1
2
X
/
-2 /
/
/t
X
CAPÍTULO IV
Funciones
55. Grafique la función
x 2;
\x)
f.
58. Si
x<0
[x l;
'
x+2
halle el valor de a para que f * =f .
(f* es la función inversa de f ).
0<x<l
-s g n (x );
f(x) = aX+^ 2 a , x e R - { - 2 } ,
x>l
A) 2
D) -3
A)
B)
B) 3
C) -2
E) 1
Y
(
1 — ■-----------1
X
59.
Sean las funciones
f: [-5 ; 5] —> R / fa = x + \
g: [-4 ; 4] -> R / S w = x -1
h: [-3 ; 3] —> R /h ^ = x
Halle el dominio de Q i*°g*of*)*
C)
1
A) x > 2
B) x e [-3 ; 3]
C) x < 3
D) x e (-3 ; 4)
D)
E)
E) x < - 2
Y
60. Dada la función f
X
X
x -3
___1
x-\
(x -l):
es cierto que
56. Halle el dominio de la función
A)
f.
I.
f es inyectiva.
x - \ l x 2 -\ 6
II. f es creciente.
x Ix + 4 ]-x
III. f posee inversa.
A) solo I
D) I, II y III
- 4 ] u [4; +°°)
B) (~°°t _ 4] u [6; +°°)
C) R - { 0 ; 4}
B) solo II
61. S ean las fu n cion es
D) (-4 ; 6)
E) <-«; -4 ] u [5; +«>
J 2.
f( 2 x - Z ) ~ k x
^ - 3 ) — 4"+1; 8 (X) - J
57. Determine el rango de la función
C2x-3) + X
g.
Halle el intervalo al cual pertenece k, de tal
4x
manera que el rango de g sea (-3 ; 3).
X +1
A) [-2; 2 ]-{0 }
D) R¿-
C) solo III
E) I y III
B) R
C) R 0+
E) [-2; 21
A) (-5 ; 11)
D) <-1; 1)
B) <-7; 1)
C) {-5 ; 1)
E) <0; 1)
331
Lumbreras Editores
f u n a fu nción co n sta n te definida por
f[x)=a, d o n d e a e s un e n te ro q u e verifica la
62. S e a
re la ció n x - 1
<a <x.
65. Analice la univalencia de la función
kx) = V lM - x + 4 x + 4Vx2 - 2 x ; x > 0
y halle la función inversa.
Calcule
x2
^(17,99)
A) ' « = 8 ^ 4 )
A) 0
B) 1
B)
C) 2
x2
f* ———
—
—
D) 3
(x) 8(x+ 4)
E) 4
63. Indique el valor de verdad de cada una de las
proposiciones.
I.
E) No existe su inversa.
[—1; 1> —> (-<*>; 0] es suryectiva
66, Resuelva el sistema de inecuaciones
x+1
x —> ----x-\
II.
D) ^ = ¿ 1 )
/ L ) = 5 - a/ 5 - x 2 + 2 x ;
x e ( -l; 0) es inyectiva
- x 2; x e (-°°; 0}
III. S(x) =
- L ; x e (0 ; +°°)
tiene inversa
vx
A) VVF
D) VFV
§/|x-2|-5 + 4/|x+3|-10<0
(I)
4/lr" ] - 3 + ^ [ 1 3 - x l > 0
(II)
A) <|>
D) (4; 7)
B) R
C) {7}
E) ( 8 ;-1 3 )
67. E sb o ce la gráfica d e la función
B) FFV
C) VVV
E) FFF
'M =
= 12x2—8 1x| + 5 1, x e [—2; 2]
A)
B)
64. Resuelva la ecuación [x j + [2 x J+ [3x]| = 14.
(11 = máximo entero)
A) <2; 3)
C)
B) (2; 2 A
C)
3’
D)
D)
E)
332
§ ;3
5
8
2’ 3
f.
E)
CAPÍTULO IV
Funciones
68. Dada la función fix)=x+ y!x2+ 9 , x e [-4 ; 4]
Halle f*, si existe.
A)
x e [ - l ; 9]
B)
xe[V,
9]
C)
^ e (l;
9}
x e (l;
9>
D)
v2+9
E) /'no es univalente
69. E sb o ce la g ráfica d e la fu nción
f.
70. D ada la fu nción
f(JC-) = ax 2+— , d e te rm in e la
condición que existe entre las cantidades
positivas a, b, c para que /'(x)> c, V x > 0.
A) a b > —
B) 6 2- 4 a c < 0
C) 27a£>2> 4c3
D) a b > c
E) 2%[ab=y[c
333
Lumbreras Editores
73. Halle el rango de la función cuya regla de co­
71. S e a la función
rrespondencia es
co sx + lco sx l
^tó­ e o s x - c o s x
x 2+8x+12 ; x e ( -6 ; - 4 }
h x )~
. slx + 2 ;
3
x e
[ - 2 ; 1)
x e [l; 4]
1 1
3
A)
-1 } u (1; +°°>
B) (-<*>;-1] u [1 ;+°°)
Determine f*, si existe.
4+V x+4;
A) f :
(x)
x e
xe[0; V3)
3 x -5 ;
x e
[2;
x e
[0 ;
V3)
3 x -5 ;
x e
[2;
3)
x
2-2 ;
3x-5;
74. Sean
(-4 ;
' x 2- 2 ;
-4 -V x + 4 ;
E) < -l;l>
3)
x e
x e
0)
D) '¿ r
2+2
f y g dos funciones tales que
/ = { ( 3 ; 1), (2; 3), (9; 2), (7; 4)};
g = { ( 2 ; 3), (7; 5), (9; 7), ( 1 1 ; - 4 ) } .
Determine (f °g) ° f* y calcule la suma de ele­
mentos del rango.
(-4 ; 0)
E) 12
D) 5
75. Dada la ecuación ||.5x[|=3x-2, calcule la
x e [o ;
suma de sus soluciones.
xe[2; 3]
A) -1
B) -2/5
E) - 2
76. Sean las funciones
ta = V T + x ; - l < x < 2
-4+ s¡x+ 4 ; x e ( - 4 ; -1)
f,
(x)
C) -7/5
D) -5/3
; xe [ o ; V3)
3 x + 5 ; xe[2; 5)
E)
C) 4
B) 2
A) 3
-4 -\ lx + 4 ; x e { - 4 ; -1)
x
[-1 ; 1]
D) {0}
0)
(-4 ;
x 2- 2 ;
-4 + V x + 4 ;
c) G r
C)
[x l; x < 0
a
g (x ) =
x 2-l; x> 0
Grafique la función f °g.
x 2+2 ; x e(o ; 4 3 )
Y
B)
Y
A)
3 x + 4 ; x e (2; 3)
72. Halle el dominio de la función
-1
f.
Y
C)
f (x )~ -3
V x2- M
V3 A
A) x e <0; 1)
B) x e (-<=; 0)
C) x e (0; + - )
D) x e ( - 0 °; 0) u <0;
E) x e
-1 )
334
k
43 X
-1
y¡ 3 X
Y
D)
1) u (1 ;
+°°)
-1
E)
& x
Y
V3 A
CAPÍTULO IV
77.
S ea
Funciones
f\ R —> [-1; 1 ] tal q ue
A) VVV
B) VFV
C) VVF
D) FVF
í-1 ; x e Q’
1; x e Q
79.
Indique el valor d e v erd ad d e las siguientes
V x . y E Q ; f M + fw = 2 f{x+y)
II.
V x , y e Q'; f M + f^ = 2 f^ x+y^
S ob re la función
f(x) = f t x ,
indique el valor d e
v erd ad d e las siguientes p ro p o sicio n es.
p ro p o sicio n es.
I.
E) F FF
I.
Es u n a función par.
II.
Es d e c re c ie n te en tod o su d om inio.
III. A dm ite infinitos c e r o s reales.
III. V x e Q , y e Q ’; f M - f w = f íy)
A) FV F
IV. V x e Q ' ; f(x + 2 )= f(x)
B) VVF
D) F F F
A) FVVV
B) VVVV
D) VFVV
78.
C) FFV
E) VVV
C) VVFV
E) VFFV
Indique el valor d e v erd ad d e las siguientes
80.
Halle el dom in io d e la fu nción f.
/w = a/U2-
x -2|-Ii - x 2I-I x +1|+^x
p ro p o sicio n es.
I.
s i ^ V ? , g M =Jf2 -» (g °0 (2 )= 4
A) ( - » ; l ) u {V 2 }
II.
S e a la función / : (-•*=; 0] —> [0; +<*>) tal
B)
que /'(x) = x 2, / e s so b rey ectiv a.
C) (-1 ; 1)
III. L a fu nción f {x)= |senx| e s univalente en
tod o su dom inio.
1]
D) <-l;2>
E) < - 2 ; l >
335
»
C
LAVES
Problemas propuestos
N IV E L 1
lA
d
lA /
d
LA
Ü L /
c
lA
a
1 1 ° /a
li>
B
L A
e
i i / r
A
'
B
7
lA /c
1 1 Z /a
L li/ B '
I A
/
d
'
I A
/
e
'
lli.
e
'
I A
/
b
Lü / '
a
*
I A
/
a
'
[2 0 /a '
N IV E L II
[ 21 / r
[3 3 / 7
1 * 5 /7
1 5 7 /i
I W
[ 2 2 / A*
134/ c '
1 * 6 / A"
[5 8 / 7
lzo/ 7
[2 3 /r
[3 s y
D
1 * 1 /7
[5 9 /b ‘
iz i
1 3 6 /7
[4 8 /7
[6 0 /7
lZg/ 7
[2 5 , B
[3 7 /B
1 4 9 /B '
A
c
IZ3 / 7
[2 6 y
D
[3 8 /C
[5 0 / 7
l® 2 / B "
lz* / 7
[2 7 y
a
[39 / c
15L
Í A
IZ5 / 7
[2 8 / A ‘
1*9 / 7
[5 2 /B
[6 4 /^
129/ A '
[4 L
[5 3 /B
I A
'
lZZ/ 7
[30
1*2 / 7
[5 4 / c
[6 6 /c '
I/® / D
111/ A
l4! / c
[5 5 /
7
[6 7 / 7
I A
[3 2 , A
IM
156/ A'
[6 8 /
[8 0 /b
[2 4 y * ‘
"
A'
a
/
a
'
Nota. Las claves con * son demostraciones.
336
e
'
l
c
/
a
b
I A
a
'
7
/
/
b
a
'
'