funciones

Orozco Angel Carlos Antonio
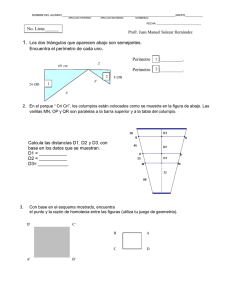
1NLSIS3A
Prof. Cesar A. Hernández Gutiérrez
Tema: FUNCIONES
Funciones Polinómicas.
Una función polinómica es aquella que está definida por un polinomio:
donde a0, a1 ... an-1, an son números reales que se llaman coeficientes del
polinomio y n es el grado del polinomio.
Las características generales de las funciones polinómicas son las siguientes:







El dominio de definición es el conjunto de los números reales (R).
Son siempre continuas.
No tienen asíntotas.
Cortan al eje X, como máximo, un número de veces igual que el grado del
polinomio.
Cortan el eje Y en el punto (0, a0).
El número de máximos y mínimos relativos es, a lo sumo, igual al grado del
polinomio menos uno.
El número de puntos de inflexión es, a lo sumo, igual al grado del polinomio
menos dos.
o Funciones polinómicas de grado 0: rectas horizontales
o Funciones polinómicas de primer grado: Rectas oblicuas
o Funciones
polinómicas
o Funciones
de
polinómicas
segundo
de
tercer
grado:
grado:
o Funciones polinómicas de cuarto grado: Cuarticas
Parábolas
Cúbicas
Funciones racionales.
Una función racional está definida como el cociente de polinomios en los
cuales el denominador tiene un grado de por lo menos 1. En otras palabras,
debe haber una variable en el denominador.
La forma general de una función racional es
polinomios y q (x) ≠ 0.
, donde p (x) y q (x) son
Ejemplos:
La función padre de una función racional es
una hipérbola.
y la gráfica es
El dominio y rango es el conjunto de todos los números reales excepto 0.
Valor excluido.
En una función racional, un valor excluido es cualquier valor de x que hace al
valor de la función y no definido. Así, estos valores deben ser excluidos del
dominio de la función.
Por ejemplo, el valor excluido de la función
cuando x = – 3, el valor de y no está definido.
es –3. Esto es,
Así, el dominio de esta función es el conjunto de todos los números reales
excepto –3.
Asíntotas.
Una asíntota es una recta que se acerca a la gráfica de la función, pero nunca
la toca. En la función padre
, tanto los ejes x y y son asíntotas. La
gráfica de la función padre se acercará más y más pero nunca tocará las
asíntotas.
Una función racional de la forma
tiene una asíntota vertical en el
valor excluido, o x = b, y una asíntota horizontal en y = c.
Funciones Irregulares.
Una función irracional es una función en cuya expresión analítica la variable
independiente X aparece debajo del símbolo de raíz.
En este apartado consideraremos únicamente funciones irracionales del tipo
con g(x) una función racional.
𝑛
𝑓(𝑥) = √𝑔(𝑥)
Si el índice n de la raíz es impar, es posible calcular la imagen de cualquier
número real, siempre y cuando la expresión g(x) sea un número real, es decir.
𝐷𝑜𝑚(𝑓) = 𝐷𝑜𝑚(𝑔)
Si el índice n de la raíz es par, para poder calcular imágenes necesitamos
que g(x) sea positiva o cero, ya que las raíces pares de un número negativo
no son números reales. Por tanto, el dominio de ƒ son las soluciones de la
inecuación 𝑔(𝑥) ≥ 0. En otras palabras, 𝐷𝑜𝑚(𝑓) = {𝑥 ∈ 𝑅 | 𝑔(𝑥) ≥ 0}.
Estudiemos ahora el caso más simple de función irracional: la función raíz
cuadrada 𝑓(𝑥) = √𝑥.
Se trata de una función en que el índice de la raíz es 2. Por tanto, su dominio
es el conjunto de soluciones de la inecuación 𝑥 ≥ 0. Así tenemos 𝐷𝑜𝑚(𝑓) =
[0 + ∞]. La imagen de la función raíz cuadrada es, como en el caso del
dominio, el conjunto de los reales mayores o igual que cero, 𝐼𝑚 = [0 + ∞].
Representación gráfica:
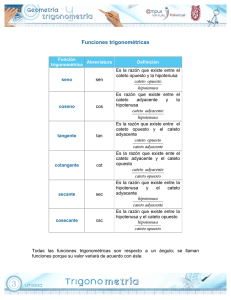
Funciones Trigonométricas.
Para definir las funciones trigonométricas del ángulo: α, del vértice A, se parte
de un triángulo rectángulo. El nombre de los lados de este triángulo rectángulo
es:



La hipotenusa (c) es el lado opuesto al
ángulo recto, o el lado más grande.
El cateto opuesto (a) es el lado opuesto al
ángulo α.
El cateto adyacente (b) es el lado adyacente
al ángulo α.
El seno de un ángulo es la relación entre la longitud del cateto opuesto y la
longitud de la hipotenusa:
sen α = opuesto/hipotenusa
El coseno de un ángulo es la relación entre la longitud del cateto adyacente
y la longitud de la hipotenusa:
cos α = adyacente/hipotenusa
La tangente de un ángulo es la relación entre la longitud del cateto opuesto
y la del adyacente:
tan α = opuesto/adyacente
La cotangente de un ángulo es la relación entre la longitud del cateto
adyacente y la del opuesto:
cot α = adyacente/opuesto
La secante de un ángulo es la relación entre la longitud de la hipotenusa y la
longitud del cateto adyacente:
sec α = hipotenusa/adyacente
6) La cosecante de un ángulo es la relación entre la longitud de la
hipotenusa y la longitud del cateto opuesto: csc α = hipotenusa/opuesto
Función Exponencial.
Se llama función exponencial de base a aquella cuya forma genérica es 𝑓(𝑥) =
𝑎 𝑥 siendo a un número positivo distinto de 1. Por su propia definición, toda
función exponencial tiene por dominio de definición el conjunto de los números
reales R.
La función exponencial puede considerarse como la inversa de la función
logarítmica
Representación gráfica de varias funciones exponenciales.
Función Logarítmica.
Una función logarítmica es aquella que genéricamente se expresa como𝑓(𝑥) =
𝑙𝑜𝑔𝑎 𝑥, siendo a la base de esta función, que ha de ser positiva y distinta de 1.
La función logarítmica es la inversa de la función 𝑙𝑜𝑔𝑎 𝑥 = 𝑏 ↔ 𝑎𝑏 = 𝑥.
Funciones polinómicas. Propiedades y características generales. (s.f.).
Recuperado 29 enero, 2020, de
http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funcione
s_elementales/teoria/polinomicas.html
Funciones polinómicas. Propiedades y características generales.. (s.f.).
Recuperado 29 enero, 2020, de
http://calculo.cc/temas/temas_bachillerato/primero_ciencias_sociales/funcione
s_elementales/teoria/polinomicas.html
Sangaku S.L. (2020) Funciones irracionales. sangakoo.com. Recuperado
de https://www.sangakoo.com/es/temas/funciones-irracionales
Qué son las funciones trigonométricas | Matemáticas Modernas. (2014, 9
septiembre). Recuperado 29 enero, 2020, de
https://matematicasmodernas.com/que-son-las-funciones-trigonometricas/
Funtzio esponentziala - hiru. (s.f.). Recuperado 29 enero, 2020, de
https://www.hiru.eus/es/matematicas/funcion-exponencial
Función logarítmica - hiru. (s.f.). Recuperado 29 enero, 2020, de
https://www.hiru.eus/es/matematicas/funcion-logaritmica