Funciones Ejercicios Resueltos

Introducción a Funciones
Nombre: ______________________________
2. Determinar si las siguientes relaciones son
funciones:
Funciones, Introducción
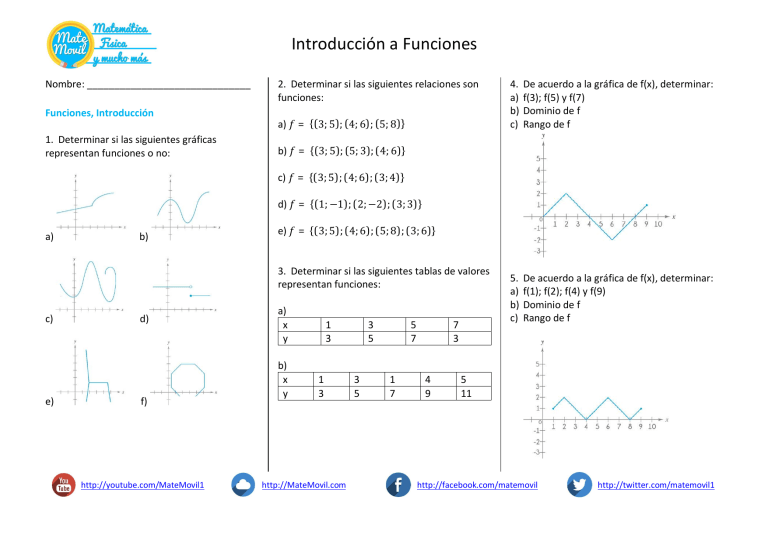
1. Determinar si las siguientes gráficas
representan funciones o no:
a)
b)
a)
= {(3; 5); (4; 6); (5; 8)}
b)
= {(3; 5); (5; 3); (4; 6)}
c)
= {(3; 5); (4; 6); (3; 4)}
d)
= {(1; −1); (2; −2); (3; 3)}
e)
= {(3; 5); (4; 6); (5; 8); (3; 6)}
3. Determinar si las siguientes tablas de valores
representan funciones:
c)
e)
d)
f)
http://youtube.com/MateMovil1
a)
x
y
b)
x
y
1
3
1
3
http://MateMovil.com
3
5
3
5
5
7
1
7
7
3
4
9
4.
a)
b)
c)
De acuerdo a la gráfica de f(x), determinar:
f(3); f(5) y f(7)
Dominio de f
Rango de f
5.
a)
b)
c)
De acuerdo a la gráfica de f(x), determinar:
f(1); f(2); f(4) y f(9)
Dominio de f
Rango de f
5
11
http://facebook.com/matemovil
http://twitter.com/matemovil1
Introducción a Funciones
Cómo graficar funciones básicas
1. Graficar la función:
4. Representar gráficamente el intervalo:
(−2; +∞)
3. A partir de la siguiente gráfica, encontrar el
dominio y rango de la función g(x)
=2 +1
5. Representar gráficamente el intervalo:
(−∞; +∞)
2. Graficar la función:
=
3. Graficar la función:
=
4. Graficar la función:
=1−
−8
5. Graficar la función ( ) = | |; siendo | | el
valor absoluto de x; teniendo en cuenta que:
− ;
<0
| |=
;
≥0
6. Representar gráficamente el intervalo:
(−5; 0]
7. Representar gráficamente el intervalo:
(−∞; +1]
8. Representar matemáticamente el siguiente
intervalo:
6. Graficar la función ( ) = √
7. Graficar la función: ( ) =
Intervalos
1. Representar gráficamente el intervalo:
[−3 ; +2]
Dominio y rango
1. Encontrar el dominio y rango de la función:
=2 +1
2. Encontrar el dominio y rango de la función
=
2. Representar gráficamente el intervalo:
(−3; +2)
5. Encontrar el dominio y rango de la función
( )=
6. Hallar el dominio y rango de la función:
( ) = √1 −
7. Encontrar el dominio y rango de la función
( )=
3. Representar gráficamente el intervalo:
(−5; 0]
http://youtube.com/MateMovil1
4. Hallar dominio y rango de la función ( ) =
√ +1
http://MateMovil.com
http://facebook.com/matemovil
http://twitter.com/matemovil1
Introducción a Funciones
Transformaciones de funciones
1. A partir de la gráfica de y = x2, graficar la
función: y = x2 – 2.
2. A partir de la gráfica de
función: = √ + 2.
3. A partir de la gráfica de
función: = | | − 3.
4. A partir de la gráfica de
función: = √ − 2.
= √ , graficar la
11. A partir de la gráfica de = √ , graficar la
función = √− ; además
= −√
= | |, graficar la
= | |, graficar la
12. A partir de la gráfica de
función: = −| | + 1
= √ , graficar la
= √ , graficar la
13. A partir de la gráfica de
función: = 2 + √− + 1.
14. A partir de la gráfica de
función: = −( + 1)
=
, graficar la
15. A partir de la gráfica de =
función: =
;
=−
, graficar la
5. A partir de la gráfica de = , graficar la
función: =
+ 3 + 3 + 1.
2
6. A partir de la gráfica de y = x , graficar la
función: y = (x – 4)2.
7. A partir de la gráfica de
función: = | − 1| + 2.
10. A partir de la gráfica de y = x2, graficar la
función: y = -x2.
= | |, graficar la
8. A partir de la gráfica de y = x2, graficar la
función: = 3 + ( + 2) .
9. A partir de la gráfica de la función
graficar la función = 2 + 1.
http://youtube.com/MateMovil1
16. A partir de la gráfica de
función = √ + 4 − 3.
18. A partir de la gráfica de
función = | − 1|
= | |, graficar la
= √ , graficar la
Función compuesta
17. A partir de la gráfica de f(x), graficar la
función y = f(2x); y = f(2x) + 1.
1. Si f(x) = x2 , g(x) = x + 1; encontrar la función
(fog)(x) y (fog)(5).
2. Si f(x) = 2x , g(x) = 1 – x ; encontrar la función
(fog)(x).
=2 ,
http://MateMovil.com
http://facebook.com/matemovil
http://twitter.com/matemovil1
Introducción a Funciones
3. Si ( ) = ; ( ) = 2 + 4; encontrar fog
y su dominio.
4. Si ( ) = ; ( ) = 2 + 4; encontrar gof
y su dominio.
5. Si ( ) = ; ( ) =
dominio.
; encontrar fog y su
6. Si ( ) = √ ; ( ) = √2 − ; encontrar
gof y su dominio.
7. Si ( ) =
√
; ( ) = ; encontrar fog y su
dominio.
8. Si ( ) =
;
Encontrar fogoh
9. Si ( ) = √ ;
Encontrar fogoh.
( )=
( )=
; ℎ( ) =
+ 2.
; ℎ( ) = √ .
10. Dada la función H(x), encontrar las
funciones f y g, tales H = fog. ( ) = ( − 3)
11. Dada la función H(x), encontrar las
funciones f y g, tales H = fog.
12. Dada la función H(x), encontrar las
funciones f y g, tales H = fog. ( ) = | + 1|
13. Se deja caer una roca en un lago, lo cual
provoca una onda circular que avanza hacia
afuera con una rapidez de 0,5 m/s.
a) Hallar la función r que modele el radio de
la onda en función del tiempo.
b) Hallar la función A que modele el área del
círculo en función del radio de la onda.
c) Hallar la función Aor; ¿qué representa
dicha función?
14. Un globo de helio está siendo inflado, y con
ello, el radio del globo aumenta a razón de
1cm/s. Encontrar la función que relaciona el
área superficial (A) del globo de helio con el
tiempo(t).
4. Determinar si la siguiente función es
sobreyectiva: : ℝ → ℝ ; ( ) = + 2
5. Determinar si la siguiente función es
sobreyectiva: : ℝ → ℝ ; ( ) =
+1
6. Determinar si la siguiente función es
sobreyectiva: : ℝ → ℝ ; ( ) = √
7. Determinar si la siguiente función es
biyectiva: ( ) =
+1
8. Determinar si la siguiente función
: [0 ; +∞) → [0 ; +∞) tal
que
( )=
+ 1 es biyectiva.
Función Inyectiva, Sobreyectiva y Biyectiva
9. Determinar si la función ( ) =
inyectiva, sobreyectiva o biyectiva.
1. Determinar si la siguiente función es
inyectiva: ( ) = + 2
Función par e impar (simetrías, paridad)
2. Determinar si la siguiente función es
inyectiva: ( ) =
+1
es
1. Determinar si la siguiente función es par o no:
( )=
+1
2. Determinar si la siguiente función es impar o
no: ( ) = +1
( )=
http://youtube.com/MateMovil1
3. Determinar si la siguiente función es
inyectiva: ( ) = √
http://MateMovil.com
http://facebook.com/matemovil
http://twitter.com/matemovil1
Introducción a Funciones
Funciones crecientes, decrecientes y
constantes
Determinar los intervalos de crecimiento y
decrecimiento de las siguientes funciones
(utilice la gráfica cuando esté en el problema):
Determinar si las siguientes funciones son pares,
impares o no tienen paridad:
3. ( ) =
+
4.
( )=3 −
5.
( )=1−
6.
( )=
7.
( ) = −7
8.
( ) = ( − 1)
9.
( )=
10.
1.
( )=
2.
( )=
+2
+1
−2
−4
( )=
11. ¿Cuál es la función que es par e impar a la
vez?
12. A partir de la gráfica, determinar si se trata
de una función par, impar o no tiene paridad.
http://youtube.com/MateMovil1
Intersecciones de una gráfica con ejes X e Y
Encontrar las intersecciones con los ejes en las
gráficas de las funciones:
1. ( ) = 2 + 2
2.
( )=2 −5
3.
( )=
−1
4.
( )=
−4
5.
( )=
+
6.
( ) = √16 −
7.
( )=4
http://MateMovil.com
−2
+3
http://facebook.com/matemovil
http://twitter.com/matemovil1
Introducción a Funciones
3.
5.
( )=
6.
4.
( )=
( )=√ +1
( )=
7. La siguiente gráfica muestra la altura del nivel
de agua en una tina de baño en función del
tiempo. Interprete la gráfica y de una
descripción de lo que puede estar ocurriendo
en la tina.
−3 ;
−3 +2
http://youtube.com/MateMovil1
http://MateMovil.com
http://facebook.com/matemovil
http://twitter.com/matemovil1