EJERCICIOS PROGRAMACION

ESCUELA SUPERIOR POLITECNICA DE CHIMBORAZO
FACULTAD DE MECÁNICA
ESCUELA DE INGENIERIA INDUSTRIAL
INGENIERIA INDUSTRIAL
ÁREA DE CIENCIAS BÁSICAS
PROGRAMACIÓN II
TEMA: GRÁFICAS BIDIMENSIONALES
1.- DATOS INFORMATIVOS
- NOMBRES Y APELLIDOS: LUIS FERNANDO CARRERA REYES
- FECHA: 2017– 02 - 20
-CORREO PERSONAL: [email protected]
- CÓDIGO:
2122
-PERIODO ACADÉMICO:
OCTUBRE – MARZO
Riobamba – Ecuador
EJERCICIO 1
La campana de Gauss es una es una representación gráfica de la distribución
normal de un grupo de datos. Esta herramienta es muy utilizada en el campo
estadístico Este gráfico se usa en variables asociadas a fenómenos naturales
como caracteres morfológicos de individuos como la estatura, el peso, edad
entre otros datos. Pues dicha función nos permite encontrar la media del grupo
de datos analizados. La función Gaussiana está establecida por constantes de
la desviación típica (a), varianza (b) , la media (c) además la ecuación es la
siguiente
(𝑥 − 𝑏) 2
𝑓(𝑥) = 𝑎 ∗ 𝑒 ∗ (−(
))
2𝑐
Si conocemos que
𝑏= 1
𝑐=
1
2√2
a) Hallar el valor máximo de la campana de Gauss para
a=1 ; a=2; a= 3 ; a=4
b) Realizar la gráfica de la campana de Gauss para cada uno de los valores
en un mismo eje cartesiano utilizando el comando Hold on
c) Insertar una leyenda en la que se muestre cual es el valor máximo de
cada curva
d) Modificar las propiedades de color y tipo de línea de cada curva
e) Insertar un título y nombre de los ejes en la gráfica
f) Insertar la cuadricula en la gráfica
% RESOLUCIÓN
% Datos de las incogrnitas
a1= 1;
a2= 2;
a3= 3;
a4= 4;
b= 1;
c=(1/2*sqrt(2))
% Formulacion de las funciones
x=linspace(-2,4,500);
y1= a1*exp(-(((x-b).^2)/(2*c^2)));
y2= a2*exp(-(((x-b).^2)/(2*c^2)));
y3= a3*exp(-(((x-b).^2)/(2*c^2)));
y4= a4*exp(-(((x-b).^2)/(2*c^2)));
% Valores máximos de las funciones
v1=max(y1)
v2=max(y2)
v3=max(y3)
v4=max(y4)
% Graficación
hold on
plot(x,y1,'b -')
plot(x,y2,'r--')
plot(x,y3,' g -.')
plot(x,y4,'y p')
title('CAMPANA DE GAUSS')
xlabel('EJE X')
ylabel('EJE Y')
legend('exp(-x^2) Valor Máximo= 1 ', '2*exp(-x^2) Valor Máximo= 2','3*exp(-x.^2)
Valor Máximo= 3','4*exp(-x.^2) Valor Máximo= 3.99')
grid on
EJERCICIO 2
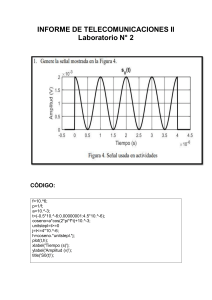
La bocina de un automóvil emite una onda de sonido que se encuentra en función
de la siguiente función matemática:
y= sin(25./x).*x;
Considerando que la máxima altura de la onda se produce a los 2 segundos de
emitida la misma
a) Determine la gráfica de disipación de la onda en función de las variables
ALTURA –TIEMPO
b) Modifique las propiedades de la gráfica para que la gráfica sea de color
amarillo y de Tipo de Línea punteada
c) Insertar un Título a la grafica
d) Insertar el nombre a los ejes de la grafica
e) Insertar rejillas en la gráfica
f) Insertar una leyenda en la Gráfica Altura – Tiempo
% RESOLUCIÓN
x=[0:0.0001:2];
y= sin(25./x).*x;
plot(x,y,'y h')
title('ONDA DE SONIDO')
xlabel('TIEMPO')
ylabel('ALTURA')
grid on
legend('Gráfica Altura - Tiempo')
EJERCICIO 3
Se desea diseñar una turbina de avión para lo cual se necesita construir un
número determinado de aletas de entrada de aire. Para la construcción de dicho
elemento se desarrolló la siguiente fórmula matemática que determinara el
número de aletas a construir
f= sin(a*tetha).*cos(a*tetha)
a) Realizar la representación gráfica de dicha función utilizando el tipo de
graficación POLAR para a =3 y a =5
Nota: Para mejor apreciación de la gráfica representarlo en u intervalo
de 0 a 2pi con un intervalo de 0.01
b) Realizar que la gráfica sea de color amarillo y de color verde
respectivamente
c) Insertar un título a cada gráfica
d) Insertar una leyenda a la gráfica especificando el número total de aletas
de entrada de aire (12 y 22 respectivamente)
%
RESOLUCIÓN
a= 3;
a1= 5;
tetha= 0:0.01:2*pi
f= sin(a*tetha).*cos(a*tetha);
subplot(2,1,1)
polar(tetha,f,'y')
f1= sin(a1*tetha).*cos(a1*tetha);
title('DISEÑO DE LA TURBINA AVIÓN')
xlabel('GRAFICA POLAR')
legend('Número de aletas de entrada de aire = 12')
hold on
subplot(2,1,2)
polar(tetha,f1,'g')
title('DISEÑO DE LA TURBINA AVIÓN')
xlabel('GRAFICA POLAR')
legend('Número de aletas de entrada de aire = 22 ')
EJERCICIO 4
Por motivos de estudio y de mejor comprensión de las funciones trigonométricas
se desea conocer el comportamiento de las funciones seno, coseno, tangente y
arco seno dentro de un mismo intervalo de valores.
a) Realice la gráfica de cada una de las funciones mencionadas
b) Utilizando el comando subplot divida la ventana de graficación para
graficar en una misma ventana las funciones anteriormente mencionadas
c) Insertar nombres de los ejes y títulos en cada gráfica
d) Insertar los siguientes colores a cada gráfica
Para la función 1 insertar el color rojo
Para la función 2 insertar el color amarillo
Para la función 3 insertar el color azul
Para la función 4 insertar el color magenta
% RESOLUCIÓN
x=-5*pi: pi/100:5*pi ;
y= sin (x)
subplot(2,2,1);
plot (x,y,'r');
title('FUNCIÓN SENO')
xlabel('EJE X')
ylabel('EJE Y')
grid on
y1= cos(x)
subplot(2,2,2);
plot (x,y1,'y');
title('FUNCIÓN COSENO')
xlabel('EJE X')
ylabel('EJE Y')
grid on
y2= tan(x)
subplot(2,2,3);
plot(x,y2,'b');
title('FUNCIÓN TANGENTE')
xlabel('EJE X')
ylabel('EJE Y')
grid on
y3= asin(x)
subplot(2,2,4);
plot(x,y3,'m');
title('FUNCIÓN ARCOSENO')
xlabel('EJE X')
ylabel('EJE Y')
grid on
EJERCICIO 5
Para el estudio matemático del dominio de funciones se conoce que
circunferencia está representada por las siguientes funciones
a)
b)
c)
d)
e)
una
𝑦 = √𝑎 − 𝑥 2
𝑦 = − √𝑎 − 𝑥 2
Graficar ambas funciones formando una circunferencia si a=4 y el
dominio de dicha función va de -2 a 2
Realizar el relleno del área bajo la curva de cada una de las funciones
con colores diferentes utilizando el comando FILL
Insertar un título a la gráfica
Insertar nombres a los ejes e insertar rejillas
Insertar una leyenda en la que indique cual es el color de cada función.
%
RESOLUCIÓN
x= -2:0.01:2
y= sqrt(4-x.^2)
z= -sqrt(4-x.^2)
plot(x,y,x,z)
fill(x,y,'y',x,z,'b')
title('DOMINIO DE LA FUNCIÓN')
legend('Funcion Positiva','Funcion Negativa')
xlabel('EJE X')
ylabel('EJE Y')
grid on
EJERCICIO 6
Diseño de gráficas bidimensionales
Diseñe 4 gráficas Polares las cuales cumplan con las siguientes condiciones
Nota: Recuerde que para realizar las espirales debe definirse los intervalos, pero
el número de valores dentro del intervalo debe ser un valor alto Ejemplo:
x=linspace(0,2*pi,1000);
a) Utilice el comando linspace para definir el intervalo de las espirales
las cuales deben tener los siguientes intervalos
1. 0 – 10 pi
2. 0 – 25 pi
3. 0 – -10 pi
4. 0 - -5pi
b) Utilizando el comando subplot divida la ventana de graficación para
graficar en una misma ventana las funciones anteriormente
mencionadas
c) Insertar un título a cada gráfica
d) Inserte diferentes colores para cada gráfica
% RESOLUCION
clear
clc
theta=linspace(0,10*pi,1000);
r=theta;
subplot(2,2,1);
polar(theta,r,'r');
title('INTERVALO DE 0-10pi')
theta=linspace(0,25*pi,300);
r=theta;
subplot(2,2,2);
polar(theta,r,'y');
title('INTERVALO DE 0-25pi')
theta=linspace(0,-10*pi,300);
r=theta;
subplot(2,2,3);
polar(theta,r,'g');
title('INTERVALO DE 0- -10pi')
theta=linspace(0,-5*pi,300);
r=theta;
subplot(2,2,4);
polar(theta,r,'m');
title('INTERVALO DE 0- -5pi')
EJERCICIO 7
Se requiere diseñar un logotipo para una empresa para lo cual un
grupo de estudiantes han desarrollado la siguiente ecuación (tita) que
representará varios polígonos y figuras que pueden servir de logotipo.
n = A;
R = 1;
tita = [0:(4*pi/n):4*pi]+pi/2;
x = R*cos(tita);
y = R*sin(tita);
a) Realizar 4 gráficas sabiendo que el valor de A es igual a:
A= 5
A= 15
A= 3
A= 20
b) Realizar el relleno con diferentes colores utilizando la función FILL
c) Insertar nombres a los ejes y leyendas
%
RESOLUCIÓN
n = 5;
R = 1;
tita = [0:(4*pi/n):4*pi]+pi/2;
x = R*cos(tita);
y = R*sin(tita);
subplot(2,2,1)
plot(x,y)
fill(x,y,'y')
xlabel('EJE X')
ylabel('EJE Y')
legend('LOGOTIPO 1')
n = 15;
R = 1;
tita = [0:(4*pi/n):4*pi]+pi/2;
x = R*cos(tita);
y = R*sin(tita);
subplot(2,2,2)
plot(x,y)
fill(x,y,'g')
xlabel('EJE X')
ylabel('EJE Y')
legend('LOGOTIPO 2')
n = 3;
R = 1;
tita = [0:(4*pi/n):4*pi]+pi/2;
x = R*cos(tita);
y = R*sin(tita);
subplot(2,2,3)
plot(x,y)
fill(x,y,'b')
xlabel('EJE X')
ylabel('EJE Y')
legend('LOGOTIPO 3')
n = 20;
R = 1;
tita = [0:(4*pi/n):4*pi]+pi/2;
x = R*cos(tita);
y = R*sin(tita);
subplot(2,2,4)
plot(x,y)
fill(x,y,'r')
xlabel('EJE X')
ylabel('EJE Y')
legend('LOGOTIPO 4')
EJERCICIO 8
Por motivos de aprendizaje un profesor de matemáticas desea facilitar la
identificación de las diferentes graficas de las funciones Cuadrática,
Exponencial, Irracional y Logarítmica para lo cual envía como tarea a sus
estudiantes el graficar en Matlab las siguientes funciones y que además lo
identifiquen con colores diferentes
Funciones:
y1= (x1.^2)+(3.*x1
y2= sqrt((2.*x2) + 1)
y3= exp(5.*x3
y4= log(1.*x4
Además se pide insertar un título en cada gráfica, nombre a los ejes cuadricula
y una leyenda para cada gráfica
}%RESOLUCION
x1= -5:0.001:5;
y1= (x1.^2)+(3.*x1);
subplot(2,2,1)
plot(x1,y1,'d g')
title('FUNCIÓN CUADRATICA')
xlabel('EJE X')
ylabel('EJE Y')
legend('FUNCIÓN 1 ')
grid on
x2= 0:0.01:20;
y2= sqrt((2.*x2) + 1);
subplot(2,2,2)
plot(x2,y2,'r s')
title('FUNCIÓN IRRACIONAL')
xlabel('EJE X')
ylabel('EJE Y')
legend('FUNCIÓN 2 ')
grid on
x3= 0:0.01:3;
y3= exp(5.*x3);
subplot(2,2,3)
plot(x3,y3,'+ b')
title('FUNCIÓN EXPONENCIAL')
xlabel('EJE X')
ylabel('EJE Y')
legend('FUNCIÓN 3 ')
grid on
x4= 0:0.01:3;
y4= log(1.*x4);
subplot(2,2,4)
plot(x3,y3,'. y')
title('FUNCIÓN LOGARITMICA')
xlabel('EJE X')
ylabel('EJE Y')
legend('FUNCIÓN 4 ')
grid on
EJERCICIO 9
Las curvas de las órbitas de 5 planetas ubicados en cierto sistema solar están
representadas por las siguientes ecuaciones
y = - x.^2
y1 = 5 - x.^2
y2 = 3 - x.^2;
y3 = 2 - x.^2;
y4 = 1 - x.^2;
a)
b)
c)
d)
%
Represente gráficamente cada una de las orbitas dadas
Asigne un color diferente a cada orbita
Asigne una leyenda a cada orbita
Agregue un título y nombre a los ejes
RESOLUCION
x = linspace(-3,3,100);
y = - x.^2;
plot(x,y,'b');
legend('PLANETA A','PLANETA B','PLANETA C','PLANETA D','PLANETA E');
title('SISTEMA SOLAR')
xlabel ('EJE X')
ylabel (' EJE Y')
hold on
y1 = 5 - x.^2;
plot(x,y1,'r');
y2 = 3 - x.^2;
plot(x,y2,'b');
y3 = 2 - x.^2;
plot(x,y3,'r');
y4 = 1 - x.^2;
plot(x,y4 ,'y');
grid on
EJERCICIO 10
El desplazamiento de una partícula se describe por las siguientes ecuaciones
lineales
1. 𝑦 = 2𝑥
de 0 a 10 segundos
1
2. 𝑦 = 2 𝑥 + 15 de 10 a 30 segundos
3. 𝑦 = −2𝑥 + 90
a)
b)
c)
d)
de 30 a 50 segundos
Graficar las ecuaciones lineales en el intervalo de tiempos establecidos
Diferenciar cada desplazamiento con un color y tipo de línea diferente
Insertar una leyenda que describa cada desplazamiento
Insertar un título a la gráfica, nombre a los ejes y a cuadricula
%
RESOLUCION
% DESPLAZAMIENTO 1
x= [0:1:10];
y= 2.*x;
plot(x,y,'y p')
% DESPLAZAMIENTO 2
hold on
x2= 10:1:30;
y2= (1/2).*x2 +15;
plot(x2,y2,'d g')
% DESPLAZAMIENTO 3
x3= 30:1:50;
y3= -2.*x3+90;
plot(x3,y3,'> r')
grid on
title('GRAFICA DISTANCIA (m) - TIEMPO (s)')
xlabel('TIEMPO(segundos)')
ylabel('DISTANCIA (metros)')
legend(' DESPLAZAMIENTO INICIAL',' DESPLAZAMIENTO INTERMEDIO',
'DESPLAMIENTO FINAL')