Presentacion-Teoremas

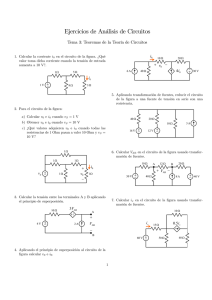
Tema 3. Teoremas de la Teoría de Circuitos
3.1 Introducción
3.2 Superposición
3.3 Transformación de fuentes
3.4 Teorema de Thevenin
3.5 Teorema de Norton
RTh
+
− VTh
A
+
v
−
i
RL
B
3.6 Máxima transferencia de potencia
Análisis de Circuitos (G-286). Grado en Ingeniería de Tecnologías de Telecomunicación
José A. Pereda, Dpto. Ing. de Comunicaciones, Universidad de Cantabria.
1
Bibliografía Básica para este Tema:
[1] C. K. Alexander, M. N. O. Sadiku, “Fundamentos de circuitos
eléctricos”, 3ª ed., McGraw-Hill, 2006.
[2] R. C. Dorf, J. A. Svoboda, “Introduction to electric circuits”,
7th ed., John Wiley & Sons, 2006.
Sadiku  Tema 4
Dorf  Tema 5
- Esta presentación se encuentra, temporalmente, en:
http://personales.unican.es/peredaj/AC.htm
2
3.1 Introducción
- Como hemos visto en temas anteriores, las ecuaciones de Kirchhoff
permiten analizar un circuito sin alterar su configuración original.
- Sin embargo, la complejidad creciente de los circuitos que se usan en
la práctica hace que los cálculos se vuelvan tediosos.
- En este tema veremos un conjunto de técnicas que permiten reducir
la complejidad que un circuito antes de proceder a su análisis:
- El principio de superposición
- La transformación de fuentes
- Los teoremas de Thevenin y Norton
3
3.2 Superposición
- Un circuito lineal es aquél que sólo tiene elementos lineales y fuentes
- Un elemento lineal es aquél cuya relación i-v es lineal:
v = a i, con a = cte
- En esta asignatura sólo se consideran circuitos lineales
- Los circuitos lineales verifican el principio de superposición
El principio de superposición establece que la tensión entre los
extremos (o corriente a través) de un elemento de un circuito
lineal es la suma algebraica de las tensiones (o corrientes) a través
de ese elemento debidas a cada una de las fuentes independientes
cuando actúa sola.
- El principio de superposición ayuda a analizar un circuito lineal con
más de una fuente independiente mediante el cálculo de la contribución
de cada fuente independiente por separado
4
3.2 Superposición
- La aplicación del principio de superposición tiene los siguientes pasos:
1. Apagar todas las fuentes independientes excepto una.
Encontrar la salida (tensión o corriente) debido a la fuente activa.
2. Repetir el paso anterior para cada una de las fuentes
independientes presentes en el circuito.
3. La contribución total vendrá dada por la suma algebraica de las
contribuciones de cada una de las fuentes independientes.
- Observaciones:
- Apagar una fuente independiente de tensión implica reemplazarla
por una fuente de tensión de 0V (cortocircuito)
- Apagar una fuente independiente de corriente implica reemplazarla
por una fuente de corriente de 0A (circuito abierto)
- Las fuentes dependientes no se modifican
5
-Ejemplo 1: Calcular v en el circuito de la figura, aplicando el principio
de superposición. Ra = 8 Ohm, Rb = 4 Ohm, Vs = 6 V, Is = 3 A
A&S-3ª Ej. 4.3
Ra
Vs +
−
+
v Rb
−
Is
6
Solución:
- Puesto que hay dos fuentes
v = v1 + v2
- v1 es la tensión debida a Vs con Is=0
- v2 es la tensión debida a Is con Vs=0
Ra
Vs +
−
- Cálculo de v1: (dejamos Is en circuito abierto)
- Aplicando la KVL: Vs = Ra i + Rb i
- luego i =
- Por tanto
Vs
6
= 0.5 A
=
Ra + Rb 8 + 4
+
v Rb
−
VS +
−
Is
Ra
i
Rb
+
v1
−
v1 = Rbi = 4 × 0.5 = 2 V
7
- Cálculo de v2: (cortocircuitamos Vs )
- Aplicando la KCL: I s =
v2 v2
+
Ra Rb
Ra Rb
8× 4
- luego v2 =
×3 = 8 V
Is =
8+ 4
Ra + Rb
- La solución final es:
Ra
+
Is
v2 Rb
−
v = v1 + v2 = 2 + 8 = 10 V
8
3.3 Transformación de fuentes
- La transformación de fuentes se usa para simplificar circuitos
Una transformación de fuentes es el proceso de sustituir una
fuente de tensión vs en serie con una resistencia R por una fuente
de corriente is en paralelo con una resistencia R, o viceversa
R
+
− vs
i
i
A
+
v
−
circuito
⇔
is
A
+
R v
−
circuito
B
B
vS = RiS
9
3.3 Transformación de fuentes
- Comprobación
R
i
A
+
v
−
+
− vs
circuito
vs v
vs = Ri + v ⇒ i = −
R R
B
i
is
A
+
R v
−
- Aplicando KCL:
circuito
B
- Aplicando KVL:
vs
is =
R
v
v
is = + i ⇒ i = is −
R
R
¡Debe cumplise para que ambos
circuitos sean equivalentes!
10
-Ejemplo 2: Calcular v0 en el circuito de la figura. Para ello, reducir el
circuito a un divisor de corriente aplicando transformación de fuentes
A&S-3ª Ej. 4.6
3Ω
2Ω
4Ω
3A
8Ω
+
v0
−
+
−
12 V
11
Solución:
3Ω
2Ω
4Ω
3A
8Ω
+
v0
−
+
−
12 V
- Comenzamos transformando la fuente de corriente a una de tensión:
vS = RiS = 4 × 3 = 12 V
4Ω
12 V
−
+
3Ω
2Ω
8Ω
+
v0
−
+
−
12 V
- Ahora, asociamos las dos resistencias en serie:
12
6Ω
12 V
−
+
3Ω
8Ω
+
v0
−
+
−
12 V
- Seguidamente, transformamos las fuentes de tensión:
vS 12
=4A
iS = =
R 3
v
12
iS = S =
=2A
R 6
2A
6Ω
8Ω
+
v0
−
3Ω
4A
- Agrupando resistencias y fuentes:
13
i0
6 Ω || 3 Ω =
6×3
= 2Ω
6+3
2A
2Ω
8Ω
+
v0
−
- Por último, usamos la fórmula del divisor de corriente:
2
i0 =
× 2 = 0.4 A
2+8
- y la ley de Ohm:
v0 = Ri0 = 8 × 0.4 = 3.2 V
14
3.4 Teorema de Thevenin
- Suele ocurrir que un elemento de un circuito sea variable (carga),
mientras que los demás permanecen fijos. Entonces, cada vez que se
cambia la carga debemos volver a analizar todo.
- El teorema de Thevenin proporciona una técnica para sustituir la parte
fija por un circuito equivalente sencillo.
El teorema de Thevenin establece que un circuito lineal de dos
terminales puede sustituirse por un circuito equivalente formado
por una fuente de tensión VTh en serie con una resistencia RTh
i
circuito lineal
de dos
terminales
RTh
A
+
v
−
carga
B
Circuito original
+
− VTh
i
A
+
v
−
carga
B
Circuito equivalente
de Thevenin
15
3.4 Teorema de Thevenin
- Cálculo de la tensión equivalente de Thevenin:
- Utilizamos como circuito de carga un circuito abierto
RTh i = 0
A
i=0A
circuito lineal
de dos
terminales
+
voc
−
+
− VTh
+
voc = VTh
−
B
B
- En esta situación se cumple
VTh = voc
16
3.4 Teorema de Thevenin
- Cálculo de la resistencia equivalente de Thevenin, RTh:
- Se ponen a cero las fuentes independientes. Entonces la RTh coincide
con la resistencia de entrada Rin vista en los terminales del circuito
A
circuito con
fuentes
independientes
puestas a cero
Rin
B
RTh
+
− VTh = 0
A
RTh = Rin
B
- Entonces
RTh = Rin (con las fuentes independientes a cero)
- Poner las fuentes independientes a cero significa:
1. Cortocircuitar las fuentes independientes de tensión
2. Dejar en circuito abierto las fuentes independientes de corriente
17
3.4 Teorema de Thevenin
- Determinación de la resistencia de entrada Rin:
- CASO 1: Circuito SIN fuentes dependientes.
1. Se ponen las fuentes independientes a cero
2. Se calcula Rin mediante asociación de resistencias
A
circuito con
fuentes
independientes
puestas a cero
Rin
B
18
-Ejemplo 3: Calcular el equivalente Thevenin del circuito de la figura
A&S-3ª Ej. 4.8
4Ω
32 V
+
−
12 Ω
1Ω
A
2A
B
19
Solución:
4Ω
32 V
+
−
1Ω
12 Ω
A
2A
B
- Comenzamos calculando la resistencia Thevenin. Para ello, ponemos a
cero las fuentes independientes y calculamos la resistencia de entrada
4Ω
12 Ω
1Ω
A
Rin
B
4 ×12
Rin = (4 Ω || 12 Ω ) + 1 Ω =
+1 = 4 Ω
4 + 12
20
- Para obtener la tensión Thevenin calculamos la tensión de circuito
abierto en los terminales A-B
4Ω
32 V
+
−
1Ω
A
i=0
12 Ω
2A
+
VTh
−
B
- Resolvemos por análisis de nudos
4Ω
- KCL: i1 + i3 = i2
- Usando la ley de Ohm:
32 − VTh
VTh
+2=
4
12
- Despajando:
32 V
+
−
i1 VTh
i3
i2
12 Ω
2A
VTh = 30 V
21
- Por tanto:
4Ω
32 V
+
−
1Ω
12 Ω
A
2A
B

4Ω
30 V
A
+
−
B
22
3.4 Teorema de Thevenin
- Determinación de la resistencia de entrada Rin:
- CASO 2: Circuito CON fuentes dependientes.
1. Se ponen las fuentes independientes a cero
2a. Se aplica una fuente de tensión v0 entre los terminales AB y se
calcula la corriente i0 que circula por la fuente.
2b. O bien, se aplica una fuente de corriente i0 entre los terminales
AB y se calcula la tensión v0 entre dichos terminales.
Entonces Rin=v0/i0
i0
A
circuito con
fuentes
independientes
puestas a cero
A
+
− v0
circuito con
fuentes
independientes
puestas a cero
B
(2a)
Rin = v0 i0
+
v0
−
i0
B
(2b)
Rin = v0 i0
23
-Ejemplo 4: Calcular el equivalente Thevenin del circuito de la figura
A&S-3ª Ej. 4.9
2 vx
+
2Ω
2Ω
5A
4Ω
+
vx
−
A
6Ω
B
24
2 vx
+
Solución:
2Ω
2Ω
4Ω
5A
+
vx
−
A
6Ω
B
- Comenzamos calculando la resistencia Thevenin. Para ello, ponemos a
cero las fuentes independientes, ponemos una fuente de tensión v0
entre los terminales y calculamos la corriente que pasa por ella.
2 vx
+
2Ω
2Ω
4Ω
+
vx
−
i0
A
6Ω
Rin = v0 i0
+
− v0
25
B
- Resolvemos por análisis de nudos:
2 vx
- Aplicando la KCL:
i2 = i1 + ix
- NUDO D: i0 + ix = i2 + i3
- Sumando C + D: i0 = i1 + i3
- NUDO C:
4Ω
- Ley Ohm:
v0 − 3v x
i0 =
2
vx
i1 =
4
2Ω
C
i1
3v x
i3 =
6
+
ix
+
vx
−
D
2Ω
i0
A
i2
i3
6Ω
+
− v0
B
VC = v x ; VD = 3v x ; VA = v0
- En función de las tensiones de nudo:
v0 − 3v x v x 3v x
= +
6
2
4
2
v
=
v0
- de donde x
9
v0 − 3v x
- De la ley de Ohm en A-D: i0 =
2
v0
= RTh = 6Ω
i0
26
- Para obtener la tensión Thevenin calculamos la tensión de circuito
abierto
2 v x ix
+
- Resolvemos por análisis de nudos:
- NUDO C:
i2 + 5 = i1 + ix
- NUDO D:
ix = i2 + i3
i1
5A
2Ω
C
4Ω
- En función de las tensiones de nudo:
+
vx
−
i2
2Ω
D
i3
i=0
6Ω
VC = v x ;
A
+
VTh
−
B
VD = VA = VTh = 3v x
2v x
vx
+ 5 = + ix
2
4
2v 3v
ix = x + x
2
6
20
vx =
V
3
VTh = 3v x = 20 V
27
3.5 Teorema de Norton
- El teorema de Norton es el dual del teorema de Thevenin
El teorema de Norton establece que un circuito lineal de dos
terminales puede sustituirse por un circuito equivalente formado
por una fuente de corriente IN en paralelo con una resistencia RN
i
circuito lineal
de dos
terminales
i
A
+
v
−
carga
B
Circuito original
IN
RN
A
+
v
−
carga
B
Circuito equivalente
de Norton
28
3.5 Teorema de Norton
- Cálculo de la corriente de Norton:
- Utilizamos como circuito de carga un corto circuito
isc
circuito lineal
de dos
terminales
isc
A
A
+
+
v=0
−
IN
RN v = 0
−
B
B
- En esta situación se cumple
I N = isc
29
3.5 Teorema de Norton
- Cálculo de la resistencia de Norton:
- Partimos del equivalente Thevenin y aplicamos transformación
de fuentes
RTh
+
− VTh
i
A
+
v
−
B
i
RN = RTh
IN
VTh
IN =
RTh
- Además, teniendo en cuenta que
RN
A
+
v
−
B
VTh = voc
I N = isc
- se obtiene
RTh = RN =
VTh voc
=
IN
isc
30
- Ejemplo 5: Calcular el equivalente Norton del circuito de la figura.
Is = 2 A, Vs = 12 V, R1 = 4 Ohm, R2 = R4 = 8 Ohm, R3 = 5 Ohm
A&S-3ª Ej. 4.11
R2
A
R1
R3
Is
Vs +
−
R4
B
31
Solución:
- Cálculo de la resistencia equivalente de Norton RN
- Ponemos a cero las fuentes independientes
R2
A
R3
R1
R4
RN
B
20 × 5
= 4Ω
RN = ( R1 + R2 + R4 ) || R3 = 20 || 5 =
20 + 5
32
- Cálculo de la fuente de corriente equivalente de Norton IN
- Calculamos la corriente de cortocircuito
+ V2 −
Is
+
R2
V1 R1
i1
−
Vs +
R4
−
−
- Malla 1: i2 = I S
- KVL para la malla 2:
V4
A
I N = isc
R3 i2
+
B
− Vs − V1 + V2 + V4 = 0
− Vs − R1 ( I S − i2 ) + R2i2 + R4i2 = 0
- Resolviendo:
i2 =
Vs + R1 I S
12 + 4 × 2
=
=1A
R1 + R2 + R4 4 + 8 + 8
I N = i2 = 1 A
33
3.6 Máxima transferencia de potencia
- En muchas situaciones prácticas un circuito se diseña para suministrar
potencia a una carga
En condiciones de circuito fuente fijo y carga variable, la
transferencia de potencia a la carga es máxima cuando la
resistencia de carga RL es igual a la resistencia del equivalente
Thevenin del circuito fuente RTh visto desde la fuente
RTh
circuito
fuente
RL
⇒
A
+
− VTh
RL
B
p = pmax ⇒ RL = RTh
34
3.6 Máxima transferencia de potencia
- Demostración
- Partimos del equivalente Thevenin
del circuito fuente
RL
v=
VTh
RTh + RL
v
VTh
i=
=
RL RTh + RL
RTh
+
− VTh
RL
2
p = vi =
V
(RTh + RL )2 Th
A
+
v
−
i
RL
B
∂p
RTh − RL
2
=
V
- Para encontrar el máximo derivamos:
Th
∂RL (RTh + RL )3
∂p
= 0 ⇒ RL = RTh
- Igualando a cero la derivada:
∂RL
∂ 2p
- Se puede comprobar que
<0
2
∂RL
VTh2
pmax =
- La potencia máxima resulta:
4 RL
35
- Ejemplo 6: Determinar el valor de RL para que la transferencia de
potencia en el circuito de la figura sea máxima. Calcular la potencia
máxima.
A&S-3ª Ej. 4.13
6Ω
12 V
+
−
12 Ω
3Ω
2Ω
A
RL
2A
B
36
Solución:
- Comenzaremos determinando el equivalente Thevenin del
circuito fuente
- Cálculo de la resistencia Thevenin RTh
6Ω
3Ω
12 Ω
2Ω
A
RTh
B
RTh = (6Ω || 12Ω ) + 3Ω + 2Ω =
6 ×12
+3+ 2 = 9 Ω
6 + 12
37
- Cálculo de la tensión Thevenin VTh
+
12 V
+
−
6Ω
− +
3Ω
+
2Ω
A
+
+
i2 v x
−
12 Ω
i1
−
−
2A
VTh
−
B
- Malla 1: − 12 + 6i1 + 12(i1 + 2) = 0
- Malla 2: i2 = −2 A
- Cálculo de VTh:
6Ω
VTh = 12 − 6i1 − 3i2
VTh = 22 V
12 V
+
−
i1
2
i1 = − A
3
3Ω
i2
2Ω
i=0
A
+
VTh
−
B
38
- Cálculo de la potencia máxima
RTh
A
+
− VTh
RL = RTh
B
pmax
22 2
VTh2
= 13.44 W
=
=
4 RL 4 × 9
39