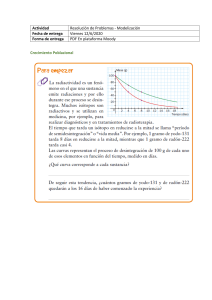
EJERCICIO 3.38M DATOS DISPONIBLES: Ecuación General : 𝑃1 𝛾 1 𝑣1 2 )) 𝑔 + 𝑧1 + (2 ( + ℎ𝐴 + ℎ𝑅 = 𝑃2 𝛾 1 𝑣2 2 )) + 𝑔 + 𝑧2 + (2 ( ℎ𝐿 𝑃2 = 140𝐾𝑁⁄ 𝑚2 𝛾 = (1.10) (9.81𝐾𝑁⁄ 𝑚3 ) = 10.791𝐾𝑁⁄ 𝑚3 𝜇 = 2 𝑥 10−3 D = 0.025𝑚 Q = 95𝐿⁄𝑚 L = 85𝑚 𝑃𝐴 = ℎ𝐴 𝑊 = ℎ𝐴 𝛾𝑄 DESAROLLO a) 𝑃𝐴 = ? Considerando la Ecuación General y que en el estanque en la superficie 𝑃1 = 0 y 𝑣1 = 0 podemos decir que: ℎ𝐴 = 𝑃2 1 𝑣2 2 + (𝑧2 − 𝑧1 ) + ( ( )) + ℎ𝐿 𝛾 2 𝑔 1𝑚3⁄ 95𝐿⁄ 𝑄 𝑚𝑖𝑛 𝑠 𝑣2 = = 𝑥 = 3.23𝑚⁄𝑠 𝜋(0,025𝑚 )2 (1000 ∗ 60)𝐿⁄ 𝐴 𝑚𝑖𝑛 4 ∴ 1 𝑣2 2 1 (3.23𝑚 )2 ) = 0.530𝑚 ( )= ( 2 𝑔 2 9.81𝑚⁄ 2 𝑠 𝐿 1 𝑣2 2 )) 𝑔 ℎ𝐿 = 𝑓 𝐷 (2 ( ∴ 𝑓 =? Para buscar “ 𝑓 “ , procedo a calcular el numero de Reynolds y Rugosidad promedio para luego buscar en el diagrama de Moody la solución. 𝑝 = 𝑔𝑒 𝑝ℎ20 = 1.10 ∗ 1000 = 1100𝐾𝑔⁄ 𝑚3 𝑁𝑅 = 𝑝𝑣𝐷 𝜇 = 1100∗3.23∗0.025 2∗10−3 = 4441.25 ∴ Turbulento 𝜀∆ = 𝜀𝑇𝑢𝑏𝑜 𝑃𝑙𝑎𝑠𝑡𝑖𝑐𝑜 𝐷 = 0.0015 0.025 Según Diagrama de Moody: = 0.06 𝑓 ≈ 0.021 Entonces: ℎ𝐿 = 0.021 ∗ ( 85 ) ∗ 0.530 = 37.86𝑚 0.025 Entonces: ℎ𝐴 = 140𝐾𝑁⁄ 𝑚2 10.791𝐾𝑁⁄ + (10𝑚 − 2.7𝑚 ) + 0.530𝑚 + 37.86𝑚 = 58.67𝑚 𝑚3 Entonces: 𝑃𝐴 = ℎ𝐴 𝛾𝑄 = 58.67𝑚 ∗ 10.791𝐾𝑁⁄ 𝑚 ∗( 3 95 ) 3 = 1,002𝐾𝑁∗𝑚⁄𝑠 ≅ 𝟏 𝒌𝑾 60000 𝑚 ⁄𝑠 b) 𝑃3 = ? *Llamare “𝑃3 “a la presión de salida de la bomba* si: 𝑃3 1 𝑣3 2 𝑃2 1 𝑣2 2 + 𝑧3 + ( ( )) − ℎ𝐿 = + 𝑧2 + ( ( )) 𝛾 2 𝑔 𝛾 2 𝑔 Entonces: 𝑃3 = 𝑃2 + (( 𝑧2 − 𝑧3 ) + ℎ𝐿 )𝛾 = 140𝐾𝑃𝐴 + ((10𝑚 − 1.5𝑚 ) + 37.86𝑚 ) (10.791𝐾𝑁⁄ 𝑚3 𝑃3 = 𝟔𝟒𝟎𝑲𝑷𝑨 )