Funciones Racionales y Potenciales. Asíntotas

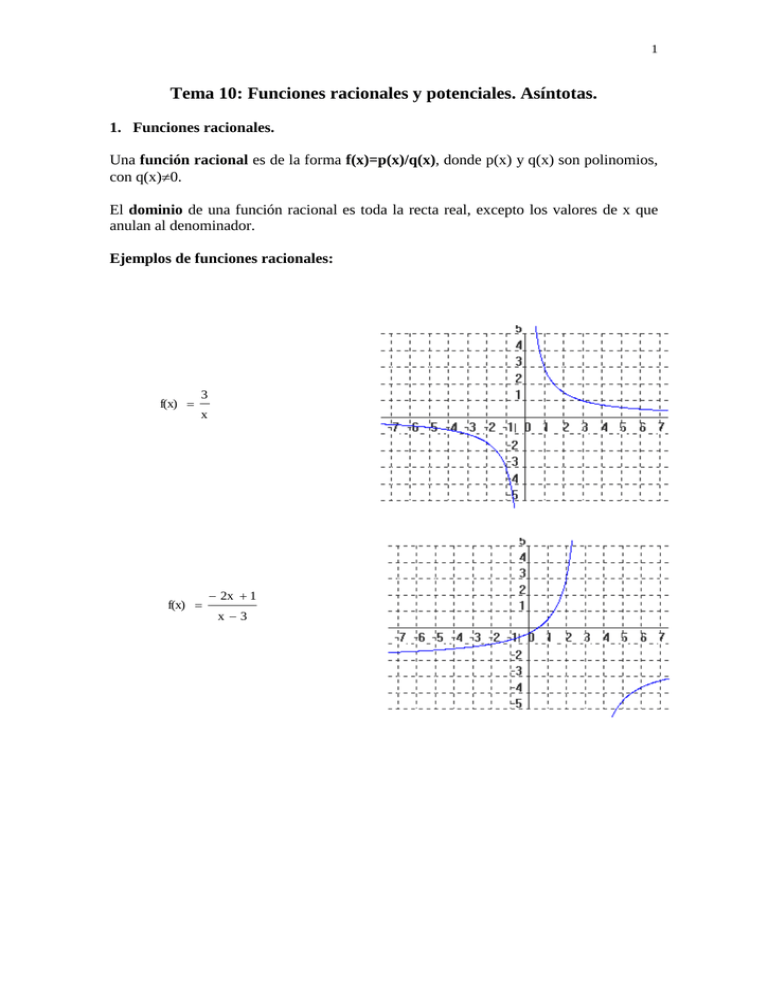
1
Tema 10: Funciones racionales y potenciales. Asíntotas.
1. Funciones racionales.
Una función racional es de la forma f(x)=p(x)/q(x), donde p(x) y q(x) son polinomios,
con q(x)0.
El dominio de una función racional es toda la recta real, excepto los valores de x que
anulan al denominador.
Ejemplos de funciones racionales:
f(x) 
3
x
f(x) 
 2x  1
x3
2
2. Funciones potenciales.
Una función potencial es de la forma f(x)=axn, donde a y n pueden ser cualquier par de
números reales.
2.1
Funciones potenciales pares.
Una función potencial par es de la forma f(x)=axn, con a>0 y n un número natural par.
Propiedades:





El dominio de la función es la recta real 
El recorrido de la función es el intervalo [0,), ya que la potencia par de un número
es siempre positivo.
La función es simétrica respecto del eje Y, ya que f(x)=f(-x).
La función es continua en todo su dominio.
La función es creciente para x<0 y creciente para x>0.
Ejemplos:
f(x)  x
2
f(x)  2x
8
3
2.2
Funciones potenciales impares.
Una función potencial par es de la forma f(x)=axn, con a>0 y n un número natural
impar.
Propiedades:





El dominio de la función es la recta real 
El recorrido de la función es. la recta real 
La función es simétrica respecto del origen, ya que f(-x)=-f(x).
La función es continua en todo su dominio.
La función es siempre creciente.
Ejemplos:
f(x)  x
3
f(x)  x
9
4
3.
Asíntotas.
3.1
Asíntotas horizontales.
Una recta horizontal y=b es una asíntota horizontal de una función f(x) si:
lim
x  
f(x)  b o
lim
x  
f(x)  b
Ejemplo:
f(x) 
- 2x
x
2
2
1
Al tender x a + o a - la función se aproxima a –2, ya que:
lim
x 
- 2x
2
2
x 1
 2
Se dice entonces que la recta y=-2 es una asíntota horizontal.
Una función f(x) tiene una asíntota horizontal en y=b si existe alguno de los
límites:
lim
x  
f(x)  b o
lim
x  
f(x)  b
5
OBSERVACIONES:


Una función tiene como máximo dos asíntotas horizontales: cuando x+ o
cuando x-.
La gráfica de una función puede cortar a su asíntota horizontal.
Ejemplo de una función cuya gráfica corta a su asíntota horizontal
f(x) 
1- x
x
2
6
Ejercicio resuelto:
Hallar las asíntotas horizontales de la función:
5
f(x) 
x

3
Para hallar las asíntotas horizontales calculamos el límite de la función cuando x
tiende a + y -.
lim
x  
5
0
x -3
lim
x  
5
0
x -3
Por tanto y=0 es una asíntota horizontal
Ejercicio:
a)
Hallar las asíntotas horizontales de la función:
2x
f(x) 
3x
1
7
3.2
Asíntotas verticales:
La recta x=k es una asíntota vertical de f(x) si existe alguno de los límites
siguientes:
lim f(x)  
x k
; lim f(x)  
x k

; lim f(x)  
xk

Ejemplo:
f(x) 
1
x
2
Cuando x se aproxima a 0, la función tiende a +.
Se dice que la recta x=0 es una asíntota vertical de la función.
OBSERVACIONES:



Una función puede tener cualquier número de asíntotas verticales.
La gráfica de una función racional no corta a sus asíntotas verticales.
Las asíntotas verticales de las funciones racionales se obtienen para los valores
de x que anulan al denominador pero no al numerador.
8
Ejercicio resuelto:
Dada la función
2x  1
f(x) 
x
2
 6x  7
Hallar sus asíntotas verticales.
La función tiende a  cuando el denominador se anula; por tanto, x2+6x-7=0, de
donde x=1 y x=-7 son las asíntotas verticales.
9
Ejercicios:
a)
f(x) 
Dada la función:
2x  7
3
x x
2
 12x
Hallar, si las hay, sus asíntotas. Tanto horizontales como verticales.
b)
Dada la función:
7
f(x) 
x
2
1
Hallar, si las hay, sus asíntotas. Tanto horizontales como verticales.
10
3.3
Asíntotas oblicuas.
Limitamos el estudio de estas asíntotas al caso de las funciones racionales.
Una función f(x) tiene una asíntota oblicua en y=mx+n si cuando x se
verifica que f(x) mx+n.
Una función racional tiene una asíntota oblicua si el grado del numerador es una
unidad mayor que el grado del denominador.
La asíntota oblicua es igual al cociente que se obtiene al dividir el numerador
entre el denominador.
Dividendo
divisor
D(x)
 cociente
d(x)
c(x) 
resto r(x)
divisor
d(x)
OBSERVACIONES:


La gráfica de una función puede cortar a su asíntota oblicua.
Si una función racional tiene una asíntota oblicua no puede tener asíntota horizontal,
y recíprocamente.
Ejercicio resuelto:
Dada la función:
f(x) 
x
2
 x 1
x
Hallar, si las hay, sus asíntotas oblicuas.
11
Dividiendo el numerador entre el denominador resulta
f(x) 
x
2
 x 1
 x 1
x
1
x
A medida que x tiende a  se verifica que 1/x tiende a 0, y en consecuencia la función:
f(x) 
x
2
 x 1
x
Se aproxima a la recta y=x-1.
Se dice que la recta y=x-1 es una asíntota oblicua.
Ejercicios:
Hallar las asíntotas de las siguientes funciones:
a)
2x
f(x) 
x
2
 16
b)
f(x) 
6x
2
1
2x
2
5
12
c)
f(x) 
5x
3
3x
2
2
d)
f(x) 
3x
2
5x
1
3