integrales dobles problema

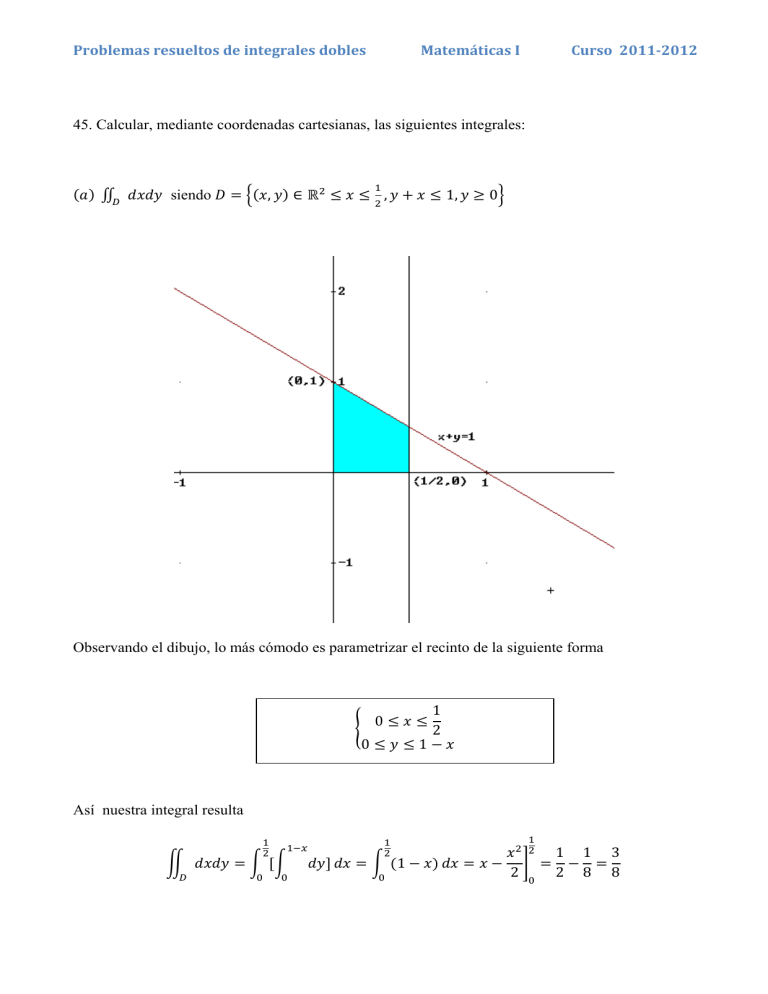
Problemas resueltos de integrales dobles
Matemáticas I
Curso 2011­2012
45. Calcular, mediante coordenadas cartesianas, las siguientes integrales:
siendo
,
,
1,
0
Observando el dibujo, lo más cómodo es parametrizar el recinto de la siguiente forma
0
0
1
1
2
Así nuestra integral resulta
1
2
1
2
1
8
3
8
Problemas resueltos de integrales dobles
Matemáticas I
Curso 2011­2012
Este valor coincide además con el área del recinto (puedes calcularla con las fórmulas básicas de
cálculo de áreas de figuras regulares, pues el recinto está formado por un triángulo y un rectángulo);
pero esto ya lo sabíamos, porque una el área de un recinto
siendo
,
/0
es precisamente
,
1,
0
Como el recinto es el mismo, parametrizamos de igual forma la integral (sólo cambia el integrando)
Realizamos primero la integral indefinida respecto de la variable
calculando una primitiva
2
Así nuestra integral resulta
1
2
1
2
1
2
1
1
1
2 8
2 5
2
1
2 12
2
8
11
2 15
11
3840
5
12
Problemas resueltos de integrales dobles
siendo
,
/
Matemáticas I
16,
,
6
,
Curso 2011­2012
0,
1
Problemas resueltos de integrales dobles
Matemáticas I
Curso 2011­2012
En esta ocasión hemos dividido el recinto en dos como se ve en el dibujo para tomar con referencia fija
la variable , quedando la variable
acotada entre dos funciones de . Así resultan integrales que se
pueden resolver. Si hubiésemos invertido los papeles de las variables (la
variable
entre valores fijos y la
acotada entre funciones de , necesitamos 3 recintos diferentes y las integrales resultantes
tienen un poco más de dificultad, pero también salen)
Así los recintos parametrizados son:
1
2
2
4
6
Así nuestra integral queda:
1
1
2
2
6
1
2
1
2
36
12
1
2 2
1 27
2 2
16
1
2
12
1
2
36 ln| |
36ln 2
3
4
1 256
4
4
1
16
4
256
64
3
15
4
18 ln 2
Problemas resueltos de integrales dobles
siendo
,
Matemáticas I
/1
2, 0
1
2
√
Curso 2011­2012
,
La parametrización del recinto puede ser
0
Por tanto esta integral se puede resolver
√
√
√
2
2
Problemas resueltos de integrales dobles
√
2
1
2
Matemáticas I
1
2
Curso 2011­2012
3
1
2
2
2
4
3
4
Donde la primitiva de la última integral se ha calculado por partes haciendo (puede comprobarlo el
alumno)
2
1
siendo
,
/
1,
,
1
Problemas resueltos de integrales dobles
Matemáticas I
Curso 2011­2012
Observando de nuevo el dibujo tenemos una parametrización fácil del recinto
1
2
1
1
1
Así nuestra integral quedaría
2
2
2
1
1
2
2
1
2
1
2
2
1
2
1
1
1
2
1
2
1
3
4
1
Problemas resueltos de integrales dobles
siendo
,
/
Matemáticas I
0,
1
1,
Curso 2011­2012
2
1
Problemas resueltos de integrales dobles
Matemáticas I
Curso 2011­2012
los recintos parametrizados son:
2
1
0
1
2
0
2
1
2
1
2
2
3
3
1
3
4
1
2
2
1
2
2
3
(Termine el alumno las operaciones y así practica)
1