Financiación externa: emisión de acciones

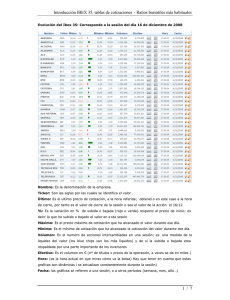
Tema 5: FINANCIACIÓN EXTERNA
(Emisión de Acciones)
Dirección Financiera I
Grupo 3e4
Prof. Fernando Úbeda
Las Acciones como fuente de
financiación
• Las acciones son partes alícuotas del capital social
de la empresa.
– Lleva implícito control de la empresa
– Retribución mediante dividendos
• Se emiten a la par o por encima de la par.
– Prima de emisión deben quedar recogidas en las reservas
• Valor teórico de la acción
Precio Teórico

Capital  Reservas
Número de acciones
• Valor de mercado de la acción
en circulació
n
La emisión de acciones
•
•
•
•
•
VENTAJAS
No costituyen un coste fijo
No se amortizan
Son una garantía para los
acreedores (efecto
expansión)
Más liquidez que la deuda
Los rendimientos de las
acciones tienen un mejor
tratamiento fiscal que los
rendimientos de la deuda
DESVENTAJAS
• Accionistas no deseados
• Son una fuente de
financiación costosa
• Los dividendos no son un
gasto fiscalmente
deducibles.
Valoración de Acciones
D1
P0 
P1 

(1  k )
D2

(1  k )
P1
(1  k )
P2
(1  k )
D 2  P2
P0 
P0 
D1
(1  k )
D1
(1  k )


(1  k )
(1  k )
D2
(1  k )
2
t

D1
(1  k )
D 2  P2
(1  k )

D3
(1  k )

3
 
2
Dt
 (1  k )
t 1
t
Patrones Básicos de Comportamiento
Dividendo
por
Acción
g2
Crecimiento
Diferencial Crecimiento
Constante
g
g1
Crecimiento 0
g=0
Años
Valoración de Acciones
Crecimiento Cero
Crecimiento Cero
g  0   t , Dt  D
P0  Da   k  D
1  (1  k )
k


D
k
Valoración de Acciones
Crecimiento Constante
 t , D t 1  D t (1  g )
P0 
D 0 (1  g )
(1  k )

D 0 (1  g )
(1  k )
2

2
D 0 (1  g )
(1  k )
3
 
3
D 0 (1  g )
(1  k )
n

n

1 k
1 g
P0 (1  k )
(1  g )
 D0 
D 0 (1  g )
(1  k )
P0 (1  k )
(1  g )
k  g;n  

D 0 (1  g )
(1  k )
 P0  D 0 
D 0 (1  g )
kg
 
D 0 (1  g )
(1  k )
 (1  k )

P0 
 1  D 0
(
1

g
)


P0 
2
2
n
n

t 1
D 0 (1  g )
(1  k )
D 0 (1  g )
n 1
n 1
(1  k )
t
Valoración de Acciones
Crecimiento Diferencial
g1
g3
g2

0
T
P0 
T’
T

t 1
D 0 (1  g 1 )
(1  k )
t
T
t
 (1  k )
T

t T
D T (1  g 2 )
(1  k )
t
t
 (1  k )
T 
D T ´ (1  g 1 )
k  g3
T  1
¿De dónde viene k y g?
BN
t 1
 BN t  A  k
P
1
BN
BN
T
t 1
BN
t

BN
t
BN
t
A

BN
k
kg
t
1  g  1  % BN no distribuid
g  % BN no distribuid
k  ROE
D1
ok
ok
k 
D
P
g
Ejemplo ENDESA
1994
D
g1
g2
P
k
Crecimiento Cero
Crecimiento Constante
Crecimiento Diferencial
0,24 €
0,24 €
0,29 €
0
18,82%
18,82% 1994-2000
4,62%
7,89 €
7,89 €
2,94 €
3,04%
22,4%
22,4%
Los flujos de caja como variable
aleatoria
FC it
t
E  FC t  
m

p it FC it
i 1
E  FC t 
m

za :  FC it  E ( FC t )
Semivarian
*

2
p it
i 1
*
FC it
Flujos caja posibles menores a la media en el momento t
m
Varianza
:
2
 FC t    FC it
i 1
 E ( FC t )

2
p it
¿Qué es la diversificación?
Temporada Lluviosa
Temporada Soleada
Esperanza
Desviación Típica
Fabricante
de Paraguas
50%
-25%
12,50%
37,50%
Centro
Turístico
Probabilidad
-25%
50%
50%
50%
12,50%
37,50%
Diversificación
Ponderaciones
Temporada Lluviosa
Temporada Soleada
Media
Desv. Típica
Fabricante
de Paraguas
50%
13%
13%
13%
0%
Centro
Turístico
50%
Esperanza y Varianza de dos Variables
Aleatorias
E ( i   k )  E ( i )  E ( k )
E ( k  i )  kE ( i )
 ( i   k )   ( i )   ( k )  2 Cov ( i ,  k ) 
2
2
2
  ( i )   ( k )  2  i , k  ( i ) ( k )
2
2
 ( k  i )  k  ( i )
2
Covarianza
2
: Cov  i ,  k  
2
n
 
j 1
i
 E ( i )  k  E ( k )  p j
 i ,k 
Cov ( i ,  k )
 ( i ) ( k )
Ejemplo de Diversificación Perfecta
Temporada Lluviosa
Temporada Soleada
Esperanza
Desviación Típica
Cov
Fabricante
de Paraguas
50%
-25%
12,50%
37,50%
Centro
Turístico
Probabilidad
-25%
50%
50%
50%
12,50%
37,50%
Coeficiente de
-0,141 Correlación
-1
La diversificación en la realidad
Riesgo
Mercado Local
Ganancia
Diversificación
Internacional
Mercado Internacional
Riesgo Sistemático
Número de Acciones
Concepto de Cartera Eficiente
• El CAPM (Capital Asset Price Model).
Markovitz (1959), Tobin (1958)
r
n
min
1
2
ww
i
j
i , j 1
i, j
M
rf
n
wr
i i
r
i 1
n
w
i 1
i
1

Activo Sin Riesgo
Cartera de Mercado
Beta deseada
0
0,5
1
1,5
10%
15%
Composición de la Cartera
1,00 € Activo sin Riesgo
0,50 € Activo sin Riesgo
0,50 € Cartera de Mercado
1,00 € Cartera de Mercado
0,50 € Deuda
1,50 € Cartera de Mercado
10 %
0 ,5  ( 0 ,10 )  0 ,5  ( 0 ,15 )  0 ,125
15 %
 0 ,5  ( 0 ,10 )  1,5  ( 0 ,15 )  0 ,175
Teoría de selección de carteras. El concepto de
Beta del mercado
• Simplifiación de Sharpe (1963) y Treynor
(1965)
 rM  r f
ri  r f  
2
 M

 i , M  r f   i ( rM  r f )


Tasa de
Rentabilidad
Rentabilidad
Del Mercado
1
Riesgo Sistemático (Beta)
Riesgo Rentabilidad Fondos de Inversión
Década de los setenta
Rentabilidad
Fondo
Crecimiento y
Renta
Mercado
Fondo
Mixto
1
Beta
Riesgo Rentabilidad Fondos de Inversión
Fondo de
Crecimiento
Rentabilidad
Rentabilidad
Fondo
Mixto
Fondo
Crecimiento y
Renta
Mercado
Mercado
Fondo de
Crecimiento
Fondo
Mixto
(1969-74)
Fondo
Crecimiento Beta
y
Renta
Beta
(1974-88)
La pendiente es inferior a la esperada
• Una cartera con beta cero no tiene los mismos
resultados que el activo libre de riesgo
Rentabilidad
Relación Teórica
Relación Real
Rentabilidad
Libre de Riesgo
Beta
Inestabilidad a corto y largo plazo.
• Para periodos cortos rendimiento y riesgo pueden
tener una relación negativa
Rentabilidad media mensual
271 Fondos
(1981-1991)

Problemas Metodológicos
• Se calcula sobre datos históricos
– No incorpora la información actual
• ¿El índice de mercado realmente mide
adecuadamente el riesgo sistemático?.
Teoría de selección de carteras. Valoración de
acciones por arbitraje (APT)
• Modelo Unifactorial
w  b j ( b j  bi )
ri  a i  bi f


r  wa i  (1  w ) a j  wb i  (1  w ) b j f  r f
ai  0
0  rf
bi
c
ri   0  bi c  bi f   0  bi 1
• APT Ross (1965), Chen, Roll y Ross (1986)
m
m
ri  a i 
b
j 1
i, j
fj
ri   0 
b
j 1
i, j
j
Derecho Preferente de Suscripción
• El valor de emisión suele ser inferior al de mercado:
– Garantizar la colocación
– Bonificación a los accionistas.
d s  Pv  Pp
Pv  Pp  d s
Pp  Pv  d s  Pe  nd s
ds 
Pv  Pe
n 1
Ejemplo
Capital social
Número de Acciones
Valor Nominal
Reservas
Remanente de Ejercicios Anteriores
Total
Emisión
Prima de emisión
Valor de Emisión
Pv 
5.000 acciones
130%
1.300
30 . 000 . 000
8.000.000
2.000.000
30.000.000
Pe  1,3  1 . 000  1 . 300
 1 . 500
30 . 000 . 000  6 . 500 . 000
25 . 000
d s  1 . 500  1 . 460  40
n
20.000
1.000
Incr. Capital Social
Incr. Reservas
20 . 000
Pp 
20.000.000
1 . 500  1 . 300
40
1  4
 1 . 460
5.000.000
1.500.000