UNIVERSIDAD DISTRITAL FRANCISCO JOSE DE CALDAS
FACULTAD DE INGENIERIA
PROYECTO CURRICULAR INGENIERIA ELECTRONICA
COMUNICACIONES DIGITALES
CODIFICADORES DE LINEA
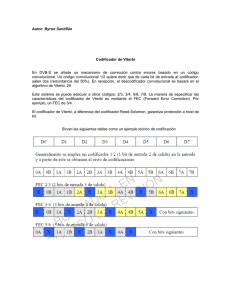
Nombre: Willinton Jahir Martin Leguizamón
Cód. 20142005143
1. Codificador AMI:
Este codificador trabaja con los ceros como nivel bajo ósea cero lógico, mientras que los
unos como nivel positivos o negativos de voltaje dependiendo de la secuencia, por
ejemplo si en una secuencia se encuentra el primer uno este será un nivel positivo de
voltaje y cuando se encuentre el segundo uno este será un nivel negativo de voltaje,
cuando encuentra el siguiente uno vuelve a ser un nivel positivo de voltaje, de esta forma
continua la secuencia, la siguiente figura muestra lo mencionado anteriormente:
Señal del codificador AMI
Paso 1:
Por lo dicho anteriormente se puede representar el comportamiento de la señal mediante
estados lógicos de la siguiente manera:
1/+V
0/0V
S0
S1
1/-V
Diagrama de estados AMI
Paso 2:
Con estos estados se realizan las siguientes matrices de transición:
0/0V
𝑇0 =
1 0
0 1
, 𝑇1 =
0 1
1 0
Paso 3:
Ahora se obtienen los vectores de cada estado:
𝑆0 =
1
,
0
0
𝑆1 = ,
1
𝑏𝑘
𝑆 = ̅̅̅
𝑏𝑘
A partir de los estados y matrices de transición se realiza la siguiente ecuación:
𝑏𝑘+1
1 0
0 1 𝑏𝑘
= {𝑎
̅̅̅̅
+ 𝑎𝑘
} ̅̅̅
𝑘
̅̅̅̅̅̅
0 1
1 0 𝑏
𝑏𝑘+1
𝑘
Con esta esta ecuación se realizan las ecuaciones que describen el comportamiento de
forma circuital:
𝑏 = (~𝑎𝑇0 + 𝑎𝑇1 )𝑏
𝑏𝑘+1 = ̅̅̅𝑏
𝑎𝑘 𝑘 + 𝑎𝑘 ̅̅̅
𝑏𝑘
̅̅̅̅̅̅
𝑏𝑘+1 = ̅̅̅𝑏
𝑎𝑘 ̅̅̅𝑘 + 𝑎𝑘 𝑏𝑘
Paso 4:
Diseño del codificador AMI en base a las ecuaciones anteriores:
Paso 5:
Diseño del decodificador AMI:
2. Codificador CMI:
Este codificador, es similar al codificador AMI la única diferencia es que en cero trabaja
con una señal que saca el CLOCK que se introduce, mientras que los unos como nivel
positivos o negativos de voltaje dependiendo de la secuencia, interpolando el nivel de
voltaje anterior del uno previo, la siguiente figura muestra lo mencionado anteriormente:
Señal del codificador CMI
Paso 1:
Por lo dicho anteriormente se puede representar el comportamiento de la señal mediante
estados lógicos de la siguiente manera:
1/+V
0/Sa (t)
S0
S1
0/ Sa (t)
1/-V
Diagrama de estados CMI
Señal 𝑺𝒂 (𝒕) para la transición con cero
Paso 2:
Con estos estados se realizan las siguientes matrices de transición:
𝑇0 =
1 0
0 1
, 𝑇1 =
0 1
1 0
Paso 3:
Ahora se obtienen los vectores de cada estado:
𝑆0 =
1
,
0
0
𝑆1 = ,
1
𝑏𝑘
𝑆 = ̅̅̅
𝑏𝑘
A partir de los estados y matrices de transición se realiza la siguiente ecuación:
𝑏𝑘+1
1 0
0 1 𝑏𝑘
= {𝑎
̅̅̅̅
+ 𝑎𝑘
} ̅̅̅
𝑘
̅̅̅̅̅̅
0 1
1 0 𝑏
𝑏𝑘+1
𝑘
Con esta esta ecuación se realizan las ecuaciones que describen el comportamiento de
forma circuital:
𝑏 = (~𝑎𝑇0 + 𝑎𝑇1 )𝑏
𝑏𝑘+1 = ̅̅̅𝑏
𝑎𝑘 𝑘 + 𝑎𝑘 ̅̅̅
𝑏𝑘
̅̅̅̅̅̅
𝑏𝑘+1 = ̅̅̅𝑏
𝑎𝑘 ̅̅̅𝑘 + 𝑎𝑘 𝑏𝑘
Paso 4:
Diseño del codificador CMI en base a las ecuaciones anteriores:
Paso 5:
Diseño del decodificador CMI:
3. Codificador MLT-3:
Para este codificador se tienen en cuenta nivel de voltaje positivo, negativo y cero de tal
forma que se cumpla que se cumpla, la secuencia de la señal MLT-3, que para el caso
cuando existe un uno interpola el anterior a este y el siguiente duplica el efecto por decirlo
de algún modo del anterior, pero el siguiente vuelve a interpolar al anterior y el que le
sigue a continuación duplica el efecto y así se repite el proceso, esto solo para los unos,
ya que los ceros si hacen que el nivel de voltaje siempre sea cero, como se aprecia en la
siguiente figura:
Señal del codificador MLT-3
Paso 1:
Por lo dicho anteriormente se puede representar el comportamiento de la señal mediante
estados lógicos de la siguiente manera:
1/+V
S1
S3
S2
1/0v
1/0v
S0
1/-V
Diagrama de estados MLT-3
Paso 2:
Con estos estados se realizan las siguientes matrices de transición:
1
0
𝑇0 =
0
0
0
1
0
0
0
0
1
0
0
0
,
0
1
0
1
𝑇1 =
0
0
0
0
1
0
0
0
0
1
1
0
0
0
Paso 3:
Ahora se obtienen los vectores de cada estado:
1
0
𝑆0 = ,
0
0
0
1
𝑆1 = ,
0
0
0
0
𝑆2 = ,
1
0
0
0
𝑆3 = ,
0
1
0
0
𝑏𝑘 𝑑𝑘 =
1
1
0
1
0
1
A partir de los estados y matrices de transición se realiza la siguiente ecuación:
̅̅̅̅̅̅
̅̅̅̅̅̅
𝑏𝑘+1 𝑑
𝑘+1
̅̅̅̅̅̅
𝑏
𝑑
𝑘+1
𝑘+1
= {𝑎
̅̅̅̅
𝑘
̅̅̅̅̅̅
𝑏𝑘+1 𝑑
𝑘+1
𝑏𝑘+1 𝑑𝑘+1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
1
+ 𝑎𝑘
0
0
0
0
1
0
0
0
0
1
𝑏𝑘
1 ̅̅̅
𝑏
0 ̅̅̅
} 𝑘
0 𝑏𝑘
0 𝑏𝑘
̅̅̅
𝑑𝑘
𝑑𝑘
̅̅̅
𝑑𝑘
𝑑𝑘
Con esta esta ecuación se realizan las ecuaciones que describen el comportamiento de
forma circuital:
𝑏𝑑 = (~𝑎𝑘 𝑇0 + 𝑎𝑘 𝑇1 )𝑏𝑑
̅̅̅̅̅̅
𝑏𝑘+1 ̅̅̅̅̅̅
𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 ̅̅̅𝑘 ̅̅̅
𝑑𝑘 ) + 𝑎𝑘 (𝑏𝑘 𝑑𝑘 ) (1)
̅̅̅̅̅̅
̅̅̅𝑘 ̅̅̅
𝑏𝑘+1 𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 ̅̅̅𝑘 𝑑𝑘 ) + 𝑎𝑘 (𝑏
𝑑𝑘 ) (2)
̅̅̅𝑘 𝑑𝑘 ) (3)
𝑏𝑘+1 ̅̅̅̅̅̅
𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 𝑘 ̅̅̅
𝑑𝑘 ) + 𝑎𝑘 (𝑏
𝑏𝑘+1 𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 𝑘 𝑑𝑘 ) + 𝑎𝑘 (𝑏𝑘 ̅̅̅
𝑑𝑘 ) (4)
Sumando (3) y (4) obtenemos 𝑏𝑘+1 y sumando (2) y (4) se obtiene 𝑑𝑘+1 :
̅̅̅𝑘 𝑑𝑘 + 𝑏𝑘 ̅̅̅
𝑏𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 𝑑𝑘 ) + 𝑎𝑘 (𝑏
𝑑𝑘 )
Reduciendo:
𝑏𝑘+1 = ̅̅̅𝑏
𝑎𝑘 𝑘 + 𝑎𝑘 (𝑏𝑘 ⊕ 𝑑𝑘 )
Ahora para 𝑑𝑘+1 :
𝑑𝑘+1 = ̅̅̅𝑑
𝑎𝑘 𝑘 + 𝑎𝑘 ̅̅̅
𝑑𝑘
Reduciendo:
𝑑𝑘+1 = 𝑎𝑘 ⊕ 𝑑𝑘
Paso 4:
Diseño del codificador MLT-3 en base a las ecuaciones anteriores:
Paso 5:
Diseño del decodificador MLT-3:
4. Codificador Miller modificado:
Para este codificador se realiza un análisis a partir de tres señales que permitirán
identificar cada uno de los estados y su transición, para este existe una cuando hubo un
cero antes y después hay otro, otra señal la cual se activa cuando existe un uno
anteriormente y luego un cero, y por ultimo una cuando hay un uno. A continuación se
presenta un diagrama del comportamiento del codificador y más adelante se mostraran
las señales dichas con anterioridad:
Señal del codificador Miller modificado
Paso 1:
Por lo dicho anteriormente se puede representar el comportamiento de la señal mediante
estados lógicos de la siguiente manera:
1/Sc (t)
S1
S3
S2
1/Sc (t)
0/Sb (t)
S0
0/Sa (t)
Diagrama de estados Miller modificado
Señal 𝑺𝒂 (𝒕) para 0 cuando antes hay 0 Señal 𝑺𝒃 (𝒕) para 0 cuando antes hay 1
Señal 𝑺𝒄 (𝒕) para 1
Paso 2:
Con estos estados se realizan las siguientes matrices de transición:
0
0
𝑇0 =
0
1
0
0
1
0
0
0
0
1
0
0
,
0
1
0
1
𝑇1 =
0
0
0
1
0
0
1
0
0
0
1
0
0
0
Paso 3:
Ahora se obtienen los vectores de cada estado:
1
0
𝑆0 = ,
0
0
0
1
𝑆1 = ,
0
0
0
0
𝑆2 = ,
1
0
0
0
𝑆3 = ,
0
1
0
0
𝑏𝑘 𝑑𝑘 =
1
1
0
1
0
1
A partir de los estados y matrices de transición se realiza la siguiente ecuación:
̅̅̅̅̅̅
𝑏𝑘+1
̅̅̅̅̅̅
𝑏
𝑘+1
𝑏𝑘+1
𝑏𝑘+1
̅̅̅̅̅̅
𝑑𝑘+1
𝑑𝑘+1
= {𝑎
̅̅̅̅
𝑘
̅̅̅̅̅̅
𝑑𝑘+1
𝑑𝑘+1
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
+ 𝑎𝑘
0
0
1
0
0
1
0
0
1
0
0
0
𝑏𝑘
1 ̅̅̅
𝑏
0 ̅̅̅
} 𝑘
0 𝑏𝑘
0 𝑏𝑘
̅̅̅
𝑑𝑘
𝑑𝑘
̅̅̅
𝑑𝑘
𝑑𝑘
Con esta esta ecuación se realizan las ecuaciones que describen el comportamiento de
forma circuital:
𝑏𝑑 = (~𝑎𝑘 𝑇0 + 𝑎𝑘 𝑇1 )𝑏𝑑
̅̅̅̅̅̅
𝑏𝑘+1 ̅̅̅̅̅̅
𝑑𝑘+1 = 𝑎𝑘 (𝑏𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 𝑑𝑘 ) (1)
̅̅̅̅̅̅
̅̅̅𝑘 ̅̅̅
𝑏𝑘+1 𝑑𝑘+1 = 𝑎𝑘 (𝑏
𝑑𝑘 + ̅̅̅
𝑏𝑘 𝑑𝑘 ) (2)
𝑏𝑘+1 ̅̅̅̅̅̅
𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 ̅̅̅
𝑘 𝑑𝑘 ) (3)
̅̅̅
̅̅̅
𝑏𝑘+1 𝑑𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 ̅̅̅
𝑘 𝑑𝑘 + 𝑏𝑘 𝑑𝑘 + 𝑏𝑘 𝑑𝑘 ) (4)
Sumando (3) y (4) obtenemos 𝑏𝑘+1 y sumando (2) y (4) se obtiene 𝑑𝑘+1 :
𝑏𝑘+1 = ̅̅̅(𝑏
𝑎𝑘 ̅̅̅
𝑎𝑘 ̅̅̅𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 𝑑𝑘 )
𝑘 𝑑𝑘 ) + ̅̅̅(𝑏
Reduciendo:
𝑏𝑘+1 = ̅̅̅
𝑎𝑘
Ahora para 𝑑𝑘+1 :
̅̅̅𝑘 ̅̅̅
𝑑𝑘+1 = 𝑎𝑘 (𝑏
𝑑𝑘 + ̅̅̅
𝑏𝑘 𝑑𝑘 ) + ̅̅̅(𝑏
𝑎𝑘 ̅̅̅𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 ̅̅̅
𝑑𝑘 + 𝑏𝑘 𝑑𝑘 )
Reduciendo:
𝑑𝑘+1 = 𝑎𝑘 ̅̅̅
𝑏𝑘 + ̅̅̅(𝑑
𝑎𝑘 ̅̅̅
𝑘 + 𝑏𝑘 )
Paso 4:
Diseño del codificador Miller modificado en base a las ecuaciones anteriores:
Paso 5:
Diseño del decodificador Miller modificado: