A2S2 P

Universidad Diego Portales.
Escuela de Industrias, Facultad de Ingeniería.
Gestión de Operaciones; 1er semestre de 2013.
Profesor: Mauricio Varas.
Ayudantes: Diego Espinoza y Daniel Santelices.
Ayudantía N° 2 S2
Problema 1
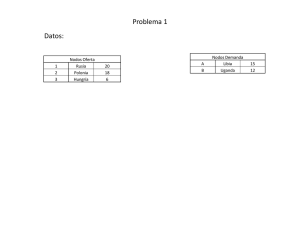
Un fabricante de motos puede vender en Libia y Uganda. La demanda en cada país es de 15 y
12 unidades mensuales respectivamente. El fabricante tiene tres fábricas: una en Rusia, otra
en Polonia y otra en Hungría, que pueden producir 20, 18 y 6 unidades mensuales
respectivamente. La siguiente tabla muestra las utilidades por unidad transportada.
Rusia
Polonia
Hungría
Libia
8
7
5
Uganda
6
7
9
a) Trabaje el problema como minimización de costos (para ello utilice la transformación vista
en clases cij = maxij {uij} - uij) y encuentre la solución óptima utilizando como solución básica
factible inicial aquel que entrega el método de la esquina nor-oeste.
Respuesta:
En primer lugar, se deben transformar las utilidades en costos. Aplicando la transformación:
Rusia
Polonia
Hungría
Libia
1
2
4
Uganda
3
2
0
Agregamos un destino ficticio para balancear la demanda (puesto que existe un exceso de
producción), con esto el tablero inicial es el siguiente:
Rusia
Polonia
Hungría
Dda.
Libia
1
2
4
15
Uganda
3
2
0
12
Fict.
4
4
4
17
Of.
20
18
6
El método de la esq. N/O nos entrega la siguiente solución inicial:
It. 1
Rusia
Polonia
Hungría
Dda.
Libia
15
Uganda
5
7
15
Fict.
Of.
20
18
6
11
6
17
12
Evaluando optimalidad:
It. 1
Rusia
Polonia
Hungría
Dda.
Libia
1
-2
-4
15
1
Uganda
3
2
2
12
3
Fict.
1
4
4
17
5
Of.
20
18
6
0
-1
-1
Se obtiene que es atractivo enviar desde Hungría a Uganda. Con esto se calcula la solución de
la segunda iteración y se evalúa optimalidad:
It. 2
Rusia
Polonia
Hungría
Dda.
Libia
15
Fict.
15
Uganda
5
1
6
12
It. 2
Rusia
Polonia
Hungría
Dda.
Libia
1
-2
-6
15
1
Uganda
3
2
0
12
3
Fict.
1
4
-2
17
5
Of.
20
18
6
Libia
15
Uganda
Fict.
5
12
Of.
20
18
6
17
Of.
20
18
6
17
Tercera iteración:
It. 3
Rusia
Polonia
Hungría
Dda.
15
6
6
12
17
0
-1
-3
It. 3
Rusia
Polonia
Hungría
Dda.
Libia
1
-1
-3
15
1
Uganda
-1
2
0
12
2
Fict.
4
4
0
17
4
Of.
20
18
6
0
0
0
La solución acá obtenida es óptima.
b) Dé respuesta a las siguientes preguntas.
i)
Al emplear el método de transporte para resolver este problema:
a.
b.
c.
d.
Un país artificial debe ser agregado.
Una planta artificial debe ser agregada.
Un destino artificial debe ser agregado (X).
Ninguna de las anteriores.
ii) Aplicando el Método de la Esquina Noroeste, ¿Cuál es el número de motos que se enviaría
a Uganda desde Polonia, en la segunda iteración? Considere como primera iteración a la
solución inicial. Asigne costos a los arcos ficticios de acuerdo al criterio del máximo.
Número de motos: 1 (ver tablero de la iteración 2).
iii) Con el Método de Costo Mínimo (bajo las condiciones de la pregunta 2) la solución inicial
es:
a.
b.
c.
d.
Óptima y no degenerada.
Óptima y degenerada.
No Óptima y no degenerada.
No Óptima y degenerada.
La solución Inicial según este método es la siguiente:
It. 1
Rusia
Polonia
Hungría
Dda.
Libia
15
15
Uganda
6
6
12
Fict.
5
12
Of.
20
18
6
17
Esta solución corresponde a la óptima (se sabe porque ya se obtuvo anteriormente,
si no se podría evaluar con el tablero de optimalidad). No es degenerada porque
tiene 5 flujos distintos de cero (5 = número de orígenes + número de destinos – 1).
iv) En el óptimo, ¿Qué país (o países) envían la totalidad de su producción de motos?
País(es): Sólo Hungría (es el único que no envía nada al destino ficticio).
v) Las utilidades mensuales para la solución óptima son de:
Utilidades: Se deben considerar las utilidades (no los costos transformados) de los
destinos no ficticios: 15*8 + 6*7 + 6*9 = 216.
vi) ¿Cuándo se debe balancear un problema de transporte antes de trabajar? (Marque la
o las alternativas correctas).
a.
b.
c.
d.
e.
Cuando el número de orígenes difiere del de destinos.
Cuando se desea maximizar utilidades en lugar de minimizar costos.
Cuando la oferta y la demanda total no coinciden (X).
Cuando se presenta una variable degenerada.
Ninguna de las anteriores.
Problema 2
a)
Considere el problema de transporte cuyos costos, ofertas y demandas se presentan en la
tabla. Encuentre una solución inicial (indicando claramente cuáles son las variables
básicas) aplicando el método del costo mínimo. Asigne a los arcos ficticios (de haberlos) el
mayor costo de la tabla. En caso de necesitar romper algún tipo de empate, deje claro qué
opción escoge.
A
10
11
7
150
1
2
3
Demanda
B
14
12
15
100
Oferta
50
300
100
Respuesta:
Balanceamos el problema:
1
2
3
Demanda
A
10
11
7
150
B
14
12
15
100
F
15
15
15
200
Oferta
50
300
100
Asignamos flujos (entre paréntesis) partiendo por los costos menores (los valores en negrita
corresponden a celdas básicas):
1
2
3
Demanda
A
10
(50)
11
7
(100)
150
B
14
F
15
Oferta
50
12
15 (0)
15
15 (0)
300
100
100
200
Al momento de asignar 50 al flujo en 1A nos vemos en la opción de cerrar la columna A o la fila
1. Si cerramos la columna A (equivalente a pensar que la oferta en 1 es 50 + ε):
1
2
3
Demanda
A
10
(50)
11 (0)
7
(100)
150
B
14 (0)
F
15 (0)
12
(100)
15 (0)
15
(200)
15 (0)
100
200
Oferta
50
300
100
En el último paso se podía tomar en cualquier orden las celdas 1F y 2F, pero en ambos casos se
llega directo al mismo resultado.
Si se cerraba la fila 1 (equivalente a pensar que la demanda en A es 150 + ε):
A
10
(50)
11 (0)
1
2
3
7
(100)
150
Demanda
B
14 (0)
F
15 (0)
12
(100)
15 (0)
15
(200)
15 (0)
100
Oferta
50
300
100
200
b) Explique una forma de resolver un problema de maximización con el método de
transporte.
Respuesta:
Se puede hacer de cualquiera de estas formas, donde uij corresponde a la utilidad que se desea
maximizar:
c) Realice una iteración para el problema de transporte cuyos datos se presentan. Considere
como solución inicial la solución donde las variables básicas son la columna A y la fila 3
completas. Indique si la solución obtenida es óptima.
1
2
3
Demanda
A
15
12
10
100
B
18
20
22
60
C
20
24
16
40
D
22
20
18
30
Oferta
50
50
130
Respuesta:
La solución inicial es:
A
50
50
0
100
1
2
3
Demanda
B
C
D
60
60
40
40
30
30
Oferta
50
50
130
Calculamos los costos reducidos (entre paréntesis):
1
2
3
Demanda
vj
A
50
50
0
100
15
B
(-9)
(-4)
60
60
27
C
(-1)
(6)
40
40
21
D
(-1)
(0)
30
30
23
Oferta
50
50
130
ui
0
-3
-5
Se debe aumentar el flujo en 1B. El ciclo se completa con 1A, 3A, y 3B. Lo máximo a descontar
de 1A y 3B serían 50 unidades de flujo, obteniendo la siguiente solución:
A
1
2
3
Demanda
vj
50
50
100
B
50
C
D
10
60
40
40
30
30
Oferta
50
50
130
ui
Para determinar si es óptima calculamos los costos reducidos:
1
2
3
Demanda
vj
A
(9)
50
50
100
6
B
50
(-4)
10
60
18
C
(8)
(6)
40
40
12
D
(8)
(0)
30
30
14
Oferta
50
50
130
ui
0
6
4
Esta solución no es óptima ya que tiene un costo reducido negativo, que permitiría disminuir
los costos actuales.