Análisis Estructural: Modelado, Computación e Interpretación
Anuncio

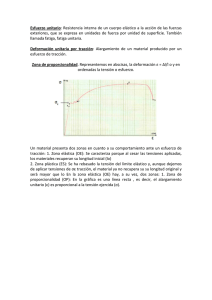
CAPÍTULO 1 Introducción El análisis estructural rara vez es, si es que alguna vez, un fin en sí mismo. Más bien, casi siempre es solo una herramienta para uso en diseño estructural. Hay tres fases distintas en el análisis estructural, a saber, "cálculo de modelos" e "interpretación". Este capítulo sostiene que, para la mayoría de los ingenieros, las fases de modelado e interpretación son, con mucho, las más importantes. La fase de cómputo involucra la teoría del análisis estructural, así como los métodos de compilación. Esta fase es relativamente poco importante. Este capítulo también señala que hay muchas razones diferentes para realizar un análisis estructural y muchos tipos diferentes de análisis, todos con diferentes necesidades de modelado e interpretación. Este capítulo considera los siguientes temas. Las tres fases del análisis estructural (modelado, computación e interpretación y su importancia relativa). Demandas, capacidades y relaciones demanda / capacidad. Evaluación del desempeño vs. diseño directo. Capacidad de diseño. Análisis elástico versus inelástico Carga estática vs. carga dinámica Pequeños desplazamientos vs. grandes desplazamientos. Análisis de demanda vs, análisis de capacidad Estos temas son considerados brevemente en este capítulo. Forman una base para capítulos posteriores. LAS FASES DEL ANÁLISIS ESTRUCTURAL. Modelado No hace falta decir que el análisis estructural no se lleva a cabo en estructuras reales, sino en modelos de estructuras reales. El desafío en la fase de modelado es configurar un modelo de análisis útil. Algunos puntos clave son los siguientes. Un modelo de análisis debe captar los aspectos importantes del comportamiento de la estructura real. Un modelo útil hace esto con suficiente precisión, economía y detalle para propósitos prácticos. Un modelo no tiene que ser "exacto", y nunca lo será. Un modelo casi siempre será un modelo de "elemento de nodo", que consiste en nodos rígidos conectados por elementos deformables. Vea el Capítulo 2 para una descripción detallada Una tarea importante es elegir las condiciones adecuadas y asignarles propiedades como rigidez y resistencia. Esta es una tarea desafiante que requiere habilidad y juicio. Una segunda tarea importante es elegir las medidas de demanda y capacidad adecuadas para evaluar el desempeño. Esto también requiere habilidad y juicio. Solo porque un modelo de análisis se parece a la estructura real no significa que tenga el mismo comportamiento. Las representaciones gráficas elaboradas de las estructuras son agradables y pueden ser útiles. Sin embargo, un modelo de análisis que se parece a la estructura real no necesariamente se comporta como tal. 1.2.2 Interpretación El final de la fase de modelado es un modelo de análisis detallado. El final de la fase de cálculo es un conjunto de "resultados" para el modelo, que consiste principalmente en desplazamientos en los nodos y fuerzas en los elementos (pero también incluye otras cosas). El desafío en la fase de interpretación es utilizar estos resultados para tomar decisiones de diseño para la estructura real. Algunos puntos clave son los siguientes. (1) Es importante considerar el propósito del análisis e interpretar los resultados de una manera que apoye ese propósito. El análisis no es un fin en sí mismo, y no existe un procedimiento de talla única para interpretar los resultados del análisis. (2) En la mayoría de los libros de texto de análisis estructural, es probable que los resultados de un análisis sean una forma desviada y un diagrama de momento de flexión. Estos pueden ser interesantes, pero pueden no ser muy útiles para tomar decisiones de diseño. Para tomar decisiones de diseño es necesario pensar en términos de demandas, capacidades y relaciones demanda / capacidad. 3. A menudo puede haber errores en un modelo de análisis, y posiblemente también en los cálculos numéricos. Es importante verificar que los resultados parecen razonables. 4. Siempre tenga en cuenta que los resultados son para el modelo de análisis, no para la estructura real. Un modelo de análisis nunca será una representación exacta de la estructura real, y no es necesario que lo sea. Sin embargo, debe estar lo suficientemente cerca para propósitos prácticos. Computación La computación, como se define en este libro, incluye todo lo que no está incluido en el modelado y la interpretación. Dado un modelo de análisis, la fase de cálculo implica todo lo que se necesita para obtener los resultados del análisis. Este puede ser un proceso complejo, que involucra la lógica compleja de la teoría de elementos finitos, y cálculos numéricos extremadamente grandes. Algunos puntos clave son los siguientes. (1) Los cálculos numéricos (dado el modelo de análisis, obtener los resultados del análisis) se realizarán casi siempre por computadora. Dado que los costos del desarrollo de programas informáticos son grandes, y el desarrollo requiere una gran cantidad de conocimientos especializados, un programa informático comercial casi siempre será la opción más económica. Los ingenieros confían en gran medida en la habilidad y experiencia de los desarrolladores de programas informáticos. (2) Los muchos ingenieros que usan programas de computadora necesitan una comprensión básica de la fase de cómputo. Este libro está dirigido principalmente a esos ingenieros. Uno de los objetivos del libro es proporcionar esta comprensión básica. Los pocos ingenieros que escriben programas de computadora necesitan una comprensión profunda de la fase de cómputo. El desarrollo de programas informáticos se ha convertido en una tarea especializada. Este libro no considera detalles computacionales. Importancia relativa de las tres fases Para un ingeniero que utiliza el análisis estructural como una herramienta práctica, existen dos desafíos principales. El primer desafío es configurar un modelo de análisis que dé resultados útiles. El segundo es usar esos resultados para tomar decisiones de diseño. Los detalles computacionales de cómo se obtienen los resultados son de importancia secundaria; pueden ser, y deben ser, atendidos por el programa de computadora (es decir, por los ingenieros que escribieron el programa). Para la mayoría de los ingenieros, las fases de modelado e interpretación son de primordial importancia, y la fase de cálculo es mucho menos importante. Para un ingeniero que escribe programas de computadora (lo más probable es que sea un equipo, no un solo individuo), la fase de cómputo es primordial. Sin embargo, las fases de modelado e interpretación también son importantes (además del diseño de la interfaz, la representación gráfica realista y muchos otros). cosas). Como muestra este libro, el modelado y la interpretación son tareas complejas. Si un desarrollador de programas no le proporciona al usuario una herramienta práctica y eficiente para modelar e interpretar, es poco probable que el programa tenga éxito. Cuando se usa un programa de computadora como una herramienta práctica, la productividad puede aumentar si el programa tiene funciones automatizadas para modelar e interpretar. Los ingenieros pueden esperar el día en que el programa de computadora cree el modelo de análisis automáticamente, realice rápidamente los cálculos numéricos y presenta los resultados exactamente de la manera en que son necesarios. Esto ya se puede hacer para estructuras relativamente simples, y es un objetivo que los desarrolladores de programas se esfuerzan por alcanzar. Puede llegar el día en que se pueda realizar un modelado automatizado para estructuras y análisis de todo tipo. Demanda y capacidad 1.4.1 Evaluación del desempeño El análisis estructural es principalmente una herramienta para evaluar el desempeño de un estructura. El diseño de una estructura por lo general procederá a través de un número. De fases, desde preliminar hasta diseño final. En las fases preliminares el Las proporciones y dimensiones globales de la estructura se refinan progresivamente, y en las fases finales, se detallan el tamaño de los miembros y otros detalles Es probable que el análisis estructural se utilice de manera más bien informal para Diseño preliminar, utilizando modelos simplificados, y más formalmente en el final. Diseño, utilizando modelos más detallados. En cada fase, el análisis estructural es un Herramienta para evaluar el desempeño de la estructura, considerando la capacidad de servicio Bajo cargas comunes y seguridad bajo condiciones de cargas extremas. · El rendimiento casi siempre se evalúa comparando las demandas y Capacidades. Algunos ejemplos simples son los siguientes: 1. Si la desviación en un punto es una preocupación por la capacidad de servicio, El valor de la demanda podría ser la desviación calculada en el punto. La correspondiente capacidad es la desviación permisible. 2. Si la resistencia a la flexión de una viga es un problema de seguridad, un valor de la demanda podría ser el momento de flexión calculado en una sección transversal en ella y La capacidad correspondiente es la resistencia a la flexión en esa sección. 3. Si se permite el rendimiento de una estructura, un problema de seguridad para una viga podría ser si la cantidad de rendimiento en flexión supera la capacidad dúctil (la capacidad de ceder sin pérdida excesiva de resistencia por fractura, pandeo u otras causas). La viga puede ser Modelado utilizando bisagras de plástico. Un valor de demanda podría ser la Rotación calculada en una bisagra particular. La capacidad correspondiente Es la rotación permitida en esa bisagra. 4. Si el costo de reparar un edificio después de un terremoto es una preocupación económica, la demanda podría Ser el costo de reparación calculado. La capacidad correspondiente es el costo aceptable. Este tipo de comparación capacidad vs demanda requiere análisis complejos, tanto en la demanda y la capacidad, y en el momento de escribir esto está muy lejos de convirtiéndose en una práctica habitual. Cuando el análisis estructural se utiliza para la evaluación del desempeño, una vista simplificada del proceso es la siguiente: (1) La geometría de la estructura y los tamaños de los miembros (incluidos detalles de refuerzo, etc.) son conocidos con suficiente detalle para que la estructura sea Modelada y analizada. (2) Se identifican medidas de capacidad de demanda de varios tipos (desplazamientos, Momentos de flexión, rotaciones de bisagras de plástico, etc.). (3) La estructura se modela y analiza, y los valores de demanda son Obtenidos a partir de los resultados del análisis. (4) Los valores de capacidad correspondientes son elegidos o calculados, usando Juicio, fórmulas de código de construcción, etc. (5) Se calculan las relaciones demanda / capacidad (D / C). (6) Si ninguna relación DIC excede de 1, el rendimiento es satisfactorio. Si el rendimiento no es satisfactorio, la estructura debe ser modificada, y / o el modelo de análisis debe ser refinado para proporcionar Los valores más precisos de demanda y / o los valores de capacidad deben ser refinados. 1.4.2 Diseño directo El análisis estructural también se puede utilizar para el diseño directo. Una vista simplificada del proceso es el siguiente: (1) Se conoce la geometría estructural general, pero no todos los tamaños de miembros El objetivo es determinar el tamaño de los miembros. (2) Se configura un modelo de análisis, utilizando el tamaño estimado de los miembros. (3) Se analiza la estructura y se calcula las demandas de fuerza de los miembros. (4) El tamaño de los miembros se calcula para satisfacer estas demandas. Este es elAspecto "diseño directo". (5) Si el tamaño de los miembros cambia significativamente de los tamaños estimados, la iteración puede ser necesaria. Por supuesto, nunca es tan simple. Sin embargo, hay diferencias importantes entre los análisis que se utilizan para el diseño directo y los que se utilizan para la evaluación del desempeño. Es importante tener claro qué se espera del análisis y exactamente cómo se utilizarán los resultados del mismo. 1.5 ANÁLISIS ELÁSTICO VS. INELÁSTICO 1.5.1 Comportamiento de un componente estructural El análisis estructural hace uso de las relaciones entre fuerzas o cargas y Deformaciones o desplazamientos correspondientes. En este libro, el término "relación fuerza-deformación" se utiliza para una estructura· Componente en un modelo de análisis. La "fuerza" puede ser la fuerza axial en una barra, el momento de flexión en una bisagra de plástico, fuerza de corte, tensión normal, corte Estrés, etc., según el tipo de componente. La correspondiente "deformación". Puede ser de extensión axial, rotación de la bisagra plástica, etc. El término "relación de carga-desplazamiento" se utiliza para una estructura completa o un modelo de análisis completo. La relación carga-desplazamiento para una estructura completa depende de las relaciones de fuerza-deformación de sus componentes. La relación fuerza-deformación para un componente estructural típico tiene la forma que se muestra en la Figura 1.1. La relación carga-desplazamiento para una estructura completa Es probable que tenga una forma similar. Fuerza-deformación relacionado a un componente estructural típico Las partes clave de la relación son las siguientes. (1) Comportamiento inicial que es esencialmente lineal. (2) Primer rendimiento, en un punto que puede o no estar bien definido. (3) Una región de fuerza creciente (endurecimiento por deformación). (4) Fuerza definitiva. (5) Límite dúctil, en un punto que puede o no estar bien definido. (6) Pérdida de resistencia progresiva. · (7) Resistencia residual, donde la resistencia se estabiliza. (8) Posible fallo completo. (9) Descarga-recarga cíclica, con un bucle de histéresis. (10) Degradación cíclica, donde la rigidez, resistencia y / o ductilidad progresivamente deteriorarse. 1.5.2 Comportamiento elástico vs. Inelástico En la Figura 1.1, el componente tiene un comportamiento lineal (o muy lineal) hasta el primer rendimiento. El comportamiento en esta región es esencialmente elástico, lo que significa que cuando se aplica una fuerza al componente, almacena energía de tensión, y cuando La fuerza se elimina esta energía se recupera. Si la fuerza sobre el componente Supera la fuerza de rendimiento, el comportamiento se vuelve no lineal e inelástico. Por Comportamiento inelástico solo una parte de la energía es recuperada. cuando la fuerza es remota. "Elástico" no es necesariamente lo mismo que "lineal". Un componente es elástico si todo El trabajo realizado en el componente a medida que se deforma se almacena como energía recuperable de deformación. Los componentes elásticos suelen ser lineales, pero pueden ser no lineales. Un ejemplo es un resorte que tiene un hueco. La rigidez del componente es cero cuando la brecha está abierta, y aumenta cuando la brecha se cierra. Desde la rigidez Esto cambia el comportamiento no lineal, pero el resorte es elástico. En un componente inelástico, parte del trabajo realizado en el componente como Las deformaciones se disipan, como el trabajo plástico, la fricción, la energía de las facturas, etc. El componente inelástico siempre será no lineal. 1.5.3 Diseño basado en la fuerza utilizando análisis elástico El enfoque tradicional del diseño estructural es hacer que la estructura sea lo suficiente fuerte para resistir las cargas externas con un comportamiento esencialmente elástico. También es importante para satisfacer los requisitos de servicio, lo que generalmente significa proporcionando suficiente rigidez para controlar las desviaciones y vibraciones. Para el diseño basado en la resistencia, el análisis estructural puede ser elástico, y su principal propósito es calcular las demandas de fuerza sobre los componentes estructurales, Las capacidades de fuerza correspondientes se obtienen, en la mayoría de los casos, de fórmulas en códigos de diseño. La capacidad de fuerza de una fórmula de código suele ser algo más bajo que la fuerza última real. Si la demanda de fuerza en un solo componente está cerca de su capacidad de fuerza, Podría haber una deformación inelástica significativa del componente. Si una proporción sustancial de los componentes en una estructura están cerca de sus capacidades de fuerza, podría haber una deformación inelástica significativa de la estructura en su conjunto. Por lo tanto, el comportamiento de la estructura podría ser significativamente inelástico bajo las cargas de diseño, y el análisis de elasticidad no es necesariamente preciso Esto es especialmente cierto si el diseño de una estructura es optimizado para reducir su peso, de modo que muchos de los componentes están completamente estresados, Sin embargo, décadas de experiencia han demostrado que el análisis elástico es lo suficientemente preciso para la mayoría de los propósitos de diseño. Para tener en cuenta la incertidumbre en la carga, las cargas esperadas se multiplican Por factores de carga que aumentan las exigencias de fuerza. Por ejemplo, el cálculo de la carga por gravedad para la demanda podría ser 1.2 veces la carga muerta calculada más 1.6 veces la carga viva esperada. Para tener en cuenta la incertidumbre en el componente fuerza, las capacidades de fuerza estimadas se multiplican por capacidad factores de reducción (o factores de resistencia), típicamente entre aproximadamente 0,75 y 0.9. Componentes que son especialmente importantes para la integridad de una estructura. Pueden asignarse menores factores de reducción de capacidad. En algunos casos La demanda calculada de un componente se puede multiplicar por una demanda factor de aumento Los detalles se pueden encontrar en los códigos de diseño y no es tan importante para este libro Los puntos importantes son que el análisis elástico puede ser utilizado, y el propósito principal del análisis es calcular las demandas de fuerza. 1.5.4 Diseño basado en la fuerza utilizando análisis inelástico Diseño basado en la fuerza que utiliza análisis elástico considera la fuerza en el componente nivel. La fuerza de la estructura en su conjunto no es explícitamente calculada. Una alternativa podría ser considerar la fortaleza en el nivel de la estructura, utilizando la carga externa como la demanda y la resistencia de la estructura como la capacidad. Por esta alternativa, la demanda es conocida y estructural. El análisis se utiliza para calcular la capacidad. Esta es una forma más directa asegurando suficiente fuerza, y tiene el potencial de producir más Diseños económicos. Sin embargo, es poco práctico para la mayoría de las estructuras, por las siguientes razones: 1. La capacidad de resistencia calculada de la estructura puede depender en gran medida de los supuestos de modelado. Un posible enfoque es modelar (o intentar modelar) de todos modos el comportamiento que puedan contribuir significativamente al colapso de la estructura. Esto incluye relativamente simple Modos de comportamiento tales como flexión inelástica en vigas (bisagra de plástico). formación), las más complejas como la columna de pandeo, muy Las complejas como la cizalla inelástica en muros de hormigón armado, y Los extremadamente complejos como la fractura por fragilidad en soldaduras. Este enfoque No es meramente poco práctico, es imposible. Para una estructura compleja. Incluso el modelo de análisis más sofisticado no puede esperar tener en cuenta para todos los efectos significativos. 2. Un enfoque más práctico es limitar deliberadamente los modos de comportamiento que contribuyen al colapso. Por ejemplo, se puede prevenir el corte inelástico en paredes de concreto reforzado, al exigir que la resistencia al corte sea lo suficientemente grande como para que nunca se produzca el comportamiento inelástico del corte. Por lo tanto, la cizalla inelástica no tiene que ser considerada, Y el modelo de análisis es más sencillo y más confiable. Dado que es probable que el corte inelástico sea frágil, también es probable que mejore el rendimiento de la estructura bajo cargas extremas. Este es un ejemplo de "diseño de capacidad". 3. Incluso cuando se usa el diseño de capacidad, el cálculo directo de la resistencia de la estructura requiere un análisis inelástico, que es mucho más complejo y costoso que el análisis elástico. una complicación es que solo se requieren las rigideces de los componentes para un análisis elástico, mientras que las rigideces, las resistencias, el comportamiento de endurecimiento por deformación y otras propiedades son necesarias para un análisis inelástico. Se puede crear un modelo elástico basado en estimaciones aproximadas de los tamaños de los miembros, y se puede actualizar fácilmente a medida que los tamaños se determinan con mayor precisión (muchos programas de computadora lo harán automáticamente). Esto no es tan fácil para un modelo inelástico. 4. Hay muchos efectos que deben tenerse en cuenta en el diseño, además de las cargas externas. Estos incluyen expansión térmica, fluencia (especialmente en concreto reforzado) y movimiento de cimientos. Algunos de estos afectan solo la capacidad de servicio, no la resistencia. Sin embargo, esto tiene que ser verificado. Es mucho más fácil tener en cuenta estos efectos en el análisis elástico. Para la mayoría de las estructuras, es probable que el análisis elástico sea el enfoque estándar para el futuro previsible. Una excepción es el diseño de estructuras para resistir grandes terremotos, como se considera en la siguiente sección. 1.5.S Deformación- Diseño basado para cargas de terremotos Para el diseño resistente a terremotos, existe una alta probabilidad de que ocurra un pequeño terremoto durante la vida útil de la estructura y una baja probabilidad de un gran terremoto. Para un terremoto pequeño, una estructura generalmente será diseñada para permanecer esencialmente elástica. Sin embargo, para un gran terremoto, generalmente se argumenta que no es económico diseñar la estructura para que permanezca elástica, y es una práctica común permitir un comportamiento sustancial e inelástico. Por lo tanto, para un gran terremoto, es probable que la demanda de resistencia elástica en una estructura exceda su capacidad de resistencia. Esto se ilustra en la Figura 1.2. Si la carga sísmica fuera una carga estática, actuando durante un período de tiempo sostenido, la estructura colapsaría. Sin embargo, las cargas sísmicas fluctúan rápidamente. Una carga que excede la resistencia de la estructura puede aplicarse varias veces durante un terremoto, pero como la carga es dinámica y actúa solo por un corto tiempo, no necesariamente causa colapso. Como se muestra en la Figura 1.2, el desplazamiento máximo de la estructura puede ser aceptable, y aunque algunos componentes estructurales se vuelven inelásticos, la estructura puede funcionar satisfactoriamente. Para aquellos componentes que se vuelven inelásticos, la preocupación por el diseño es la deformación, no la resistencia. Para un desempeño satisfactorio, la demanda de deformación en un componente inelástico generalmente debe ser más pequeña que su límite dúctil (como se define en la Figura 1.1. El enfoque más racional para un gran terremoto es utilizar el análisis inelástico. Esto tiene las siguientes ventajas. 1. Para los componentes que se vuelven inelásticos, la principal preocupación para el diseño es la deformación (o ductilidad), no la resistencia. El análisis inelástico puede calcular las demandas de deformación directamente. El análisis elástico no puede. 2. Cuando una estructura se vuelve inelástica, las fuerzas en. la estructura se puede redistribuir, y la distribución de fuerzas en la estructura puede ser muy diferente de la calculada por el análisis elástico. Esto puede tener efectos sustanciales en el comportamiento de la estructura. El análisis inelástico explica la redistribución de la fuerza. El análisis elástico no lo hace. 3. Cuando se usa el diseño de capacidad, las demandas de fuerza deben calcularse para aquellos componentes que deben permanecer elásticos. Por ejemplo, si no se permite el corte inelástico en un muro de concreto reforzado, se debe calcular la demanda de fuerza de corte, y el muro debe diseñarse con una capacidad de fuerza de corte que exceda la demanda. En un análisis inelástico, las demandas de fuerza calciladas para un componente pueden depender de la resistencia de sus componentes circundantes o de la resistencia del propio componente. Por ejemplo, la demanda de fuerza de corte en una pared puede depender de su resistencia a la flexión. Esto se puede explicar directamente en un análisis inelástico, lo que significa que el diseño de la capacidad se puede aplicar de manera más racional. El diseño de la capacidad todavía se puede utilizar con análisis elástico, como se considerará más adelante, pero es un proceso menos directo. Para una estructura simple, el análisis estático inelástico (análisis "push over" estático) puede ser suficiente. Para una estructura grande o compleja, el análisis dinámico inelástico puede ser necesario. 1.5.6 Fuerza-Diseño basado para cargas de terremotos No es esencial utilizar el análisis inelástico para el diseño resistente a terremotos. Para propósitos de diseño es posible usar análisis elástico, considerando el comportamiento inelástico implícitamente en lugar de explícitamente. Si una estructura fue diseñada para permanecer elástica en un gran terremoto, se aplicarán cargas que correspondan a este terremoto, y los componentes estructurales se diseñarán para las demandas de fuerza calculadas utilizando un análisis elástico. Llame a estas "demandas de fuerza elástica". Cuando se permite el comportamiento inelástico, el procedimiento habitual es diseñar los componentes para demandas de fuerza que son sustancialmente más pequeñas que las demandas elásticas. Estas demandas se obtienen aplicando una "modificación de respuesta. Coeficiente "o" factor R "a las demandas de fuerza elástica, donde este coeficiente depende de la ductilidad del componente y su importancia en la estructura. Por ejemplo, si un componente es muy dúctil, podría diseñarse para una demanda de fuerza de, por ejemplo, 1/8 de la demanda de fuerza elástica (un factor R de 8). Esto significa que el componente es relativamente débil y es probable que tenga una Deformación inelástica. A la inversa, si un componente es muy frágil, podría diseñarse para la demanda total de fuerza elástica (un factor R de 1). Tal componente es relativamente fuerte y es probable que tenga poca o ninguna deformación inelástica. Por lo tanto, este método tiende a producir estructuras que tienen un comportamiento deseable, ahorrando dinero al permitir que los componentes dúctiles se vuelvan inelásticos y preservando la seguridad al mantener elásticos los componentes quebradizos. Además, es un método práctico porque es básicamente un diseño basado en la fuerza que utiliza análisis elástico. Sin embargo, el análisis elástico no tiene en cuenta la redistribución de la fuerza, ya que una estructura se vuelve inelástica y, por lo tanto, el uso de este método no garantiza necesariamente que la estructura funcionará bien. En algunos casos, el análisis elástico puede incluso dar información engañosa. El método puede ser más confiable cuando se combina con el diseño de capacidad, como se considera en la siguiente sección. El método no debe usarse a ciegas Esto enfatiza que no es necesario que un análisis sea "exacto", solo tiene que proporcionar resultados que sean lo suficientemente precisos para los propósitos de diseño. Con una buena ingeniería, las estructuras que están diseñadas con análisis elástico pueden funcionar bien en grandes terremotos. 1.5.7 Diseño de capacidad utilizando análisis elástico En la forma básica del diseño basado en la resistencia, el análisis elástico se utiliza para calcular las demandas de fuerza en los componentes estructurales, y los componentes están diseñados para tener capacidades de resistencia iguales o superiores a las demandas. Este proceso debe modificarse cuando se utiliza el diseño de la capacidad. Como ejemplo, considere una estructura de marco de concreto reforzado donde se permite la flexión inelástica en las vigas, pero donde el comportamiento de corte debe ser esencialmente elástico. Esto se puede hacer porque los moldes de hormigón armado pueden ser dúctiles en flexión, pero tienden a ser frágiles en cizallamiento. Como se consideró en la sección anterior, cuando se usa el análisis elástico para cargas sísmicas, es usual permitir implícitamente un comportamiento inelástico, utilizando factores R, una forma de explicar la ductilidad relativa es usar un factor R menor para el corte que para doblar. Sin embargo, existe un método mejor y más directo, utilizando el diseño de capacidad. Para ilustrar esto, considere el marco en la Figura l.3 (a). La figura muestra las cargas de gravedad más una carga lateral estática para representar un terremoto. Para estas cargas, la Figura 1.3 (b) muestra las demandas de momento de flexión. Estas son las demandas elásticas, con los momentos de cargas sísmicas divididos por un factor R. Para una viga de concreto reforzado, este factor puede ser tan alto como 8. Como se muestra en la figura, es probable que la resistencia real de la viga en la flexión sea significativamente mayor que la demanda del momento de flexión, por dos razones principales, como sigue. 1. Es probable que el área de refuerzo sea más grande que el área necesaria para proporcionar una capacidad que sea exactamente igual a la demanda. 2. Es probable que las resistencias reales del material sean mayores que las asumidas para el diseño. Para diseñar la viga, es habitual aplicar un factor de reducción de capacidad a la resistencia a la flexión nominal, o esperada, para tener en cuenta la incertidumbre. Para estimar la capacidad de resistencia a la flexión real, deben usarse las resistencias de material esperadas (o más), sin factor de reducción de capacidad. Utilizando capacidad de diseño, la cizalla. las demandas de fuerza se basan en el diagrama de momentos discontinuos de la Figura 1.3 (b). Dado que las fuerzas de corte dependen de los momentos de flexión, y dado que los momentos de flexión son los valores máximos que pueden alcanzarse independientemente de la resistencia del terremoto, si el haz está diseñado para estas fuerzas de corte, el comportamiento en corte es siempre esencialmente elástico. Una alternativa es usar diferentes factores R para doblar y cortar, y diseñar la viga para las demandas calculadas. Esto puede o no lograr el objetivo de mantener el comportamiento de corte esencialmente elástico. El diseño de capacidades es un enfoque más racional. 1.6 Análisis estático vs. Dinámico Las cargas externas en una estructura pueden ser estáticas o dinámicas. La mayoría de las cargas son en realidad dinámicas, pero para fines de análisis se puede suponer que una carga es estática si se aplica lentamente (en relación con el período de vibración de la estructura). Para el caso estático, las cargas externas en la estructura son resistidas completamente por las fuerzas estáticas en los componentes estructurales. Para el caso dinámico, las cargas externas también pueden resistirse por fuerzas de inercia asociadas con la masa de la estructura. Si las fuerzas de inercia y las fuerzas en los componentes estructurales actúan en la misma dirección, las fuerzas de los componentes son más pequeñas de lo que serían para las mismas cargas aplicadas de forma estática. Si la inercia y las fuerzas de los componentes actúan en direcciones opuestas, las fuerzas de los componentes son más grandes de lo que serían para las mismas cargas aplicadas de forma estática. En general, las fuerzas de inercia y componentes actúan en direcciones variables en diferentes partes de la estructura y en diferentes momentos del análisis, y las interacciones entre las fuerzas son complejas. Las fuerzas de inercia dependen de la aceleración y varían linealmente con la aceleración (Suponiendo que la masa no cambie). También puede haber fuerzas "viscosas" que dependen de la velocidad. La experiencia muestra que cuando una estructura se carga dinámicamente, hay una pérdida de energía (disipación de energía), incluso si la estructura es elástica. Es común suponer que la disipación de energía es causada por un mecanismo de amortiguamiento viscoso, que implica la presencia de fuerzas dependientes de la velocidad. Estas fuerzas pueden depender lineal o no linealmente de la velocidad, dependiendo del supuesto mecanismo de amortiguamiento viscoso. Una complicación adicional es que la relación fuerza-deformación para un componente estructural puede depender de la tasa de deformación del componente, que a su vez depende de la velocidad. Por ejemplo, un componente puede ser sustancialmente más fuerte cuando se carga dinámicamente, con una alta tasa de deformación, que cuando se carga estáticamente. 1.7 ANÁLISIS DE DESPLAZAMIENTOS PEQUEÑOS VS. GRANDES 1.7.1 Descripción general Si una estructura tiene componentes inelásticos, su comportamiento será no lineal, como se consideró anteriormente. Esto generalmente se denomina no linealidad material. También puede haber un comportamiento no lineal cuando una estructura experimenta grandes desplazamientos, incluso si permanece elástica. Esto generalmente se conoce como. No linealidad geométrica. Existen dos causas de la no linealidad geométrica, la primera basada en el equilibrio y la segunda en la compatibilidad (continuidad). Esta sección da breves explicaciones. El capítulo 6 entra en más detalle. 1.7.2 Equilibrio Cuando se carga una estructura cambia de forma. En rigor, equilibrio. Entre las cargas externas y las fuerzas internas se deben satisfacer en la posición deformada de la estructura. Sin embargo, si los desplazamientos son pequeños, puede ser una aproximación razonable considerar el equilibrio en la posición inicial, no deformada. Como esta posición es fija, las relaciones de equilibrio son lineales. por ejemplo, duplicar las cargas externas duplica exactamente las fuerzas internas (suponiendo que no haya material no lineal). Si los desplazamientos no son pequeños, se debe considerar el equilibrio en la posición deformada En este caso las relaciones de equilibrio no son lineales. (duplicar las cargas externas no duplica exactamente las fuerzas internas). Esto se ilustra en la Figura 1.4. (a) POSICION NO DEFORMADA (b) POSICION DEFORMADA FORCE IN SPRING (FUERZA EN PRIMAVERA) Figura 1.4 Equilibrio en posiciones no deformadas y deformadas La figura 1.4 (a) muestra la posición no deformada. El momento de flexión en la base fijada debe ser cero, por lo que mediante un simple equilibrio la fuerza en el resorte es igual a la carga horizontal. La Figura 1.4b) muestra la posición deformada, asumiendo que el resorte Comprime y la parte superior de la barra se mueve horizontalmente en una cantidad A. Nuevamente, el momento de flexión en la base es cero, para satisfacer el equilibrio La fuerza en el resorte debe ser mayor que la carga aplicada. Además, la primavera. La fuerza no es proporcional a la carga. Por ejemplo, si P y H se duplican, La fuerza en el resorte más que se duplica. 1.7.3 Compatibilidad (Continuidad) Existe una relación geométrica entre los desplazamientos de una estructura. y las deformaciones de sus componentes. La figura 1.5 muestra tal relación. (a)Desplazamiento Impuesto (b) Relación de compatibilidad Deformed lenght (longitud deformada) bar extensión (extensión de la barra) Figura 1.5 Relación de compatibilidad no lineal En la Figura 15 (a), la parte superior de la barra se mueve horizontalmente. Por lo tanto, la barra debe extender para mantener la continuidad. La figura 1.5 (b) muestra la relación entre Desplazamiento y barra de tensión. La extensión de la barra es la longitud deformada. menos la longitud no deformada, h. Para un desplazamiento horizontal muy pequeño, la extensión de la barra está cerca de cero (en el límite, para un desplazamiento muy pequeño, la extensión de la barra es exactamente cero). Para mayores desplazamientos se extiende la barra, con un no lineal. Relación entre desplazamiento y extensión. 1.7.4 Tipos de análisis Para el análisis los efectos de los grandes desplazamientos en las relaciones de equilibrio y compatibilidad pueden tratarse por separado. En consecuencia, hay tres tipos diferentes de análisis que pueden llevarse a cabo, de la siguiente manera. (1) Análisis de pequeños desplazamientos. El equilibrio se considera en la posición no deformada y, por compatibilidad, se supone que los desplazamientos son muy pequeños. (2) Verdadero análisis de grandes desplazamientos. El equilibrio se considera en la posición deformada y, por compatibilidad, se supone que los desplazamientos son finitos. (3) Análisis P-A. El equilibrio se considera en la posición deformada y, por compatibilidad, se supone que los desplazamientos son muy pequeños. Hay un cuarto tipo (posición deformada para el equilibrio, pequeños desplazamientos). de compatibilidad), pero esto nunca se utiliza. La figura 1.6 ilustra la diferencia para una estructura simple. (a) Pequeños desplazamientos (c) grandes desplazamientos Moves horizontaly ( movimientos horizontales) Forcé in spring ( fuerzas horizontales) Force in bar (fuerza en la barra) Figura 1.6 Diferentes tipos de análisis Para esta estructura, asuma que la barra está rígida axialmente, de modo que tiene una resistencia despreciable. Deformación axial. La figura 1.6 (a) muestra las cargas y fuerzas para pequeños análisis de desplazamientos, Figura 1.6 (b) para el análisis P-A y Figura 1.6 (c) para análisis de grandes desplazamientos. Tenga en cuenta que en la Figura 1.6 (c) se supone que el resorte permanece horizontal. Las diferencias entre los tres métodos dependen de los valores relativos de las cargas P y H, y en el desplazamiento A. Considere dos casos de ejemplo como sigue. (1) P-0 y & / h = 0.1 (es decir, 10% de relación de deriva, que es una deriva muy grande para la mayoría de las estructuras). Para los tres métodos, la fuerza en el resorte es H y la fuerza en la barra es cero. La única diferencia es que la vertical Análisis de desplazamientos pequeños vs. grandes el desplazamiento es insignificante para los pequeños desplazamientos y los análisis de P-A, y es igual a un pequeño valor (0.005) para el análisis de grandes desplazamientos. (2) P / H 5, h-0,10. Para el caso de pequeños desplazamientos, las fuerzas en el resorte y la barra son respectivamente H y P. Para el caso P-A, las fuerzas son 1.5 H y 0.995P. Para el caso de grandes desplazamientos, las fuerzas son 1.503H y 0.995P. Los desplazamientos verticales son esencialmente los mismos que para P = 0. Estos ejemplos muestran que el análisis de pequeños desplazamientos puede ser erróneo cuando hay cargas de gravedad sustanciales y grandes desviaciones, pero solo en la fuerza en el resorte (en la segunda muestra anterior hay un error del 50% en la fuerza del resorte). Para los tres análisis, la fuerza axial en la barra está muy cerca de P (porque cos @ está muy cerca de 1.0). Cuando se comparan los análisis de P-A y de gran desplazamiento, hay muy poca diferencia en las fuerzas del resorte. La única diferencia significativa es que la desviación vertical calculada es cero para el análisis P-A y un pequeño valor para el análisis de grandes desplazamientos. Estos ejemplos representan aproximadamente una estructura de construcción de un solo piso (el resorte modela la rigidez horizontal). Indican que puede ser importante considerar los efectos de PA, pero que no es necesario considerar desplazamientos grandes verdaderos. Esto es importante porque el análisis P-4 puede ser mucho más eficiente computacionalmente que el análisis de grandes desplazamientos. Para estructuras de edificios bajo gravedad más cargas laterales, a menudo es importante considerar los efectos P-A, pero rara vez es necesario considerar verdaderos grandes desplazamientos. 1.7.5 Efecto catenario El tipo de comportamiento escrito en la sección anterior no se aplica a todas las estructuras. La figura 1.7 muestra el comportamiento de un tipo diferente. Análisis de grandes desplazamientos Barras o cables flexibles Predice un aumento de rigidez Pequeños desplazamientos P - ∆ Los análisis predicen p=0 Figura 1.7 Efecto catenario. En este ejemplo, a medida que la estructura se desvía, se vuelve cada vez más rígida. Esto generalmente se conoce como el efecto "catenaria". Sólo un análisis de grandes desplazamientos explica este efecto. La razón es que el análisis de pequeños desplazamientos y los análisis P-A asumen una relación de compatibilidad lineal entre el desplazamiento de la estructura y la extensión de la barra. En este ejemplo, la relación de compatibilidad lineal da una extensión de barra cero, incluso para valores grandes de A. Por consiguiente, la fuerza de la barra es cero y, por lo tanto, P = 0 en las posiciones deformadas y deformadas. El análisis de grandes desplazamientos utiliza una relación de compatibilidad no lineal, como en la Figura 1.5, y por lo tanto explica el efecto catenario. Una diferencia importante entre el material y la no linealidad geométrica es que la no linealidad geométrica tiene dos causas bien definidas (equilibrio y compatibilidad), ambas regidas por reglas matemáticas claras, mientras que la no linealidad material puede tener muchas causas y muchas formas. Nuestro conocimiento de la no linealidad del material depende casi completamente de lo que observamos en experimentos con estructuras reales y componentes estructurales. En este ejemplo, a medida que la estructura se desvía, se vuelve cada vez más rígida. Esto generalmente se conoce como el efecto "catenaria". Sólo un análisis de grandes desplazamientos explica este efecto. La razón es que los pequeños desplazamientos y los análisis P- ~ asumen una relación de compatibilidad lineal entre el desplazamiento de la estructura y la extensión de la barra. En este ejemplo, la relación de compatibilidad lineal da una extensión de barra cero, incluso para valores grandes de fl. En consecuencia, la fuerza de la barra es cero y, por lo tanto, P = 0 tanto en la posición deformada como en la no deformada. El análisis de grandes desplazamientos utiliza una relación de compatibilidad no lineal, como en la Figura 1.5, y él explica el efecto catenario. Una diferencia importante entre el material y la no linealidad geométrica es que la no linealidad geométrica tiene dos causas bien definidas (equilibrio y compatibilidad), las cuales están regidas por reglas matemáticas claras, mientras que la no linealidad del material puede tener muchas causas y muchas opciones. Nuestro conocimiento de la no linealidad del material depende casi por completo de lo que observamos en experimentos con estructuras reales y componentes estructurales. 1.8 ANÁLISIS DE DEMANDA VS. ANÁLISIS DE CAPACIDAD 1.8.1 Descripción general En la mayoría de los casos, el análisis estructural se utiliza para calcular los valores de la demanda para la evaluación del desempeño o el diseño directo. También es posible utilizar el análisis estructural para calcular los valores de capacidad. Este es un proceso muy diferente. Hay cuatro tipos generales de análisis, como sigue. (1) Demanda de fuerza. Este es, con mucho, el tipo de análisis más común. El análisis se utiliza para calcular los momentos de flexión, las fuerzas de corte, etc. Las capacidades correspondientes se obtienen a partir de códigos de diseño u otras fuentes. (2) Demanda de deformación. La mayoría de los análisis inelásticos son de este tipo. El análisis se utiliza para calcular las rotaciones de las bisagras de plástico, las tensiones de corte, etc. (3) Capacidad de fuerza. El análisis, en lugar del experimento, se usa para estimar la resistencia de una estructura o componente estructural. 4) Capacidad de deformación. El análisis, en lugar del experimento, se usa para estimar la relación fuerza deformación para un componente estructural (o posiblemente la relación cargadesplazamiento para una estructura). A partir de esta relación, se puede hacer una estimación de la deformación máxima que se puede imponer sobre el componente (es decir, su capacidad de deformación). Esta sección da algunos ejemplos de análisis de capacidad. 1.8.2 Carga lateral al primer rendimiento Este es un ejemplo de un análisis de capacidad de fuerza. Es un ejemplo artificial, pero ilustra el proceso. Supongamos que se requiere que la estructura del bastidor permanezca elástica (sin formación de bisagras plásticas) bajo la gravedad combinada y la carga lateral estática (que representa, por ejemplo, la carga del viento). Supongamos que (a) se conoce la carga de gravedad, tanto en distribución como en magnitud, y (b) se conoce la distribución de la carga lateral pero no su magnitud. Es necesario calcular la magnitud de la carga lateral en la que el marco deja de ser elástico (es decir, en el que se forma la primera articulación). Esta magnitud de carga lateral es la capacidad elástica del bastidor. El análisis es fácil de realizar. Los pasos son los siguientes: (1) Configurar un modelo elástico de la estructura. (2) Identifique todos los lugares donde se pueden formar las bisagras de plástico. Calcule las capacidades de los momentos de flexión en estos lugares. (3) Analizar para la carga de gravedad. (4) Agregue la carga lateral y aumente progresivamente la magnitud de la carga hasta que la demanda del momento de flexión en una de las ubicaciones de bisagra potenciales supere la capacidad del momento de flexión. (Como alternativa, dado que el comportamiento es lineal, realice análisis separados para la carga de gravedad y la unidad lateral de carga, luego calcule la magnitud de carga lateral mínima necesaria para obtener una relación D / C igual a 1.0). (5) Esta magnitud de carga es el requisito lateral requerido. capacidad de carga. Tenga en cuenta que no es necesario configurar un modelo inelástico con bisagras de plástico. 1.8.3 Intensidad del terremoto en el colapso Este es un ejemplo más realista de un análisis de capacidad de fuerza. Se han utilizado análisis de este tipo para estimar las probabilidades de colapso de las estructuras reales. Considere una estructura de bastidor con una carga de gravedad conocida y un movimiento de tierra de terremoto específico. Para el movimiento del terreno, se conoce la variación de la aceleración del terreno con el tiempo, pero la intensidad puede variar (es decir, las aceleraciones del terreno se pueden escalar hacia arriba o hacia abajo). Calcule la intensidad del terremoto requerida para colapsar la estructura. Esta intensidad es la capacidad de colapso del marco. El proceso para calcular la capacidad de colapso generalmente se denomina "análisis dinámico incremental". Los pasos son los siguientes: (1) Configurar un modelo inelástico de la estructura. (2) Analizar para la carga de gravedad. (3) Elija una intensidad para el terremoto y ejecute un análisis dinámico inelástico, manteniendo constante la carga de gravedad. Determine si la estructura se derrumba. Vea a continuación para un comentario sobre esto. (4) Repita el análisis para una cantidad de intensidades de terremoto (generalmente en aumento progresivo). H todo va bien, con cierta intensidad la estructura no colapsará, y con una intensidad ligeramente mayor colapsará. (5) Esto determina la capacidad de colapso, dentro de una tolerancia que depende del número de intensidades de terremotos que se consideran. El objetivo general es similar al del ejemplo anterior, es decir, calcular una capacidad. Sin embargo, los detalles son dramáticamente diferentes. Es relativamente fácil configurar un modelo de análisis elástico y verificar las relaciones DIC de resistencia. Es mucho más difícil configurar un modelo que explique los muchos tipos de comportamiento inelástico que puede influir en el colapso y realizar un análisis dinámico significativo de dicho modelo. Es probable que los análisis de este tipo sean muy aproximados, y los resultados del análisis pueden depender en gran medida de los supuestos en el modelo de análisis. 1.8.4 Fuerza de flexión de una viga Los dos ejemplos anteriores consideraron estructuras completas. Este ejemplo considera una pequeña parte de una estructura completa. Este es también un análisis de la capacidad de fuerza. Supongamos que una viga de hormigón armado tiene una sección transversal compleja, por lo que no se aplican las fórmulas utilizadas únicamente para calcular la capacidad del momento de flexión. El análisis estructural podría usarse para calcular esta capacidad, de la siguiente manera: (1) Configure un modelo de análisis que consista en una longitud corta de la viga, cargada de modo que la viga tenga un momento de flexión constante (es decir, flexión pura). (2) Divida la sección transversal de la viga en varias "fibras" o "filamentos" longitudinales, algunas representando concreto y algo de acero. (3) Modele las fibras de concreto utilizando un modelo de material inelástico que tenga en cuenta el agrietamiento y la trituración. (4) Modele las fibras de acero utilizando un material inelástico que tenga en cuenta el rendimiento y el endurecimiento por deformación. (5) Suponga que las secciones planas permanecen planas, como es habitual en la teoría de vigas. (6) Realice un análisis inelástico, aumentando progresivamente el momento de flexión hasta alcanzar la fuerza máxima. 1.8.5 Capacidad de rotación de la bisagra de plástico Este es un ejemplo de un análisis de capacidad de deformación. El comportamiento inelástico de las vigas en la flexión a menudo se puede modelar utilizando bisagras de plástico. Esto se muestra en la Figura 1.8. La viga se modela como una viga elástica con bisagras de plástico en cada extremo. Una bisagra de plástico es inicialmente rígida y comienza a girar a primera velocidad. Las propiedades de una bisagra plástica incluyen su resistencia a la flexión y su capacidad de rotación, que para este ejemplo es la rotación en el límite dúctil. Cuando se modela una viga inelástica utilizando bisagras de plástico, se supone que todas las deformaciones inelásticas se concentran en las bisagras y que el resto de la viga permanece elástica. Como es probable que el comportamiento inelástico en una viga real se distribuya en una longitud significativa de la viga, una bisagra de plástico de longitud cero es una aproximación. La figura 1.9 muestra cómo se pueden determinar las propiedades de una bisagra plástica. La figura l.9 (a) muestra una viga con momentos finales iguales y opuestos. La figura l.9 (b) muestra un modelo de la viga, con bisagras de plástico. Si se conoce la relación entre el momento final y la rotación final total, las propiedades de la bisagra plástica se pueden determinar como se muestra en la Figura l.9 (c). Las propiedades plásticas de la bisagra se determinan generalmente experimentalmente, Sin embargo, para este ejemplo, suponga que la viga tiene una sección de acero de pared delgada para la cual no se dispone de resultados experimentales. Las propiedades plásticas de la bisagra se determinan generalmente experimentalmente. Sin embargo, para este ejemplo, suponga que la viga tiene una sección de acero de pared delgada para la cual no se dispone de resultados experimentales. Las propiedades de la bisagra plástica deben ser estimadas por análisis. Las principales propiedades que deben calcularse son la resistencia a la flexión y la capacidad de rotación de la bisagra, que es la rotación en el límite dúctil. Estos pueden calcularse realizando un análisis inelástico de una viga en voladizo, como se muestra en la Figura 1.10. carga Estimación de las propiedades de la bisagra por análisis. a) Realizar con momentos finales b) Voladizo en equilibrio c) Modelo de elementos finitos La figura 1.10 (a) muestra la viga. La figura 10.1 (b) muestra un voladizo equivalente. La Figura 1.10 (c) muestra el tipo de malla de elementos finitos que podría usarse para Analizar el voladizo. Los elementos en la región de la bisagra deben tener en cuenta el rendimiento del acero, con el fin de Para calcular la resistencia a la flexión. Más importante aún, el límite dúctil para el es probable que la viga esté gobernada por el pandeo local de la sección de acero, por lo que Los elementos también deben tener en cuenta la no linealidad geométrica. El pandeo El comportamiento puede ser sensible a las imperfecciones geométricas en la viga, como variaciones en el espesor de la pared y distorsiones locales causadas por la soldadura de la conexión final La relación tensión-deformación para el acero puede ser incierta. y puede variar de un punto a otro en la viga. Este es un análisis de capacidad, donde el análisis se utiliza como un sustituto de experimentar. Aunque la estructura es pequeña, puede ser difícil de configurar un modelo de análisis preciso, especialmente si se debe considerar la deformación cíclica. 1.8.6 Conclusión para esta sección La mayoría de los análisis estructurales son análisis de demanda, donde el objetivo es estimar Exigencias de fuerza o deformación. En un análisis de capacidad el objetivo es estimar una resistencia o capacidad de deformación. El objetivo del análisis de capacidad es esencialmente una simulación "exacta". Esto puede ser difícil cuando hay un comportamiento inelástico complejo que involucra cosas tales como fractura y pandeo local en acero o trituración, agrietamiento, corte inelástico y Bond antideslizante en hormigón armado. Los análisis de capacidad deben usarse con cautela. Como regla general, las capacidades que son determinados por experimento es probable que sean más confiables. 1.9 Conclusión para este capítulo. Existen diferentes tipos de análisis estructural, con diferentes objetivos. Es importante tener claro el propósito del análisis, los resultados requeridos, y cómo se utilizan los resultados. La mayoría de los análisis son análisis de demanda, donde el propósito es calcular la fuerza y / o. Demandas de deformación. Las capacidades correspondientes se obtienen de otras fuentes, como el diseño. Algunos análisis pueden ser Análisis de capacidad, donde el propósito es calcular la resistencia y / o la capacidad de deformación. Las demandas correspondientes se obtienen de otras fuentes. El análisis de capacidad es más difícil que análisis de la demanda. Un análisis nunca puede ser "exacto". Es literalmente imposible usar -análisis para realizar una simulación exacta de una estructura real, sin importar cuánta computación El poder está disponible o qué tan complejo es el modelo. El análisis estructural está en el mejor de los casos, aproximado, y siempre se debe utilizar con una gran dosis de ingeniería y juicio. 1.10 Temas para los siguientes capítulos. Este libro se ocupa principalmente de los modelos de análisis de "elemento finito" o Tipo "nodo-elemento", que consiste en nodos y elementos discretos. Es importante para entender lo que significa un "modelo de análisis". El capitulo 2 describe Las características y limitaciones de los modelos nodo-elemento. La parte computacional del análisis casi siempre se hace usando el Método de rigidez directa. Para los ingenieros que realizan análisis prácticos, no es necesario comprender los detalles de este método, pero es importante tener una comprensión global del proceso. Esto se trata en el Capítulo 3. El paso más importante para configurar un modelo de nodo-elemento es elegir el Elementos y Cl $ firmándolos de propiedades. En general, se puede hacer un elemento de una serie de componentes, con rigidez, resistencia y otras propiedades. Para entender las características y limitaciones de un elemento, es importante comprender el comportamiento de sus componentes subyacentes, y Las suposiciones que se hacen para capturar este comportamiento en un análisis. modelo. El capítulo 4 considera el comportamiento de los componentes, con énfasis en el material. no linealidad. Este capítulo está limitado a componentes "uniaxiales", donde El componente tiene una sola fuerza (como la fuerza axial en una barra) y una sola Deformación correspondiente (como la extensión de la barra). Capitulo 5 también considera la no linealidad del material, pero para componentes con fuerza deformación multiaxial relaciones con la interacción. Un ejemplo es la fuerza P-M-M. y la Interacción en una columna. Los capítulos 4 y 5 consideran principalmente la no linealidad material. Geométrico la no linealidad es un tema aparte que puede ser importante tanto en la estructura nivel y el nivel de elemento. El capítulo 6 considera varios aspectos de la geometría. no linealidad, incluidas las contrapartes P-.1 \ y P-0, la inestabilidad y el Pandeo de columnas, vigas y estructuras completas. Capítulo. 7 considera algunos otros aspectos del comportamiento estructural, incluyendo Mecanismos plásticos, redundancia, componentes no estructurales y energía equivalente