FUNDACION CENTRO COLOMBIANO DE ESTUDIOS PROFESIONALES. AREA: ESTADISTICA INFERENCIAL PERIODO ACADEMICO: II-2010

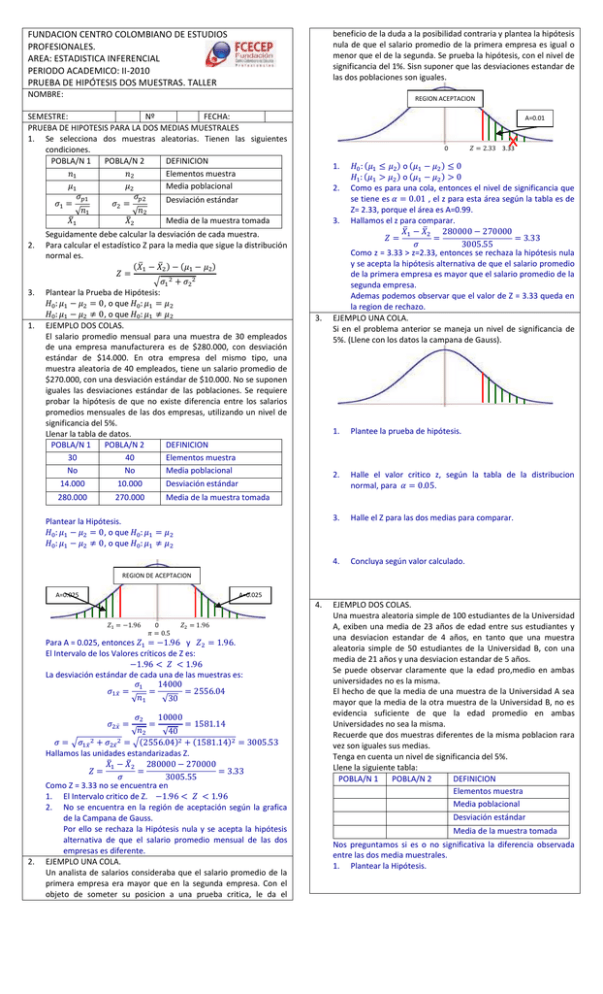
beneficio de la duda a la posibilidad contraria y plantea la hipótesis
nula de que el salario promedio de la primera empresa es igual o
menor que el de la segunda. Se prueba la hipótesis, con el nivel de
significancia del 1%. Sisn suponer que las desviaciones estandar de
las dos poblaciones son iguales.
FUNDACION CENTRO COLOMBIANO DE ESTUDIOS
PROFESIONALES.
AREA: ESTADISTICA INFERENCIAL
PERIODO ACADEMICO: II-2010
PRUEBA DE HIPÓTESIS DOS MUESTRAS. TALLER
NOMBRE:
REGION ACEPTACION
SEMESTRE:
Nº
FECHA:
PRUEBA DE HIPOTESIS PARA LA DOS MEDIAS MUESTRALES
1. Se selecciona dos muestras aleatorias. Tienen las siguientes
condiciones.
POBLA/N 1
POBLA/N 2
DEFINICION
𝑛1
𝑛2
Elementos muestra
𝜇1
𝜇2
Media poblacional
𝜎𝑝1
𝜎𝑝2
Desviación estándar
𝜎1 =
𝜎2 =
√𝑛1
√𝑛2
Media de la muestra tomada
𝑋̅1
𝑋̅2
2.
3.
1.
Seguidamente debe calcular la desviación de cada muestra.
Para calcular el estadístico Z para la media que sigue la distribución
normal es.
(𝑋̅1 − 𝑋̅2 ) − (𝜇1 − 𝜇2 )
𝑍=
√𝜎1 2 + 𝜎2 2
Plantear la Prueba de Hipótesis:
𝐻0 : 𝜇1 − 𝜇2 = 0, o que 𝐻0 : 𝜇1 = 𝜇2
𝐻0 : 𝜇1 − 𝜇2 ≠ 0, o que 𝐻0 : 𝜇1 ≠ 𝜇2
EJEMPLO DOS COLAS.
El salario promedio mensual para una muestra de 30 empleados
de una empresa manufacturera es de $280.000, con desviación
estándar de $14.000. En otra empresa del mismo tipo, una
muestra aleatoria de 40 empleados, tiene un salario promedio de
$270.000, con una desviación estándar de $10.000. No se suponen
iguales las desviaciones estándar de las poblaciones. Se requiere
probar la hipótesis de que no existe diferencia entre los salarios
promedios mensuales de las dos empresas, utilizando un nivel de
significancia del 5%.
Llenar la tabla de datos.
POBLA/N 1
POBLA/N 2
DEFINICION
30
40
Elementos muestra
No
No
Media poblacional
14.000
10.000
Desviación estándar
280.000
270.000
Media de la muestra tomada
A=0.01
𝑍 = 2.33 3.33
0
𝐻0 : (𝜇1 ≤ 𝜇2 ) o (𝜇1 − 𝜇2 ) ≤ 0
𝐻1 : (𝜇1 > 𝜇2 ) o (𝜇1 − 𝜇2 ) > 0
2. Como es para una cola, entonces el nivel de significancia que
se tiene es 𝛼 = 0.01 , el z para esta área según la tabla es de
Z= 2.33, porque el área es A=0.99.
3. Hallamos el z para comparar.
𝑋̅1 − 𝑋̅2 280000 − 270000
𝑍=
=
= 3.33
𝜎
3005.55
Como z = 3.33 > z=2.33, entonces se rechaza la hipótesis nula
y se acepta la hipótesis alternativa de que el salario promedio
de la primera empresa es mayor que el salario promedio de la
segunda empresa.
Ademas podemos observar que el valor de Z = 3.33 queda en
la region de rechazo.
EJEMPLO UNA COLA.
Si en el problema anterior se maneja un nivel de significancia de
5%. (Llene con los datos la campana de Gauss).
1.
3.
Plantear la Hipótesis.
𝐻0 : 𝜇1 − 𝜇2 = 0, o que 𝐻0 : 𝜇1 = 𝜇2
𝐻0 : 𝜇1 − 𝜇2 ≠ 0, o que 𝐻0 : 𝜇1 ≠ 𝜇2
1.
Plantee la prueba de hipótesis.
2.
Halle el valor critico z, según la tabla de la distribucion
normal, para 𝛼 = 0.05.
3.
Halle el Z para las dos medias para comparar.
4.
Concluya según valor calculado.
REGION DE ACEPTACION
A=0.025
A=0.025
4.
𝑍1 = −1.96
0
𝜋 = 0.5
𝑍2 = 1.96
Para A = 0.025, entonces 𝑍1 = −1.96 y 𝑍2 = 1.96.
El Intervalo de los Valores críticos de Z es:
−1.96 < 𝑍 < 1.96
La desviación estándar de cada una de las muestras es:
𝜎1
14000
𝜎1𝑥̅ =
=
= 2556.04
𝑛
√ 1
√30
𝜎2
10000
=
= 1581.14
𝑛
√ 2
√40
𝜎 = √𝜎1𝑥̅ 2 + 𝜎2𝑥̅ 2 = √(2556.04)2 + (1581.14)2 = 3005.53
Hallamos las unidades estandarizadas Z.
𝑋̅1 − 𝑋̅2 280000 − 270000
𝑍=
=
= 3.33
𝜎
3005.55
Como Z = 3.33 no se encuentra en
1. El Intervalo critico de Z. −1.96 < 𝑍 < 1.96
2. No se encuentra en la región de aceptación según la grafica
de la Campana de Gauss.
Por ello se rechaza la Hipótesis nula y se acepta la hipótesis
alternativa de que el salario promedio mensual de las dos
empresas es diferente.
EJEMPLO UNA COLA.
Un analista de salarios consideraba que el salario promedio de la
primera empresa era mayor que en la segunda empresa. Con el
objeto de someter su posicion a una prueba critica, le da el
𝜎2𝑥̅ =
2.
EJEMPLO DOS COLAS.
Una muestra aleatoria simple de 100 estudiantes de la Universidad
A, exiben una media de 23 años de edad entre sus estudiantes y
una desviacion estandar de 4 años, en tanto que una muestra
aleatoria simple de 50 estudiantes de la Universidad B, con una
media de 21 años y una desviacion estandar de 5 años.
Se puede observar claramente que la edad pro,medio en ambas
universidades no es la misma.
El hecho de que la media de una muestra de la Universidad A sea
mayor que la media de la otra muestra de la Universidad B, no es
evidencia suficiente de que la edad promedio en ambas
Universidades no sea la misma.
Recuerde que dos muestras diferentes de la misma poblacion rara
vez son iguales sus medias.
Tenga en cuenta un nivel de significancia del 5%.
Llene la siguiente tabla:
POBLA/N 1
POBLA/N 2
DEFINICION
Elementos muestra
Media poblacional
Desviación estándar
Media de la muestra tomada
Nos preguntamos si es o no significativa la diferencia observada
entre las dos media muestrales.
1. Plantear la Hipótesis.
Un constructor está considerando dos lugares alternativos para un
centro comercial regional. Como los ingresos de los hogares de la
comunidad son una consideración importante en esa selección,
desea probar la hipótesis nula de que no existe diferencia entre el
ingreso promedio por hogar en las dos comunidades. Consiente
con esta hipótesis, supone que la desviación estándar del ingreso
por hogar es también igual en las dos comunidades. Para una
muestra de 30 hogares de la primera comunidad, encuentra que el
ingreso diario promedio es de $35.500, con desviación estándar de
$1.800. Para la otra muestra de 40 familias de la segunda
comunidad, $34.600 de salario promedio diario y desviación
estándar de $2.400. Pruebe la hipótesis nula en el nivel de
significancia del 5%.
POBLA/N 1
POBLA/N 2
DEFINICION
30
40
Elementos muestra
No
No
Media poblacional
REGION ACEPTACION
A=
A=
A=
𝑍1 =
2.
0
𝑍2 =
Calculamos las desviaciones estandar de cada una de las
muestras.
𝜎1𝑥̅ =
𝜎1
√𝑛1
=
𝜎2𝑥̅ =
𝜎2
√𝑛2
=
𝜎 = √𝜎1𝑥̅ 2 + 𝜎2𝑥̅ 2 =
3.
Hallamos las unidades estandarizadas Z.
𝑍=
5.
𝑋̅1 −𝑋̅2
𝜎
=
El intervalo de valores criticos de Z.
5.
Concluya.
35.500
34.600
Media de la muestra tomada
𝑍1 = −1.96
A=
A=
7.
𝑍1
0
𝑍2 =
Nos preguntamos si es o no significativa la diferencia
observada entre las dos media muestrales.
Plantear la Hipótesis.
Calculamos las desviaciones estandar de cada una de las
muestras.
𝜎1
√𝑛1
=
𝜎2𝑥̅ =
𝜎2
√𝑛2
=
𝜎2
2400
=
= 379.47
√𝑛2
√40
𝜎 = √𝜎1𝑥̅ 2 + 𝜎2𝑥̅ 2 = √(328.63)2 + (379.47)2 = 501.99
12. Hallamos las unidades estandarizadas Z.
𝑋̅1 − 𝑋̅2 35500 − 34600
𝑍=
=
= 1.79
𝜎
501.99
13. El intervalo de valores criticos de Z.
−1.96 < 𝑍 < 1.96
Observamos que z = 1.79 se encuentra en la region de aceptacion,
por lo tanto no se rechaza la hipótesis nula, de que los ingresos
promedios diario de cada familia no son diferentes con un nivel de
significancia del 0.05.
EJERCICIO DE COLA DEL EXTREMO SUPERIOR.
Si antes de recolectar los datos, el constructor considero que el
ingreso de la primera comunidad familiar pudiera ser mayor que el
de la segunda comunidad. Con el objeto de someter esta
evaluación a una prueba critica, le otorgo el beneficio de la duda a
la otra posibilidad y planteo la hipótesis nula 𝐻0 : (𝜇1 ≤ 𝜇2 ).
Pruebe esta hipótesis con un nivel de significancia del 5%, con la
suposición adicional de que los valores de las desviaciones
estándar para las dos poblaciones no son necesariamente iguales.
Datos del ejercicio anterior.
REGION ACEPTACION
A=
0
𝑍=
𝜎 = √𝜎1𝑥̅ 2 + 𝜎2𝑥̅ 2 =
1.
Plantear prueba de hipótesis
7.
2.
Valor critico de Z para una sola cola del extremo superior,
según tabla de distribucion normal.
3.
Hallamos el z para comparar.
Hallamos las unidades estandarizadas Z.
𝑍=
8.
𝑋̅1 −𝑋̅2
𝜎
=
El intervalo de valores criticos de Z.
𝑍=
9.
6.
𝑍2 = 1.96
𝜎2𝑥̅ =
REGION ACEPTACION
A=
0
Nos preguntamos si es o no significativa la diferencia observada
entre las dos media muestrales.
Plantear la Hipótesis.
10. 𝐻0 : 𝜇1 − 𝜇2 = 0, o que 𝐻0 : 𝜇1 = 𝜇2
𝐻0 : 𝜇1 − 𝜇2 ≠ 0, o que 𝐻0 : 𝜇1 ≠ 𝜇2
11. Calculamos las desviaciones estandar de cada una de las
muestras.
𝜎1
1800
𝜎1𝑥̅ =
=
= 328.63
𝑛
√ 1
√30
Media de la muestra tomada
𝜎1𝑥̅ =
A=0.025
A=0.95
Desviación estándar
6.
Desviación estándar
A=0.025
EJEMPLO DE DOS COLAS.
Para comparar la vida útil media de dos marcas de Pilas doble A, se
selecciono una muestra de 100 pilas de la marca X y 100 pilas de la
marca Y. La muestra de la marca X, tiene una vida útil media de 47
horas y una desviacion estandar de 4 horas, en tanto que la
muestra de la marca Y, tiene una vida útil media de 48 horas y una
desviacion estandar de 3 horas. Es significativa la diferencia entre
las dos medias muestrales al nivel de significancia del 0.05.
Llene la siguiente tabla con los datos del problema.
POBLA/N 1
POBLA/N 2
DEFINICION
Elementos muestra
Media poblacional
2.
2.400
REGION ACEPTACION
4.
1.
1.800
Concluya.
EJERCICIO DE DOS COLAS.
4.
𝑋̅1 −𝑋̅2
𝜎
=
Concluya
Lic. Simeón Cedano Rojas
PRUEBA DE HIPÓTESIS DOS MUESTRAS.DOXC