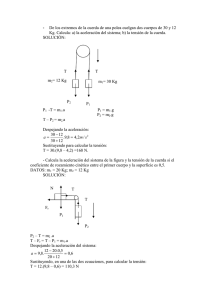
20 kg 6 kg 30º 12 kg 2 kg 20º 15 kg 10 kg

DINÁMICA (II)
CÁLCULO DE LA ACELERACIÓN Y DE LA TENSIÓN.
1.-
Colgamos dos objetos de 20 kg y 15 kg respectivamente de los extremos de la
cuerda de una polea. Calcula:
a) la aceleración del sistema
b) la tensión de la cuerda.
2.-
a) ¿Se moverá el sistema de la figura? En caso de que lo
haga calcula la aceleración. Si no lo hace, calcula la fuerza
con que habrá que empujar la caja de 20 kg para que
empiece a moverse.
20 kg
b) ¿Cuál será la tensión de la cuerda si no aplicamos ninguna
fuerza?
6 kg
El coeficiente de rozamiento entre el cuerpo de 20 kg y la
superficie es 0,4.
3.-
4.-
¿Se moverá el sistema de la figura? Calcula la tensión de la
cuerda y en caso afirmativo, también la aceleración del
sistema. Sabemos que el coeficiente de rozamiento entre el
cuerpo de 12 kg y la superficie es 0,18.
12 kg
30º
Calcula la aceleración del sistema de la figura y la tensión
de la cuerda si:
a) no hay rozamiento;
b) el coeficiente de rozamiento entre el objeto de
15 kg y la superficie es de 0,3.
15 kg
20º
DINÁMICA DEL MOVIMIENTO CIRCULAR UNIFORME.
5.-
Atamos un objeto de 1,5 kg a una cuerda de 1 m de longitud y lo hacemos girar
en un plano horizontal, sobre el que se apoya y con el que no tiene rozamiento,
a 60 rpm. Calcula la tensión de la cuerda.
6.-
a) Un coche de 800 kg, gira con una velocidad constante de 120 km/h en una
curva sin peralte de 100 m de radio. Calcula el valor de la fuerza centrípeta.
b) Si al aumentar la velocidad en dicha curva hasta los 135 km/h empezara a
derrapar, ¿cuál sería el coeficiente de rozamiento?
7.-
2 kg
¿Con qué velocidad máxima podrá tomar un coche una curva plana de 90 m de
radio sin derrapar sabiendo que el coeficiente de rozamiento estático de
deslizamiento entre los neumáticos y la carretera es de 0,25?
10 kg
8.-
Hacemos girar en el aire una esfera atada al extremo de una cuerda de 80 cm
de longitud con una celeridad constante describiendo un péndulo cónico. Si la
cuerda forma un ángulo de 30º con la vertical, calcula:
a) el módulo de la velocidad de la bola
b) el tiempo que tarda la esfera en dar una vuelta completa
c) el ángulo que debería formar con la vertical para llevar una celeridad
doble.
SOLUCIONES
1.-
P1 = m1 · g = 20 kg · 9,8 m/s2 = 196 N ; P2 = m2 · g = 15 kg · 9,8 m/s2 = 147 N
a) El objeto que caerá será el de mayor peso, es decir P1, con lo que el cuerpo 2
ascenderá. Aplicando las ecuaciones escalares a cada objeto tendremos:
P1 – T = 20 kg · a ;
T – P2 = 15 kg · a
Sumando ambas ecuaciones escalares desparece la tensión y nos queda la
ecuación global (puedes resolver el sistema de ecuaciones por cualquier método)
P1 – P2 = 196 N – 147 N = (20 kg + 15 kg) · a ⇒ a = 1,4 m/s2.
b) Despejando T de cualquiera de las dos ecuaciones escalares (en este caso
elegimos la segunda) y sustituyendo el valor de a obtenido anteriormente,
tendremos:
T = P2 + 15 kg · a = 147 N + 15 kg · 1,4 m/s2 = 168 N
2.-
a) Sea 1 el objeto que cuelga y 2 el que está en el plano horizontal; calculamos
las fuerzas que están en la dirección del posible movimiento son:
P1 = m1 · g = 6 kg · 9,8 m/s2 = 58,8 N; Froz = 0,4 · 20 kg · 9,8 m/s2 = 78,4 N
Como P1 < Froz . Por tanto, habrá que empujar la caja de 20 kg para que se inicie
el movimiento con una fuerza F.
Σ F = P1 + F – Froz = 0 ⇒
F = 78,4 N – 58,8 N ⇒ F = 19,6 N.
b) Como no hay movimiento P1 – T = 0 ; T – Froz = 0
Despejando T de cualquiera de ellas tendremos:
3.-
T = 58,8 N
Sea 1 el objeto que cuelga y 2 el de 12 kg; calculamos las fuerzas que están en
la dirección del posible movimiento son:
P1 = m1 · g = 2 kg · 9,8 m/s2 = 19,6 N;
Froz = 0,18 · 12 kg · 9,8 m/s2 · cos 30º = 18,3 N
Px2 = m2 · g = 12 kg · 9,8 m/s2 · sen 30º = 58,8 N;
Como Px2 > P1 de haber movimiento éste se producirá hacia la izquierda; con lo
Froz actuaría hacia la derecha. Como Px2 > P1 + Fremax habrá movimiento y el
objeto de 12 kg en su bajada hará subir al de 2 kg. Una vez que sabemos que
hay movimiento necesitamos calcular,.
Aplicamos la segunda ley de la dinámica a cada uno de los cuerpos: Σ F = m · a
Px2 – T – Froz = 12 kg · a ;
T – P1 = 2 kg · a
Sumando ambas ecuaciones se elimina T:
Px2 –Froz –P1 = 58,8 N – 18,3 N – 19,6 N = 14 kg · a ⇒ a = 1,49 m/s2
Despejando T de la segunda ecuación tendremos: T = 19,6 N + 2 kg · 1,49 m/s2
= 22,58 N
4.-
a) Sea 1 el objeto que cuelga y 2 el del plano inclinado; calculamos las fuerzas
que están en la dirección del posible movimiento son:
P1 = m1 · g = 10 kg · 9,8 m/s2 = 98 N;
Px2 = m2 · g = 15 kg · 9,8 m/s2 · sen 20º = 50,3 N;
Como P1 > Px2 el movimiento se producirá hacia la derecha, con el que el cuerpo
de 10 kg hará subir al de 15 kg.
P1 –T = 10 kg · a ;
T – Px2 = 15 kg · a
Sumando ambas ecuaciones tendremos:98 N – 50,3 N = 25 kg a ⇒ a = 1,9 m/s2
Sustituyendo a en cualquiera de las otras ecuaciones obtenemos que: T = 79 N.
b) Calculamos la fuerza de rozamiento: Froz= 0,3·15 kg·9,8 m/s2 · cos 20º = 41,4 N
Las ecuaciones para cada objeto ahora son:
P1 –T = 10 kg · a ;
T – Px2 – Frc = 15 kg · a
Sumando: (resuelve el sistema por el método que quieras)
P1 – Px2 – Froz = 98 N – 50,3 N – 41,4 N = 25 kg · a ⇒ a = 0,25 m/s2 ; T = 95,5 N.
5.-
Pasamos ω al sistema internacional: ω =
En este caso T es la fuerza centrípeta:
60 vueltas 2π rad min 2π rad
×
×
=
min
vuelta 60 s
s
 2π rad 
T = m × ω × R = 1,5 kg × 
 × 1 m = 59, 2 N
 s 
2
2
6.-
a) Pasamos v al sistema internacional: v = 120
2
m

33, 3 

2
v
s
Fc = m × = 800 kg × 
= 8890N
R
100 m
km
h
1000m
m
×
×
= 33, 3
h 3600 s
km
s
km
h
1000m
m
×
×
= 37,5
;
h 3600 s
km
s
2
m

 37, 5 
v '2
s
Fc ' = m ×
= 800 kg × 
= 11250 N
R
100 m
b) v ' = 135
En el momento en que empieza a derrapar Froz = Fc, luego Froz = 11250 N.
Como no tiene peralte: N = P ⇒
µe =
Fre
11250 N
=
= 1, 43
N 800 kg × 9,8 m
s2
v = µ × R × g = 0, 25 × 90 m × 9,8
m
m
= 220,5
2
s
s
7.-

8.-
 a) La tensión de la cuerda se descompone es sus componentes Tx que actúa
como fuerza centrípeta y Ty que contrarresta el peso de la esfera:
Tx = T × sen 30º =
m × v2
m × v2
m × v2
=
⇒T =
R
0,8 m × sen 30º
0,8 m × sen 2 30º
Ty = T × cos 30º = m × g ⇒ T =
m× g
cos 30º
Igualando T y eliminando m:
v2
g
0,8 m × 0, 25 × 9,8 m s 2
m
=
⇒v=
= 1, 5
0,8 m × 0, 25 0,866
0,866
s
b) El periodo T (no confundir con la tensión) es el tiempo que tarda en
dar una vuelta completa:
T=
2π R 6, 28 × 0,8 m
=
= 3, 35 s
v
1,5 m s
c)
v2
g
1 − sen 2α 0,8 m × 9,8 m s 2
=
⇒
=
= 0,871
2
0,8 m × sen 2α cos α
sen 2α
( 3, 0 m s )
Llamando x = sen α obtenemos:
1 − x2
1 − x2
=
0,871
⇒
= 0,8712 = 0, 759
2
4
x
x
Como sale una ecuación bicuadrada llamamos y = x 2 con lo que nos
queda: 0, 759 y 2 + y − 1 = 0
Resolviendo queda que: y = 0,665 ⇒ x = 0,815 ⇒ α = arcsen 0,815 =
54,6º