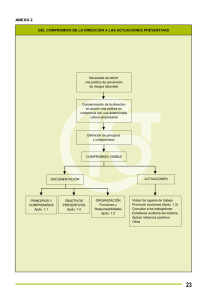
Más información
Anuncio

CMAT – Cálculo Mecánico de Líneas Eléctricas Aéreas A.T. Presentación El programa CMAT es uno de los módulos del paquete integrado de instalaciones en urbanización. Un módulo común para todas las instalaciones del paquete es la “Configuración de la urbanización”. Este módulo permite definir gráficamente la urbanización, medio rural, parcela, etc, donde dibujar todas las infraestructuras (electricidad, abastecimiento, etc). Visión general del módulo Configuración Urbanización - Posibilidad de cargar el dibujo de la urbanización en DWG, DXF, BMP, TIF y JPG. - Posibilidad de activar o desactivar capas de las imágenes importadas. - Posibilidad de cambiar el color de las imágenes importadas. - Posibilidad de capturar sólo una zona de la imagen de fondo. Más potente aún es la posibilidad de importar los datos del terreno automáticamente, pudiendo el programa leer una nube de puntos en planta, una traza del terreno donde irá situada la línea eléctrica, un perfil longitudinal realizado por un topógrafo o un fichero de texto con todos los puntos. A grandes rasgos, el programa CMAT presenta 6 zonas bien diferenciadas. - Menú general de opciones (Proyecto, Edición, Ver, Componentes Terreno y Red, Calcular, Resultados y Ayuda). - Botonera de acceso directo a los comandos más usuales (nuevo, abrir, salvar, cortar ramas y/o nudos, copiar ramas y/o nudos, pegar ramas y/o nudos, deshacer, calcular el proyecto completo, acceder al anexo de cálculo, acceder a la medición del proyecto, generar los esquemas en fichero DXF, imprimir, presentación previa, acceso a las bases de datos, ayuda, replanteo automático y ver perfil). - Paleta de Componentes Gráficos (tipo de nudos) para la definición de la topografía del terreno (punto para cambio de cota o dirección, cruce con otra línea eléctrica o de telecomunicaciones, cruce con carreteras, ferrocarriles, etc) y de la línea eléctrica aérea (apoyos de fin de línea, de alineación, de ángulo, etc). - Paleta de Herramientas con todas las funciones gráficas de diseño (enlace de nudos, rotar, modo orto, zoom ventana, zoom en tiempo real, encuadre en tiempo real, zoom previo, zoom todo, redibuja y borrar líneas). - Ventana de Propiedades de Componentes, donde definir los datos del terreno (cota, datos de cruzamientos, etc) y de la línea eléctrica aérea (función y constitución de los apoyos, tipo de cruceta, tipo de conductor, tense máximo, etc). - Zona de edición gráfica, donde se dibuja la red eléctrica aérea (es la zona donde se ve reflejado este ejemplo). Visión general del programa CMAT - Control total de la instalación, pues es posible observar el dibujo completo de la línea de un simple vistazo. - Diseño de la instalación de forma muy sencilla e intuitiva. - Accesibilidad instantánea a todas las opciones y funciones que incorpora el programa. - Modificación instantánea de cualquier dato o parámetro de un nudo, línea o conjunto de éstos, con una simple selección de la zona deseada y aplicación de los nuevos valores. A la hora de calcular un proyecto, se puede acceder a las Condiciones Generales y consultar, definir o modificar los datos o hipótesis de partida. Los valores por defecto son los más usuales. Condiciones generales del proyecto - Modo de cálculo: Diseño, para el cálculo automático de esfuerzos en punta y altura de apoyos, o Comprobación, dando la posibilidad al usuario de fijar la altura de los apoyos y atender a las advertencias del programa si ésta no es correcta. - Tensión de la línea (V), velocidad del viento y temperatura para la hipótesis de flecha máxima - Tense máximo de cálculo (igual para toda la línea o posibilidad de ser diferente en cada cantón). - Posibilidad de considerar la hipótesis de Hielo + Viento en las Hipótesis de Tracción máxima. - Posibilidad de tener 2 conductores distintos en líneas de doble circuito. - Comprobación del EDS máximo. - Distancias de seguridad para la protección de la Avifauna. - Distancias de seguridad reglamentarias (distancia mínima del conductor al terreno y a masa, distancias horizontales a cruzamientos y distancias verticales a cruzamientos) para conductores desnudos, recubiertos y aislados en haz. - Simbología gráfica a gusto del usuario. Las bases de datos del programa muestran las características de los apoyos, crucetas, conductores y aisladores. Es posible su modificación o ampliación. Los valores indicados se utilizarán para realizar el cálculo de la línea aérea (a la hora de seleccionar un apoyo normalizado, calcular la línea con un conductor homologado por las compañías eléctricas, etc). Bases de Datos de Apoyos y Crucetas - Existe una gran gama de fabricantes y es posible añadir tantos como el usuario desee. Es posible copiar fabricantes, constituciones, crucetas, etc. - Figuran todos los tipos de apoyos: de perfiles metálicos, de hormigón vibrado, de hormigón vibrado hueco, de chapa metálica rectangular y de chapa metálica circular o poligonal regular. - Figuran todos los tipos de crucetas normalizadas: montaje 0 (horizontal), montaje I (triángulo), tresbolillo, bandera, boveda normal, bóveda recta y doble circuito. - Aparecen los esfuerzos normalizados para cada apoyo: esfuerzo nominal o útil en punta, esfuerzo secundario en apoyos de sección asimétrica, esfuerzo vertical, esfuerzo de torsión, etc. - Se incluyen todas las dimensiones para cada esfuerzo, cogolla del apoyo, longitud de la cabeza para apoyos con cabeza recta, etc. Bases de Datos de Cables Recubiertos y Aislados en haz) (Desnudos, - Existe una gran gama de conductores y es posible añadir tantos como el usuario desee. - Figuran todas las características técnicas de los conductores: denominación, sección, diámetro, carga de rotura, peso propio, etc. Bases de Datos de Aisladores - Existe una gran gama de aisladores y es posible añadir tantos como el usuario desee. - Figuran todas las características técnicas de los aisladores: denominación, carga de rotura, diámetro, línea de fuga, etc. - Aisladores de vidrio, cerámicos, poliméricos, etc. Para realizar el cálculo mecánico de una línea eléctrica aérea se comenzará dibujando el perfil longitudinal en planta, por lo tanto, se accederá a la Paleta de Componentes (tipos de nudos de terreno), se hará un clic con el botón izquierdo del ratón sobre el icono deseado (punto de terreno para realizar un cambio de cota o de itinerario, cruzamiento, etc), se desplazará hasta la zona de edición gráfica elegida por el usuario y se hará otro clic sobre el botón izquierdo. Cada vez que se hace un clic, se introduce en la línea un nudo de terreno (cambio de cota, de dirección, cruce, etc) y una rama que lo une a un nudo anterior, del que parte (la rama identifica la zona donde está situada la línea, según la altitud sobre el nivel del mar: A, B o C). De gran ayuda resulta disponer de la planta topográfica cargada como imagen de fondo (DWG, DXF, BMP o TIF), pues con sólo ir colocando los puntos en los lugares deseados por el usuario, quedará establecida automáticamente la distancia entre ellos. También es posible prefijar esta distancia. Más potente aún es la posibilidad de importar los datos del terreno automáticamente, pudiendo el programa leer una nube de puntos en planta, una traza del terreno donde irá situada la línea eléctrica, un perfil longitudinal realizado por un topógrafo o un fichero de texto con todos los puntos. Ventana de Propiedades de nudos de terreno - Tipo nudo, para la modificación de uno o varios nudos ya introducidos. - Denominación de nudos de terreno y cruzamientos. - Posibilidad de fijar la longitud entre singularidades (puntos) del terreno y el ángulo respecto al tramo anterior (coordenadas polares). - Definición del perfil en planta, considerando desniveles entre nudos o cotas absolutas. - Datos de Cruzamientos: anchura, altura, distancia de cruce a líneas existentes y tensión de éstas. Una vez definido el terreno, para ubicar los apoyos se puede hacer un replanteo automático o situar éstos en los lugares establecidos por el usuario; para ello se accederá a la Paleta de Componentes, se hará un clic con el botón izquierdo del ratón sobre el icono deseado (apoyo fin de línea, apoyo de perfiles metálicos, cruceta horizontal, etc), se desplazará hasta la zona de edición gráfica elegida por el usuario (sobre la topografía definida anteriormente) y se hará otro clic sobre el botón izquierdo. Cada vez que hacemos un clic introducimos un apoyo (ángulo, alineación, etc) y un vano (LA-56, etc) que lo une al nudo anterior, del que parte. Los apoyos y vanos se pueden introducir tanto en planta como en perfil, según sea más cómodo para el usuario. De esta manera tan sencilla se realiza una línea de gran longitud en muy pocos minutos. Las características de la línea aérea (tipo de apoyo, sección del cable, etc), en el proceso de introducción de la línea, quedarán definidas en la Ventana de Propiedades (datos y parámetros). Esta ventana también se utilizará para modificar características de apoyos y vanos ya dibujados. Ventana de Propiedades de apoyos y vanos - Función, constitución y fabricante, para la modificación de uno o varios apoyos ya introducidos. Tipo de cruceta o montaje. - Denominación de apoyos, para su identificación en el anexo y planos. - Posibilidad de fijar la dimensión mínima de las crucetas. - Posibilidad de fijar la longitud de los vanos. - Posibilidad de fijar la altura de los apoyos. - Posibilidad de fijar el esfuerzo útil en punta mínimo. - Posibilidad de incluir esfuerzos verticales adicionales (transformadores, etc). - Cimentaciones monobloque o por zapatas aisladas. - Designación del conductor y número de conductores por fase o haces. Conductores desnudos, recubiertos y aislados en haz. - Coeficiente de seguridad del conductor (para obtener el tense máximo del cantón) y coeficiente de seguridad de apoyos (normal o reforzado). - Denominación del aislador y nivel de aislamiento requerido. - Desviación horizontal de las catenarias por la acción del viento. - Posibilidad de incluir dos crucetas en un mismo apoyo (principal y derivación). Editor de haces (cables aislados en haz) - Posibilidad de definir haces de distinta sección en cada vano. - Coeficiente de seguridad (tracción máxima de cálculo) para cada haz. - Distancia de fijación de cada haz hasta la cogolla. Una vez diseñada la línea eléctrica, el programa calcula automáticamente (según las especificaciones del Reglamento sobre condiciones técnicas y garantías de seguridad en líneas eléctricas de alta tensión) todas las tensiones y flechas en hipótesis reglamentarias, tensiones y flechas de tendido, cálculo de apoyos, apoyos adoptados, cálculo de cimentaciones, cálculo de las cadenas de aisladores, esfuerzos verticales sin sobrecarga para detectar apoyos colgados y distancias de seguridad, realizando simultáneamente el perfil longitudinal con dibujo automático de catenarias. En dicho cálculo, considera la ecuación de la catenaria, la ecuación del cambio de condiciones, en apoyos los esfuerzos horizontales, verticales y de torsión, fórmula de Sulzberger para el cálculo de cimentaciones, etc. Una vez calculado el proyecto se puede acceder a los resultados desde tres puntos de vista: - Haciendo un zoom ventana sobre la planta o perfil longitudinal y observando minuciosamente todos los datos obtenidos. Accediendo a los resultados del proyecto: Memoria Descriptiva, Anexo de Cálculos, Pliego de Condiciones, Medición y Planos. - Abriendo las ventanas de Tensiones y flechas en hipótesis reglamentarias, Tensiones y flechas de tendido, Cálculo de apoyos, Apoyos adoptados, Cálculo de cimentaciones, Cálculo de aisladores, Esfuerzos verticales sin sobrecarga para detectar apoyos colgados y Distancias de seguridad. Tensiones y reglamentarias flechas en hipótesis - Vano de regulación, hipótesis de tensión máxima, hipótesis de flecha máxima, hipótesis de flecha mínima, hipótesis de cálculo de apoyos y desviación horizontal de las catenarias por la acción del viento. Tensiones y flechas de tendido - Tensiones y flechas a diferentes temperaturas (0 ºC, 10 ºC, etc) para el tendido de la línea. Cálculo de apoyos - Esfuerzos verticales (V) y horizontales (T, L, Lt) sobre los apoyos en las 4 hipótesis reglamentarias (Viento, Hielo, Desequilibrio y Rotura), y distancia mínima de conductores en el apoyo. Obtención automática del perfil longitudinal. Perfil longitudinal de la línea - Plano de comparación, tipo de conductor y tensión (V). - Denominación de apoyos, cotas del terreno, desniveles, distancias parciales, distancias al origen, longitud de los vanos y zona (A, B o C). - Tipo y constitución de los apoyos, esfuerzo nominal y altura total, tipo de cruceta o montaje y separación entre conductores, tipo de aislador, nº de elementos por cadena y nº de cadenas de amarre o suspensión. - Acotado de cruzamientos y señalización de ángulos. Características Principales Proyecto - - - - Crear un proyecto nuevo. Abrir un proyecto existente. Salvar un proyecto a disco. Salvar un proyecto existente con otro nombre diferente al que se identificó por primera vez (salvar como) y así tener dos proyectos iguales con nombres diferentes. Cargar una imagen de fondo en formato DXF, DWG, BMP o TIF (planos vectoriales o escaneados), que nos servirá para diseñar la línea gráficamente, olvidándonos de la incómoda toma de datos previos que siempre era necesaria antes de introducir los trabajos en el ordenador (longitud de ramas, ángulos, etc), pues al diseñar y dibujar sobre un plantilla real, con sólo posicionar el cursor del ratón en la zona de edición gráfica, obtenemos las coordenadas de cada nudo. Posibilidad de importar los datos del terreno automáticamente, pudiendo el programa leer una nube de puntos en planta (DWG o DXF), una traza del terreno (DWG o DXF) donde irá situada la línea eléctrica, un perfil longitudinal (DWG o DXF) realizado por un topógrafo o un fichero de texto (CSV o TXT) con todos los puntos. Acceder a las condiciones generales del proyecto que se vaya a realizar. Esta opción permite: Trabajar en modo diseño, para calcular automáticamente la altura y esfuerzo de los apoyos, o en modo comprobación, si se desea fijar la altura de éstos. Definir o modificar la tensión de trabajo (V). Modificar la velocidad del viento. Variar la temperatura en la hipótesis de flecha máxima. Indicar la densidad del hormigón para calcular las cimentaciones en el sistema de zapatas aisladas. Tense máximo igual para toda la línea o posibilidad de ser diferente para cada cantón (tensión adecuada al coeficiente de seguridad reglamentario o al EDS). Comprobación del EDS máximo, según disponga la línea o no de amortiguadores. Posibilidad de considerar la hipótesis de Hielo + Viento en las Hipótesis de Tracción máxima (si es requerido por la compañía suministradora o el técnico lo considera oportuno). Distancias de seguridad para la protección de la Avifauna (RD 1432/2008 y demás disposiciones de CCAA). Distancias entre conductor y armado y entre conductores en suspensión y amarre, distancia entre la semicruceta inferior y el conductor superior en armados tresbolillo, bandera y doble circuito y distancia entre el conductor central y la cabeza del poste en armados tipo bóveda. Posibilidad de modificar la distancia de los conductores al suelo y a masa y las distancias verticales y horizontales a todo tipo de cruzamientos (datos por defecto según RLAT). Simbología gráfica: posibilidad de variar el factor de escala de textos y símbolos, de definir la leyenda en vanos, de variar el color de apoyos, vanos, cruces, etc, de representar los vanos con distintos tipos de líneas, de mostrar en los perfiles todos los itinerarios de inicio a fin o sólo lo tramos diferentes, de variar el factor de escala de textos en la guitarra del perfil, etc. Acceder a las bases de datos del programa, para su consulta, modificación o ampliación. Estas contienen: Apoyos de perfiles metálicos, de hormigón vibrado, de hormigón vibrado hueco, de chapa metálica con sección rectangular y de chapa metálica con sección circular o poligonal regular. Esfuerzo nominal o principal, esfuerzo secundario en apoyos de sección asimétrica, esfuerzo en punta coincidente con torsión, esfuerzo vertical con y sin torsión, esfuerzo de torsión y distancia de aplicación de este esfuerzo. Dimensiones de los diferentes tipos de apoyos. Crucetas o armados en montaje Horizontal, Triángulo, Tresbolillo, Bandera, Bóveda triangular, Bóveda plana y Daoble circuito. Diferentes fabricantes y posibilidad de añadir otros por parte del usuario. Posibilidad de copiar fabricantes, esfuerzos, dimensiones, etc. Conductores desnudos, recubiertos y aislados en haz. Dimensiones, carga de rotura, etc. Posibilidad de especificar otros tipos por parte del usuario. Aisladores de tipo caperuza y vástago, poliméricos, etc. Dimensiones, carga de rotura, etc. Posibilidad de especificar otros tipos por parte del usuario. Seleccionar o cambiar el editor de textos que lleva el programa por defecto y dar la posibilidad de visualizar la memoria descriptiva, el anexo de cálculo, el pliego de condiciones y la medición en otro elegido por el usuario (word, wordperfect, etc). Fijar la escala de impresión o ajustar al formato deseado. Hacer una presentación previa del esquema de la línea antes de la salida directa a impresora o a ploter. Imprimir el gráfico que se esté viendo en ese momento en la zona de edición gráfica. Edición Deshacer operaciones realizadas anteriormente. Cortar líneas y nudos de la línea aérea. Copiar líneas y nudos de la línea aérea. Pegar líneas y nudos, anteriormente cortados o copiados, en determinados lugares del dibujo. Enlazar nudos de la línea aérea, si el usuario había dejado tramos desconectados. Trabajar en modo Orto, definiendo la red según unos ejes ficticios de un sistema de coordenadas cartesianas X,Y. Rotar partes o toda la línea aérea. Renumerar los nudos y ramas de la línea aérea. Borrar líneas y nudos de la línea aérea. Ver Los Datos del terreno (cotas de los puntos, zona, etc) y de la línea aérea (tipo de apoyo, sección del conductor, etc) en forma de tabla. La Ventana de Resultados de Tensiones y Flechas en Hipótesis Reglamentarias, para ver el cálculo del vano de regulación, tense máximo y flecha máxima según zona A, B o C (RLAT), flecha mínima, hipótesis de cálculo de apoyos y desviación horizontal de las catenarias por la acción del viento. La Ventana de Resultados de Tensiones y Flechas de Tendido, para ver el tense y la flecha de la línea a las diferentes temperaturas (- 20 ºC, -15 ºC, -10 ºC, -5 ºC, 0 ºC, 5 ºC, 10 ºC, etc). EDS en cada vano. La Ventana de Cálculo de Apoyos, para ver el cálculo de los apoyos en las hipótesis reglamentarias (Viento, Hielo, Desequilibrio de Tracciones y Rotura), según Zona A, B o C (RLAT). Esfuerzo horizontal en dirección transversal a la línea (T), esfuerzo horizontal en dirección longitudinal (L), esfuerzo o carga vertical (V) y esfuerzo horizontal de torsión (Lt) descentrado respecto al eje del apoyo. La Ventana de Apoyos Adoptados, para ver las características de los apoyos seleccionados (esfuerzo nominal o útil en punta, altura total, etc). La Ventana de Crucetas Adoptadas, para ver las características de las crucetas seleccionadas (dimensiones de brazos, etc). La Ventana de Cálculo de Cimentaciones, para ver el cálculo de las cimentaciones por el método de Sulzberger en cimentaciones monobloque (momento al vuelco por el conductor, momento al vuelco por el viento, momento absorbido por la cimentación, etc) o el cálculo de cimentaciones mediante zapatas aisladas. La Ventana de Dimensiones de Cimentaciones, para ver las características de las cimentaciones adoptadas (ancho, alto, etc). La Ventana de Cálculo de Cadenas de Aisladores, para ver el cálculo eléctrico y mecánico de los aisladores. La Ventana de Cálculo de Esfuerzos verticales sin Sobrecarga, para detectar apoyos que pudieran quedar colgados. La lista de Mensajes de errores o advertencias. Redibujar el esquema. Zooms de todo tipo (zoom ventana, zoom en tiempo real, encuadre en tiempo real, zoom previo, zoom todo, etc). Vista global, con el fin de no perder nunca la referencia de la zona del dibujo en la que estamos trabajando. Visualizar u ocultar la imagen de fondo (planta de un topográfico, etc) anteriormente cargada. Visualizar u ocultar los nudos-ramas, el texto de los nudos y el texto de las ramas de la red eléctrica. Cambiar el color de fondo de la zona de edición gráfica. Nudos Paleta de Componentes Gráficos (nudos de terreno) para diseñar el perfil longitudinal de la línea aérea (nudo o punto del terreno para cambiar de cota o de dirección, cruzamiento con una línea eléctrica aérea AT existente, cruzamiento con una línea eléctrica aérea BT existente, cruzamiento con una línea de telecomunicaciones existente, cruzamiento con una carretera del estado existente -autopista, autovía, vía rápida, carretera nacional, etc-, cruzamiento con una carretera no estatal, cruzamiento con una línea de ferrocarril no electrificada, cruzamiento con una línea de ferrocarril electrificada, cruzamiento con un teleférico para transporte de personas, cruzamiento con un río o canal (navegable o flotable) y cruzamiento con un edificio. Paleta de Componentes Gráficos (apoyos) para situar apoyos a lo largo del perfil (entronque o conexión a una línea eléctrica aérea ya existente, punto de fijación a una pared o muro, apoyo fin de línea, apoyo de anclaje en alineación, apoyo de anclaje en ángulo, apoyo de alineación con cadenas de suspensión, apoyo de alineación con cadenas de amarre, apoyo de ángulo con cadenas de suspensión, apoyo de ángulo con cadenas de amarre y apoyo de estrellamiento o derivación). Ventana de Propiedades de nudos de terreno Tipo nudo, para la modificación de uno o varios nudos ya introducidos. Denominación de cruzamientos. Posibilidad de fijar la distancia y el ángulo entre singularidades (puntos) del terreno (coordenadas polares). Zona geográfica donde está situada la línea: A, B o C. Cota de los puntos del terreno. Datos de cruzamientos: anchura de carreteras, líneas eléctricas, etc. Ventana de Propiedades de apoyos y vanos Función o Tipo de apoyo: entronque, fijación a una pared o muro, fin de línea, anclaje (alineación o ángulo), alineación (suspensión o amarre), ángulo (suspensión o amarre) y estrellamiento. Constitución del apoyo: celosía cabeza cónica, celosía cabeza recta, presilla cabeza cónica, presilla cabeza recta, hormigón vibrado, hormigón vibrado hueco, chapa metálica con sección rectangular y chapa metálica con sección circular o poligonal regular. Cruceta empleada: horizontal, triángulo, tresbolillo, bandera, bóveda triangular, bóveda plana y doble circuito. Fabricante empleado. Posibilidad de fijar la dimensión mínima de las crucetas. Posibilidad de fijar la longitud de los vanos. Posibilidad de fijar la altura total de los apoyos. Posibilidad de fijar el esfuerzo nominal o útil en punta mínimo. Posibilidad de definir cargas verticales adicionales (peso de transformadores, etc). Posibilidad de calcular cimentaciones monobloque (apoyo empotrado o sobre placa base) o por zapatas aisladas. Denominación del conductor (LA-30, LA-56, LA-110, etc) y nº de conductores por fase (desnudos y recubiertos). Posibilidad de tener haces de distinta sección y características en el mismo vano (aislados en haz). Distancia de fijación de cada haz hasta la cogolla. Color de cada haz. Coeficiente de seguridad del conductor, para obtener el tense máximo del cantón. Coeficiente de seguridad del apoyo (normal o reforzado). Denominación del aislador (U40B, U70BS, etc) y nivel de aislamiento requerido (cm/kV). Desviación horizontal de las catenarias por la acción del viento. Posibilidad de incluir dos crucetas en un mismo apoyo (principal y derivación). Cálculos Cálculo de tensiones y flechas en las hipótesis reglamentarias (RLAT), tensiones y flechas para el tendido de línea y EDS, cálculo de apoyos en todas las hipótesis reglamentarias (RLAT), apoyos adoptados, crucetas adoptadas, cálculo de cimentaciones por el método de Sulzberger en cimentaciones monobloque, cálculo de cimentaciones mediante zapatas aisladas, cálculo de las cadenas de aisladores, cálculo de esfuerzos verticales sin sobrecarga para detectar apoyos colgados y distancias de seguridad, o sea, el cálculo mecánico completo de la línea eléctrica aérea de alta tensión. Resultados La Memoria Descriptiva muestra las características de la línea aérea B.T. Permite ser cargada en el editor de textos del programa o en el seleccionado por el usuario (word, wordperfect, etc, mediante la opción Cambiar Editor), presentar, visualizar, editar, imprimir y generar dicho documento en fichero RTF, de intercambio con cualquier editor de textos. El Anexo de cálculo proporciona un resumen de fórmulas generales (ecuación de la catenaria, ecuación del cambio de condiciones, esfuerzos en apoyos, etc), datos generales de la línea (zona, tensión eléctrica, etc) y de los conductores (denominación, peso propio, peso propio más sobrecarga de viento, etc), cálculo de la distancia de los conductores al terreno y a masa (al apoyo), cálculo de la distancia entre conductores, desviación de las cadenas de suspensión por la acción del viento (acercamiento de la cadena al apoyo), cálculo de tensiones y flechas en las hipótesis reglamentarias (tensión máxima, flecha máxima, etc), desviación horizontal de las catenarias por la acción del viento (para proximidades a edificaciones, etc), tensiones y flechas de tendido (a todas las temperaturas), cálculo de apoyos (en las 4 hipótesis reglamentarias: Viento, Hielo, Desequilibrio y Rotura), apoyos adoptados (esfuerzos en punta, altura total, esfuerzos de torsión, etc), crucetas adoptadas (brazos, etc), cálculo de cimentaciones, cimentaciones adoptadas, cálculo de las cadenas de aisladores (cálculo eléctrico y mecánico, nº de elementos por cadena, etc) y cálculo de esfuerzos verticales sin sobrecarga. El Pliego de Condiciones muestra de forma minuciosa las características constructivas y de ejecución de todas las instalaciones proyectadas, así como las responsabilidades que debe asumir cada una de las partes que intervienen en la ejecución de la obra. Permite ser cargado en el editor de textos del programa o en el seleccionado por el usuario (word, wordperfect, etc, mediante la opción Cambiar Editor), presentar, visualizar, editar, imprimir y generar dicho documento en fichero RTF, de intercambio con cualquier editor de textos. La Medición muestra el cómputo de toda la aparamenta eléctrica que interviene en el cálculo (cableado eléctrico, apoyos y cimentaciones). Permite cargar los resultados en el editor de textos del programa o en el seleccionado por el usuario (word, wordperfect, etc, mediante la opción Cambiar Editor), presentar, visualizar, editar, imprimir y generar dicho documento en fichero RTF, de intercambio con cualquier editor de textos. Los Planos muestran las características generales del proyecto calculado, en planta y perfil, con dibujo automático de catenarias. Planos de cimentaciones y crucetas acotadas. Salida directa a impresora o generación en fichero DXF, de intercambio con cualquier programa de CAD. Ayudas El programa proporciona ayudas técnicas muy didácticas de cada una de las opciones y campos establecidos. Incorpora también filosofía de trabajo del programa, ejemplos prácticos resueltos, etc. Toda esta información queda además recogida en los manuales correspondientes. Memoria Descriptiva 1. ANTECEDENTES Y FINALIDAD DE LA INSTALACION. 2. OBJETO DEL PROYECTO. 3. REGLAMENTACION Y DISPOSICIONES OFICIALES Y PARTICULARES. 4. TRAZADO DE LA LINEA. 5. CRUZAMIENTOS Y PARALELISMOS. 5.1. GENERALIDADES. 5.2. DISTANCIAS A OTRAS LINEAS ELECTRICAS AEREAS O DE TELECOMUNICACION. 5.3. DISTANCIAS A CARRETERAS. 5.4. DISTANCIAS A FERROCARRILES SIN ELECTRIFICAR. 5.5. DISTANCIAS A FERROCARRILES ELECTRIFICADOS, TRANVIAS Y TROLEBUSES. 5.6. DISTANCIAS A TELEFERICOS Y CABLES TRANSPORTADORES. 5.7. DISTANCIAS A RIOS Y CANALES, NAVEGABLES O FLOTABLES. 5.8. PASO POR ZONAS. 6. MATERIALES. 7. CONDUCTORES. 7.1. CONDUCTORES DE ALUMINIO. 7.2. CONDUCTORES DE ACERO. 7.3. CONDUCTORES DE COBRE. 7.4. EMPALMES Y CONEXIONES. 8. HERRAJES Y ACCESORIOS. 9. AISLADORES. 10. CRUCETAS. 11. APOYOS. 11.1. APOYOS METALICOS. 11.2. APOYOS DE HORMIGON. 11.3. NUMERACION, MARCADO Y AVISOS DE RIESGO ELECTRICO. 12. ELEMENTOS DEL SISTEMA DE PUESTA A TIERRA Y CONDICIONES DE MONTAJE. 12.1. ELECTRODOS DE PUESTA A TIERRA. 12.2. LINEAS DE TIERRA. 12.3. CONEXION DE LOS APOYOS A TIERRA. 13. CIMENTACIONES. 14. ENTRONQUE. 15. PROTECCION DE LA AVIFAUNA. 15.1. PROTECCION CONTRA LA ELECTROCUCION. 15.2. PROTECCION CONTRA LA COLISION. 16. PLANOS 17. CONCLUSION SEGURIDAD, HIGIENE Y SALUD EN EL TRABAJO 1. PREVENCION DE RIESGOS LABORALES. 1.1. INTRODUCCION. 1.2. DERECHOS Y OBLIGACIONES. 1.3. SERVICIOS DE PREVENCION. 1.4. CONSULTA Y PARTICIPACION DE LOS TRABAJADORES. 2. DISPOSICIONES MINIMAS EN MATERIA DE SEÑALIZACION DE SEGURIDAD Y SALUD EN EL TRABAJO. 2.1. INTRODUCCION. 2.2. OBLIGACION GENERAL DEL EMPRESARIO. 3. DISPOSICIONES MINIMAS DE SEGURIDAD Y SALUD PARA LA UTILIZACION POR LOS TRABAJADORES DE LOS EQUIPOS DE TRABAJO. 3.1. INTRODUCCION. 3.2. OBLIGACION GENERAL DEL EMPRESARIO. 4. DISPOSICIONES MINIMAS DE SEGURIDAD Y SALUD EN LAS OBRAS DE CONSTRUCCION. 4.1. INTRODUCCION. 4.2. ESTUDIO BASICO DE SEGURIDAD Y SALUD. 4.3. DISPOSICIONES ESPECIFICAS DE SEGURIDAD Y SALUD DURANTE LA EJECUCION DE LAS OBRAS. 5. DISPOSICIONES MINIMAS DE SEGURIDAD Y SALUD RELATIVAS A LA UTILIZACION POR LOS TRABAJADORES DE EQUIPOS DE PROTECCION INDIVIDUAL 5.1. INTRODUCCION. 5.2. OBLIGACIONES GENERALES DEL EMPRESARIO. Anexo de Cálculos 1. RESUMEN DE FORMULAS. 2. DATOS GENERALES DE LA LINEA. 3. DISTANCIAS DE SEGURIDAD. 4. ANGULO DE DESVIACION DE LA CADENA DE AISLADORES. 5. TENSIONES Y FLECHAS EN HIPOTESIS REGLAMENTARIAS. 6. TENSIONES Y FLECHAS DE TENDIDO. 7. CALCULO DE APOYOS. 8. APOYOS ADOPTADOS. 9. CRUCETAS ADOPTADAS. 10. CALCULO DE CIMENTACIONES. 11. CALCULO DE CADENAS DE AISLADORES. 12. ESFUERZOS VERTICALES SIN SOBRECARGA. 1. RESUMEN DE FORMULAS. 1.1. TENSION MAXIMA EN UN VANO (Apdo. 3.2.1). La tensión máxima en un vano se produce en los puntos de fijación del conductor a los apoyos. TA = P0 ·YA = P0 · c · cosh (XA/c) = P0 · c ·cosh [(Xm - a/2) / c] TB = P0 ·YB = P0 · c · cosh (XB/c) = P0 · c ·cosh [(Xm+ a/2) / c] Pv = K · d / 1000 K=60·(v/120)² daN/m² si d ≤16 mm y v ≥ 120 Km/h K=50·(v/120)² daN/m² si d >16 mm y v ≥ 120 Km/h Pvh = K · D / 1000 K=60·(v/120)² daN/m² si d ≤16 mm y v ≥ 60 Km/h Ph = K · √d K=50·(v/120)² daN/m² si d >16 mm y v ≥ 60 Km/h K=0.18 Zona B K=0.36 Zona C P0 = √ (Pp² + Pv²) Zona A, B y C. Hipótesis de viento. P0 = Pp + Ph Zonas B y C. Hipótesis de hielo. P0 = √ [(Pp + Ph )² + Pvh²] Zonas B y C. Hipótesis de hielo + viento. Cuando sea requerida por la empresa eléctrica. c = T0h / P0 Xm = c · ln [z + √(1+z²)] z = h / (2·c·senh a/2c) Siendo: v = Velocidad del viento (Km/h). TA = Tensión total del conductor en el punto de fijación al primer apoyo del vano (daN). TB = Tensión total del conductor en el punto de fijación al segundo apoyo del vano (daN). P0 = Peso total del conductor en las condiciones más desfavorables (daN/m). Pp = Peso propio del conductor (daN/m). Pv = Sobrecarga de viento (daN/m). Pvh = Sobrecarga de viento incluido el manguito de hielo (daN/m). Ph = Sobrecarga de hielo (daN/m). d = diámetro del conductor (mm). D = diámetro del conductor incluido el espesor del manguito de hielo (mm). Y = c · cosh (x/c) = Ecuación de la catenaria. c = constante de la catenaria. YA = Ordenada correspondiente al primer apoyo del vano (m). YB = Ordenada correspondiente al segundo apoyo del vano (m). XA = Abcisa correspondiente al primer apoyo del vano (m). XB = Abcisa correspondiente al segundo apoyo del vano (m). Xm= Abcisa correspondiente al punto medio del vano (m). a = Proyección horizontal del vano (m). h = Desnivel entre los puntos de fijación del conductor a los apoyos (m). T0h = Componente Horizontal de la Tensión en las condiciones más desfavorables o Tensión Máxima Horizontal (daN). Es constante en todo el vano. 1.2. VANO DE REGULACION. Para cada tramo de línea comprendida entre apoyos con cadenas de amarre, el vano de regulación se obtiene del siguiente modo: ar = √ (∑ a3 / ∑ a) 1.3. TENSIONES Y FLECHAS DE LA LINEA EN DETERMINADAS CONDICIONES. ECUACION DEL CAMBIO DE CONDICIONES. Partiendo de una situación inicial en las condiciones de tensión máxima horizontal (T0h), se puede obtener una tensión horizontal final (Th) en otras condiciones diferentes para cada vano de regulación (tramo de línea), y una flecha (F) en esas condiciones finales, para cada vano real de ese tramo. La tensión horizontal en unas condiciones finales dadas, se obtiene mediante la Ecuación del Cambio de Condiciones: [δ · L0 · (t - t0)] + [L0/(S·E) · (Th - T0h)] = L - L0 L0 = c0·senh[(Xm0+a/2) / c0] - c0·senh[(Xm0-a/2) / c0] c0 = T0h/P0 ; Xm0 = c0 · ln[z0 + √(1+z0²)] z0 = h / (2·c0·senh a/2c0) L = c·senh[(Xm+a/2) / c] - c·senh[(Xm-a/2) / c] c = Th/P ; Xm = c · ln[z + √(1+z² )] z = h / (2·c·senh a/2c) Siendo: δ = Coeficiente de dilatación lineal. L0 = Longitud del arco de catenaria en las condiciones iniciales para el vano de regulación (m). L = Longitud del arco de catenaria en las condiciones finales para el vano de regulación (m). t0 = Temperatura en las condiciones iniciales (ºC). t = Temperatura en las condiciones finales (ºC). S = Sección del conductor (mm²). E = Módulo de elasticidad (daN/mm²). T0h = Componente Horizontal de la Tensión en las condiciones más desfavorables o Tensión Máxima Horizontal (daN). Th = Componente Horizontal de la Tensión o Tensión Horizontal en las condiciones finales consideradas, para el vano de regulación (daN). a = ar (vano de regulación, m). h = Desnivel entre los puntos de fijación del conductor a los apoyos, en tramos de un solo vano (m). h = 0, para tramos compuestos por más de un vano. Obtención de la flecha en las condiciones finales (F), para cada vano real de la línea: F = YB - [h/a · (XB - Xfm)] - Yfm Xfm = c · ln[h/a + √(1+(h/a)²)] Yfm = c · cosh (Xfm/c) Siendo: YB = Ordenada de uno de los puntos de fijación del conductor al apoyo (m). XB = Abcisa de uno de los puntos de fijación del conductor al apoyo (m). Yfm = Ordenada del punto donde se produce la flecha máxima (m). Xfm = Abcisa del punto donde se produce la flecha máxima (m). h = Desnivel entre los puntos de fijación del conductor a los apoyos (m). a = proyección horizontal del vano (m). 1.3.1. Tensión máxima (Apdo. 3.2.1). Condiciones iniciales a considerar en la ecuación del cambio de condiciones. a) Zona A. - Tracción máxima viento. t = - 5 ºC. Sobrecarga: viento (Pv). b) Zona B. - Tracción máxima viento. t = -10 ºC. Sobrecarga: viento (Pv). - Tracción máxima hielo. t = -15 ºC. Sobrecarga: hielo (Ph). - Tracción máxima hielo + viento. (Cuando sea requerida por la empresa eléctrica). t = -15 ºC. Sobrecarga: viento (Pvh). Sobrecarga: hielo (Ph). c) Zona C. - Tracción máxima viento. t = -15 ºC. Sobrecarga: viento (Pv). - Tracción máxima hielo. t = -20 ºC. Sobrecarga: hielo (Ph). - Tracción máxima hielo + viento. (Cuando sea requerida por la empresa eléctrica). t = -20 ºC. Sobrecarga: viento (Pvh). Sobrecarga: hielo (Ph). 1.3.2. Flecha máxima (Apdo. 3.2.3). Condiciones finales a considerar en la ecuación del cambio de condiciones. a) Hipótesis de viento. t = +15 ºC. Sobrecarga: Viento (Pv). b) Hipótesis de temperatura. t = + 50 ºC. Sobrecarga: ninguna. c) Hipótesis de hielo. t = 0 ºC. Sobrecarga: hielo (Ph). Zona A: Se consideran las hipótesis a) y b). Zonas B y C: Se consideran las hipótesis a), b) y c). 1.3.3. Flecha mínima. Condiciones finales a considerar en la ecuación del cambio de condiciones. a) Zona A. t = -5 ºC. Sobrecarga: ninguna. b) Zona B. t = -15 ºC. Sobrecarga: ninguna. c) Zona C. t = -20 ºC. Sobrecarga: ninguna. 1.3.4. Desviación cadena aisladores. Condiciones finales a considerar en la ecuación del cambio de condiciones. t = -5 ºC en zona A, -10 ºC en zona B y -15 ºC en zona C. Sobrecarga: mitad de Viento (Pv/2). 1.3.5. Hipótesis de Viento. Cálculo de apoyos. Condiciones finales a considerar en la ecuación del cambio de condiciones. t = -5 ºC en zona A, -10 ºC en zona B y -15 ºC en zona C. Sobrecarga: Viento (Pv). 1.3.6. Tendido de la línea. Condiciones finales a considerar en la ecuación del cambio de condiciones. t = -20 ºC (Sólo zona C). t = -15 ºC (Sólo zonas B y C). t = -10 ºC (Sólo zonas B y C). t = -5 ºC. t = 0 ºC. t = + 5 ºC. t = + 10 ºC. t = + 15 ºC. t = + 20 ºC. t = + 25 ºC. t = + 30 ºC. t = + 35 ºC. t = + 40 ºC. t = + 45 ºC. t = + 50 ºC. Sobrecarga: ninguna. 1.4. LIMITE DINAMICO "EDS". EDS = (Th / Qr) · 100 < 15 Siendo: EDS = Every Day Estress, esfuerzo al cual están sometidos los conductores de una línea la mayor parte del tiempo, correspondiente a la temperatura media o a sus proximidades, en ausencia de sobrecarga. Th = Componente Horizontal de la Tensión o Tensión Horizontal en las condiciones finales consideradas, para el vano de regulación (daN). Zonas A, B y C, tª = 15 ºC. Sobrecarga: ninguna. Qr = Carga de rotura del conductor (daN). 1.5. HIPOTESIS CALCULO DE APOYOS (Apdo. 3.5.3). Apoyos de líneas situadas en zona A (Altitud inferior a 500 m). TIPO DE APOYO Alineación Suspensión TIPO DE ESFUERZO V T HIPOTESIS 1ª (Viento) Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Alineación Amarre V T Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Angulo Suspensión V T Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT L Angulo Amarre V T L Anclaje Alineación V T Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT Res. Angulo (apdo. 3.1.6) L = RavL Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Anclaje Angulo y V Estrellam. T L Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT Res. Angulo (apdo. 3.1.6) L = RavL HIPOTESIS 2ª (Hielo) HIPOTESIS 3ª (Des. Tracciones) Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc HIPOTESIS 4ª (Rotura cond.) Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Des. Tracc. (apdo. 3.1.4.1) L = Dtv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Rot. Cond. (apdo. 3.1.5.1) Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Des. Tracc. (apdo. 3.1.4.2) L = Dtv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Des. Tracc. (apdo. 3.1.4.1) Res. Angulo (apdo. 3.1.6) T = RavdT Des. Tracc. (apdo. 3.1.4.1) Res. Angulo (apdo. 3.1.6) L = RavdL Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Des. Tracc. (apdo. 3.1.4.2) Res. Angulo (apdo. 3.1.6) T = RavdT Des. Tracc. (apdo. 3.1.4.2) Res. Angulo (apdo. 3.1.6) L = RavdL Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Rot. Cond. (apdo. 3.1.5.2) Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Rot. Cond. (apdo. 3.1.5.1) Res. Angulo (apdo. 3.1.6) T = RavrT Rot. Cond. (apdo. 3.1.5.1) Res. Angulo (apdo. 3.1.6) L = RavrL ; Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Rot. Cond. (apdo. 3.1.5.2) Res. Angulo (apdo. 3.1.6) T = RavrT Rot. Cond. (apdo. 3.1.5.2) Res. Angulo (apdo. 3.1.6) L = RavrL ; Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Des. Tracc. (apdo. 3.1.4.3) L = Dtv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Des. Tracc. (apdo. 3.1.4.3) Res. Angulo (apdo. 3.1.6) T = RavdT Des. Tracc. (apdo. 3.1.4.3) Res. Angulo (apdo. Rot. Cond. (apdo. 3.1.5.3) Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Rot. Cond. (apdo. 3.1.5.3) Res. Angulo (apdo. 3.1.6) T = RavrT Rot. Cond. (apdo. 3.1.5.3) Res. Angulo (apdo. 3.1.6) L = RavdL Fin de línea V T L Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc Des. Tracc. (apdo. 3.1.4.4) L = Dtv V = Esfuerzo vertical T = Esfuerzo transversal 3.1.6) L = RavrL ; Lt = Rotv Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv - Pcvr + Pca·nc Rot. Cond. (apdo. 3.1.5.4) Lt = Rotv L = Esfuerzo longitudinal Lt = Esfuerzo de torsión Para la determinación de las tensiones de los conductores se considerarán sometidos a una sobrecarga de viento (apdo. 3.1.2) correspondiente a una velocidad mínima de 120 Km/h y a la temperatura de -5 ºC. En los apoyos de alineación y ángulo con cadenas de suspensión y amarre se prescinde de la 4ª hipótesis si se verifican simultáneamente las siguientes condiciones (apdo. 3.5.3) : - Tensión nominal de la línea hasta 66 kV. - La carga de rotura del conductor es inferior a 6600 daN. - Los conductores tienen un coeficiente de seguridad de 3, como mínimo. - El coeficiente de seguridad de los apoyos y cimentaciones en la hipótesis tercera es el correspondiente a las hipótesis normales. - Se instalen apoyos de anclaje cada 3 kilómetros como máximo. Apoyos de líneas situadas en zonas B y C (Altitud igual o superior a 500 m). TIPO DE APOYO Alineación Suspensión TIPO DE ESFUERZO V T HIPOTESIS 1ª (Viento) Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc HIPOTESIS 2ª (Hielo) Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc HIPOTESIS 3ª (Des. Tracciones) Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc HIPOTESIS 4ª (Rotura cond.) Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Des. Tracc. (apdo. 3.1.4.1) L = Dth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Rot. Cond. (apdo. 3.1.5.1) Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Des. Tracc. (apdo. 3.1.4.2) L = Dth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT Res. Angulo (apdo. 3.1.6) T = RahT Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT Res. Angulo (apdo. 3.1.6) L = RavL Res. Angulo (apdo. 3.1.6) T = RahT Res. Angulo (apdo. 3.1.6) L = RahL Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Des. Tracc. (apdo. 3.1.4.2) Res. Angulo (apdo. 3.1.6) T = RahdT Des. Tracc. (apdo. 3.1.4.2) Res. Angulo (apdo. 3.1.6) L = RahdL Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Rot. Cond. (apdo. 3.1.5.2) Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Rot. Cond. (apdo. 3.1.5.1) Res. Angulo (apdo. 3.1.6) T = RahrT Rot. Cond. (apdo. 3.1.5.1) Res. Angulo (apdo. 3.1.6) L = RahrL ; Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Rot. Cond. (apdo. 3.1.5.2) Res. Angulo (apdo. 3.1.6) T = RahrT Rot. Cond. (apdo. 3.1.5.2) Res. Angulo (apdo. 3.1.6) L = RahrL ; Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Des. Tracc. (apdo. 3.1.4.3) L = Dth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Viento. (apdo. 3.1.2) Res. Angulo (apdo. 3.1.6) T = Fvc + Eca·nc + RavT Res. Angulo (apdo. 3.1.6) T = RahT Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Alineación Amarre V T Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Angulo Suspensión V T L Angulo Amarre V T L Anclaje Alineación V T Viento. (apdo. 3.1.2) T = Fvc + Eca·nc L Anclaje Angulo y V Estrellam. T Des. Tracc. (apdo. 3.1.4.1) Res. Angulo (apdo. 3.1.6) T = RahdT Des. Tracc. (apdo. 3.1.4.1) Res. Angulo (apdo. 3.1.6) L = RahdL Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Des. Tracc. (apdo. 3.1.4.3) Res. Angulo (apdo. 3.1.6) T = RahdT Rot. Cond. (apdo. 3.1.5.3) Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Rot. Cond. (apdo. 3.1.5.3) Res. Angulo (apdo. 3.1.6) T = RahrT L Fin de línea V T L Res. Angulo (apdo. 3.1.6) L = RavL Res. Angulo (apdo. 3.1.6) L = RahL Cargas perm. (apdo. 3.1.1) Viento. (apdo. 3.1.2) V = Pcv + Pca·nc Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch + Pca·nc Viento. (apdo. 3.1.2) T = Fvc + Eca·nc Des. Tracc. (apdo. 3.1.4.4) L = Dtv Des. Tracc. (apdo. 3.1.4.4) L = Dth V = Esfuerzo vertical T = Esfuerzo transversal Des. Tracc. (apdo. 3.1.4.3) Res. Angulo (apdo. 3.1.6) L = RahdL L = Esfuerzo longitudinal Rot. Cond. (apdo. 3.1.5.3) Res. Angulo (apdo. 3.1.6) L = RahrL ; Lt = Roth Cargas perm. (apdo. 3.1.1) Hielo (apdo. 3.1.3) V = Pch - Pchr + Pca·nc Rot. Cond. (apdo. 3.1.5.4) Lt = Roth Lt = Esfuerzo de torsión Para la determinación de las tensiones de los conductores se considerará: Hipótesis 1ª : Sometidos a una sobrecarga de viento (apdo. 3.1.2) correspondiente a una velocidad mínima de 120 Km/h y a la temperatura de -10 ºC en zona B y -15 ºC en zona C. Resto hipótesis : Sometidos a una sobrecarga de hielo mínima (apdo. 3.1.3) y a la temperatura de -15 ºC en zona B y -20 ºC en zona C. En los apoyos de alineación y ángulo con cadenas de suspensión y amarre se prescinde de la 4ª hipótesis si se verifican simultáneamente las siguientes condiciones (apdo. 3.5.3) : - Tensión nominal de la línea hasta 66 kV. - La carga de rotura del conductor es inferior a 6600 daN. - Los conductores tienen un coeficiente de seguridad de 3, como mínimo. - El coeficiente de seguridad de los apoyos y cimentaciones en la hipótesis tercera es el correspondiente a las hipótesis normales. - Se instalen apoyos de anclaje cada 3 kilómetros como máximo. 1.5.1. Cargas permanentes (Apdo. 3.1.1). Se considerarán las cargas verticales debidas al peso de los distintos elementos: conductores con sobrecarga (según hipótesis), aisladores, herrajes. En todas las hipótesis en zona A y en la hipótesis de viento en zonas B y C, el peso que gravita sobre los apoyos debido al conductor y su sobrecarga "Pcv" será: Pcv = Lv · Ppv · cos α · n (daN) Pcvr = Lv · Ppv · cos α · nr (daN) Siendo: Lv = Longitud del conductor que gravita sobre el apoyo en las condiciones de -5 ºC (zona A), -10 ºC (zona B) o -15 ºC (zona C) con sobrecarga de viento (m). Ppv = Peso propio del conductor con sobrecarga de viento (daN/m). Pcvr = Peso que gravita sobre los apoyos de los conductores rotos con sobrecarga de viento para la 4ª hipótesis (daN). α = Angulo que forma la resultante del viento con el peso propio del conductor. n = número total de conductores. nr = número de conductores rotos en la 4ª hipótesis. En todas las hipótesis en zonas B y C, excepto en la hipótesis 1ª de Viento, el peso que gravita sobre los apoyos debido al conductor y su sobrecarga "Pch" será: Pch = Lh · Pph · n (daN) Pchr = Lh · Pph · nr (daN) Siendo: Lh = Longitud del conductor que gravita sobre el apoyo en las condiciones de -15 ºC (zona B) o -20 ºC (zona C) con sobrecarga de hielo (m). Pph = Peso propio del conductor con sobrecarga de hielo (daN/m). Pphr = Peso que gravita sobre los apoyos de los conductores rotos con sobrecarga de hielo para la 4ª hipótesis (daN). n = número total de conductores. nr = número de conductores rotos en la 4ª hipótesis. En todas las zonas y en todas las hipótesis habrá que considerar el peso de los herrajes y la cadena de aisladores "Pca", así como el número de cadenas de aisladores del apoyo "nc". 1.5.2. Esfuerzos del viento (Apdo. 3.1.2). - El esfuerzo del viento sobre los conductores "Fvc" en la hipótesis 1ª para las zonas A, B y C se obtiene de la siguiente forma: Apoyos alineación Fvc = (a1 · d1 · n1 + a2 · d2 · n2)/2 · k (daN) Apoyos fin de línea Fvc = a/2 · d · n · k (daN) Apoyos de ángulo y estrellamiento Fvc = ∑ ap /2 · dp · np · k (daN) Siendo: a1 = Proyección horizontal del conductor que hay a la izquierda del apoyo (m). a2 = Proyección horizontal del conductor que hay a la derecha del apoyo (m). a = Proyección horizontal del conductor (m). ap = Proyección horizontal del conductor en la dirección perpendicular a la bisectriz del ángulo (apoyos de ángulo) y en la dirección perpendicular a la resultante (apoyos de estrellamiento) (m). d, d1, d2, dp = Diámetro del conductor(m). n, n1, n2, np = nº de haces de conductores. v = Velocidad del viento (Km/h). K = 60·(v/120)² daN/m² si d ≤16 mm y v ≥ 120 Km/h K = 50·(v/120)² daN/m² si d >16 mm y v ≥ 120 Km/h - En la hipótesis 1ª para las zonas A, B y C habrá que considerar el esfuerzo del viento sobre los herrajes y la cadena de aisladores "Eca", así como el número de cadenas de aisladores del apoyo "nc". 1.5.3. Desequilibrio de tracciones (Apdo. 3.1.4) - En la hipótesis 1ª (sólo apoyos fin de línea) en zonas A, B y C y en la hipótesis 3ª en zona A (apoyos alineación, ángulo, estrellamiento y anclaje), el desequilibrio de tracciones "Dtv" se obtiene: Apoyos de alineación con cadenas de suspensión. Dtv = 8/100 · Th · n (daN) Dtv = Abs( (Th1· n1 ) – (Th2 · n2 ) ) (daN) Apoyos de alineación con cadenas de amarre. Dtv = 15/100 · Th · n (daN) Dtv = Abs( (Th1· n1 ) – (Th2 · n2 ) ) (daN) Apoyos de ángulo con cadenas de suspensión. Dtv = 8/100 · Th · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos de ángulo con cadenas de amarre. Dtv = 15/100 · Th · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos de anclaje de alineación. Dtv = 50/100 · Th · n (daN) Dtv = Abs( (Th1· n1 ) – (Th2 · n2 ) ) (daN) Apoyos de anclaje en ángulo y estrellamiento. Dtv = 50/100 · Th · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos fin de línea Dtv = 100/100 · Th · n (daN) Siendo: n, n1, n2 = número total de conductores. Th, Th1, Th2 = Componente horizontal de la tensión en las condiciones de -5 ºC (zona A), -10 ºC (zona B) y -15 ºC (zona C) con sobrecarga de viento (daN). - En la hipótesis 2ª (fin de línea) y 3ª (alineación, ángulo, estrellamiento y anclaje) en zonas B y C, el desequilibrio de tracciones "Dth" se obtiene: Apoyos de alineación con cadenas de suspensión. Dth = 8/100 · T0h · n (daN) Dth = Abs( (T0h1· n1 ) – (T0h2 · n2 ) ) (daN) Apoyos de alineación con cadenas de amarre. Dth = 15/100 · T0h · n (daN) Dth = Abs( (T0h1· n1 ) – (T0h2 · n2 ) ) (daN) Apoyos de ángulo con cadenas de suspensión. Dth = 8/100 · T0h · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos de ángulo con cadenas de amarre. Dth = 15/100 · T0h · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos de anclaje en alineación. Dth = 50/100 · T0h · n (daN) Dth = Abs( (T0h1· n1 ) – (T0h2 · n2 ) ) (daN) Apoyos de anclaje en ángulo y estrellamiento. Dth = 50/100 · T0h · n (daN) Este esfuerzo se combinará con la resultante de ángulo. Apoyos fin de línea Dth = 100/100 · T0h · n (daN) Siendo: n, n1, n2 = número total de conductores. T0h ,T0h1 ,T0h2 = Componente horizontal de la tensión en las condiciones -15 ºC (Zona B) y -20 ºC (Zona C) con sobrecarga de hielo (daN). 1.5.4. Rotura de conductores (Apdo. 3.1.5) - El esfuerzo debido a la rotura de conductores "Rotv" en zona A, aplicado en el punto donde produzca la solicitación más desfavorable produciendo un esfuerzo de torsión, se obtiene: Apoyos de alineación y de ángulo con cadenas de suspensión - Se prescinde siempre que se cumplan las condiciones especificadas en el apdo 3.5.3. - Si no se cumplen esas condiciones, se considerará el esfuerzo unilateral correspondiente a la rotura de un solo conductor "Rotv", aplicado en el punto que produzca la solicitación más desfavorable. Rotv = T0h (daN) Apoyos de alineación y de ángulo con cadenas de amarre - Se prescinde siempre que se cumplan las condiciones especificadas en el apdo 3.5.3. - Si no se cumplen esas condiciones, se considerará el esfuerzo unilateral correspondiente a la rotura de un solo conductor "Rotv", aplicado en el punto que produzca la solicitación más desfavorable. Rotv = T0h (daN) Apoyos de anclaje en alineación, anclaje en ángulo y estrellamiento Rotv = T0h (simplex, un sólo conductor por fase) (daN) Rotv = T0h · ncf · 0,5 (dúplex, tríplex, cuadruplex; dos, tres o cuatro conductores por fase) (daN) Fin de línea Rotv = T0h · ncf (daN) Rotv = 2 ·T0h · ncf (montaje tresbolillo y bandera) (daN) Siendo: ncf = número de conductores por fase. T0h = Componente horizontal de la tensión en las condiciones de -5 ºC (zona A), -10 ºC (zona B) y -15 ºC (zona C) con sobrecarga de viento (daN). - El esfuerzo debido a la rotura de conductores "Roth" en zonas B y C, aplicado en el punto donde produzca la solicitación más desfavorable produciendo un esfuerzo de torsión, se obtiene: Apoyos de alineación y de ángulo con cadenas de suspensión - Se prescinde siempre que se cumplan las condiciones especificadas en el apdo 3.5.3. - Si no se cumplen esas condiciones, se considerará el esfuerzo unilateral correspondiente a la rotura de un solo conductor "Roth", aplicado en el punto que produzca la solicitación más desfavorable. Roth = T0h (daN) Apoyos de alineación y de ángulo con cadenas de amarre - Se prescinde siempre que se cumplan las condiciones especificadas en el apdo 3.5.3. - Si no se cumplen esas condiciones, se considerará el esfuerzo unilateral correspondiente a la rotura de un solo conductor "Roth", aplicado en el punto que produzca la solicitación más desfavorable. Roth = T0h (daN) Apoyos de anclaje en alineación, anclaje en ángulo y estrellamiento Roth = T0h (simplex, un sólo conductor por fase) (daN) Roth = T0h · ncf · 0,5 (dúplex, tríplex, cuadruplex; dos, tres o cuatro conductores por fase) (daN) Fin de línea Roth = T0h · ncf (daN) Roth = 2 ·T0h · ncf (montaje tresbolillo y bandera) (daN) Siendo: ncf = número de conductores por fase. T0h = Componente horizontal de la tensión en las condiciones de -15 ºC (Zona B) y -20 ºC (Zona C) con sobrecarga de hielo (daN). 1.5.5. Resultante de ángulo (Apdo. 3.1.6) El esfuerzo resultante de ángulo "Rav" de las tracciones de los conductores en la hipótesis 1ª para las zonas A, B y C se obtiene del siguiente modo: Rav = √((Th1· n1)² +(Th2· n2 )² − 2 · (Th1· n1 ) · (Th2· n2) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Rav" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RavL" y otro en dirección transversal a la línea "RavT". Siendo: n1, n2 = Número de conductores. Th1, Th2 = Tensiones horizontales en las condiciones de -5 ºC (zona A), -10 ºC (zona B) y -15 ºC (zona C) con sobrecarga de viento (daN). α = Angulo que forman Th1 y Th2 (gr. sexa.). El esfuerzo resultante de ángulo "Rah" de las tracciones de los conductores en la hipótesis 2ª para las zonas B y C se obtiene del siguiente modo: Rah = √((Th1· n1)² +(Th2· n2)² − 2 · (Th1· n1 ) · (Th2· n2) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Rah" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RahL" y otro en dirección transversal a la línea "RahT". Siendo: n1, n2 = Número de conductores. Th1, Th2 = Tensiones horizontales en las condiciones de -15 ºC (zona B) y -20 ºC (zona C) con sobrecarga de hielo (daN). α = Angulo que forman Th1 y Th2 (gr. sexa.). El esfuerzo resultante de ángulo "Ravd" de las tracciones de los conductores en la hipótesis 3ª para la zona A se obtiene del siguiente modo: Ravd = √((Th1· n1)² +(Th1· n1 - Dtv)² − 2 · (Th1· n1 ) · (Th1· n1 - Dtv) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Ravd" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RavdL" y otro en dirección transversal a la línea "RavdT". Siendo: n1 = Número de conductores. Th1 = Tensiones horizontales en las condiciones de -5 ºC (zona A), -10 ºC (zona B) y -15 ºC (zona C) con sobrecarga de viento (daN). Dtv = Desequilibrio de tracciones en la hipótesis de viento. α = Angulo que forman Th1 y (Th1 - Dtv) (gr. sexa.). El esfuerzo resultante de ángulo "Rahd" de las tracciones de los conductores en la hipótesis 3ª para las zonas B y C se obtiene del siguiente modo: Rahd = √((Th1· n1)² +(Th1· n1 - Dth)² − 2 · (Th1· n1 ) · (Th1· n1 - Dth) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Rahd" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RahdL" y otro en dirección transversal a la línea "RahdT". Siendo: n1 = Número de conductores. Th1 = Tensiones horizontales en las condiciones de -15 ºC (zona B) y -20 ºC (zona C) con sobrecarga de hielo (daN). Dth = Desequilibrio de tracciones en la hipótesis de hielo. α = Angulo que forman Th1 y (Th1 - Dth) (gr. sexa.). El esfuerzo resultante de ángulo "Ravr" de la rotura de conductores en la hipótesis 4ª para la zona A se obtiene del siguiente modo: Ravr = √((Th1· n1)² +(Th2· n2 )² − 2 · (Th1· n1 ) · (Th2· n2) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Ravr" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RavrL" y otro en dirección transversal a la línea "RavrT". Siendo: n1, n2 = Número de conductores quitando los conductores que se han roto. Th1, Th2 = Tensiones horizontales en las condiciones de -5 ºC (zona A), -10 ºC (zona B) y -15 ºC (zona C) con sobrecarga de viento (daN). α = Angulo que forman Th1 y Th2 (gr. sexa.). El esfuerzo resultante de ángulo "Rahr" de la rotura de conductores en la hipótesis 4ª para las zonas B y C se obtiene del siguiente modo: Rahr = √((Th1· n1)² +(Th2· n2)² − 2 · (Th1· n1 ) · (Th2· n2) · cos [180 - α] ) (daN) El esfuerzo resultante de ángulo "Rahr" se descompondrá en dos esfuerzos, uno en dirección longitudinal a la línea "RahrL" y otro en dirección transversal a la línea "RahrT". Siendo: n1, n2 = Número de conductores quitando los conductores que se han roto. Th1, Th2 = Tensiones horizontales en las condiciones de -15 ºC (zona B) y -20 ºC (zona C) con sobrecarga de hielo (daN). α = Angulo que forman Th1 y Th2 (gr. sexa.). *Nota: En los apoyos de estrellamiento las operaciones anteriores se han realizado tomando las tensiones dos a dos para conseguir la resultante total. 1.5.6. Esfuerzos descentrados En los apoyos fin de línea, cuando tienen el montaje al tresbolillo o bandera, aparecen por la disposición de la cruceta esfuerzos descentrados en condiciones normales, cuyo valor será: Esdt = T0h · ncf (daN) (tresbolillo) Esdb = 3 · T0h · ncf (daN) (bandera) Siendo: ncf = número de conductores por fase. T0h = Componente horizontal de la tensión en las condiciones más desfavorables de tensión máxima. 1.5.7. Esfuerzos equivalentes Los esfuerzos horizontales de los apoyos vienen especificados en un punto de ensayo, situado en la cogolla (excepto en los apoyos de hormigón y de chapa metálica que están 0,25 m por debajo de la cogolla). Si los esfuerzos están aplicados en otro punto se aplicará un coeficiente reductor o de mayoración. - Coeficiente reductor del esfuerzo nominal. Se aplica para esfuerzos horizontales a mayor altura del punto de ensayo, cuyo valor será: Apoyos de celosía y presilla K = 4,6 / (HS + 4,6) Apoyos de hormigón K = 5,4 / (HS + 5,25) Apoyos de chapa metálica K = 4,6 / (HS + 4,85) - Coeficiente de mayoración del esfuerzo nominal. Se aplica para esfuerzos horizontales a menor altura del punto de ensayo, cuyo valor será: K = HEn / HF Por tanto los esfuerzos horizontales aplicados en el punto de ensayo serán: T = Tc / K L = Lc / K El esfuerzo horizontal equivalente soportado por el apoyo será: - Existe solamente esfuerzo transversal. F=T - Existe solamente esfuerzo longitudinal. F=L - Existe esfuerzo transversal y longitudinal simultáneamente. En apoyos de celosía, presilla, hormigón vibrado hueco y chapa circular. F=T+L En apoyos de hormigón vibrado y chapa rectangular con viento sobre la cara secundaria. F = RU · T + L En apoyos de hormigón vibrado y chapa rectangular sin viento o con viento sobre la cara principal. F = T + RN · L El esfuerzo de torsión aplicado en el punto de ensayo será: Lt = Ltc · Dc / Dn En apoyos de hormigón vibrado y chapa rectangular el apoyo se orienta con su esfuerzo nominal principal en dirección del esfuerzo mayor (T o L). Siendo: HEn = Distancia desde el punto de ensayo de los esfuerzos horizontales hasta el terreno (m). HS = Distancia por encima de la cogolla, donde se aplican los esfuerzos horizontales (m). HF = Distancia desde punto de aplicación de los esfuerzos horizontales hasta el terreno (m). Dn = Distancia del punto de ensayo del esfuerzo de torsión al eje del apoyo (m). Dc = Distancia del punto de aplicación de los conductores al eje del apoyo (m). Hv = Altura del punto de aplicación del esfuerzo del viento (m). Eva = Esfuerzo del viento sobre el apoyo (daN). EvaRed = Esfuerzo del viento sobre el apoyo reducido al punto de ensayo (daN). EvaRed = Eva · Hv / HEn RU = Esfuerzo nominal principal / (Esfuerzo nominal secundario – EvaRed). RN = Esfuerzo nominal principal / Esfuerzo nominal secundario. Tc = Esfuerzo transversal en el punto de aplicación de los conductores (daN). Lc = Esfuerzo longitudinal en el punto de aplicación de los conductores (daN). Ltc = Esfuerzo de torsión en el punto de aplicación de los conductores (daN). F = Esfuerzo horizontal equivalente (daN). T = Esfuerzo transversal en el punto de ensayo (daN). L = Esfuerzo longitudinal en el punto de ensayo (daN). Lt = Esfuerzo de torsión en el punto de ensayo (daN). 1.5.8. Apoyo adoptado El apoyo adoptado deberá soportar la combinación de esfuerzos considerados en cada hipótesis (V,F,Lt). A estos esfuerzos se le aplicará un coeficiente de seguridad si el apoyo es reforzado. - Hipótesis sin esfuerzo de torsión. El esfuerzo horizontal debe cumplir la ecuación: En ≥ F En apoyos de hormigón el esfuerzo vertical debe cumplir la ecuación: Vn ≥ V En apoyos que no sean de hormigón se aplicará la ecuación resistente: (3 · Vn) ≥ V (5 · En + Vn) ≥ (5 · F + V) - Hipótesis con esfuerzo de torsión. El esfuerzo horizontal debe cumplir la ecuación: Ent ≥ F El esfuerzo vertical debe cumplir la ecuación: Vnt ≥ V El esfuerzo de torsión debe cumplir la ecuación: ET ≥ Lt Siendo: V = Cargas verticales. F = Esfuerzo horizontal equivalente. Lt = Esfuerzo de torsión. En = Esfuerzo nominal sin torsión del apoyo. Ent = Esfuerzo nominal con torsión del apoyo. Vn = Esfuerzo vertical sin torsión del apoyo. Vnt = Esfuerzo vertical con torsión del apoyo. ET = Esfuerzo de torsión del apoyo. 1.6. CIMENTACIONES (Apdo. 3.6). Las cimentaciones se podrán realizar mediante zapatas monobloque o zapatas aisladas. En ambos casos se producirán dos momentos, uno debido al esfuerzo en punta y otro debido al viento sobre el apoyo. Estarán situados los dos momentos, horizontalmente en el centro del apoyo y verticalmente a ras de tierra. Momento debido al esfuerzo en punta El momento debido al esfuerzo en punta "Mep" se obtiene: Mep = Ep · HL Siendo: Ep = Esfuerzo en punta (daN). HL = Altura libre del apoyo (m). Momento debido al viento sobre el apoyo El momento debido al esfuerzo del viento sobre el apoyo "Mev" se obtiene: Mev = Eva · Hv Siendo: Eva = Esfuerzo del viento sobre el apoyo (daN). Según apdo. 3.1.2.3 se obtiene: Eva = 170 · (v/120)² · η · S (apoyos de celosía). Eva = 100 · (v/120)² · S (apoyos con superficies planas). Eva = 70 · (v/120)² · S (apoyos con superficies cilíndricas). v = Velocidad del viento (Km/h). S = Superficie definida por la silueta del apoyo (m²). η = Coeficiente de opacidad. Relación entre la superficie real de la cara y el área definida por su silueta. Hv = Altura del punto de aplicación del esfuerzo del viento (m). Se obtiene: Hv = H/3 · (d1 + 2·d2) / (d1 + d2) (m) H = Altura total del apoyo (m). d1 = anchura del apoyo en el empotramiento (m). d2 = anchura del apoyo en la cogolla (m). 1.6.1. Zapatas Monobloque. Las zapatas monobloque están compuestas por macizos de hormigón de un solo bloque. Momento de fallo al vuelco Para que un apoyo permanezca en su posición de equilibrio, el momento creado por las fuerzas exteriores a él ha de ser absorbido por la cimentación, debiendo cumplirse por tanto: Mf ≥ 1,65 · (Mep + Mev) Siendo: Mf = Momento de fallo al vuelco. Momento absorbido por la cimentación (daN · m). Mep = Momento producido por el esfuerzo en punta (daN · m). Mev = Momento producido por el esfuerzo del viento sobre el apoyo (daN · m). Momento absorbido por la cimentación El momento absorbido por la cimentación "Mf" se calcula por la fórmula de Sulzberger: Mf = [139 · C2 · a · h4] + [a3 · (h + 0,20) · 2420 · ( 0,5 - 2/3·√(1,1 · h/a · 1/10·C2) )] Siendo: C2 = Coeficiente de compresibilidad del terreno a la profundidad de 2 m (daN/cm3). a = Anchura del cimiento (m). h = Profundidad del cimiento (m). 1.6.2. Zapatas Aisladas. Las zapatas aisladas están compuestas por un macizo de hormigón para cada pata del apoyo. Fuerza de rozamiento de las tierras Cuando la zapata intenta levantar un volumen de tierra, este opone una resistencia cuyo valor será: Frt = δ t · ∑ (γ 2 · L) ·tg [φ/2] Siendo: δ t = Densidad de las tierras de que se trata ( 1600 daN/ m3 ). γ = Longitudes parciales del macizo, en m. L = Perímetro de la superficie de contacto, en m. φ = Angulo de las tierras ( generalmente = 45º ). Peso de la tierra levantada El peso de la tierra levantada será: Pt = Vt · δ t , en daN. Siendo: Vt = 1/3· h · (Ss + Si + √( Ss · Si )) ; volumen de tierra levantada, que corresponde a un tronco de pirámide, en m3 . δ t = Densidad de la tierra, en daN/ m3 . h = Altura del tronco de pirámide de la tierra levantada, en m. Ss = Superfice superior del tronco de pirámide de la tierra levantada, en m2 . Si = Superfice inferior del tronco de pirámide de la tierra levantada, en m2 . Al volumen de tierra “ Vt “, habrá que quitarle el volumen del macizo de hormigón que hay enterrado. Peso del macizo de hormigón El peso del macizo de hormigón de la zapata será: Ph = Vh · δ h , en daN. Siendo: δ h = Densidad del macizo de hormigón, en daN/ m3 . Vh = ∑ Vhi ; los volumenes “ Vhi ” pueden ser cubos, pirámides o troncos de pirámide, en m3 . Vi = 1/3 · h · (Ss + Si + √( Ss · Si )) ; volumen del tronco de pirámide, en m3 . Vi = 1/3 · h · S ; volumen de la pirámide, en m3 . Vi = h · S ; volumen del cubo, en m3 . h = Altura del cubo, pirámide o tronco de pirámide, en m. Ss = Superfice superior del tronco de pirámide, en m2 . Si = Superfice inferior del tronco de pirámide, en m2 . S = Superfice de la base del cubo o pirámide, en m2 . Esfuerzo vertical debido al esfuerzo en punta El esfuerzo vertical que tiene que soportar la zapata debido al esfuerzo en punta "Fep" se obtiene: Fep = 0,5 · (Mep + Mev · f) / Base , en daN. Siendo: Mep = Momento producido por el esfuerzo en punta, en daN · m. Mev = Momento producido por el esfuerzo del viento sobre el apoyo, en daN · m. f = Factor que vale 1 si el coeficiente de seguridad del apoyo es normal y 1,25 si el coeficiente de seguridad es reforzado. Base = Base del apoyo, en m. Esfuerzo vertical debido a los pesos Sobre la zapata actuarán esfuerzos verticales debidos a los pesos, el valor será: FV = TV /4 + Pa /4 + Pt + Ph , en daN. Siendo: TV = Esfuerzos verticales del cálculo de los apoyos, en daN. Pa = Peso del apoyo, en daN. Pt = Peso de la tierra levantada, en daN. Ph = Peso del hormigón de la zapata, en daN. Esfuerzo total sobre la zapata El esfuerzo total que actúa sobre la zapata será: FT = Fep + FV , en daN. Siendo: Fep = Esfuerzo debido al esfuerzo en punta, en daN. FV = Esfuerzo debido a los esfuerzos verticales, en daN. Comprobación de las zapatas Si el esfuerzo total que actúa sobre la zapata tiende a levantar el macizo de hormigón, habrá que comprobar el coeficiente de seguridad ”Cs“, cuyo valor será: Cs = ( FV + Frt ) / Fep > 1,5 . Si el esfuerzo total que actúa sobre la zapata tiende a hundir el macizo de hormigón, habrá que comprobar que el terreno tiene la debida resistencia ”Rt“, cuyo valor será: Rt = FT / S , en daN/cm2 . Siendo: FV = Esfuerzo debido a los esfuerzos verticales, en daN. Frt = Esfuerzo de rozamiento de las tierras, en daN. Fep = Esfuerzo debido al esfuerzo en punta, en daN. FT = Esfuerzo total sobre la zapata, en daN. S = Superficie de la base del macizo, en cm2 . 1.7. CADENA DE AISLADORES. 1.7.1. Cálculo eléctrico El grado de aislamiento respecto a la tensión de la línea se obtiene colocando un número de aisladores suficiente "NAis", cuyo número se obtiene: NAis = Nia · Ume / Llf Siendo: NAis = número de aisladores de la cadena. Nia = Nivel de aislamiento recomendado según las zonas por donde atraviesa la línea (cm/kV). Ume = Tensión más elevada de la línea (kV). Llf = Longitud de la línea de fuga del aislador elegido (cm). 1.7.2. Cálculo mecánico Mecánicamente, el coeficiente de seguridad a la rotura de los aisladores "Csm" ha de ser mayor de 3. El aislador debe soportar las cargas normales que actúan sobre él. Csmv = Qa / (Pv+Pca) > 3 Siendo: Csmv = coeficiente de seguridad a la rotura de los aisladores con cargas normales. Qa = Carga de rotura del aislador (daN). Pv = El esfuerzo vertical transmitido por los conductores al aislador (daN). Pca = Peso de la cadena de aisladores y herrajes (daN). El aislador debe soportar las cargas anormales que actúan sobre él. Csmh = Qa / (Toh·ncf) > 3 Siendo: Csmh = coeficiente de seguridad a la rotura de los aisladores con cargas anormales. Qa = Carga de rotura del aislador (daN). Toh = Tensión horizontal máxima en las condiciones más desfavorables (daN). ncf = número de conductores por fase. 1.7.3. Longitud de la cadena La longitud de la cadena Lca será: Lca = NAis · LAis (m) Siendo: Lca = Longitud de la cadena (m). NAis = número de aisladores de la cadena. LAis = Longitud de un aislador (m). 1.7.4. Peso de la cadena El peso de la cadena Pca será: Pca = NAis · PAis (daN) Siendo: Pca = Peso de la cadena (daN). NAis = número de aisladores de la cadena. PAis = Peso de un aislador (daN). 1.7.5. Esfuerzo del viento sobre la cadena El esfuerzo del viento sobre la cadena Eca será: Eca = k · (DAis / 1000) · Lca (daN) Siendo: Eca = Esfuerzo del viento sobre la cadena (daN). k = 70 · (v/120)² . Según apdo 3.1.2.2. v = Velocidad del viento (Km/h). DAis = Diámetro máximo de un aislador (mm). Lca = Longitud de la cadena (m). 1.8. DISTANCIAS DE SEGURIDAD. 1.8.1. Distancia de los conductores al terreno La altura de los apoyos será la necesaria para que los conductores, con su máxima flecha vertical, queden situados por encima de cualquier punto del terreno o superficies de agua no navegables a una altura mínima de: D = Dadd + Del = 5,3 + Del (m), mínimo 6 m. Siendo: Dadd = Distancia de aislamiento adicional (m). Del = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase y objetos a potencial de tierra en sobretensiones de frente lento o rápido, según tabla 15 del apdo. 5.2 (m). 1.8.2. Distancia de los conductores entre sí La distancia de los conductores entre sí "D" debe ser como mínimo: D = k·√(F + L) + k' · Dpp (m). Siendo: k = Coeficiente que depende de la oscilación de los conductores con el viento, según tabla 16 del apdo. 5.4.1. L = Longitud de la cadena de suspensión (m). Si la cadena es de amarre L=0. F = Flecha máxima (m). k' = 0,75. Dpp = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase durante sobretensiones de frente lento o rápido, según tabla 15 del apdo. 5.2 (m). 1.8.3. Distancia de los conductores al apoyo La distancia mínima de los conductores al apoyo "ds" será de: ds = Del (m), mínimo de 0,2 m. Siendo: Del = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase y objetos a potencial de tierra en sobretensiones de frente lento o rápido, según tabla 15 del apdo. 5.2 (m). 1.9. ANGULO DE DESVIACION DE LA CADENA DE SUSPENSION. Debido al esfuerzo del viento sobre los conductores, las cadenas de suspensión en apoyos de alineación y de ángulo sufren una desviación respecto a la vertical. El ángulo máximo de desviación de la cadena "γ" no podrá ser superior al ángulo "µ" máximo permitido para que se mantenga la distancia del conductor al apoyo. tg γ = (Pv + Eca/2) / (P-XºC+V/2 + Pca/2) = Etv / Pt , en apoyos de alineación. tg γ = (Pv·cos[(180-α)/2] + Rav + Eca/2) / (P-XºC+V/2 + Pca/2) = Etv / Pt , en apoyos de ángulo. Siendo: tg γ = Tangente del ángulo que forma la cadena de suspensión con la vertical, al desviarse por la acción del viento. Pv = Esfuerzo de la mitad de la presión de viento sobre el conductor (120 km/h) (daN). Eca = Esfuerzo de la mitad de la presión de viento sobre la cadena de aisladores y herrajes (120 km/h) (daN). P-XºC+V/2 = Peso total del conductor que gravita sobre el apoyo en las condiciones de una Tª X (5 ºC en zona A, -10 ºC en zona B, -15 ºC en zona C) con sobrecarga mitad de la presión de viento (120 km/h) (daN). Pca = Peso de la cadena de aisladores y herrajes (daN). α = Angulo que forman los conductores de la línea (gr. sexa.). Rav = Resultante de ángulo en las condiciones de -5 ºC en zona A, -10 ºC en zona B y -15 ºC en zona C con sobrecarga mitad de la presión de viento (120 km/h) (daN). Si el valor del ángulo de desviación de la cadena "γ" es mayor del ángulo máximo permitido "µ", se deberá colocar un contrapeso de valor: G = Etv / tg µ - Pt 1.10. DESVIACION HORIZONTAL DE LAS CATENARIAS POR LA ACCION DEL VIENTO. dH = z · senα Siendo: dH = Desviación horizontal de las catenarias por la acción del viento (m). z = Distancia entre el punto de la catenaria y la recta de unión de los puntos de sujeción (m). α = Angulo que forma la resultante del viento con el peso propio del conductor. 2. DATOS GENERALES DE LA INSTALACION. Tensión de la línea: 20 kV. Tensión más elevada de la línea: 24 kV. Velocidad del viento: 120 km/h. Zonas: B. CONDUCTOR. Denominación: LA-56 (47-AL1/8-ST1A). Sección: 54.6 mm2 . Diámetro: 9.45 mm. Carga de Rotura: 1640 daN. Módulo de elasticidad: 7900 daN/mm2 . Coeficiente de dilatación lineal: 19.1 · 10-6 . Peso propio: 0.185 daN/m. Peso propio más sobrecarga de viento: 0,596 daN/m. Peso propio más sobrecarga con la mitad del viento: 0,339 daN/m. Peso propio más sobrecarga de hielo (Zona B): 0,738 daN/m. Peso propio más sobrecarga de hielo (Zona C): 1,292 daN/m. 3. DISTANCIAS DE SEGURIDAD. 3.1. Distancia de los conductores al terreno La altura de los apoyos será la necesaria para que los conductores, con su máxima flecha vertical, queden situados por encima de cualquier punto del terreno o superficies de agua no navegables a una altura mínima de. dstdes = Dadd + Del = 5,3 + 0,22 = 5,52 m.; mínimo 6m. dstdes = 6 m. dstais = 6 m. dstrec = 6 m. Siendo: Dadd = Distancia de aislamiento adicional, para asegurar el valor Del con el terreno. Del = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase y objetos a potencial de tierra en sobretensiones de frente lento o rápido. 3.2. Distancia de los conductores entre sí La distancia de los conductores entre sí D debe ser como mínimo: Ddes = k·√(F + L) + k´·Dpp Drec = 1/3·k·√(F + L) + k´·Dpp Siendo: k = Coeficiente que depende de la oscilación de los conductores con el viento, según tabla 16 del apdo. 5.4.1. L = Longitud de la cadena de suspensión (m). Si la cadena es de amarre L=0. F = Flecha máxima (m). Dpp = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase durante sobretensiones de frente lento o rápido. apoyo 1 Ddes = 0,65·√(4,22 + 0) + 0,75·0,25 = 1,52 m apoyo 2 Cruceta Principal Ddes = 0,65·√(4,22 + 0) + 0,75·0,25 = 1,52 m Cruceta de Derivación Ddes = 0,65·√(1,89 + 0) + 0,75·0,25 = 1,08 m apoyo 3 Ddes = 0,65·√(1,89 + 0,62) + 0,75·0,25 = 1,22 m apoyo 4 Ddes = 0,65·√(1,89 + 0) + 0,75·0,25 = 1,08 m apoyo 5 Ddes = 0,65·√(2,03 + 0) + 0,75·0,25 = 1,11 m apoyo 6 Ddes = 0,65·√(2,03 + 0) + 0,75·0,25 = 1,11 m 3.3. Distancia de los conductores al apoyo La distancia mínima de los conductores al apoyo dsa será de: dsa = Del = 0,22 m.; mínimo 0,2 m. dsa = 0,22 m. Siendo: Del = Distancia de aislamiento en el aire mínima especificada, para prevenir una descarga disruptiva entre conductores de fase y objetos a potencial de tierra en sobretensiones de frente lento o rápido. 4. ANGULO DE DESVIACION DE LA CADENA DE SUSPENSION. Debido al esfuerzo del viento sobre los conductores, las cadenas de suspensión en los apoyos sufren una desviación respecto a la vertical. El ángulo máximo de desviación de la cadena α no podrá ser superior al ángulo β máximo permitido para que se mantenga la distancia del conductor al apoyo. tg γ = (Pv + Eca/2) / (P-XºC+V/2 + Pca/2) = Etv / Pt , en apoyos de alineación. tg γ = (Pv·cos[(180-α)/2] + Rav+ Eca/2) / (P-XºC+V/2 + Pca/2) = Etv / Pt , en apoyos de ángulo. Siendo: tg γ = Tangente del ángulo que forma la cadena de suspensión con la vertical, al desviarse por la acción del viento. Pv = Esfuerzo de la mitad de la presión de viento sobre el conductor (120 km/h) (daN). Eca = Esfuerzo de la mitad de la presión de viento sobre la cadena de aisladores y herrajes (120 km/h) (daN). P-XºC+V/2 = Peso total del conductor que gravita sobre el apoyo en las condiciones de una Tª X (- 5 ºC en zona A, -10 ºC en zona B, -15 ºC en zona C) con sobrecarga mitad de la presión de viento (120 km/h) (daN). Pca = Peso de la cadena de aisladores y herrajes (daN). α = Angulo que forman los conductores de la línea (gr. sexa.). Rav = Resultante de ángulo en las condiciones de -5 ºC en zona A, -10 ºC en zona B y -15 ºC en zona C con sobrecarga mitad de la presión de viento (120 km/h) (daN). Si el valor del ángulo de desviación de la cadena "γ" es mayor del ángulo máximo permitido "µ", se deberá colocar un contrapeso de valor: G = Etv / tg µ - Pt Apoyos con cadenas de suspensión. apoyo 3 tg γ = (Pv + Eca/2) / (P-10ºC+V/2 + Pca/2) = (27,79 + 2,69/2) / (19,32 + 6,68/2) = 1,29. γ = 52,13º µ = 68,5º 5. TENSIONES Y FLECHAS EN HIPOTESIS REGLAMENTARIAS. Vano 1-2 2-3 3-4 2-5 5-6 Vano Conductor LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Conductor Longit. Desni. (m) (m) 152 0,65 152 453,6 543,5 98 1,1 98 467,6 545 98 0,5 98 467,6 545 101 -1,57 101 466,4 544,7 102 -3,03 102 465,4 544 Longit. (m) 1-2 2-3 3-4 2-5 5-6 Vano LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Conductor 2-3 3-4 2-5 5-6 LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Desni. (m) Vano Regula. (m) Hipótesis de Flecha Máxima 15ºC+V 50ºC 0ºC+H Th(daN) F(m) Th(daN) F(m) Th(daN) F(m) -20ºC+H+V Toh(daN) Hipótesis Flecha Mínima -5ºC -15ºC -20ºC F(m) F(m) F(m) 152 0,65 152 409,7 4,21 126,7 4,22 513,1 4,16 2,87 98 1,1 98 388,2 1,85 117,8 1,89 492,4 1,8 0,75 98 0,5 98 388,2 1,85 117,8 1,89 492,4 1,8 0,75 101 -1,57 101 389,7 1,95 118,5 1,99 493,8 1,91 0,83 102 -3,03 102 389,8 1,99 118,6 2,03 493,8 1,95 0,86 Longit. (m) 1-2 Vano Hipótesis de Tensión Máxima Regula. -5ºC+V -10ºC+V -15ºC+H -15ºC+H+V -15ºC+V -20ºC+H (m) Toh(daN) Toh(daN) Toh(daN) Toh(daN) Toh(daN) Toh(daN) Desni. (m) Vano Regula. (m) -5ºC+V Th(daN) Hipótesis de Cálculo Apoyos -10ºC+V -15ºC+H -15ºC+V -20ºC+H Th(daN) Th(daN) Th(daN) Th(daN) Desviación Cadenas Aisladores -5ºC+V/2 -10ºC+V/2 -15ºC+V/2 Th(daN) Th(daN) Th(daN) 152 0,65 152 453,6 543,5 292,4 98 1,1 98 467,6 545 349,2 98 0,5 98 467,6 545 349,2 101 -1,57 101 466,4 544,7 344,1 102 -3,03 102 465,4 544 341,8 6. TENSIONES Y FLECHAS DE TENDIDO. Vano 1-2 2-3 3-4 2-5 5-6 Conductor LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Vano 1-2 2-3 3-4 2-5 5-6 Conductor LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Vano 1-2 2-3 3-4 2-5 5-6 Conductor LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) LA-56 (47-AL1/8ST1A) Long. (m) Desni. (m) V.Reg. (m) -20ºC T(daN) F(m) -15ºC T(daN) F(m) -10ºC T(daN) F(m) -5ºC T(daN) F(m) 0ºC T(daN) F(m) 152 0,65 152 186,4 2,87 179,1 2,98 172,5 3,1 166,4 3,21 98 1,1 98 295,7 0,75 268,8 0,83 244,5 0,91 223,2 1 98 0,5 98 295,7 0,75 268,8 0,83 244,5 0,91 223,2 1 101 -1,57 101 285,1 0,83 259,7 0,91 237,1 1 217,2 1,09 102 -3,03 102 281 0,86 256,2 0,94 234,2 1,03 214,8 1,12 Long. (m) Desni. (m) V.Reg. (m) 5ºC T(daN) F(m) 10ºC T(daN) F(m) 15ºC T(daN) F(m) 20ºC T(daN) F(m) 25ºC T(daN) F(m) 152 0,65 152 160,9 3,32 155,9 3,43 151,2 3,54 146,9 3,64 142,9 3,74 98 1,1 98 204,5 1,09 188,4 1,18 174,6 1,27 162,7 1,37 152,5 1,46 98 0,5 98 204,5 1,09 188,4 1,18 174,6 1,27 162,7 1,37 152,5 1,46 101 -1,57 101 200 1,18 185 1,28 172,2 1,37 161,1 1,46 151,5 1,56 102 -3,03 102 198,1 1,22 183,6 1,31 171,1 1,41 160,3 1,5 150,9 1,6 Long. (m) Desni. (m) V.Reg. (m) 30ºC T(daN) F(m) 35ºC T(daN) F(m) 40ºC T(daN) F(m) 45ºC T(daN) F(m) 50ºC T(daN) F(m) EDS 152 0,65 152 139,2 3,84 135,7 3,94 132,5 4,04 129,5 4,13 126,7 4,22 9,22 98 1,1 98 143,6 1,55 135,9 1,63 129,1 1,72 123,1 1,81 117,8 1,89 10,65 98 0,5 98 143,6 1,55 135,9 1,63 129,1 1,72 123,1 1,81 117,8 1,89 10,65 101 -1,57 101 143,1 1,65 135,8 1,74 129,4 1,82 123,6 1,91 118,5 1,99 10,5 102 -3,03 102 142,7 1,69 135,6 1,78 129,2 1,86 123,6 1,95 118,6 2,03 10,43 7. CALCULO DE APOYOS. Apoyo Tipo Angulo Relativo Hipótesis 1ª (Viento) (-5:A/-10:B/-15:C)ºC+V gr.sexa. Fin Línea Estrellam. 1,1°; apo.3 Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI 1 2 3 4 5 6 Apoyo 1 2 3 4 5 6 Tipo Angulo Relativo V (daN) 60,5 161,3 77,2 T (daN) 145,7 1.592,8 205,4 L (daN) 1.360,8 28,3 1.402,8 49,5 99,6 102,6 175,5 35,5 103 Hipótesis 2ª (Hielo) (-15:B/-20:C)ºC+H Lt (daN) 2,8 463,3 247,4 1.598 288,4 T (daN) 1.598 136,9 L (daN) 1.630,4 2,6 Lt (daN) 8,1 1.634,9 288,4 1.396,2 84,5 Hipótesis 3ª (Desequilibrio de tracciones) (-5:A)ºC+V (-15:B/-20:C)ºC+H V (daN) T (daN) L (daN) Lt (daN) gr.sexa. Fin Línea Estrellam. 1,1°; apo.3 Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI V (daN) 181,7 463,3 247,4 2,6 146,8 698,9 8,1 1.631,9 Hipótesis 4ª (Rotura de conductores) Dist.Lt (-5:A)ºC+V (-15:B/-20:C)ºC+H V (daN) T (daN) L (daN) Lt (daN) (m) 127,8 634 1,5 433,2 1.213,4 10,2 462,3 1,5 1 2 3 Tipo Fin Línea Estrellam. Alin. Susp. Constitución Coefic. Segur. Celosia recto R Celosia recto R Celosia recto N Angulo (m) 1,52 1,52/1.08 1,22 98 454,1 1,5 1,08 234,5 453,9 1,5 1,11 63 453,3 1,5 1,11 8. APOYOS ADOPTADOS. Apoyo Dist.Min. Cond. Altura Esf. Esf. Esf.punta Esf.Ver. Total Nominal Secund. c.Tors. s.Tors. gr.sexa. (m) (daN) (daN) (daN) (daN) 12 3.000 800 16 4.500 3.000 800 10 500 600 Esf.Ver. c.Tors. (daN) 800 800 600 Esfuer. Dist. Torsión Torsión (daN) (m) 1.400 1,5 1.400 1,5 500 1,5 Peso (daN) 4 5 6 Fin Línea CTP Anc. Alin. Fin Línea CTI Celosia recto N Celosia recto R Celosia recto R 10 14 10 2.000 1.000 3.000 600 600 800 600 600 800 1.400 700 1.400 1,5 1,5 1,5 9. CRUCETAS ADOPTADAS. Apoyo 1 2 2 3 Tipo Fin Línea Estrellam. Estrellam. Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI 4 5 6 Constitución Celosia recto Celosia recto Celosia recto Celosia recto Montaje D.Cond. Cruceta Horizontal Atir. Tresbolillo Atir. Horizontal Bóveda Triang. (m) 1,75 2,33 1,25 2,07 a b c d e f g Brazo Brazo Brazo D.Vert. D.eje D.ref. Altura Superior Medio Inferior Brazos jabalcón jabalcón Tirante (m) (m) (m) (m) (m) (m) (m) 1,75 0,6 1 1 1,25 1,2 0,6 1,25 2 0,55 0,6 1 1,1 0,6 (daN) 80 75 55 195 55 Celosia recto Horizontal Atir. 1,25 1,25 Celosia recto Tresbolillo Atir. 2,33 1 Celosia recto Horizontal Atir. 1,25 1,25 0,6 1 1,25 1,2 Peso 0,6 75 0,6 55 10. CALCULO DE CIMENTACIONES. Apoyo 1 2 3 4 5 6 Apoyo 1 2 3 Tipo Esf.Util Alt.Libre Punta Apoyo (daN) (m) Fin Línea 3.000 9,95 Est.rel.lam, 4.500 13,6 A.lin, Susp. 500 8,8 Fin Línea 2.000 8,2 CTP Anc, Alin. 1.000 12,45 Fin Línea 3.000 8 CTI Tipo Fin Línea Estrellam. Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI 4 5 6 Mom.Producido Esf.Vie. Alt.Vie. Mom.Producido por el conduc. Apoyos Apoyos Viento Apoyos (daN.m) (daN) (m) (daN.m) 29.850 370,3 4,5 1.667,5 61.200 520 5,97 3.105,6 4.400 241,8 4,07 983,3 Momento Total Fuerzas externas (daN.m) 31.517,5 64.305,7 5.383,3 16.400 271,6 3,81 1.033,8 17.433,8 12.450 384,1 5,52 2.120,5 14.570,5 24.000 288,2 3,72 1.071,8 25.071,8 Volum. Horm. (m3) Peso Horm. (daN) Ancho Alto Cimen. Cimen. A(m) 1,24 1,45 1,1 MONOBLOQUE Coefic. Mom.Absorbido Comp. por la cimentac. (daN.m) H(m) (daN/m3) 2,3 10 52.902,37 2,65 10 107.920,83 1,45 10 8.989,64 1,07 2,05 10 28.956,78 1,36 1,8 10 24.952,69 1,09 2,25 10 41.898,04 ZAPATAS Dens. Peso Tierra Tierra 3 (Kg/m ) (daN) Volum. Tierra (m3) AISLADAS Esf.Roz. Esf. Tierra Montan. (daN) (daN) Esf. Vert. (daN) Coef. Seg. 11. CALCULO DE CADENAS DE AISLADORES. Apoyo 1 2 3 Fin Línea Estrellam. Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI 4 5 6 Apoyo 1 2 3 4 5 6 Tipo Tipo Fin Línea Estrellam. Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI Denom. U40B U40B U40B Qa (daN) 4.000 4.000 4.000 Diam. Aisl. (mm) 175 175 175 Llf (mm) 190 190 190 Long. Aisl. Peso Aisl. (m) (daN) 0,11 1,67 0,11 1,67 0,11 1,67 U40B 4.000 175 190 0,11 U40B 4.000 175 190 0,11 1,67 U40B 4.000 175 190 0,11 1,67 N.Cad. 3 C.Am. 9 C.Am. 3 C.Su. Denom. U40B U40B U40B N.Ais. 4 4 4 Nia Lca (cm/KV) (m) 2,5 0,62 2,5 0,62 2,5 0,62 L.Alarg. (m) 1,67 Pca (daN) 6,68 6,68 6,68 Eca (daN) 5,39 5,39 5,39 Pv+Pca Csmv (daN) 60,56 66,05 65,23 61,33 82,48 48,5 Toh · ncf Csmh (daN) 543,47 7,36 544,97 7,34 55,6 71,94 3 C.Am. U40B 4 2,5 0,62 6,68 5,39 45,65 87,63 544,97 7,34 6 C.Am. U40B 4 2,5 0,62 6,68 5,39 60,58 66,02 544,67 7,34 3 C.Am. U40B 4 2,5 0,62 6,68 5,39 28,18 141,94 543,97 7,35 Res.Cálc. Tierra (daN/cm2) 12. CALCULO DE ESFUERZOS VERTICALES SIN SOBRECARGA. Apoyo 1 2 3 4 5 6 Tipo Fin Línea Estrellam. Alin. Susp. Fin Línea CTP Anc. Alin. Fin Línea CTI Esf.Vert. -20ºC (daN) Esf.Vert. -15ºC Esf.Vert. -5ºC (daN) (daN) 59,9 60 163,3 162,6 79,9 79 51,7 51 108,2 106,3 23,3 27,5 Pliego de Condiciones Condiciones Generales 1. OBJETO. 2. CAMPO DE APLICACION. 3. DISPOSICIONES GENERALES. 3.1. CONDICIONES FACULTATIVAS LEGALES. 3.2. SEGURIDAD EN EL TRABAJO. 3.3. SEGURIDAD PUBLICA. 4. ORGANIZACION DEL TRABAJO. 4.1. DATOS DE LA OBRA. 4.2. REPLANTEO DE LA OBRA. 4.3. MEJORAS Y VARIACIONES DEL PROYECTO. 4.4. RECEPCION DEL MATERIAL. 4.5. ORGANIZACION. 4.6. FACILIDADES PARA LA INSPECCION. 4.7. ENSAYOS. 4.8. LIMPIEZA Y SEGURIDAD EN LAS OBRAS. 4.9. MEDIOS AUXILIARES. 4.10. EJECUCION DE LAS OBRAS. 4.11. SUBCONTRATACION DE OBRAS. 4.12. PLAZO DE EJECUCION. 4.13. RECEPCION PROVISIONAL. 4.14. PERIODOS DE GARANTIA. 4.15. RECEPCION DEFINITIVA. 4.16. PAGO DE OBRAS. 4.17. ABONO DE MATERIALES ACOPIADOS. 5. DISPOSICION FINAL. Condiciones Técnicas para la Obra Civil y Montaje de Líneas Eléctricas Aéreas de Alta Tensión 1. OBJETO Y CAMPO DE APLICACION. 2. EJECUCION DEL TRABAJO. 2.1. REPLANTEO DE LOS APOYOS. 2.2. APERTURA DE HOYOS. 2.3. TRANSPORTE, ACARREO Y ACOPIO A PIE DE HOYO. 2.4. CIMENTACIONES. 2.5. ARMADO E IZADO DE APOYOS. 2.6. PROTECCION DE LAS SUPERFICIES METALICAS. 2.7. TENDIDO, TENSADO Y ENGRAPADO DE LOS CONDUCTORES. 2.8. REPOSICION DEL TERRENO. 2.9. NUMERACION DE APOYOS. AVISOS DE PELIGRO ELECTRICO. 2.10. TOMAS DE TIERRA. 3. MATERIALES. 3.1. RECONOCIMIENTO Y ADMISION DE MATERIALES. 3.2. APOYOS. 3.3. HERRAJES. 3.4. AISLADORES. 3.5. CONDUCTORES. 4. RECEPCION DE OBRA. 4.1. CALIDAD DE CIMENTACIONES. 4.2. TOLERANCIAS DE EJECUCION. 4.3. TOLERANCIAS DE UTILIZACION. Medición MEDICION DE CONDUCTORES Designación(mm²) Total(m) LA-56 (47-AL1/8-ST1A) Pu(Euros) Ptotal(Euros) 1654.55 MEDICION DE CADENAS DE AISLADORES Designación Total(ud.) Pu(Euros) U40B-4 El. Ptotal(Euros) 27 MEDICION DE APOYOS Constitución Esf.Util Altura Total Celosía recto Celosía recto Celosía recto Celosía recto Celosía recto Celosía recto 3000 3000 4500 500 2000 1000 12 10 16 10 10 14 Total(ud.) Pu(Euros) Ptotal(Euros) 1 1 1 1 1 1 MEDICION DE CRUCETAS Constitución Esf.Max. Horizontal Atir. Horizontal Atir. Tresbolillo Atir. Horizontal Bóveda Triang 4500 4500 4500 4500 9000 Dist.Cond. 1.75 1.25 2.33 1.25 2.07 Total(ud.) Pu(Euros) Ptotal(Euros) 1 2 2 1 1 MEDICION DE CIMENTACIONES EXCAVACION Apoyo Excav.Pozo Zap.(m³) N.Zapatas 1 2 3 4 5 6 3.54 5.57 1.75 2.35 3.33 2.67 Pu(Euros) Ptotal(Euros) 1 1 1 1 1 1 HORMIGON Apoyo Vol.Horm.Zap.(m³) 1 2 3 4 5 6 3.97 6.17 2.1 2.67 3.85 3.01 N.Zapatas 1 1 1 1 1 1 Pu(Euros) Ptotal(Euros)