CONTENIDOS 1ERO-3ERO BACH
Anuncio
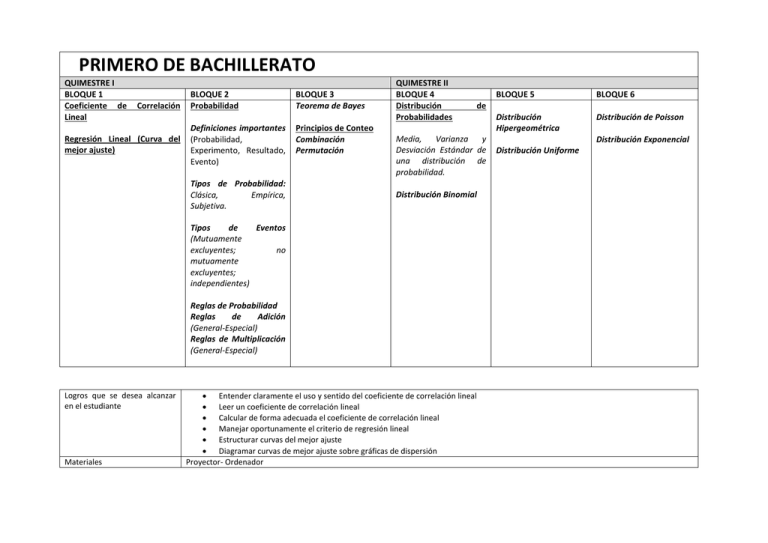
PRIMERO DE BACHILLERATO QUIMESTRE I BLOQUE 1 Coeficiente de Lineal Correlación Regresión Lineal (Curva del mejor ajuste) BLOQUE 2 Probabilidad BLOQUE 3 Teorema de Bayes Definiciones importantes (Probabilidad, Experimento, Resultado, Evento) Principios de Conteo Combinación Permutación Tipos de Probabilidad: Clásica, Empírica, Subjetiva. QUIMESTRE II BLOQUE 4 Distribución Probabilidades Media, Varianza y Desviación Estándar de una distribución de probabilidad. Distribución Binomial Tipos de Eventos (Mutuamente excluyentes; no mutuamente excluyentes; independientes) Reglas de Probabilidad Reglas de Adición (General-Especial) Reglas de Multiplicación (General-Especial) Logros que se desea alcanzar en el estudiante Materiales BLOQUE 5 BLOQUE 6 Distribución Hipergeométrica Distribución de Poisson de Entender claramente el uso y sentido del coeficiente de correlación lineal Leer un coeficiente de correlación lineal Calcular de forma adecuada el coeficiente de correlación lineal Manejar oportunamente el criterio de regresión lineal Estructurar curvas del mejor ajuste Diagramar curvas de mejor ajuste sobre gráficas de dispersión Proyector- Ordenador Distribución Exponencial Distribución Uniforme BLOQUE 1 Coeficiente de Correlación Lineal El coeficiente de correlación lineal “r”, es un estadígrafo adimensional que intenta demostrar si existe influencia de una variable llamada independiente sobre otra llamada dependiente, además intenta medir la proporcionalidad directa o inversa de una variable sobre otra. Sus valores pueden estar entre -1 y 1. RELACIÓN INVERSA NEGATIVA RELACIÓN DIRECTA POSITIVA -1 a -0.5 -0.5 a 0 0 a 0.5 0.5 a 1 FUERTE DÉBIL DÉBIL FUERTE 𝑟= 𝑆𝑆𝑥𝑦 √𝑆𝑆𝑥 ∗ 𝑆𝑆𝑦 2 (∑ ) 𝑋 𝑆𝑆𝑥 = ∑ 𝑋 2 − 𝑛 2 (∑ ) 𝑌 𝑆𝑆𝑦 = ∑ 𝑌 2 − 𝑛 ∑𝑋 ∗ ∑𝑌 𝑆𝑆𝑥𝑦 = ∑ 𝑋𝑌 − 𝑛 Pasos para calcular el coeficiente de correlación lineal 1. Encontrar valores de x al cuadrado 2. Encontrar valores de y al cuadrado 3. Encontrar la multiplicación de X por Y 4. Hallas sumatorias de X, Y, X2, Y2; XY. 5. Aplicar fórmulas de sumas de cuadrados. 6. Reemplazar en fórmula del coeficiente de correlación lineal 7. Obtener conclusiones de coeficiente Ejemplo 1: En una clase de Literatura el profesor Thompson, encuesta a sus alumnos sobre el tiempo de estudio previo al examen, esto lo hace antes de darles las calificaciones, su interés es conocer si existe alguna correlación entre las horas de estudio y la calificación. 𝑆𝑆𝑥 = 13.8 − 𝑟= 7.5 √2.55∗24.32 (7.5)2 5 = = 2.55 7.5 7.875 Alumno Horas de Calificación (Y) estudio (X) X^2 Y^2 XY A B C D E 2,5 1,5 1 0,5 2 9,6 7,6 6,2 3 8 6,25 2,25 1 0,25 4 92,16 57,76 38,44 9 64 24 11,4 6,2 1,5 16 7,5 34,4 13,8 261 59,1 𝑆𝑆𝑦 = 261 − (34.4)2 5 = 24.32 𝑆𝑆𝑥𝑦 = 59.1 − 10 Calificación = 7.5 El coeficiente de correlación lineal es positivo y fuerte, lo que quiere decir que existe una relación directa entre las horas de estudio y las calificaciones. A más horas de estudio más alta será la calificación, y viceversa, y que su valor sea próximo a 1, indica que existe una fuerte influencia de las horas de estudio respecto a las calificaciones. 12 8 6 4 2 0 0.5 5 = 0.95238 Gráfico de Dispersión 0 7.5∗34.4 1 Horas de Estudio 1.5 2 2.5 3 Ejemplo 2: La empresa “LADY GUADA” que se dedica a organizar eventos sociales, desea conocer si existe influencia entre la inversión mensual que se realiza en publicidad y el nivel de ingresos en eventos. 𝑆𝑆𝑥 = 330000 − 𝑟= 197500 √88000∗495000 (1100)2 5 = Mes Gasto Ventas (Y) Publicidad (X) X^2 Y^2 XY Mayo Junio Julio Agosto Septiembre $ 200,00 $ 250,00 $ 450,00 $ 150,00 $ 50,00 $ 1.200,00 $ 1.350,00 $ 1.600,00 $ 850,00 $ 750,00 40000 62500 202500 22500 2500 1440000 1822500 2560000 722500 562500 240000 337500 720000 127500 37500 1100 5750 330000 7107500 1462500 = 88000 197500 208710.32 𝑆𝑆𝑦 = 7107500 − (5750)2 5 = 495000 𝑆𝑆𝑥𝑦 = 1462500 − Ventas = 197500 El coeficiente de correlación lineal es positivo y fuerte, lo que quiere decir que existe una relación directa entre el gasto en publicidad y el nivel de ventas de un mes en específico. A más gasto en publicidad mayores ventas y viceversa, y que su valor sea próximo a 1, indica que existe una fuerte influencia del gasto en publicidad sobre las ventas mensuales. $ 1,800.00 $ 1,600.00 $ 1,400.00 $ 1,200.00 $ 1,000.00 $ 800.00 $ 600.00 $ 400.00 $ 200.00 $ 0.00 $ 50.00 5 = 0.9462 Gráfico de Dispersión $ 0.00 1100∗5750 $ 100.00 $ 150.00 $ 200.00 $ 250.00 $ 300.00 Gasto Publicidad $ 350.00 $ 400.00 $ 450.00 $ 500.00 Ejemplo 3: La empresa “Medias Don Gato”, que se dedica a la confección de medias desea conocer si existe una relación entre el nivel de ausentismo de sus empleados en un mes y su producción mensual. 𝑆𝑆𝑥 = 525 − 𝑟= (47)2 5 −3402 √83.2∗167720 = Mes Ausentismo (X) Producción en X^2 miles de pares (Y) Y^2 XY Agosto Septiembre Octubre Noviembre Diciembre 12 5 6 8 16 900 1250 1000 950 680 144 25 36 64 256 810000 1562500 1000000 902500 462400 10800 6250 6000 7600 10880 47 4780 525 4737400 41530 = 83.2 −3402 3735.54 𝑆𝑆𝑦 = 4737400 − (4780)2 5 = 167720 𝑆𝑆𝑥𝑦 = 41530 − 47∗4780 5 = −3402 = −0.9107 Gráfico de Dispersión 1400 El coeficiente de correlación lineal es negativo y fuerte, lo que quiere decir que existe una relación inversa entre el nivel de ausentismo mensual y el nivel de producción. A más ausentismo menor producción y viceversa, y que su valor sea próximo a -1, indica que existe una fuerte influencia del nivel de ausentismo sobre la producción mensual. Producción Mensual 1200 1000 800 600 400 200 0 0 2 4 6 8 10 Nivel de Ausentismo 12 14 16 18 Ejercicios de Tarea: En los siguientes ejercicios, calcule el coeficiente de correlación lineal, exprese sus conclusiones y trace el gráfico de dispersión. 1. Se desea conocer si existe correlación entre la edad de una persona y el tiempo que demora en recorrer 100 metros. Edad (años) 4 5 6 11 15 18 2. Tiempo (Seg) 27 25 26 23 20 19 ¿Qué relación existirá entre la cantidad de personas que entran diariamente a un local comercial y su nivel de ventas? Personas 20 40 30 15 29 50 Ventas $ 120,00 $ 250,00 $ 180,00 $ 130,00 $ 356,00 $ 500,00 3. Tome una muestra de 20 alumnos y mida su estatura y peso, calcule la correlación lineal, explique sus conclusiones y obtenga el gráfico de dispersión 4. Forme 4 muestras (ABCD) de n=10; con 100RAN# (Números aleatorios de una calculadora científica). Calcule el coeficiente de correlación lineal, explique su conclusión y grafique el diagrama de dispersión, para los pares de muestras AB; AC; AD; BC; BD; CD. 5. Cree 3 casos de estudio reales donde se pueda aplicar criterios de correlación lineal y resuélvalo. 6. Resuelva de forma analítica el siguiente ejercicio X 2𝑎 + 𝑏 3𝑎 𝑎2 + 𝑏 −1 −4𝑎 Y 3𝑎 − 2𝑏 4𝑏 5𝑏 −2𝑏 Regresión Lineal La regresión lineal es un proceso matemático que sirve para encontrar la curva del mejor ajuste, que representa una función lineal que intentan modelar el comportamiento más aproximado de los datos en una gráfica de dispersión. Además servirá para realizar pronósticos dentro del dominio de la gráfica. 𝑦̂ = 𝑏0 + 𝑏1 𝑥 𝑆𝑆𝑥𝑦 𝑏0 = 𝑆𝑆𝑥 𝑏1 = 𝑌̅ − 𝑏1 𝑋̅ Pasos para aplicar regresión lineal 1. Encontrar valores de x al cuadrado 2. Encontrar la multiplicación de X por Y 3. Hallas sumatorias de X, Y, X2, XY. 4. Aplicar fórmulas de sumas de cuadrados, de XY y de X. 5. Reemplazar en la fórmula de bo y en la fórmula de b1 ((pendiente)) 6. Formar curva del mejor ajusta 7. Graficar curva del mejor ajuste con los valores mínimo y máximo de los valores de X. 8. Pronosticar lo solicitado Ejemplo 1: En una clase de Literatura el profesor Thompson, encuesta a sus alumnos sobre el tiempo de estudio previo al examen, esto lo hace antes de darles las calificaciones, su interés es conocer si existe alguna correlación entre las horas de estudio y la calificación, y PRONOSTICAR cuánto sacará en nota un alumno que estudio 2.3 horas. 𝑆𝑆𝑥 = 13.8 − (7.5)2 Alumno Horas de Calificación (Y) estudio (X) X^2 Y^2 XY A B C D E 2,5 1,5 1 0,5 2 9,6 7,6 6,2 3 8 6,25 2,25 1 0,25 4 92,16 57,76 38,44 9 64 24 11,4 6,2 1,5 16 7,5 34,4 13,8 261 59,1 𝑆𝑆𝑥𝑦 = 59.1 − 7.5∗34.4 = 2.55 5 5 = 7.5 𝑏𝑜 = 𝑌̅ − 𝑏1 𝑋̅ = 6.88 − 2.94 ∗ 1.5=2.47 𝑦̂ = 2.47 + 2.94𝑥 CURVA DEL MEJOR AJUSTE: Gráfico de Dispersión 12 Pronóstico para 2.3 horas. 10 Calificación 𝑦̂ = 2.47 + 2.94(2.3) 𝑦̂ = 2.47 + 6.762 𝑦̂ = 9.23 y = 2,94x + 2,47 8 6 4 2 0 0 0.5 1 1.5 2 Horas de Estudio 2.5 3 𝑏1 = 𝑆𝑆𝑥𝑦 𝑆𝑆𝑥 = 7.5 2.55 = 2.94 Ejemplo 2: La empresa “LADY GUADA” que se dedica a organizar eventos sociales, desea conocer si existe influencia entre la inversión mensual que se realiza en publicidad y el nivel de ingresos en eventos. Y PRONOSTICAR cuál será su venta estimada con un gasto en publicidad de USD 380.00. 𝑆𝑆𝑥 = 330000 − (1100)2 5 Mes Gasto Ventas (Y) Publicidad (X) X^2 Y^2 XY Mayo Junio Julio Agosto Septiembre $ 200,00 $ 250,00 $ 450,00 $ 150,00 $ 50,00 $ 1.200,00 $ 1.350,00 $ 1.600,00 $ 850,00 $ 750,00 40000 62500 202500 22500 2500 1440000 1822500 2560000 722500 562500 240000 337500 720000 127500 37500 1100 5750 330000 7107500 1462500 = 88000 𝑆𝑆𝑥𝑦 = 1462500 − 1100∗5750 5 = 197500 𝑏1 = 𝑆𝑆𝑥𝑦 𝑆𝑆𝑥 = 197500 88000 𝑏𝑜 = 𝑌̅ − 𝑏1 𝑋̅ = 1150 − 2.24 ∗220 = 657.2 CURVA DEL MEJOR AJUSTE: 𝑦̂ = 657.2 + 2.24𝑥 Ventas Gráfico de Dispersión $ 1,800.00 $ 1,600.00 $ 1,400.00 $ 1,200.00 $ 1,000.00 $ 800.00 $ 600.00 $ 400.00 $ 200.00 $ 0.00 $ 0.00 Pronóstico para un gasto de USD 380.00 y = 2,2443x + 657,2 $ 100.00 $ 200.00 $ 300.00 Gasto Publicidad 𝑦̂ = 657.20 + 2.24(380) 𝑦̂ = 657.20 + 851.12 𝑦̂ = 1508.40 $ 400.00 $ 500.00 = 2.24 Ejemplo 3: La empresa “Medias Don Gato”, que se dedica a la confección de medias desea conocer si existe una relación entre el nivel de ausentismo de sus empleados en un mes y su producción mensual. Se desea PRONOSTICAR el nivel de producción si se logra establecer el ausentismo en 7 personas por mes. 𝑆𝑆𝑥 = 525 − (47)2 5 Mes Ausentismo (X) Producción en X^2 miles de pares (Y) Y^2 XY Agosto Septiembre Octubre Noviembre Diciembre 12 5 6 8 16 900 1250 1000 950 680 144 25 36 64 256 810000 1562500 1000000 902500 462400 10800 6250 6000 7600 10880 47 4780 525 4737400 41530 = 83.2 𝑆𝑆𝑥𝑦 = 41530 − 47∗4780 5 = −3402 𝑏1 = 𝑆𝑆𝑥𝑦 𝑆𝑆𝑥 = −3402 83.2 = −40.88 𝑏𝑜 = 𝑌̅ − 𝑏1 𝑋̅ = 956 + 40.88 ∗9.4 = 1340.27 𝑦̂ = 1340.27 − 40.88𝑥 CURVA DEL MEJOR AJUSTE: Gráfico de Dispersión Pronóstico para ausentismo de 7 personas por mes. Producción Mensual 1400 𝑦̂ = 1340.27 − 40.88(7) 𝑦̂ = 1340.27 − 286.16 𝑦̂ =1054.11 1200 1000 800 600 y = -40.889x + 1340.4 400 200 0 0 2 4 6 8 10 Nivel de Ausentismo 12 14 16 18 Ejercicios de Tarea: En los siguientes ejercicios, calcule el coeficiente de correlación lineal, exprese sus conclusiones y trace el gráfico de dispersión. 1. Se desea conocer si existe correlación entre la edad de una persona y el tiempo que demora en recorrer 100 metros. PRONOSTIQUE EL TIEMPO PARA EDAD 13 AÑOS. Edad (años) 3 5 6 11 16 18 2. Tiempo (Seg) 27 25 26 23 20 19 ¿Qué relación existirá entre la cantidad de personas que entran diariamente a un local comercial y su nivel de ventas? PRONOSTIQUE LAS VENTAS PARA UN INGRESO DE 36 PERSONAS. Personas 22 40 32 15 29 55 Ventas $ 120,00 $ 250,00 $ 180,00 $ 130,00 $ 356,00 $ 500,00 1. Tome una muestra de 20 alumnos y mida su estatura y peso, calcule la correlación lineal, explique sus conclusiones y obtenga el gráfico de dispersión. PRONOSTIQUE EL PESO PARA UNA ESTATURA DE 1.65M. 2. Forme 4 muestras (ABCD) de n=10; con 50RAN# (Números aleatorios de una calculadora científica). Calcule el coeficiente de correlación lineal, explique su conclusión y grafique el diagrama de dispersión, para los pares de muestras AB; AC; AD; BC; BD; CD. ENCUENTRE EN TODOS LOS CASOS LA CURVA DEL MEJOR AJUSTE. 3. Cree 3 casos de estudio reales donde se pueda aplicar criterios de REGRESIÓN LINEAL 4. Resuelva de forma analítica el siguiente ejercicio X Y 2𝑎 3𝑎 3𝑎 4𝑏 𝑏 −1 5𝑏 −4𝑎 −2𝑏 BLOQUE 2 Probabilidad Se define como la posibilidad de que un evento suceda o no. Está representada por un valor entre 0 y 1, que se pueden aproximar a porcentajes multiplicando por 100 y agregando el símbolo %. No existen probabilidades negativas. Si una probabilidad llega a ser 1 quiere decir que es cierta, siempre sucederá, por ejemplo, la probabilidad de que sienta hambre luego de transcurridas 15 horas sin ingerir ningún alimento. Si una probabilidad es muy cercana a cero la llamamos débil y quiere decir que es muy poco probable que ese evento ocurra. Si una probabilidad es próxima a 0.5, es una probabilidad medio o incierta, que no estamos seguros si puede o no ocurrir. Definiciones importantes Experimento: Es el conjunto de condiciones controlados que se crean para medir o comprobar un supuesto. Evento: Son los acciones que se presentan como resultado de un experimento. Resultado: Afirmaciones o negaciones dadas por los eventos provenientes de un experimento. Ejemplo Experimento: Preparar las hojas de tabulación de datos, y recolectar edades de alumnos. Evento: La mayoría de hombres no quisieron responder. Resultado: La mayor cantidad de personas encuestadas fueron mujeres con un promedio de 17.5 años por estudiante. Tipos de Probabilidad: Clásica, Empírica, Subjetiva. Subjetiva: Es aquella que nunca ha sucedido antes, está basada en la intuición de las personas, conociendo otro tipo de datos, por ejemplo: La probabilidad de que una mujer sea presidenta de los Estados Unidos. Empírica: Se presenta cuando se realiza un análisis de datos históricos, que han sucedido en tiempo s anteriores, y nos permiten realizar una aproximación de pronósticos. Por ejemplo: En cierta población, el año anterior nacieron 50 bebes, de los cuales 40 eran mujeres y 10 hombres; por lo que se dice que existe una probabilidad de 80% de que en el año siguiente nazcan mujeres y un 20% para hombres. Clásica: Es la más común, y basa su cálculo en las observaciones tangibles o constantes durante una observación, es equivalente al número de éxitos dividido para el número de total de observaciones, por ejemplo: Pensemos que tenemos una mano de 5 barajas donde 2 de las mismas son cartas altas y 3 son cartas bajas, la probabilidad de sacar una carta alta es 2 de 5 (40%) y la probabilidad de obtener una carta alta es 3 de 5 (60%) Tipos de Eventos (Mutuamente excluyentes; no mutuamente excluyentes; independientes) Los eventos pueden ser mutuamente excluyentes cuando no podrían suceder al mismo tiempo, y lógicamente en un diagrama de VEN se encuentran separados, por ejemplo: La probabilidad de encontrar un auto que sea moto, los eventos ser auto y ser moto, son mutuamente excluyentes, porque no existe una máquina que al mismo tiempo pueda ser auto y pueda ser moto. AUTO MOTO Nótese que no hay intersección porque no existirían elementos que compartan las dos características. Los eventos no mutuamente excluyentes son aquellos que pueden suceder al mismo tiempo, regularmente cruzan variables de diferente caracterización, por ejemplo: Que un automóvil pase frente a nosotros y sea Verde o Deportivo, en este caso existen autos verdes que no son deportivos, autos deportivos que no son verdes, y también existen autos deportivos que si son verdes, por lo tanto el diagrama se dibuja con alguna interesección. AUTO DEPORTIVO AUTO VERDE Reglas de Probabilidad Las reglas de probabilidad son parámetros que deben ser aplicados siempre que se note casos específicos de eventos mutuamente excluyentes o no mutuamente excluyentes, al igual forma que eventos dependientes e independientes. Reglas de Adición Las reglas de adición se deben usar cuando se desea comprobar la probabilidad de que dos eventos sucendan en tiempos diferentes, es decir el uno o el otro pero no los dos al mismo tiempo. La Regla General dice que si se desea calcular que puedan suceder dos eventos que son mutuamente excluyentes, se deben sumar las probabilidades. La Regla Especial dice que si se desea calcular que puedan suceder dos eventos que son NO mutuamente excluyentes, se deben sumar las probabilidades y restar la multiplicación de las mismas, es decir restar la intersección. Reglas de Multiplicación Las reglas de multiplicación se deben usar cuando se desea comprobar la probabilidad de que dos eventos sucedan al mismo tiempo. La Regla General se debe utilizar para eventos independientes, es decir que la ocurrencia del uno afecta en nada a la ocurrencia del otro. P(A y B) = P(A) * P(B) La Regla Especial, se utiliza para eventos dependientes donde la ocurrencia de un evento afecta a que el otro pueda o no suceder. P(A/B)= P(A)*P(B/A) se lee como al probabilidad de A dado que B sucedió. Ejercicio de Probabilidad: 1. Una urna tiene ocho bolas rojas, 5 amarilla y siete verdes. Si se extrae una bola al azar calcular la probabilidad de: a. Sea roja. b. Sea verde. c. Sea amarilla. d. No sea roja. e. No sea amarilla. 2. Se extrae una bola de una urna que contiene 4 bolas rojas, 5 blancas y 6 negras, ¿cuál es la probabilidad de que la bola sea roja o blanca? ¿Cuál es la probabilidad de que no sea blanca? 3. En una clase hay 10 alumnas rubias, 20 morenas, cinco alumnos rubios y 10 morenos. Un día asisten 45 alumnos, encontrar la probabilidad de que un alumno: a. Sea hombre. b. Sea mujer morena. c. Sea hombre o mujer. 4. Un dado está trucado, de forma que las probabilidades de obtener las distintas caras son proporcionales a los números de estas. Hallar: a. La probabilidad de obtener el 6 en un lanzamiento. b. La probabilidad de conseguir un número impar en un lanzamiento. c. Se lanzan dos dados al aire y se anota la suma de los puntos obtenidos. Se pide: d. La probabilidad de que salga el 7. e. La probabilidad de que el número obtenido sea par. f. La probabilidad de que el número obtenido sea múltiplo de tres. 5. Se lanzan tres dados. Encontrar la probabilidad de que: a. alga 6 en todos. b. Los puntos obtenidos sumen 7. 6. Hallar la probabilidad de que al levantar unas fichas de dominó se obtenga un número de puntos mayor que 9 o que sea múltiplo de 4. 7. Busca la probabilidad de que al echar un dado al aire, salga: a. Un número par. b. Un múltiplo de tres. c. Mayor que cuatro. 8. Hallar la probabilidad de que al lanzar al aire dos monedas, salgan: a. Dos caras. b. Dos cruces. c. Una cara y una cruz. 9. En un sobre hay 20 papeletas, ocho llevan dibujado un coche las restantes son blancas. Hallar la probabilidad de extraer al menos una papeleta con el dibujo de un coche: a. Si se saca una papeleta. b. Si se extraen dos papeletas. c. Si se extraen tres papeletas. SEGUNDO DE BACHILLERATO QUIMESTRE I BLOQUE 1 BLOQUE 2 BLOQUE 3 Distribución Normal Función Campana de Gauss Aproximación Normal a Binomial Teorema central Áreas bajo la curva Métodos de Muestreo El Emprendedor Cree una idea de negocio ¿Qué es un emprendedor? Descubra su vocación ¿Quién es emprender? Desarrollo de un banco de ideas Análisis subjetivo de las oportunidades de las ideas del límite QUIMESTRE II BLOQUE 4 BLOQUE 5 BLOQUE 6 Intervalos de Confianza Para medias poblacionales Intervalos de Confianza Para proporciones poblacionales Aplicación del Factor de Corrección poblacional Tamaño adecuado de la muestra Estudio de las oportunidades para las ideas de negocio Costos Inversión Plan financiero Directos Gastos pre-operativos Plan de costos y ventas Mercado Indirectos Gastos operativos Utilidades Clientes Precios Fuentes financiamiento Estudio de los requerimientos para la empresa seleccionada Personal humano Recursos materiales Recursos técnicos Materiales Flujo de caja Demanda Competencia Logros que se desea alcanzar en el estudiante de Conocer todas las propiedades del distribución normal Encontrar áreas bajo la curva de distribución normal para resolver problemas EMPRENDIMIENTO Conocer si tienen un perfil emprendedor Ubicar sus mayores fortalezas como potenciales emprendedores Reconocer las oportunidades del entorno en el que desean emprender Proyector- Ordenador Forma legal empresa de la Bloque 1 Distribución Normal La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar. Propiedades de la distribución normal: La distribución normal posee ciertas propiedades importantes que conviene destacar: Tiene una única moda, que coincide con su media y su mediana. La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre a 1. Es simétrica con respecto a su media . Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor. La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica ( ). Cuanto mayor sea , más aplanada será la curva de la densidad. La forma de la campana de Gauss depende de los parámetros y (Figura 3). La media indica la posición de la campana, de modo que para diferentes valores y es teóricamente posible. El área total bajo la curva es, por tanto, igual de la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución. Es importante conocer que, a partir de cualquier variable X que siga una distribución estándar, sin más que efectuar la transformación: , se puede obtener otra característica Z con una distribución normal Áreas Bajo la Curva Normal A través de métodos de integración se pude encontrar el área bajo la curva normal, sin embargo estos ya están plasmados en la tabla Z, donde una vez estandarizados los valores se debe encontrar el entero y el primero decimal en la columna y el segundo decimal en las filas, y el valor que coincida entre los dos es el área bajo la curva, desde la media hasta el valor estandarizado. TABLA DE ÁREAS Z Z 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 0 0,0000 0,0398 0,0793 0,1179 0,1554 0,1915 0,2257 0,2580 0,2881 0,3159 0,3413 0,3643 0,3849 0,4032 0,4192 0,4332 0,4452 0,4554 0,4641 0,4713 0,4772 0,4821 0,4861 0,4893 0,4918 0,4938 0,4953 0,4965 0,4974 0,4981 0,4987 0,01 0,0040 0,0438 0,0832 0,1217 0,1591 0,1950 0,2291 0,2611 0,2910 0,3186 0,3438 0,3665 0,3869 0,4049 0,4207 0,4345 0,4463 0,4564 0,4649 0,4719 0,4778 0,4826 0,4864 0,4896 0,4920 0,4940 0,4955 0,4966 0,4975 0,4982 0,4987 0,02 0,0080 0,0478 0,0871 0,1255 0,1628 0,1985 0,2324 0,2642 0,2939 0,3212 0,3461 0,3686 0,3888 0,4066 0,4222 0,4357 0,4474 0,4573 0,4656 0,4726 0,4783 0,4830 0,4868 0,4898 0,4922 0,4941 0,4956 0,4967 0,4976 0,4982 0,4987 0,03 0,0120 0,0517 0,0910 0,1293 0,1664 0,2019 0,2357 0,2673 0,2967 0,3238 0,3485 0,3708 0,3907 0,4082 0,4236 0,4370 0,4484 0,4582 0,4664 0,4732 0,4788 0,4834 0,4871 0,4901 0,4925 0,4943 0,4957 0,4968 0,4977 0,4983 0,4988 0,04 0,0160 0,0557 0,0948 0,1331 0,1700 0,2054 0,2389 0,2704 0,2995 0,3264 0,3508 0,3729 0,3925 0,4099 0,4251 0,4382 0,4495 0,4591 0,4671 0,4738 0,4793 0,4838 0,4875 0,4904 0,4927 0,4945 0,4959 0,4969 0,4977 0,4984 0,4988 0,05 0,0199 0,0596 0,0987 0,1368 0,1736 0,2088 0,2422 0,2734 0,3023 0,3289 0,3531 0,3749 0,3944 0,4115 0,4265 0,4394 0,4505 0,4599 0,4678 0,4744 0,4798 0,4842 0,4878 0,4906 0,4929 0,4946 0,4960 0,4970 0,4978 0,4984 0,4989 0,06 0,0239 0,0636 0,1026 0,1406 0,1772 0,2123 0,2454 0,2764 0,3051 0,3315 0,3554 0,3770 0,3962 0,4131 0,4279 0,4406 0,4515 0,4608 0,4686 0,4750 0,4803 0,4846 0,4881 0,4909 0,4931 0,4948 0,4961 0,4971 0,4979 0,4985 0,4989 0,07 0,0279 0,0675 0,1064 0,1443 0,1808 0,2157 0,2486 0,2794 0,3078 0,3340 0,3577 0,3790 0,3980 0,4147 0,4292 0,4418 0,4525 0,4616 0,4693 0,4756 0,4808 0,4850 0,4884 0,4911 0,4932 0,4949 0,4962 0,4972 0,4979 0,4985 0,4989 0,08 0,0319 0,0714 0,1103 0,1480 0,1844 0,2190 0,2517 0,2823 0,3106 0,3365 0,3599 0,3810 0,3997 0,4162 0,4306 0,4429 0,4535 0,4625 0,4699 0,4761 0,4812 0,4854 0,4887 0,4913 0,4934 0,4951 0,4963 0,4973 0,4980 0,4986 0,4990 0,09 0,0359 0,0753 0,1141 0,1517 0,1879 0,2224 0,2549 0,2852 0,3133 0,3389 0,3621 0,3830 0,4015 0,4177 0,4319 0,4441 0,4545 0,4633 0,4706 0,4767 0,4817 0,4857 0,4890 0,4916 0,4936 0,4952 0,4964 0,4974 0,4981 0,4986 0,4990 Ejemplo: Se sabe que los pesos de un grupo de estudiantes se distribuyen normalmente, con una media de 70Kg, y desviación estándar de 4.8Kg. Si se selecciona uno al azar cual es la probabilidad de que este: a) Se de peso mayor que 75Kg b) Pese entre 62 y 73Kg c) Pese menos de 60Kg Z 1,04 Área Z=1,04 0,3508 Cola superior 0,1492 x=62 x=73 Z -1,67 Z 0,63 Área Z=1,04 0,4525 Área Z=1,04 0,2357 Área Total 0,6882 x=60 Z -2,08 Área Z=1,04 0,4812 Cola inferior 0,0188 Ejercicios: 1. En una distribución normal de media 4 y desviación típica 2, calcular el valor de a para que: P(X ≤ 0.5934) 2. En una ciudad se estima que la temperatura máxima en el mes de junio sigue una distribución normal, con media 23° y desviación típica 5°. Calcular el número de días del mes en los que se espera alcanzar máximas entre 21° y 27°. 3. La media de los pesos de 500 estudiantes de un colegio es 70 kg y la desviación típica 3 kg. Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan: a. b. c. d. Entre 60 kg y 75 kg. Más de 90 kg. Menos de 64 kg. 55.64 kg o menos. 4. Se supone que los resultados de un examen siguen una distribución normal con media 78 y desviación típica 36. Se pide: a. ¿Cuál es la probabilidad de que una persona que se presenta el examen obtenga una calificación superior a 72? b. Si se sabe que la calificación de un estudiante es mayor que 72 ¿cuál es la probabilidad de que su calificación sea, de hecho, superior a 84? 5. Tras un test de cultura general se observa que las puntuaciones obtenidas siguen una distribución una distribución N(65, 18). Se desea clasificar a los examinados en tres grupos (de baja cultura general, de cultura general aceptable, de excelente cultura general) de modo que hay en el primero un 20% la población, un 65% el segundo y un 15% en el tercero. ¿Cuáles han de ser las puntuaciones que marcan el paso de un grupo al otro? 6. Varios test de inteligencia dieron una puntuación que sigue una ley normal con media 100 y desviación típica 15. a. b. c. Determinar el porcentaje de población que obtendría un coeficiente entre 95 y 110. ¿Qué intervalo centrado en 100 contiene al 50% de la población? En una población de 2500 individuos ¿cuántos individuos se esperan que tengan un coeficiente superior a 125? DESARROLLO DE EMPRENDEDORES ¿Qué es un emprendedor? Es un individuo que es capaz de acometer un proyecto rechazado por la mayoría. Sabe interpretar las características reales del entorno a pesar de que no son aparentes. Es capaz de luchar ante cualquier inconveniente que se les atraviesa a su estrategia y no le teme al fracaso. Además, es capaz de crear un grupo con motivación suficiente que le da el apoyo que necesita. "Un emprendedor es alguien que "acomete" un proyecto que implica trabajo o presenta dificultades; toda persona que tenga iniciativa y decisión de llevar adelante un proyecto empresarial " El emprendedor empresarial además de haber llevado adelante el proyecto, este debe reportarles un beneficio comercial. Los proyectos militares, científicos o educativos reportan beneficios pero no económicos sino sociales. La naturaleza del proyecto empresarial está enraizada en el mercado. Debe satisfacer una necesidad expresada por el mercado. "El emprendedor modelo tiene una gran necesidad de realización personal. Es una persona con ilusiones, llena de energía y de creatividad, tiene confianza en sí mismo, se compromete entera y totalmente. Ama los riesgos moderados y quiere ser independiente y autónomo. Estas características se encuentran en diferentes grados en cualquier emprendedor. No es que todos los individuos los posean, sin embargo en nuestra sociedad, existe un buen número de personas que pueden convertirse en emprendedores, en una proporción semejante a la que tienen otras ciudades, esto es, alrededor del 10% de la población. Si el número de empresas correspondiera al de las personas que tienen las características básicas de los emprendedores, habría al menos un 50% más de empresas de las que hay ahora" La función específica de los emprendedores es la capacidad para tomar los factores de la producción -tierra, trabajo y capital- y usarlos para producir bienes o servicios nuevos. El emprendedor percibe oportunidades que otros ejecutivos de empresas no ven o no les interesan. Algunos emprendedores usan información, al alcance de todos, para producir algo nuevo. "Básicamente, el emprendedor detecta una necesidad y, después, reúne la mano de obra, los materiales y el capital que se necesita para satisfacer esa necesidad." En esencia, un emprendedor crea una organización como medio para ofrecer algo nuevo a los clientes, empleados u otros grupos de interés. Características de un Emprendedor Búsqueda de oportunidades e iniciativa o ¿Qué oportunidades se desarrollarían en su barrio o con grupos de amigos? Persistencia o ¿Por qué creen que es importante persistir? Cumplimiento o ¿Es necesario cuantificar las metas? Exigir eficiencia y calidad o ¿Al hacer algo es importante la calidad de esto? Correr riesgos calculados o ¿Por qué debemos calcular los riesgos? ¿Cómo podemos hacerlo? Fijar metas o ¿Cómo se pueden plantear metas? ¿Siempre deben ser las mismas? Búsqueda de información o ¿Por qué es importante información de primera mano? Planificación sistemática y seguimiento o ¿Qué rol cumple la planificación en el emprendimiento? Persuasión y redes de apoyo o ¿Para qué asociarse? ¿Es bueno? Autoconfianza e independencia o ¿Si emprendo algo es posible que me vaya bien o mal inicialmente? ¿Por qué? Ejercicios de aplicación: Realizar el TEST propuesto en el link http://www.unet.edu.ve/~ilabarca/test1.htm e imprimir el resultado. Investigue en su comunidad o región personas que han emprendido y sus resultados. Encueste a un emprendedor y pregúntele: ¿Qué fue lo más complejo al inicio del emprendimiento? ¿Cómo venció el temor al emprender? ¿Volvería a emprender en otro campo? ¿Cuál fue su mejor y su peor decisión al momento de emprender? Investigue en la revista Líderes un emprendimiento y realice un comentario de esto (cada lunes se publica la revista, esta es una tarea continua) Visite el Link http://www.100ideasparaemprender.com/home/ y escoja un tipo de emprendimiento y coméntelo (exposición en clase.) BLOQUE 2 Aproximación Normal a Binomial. Una distribución binomial B(n,p) se puede aproximar por una distribución normal, siempre que n sea grande y p no esté muy próxima a 0 o a 1. La aproximación consiste en utilizar una distribución normal con la misma media y desviación típica que la distribución binomial. Condiciones de uso de la aproximación Modelo Supóngase una distribución de probabilidad binomial, con n = 40 y u = 0.55. Calcule lo siguiente: a. La media y la desviación estándar de la variable aleatoria. b. La probabilidad de que x sea igual o superior a 25. c. La probabilidad de que x sea igual o inferior a 15. d. La probabilidad de que x este entre 15 y 25 , inclusive Un estudio realizado por el club de acondicionamiento físico Taurus Health club, revelo que 30% de sus socios nuevos tienen sobrepeso considerable. Una promoción para membrecías en la zona metropolitana dio como resultado la descripción de 500 socios nuevo. a) Se ha planteado utilizar la aproximación normal a la binomial para determinar la probabilidad de que 175 o más de los miembros nuevos tengan sobrepeso considerable. ¿Se puede calificar este problema como binomial? Explique su respuesta. Sí, porque existen dos resultados posibles el uno que tienen sobrepeso y el otro que no tienen sobrepeso. - El número de éxitos es el resultado de socios con sobrepeso. - Los ensayos son independientes. - Su probabilidad va a ser igual en los ensayos que es 0,3 b) ¿Cuál es la probabilidad de que 175 o más de los sociosnuevos tengan sobrepeso? c) ¿Cuál es la probabilidad de que 140 o más de los socios recientes tengan sobrepeso? La empresa de asuntos fiscales Theresa Tax Service se especializa en la elaboración de declaraciones de impuestos de clientes profesionales (médicos, dentistas, contadores, abogados). Una auditoria reciente de las declaraciones indicó que 5% de las declaraciones del año anterior preparadas por la empresa tenían algún error. Suponiendo que la tasa continúe en este año, y la empresa elaboró 60 declaraciones, cuál es la probabilidad de que cometa algún error en: a. Más de 6 declaraciones? b. Al menos 6 declaraciones? c. Exactamente 6 declaraciones? Métodos de Muestreo. Llamamos muestreo al efecto de tomar una muestra, debido a que es imposible estudiar poblaciones completas, y para realizarlo se debe tomar en cuenta la naturaleza de las pruebas y el tamaño de la población, se puede realizar en los siguientes modelos: Aleatorio Simple, Sistemático, Estratificado y por Conglomerados. Muestreo aleatorio simple Una muestra aleatoria simple es seleccionada de tal manera que cada muestra posible del mismo tamaño tiene igual probabilidad de ser seleccionada de la población. Para obtener una muestra aleatoria simple, cada elemento en la población tiene la misma probabilidad de ser seleccionado, el plan de muestreo puede no conducir a una muestra aleatoria simple. Por conveniencia, este método pude ser reemplazado por una tabla de números aleatorios. Cuando una población es infinita, es obvio que la tarea de numerar cada elemento de la población es infinita, es obvio que la tarea de numerar cada elemento de la población es imposible. Por lo tanto, ciertas modificaciones del muestreo aleatorio simple son necesarias. Los tipos más comunes de muestreo aleatorio modificado son sistemáticos, estratificados y de conglomerados. Muestreo sistemático. Una muestra sistemática es obtenida cuando los elementos son seleccionados en una manera ordenada. La manera de la selección depende del número de elementos incluidos en la población y el tamaño de la muestra. El número de elementos en la población es, primero, dividido por el número deseado en la muestra. El cociente indicará si cada décimo, cada onceavo, o cada centésimo elemento en la población van a ser seleccionado. El primer elemento de la muestra es seleccionado al azar. Por lo tanto, una muestra sistemática puede dar la misma precisión de estimación acerca de la población, que una muestra aleatoria simple cuando los elementos en la población están ordenados al azar. Muestreo Estratificado Para obtener una muestra aleatoria estratificada, primero se divide la población en grupos, llamados estratos, que son más homogéneos que la población como un todo. Los elementos de la muestra son entonces seleccionados al azar o por un método sistemático de cada estrato. Las estimaciones de la población, basadas en la muestra estratificada, usualmente tienen mayor precisión (o menor error muestral) que si la población entera muestreada mediante muestreo aleatorio simple. El número de elementos seleccionado de cada estrato puede ser proporcional o desproporcional al tamaño del estrato en relación con la población. Muestreo de conglomerados. Para obtener una muestra de conglomerados, primero dividir la población en grupos que son convenientes para el muestreo. En seguida, seleccionar una porción de los grupos al azar o por un método sistemático. Finalmente, tomar todos los elementos o parte de ellos al azar o por un método sistemático de los grupos seleccionados para obtener una muestra. Bajo este método, aunque no todos los grupos son muestreados, cada grupo tiene una igual probabilidad de ser seleccionado. Por lo tanto la muestra es aleatoria. Una muestra de conglomerados, usualmente produce un mayor error muestral (por lo tanto, da menor precisión de las estimaciones acerca de la población) que una muestra aleatoria simple del mismo tamaño. Los elementos individuales dentro de cada "conglomerado" tienden usualmente a ser iguales. Por ejemplo la gente rica puede vivir en el mismo barrio, mientras que la gente pobre puede vivir en otra área. No todas las áreas son muestreadas en un muestreo de áreas. La variación entre los elementos obtenidos de las áreas seleccionadas es, por lo tanto, frecuentemente mayor que la obtenida si la población entera es muestreada mediante muestreo aleatorio simple. Esta debilidad puede reducida cuando se incrementa el tamaño de la muestra de área. El incremento del tamaño de la muestra puede fácilmente ser hecho en muestra de área. Los entrevistadores no tienen que caminar demasiado lejos en una pequeña área para entrevistar más familias. Por lo tanto, una muestra grande de área puede ser obtenida dentro de un corto período de tiempo y a bajo costo. Por otra parte, una muestra de conglomerados puede producir la misma precisión en la estimación que una muestra aleatoria simple, si la variación de los elementos individuales dentro de cada conglomerado es tan grande como la de la población. Ejercicios Estructure 5 ejemplos de cada tipo de muestreo Aplique cada uno de los muestreos a la prueba: “Conocer la talla de calzado promedio de los alumnos del colegio Lev Vygotsky” TERCERO DE BACHILLERATO QUIMESTRE I BLOQUE 1 Pruebas de Hipótesis (Unilateral y bilateral) BLOQUE 2 Análisis de la Varianza BLOQUE 3 Regresión simple correlación y QUIMESTRE II BLOQUE 4 Regresión múltiple y correlación Datos de Series de Tiempo ANOVA a una vía Para medias poblacionales Pruebas de hipótesis Modelo de Regresión Múltiple ANOVA a dos vías Para poblacionales proporciones BLOQUE 5 Análisis de Series de tiempo Técnicas de suavizamiento Intervalos de confianza Comparaciones por pares Multicolinealidad Coeficiente determinación de Variables dummy Modelos Curvilíneos Logros que se desea alcanzar en el estudiante Materiales Entender el uso y beneficios de las pruebas de hipótesis Desarrollar ordenada y estructuradamente los pasos para realizar una prueba de hipótesis. Comprender el procedimiento para una prueba de hipótesis para medias y proporciones poblacionales Reconocer los errores tipo de las pruebas de hipótesis Proyector- Ordenador BLOQUE 6 PROYECTO APLICACIÓN DE CONOCIMIENTOS DE OCTAVO A TERCERO DE BACHILLERATO BLOQUE 1 Pruebas de Hipótesis Las pruebas de hipótesis en Estadística son la base fundamental de la inferencia, es decir el criterio más claro para comprobar si un comportamiento muestral se aproxima a uno poblacional. Dentro de la prueba de hipótesis existe la capacidad de comprobar si una teoría es cierta o si no lo es, es decir si se acepta o rechaza, todo esto asumiendo distribuciones normales o aproximaciones a normalidad, para ellos se deberá utilizar los estadísticos Z y T de Student. PASOS PARA APLICAR UNA PRUEBA DE HIPÓTESIS Paso 1: Plantear la hipótesis nula Ho y la hipótesis alternativa H1. Cualquier investigación estadística implica la existencia de hipótesis o afirmaciones acerca de las poblaciones que se estudian. La hipótesis nula (Ho) se refiere siempre a un valor especificado del parámetro de población, no a una estadística de muestra. La letra H significa hipótesis y el subíndice cero no hay diferencia. Por lo general hay un "no" en la hipótesis nula que indica que "no hay cambio" Podemos rechazar o aceptar Ho. La hipótesis nula es una afirmación que no se rechaza a menos que los datos muestrales proporcionen evidencia convincente de que es falsa. El planteamiento de la hipótesis nula siempre contiene un signo de igualdad con respecto al valor especificado del parámetro. La hipótesis alternativa (H1) es cualquier hipótesis que difiera de la hipótesis nula. Es una afirmación que se acepta si los datos muestrales proporcionan evidencia suficiente de que la hipótesis nula es falsa. Se le conoce también como la hipótesis de investigación. El planteamiento de la hipótesis alternativa nunca contiene un signo de igualdad con respecto al valor especificado del parámetro. Paso 2: Seleccionar el nivel de significancia. Nivel de significancia es la probabilidad de rechazar la hipótesis nula cuando es verdadera. Se le denota mediante la letra griega α, también es denominada como nivel de riesgo, este término es más adecuado ya que se corre el riesgo de rechazar la hipótesis nula, cuando en realidad es verdadera. Este nivel esta bajo el control de la persona que realiza la prueba. Si suponemos que la hipótesis planteada es verdadera, entonces, el nivel de significación indicará la probabilidad de no aceptarla, es decir, estén fuera de área de aceptación. El nivel de confianza (1-α), indica la probabilidad de aceptar la hipótesis planteada, cuando es verdadera en la población. La distribución de muestreo de la estadística de prueba se divide en dos regiones, una región de rechazo (conocida como región crítica) y una región de no rechazo (aceptación). Si la estadística de prueba cae dentro de la región de aceptación, no se puede rechazar la hipótesis nula. La región de rechazo puede considerarse como el conjunto de valores de la estadística de prueba que no tienen posibilidad de presentarse si la hipótesis nula es verdadera. Por otro lado, estos valores no son tan improbables de presentarse si la hipótesis nula es falsa. El valor crítico separa la región de no rechazo de la de rechazo. Tipos de errores Cualquiera sea la decisión tomada a partir de una prueba de hipótesis, ya sea de aceptación de la Ho o de la Ha, puede incurrirse en error: Un error tipo I se presenta si la hipótesis nula Ho es rechazada cuando es verdadera y debía ser aceptada. La probabilidad de cometer un error tipo I se denomina con la letra alfa α Un error tipo II, se denota con la letra griega β se presenta si la hipótesis nula es aceptada cuando de hecho es falsa y debía ser rechazada. En cualquiera de los dos casos se comete un error al tomar una decisión equivocada. Para que cualquier ensayo de hipótesis sea bueno, debe diseñarse de forma que minimice los errores de decisión. En la práctica un tipo de error puede tener más importancia que el otro, y así se tiene a conseguir poner una limitación al error de mayor importancia. La única forma de reducir ambos tipos de errores es incrementar el tamaño de la muestra, lo cual puede ser o no ser posible. La probabilidad de cometer un error de tipo II denotada con la letra griega beta β, depende de la diferencia entre los valores supuesto y real del parámetro de la población. Como es más fácil encontrar diferencias grandes, si la diferencia entre la estadística de muestra y el correspondiente parámetro de población es grande, la probabilidad de cometer un error de tipo II, probablemente sea pequeña. El estudio y las conclusiones que obtengamos para una población cualquiera, se habrán apoyado exclusivamente en el análisis de una parte de ésta. De la probabilidad con la que estemos dispuestos a asumir estos errores, dependerá, por ejemplo, el tamaño de la muestra requerida. Las contrastaciones se apoyan en que los datos de partida siguen una distribución normal Existe una relación inversa entre la magnitud de los errores α y β: conforme a aumenta, β disminuye. Esto obliga a establecer con cuidado el valor de a para las pruebas estadísticas. Lo ideal sería establecer α y β.En la práctica se establece el nivel α y para disminuir el Error β se incrementa el número de observaciones en la muestra, pues así se acortan los limites de confianza respecto a la hipótesis planteada .La meta de las pruebas estadísticas es rechazar la hipótesis planteada. En otras palabras, es deseable aumentar cuando ésta es verdadera, o sea, incrementar lo que se llama poder de la prueba (1- β). La aceptación de la hipótesis planteada debe interpretarse como que la información aleatoria de la muestra disponible no permite detectar la falsedad de esta hipótesis. Paso 3: Cálculo del valor estadístico de prueba Valor determinado a partir de la información muestral, que se utiliza para determinar si se rechaza la hipótesis nula., existen muchos estadísticos de prueba para nuestro caso utilizaremos los estadísticos z y t. La elección de uno de estos depende de la cantidad de muestras que se toman, si las muestras son de la prueba son iguales a 30 o más se utiliza el estadístico z, en caso contrario se utiliza el estadístico t. Tipos de prueba a) Prueba bilateral o de dos extremos: la hipótesis planteada se formula con la igualdad Ejemplo H0 : µ = 200 H1 : µ ≠ 200 b) Pruebas unilateral o de un extremo: la hipótesis planteada se formula con ≥ o ≤ H0 : µ ≥ 200 H0 : µ ≤ 200 H1 : µ < 200 H1 : µ > 200 En las pruebas de hipótesis para la media (μ), cuando se conoce la desviación estándar (σ) poblacional, o cuando el valor de la muestra es grande (30 o más), el valor estadístico de prueba es z y se determina a partir de: El valor estadístico z, para muestra grande y desviación estándar poblacional desconocida se determina por la ecuación: En la prueba para una media poblacional con muestra pequeña y desviación estándar poblacional desconocida se utiliza el valor estadístico t. Paso 4: Formular la regla de decisión Se establece las condiciones específicas en la que se rechaza la hipótesis nula y las condiciones en que no se rechaza la hipótesis nula. La región de rechazo define la ubicación de todos los valores que son tan grandes o tan pequeños, que la probabilidad de que se presenten bajo la suposición de que la hipótesis nula es verdadera, es muy remota Valor critico: Es el punto de división entre la región en la que se rechaza la hipótesis nula y la región en la que no se rechaza la hipótesis nula. Paso 5: Tomar una decisión. En este último paso de la prueba de hipótesis, se calcula el estadístico de prueba, se compara con el valor crítico y se toma la decisión de rechazar o no la hipótesis nula. Tenga presente que en una prueba de hipótesis solo se puede tomar una de dos decisiones: aceptar o rechazar la hipótesis nula. Debe subrayarse que siempre existe la posibilidad de rechazar la hipótesis nula cuando no debería haberse rechazado (error tipo I). También existe la posibilidad de que la hipótesis nula se acepte cuando debería haberse rechazado (error de tipo II). Pruebas de Hipótesis para Proporciones Cuando el objetivo del muestreo es evaluar la validez de una afirmación con respecto a la proporción de una población, es adecuado utilizar una prueba de una muestra. La metodología de prueba depende de si el número de observaciones de la muestra es grande o pequeño. Como se habrá observado anteriormente, las pruebas de grandes muestras de medias y proporciones son bastante semejantes. De este modo, los valores estadísticos de prueba miden la desviación de un valor estadístico de muestra a partir de un valor propuesto. Y ambas pruebas se basan en la distribución normal estándar para valores críticos. Quizá la única diferencia real entre las ambas radica en la forma corno se obtiene la desviación estándar de la distribución de muestreo. Esta prueba comprende el cálculo del valor estadístico de prueba Z Posteriormente este valor es comparado con el valor de Z, obtenido a partir de una tabla normal a un nivel de significación seleccionado. Como ocurrió con la prueba de medias de una muestra, las pruebas de proporciones pueden ser de una o dos colas. BLOQUE 2 Análisis de la Varianza El análisis de la varianza parte de los conceptos de regresión lineal. El primer concepto fundamental es que todo valor observado puede expresarse mediante la siguiente función: Donde Y sería el valor observado (variable dependiente), y X el valor que toma la variable independiente. Sería una constante que en la recta de regresión equivale a la ordenada en el origen, es otra constante que equivale a la pendiente de la recta, y aleatoria que añade a la función cierto error que desvía la puntuación observada de la puntuación pronosticada. Por tanto, a la función de pronóstico la podemos llamar "Y prima": Podemos resumir que las puntuaciones observadas equivalen a las puntuaciones esperadas, más el error aleatorio: (1.1) Sabiendo este concepto, podemos operar con esta ecuación de la siguiente forma: 1) Restamos a ambos lados de la ecuación (para mantener la igualdad) la media de la variable dependiente: 2) Substituimos el error por la ecuación resultante de despejar la ecuación 1.1: Por tanto... Y reorganizando la ecuación: Ahora hay que tener en cuenta que la media de las puntuaciones observadas es exactamente igual que la media de las puntuaciones pronosticadas: Por tanto: es una variable Podemos ver que nos han quedado 3 puntuaciones diferenciales. Ahora las elevamos al cuadrado para que posteriormente, al hacer el sumatorio, no se anulen: Y desarrollamos el cuadrado: Podemos ver que tenemos los numeradores de las varianzas, pero al no estar divididas por el número de casos (n), las llamamos Sumas de Cuadrados., excepto en el último término, que es una Suma Cruzada de Cuadrados (el numerador de la covarianza), y la covarianza en este caso es cero (por las propiedades de la regresión lineal, la covarianza entre el error y la variable independiente es cero). Por tanto: O lo mismo que: De un factor, que es el caso más sencillo, la idea básica del análisis de la varianza es comparar la variación total de un conjunto de muestras y descomponerla como: Dónde: es un número real relacionado con la varianza, que mide la variación debida al "factor", "tratamiento" o tipo de situación estudiado. es un número real relacionado con la varianza, que mide la variación dentro de cada "factor", "tratamiento" o tipo de situación. En el caso de que la diferencia debida al factor o tratamiento no sean estadísticamente significativa puede probarse que las varianzas muestrales son iguales: Donde: es el número de situaciones diferentes o valores del factor se están comparando. es el número de mediciones en cada situación se hacen o número de valores disponibles para cada valor del factor. Así lo que un simple test a partir de la F de Snedecor puede decidir si el factor o tratamiento es estadísticamente significativo. Existen tres clases de modelos. El Modelo de efectos fijos asume que los datos provienen de poblaciones normales las cuales podrían diferir únicamente en sus medias. El Modelo de efectos aleatorios asume que los datos describen una jerarquía de diferentes poblaciones cuyas diferencias quedan restringidas por la jerarquía. Ejemplo: El experimentador ha aprendido y ha considerado en el experimento sólo tres de muchos más métodos posibles, el método de enseñanza es un factor aleatorio en el experimento. El Modelo de efectos mixtos describe situaciones que éste puede tomar. Ejemplo: Si el método de enseñanza es analizado como un factor que puede influir donde están presentes ambos tipos de factores: fijos y aleatorios. Supuestos previos El ANOVA parte de algunos supuestos que han de cumplirse: La variable dependiente debe medirse al menos a nivel de intervalo. Independencia de las observaciones. La distribución de los residuales debe ser normal. Homocedasticidad: homogeneidad de las varianzas. La técnica fundamental consiste en la separación de la suma de cuadrados (SS, 'sum of squares') en componentes relativos a los factores contemplados en el modelo. Como ejemplo, mostramos el modelo para un ANOVA simplificado con un tipo de factores en diferentes niveles. (Si los niveles son cuantitativos y los efectos son lineales, puede resultar apropiado un análisis de regresión lineal) El número de grados de libertad (gl) puede separarse de forma similar y corresponde con la forma en que la distribución chi-cuadrado (χ² o Ji-cuadrada) describe la suma de cuadrados asociada. Tipos de modelo Modelo I: Efectos fijos El modelo de efectos fijos de análisis de la varianza se aplica a situaciones en las que el experimentador ha sometido al grupo o material analizado a varios factores, cada uno de los cuales le afecta sólo a la media, permaneciendo la "variable respuesta" con una distribución normal. Este modelo se supone cuando el investigador se interesa únicamente por los niveles del factor presentes en el experimento, por lo que cualquier variación observada en las puntuaciones se deberá al error experimental. Modelo II: Efectos aleatorios (componentes de varianza) Los modelos de efectos aleatorios se usan para describir situaciones en que ocurren diferencias incomparables en el material o grupo experimental. El ejemplo más simple es el de estimar la media desconocida de una población compuesta de individuos diferentes y en el que esas diferencias se mezclan con los errores del instrumento de medición. Este modelo se supone cuando el investigador está interesado en una población de niveles, teóricamente infinitos, del factor de estudio, de los que únicamente una muestra al azar (t niveles) están presentes en el experimento. Grados de libertad Los grados de libertad pueden descomponerse al igual que la suma de cuadrados. Así, GLtotal = GLentre + GLdentro. Los GLentre se calculan como: a - 1, donde a es el número de tratamientos o niveles del factor. Los GLdentro se calculan como N - a, donde N es el número total de observaciones o valores de la variable medida (la variable respuesta). Pruebas de significación El análisis de varianza lleva a la realización de pruebas de significación estadística, usando la denominada distribución F de Snedecor. Tablas ANOVA Una vez que se han calculado las sumas de cuadrados, las medias cuadráticas, los grados de libertad y la F, se procede a elaborar una tabla que reúna la información, denominada "Tabla de Análisis de varianza o ANOVA", que adopta la siguiente forma: Fuente de variación Suma de cuadrados Grados de libertad Cuadrado medio Intergrupo t-1 Intragrupo o Error N-t Total N-1 F
