PROBABILIDAD VARIABLES ALEATORIAS

PROBABILIDAD
Ricardo Bautista Mercado
20 de julio de 2007
Resumen
Este trabajo fue motivado por el curso de Probabilidad I, impartido
por el Dr. Raul Montes De Oca del Departamento de Matematicas de la
UAM-I, en el trimestre 07-I
VARIABLES ALEATORIAS
1. VARIABLES ALEATORIAS DISCRETAS
1.1.
Variable Aleatoria Binomial
Sea ǫ un experimento aleatorio tal que
Ω ={exito, fracaso}
p = P [{exito}]
Observación 1. P [fracaso}] = 1 − p
X =número de exitos en las n repeticiones independientes de ǫ
P [X = k] = Ckn pk (1 − p)n−k
X[Ω] = {0, 1, 2, 3, . . .}
k ∈ {0, 1, . . . , n}
Notación: X ∼ B(n, p)
Observación 2.
n
X
k=0
P [X = k] =
n
X
k=0
Ckn pk (1 − p)n−k = (p + (1 − p))n = 1
1
Ejemplo 1. I) Sea m una moneda con P ({aguila}) = 32 , P ({sol}) = 13
Suponga que lanzamos la moneda 100 veces, de manera independiente
¿cual es la probabilidad de obtener 2 aguilas o mas?
„
«
2
X ∼ B 100,
3
P [X ≥ 2]
=
=
=
1 − P [X < 2]
1 − (P [X = 0] + P [X = 1])
„ «100
„ « „ «99
1
1
2
1−
− 100
3
3
3
II) Los motores de un avión operan independientemente unos de otros
con P ({no fallar}) = 0,99 . Un avión llega a su destino siempre y
cuando no fallen al menos la mitad de sus motores
¿cual es la probabilidad de que un tetramotor llegue a su destino
exitosamente?
X ∼ B (4, 0,99)
P [X ≥ 2]
=
P [X = 2] + P [X = 3] + P [X = 4]
=
C24 (0,99)2 (0,01)2 + C34 (0,99)3 (0,01) + C44 (0,99)4
III) Se tienen N objetos de los cuales M son blancos y el resto de color
negro
si se toma una muestra de n objetos con sustitucion
¿cual es la probabilidad de obtener k objetos blancos?
«
„
M
X ∼ B n,
N
P [X = k]
=
Ckn
„
M
N
«k „
«n−k
M
1−
N
Observación 3. El muestreo sin sustitucion no se puede plantear
como binomial pues no hay independencia
2
III) Un sistema de protección contra misiles esta construido con n unidades de radar que funcionan de forma independiente, cada uno con
una probabilidad de 0.9 de detectar un misil.
a) Si n = 5 y pasa un misil, ¿cual es la probabilidad de que 4 unidades lo detecten?
!
5
P [X = 4] =
(0,9)4 (0,1) = 0,32805
4
b) ¿cual debe ser el valor de n para que la probabilidad de dectar un
misil sea 0.999?
0,999
=
=
P [X ≥ 1]
1 − (1 − 0,9)n
⇒
(1 − 0,9)n
(0,1)n
=
=
1 − 0,999
0,001
⇒
n
=
=
1.2.
log(0,001)
log(0,1)
3
Variable Aleatoria de Poisson
Lema 1. Sea θ(x) una función tal que
lı́m
x→0
θ(x)
=0
x
Sea a ∈ R. Entonces
lı́m [1 + ax + θ(x)]1/x = ea
x→0
3
Teorema 1 (Poisson). Sea Xn ∼ B(n, Pn )
n = 1, 2, . . .
Supongangase que lı́mn→+∞ Pn = 0 y que lı́mn→+∞ nPn = λ > 0
Entonces
P [Xn = k] →
λk e−λ
k!
k = 0, 1, 2, . . .
Demostración. Como n · Pn → λ cuando n → ∞
entonces
g(n) = n · Pn − λ → 0 cuando n → ∞
Por otro lado
λ
n · Pn − λ = g(n) ⇒ Pn = g(n)
+n
n
g(n)
en particular n → 0 cuando n → ∞
Luego utilizando la hipotesis Xn ∼ B(n, Pn ) tenemos que
P [Xn = k]
=
=
=
=
sea x =
P [Xn = k]
1
,
n
Ckn Pnk (1 − Pn )n−k
«k „
„
««n−k
g(n)
λ
1−
+
n
n
«n−k
„
g(n)
λ
1 n(n − 1) · · · (n − k + 1)
k
1
−
(λ
+
g(n))
−
k!
nk
n
n
„
„
«
„
«
«n „
«−k
g(n)
g(n)
1
λ
1
k−1
λ
1−
··· 1 −
(λ + g(n))k 1 − −
1− −
k!
n
n
n
n
n
n
n(n − 1) · · · (n − k + 1)
k!
„
g(n)
λ
+
n
n
entonces
=
1
k!
„
„
«
„
«
«−k
1
g(n)
1
k−1
λ
1−
··· 1 −
(λ + g(n))k (1 − λx − xg(n)) x 1 − −
n
n
n
n
λ −λ
e
k!
∴ lı́mn→∞ P [Xn = k] =
k
Observación 4. a) 0 ≤ λk! e−λ ≤ 1
P+∞ λk −λ
P
λk
b)
= e−λ +∞
k=1 k! e
k=1 k! = 1
Observación 5.
ez =
+∞ m
X
z
,
m!
k=1
∀k = 0, 1, . . .
z∈R
X =número de veces que ocurre cierto evento aleatorio, cuando sabemos que este ocurre en promedio λ veces por unidad de tiempo
P [X = k] =
X[Ω] = {0, 1, 2, . . .}
Notación: X ∼ P[λ]
4
λk −λ
e
k!
Ejemplo 2. En una carretera ocurren en promedio 2 accidentes por dia
λ=2
X ∼ P[2]
I) ¿cual es la probabilidad de que mañana no ocurra ningun accidente?
P [X = 0] = e−2 = 0,1353
II) ¿cual es la probabilidad de que ocurra al menos 1 accidente?
P [X ≥ 1] = 1 − P [X = 0] = 1 − e−2 = 1 − 0,1353 = 0,864
III)
P [4 < X ≤ 7]
=
=
=
=
P [X = 5] + P [X = 6] + P [X = 7]
25 −2 26 −2 27 −2
e + e + e
5!
6!
7!«
„
64
128
32
e−2
+
+
120
720
5040
0,051556298
Ejemplo 3. Supóngase que un deposito contiene 10000 partı́culas. la probabilidad de que una de esas partı́culas salga del depósito es igual a 0.0004
¿Cuál es la probabilidad de que ocurran más de 5 salidas? (Puede suponerse que las salidas son independientes unas de otras).
X ∼ B(10000, 0,0004)
λ = (10000)(0,0004) = 4
P [X > 5]
≈
=
=
1.3.
1 − (P [X = 0] + P [X = 1] + · · · + P [X = 5])
„ 0
«
4
41
42
43
44
−4
1−e
+
+
+
+
0!
1!
2!
3!
4!
0,2151
Variable Aleatoria Geometrica
Sea ǫ un experimento Bernoulli,
Ω = {exito, f racaso},
p := P [{exito}]
p ∈ (0, 1)
Se repite ǫ, de manera independiente, una infinidad de veces
Sea Ω′ := Ω × Ω × Ω × · · ·
5
Observación 6. ω ∈ Ω ⇔ Ω = (exito ó fracaso, exito ó fracaso, . . .)
X : Ω′ → R
X =número de repeticiones de ǫ hasta obtener exito por vez primera
X[Ω′ ] = {1, 2, 3, . . .}
P [X = k] = (1 − p)k−1 p
Notación: X ∼ G[p]
Observación 7.
+∞
X
P [X = k] =
k=1
+∞
X
k=1
+∞
X
p(1 − p)k−1 = p
(1 − p)k−1
k=1
!
=p
1
=1
1 − (1 − p)
Ejemplo 4. La probabilidad de encontrar cierto medicamento en una
farmacia es de 0.20
Calcule la probabilidad de que una persona que requiere de ese medicamento:
I) Tenga que recorrer 3 farmacias para hallarlo?
p = 0,20
P [X = 3] = (1 − p)2 p = (0,8)2 (0,20) = 0,128
II) Se vea obligada a recorrer por lo menos 3 farmacias para encontrarlo?
P [X ≥ 3]
=
=
=
1 − P [X = 1] − P [X = 2]
1 − (0,20) − (0,8)(0,20)
0,64
Ejemplo 5. Cierto atleta logra saltar la varilla a 2.28 mts de altura el
60 % de las veces. En una competencia olimpica dispone de 3 intentos y si
logra salvar esa altura ganara medalla de oro. Determine la probabilidad
de que gane dicha medalla
p = 0,6
P [{gane la medalla de oro}]
=
P [X = 1] + P [X = 2] + P [X = 3]
=
(0,6) + (0,4)(0,6) + (0,4)2 (0,6)
=
0,936
Observación 8. Se supuso que los saltos sean independientes
6
Ejemplo 6. Suponga que un joven envia muchos mensajes por é-mail a
su prometida, pero ella solo responde el 5 % de los mensajes que recibe.
¿cuantos correos debera este insistente joven enviar a su novia para tener
una probabilidad de por lo menos 0.8 de que por fin uno de ellos sea
respondido?
p = 0,05
P [{algun correo es respondido}]
P [X = 1] + P [X = 2] + · · · + P [X = n]
=
p + (1 − p)p + (1 − p)2 p + · · · + (1 − p)n−1 p
=
[1 + (1 − p) + (1 − p)2 + · · · + (1 − p)n−1 ]p
1 − (1 − p)n
p
1 − (1 − p)
1 − (1 − p)n
=
=
=
≥
0,8
⇒
(1 − p)n
≤
=
1 − 0,8
0,2
⇒
n
≥
=
log(0,2)
log(0,95)
31,38
7
1.4.
Función de distribucion acumulativa
Sea X una variable aleatoria discreta
Definimos la funcion de distribucion acumulativa de X como la función
FX : R → R dada por:
X
FX := P [X ≤ x] =
P [X = k],
x∈R
k∈X[Ω]:k≤x
Ejemplo 7. Hallar FX :
X ∼ B(3, 12 )
k
0
1
2
3
P [X = k] = Ck3 ·
1
8
3
8
3
8
1
8
` 1 ´3
2
= Ck3 ·
P [X = k]
FX =
8
0
>
>
>
>
< 18
>
>
>
>
:
4
8
7
8
1
si
si
si
si
si
8
x<0
0≤x<1
1≤x<2
2≤x<3
x≥3
1
8
FX
1.4.1. Propiedades de la distribución acumulativa asociada
a una variable aleatoria discreta
FX es creciente (i.e x < y ⇒ FX (x) ≤ FX (y))
lı́mx→∞ FX (x) = 1;
lı́mx→−∞ FX (x) = 0
FX es continua a la derecha de los puntos del rango
P [X = k] = FX (k) − FX (− k)
k ∈ X[Ω]
Ejemplo 8. Supongase que X toma los valores −1, 0, 1 con probabilidades
1 1 1
, , respectivamente
3 2 6
I) Hallar la función de probabilidad puntual de Y1 = X2
Y1 [Ω] = {0, 1}
P [Y1 = 0] = P [X2 = 0] = P [X = 0] = 12
P [Y1 = 1] = P [X2 = 1] = P [X = 1] + P [X = −1] =
1
6
+
II) Hallar la función de probabilidad puntual de Y2 = 3X + 1
Y2 [Ω] = {−2, 1, 4}
P [Y2 = −2] = P [3X + 1 = −2] = P [X = −1] =
P [Y2 = 1] = P [3X + 1 = 1] = P [X = 0] = 12
P [Y2 = 4] = P [3X + 1 = 4] = P [X = 1] = 61
9
1
3
1
3
=
1
2
Ejemplo 9. X ∼ G( 21 )

0
Y=
1
si X toma un valor par
si X toma un valor impar
Hallar la función de probabilidad puntual de Y
Y[Ω] = {0, 1}
` ´2 ` ´4 ` ´6
P [Y = 0] = 12 + 21 + 21 + · · · = 13
` ´3 ` ´5
` ´7
P [Y = 1] = 12 + 21 + 12 + + 21 + · · · =
1.5.
2
3
Variable Aleatoria Hipergeometrica
Considere N objetos tales que M de ellos cumplen cierta propiedad p,
entonces para el problema del muestreo sin substitución (con tamaño de
muestra n) se tiene el siguiente modelo probabilistico:
X =número de objetos que cumplen la propiedad p
N −M
CkM Cn−k
N
Cn
X[Ω]={k| k es un entero no negativo que cumple: k ≤ M y k ≤ N −M }
P [X = k] =
Notación: X ∼ H[N, M, k]
Ejemplo 10. En una fabrica hay 1500 lavadoras de las cuales 400 son
defectuosas. Si se toman sin sustitucion 200 lavadoras al azar, ¿cual es la
probabilidad de que al menos una de las 200 lavadoras sea defectuosa?
X ∼ H (1500, 400, 200)
P [X ≥ 1]
=
1 − P [X = 0]
=
1−
10
1100
C200
1500
C200
2. ESPACIOS DE PROBABILIDAD Y
VARIABLES ALEATORIAS
Definición 1. Sean Ω un conjunto y F una familia de subcon juntos de
Ω
Diremos que F es una σ-álgebra de subconjuntos de Ω si:
a) ∅, Ω ∈ F
b) si A ⊂ F entonces Ac ∈ F;
y
c) A1 , A2 , . . . ∈ F, entonces
∪+∞
n=1 An ∈ F
Observación 9. Sean A1 , A2 , . . . ∈ F entonces (por las leyes de DeMorgan)
´c
` +∞
∩+∞
n=1 An = ∪n=1 An
Lema 2. Si F1 , F2 son σ-álgebras de Ω entonces F1 ∩ F2 tambien es σálgebra
Demostración.
entonces
a) Como ∅, Ω ∈ Fi
i = 1, 2
∅, Ω ∈ F1 ∩ F2
b) Sea A ⊂ F1 ∩ F2 entonces Ac ∈ F1 y Ac ∈ F2
luego entonces
Ac ∈ F 1 ∩ F 1
c) Sean A1 , A2 , . . . ∈ F1 ∩ F2 , entonces
A1 , A 2 , . . . ∈ F 1
entonces
por lo tanto
A1 , A 2 , . . . ∈ F 2
∪+∞
n=1 An ∈ Fi
i = 1, 2
∪+∞
n=1 An ∈ F1 ∩ F2
i = 1, 2
Ejemplo 11. a) Sea Ω un subconjunto. Entonces F1 = {∅, Ω} y F2 =
P (ω) (conjunto potencia de Ω)
son σ-álebra de subconjuntos de Ω
b) Sean Ω un conjunto y τ ⊂ Ω τ 6= ∅
B(τ ) := ∩{F : F es σ-álgebra y F ⊇ τ }
Notación: B(τ ) := σ-álgebra de Borel de Ω
11
Definición 2. Sea Ω un subconjunto y F una σ-álgebra de subconjuntos
de Ω
Diremos que
p : F : [0, 1]
es una medida de probabilidad sobre F si:
a) P [Ω]=1;
y
b) si A1 , A2 , . . . ∈ F y son ajenos , entonces
+∞
´ X
`
P (An )
P ∪+∞
n=1 An =
n=1
A la terna (Ω, F, P ) se le llama espacio de probabilidad
Definición 3. Diremos que X es una variable aleatoria si
∀x ∈ R
[X ≤ x] := {ω ∈ Ω : X(ω) ≤ x} ∈ F
1
Observación 10. [X ≤ x] = {ω ∈ Ω : X(ω) < x} = ∪+∞
i=1 [X ≤ x− n ] ∈ F
Definición 4. Diremos que X es una variable aleatoria discreta si
X[Ω] := {X(ω) : ω ∈ Ω}
es un conjunto finito o numerable
Para una variable aleatoria discreta, con rango X[Ω] = {x1 , x2 , . . .} se
define la función de probabilidad puntual como:
PX ({xi }) := P [X = xi ],
∀i = 1, 2, . . .
Observación 11. a) 0 ≤ PX ({xi }) ≤ 1 ∀i = 1, 2 . . .
P+∞
P+∞
b)
i=1 P [X = xi ] = 1
i=1 PX ({xi }) =
2.1.
VARIABLES ALEATORIAS CONTINUAS
Definición 5. Sea X una variable aleatoria diremos que X es una variable
aleatoria continua si
P [X = x] = 0
∀x ∈ R
Observación 12. Igual que en el caso discreto, se puede definir la función
de distribucion acumulativa asociada a una variable aleatoria continua
como
F : R → R, dada F (x) = P [X ≤ x] ∀x ∈ R (esta funcion F cumple
con las propiedades obtenidas para el caso discreto)
(i) como P [X = x] = F (x) − F (− x) = 0 ⇒ F es continua
(ii) Notese que P [X ∈ R] = 1 y que no puede estar ”soportada”por un
conjunto finito o numerable
si A = {y1 , y2 , . . .}
⇒ P [X ∈ A] = P [X = y1 ] + P [X = y2 ] + · · · = 0
12
(iii) Sean a, b ∈ R, a < b
F (b) − F (a) = P [X ≤ b] − P [X ≤ a]
=
=
=
=
P [a < X ≤ b]
P [a ≤ X < b]
P [a < X < b]
P [a ≤ X ≤ b]
2.1.1. VARIABLES ALEATORIAS CONTINUAS DEFINIDAS MEDIANTE DENSIDADES
Definición 6. Sea f : R → R diremos que f es una densidad de probabilidad
si
a) f ≥ 0;
y
R +∞
b) −∞ f (x)dx = 1
Ry
Observación 13. (i) y f (x)dx = 0;
y
Rx
(ii) F (x) := −∞ f (t)dt,
x∈R
⇒ F cumple con con todas las propiedades de una funcion de distrución
de una variable aleatoria continua
Entonces por un teorema debido a Kolmogorov, existen un espacio de
probabilidad (Ω, F, p) y una variable aleatoria X : Ω → R tal que
Z x
f (t)dt,
x∈R
FX = F (X) =
−∞
13
2.2.
Ejemplos de variables aleatorias continuas
1. Variable Aleatoria Uniforme
a, b ∈ R, a < b
f (x) =

1
b−a
0
si x ∈ [a, b]
si x ∈
/ [a, b]
X =seleccion de un punto al azar de [a, b]
P [c1 ≤ X ≤ c2 ] =
Z
c2
[c1 , c2 ] ⊂ [a, b]
f (x)dx
c1
Notación: X ∼ U [a, b]
Ejemplo 12. El tiempo medido en minutos en que cierta persona
invierte en ir de la estacion de su casa al tren es un fenomeno aleatorio que sigue una ley de probabilidad uniforme en el intervalo de
20-25. ¿cual es la probabilidad de que alcance el tren que sale de la
estacion a las 7:28 AM en punto si deja su casa exactamente a las
7:05 AM
X ∼ U (20, 25)
P [{alcance el tren}]
=
=
14
P [20 ≤ X ≤ 23]
Z 23
1
3
dt =
5
5
20
2. Variable Aleatoria Exponencial
Sea λ > 0
f (x) =

λ exp−λx
0
si x ≥ 0
si x < 0
T =tiempo transcurrido hasta que cierto evento ocurre,
T[Ω] = [0, +∞)
Z
+∞
f (x)dx =
−∞
Z
+∞
0
˛+∞
˛
λe−λx dx = −e−λx ˛
0
Notación: T ∼ exp[λ]
Ejemplo 13. Supongase que un sistema contiene cierto tipo de componente cuya duracion en años está dada por una variable aleatoria
distribuida en forma exponencial con λ = 51 . Si se instalan 5 de estos
componentes en diferentes sistemas, ¿cual es la probabilidad de que
por lo menos 2 funcionen 8 años ó mas?
[Supongase que estos componentes son independientes unos de otros]
T ∼ exp
P [T ≥ 8]
=
=
Z
» –
1
5
+∞
8
1 − 15 x
e
dx
5
8
e− 5 = 0,2018
Por lo tanto la probabilidad de que un componente dure 8 años ó mas
8
es e− 5 , ahora solo falta calcular la probabilidad de que por lo menos
8
2 de los 5 componentes sigan funcionando: X ∼ B(5, e− 5 )
15
P [X ≥ 2]
=
1 − (P [X = 0] + P [X = 1])
”
”
“ 8”“
“
8 5
8 4
1 − e− 5
1 − 1 − e− 5 − 5 e− 5
=
,2666
=
=
1 − ,323814 − 0,409577
Proposición 1 (perdida de memoria de la exponencial). Sea T ∼
exp [λ]
Entonces
∀t, s > 0
P [T > s + t|T > s] = P [T > t]
Demostración.
P [T > s + t|T > s]
=
=
P [T > s + t, T > s]
P [T > s]
P [T > s + t]
pues
P [T > s]
[T > s + t] ⊆ [T > s]
por otra parte
Z
+∞
P [T > s + t|T > s]
=
P [T > s]
=
λe−λt dt
s
=
e−λs dt
por lo tanto
16
=
e−λ(s+t)
e−λs
e−λt
=
P [T > t]
3. Variable Aleatoria Normal
Observación 14. La variable aleatoria normal trata de ajustarse a
la binomial
Función de densidad normal:
1
− 1 (x−µ)2
e 2σ2
(1)
2πσ
Definición 7. Una variable aleatoria X con densidad dada por 1
será llamada variable aleatoria normal con parametros µ y σ 2 se
denota
X ∼ N (µ, σ 2 )
f (x) = √
Observación 15. X[Ω] = R
P [0 ≤ X ≤ z] = φ(z) =Área bajo la curva normal estándar de 0 a z
3.1.10
17
CALCULO DE PROBABILIDADES CON LA NORMAL
a) X∗ ∼ N (0, 1)
X∗ =Normal estándar (centrada por el eje de las y’s)
Ejemplo 14. I) P [0 ≤ X∗ ≤ 1,42] = φ(1,42) =.4222
II) P [−0,73 ≤ X∗ ≤ 0] = φ(0,73) =.2673
III) P [−1,73 ≤ X∗ ≤ 2,01] = φ(2,01) + φ(1,73) =.4778
18
IV) P [0,65 ≤ X∗ ≤ 1,26] = φ(1,26) − φ(0,65) =.1540
V) P [−1,79 ≤ X∗ ≤ −0,54] = φ(1,79) − φ(,54) = ,4633 −
,2054 =.2579
VI) P [X∗ ≥ 1,13] =
1
2
− ,3708 =.1292
19
VII) determine a tal que P [−a ≤ X∗ ≤ −0,5] = 0,004
0,004
=
=
φ(a) − φ(0,5)
φ(a) − 0,1915
entonces
φ(a) = 0,004 + 0,1915 = 0,1955
de donde
a ≈.51
b) X ∼ N (µ, σ 2 ), µ 6= 0, σ 6= 1
Proposición 2. Si Y :=
entonces
X−µ
σ
Y ∼ N (0, 1)
Demostración.
FY (y)
=
=
=
=
P [Y ≤ y]
»
–
X−µ
P
≤y
σ
P [X ≤ σy + µ]
Z σy+µ
1
− 1 (t−µ)2
√
e 2σ2
dt
2πσ
−∞
sea ξ := σ1 t − σµ
entonces dξ := σ1 dt
por lo tanto
FY (y)
=
=
Z
σy+µ
−∞
Z y
−∞
=
√
1
− 1 (t−µ)2
e 2σ2
dt
2πσ
1 2
1
√ e− 2 ξ dξ
2π
1 2
1
√ e− 2 y
2π
20
y∈R
Ejemplo 15. Sea X ∼ N (0,25, (0,02)2 )
hallar
I) P [X ≤ 0,2] ∼ P [X∗ ≤ 0,2−0,25
] = 12 − φ(2,5) = 0,0062
0,02
II) P [X ≥ 0,28] ∼ P [X∗ ≥
III) P [0,2 ≤ X ≤ 0,28]
P [0,2 ≤ X ≤ 0,28]
0,28−0,25
]
0,02
»
=
1
2
− φ(1,5) = 0,0668
X − 0,25
0,2 − 0,25
≤
≤ 1,5
0,02
0,02
∼
P
=
P [−2,5 ≤ X∗ ≤ 1,5]
=
–
φ(2,5) + φ(1,5)
=
0,4938 + 0,4332
=
0,927
Ejemplo 16. Si X ∼ N (80, 102 )
determine
I) P [X ≤ 100] ∼ P [X∗ ≤ 100−80
] = 21 + φ(2) = 0,9772
10
∗
80−80
II) P [X ≤ 80] ∼ P [X ≤ 10 ] = 12
≤ X∗ ≤ 100−80
] = φ(2) + φ(0,5) =
III) P [75 ≤ X ≤ 100] ∼ P [ 75−80
10
10
,6687
IV) P [X ≥ 75] ∼ P [X∗ ≥ 75−80
] = 12 + φ(,5) = 0,6915
10
V) P [|X−80| ≤ 19,6] ∼ P [− 19,6
≤ X∗ ≤ 19,6
] = φ(1,96)+φ(1,96) = 1,95
10
10
Observación 16.
|x| ≤ a
|x| ≥ a
⇔
x ∈ [−a, a]
⇔
x ∈ (−∞, −a] ∪ [a, +∞)
Ejemplo 17. Una maquina troqueladora produce tapas de latas cuyos
diametros estan normalmente distribuidos con σ = 0,01 pulgadas.
En que valor de µ debe ajustarse la maquinaria de tal manera que el
5 % de las tapas producidas tengan diametro que excede las 3 pulgadas
D ∼ N (µ, (0,01)2 )
0,05
=
∼
=
P [D > 3]
»
–
3−µ
P D∗ >
0,01
„
«
3−µ
1
−φ
2
0,01
21
por lo tanto
φ
entonces
„
3−µ
0,01
«
= 0,45
3−µ
≈ 1,65
0,01
⇒
µ = 3 − (0,01)(1,65) = 2,9835
22
3. VARIABLES ALEATORIAS (BIDIMENSIONALES)
Sea ǫ un experimento aleatorio con espacio de probabilidad (Ω, F, P )
Sea X : Ω → R2 , X = (X, Y) una funcion ω 7→ X(ω) = (X(ω), Y(ω))
Definición 8. Diremos que X es un vector aleatorio (bidimensional) si
[X ≤ x, Y ≤ y] ∈ F
∀x, y ∈ R
[X ≤ x, Y ≤ y] := {ω ∈ Ω : X(ω) ≤ x, Y(ω) ≤ y}
I. Caso discreto
Definición 9. Diremos que X es un vector aleatorio discreto si
X[Ω] = {(xi , yi ) : xi ∈ X[Ω], yj ∈ Y[Ω]}
es finito o numerable
3.0.1.
Función de probabilidad puntual de X
PX ({(xi , yj )})
:=
P [X = xi , Y = yi ]
=
P [{ω ∈ Ω : X(ω) = xi , Y = yj }]
Propiedades
0 ≤ PX ({(xi , yj )}) ≤ 1
XX
j
i
PX {(xi , yj )}
∀i, j
=
X X
j
=
X
P [X = xi , Y = yj ]
i
!
P [Y = yi ]
j
=
3.0.2.
P [Ω] = 1
Funciones de probabilidad puntual marginales
P [X = xi ] =
X
P [X = xi , Y = yj ],
∀i
P [X = xi , Y = yj ],
∀j
j
P [Y = yj ] =
X
i
3.0.3.
Funciones de probabilidad condicional
P [X = xi |Y = yj ] :=
P [X = xi , Y = yj ]
P [Y = yj ]
P [Y = yj |X = xi ] :=
P [X = xi , Y = yj ]
P [X = xi ]
23
Independencia
Definición 10. X y Y son independientes ssi
P [X = xi , Y = yj ] = P [X = xi ]P [Y = yj ]
∀i, j
X
Y
0
1
2
3
P [X = x]
1
2
3
6
0
0
42
42
42
42
Ejemplo 18.
2
3
4
5
14
1
42
42
42
42
42
4
5
6
7
22
2
42
42
42
42
42
6
9
12
15
P [Y = y] 42
42
42
42
{0, 1, 2}
X[Ω]
=
Y[Ω]
=
{0, 1, 2, 3}
X[Ω]
=
X[Ω] × Y[Ω]
=
=
{0, 1, 2} × {0, 1, 2, 3}
{(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3)}
Ejemplo 19.
P [X = 1, Y = 1] = PX ({(1, 1)}) =
3
42
Ejemplo 20.
P [X > Y]
=
P [{(1, 0), (2, 0), (2, 1)}]
4
5
2
+
+
42
42
42
11
42
=
=
Ejemplo 21.
P [X < 1] = P [X = 0] =
6
42
Ejemplo 22.
P [X = 0|Y = 1]
=
=
=
P [X = 0, Y = 1]
P [Y = 1]
1/42
9/42
1
9
Ejemplo 23.
P [X = 1|Y = 1]
=
=
=
24
P [X = 1, Y = 1]
P [Y = 1]
3/42
9/42
3
9
Ejemplo 24.
P [X = 2|Y = 1]
=
=
=
P [X = 2, Y = 1]
P [Y = 1]
5/9
1
5
9
Observación 17.
P [X = 0|Y = 1] + P [X = 1|Y = 1] + P [X = 2|Y = 1]
=
=
1
3
5
+ +
9
9
9
1
(veáse los ejemplos 22, 23, 24)
Observación 18.
P [X = 0, Y = 0]
=
6=
=
0
„
«2
6
42
P [X = 0] · P [Y = 0]
∴ X, Y no son independientes
II. Caso Continuo
Definición 11. Diremos que X es un vector aleatorio continuo si
∀x, y
P [X = x, Y = y] = 0
Observación 19. Igual que en el caso unidimensional tenemos:
FX (x, y) := P [X ≤ x, Y ≤ y]
3.0.4.
∀x, y
Vectores aleatorios generados por densidades
Definición 12. Una función f : R2 → R será llamada una densidad
de probabilidad si
a) f ≥ 0 (i.e f (x, y) ≥ 0
R
b) R2 f = 1
∀x, y)
Proposición 3. Sea f una densidad de probabilidad
F (x, y) =
Z
x
−∞
Z
y
f (u, v)dvdu,
−∞
x, y ∈ R
entonces
PX (A) =
Z
A
f,
A ∈ B(R2 )
25
(veáse ejemplo 11)
Ejemplo 25. Sea X = (x, y) con densidad
f (x, y) =
Z
f

e−y
0
si x ≥ 0, y > x
en otro caso
«
f (x, y)dy dx
x
0
«
Z ∞ „Z +∞
e−y dy dx
x
Z0 ∞
−x
e dx
Z
=
R2
=
=
∞
„Z
+∞
0
=
3.0.5.
1
Densidades Marginales
fX (x) =
fY (y) =
Z
Z
+∞
f (x, y)dy,
x ∈ X[Ω]
f (x, y)dx,
y ∈ Y[Ω]
−∞
+∞
−∞
Ejemplo 26. Sea f (x, y) la función de densidad dada en el ejemplo
25
entonces
fX (x)
=
=
=
Z
+∞
f (x, y)dy,
x
Z +∞
e
x
−x
e−y dy
x≥0
,
26
x ∈ [0, +∞)
fY (y)
=
=
Z
y
f (x, y)dx,
Z0 y
y ∈ [0, +∞)
e−y dx
0
=
ye−y ,
y≥0
Independencia
Definición 13. X y Y son independientes sii
f (x, y) = fX (x) · fY (y)
∀(x, y)
Ejemplo 27. Sea f (x, y) la función de densidad dada en el ejemplo
25
entonces
X y Y no son independientes, pues
f (0, 0)
=
1
6=
0
=
fX (0) · fY (0)
Calculo de Probabilidades
Ejemplo 28. Sea f (x, y) la función de densidad dada en el ejemplo
25
P [X ≥ 1|Y ≥ 2] =
27
P [X ≥ 1, Y ≥ 2]
P [Y ≥ 2]
P [X ≥ 1, Y ≥ 2]
Z Z
=
Z
=
Z
=
Z
=
=
Z
1
2
+∞
2
+∞
ye
∞
=
dy −
Z
+∞
e−y dy
2
fY (y)dy
Z2 ∞
ye−y dy
»
Z
−ye−y +
ˆ
−y
2
2
=
(ye−y − e−y )dy
2e−2
=
=
f (x, y)dydx
Z y
e−y dxdy
3e−2 − e−2
=
P [Y ≥ 2]
∞
−ye
−y
por ejemplo 26
–∞
∞
e−y dy
2
−y ˜∞
−e
2
−2
=
2e−2 + e
=
3e−2
2
Observación 20.
lı́m ye−y
y→+∞
=
=
=
y
ey
1
lı́m
y→+∞ ey
0
lı́m
y→+∞
regla de L’Hopital
entonces
P [X ≥ 1|Y ≥ 2]
=
=
=
28
P [X ≥ 1, Y ≥ 2]
P [Y ≥ 2]
2e−2
3e−2
2
3
3.0.6.
Densidades Condicionales
fY|X (y|x) :=
fX|Y (x|y) :=
f (x,y)
,
fX (x)
f (x,y)
,
fY (y)
fX (x) > 0
fY (y) > 0
29
Ejemplo 29. Sea f (x, y) la función de densidad dada en el ejemplo 25
Sea x ≥ 0 fijo
fY|X (y|x)
=
=
=
f (x, y)
fX (x)
e−y
por ejemplo 26
e−x
−(y−x)
e
Sea y > 0 fijo
fX|Y (x|y)
=
=
=
f (x, y)
fY (x)
e−y
ye−y
1
y
30
por ejemplo 26
PROBLEMA 21. Supongamos que el vector aleatorio discreto (X, Y)
está definido por
X
Y
1
2
3
1
2
1
2
1
6
1
9
1
4
0
1
8
3
0
1
5
2
15
1. Hallar las funciones de probabilidad marginales y las funciones de
probabilidad condicionales
Diga si X y Y son independientes
2. Supóngase que el vector aleatorio continuo tiene densidad
f (x, y) =

kx(x − y)
0
si 0 < x < 2, −x < y < x
en otro caso
a) Encuentre el valor de k
b) Determine fX y fY y diga si X y Y son independientes
31
3.0.7.
Densidades de funciones de variable aleatoria
Ejemplo 30. Supóngase que X ∼ U [0, 1]. Encuentre la densidad de Y =
4X2 + 2
(g(x) = 4x2 + 2,
x ∈ R)
Solución 22. a) Determinar el rango de Y
Y[Ω] = [2, 6]
Observación 23. fuera de es este rango mide 0
b) Sea y ∈ [2, 6] fijo
Observación 24.
y ∈ [2, 6]
⇔
⇔
⇔
FY (y)
=
=
=
=
=
=
P [Y ≤ y]
2≤y≤6
0≤y−2≤4
y−2
0≤
≤1
4
P [4X + 2 ≤ y]
–
»
y−2
P X2 ≤
4
"
#
r
y−2
P |X| ≤
4
#
" r
r
y−2
y−2
≤X≤
P −
4
4
q
r
Z y−2
4
y−2
1 · dt =
4
0
32
Conclusión Si y ∈ [2, 6], entonces
1
FY (y) =
(y − 2) 2
2
⇒
fY (y)
=
=
=
fY (y) =

FY′ (y)
«
„
1 1
−1
2
(y − 2)
2 2
1
1
√
4 y−2
1√1
4 y−2
0
33
si y ∈ (2, 6]
en otro caso
Ejemplo 31. Supongase que X ∼ U [0, 1]. Encuentre la densidad de Z =
eX
Solución 25. a) Determinar el rango de Z
Z[Ω] = [1, e]
Observación 26. fuera de es este rango mide 0
b) Sea z ∈ [1, e] fijo
Observación 27.
z ∈ [1, e]
FZ (z)
=
=
=
=
⇔
⇔
1≤z≤e
0 ≤ ln z ≤ 1
P [Z ≤ z]
P [exp[X] ≤ z]
P [X ≤ ln z]
Z ln z
1 · dt = ln z
0
34
Conclusión Si z ∈ [1, e], entonces
FZ (z) = ln z
⇒
fZ (z)
=
=
fZ (z) =

1
z
0
35
FZ′ (z)
1
z
si z ∈ [1, e]
en otro caso
Ejemplo 32. Sea X ∼ U [−1, 1]. Hallar la densidad de Y = 5X3 + 3
Solución 28. a) Determinar el rango de Y
Y[Ω] = [−2, 8]
Observación 29. fuera de es este rango mide 0
b) Sea y ∈ [−2, 8] fijo
Observación 30.
y ∈ [−2, 8]
⇔
⇔
⇔
FY (y)
=
=
=
=
=
−2 ≤ y ≤ 8
−5 ≤ y − 3 ≤ 5
y−3
−1 ≤
≤1
5
P [Y ≤ y]
P [5X3 + 3 ≤ y]
–
»
y−3
P X3 ≤
5
"
#
r
3 y − 3
P X≤
5
Z
q
3 y−3
5
0
36
1
1
· dt =
2
2
r
3
y−3
5
Conclusión Si y ∈ [−2, 8]\{3}, entonces
FY (y) =
1
2
„
(y − 3)
5
«1
3
⇒
fY (y)
=
=
fY (y) =
8
<
1
30
: 0
FY′ (y)
„
«2
1 (y − 3) 3
30
5
“
(y−3)
5
”2
3
si y 6= 3
si y ∈ (2, 3) ∪ (3, 6]
en otro caso
PROBLEMA 31. Supóngase que X tiene densidad

2x si 0 < x < 1
f (x) =
0
en otro caso
Encuentre las densidades de
a) Y = 3X + 1
b) Z = e−X
37
3.0.8. Densidades de la suma y del producto de variables
aleatorias independientes
Sean Z := X + Y
Densidad de la suma
FZ (z)
=
=
=
=
P [Z ≤ z]
z fijo
P [X + Y ≤ z]
Z Z
fX (x, y)dydx
x+y≤z
Z Z
f (x) · g(y)dydx
independencia
x+y≤z
=
=
=
=
Z
Z
Z
+∞
−∞
+∞
„Z
z−x
−∞
f (x)
−∞
+∞
f (x)
−∞
Z z
−∞
„Z
„Z
„Z
+∞
−∞
«
f (x) · g(y)dy dx
z−x
«
g(y)dy dx
−∞
z
−∞
«
g(u − x)du dx
«
f (x)g(u − x)dx du
cambio de variable: u = y + x
T. Fubini
⇒
R +∞
FZ′ = −∞ f (x)g(z − x)dx
∴
convolución:
fX+Y (z) =
38
Z
+∞
−∞
f (x)g(z − x)dx
Ejemplo 33. Sean X ∼ exp(λ1 ), Y ∼ exp(λ2 ). Suponga que X y
Y son independientes y que λ1 6= λ2
Hallar fX+Y
f (x) =

λ1 e−λ1 x
0
si x ≥ 0
en otro caso
g(y) =

λ2 e−λ2 y
0
si y ≥ 0
en otro caso

≥0
≥x
entonces
x
z
pues y = z − x ≥ 0
(X + Y)[Ω] = [0, ∞)
Sea z ∈ [0, +∞)
fX+Y (z)
=
=
Z
z
λ1 e−λ1 x · λ2 e−λ2 (z−x) dx
Z z
e−x(λ1 −λ2 ) dx
λ1 λ2 e−λ2 z
convolución
0
0
=
=
”
λ1 λ2 −λ2 z “ −z(λ1 −λ2 )
e
−
e
−1
λ1 − λ2
”
λ1 λ2 “ −λ1 z
− e−λ2 z
e
λ2 − λ1
39
Densidad del producto
fX·Y (z) =
Z
+∞
−∞
f (x) · g(z/x)
1
dx
|x|
Ejemplo 34. Supóngase que X y Y tienen densidades
f (x) =
g(y) =


2x
0
y 2 /9
0
si 0 < x < 1
en otro caso
si 0 < y < 3
en otro caso
respectivamente
Suponiendo X y Y independientes encuentre fX·Y

0<y<3
1
z<x
3
X · Y = [0, 3]
40
pues y =
z
x
<3
(2)
Sea z ∈ (0, 3)
fX·Y (z)
Z
=
1
1z
3
2 2
z
9
=
2x ·
z2 1 1
dx
x2 9 x
Z
dx
x2
1
1z
3
„
«
2 2 3
z
−1
9
z
´
2`
3z − z 2
9
=
=
Ejemplo 35. Sean
I : f (i)
=

R : g(r)
=

6i(1 − i)
0
2r
0
si 0 ≤ i ≤ 1
en otro caso
si 0 < r < 1
en otro caso
I, R independientes
Hallar la densidad de W = I 2 · R
I 2 [Ω] = [0, 1]
41
FI 2 (z)
=
=
=
P [I 2 ≤ z]
√
P [I ≤ z]
√
Z z
6i(1 − i)di
0
Z
√
z
idi − 6
=
6
=
3z − 2z 3/2
0
Z
√
z
i2 di
0
entonces
fI 2 (i) = FI′ 2 (i) =
por otro lado

FI 2 ·R
=
=
=
=

0≤i≤1
z<i
Z
3 − 3i1/2
0
pues r =
si 0 ≤ i ≤ 1
en otro caso
z
i
<1
1
z 1
usando 2
(3 − 2i1/2 )(2 ) di
i |i|
z
Z 1
Z 1
1
i−3/2 di
di − 4z
6z
2
z
z i
(6 − 6z) + (8z − 8z (1/2) )
√
2z − 8 z + 6
42
3.1.
ESPERANZA Y VARIANZA
3.1.1.
Esperanza
Definición 14. Sea X una variable aleatoria (discreta o continua). Se
define la esperanza como
8 P
X discreta
<
k kP [X = k],
E[X] :=
R
: ∞
xfX (x)dx, X continua
−∞
Observación 32. La esperanza de X se define solo si
X
|k|P [X = k] < +∞
k
ó
Z
∞
−∞
|x|fX (x)dx < +∞
Ejemplo 36. Encuentra E[X] en los casos siguientes:
a) X ∼ B(n, p)
E[X]
=
=
=
n
X
k=0
n
X
k=1
n
X
k=1
=
kCkn pk (1 − p)n−k
k
n!
pk (1 − p)n−k
k!(n − k)!
n(n − 1)!
pk (1 − p)n−k
(k − 1)!(n − k)!
(np)
n
X
k=1
=
(np)
n−1
X
z=0
=
(np)
=
np
n−1
X
z=0
(n − 1)!
pk−1 (1 − p)n−k
(k − 1)!(n − k)!
(n − 1)!
pz (1 − p)n−(z+1)
z!((n − 1) − z)!
Czn−1 pz (1 − p)(n−1)−z
Conclusión
Si X ∼ B(n, p) ⇒ E[X] = np
b) X ∼ U [a, b]
43
cambio de variable: z = k − 1
E[X]
=
=
=
=
=
Z
Z
+∞
xfX (x)dx
−∞
b
1
dx
b
−
a
a
Z b
1
xdx
b−a a
x
b 2 − a2
2(b − a)
a+b
2
Conclusión
Si X ∼ U [a, b] ⇒ E[X] =
a+b
2
`
´
Ejemplo 37. X ∼ B 3, 12
plo 7)
⇒
(veáse ejem-
E[X] =
44
3
2
3.1.2.
Varianza
Definición 15. Sea X una variable aleatoria (discreta o continua) con
esperanza E[X]. Se define la varianza de X como:
8 P
2
X discreta
<
k (k − E[X]) P [X = k],
var(X) :=
: R∞
(X − E[X])2 fX (x)dx, X continua
−∞
Observación 33. var(X) ≥ 0
Ejemplo 38. Hallar var(X) en los casos:
a) X ∼ B(n, p)
var(X)
=
=
=
=
=
n
X
(k − np)2 P [X = k]
k=0
n
X
k=0
n
X
k=0
n
X
k=2
n
X
k=2
=
=
k2 P [X = k] − 2np
n
X
k=1
k2 P [X = k] − (np)2
k(k − 1)
P [X = k]
k=1
por problema 36
n(n − 1)p2
n(n − 1)p2
n!
p2 pk−2 (1 − p)n−k + np − (np)2
k!(n − k)!
n
X
k=2
n−2
X
z=0
n−2
X
(n − 2)!
pk−2 (1 − p)n−k + np − (np)2
(k − 2)!(n − k)!
(n − 2)!
pz (1 − p)n−2−z + np − (np)2
z!((n − 2) − z)!
Czn−z pz (1 − p)(n−2)−z + np − (np)2
n(n − 1)p2
=
n(n − 1)p2 + np − (np)2
=
n
X
k(k − 1)Ckn pk (1 − p)n−k + np − (np)2
=
=
kP [X = k] + (np)2
z=0
(np)2 − np2 + np − (np)2
np(1 − p)
Conclusión
Si X ∼ B(n, p) ⇒ var(X) = np(1 − p)
b) X ∼ U [a, b]
45
c.v: z = k − 2
var(X)
=
=
=
=
=
=
=
=
„
«2
a+b
x−
fX (x)dx
2
−∞
Z +∞
Z +∞
(a + b)2
x2 fX (x)dx − (a + b)
xfX (x)dx +
4
−∞
−∞
Z b
2
2
(a + b)
(a + b)
1
dx −
+
x2
b
−
a
2
4
a
Z
+∞
(a + b)2
1
(b3 − a3 ) −
3(b − a)
4
(a + b)2
(b − a)(b2 + ab + a2 )
−
3(b − a)
4
4b2 + 4ab + 4a2 − 3a2 + 6ab − 3b2
12
b2 − 2ab + a2
12
(b − a)2
12
Conclusión
Si X ∼ U [a, b] ⇒ var(X) =
(b−a)2
12
cuadro de esperanzas y varianzas
variable aleatoria
B(n, p)
G(p)
P(λ)
H(N, M, n)
U [a, b]
exp(λ)
N (µ, σ 2 )
Esperanza
np
1/p
λ
M
n
N
a+b
2
1/λ
µ
46
Varianza
np(1 − p)
1−p
pz
λ
M N −n
(1
−
)
nM
N
N N −1
(b−a)2
12
2
1/λ
σ2
3.1.3.
Esperanza de funciones de variables aleatorias
Definición 16. Supongamos Y := g ◦ X = g(X), entonces
8 P
Y discreta
<
k∈Y[Ω] kP [Y = k],
E[Y] = E[g(X)] =
: R∞
yfY (y)dy,
Y continua
−∞
Ejemplo 39. Sea X ∼ U [−1, 1]
Hallar E[X2 ]
(Y = X2 )
obtención de la densidad de Y:
1◦ Y[Ω] = [0, 1]
2◦ Sea y ∈ [0, 1] fijo
FY (y)
P [Y ≤ y]
=
P [X2 ≤ y]
√
√
P [− y ≤ X ≤ y]
√
Z y
1
2
dx
2
0
√
y
=
=
=
=
Observación 34.
y ∈ [0, 1]
⇔
⇔
0≤y≤1
√
y≤1
0≤
√
y análogamente −1 ≤ − y ≤ 0
entonces
fY (y) =
8
<
:
E[Y]
=
=
1
√ ,
2 y
0,
en otro caso
Z
+∞
yfY (y)dy
−∞
Z 1
1
y √ dy
2 y
Z 1
1
1
lı́m
y 2 dy
2 ǫ→0 ǫ
1 2
· lı́m (1 − ǫ3/2 )
2 3 ǫ→0
1
3
0
=
=
=
0<y≤1
47
Teorema 2. Supongamos Y = g(X), entonces
E[Y] = E[g(X)] :=
8 P
<
k∈X[Ω] g(k)P [X = k],
: R∞
−∞
Ejemplo 40.
E[Y]
=
=
=
=
g(x)fX (x)dx,
X discreta
X continua
E[X2 ]
Z +∞
x2 fX (x)dx
Z
−∞
1
−1
1
x2 dx
2
1
3
Observación 35.
var(X)
:=
8 P
2
<
k (k − E[X]) P [X = k],
: R∞
−∞
=
X continua
2
E[(X − E[X]) ]
(g(x) = (x − E[X])2 ,
3.1.4.
rios
(X − E[X])2 fX (x)dx,
X discreta
x ∈ R)
Esperanza asociada a funciones de vectores aleato-
Teorema 3. Supongamos X = g(X, Y), entonces
E[g(X, Y)] :=
8 P P
<
x
y g(x, y)P [X = x, Y = y],
: R∞ R∞
−∞
−∞
g(x, y)fX (x, y)dxdy,
48
X, Y discreta
(X, Y) continua
3.1.5.
Propiedades de la Esperanza
1. Si X = c, entonces
E[X] = c
Observación 36. X = c
⇔
X[Ω] = {c}
P [X = c] = 1
2. Si c es constante, entonces
E[cX] = cE[X]
3. E[X + Y] = E[X] + E[Y]
Demostración. Sea
g(x, y) = x + y,
∀(x, y) ∈ R2
y supongase que (X, Y) es un vector continuo con densidad fX
X + Y = g(X, Y)
⇒
E[X + Y]
=
=
=
=
=
=
=
E[g(X, Y)]
Z +∞ Z +∞
−∞
Z +∞
Z
Z
−∞
+∞
−∞
+∞
−∞
Z +∞
Z
−∞
+∞
−∞
x
−∞
Z +∞
„Z
(x + y)fX (x, y)dxdy
xfX (x, y)dxdy +
xfX (x, y)dydx +
Z
Z
+∞
−∞
+∞
y
−∞
« Z
+∞
fX (x, y)dydx +
−∞
xfX (x)dx + E[Y]
Z
+∞
−∞
„Z
+∞
yfX (x, y)dxdy
+∞
−∞
yfY (y)dy
−∞
por definición de densidad marginal y esperanza
−∞
E[X] + E[Y]
4. Sean X y X variables aleatorias independientes, entonces
E[X · Y] = E[X] · E[Y]
49
«
fX (x, y)dx dy
Demostración. Sea
g(x, y) = x · y,
∀(x, y) ∈ R2
y supóngase que (X, Y) es un vector continuo con densidad fX
X · Y = g(X, Y)
⇒
E[X · Y]
=
E[g(X, Y)]
Z +∞ Z +∞
=
−∞
Z +∞
=
Z
=
=
−∞
y
−∞
E[X]
Z
„Z
x · yfX (x, y)dxdy
x · yfX (x)fY (y)dxdy
pues X y Y son independientes
«
+∞
xfX (x)dx fY (y)dy
−∞
+∞
yfY (y)dy
−∞
E[X] · E[Y]
=
3.1.6.
−∞
+∞
−∞
Z +∞
Propiedades de la Varianza
var(X) := E[(X − E[X])2 ]
1. Sea c es constante
Entonces
var(X + c) = var(X)
Demostración.
var(X + c)
=
=
=
=
E[(X + c − E[X + c])2 ]
E[(X + c − E[X] − c)2 ]
E[(X − E[X])2 ]
var(X)
2. Sea c una constante
Entonces
var(cX) = c2 var(X)
50
Demostración.
var(cX)
=
=
=
=
E[(cX − E[cX])2 ]
E[(cX − cE[X])2 ]
c2 E[(X − E[X])2 ]
c2 var(X)
3. Sean X y X variables aleatorias independientes, entonces
var(X + Y) = var(X) + var(Y)
Demostración.
var(X + Y)
=
=
=
=
=
=
E[((X + Y) − E[X + Y])2 ]
E[(X − E[X]) + (Y − E[Y])2 ]
var(X) + 2E[(X − E[X])(Y − E[Y])] + var(Y)
var(X) + var(Y) + 2(E[XY] − E[X]E[Y] − E[X]E[Y] + E[X]E[Y])
var(X) + var(Y) + 2(E[XY] − E[X]E[Y])
var(X) + var(Y)
51
Ejemplo 41. Suponga que X y Y son variables aleatorias independientes
con densidades:
f (x) = x83 , x > 2;
g(y) = 2y, 0 < y < 1
a) Encuentre la densidad de Z = XY
primero observe que
z
z = xy ⇒ y =
x
de donde 0 < y < 1 ⇒ 0 < z < x
f (x) =
8
<
8
x3
:
g(y) =
0
8
< 2y
:
si x > 2
en otro caso
si 0 < z < x
0
en otro caso
Sea z ∈ [0, ∞]
fXY (z)
=
=
Z
Z2 ∞
2
=
=
Sea z ∈ [2, ∞]
52
∞
„ «
1
8 2z
dx
x3 x |x|
16z
dx
x5
16z
4(2)4
z
4
fXY (z)
Z
=
∞
Zz ∞
=
z
„ «
1
8 2z
dx
x3 x |x|
16z
dx
x5
4
z3
=
por lo tanto
8
<
fXY (z) =
:
b) Obtenga E[Z] de dos maneras:
z
4
si 0 ≤ z < 2
4
z3
si z > 2
i) Usando la densidad de Z
E[Z]
Z
=
+∞
zfZ (z)dz
−∞
Z 2
=
z
z dz +
4
0
1
4
8
3
=
=
Z
2
2
Z
+∞
z
2
z dz + 4
0
Z
4
dz
z3
+∞
z −2 dz
2
ii) Directamente, sin usar la densidad de Z
E[Z]
=
E[XY]
=
E[X]E[Y]
„Z ∞
« „Z 1
«
8
x 3 dx
y(2y)dy
x
2
0
„ Z ∞
«„ Z 1
«
−2
8
x dx
2
y 2 dy
=
=
2
=
8
3
53
0
Ejemplo 42. Suponga que X es una variable aleatoria tal que E[X] = 10
y var(X) = 25
¿Para que valores positivos de a y de b tiene Y = aX − b esperanza
cero y varianza 1?
1
=
=
var(Y)
var(aX − b)
=
var(aX)
=
a2 · var(X)
=
a2 · 25
entonces
a=
0
1
5
=
E[Y]
=
E[aX − b]
=
=
a · E[X] − b
1
· 10 − b
5
entonces
b=2
54
3.1.7.
Desigualdad de Chebyschev
Sea X una variable aleatoria con esperanza y varianza, ambas finitas.
Entonces para cada δ > 0, se cumple
P [|X − E[X]| < δ] ≥ 1 −
var(X)
δ2
(3)
Observación 37.
1−
var(X)
≤ P [|X − E[X]| < δ] ≤ 1
δ2
Demostración. Supongase que X es continua
var(X)
=
=
=
E[(X − E[X])2 ]
Z +∞
(X − E[X])2 fX (x)dx
−∞
Z
Z
(X − E[X])2 fX (x)dx +
{x:|X−E[X]|<δ}
≥
=
Z
{x:|X−E[X]|≥δ}
Z
{x:|X−E[X]|≥δ}
(X − E[X])2 fX (x)dx
{x:(X−E[X])2 ≥δ 2 }
≥
=
δ2
(X − E[X])2 fX (x)dx
(X − E[X])2 fX (x)dx
Z
fX (x)dx
{x:(X−E[X])2 ≥δ 2 }
δ2
Z
fX dx
{x:P [(X−E[X])2 ≥δ 2 ]}
=
δ2
Z
fX dx
{x:P [|X−E[X]|≥δ]}
=
=
δ 2 P [|X − E[X]| ≥ δ]
δ 2 (1 − P [|X − E[X]| < δ])
⇒
P [|X − E[X]| < δ] ≥ 1 −
var(X)
δ2
Observación 38. Sea X una variable aleatoria tal que var(X) = 0. Entonces X ≡ E[X]
55
3.1.8.
Ley debil de los grandes números
Sean X1 , X2 , . . . variables aleatorias independientes e identicamente
distribuidas
Supongase que X1 tiene esperanza y varianza finitas. Denotemos, para
cada n = 1, 2, 3, . . .
Sn := X1 + X2 + · · · + Xn
Entonces para cada δ > 0 tenemos
˛
»˛
–
˛ Sn
˛
lı́m P ˛˛
− E[X1 ]˛˛ < δ = 1
n→∞
n
(para n grande
Sn
n
≈ E[X1 ])
Demostración. Note que para n = 1, 2, . . .
E[Sn ] = E[X1 + · · · + Xn ] = n · E[X1 ]
var(Sn ) = var(X1 + · · · + Xn ) = n · var(X1 )
Entonces, dado δ > 0
˛
»˛
–
˛ Sn
˛
˛
P ˛
− E[X1 ]˛˛ < δ
n
=
≥
=
=
P [|Sn − n · E[X1 ]| < n · δ]
var(Sn )
usando la desigualdad de chebyschev
n2 δ 2
n · var(X1 )
1−
n2 · δ 2
var(X1 )
1−
n · δ2
1−
por tanto, para cada n = 1, 2, . . .
˛
–
»˛
˛ Sn
˛
var(X1 )
1 ≥ P ˛˛
− E[X1 ]˛˛ < δ ≥ 1 −
n
n · δ2
se sigue entonces que cuando n → ∞:
˛
»˛
–
˛ Sn
˛
lı́m P ˛˛
− E[X1 ]˛˛ < δ = 1
n→∞
n
56
3.1.9.
Ley fuerte de los grandes números
Sean X1 , X2 , . . . variables aleatorias independientes e identicamente
distribuidas
Supongase que X1 tiene esperanza finita
Entonces,
( Snn
Sn
→ E[X1 ]
n
≈ E[X1 ], para n grande)
con probabilidad 1
Observación 39. Supongase que X ∼ B(1, p), Y ∼ B(1, p), y que X y Y
son independientes
¿Cuál es la distribución probabilistica de X + Y?
(X + Y)[Ω] = {0, 1, 2}
P [X + Y = 0]
=
P [X = 0, Y = 0]
=
(P [X = 0])2
=
(1 − p)2
C02 p0 (1 − p)2
=
P [X + Y = 1]
=
=
P [X + Y = 2]
2P [X = 0] · P [Y = 1]
C12 p(1 − p)
=
C22 p2 (1 − p)0
∴ X + Y ∼ B(2, p)
Observación 40. En general es posible demostrar por inducción que:
Si X1 , X2 , . . . , Xn son independientes y Xi ∼ B(1, p), ∀i = 1, 2, . . . , n,
entonces
X1 + X2 + · · · + Xn ∼ B(n, p)
57
Ejemplo 43 (frecuencia relativa). Sea ǫ un experimento aleatorio con
espacio de probabilidad (Ω, F, P )
Sea A un evento tal que p = P [A]
Para cada i = 1, 2, . . . , n sea Xi ∼ B(1, p) y suponga que X1 , X2 , . . . , Xn
son variables independientes.
observe que:
E[Xi ] = p
Sn
n
∀i = 1, 2, . . . , n
X1 +X2 +···+Xn
n
=
(frecuencia relativa de A)
pues Sn = X1 + X2 + · · · + Xn ∼ B(n, p)
por la ley de los grandes números
Sn
→ p = P (A),
n
3.1.10.
con probabilidad 1
Teorema Limite Central (Forma Clásica)
Teorema 4 (Teorema Limite Central). Sean X1 , X2 , . . . variables independientes identicamente distribuidas.
Supongase que X1 tiene esperanza y varianza finitas, con var(X1 ) > 0
Entonces
"
#
Z x
t2
Sn − E[Sn ]
1
lı́m P p
≤x = √
e− 2 dt
n→∞
2π −∞
var(Sn )
x ∈ R, Sn := X1 + · · · + Xn ,
n = 1, 2, . . .
Observación 41. En pocas palabras el teorema dice que si n es grande,
Sn − E[Sn ]
p
≈ X∗
var(Sn )
Observación 42. El teorema anterior se puede interpretar para X∗ ∼
N (0, 1) como sigue:
#
"
Sn − E[Sn ]
≤ x = P [X∗ = x]
lı́m P p
n→∞
var(Sn )
Observación 43. var(X) = 0 ⇒ X constante
Observación 44.
"
#
Sn − E[Sn ]
E p
var(Sn )
=
=
=
1
p
E[Sn − E[Sn ]]
var(Sn )
1
p
(E[Sn ] − E[Sn ])
var(Sn )
0
58
var
Sn − E[Sn ]
p
var(Sn )
!
=
=
=
1
p
var(Sn − E[Sn ])
var(Sn )
1
p
var(Sn )
var(Sn )
1
Observación 45. Si X ∼ B(n, p), entonces para poder aplicar el teorema
se debe satisfacer tambien lo siguiente:
X = Sn = X1 + · · · + Xn
Xi ∼ B(1, p),
∀i = 1, 2, . . . , n
X1 , . . . , Xn son independientes
Ejemplo 44 (Aproximacion normal a la Binomial). Sea X ∼ B(900, 12 )
entonces
E[X] = (900)( 21 ) = 450
var(X) = (900)( 21 )(1 − 21 ) = 225
X = S900 por observación 40
P [X ≥ 500]
=
=
≈
=
P [400 ≤ X ≤ 500]
=
=
=
P [X = 420]
=
=
=
=
=
=
P [S900 ≥ 500]
"
#
S900 − E[S900 ]
500 − 450
p
√
P
≥
225
var(S900 )
P [X∗ ≥ 3,33]
0,0004
P [400 ≤ S900 ≤ 500]
#
"
S900 − E[S900 ]
500 − 450
400 − 450
√
≤ √
P
≤ p
225
225
var(S900 )
0,9992
P [419,5 ≤ X ≤ 420,5]
–
»
420,5 − 450
419,5 − 450
∗
√
√
≤X ≤
P
225
225
∗
P [−2,63 ≤ X ≤ −1,96]
φ(2,03) − φ(1,96)
0,4788 − 0,4750
0,0638
59
PROBLEMA 46. Al sumar números, una computadora aproxima cada
número al entero mas próximo. Supongase que todos los errores de aproximación son independientes y que están distribuidos uniformemente en
[-0.5,0.5]. Si se suman 1500 números, ¿cuál es la probabilidad de que el
valor absoluto del error total exceda a 15?
Solución 47.
8
< Xi = errores de aproximación
:
Xi ∼ U [−0.5, 0.5]
i = 1, 2, . . . , 1500
∀i = 1, 2, . . . , 1500
S1500 = X1 + · · · + X1500
P [|S1500 | > 15]
=
≈
=
=
=
=
P [S1500 > 15] + P [S1500 < −15]
15 − 0
−15 − 0
P [X∗ >
] + P [X∗ <
]
11.18
11.18
P [X∗ > 1,341] + P [X∗ < −1,341]
2P [X∗ > 1,341]
«
„
1
− φ(1,341)
2
2
0.1802
PROBLEMA 48. Supongase que los tiempos de espera para los clientes
que pasan por una caja registradora a la salida de una tienda son variables
aleatorias independientes e identicamente distribuidas con esperanza 1.5
minutos y varianza 1.0
Aproxime la probabilidad de que se pueda atender a 100 clientes en
menos de 120 minutos.
Solución 49.
Xi = tiempo de espera del i-esimo cliente
i = 1, 2, . . . , 100
S100 = X1 + · · · + X100
P [S100 ≤ 120]
≈
=
=
=
120 − 150
]
10
∗
P [X ≤ 3]
1
+ φ(3)
2
0.9974
P [X∗ ≤
60
PROBLEMA 50. Supongase que tenemos 20 voltajes vi , i = 1, 2, . . . , 20
con ruido independiente
P que se reciben en lo que se llama un ”sumador
de voltaje”. Sea V = 20
i=1 vi donde se supone que vi ∼ U [0, 10] para toda
i = 1, . . . , 20
Aproxime P [V > 105]
Solución 51.
8
< Xi = voltajes con ruido
S20 = V
:
Xi ∼ U [0, 10]
P [V > 105]
=
≈
=
=
=
i = 1, 2, . . . , 20
∀i = 1, 2, . . . , 20
P [S20 > 105]
105 − 100
P [X∗ >
]
12.90
∗
P [X > 0.3875]
1
− φ(0,3875)
2
0.352
61
PROBLEMA 52. a) Sea c una constante y X una variable aleatoria
con E[X] = µ y var(X) = σ 2
Demuestre que
E[(X − c)2 ] = (µ − c)2 + σ 2
b) Supongase que E[(X − c)2 ] se piensa como función de c,
es decir
g(c) = E[(X − c)2 ],
c∈R
¿Para que valor de c, g alcanza su mı́nimo?
Solución 53. a)
E[(X − c)2 ]
=
=
=
=
E[X2 ] − 2cµ + c2 + µ2 − µ2
(µ − c)2 + (E[X2 ] − µ2 )
(µ − c)2 + (E[X2 − (E[X])2 ])
(µ − c)2 + var(X)
b) c = µ
PROBLEMA 54. Construya un ejemplo de una distribución de probabilidad cuya esperanza exista pero su varianza no (es decir esperanza finita
y varianza infinita)
Observación 55. Sea X una variable aleatoria tal que la función de
probabilidad puntual esta definida según la siguiente regla:
P [X = n] =
1 1
,
π / 6 n2
n=
entonces
E[X]
=
+∞
X
n=1
=
+∞
X
n=1
=
=
n · P [X = n]
n·
1 1
π 2 /6 n2
+∞
1 X1
π 2 /6 n=1 n
+∞
62
1, 2, . . .
| {z }
rango de X
Observación 56.
Sn − E[Sn ]
p
var(Sn )
1
(Sn − E[Sn ])
n
p
1
var(Sn )
n
Sn
− E[ Snn ]
n
=
=
q
1
var(Sn )
n2
− E[ Snn ]
q
var( Snn )
Sn
n
=
X∗
≈
para n grande
Ejemplo 45. Supongase que un instrumento electrónico tiene una duración T que está distribuida exponencialmente con parametro λ =0.001
Si se prueban 100 de tales instrumentos (lo que da valores observados:
T1 , . . . , T100 )
¿Cuál es la probabilidad de que 950 < T < 1100?
Observación 57. T =
E[T]
T1 +···+T100
100
=
=
=
=
=
=
q
var(T)
=
=
=
=
=
=
E
»
T1 + · · · + T100
100
–
1
E[T1 + · · · + T100 ]
100
100
E[T1 ]
100
E[T1 ]
1
λ
1000
s
var
„
T1 + · · · + T100
100
«
1 p
var(T1 + · · · + T100 )
100
10 p
var(T1 )
100
r
1
1
10 λ2
„
«
1
1
10 0,001
100
Observación 58. Se supuso que T1 , . . . , T100 son independientes
63
P [950 < T < 1100]
»
1100 − 1000
950 − 1000
∗
<T <
100
100
≈
P
=
P [−0,5 < T < 1]
=
0,5328
∗
–
PROBLEMA 59. Sean X1 , X2 , . . . variables independientes identicamente distribuidas
Supongase que E[X1 ] = λ y que var(X1 ) = q
Utilice el teorema lı́mite central para determinar el menor valor de n
para el cual
˛
»˛
–
˛ Sn
˛
˛
˛
P ˛
− λ˛ < 0,3 ≥ 0,95
n
donde Sn := X1 + · · · + Xn
64
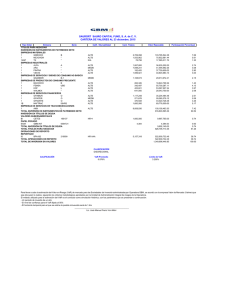
Áreas bajo la curva
normal estándar
de 0 a z
z
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
3.2
3.3
3.4
3.5
0
.0000
.0000
.0000
.1179
.1179
.1179
.2258
.2258
.2258
.3159
.3159
.3159
.3159
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
2
.0040
.0040
.0040
.1217
.1217
.1217
.2291
.2291
.2291
.3186
.3186
.3186
.3186
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
2
.0080
.0080
.0080
.1255
.1255
.1255
.2324
.2324
.2324
.3212
.3212
.3212
.3212
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
.4987
3
.0120
.0120
.0120
.1293
.1293
.1293
.2357
.2357
.2357
.3238
.3238
.3238
.3238
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
65
4
.0160
.0160
.0160
.1331
.1331
.1331
.2389
.2389
.2389
.3264
.3264
.3264
.3264
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
.4988
5
.0199
.0199
.0199
.1368
.1368
.1368
.2422
.2422
.2422
.3289
.3289
.3289
.3289
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
6
.0239
.0239
.0239
.1406
.1406
.1406
.2454
.2454
.2454
.3315
.3315
.3315
.3315
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
7
.0279
.0279
.0279
.1443
.1443
.1443
.2486
.2486
.2486
.3340
.3340
.3340
.3340
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
.4989
8
.0319
.0319
.0319
.1480
.1480
.1480
.2518
.2518
.2518
.3365
.3365
.3365
.3365
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
9
.0359
.0359
.0359
.1517
.1517
.1517
.2549
.2549
.2549
.3389
.3389
.3389
.3389
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
.4990
PROBABILIDAD
CONDICIONAL
Sea ǫ un experimento con espacio muestral Ω
Proposición 4.
P (Ac ) = 1 − P (A)
para todo evento A
Proposición 5.
P (B\A) = P (B) − P (A ∩ B)
Proposición 6.
P (A ∪ B) = P (A) + P (B) − P (A ∩ B)
Observación 60. En general
P (A1 ∪A2 ∪· · ·∪An ) =
n
X
P (Ak )−
k=1
X
i<k
Definición 17.
P (A|B) :=
P (Ai ∩Aj )+
X
i<k<j
P (Ai ∩Ak ∩Aj )−· · ·+(−1)n−1 P (A1 ∩· · ·∩An )
P (A ∩ B)
P (B)
Teorema 5 (Teorema de la multiplicación). Sean A1 , A2 , . . . , Am eventos
tales que P (A1 ∩ · · · ∩ Am ) > 0. Entonces
P (A1 ∩· · ·∩Am ) = P (A1 )·P (A2 |A1 )·P (A3 |A1 ∩A2 ) · · · P (Am |A1 ∩A2 ∩· · ·∩Am−1 )
Definición 18. Diremos que los eventos A1 , . . . , An forman una partición
de Ω si
a) Ai ∩ Aj = ∅ si i 6= j
b) Ω = A1 ∪ A2 ∪ · · · ∪ An
c) P (Ai ) > 0
∀i = 1, . . . , n
Teorema 6 (Teorema de la probabilidad total). Sea {Ai }n
i=1 una partición de Ω. Entonces, si A es un evento tenemos que
P (A) =
n
X
P (A|Ai )P (Ai )
i=1
Demostración. A = (A ∩ A1 ) ∪ (A ∩ A2 ) ∪ · · · ∪ (A ∩ An )
entonces
P (A) =
n
X
i=1
P (A ∩ Ai ) =
66
n
X
i=1
P (A|Ai ) · P (Ai )
Teorema 7 (Fórmula de Bayes). Supongase las hipótesis del Teorema
anterior. Sea Ak un elemento de la partición y sea A un evento, con
P (A) > 0. Entonces
P (Ak |A) =
P (Ak ∩ A)
P (A|Ak ) · P (Ak )
= Pn
P (A)
i=1 P (A|Ai ) · P (Ai )
Ejemplo 46. Un motor V8 de autómovil tiene tres soportes independientes, cuyas probabilidades de romperse en un lapso de 8 años son, respectivamente, 0.2, 0.4 y 0.3 %. Si el conductor del vehı́culo percibe el ruido
caracterı́stico de dos soportes quebrados, halle la probabilidad de que se
hayan roto los soportes primero y segundo.
Llamemos pi la probabilidad de que se haya roto el soporte i y qi la
probabilidad de que no se haya roto el soporte i
B1
=
B2
=
B3
=
p1
=
0,2
p2
=
0,4
p3
=
0,3
{ se rompieron 1 y 2 pero no el 3}
{ se rompieron 1 y 3 pero no el 2}
{ se rompieron 2 y 3 pero no el 1}
P (B1 )
=
p1 p2 q3
P (B2 )
=
p1 q2 p3
P (B3 )
=
q1 p2 p3
Sea A = {se rompieron 2 soportes}
P (A) =
3
X
P (Bi ) = 0,1880
i=1
Aplicando Bayes obtenemos:
P (B1 |A)
=
=
=
P (B1 )P (A|B1 )
P (A)
p1 p2 q3
P (A)
0,2978
67
Índice
1. VARIABLES ALEATORIAS DISCRETAS
1.1. Variable Aleatoria Binomial . . . . . . . . . . . . . . . . .
1.2. Variable Aleatoria de Poisson . . . . . . . . . . . . . . . .
1.3. Variable Aleatoria Geometrica . . . . . . . . . . . . . . . .
1.4. Función de distribucion acumulativa . . . . . . . . . . . .
1.4.1. Propiedades de la distribución acumulativa asociada
a una variable aleatoria discreta . . . . . . . . . .
1.5. Variable Aleatoria Hipergeometrica . . . . . . . . . . . . .
.
.
.
.
. 9
. 10
2. ESPACIOS DE PROBABILIDAD Y VARIABLES ALEATORIAS
2.1. VARIABLES ALEATORIAS CONTINUAS . . . . . . . . .
2.1.1. VARIABLES ALEATORIAS CONTINUAS DEFINIDAS MEDIANTE DENSIDADES . . . . . . . . .
2.2. Ejemplos de variables aleatorias continuas . . . . . . . . . .
3. VARIABLES ALEATORIAS (BIDIMENSIONALES)
3.0.1. Función de probabilidad puntual de X . . . . . . . .
3.0.2. Funciones de probabilidad puntual marginales . . . .
3.0.3. Funciones de probabilidad condicional . . . . . . . .
3.0.4. Vectores aleatorios generados por densidades . . . .
3.0.5. Densidades Marginales . . . . . . . . . . . . . . . . .
3.0.6. Densidades Condicionales . . . . . . . . . . . . . . .
3.0.7. Densidades de funciones de variable aleatoria . . . .
3.0.8. Densidades de la suma y del producto de variables
aleatorias independientes . . . . . . . . . . . . . . .
3.1. ESPERANZA Y VARIANZA . . . . . . . . . . . . . . . . .
3.1.1. Esperanza . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2. Varianza . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.3. Esperanza de funciones de variables aleatorias . . . .
3.1.4. Esperanza asociada a funciones de vectores aleatorios
3.1.5. Propiedades de la Esperanza . . . . . . . . . . . . .
3.1.6. Propiedades de la Varianza . . . . . . . . . . . . . .
3.1.7. Desigualdad de Chebyschev . . . . . . . . . . . . . .
3.1.8. Ley debil de los grandes números . . . . . . . . . . .
3.1.9. Ley fuerte de los grandes números . . . . . . . . . .
3.1.10. Teorema Limite Central (Forma Clásica) . . . . . . .
68
1
1
3
5
8
11
12
13
14
23
23
23
23
25
26
29
32
38
43
43
45
47
48
49
50
55
56
57
58