Cinemática de sistemas de partículas - prof.usb.ve.

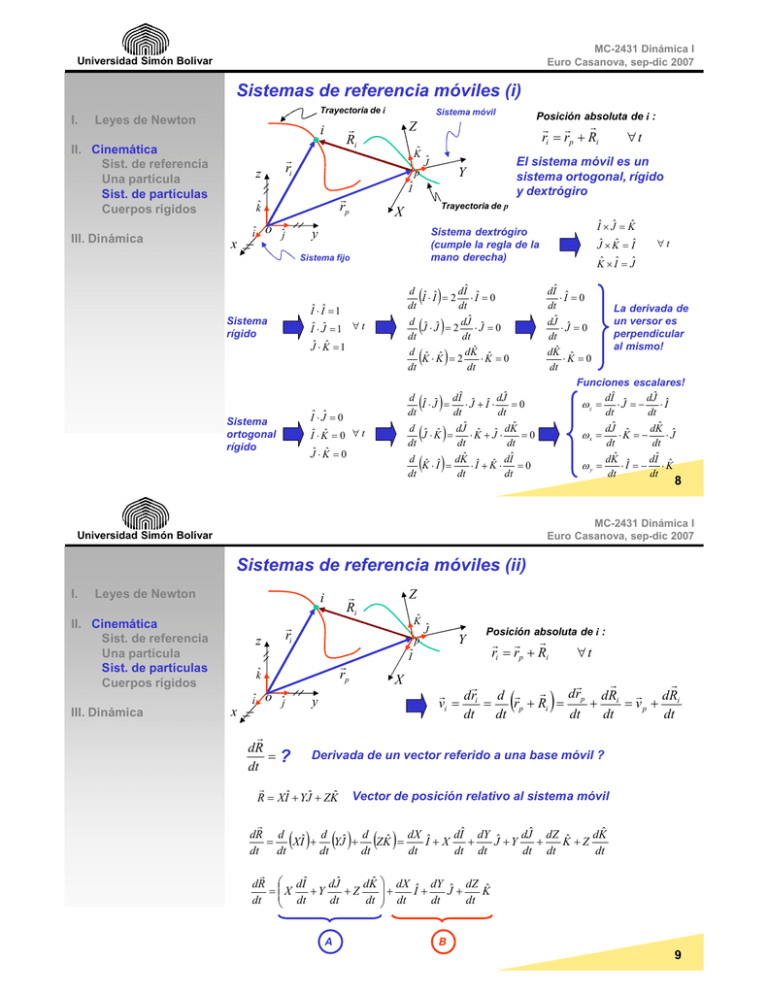
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (i)
I.
Trayectoria de i
Leyes de Newton
III. Dinámica
r
Ri
i
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
x
Ĵ
Iˆ
Trayectoria de p
X
Sistema fijo
( )
( )
Jˆ ⋅ Kˆ = 1
(
( )
(
Jˆ ⋅ Kˆ = 0
La derivada de
un versor es
perpendicular
al mismo!
Funciones escalares!
dIˆ
dJˆ
ω z = ⋅ Jˆ = − ⋅ Iˆ
dt
dt
ˆ
dJ ˆ
dKˆ ˆ
ωx =
⋅K = −
⋅J
dt
dt
dKˆ ˆ
dIˆ
ωy =
⋅ I = − ⋅ Kˆ
dt
dt
d ˆ ˆ dIˆ ˆ ˆ dJˆ
I⋅J = ⋅J +I ⋅
=0
dt
dt
dt
d ˆ ˆ dJˆ ˆ ˆ dKˆ
J ⋅K =
⋅K + J ⋅
=0
dt
dt
dt
d ˆ ˆ dKˆ ˆ ˆ dIˆ
K⋅I =
⋅I + K ⋅ = 0
dt
dt
dt
Iˆ ⋅ Jˆ = 0
Iˆ ⋅ Kˆ = 0 ∀ t
Sistema
ortogonal
rígido
)
∀t
Kˆ × Iˆ = Jˆ
dIˆ ˆ
⋅I =0
dt
dJˆ ˆ
⋅J = 0
dt
dKˆ ˆ
⋅K =0
dt
d ˆ ˆ
dIˆ
I ⋅ I = 2 ⋅ Iˆ = 0
dt
dt
d ˆ ˆ
dJˆ
J ⋅ J = 2 ⋅ Jˆ = 0
dt
dt
d ˆ ˆ
dKˆ ˆ
K⋅K = 2
⋅K = 0
dt
dt
Iˆ ⋅ Iˆ = 1
Iˆ ⋅ Jˆ = 1 ∀ t
Sistema
rígido
Iˆ × Jˆ = Kˆ
Jˆ × Kˆ = Iˆ
Sistema dextrógiro
(cumple la regla de la
mano derecha)
y
ĵ
∀t
El sistema móvil es un
sistema ortogonal, rígido
y dextrógiro
Y
p
r
rp
o
r r r
ri = rp + Ri
K̂
k̂
Posición absoluta de i :
Z
r
ri
z
iˆ
Sistema móvil
)
( )
8
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (ii)
I.
Leyes de Newton
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
K̂
r
rp
o
r
dR
=?
dt
Y
Posición absoluta de i :
Iˆ
X
y
ĵ
Ĵ
p
k̂
x
Z
r
ri
z
iˆ
III. Dinámica
r
Ri
i
r r r
ri = rp + Ri
∀t
r
r
r
r
drp dRi r dRi
r dri d r r
vi =
rp + Ri =
=
+
= vp +
dt
dt
dt
dt
dt
(
)
Derivada de un vector referido a una base móvil ?
r
R = XIˆ + YJˆ + ZKˆ
Vector de posición relativo al sistema móvil
r
dR d ˆ d ˆ d
dX ˆ
dIˆ dY ˆ
dJˆ dZ ˆ
dKˆ
=
XI + YJ +
ZKˆ =
I+X
+
J +Y
+
K +Z
dt
dt
dt
dt
dt
dt dt
dt dt
dt
( )
( )
( )
r
dR ⎛ dIˆ
dJˆ
dKˆ ⎞ dX ˆ dY ˆ dZ ˆ
⎟+
= ⎜⎜ X
+Y
+Z
I+
J+
K
dt ⎝ dt
dt
dt ⎟⎠ dt
dt
dt
A
B
9
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (iii)
I.
Leyes de Newton
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
III. Dinámica
⎛ dIˆ
dJˆ
dKˆ ⎞ ⎛ dIˆ ˆ
dJˆ ˆ
dKˆ ˆ ⎞ ˆ ⎛ dIˆ ˆ
dJˆ ˆ
dKˆ ˆ ⎞ ˆ
⎟
⎜X
⎟ ⎜
⎟ ⎜
⎜ dt + Y dt + Z dt ⎟ = ⎜ X dt ⋅ I + Y dt ⋅ I + Z dt ⋅ I ⎟ I + ⎜ X dt ⋅ J + Y dt ⋅ J + Z dt ⋅ J ⎟ J +
⎝
⎠ ⎝
⎠ ⎝
⎠
ˆ
ˆ
ˆ
⎛ dI ˆ
dJ ˆ
dK ˆ ⎞ ˆ
+ ⎜⎜ X
⋅ K +Y
⋅K + Z
⋅ K ⎟⎟ K
A
dt
dt
dt
⎝
⎠
dIˆ ˆ dJˆ ˆ dKˆ ˆ
⋅I =
⋅J =
⋅K = 0
dt
dt
dt
Recordando :
ωz =
dIˆ ˆ
dJˆ
dJˆ ˆ
dKˆ ˆ
dKˆ ˆ
dIˆ
⋅ J = − ⋅ Iˆ ; ω x =
⋅K = −
⋅ J ; ωy =
⋅ I = − ⋅ Kˆ
dt
dt
dt
dt
dt
dt
Iˆ
⎛ dIˆ
dJˆ
dKˆ ⎞
ˆ
ˆ
ˆ
⎜X
⎟
⎜ dt + Y dt + Z dt ⎟ = (− Yω z + Zω y )I + ( Xω z − Zω x )J + (− Xω y + Yω x )K = ω x
⎝
⎠
X
r
Definiendo : ω = ω x Iˆ + ω y Jˆ + ω z Kˆ
Jˆ
Kˆ
ωy ωz
Y
Z
Velocidad Angular Absoluta del sistema pXYZ:
⎛ dIˆ
dJˆ
dKˆ ⎞ r
⎜X
⎟
⎜ dt + Y dt + Z dt ⎟ = ω × R
⎝
⎠
A
10
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (iv)
I.
Leyes de Newton
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
III. Dinámica
r
dX ˆ dY ˆ dZ ˆ & ˆ & ˆ & ˆ DR
I+
J+
K = XI + YJ + ZK =
dt
dt
dt
Dt
Derivada relativa a pXYZ
(como si pXYZ no se moviera!)
B
A
B
r
r
dR r r DR
=ω×R+
dt
Dt
Regla general para derivar un vector
referido a una base móvil
Derivadas de los versores de la base móvil
(Relaciones de Poisson)
dIˆ r ˆ
=ω×I
dt
dJˆ r ˆ
=ω×J
dt
dKˆ r ˆ
=ω×K
dt
DIˆ DJˆ DKˆ r
=
=
=0
Dt
Dt
Dt
Siméon Poisson
(1781-1840)
11
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (v) : Velocidad
I.
Leyes de Newton
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
K̂
Y
Iˆ
r
rp
o
Ĵ
p
k̂
x
Z
r
ri
z
iˆ
III. Dinámica
r
Ri
i
Posición absoluta de i :
r r r
ri = rp + Ri
X
y
ĵ
∀t
r
r
r
r
drp dRi r
r dri d r r
v r DRi
vi =
r + Ri =
=
+
= v p + ω × Ri +
dt
dt p
dt
dt
Dt
r
r
DRi
Definiendo : VRi =
Dt
r r v
r r
vi = v p + ω × Ri + VRi
(
r
vp
r
ω
r
Ri
v
VRi
)
Velocidad absoluta del punto p
Velocidad angular absoluta del sistema pXYZ
Vector posición de i respecto a pXYZ
Velocidad relativa de i respecto a pXYZ
12
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (vi) : Aceleración
I.
Leyes de Newton
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
III. Dinámica
r
r dvi d r
v r v
v p + ω × Ri + VRi =
ai =
=
dt
dt
r
v
dv
dω r v ⎛ v r
= p+
× Ri + ω × ⎜⎜ ω × Ri
dt
dt
⎝
v
r dω
Definiendo :
α=
dt
(
)
(
(
r
v
v
dω r v dRi dVRi
+
× Ri + ω ×
+
dt
dt
dt
dt
r
v
DRi ⎞ v v
D VRi
⎟⎟ + ω × VRi +
+
Dt ⎠
Dt
r
r
DVRi
ARi =
Dt
r
dv p
)
)
Aceleración
de Coriolis
v
r r v v r
r v
v v
ai = a p + α × Ri + ω × ω × Ri + 2ω × VRi + ARi
r
ap
r
αp
r
Ri
r
ω
v
VRi
r
ARi
Aceleración absoluta del punto p
Aceleración angular absoluta del sistema pXYZ
Vector posición de i respecto a pXYZ
Gustave Coriolis
(1792-1843)
Velocidad angular absoluta del sistema pXYZ
Velocidad relativa de i respecto a pXYZ
Aceleración relativa de i respecto a pXYZ
13
MC-2431 Dinámica I
Euro Casanova, sep-dic 2007
Universidad Simón Bolívar
Sistemas de referencia móviles (vii) : Movimiento
I.
Z
Leyes de Newton
K̂
II. Cinemática
Sist. de referencia
Una partícula
Sist. de partículas
Cuerpos rígidos
k̂
Z
K̂
r
rp ( t1 )
z
x
Y
Ĵ
p
Iˆ
X
o
iˆ
Z
r
rp ( t 0 )
X
III. Dinámica
Ĵ
p
Iˆ
∀t
Y
K̂
Traslación
pura
Ĵ
p
r
rp ( t2 )
ĵ
Z′
z
r
X
Iˆ
X
ĵ
K̂
p Ĵ
r
rp
k̂
x
r
ω=0
r r
α =0
Y
y
Z
o
dIˆ dJˆ dKˆ r
=
=
=0
dt
dt
dt
Iˆ
Rotación pura
respecto a p
iˆ
r
r
vp ≠ 0
Y′
Y′
Y
∀t
r
r
vp = 0 ⇒
r
r
ap = 0
dIˆ dJˆ dKˆ
Al menos 2 de :
;
;
dt dt dt
deben ser no nulas
r
r
ω≠0
X′
y
14