(análisis del parámetro a en la función potencia).
Anuncio

Segundo Año Medio
Profesor: Andrés Millán
Unidad: FUNCIÓN POTENCIA
Contenido: ANÁLISIS DE PARÁMETROS
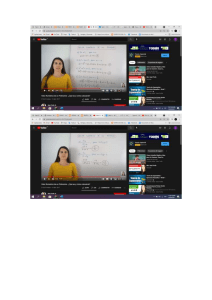
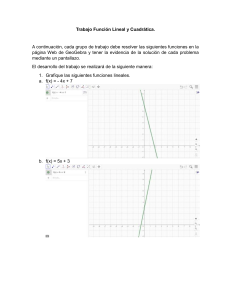
ANÁLISIS DEL PARÁMETRO “a” EN LA FUNCIÓN POTENCIA
Nombre:
Fecha:
Presentación
Objetivo de la clase: Analizar las relaciones entre gráficos, los exponentes y los parámetros en la función
potencia.
𝑓(𝑥) = 𝑎𝑥 𝑛
𝑐𝑜𝑛 𝑎 ∈ ℝ − {0}
∧
𝑛 ∈ ℕ − {1}
Actividad. Desarrolla ordenadamente en tu cuaderno
Desarrolle las siguientes actividades en la guía o en su cuaderno.
1- Determine la forma de la gráfica de las siguientes funciones potencia, indicando el coeficiente “a” y el
exponente “n”.
Función
𝑓(𝑥) = 𝑥 3
a
n
Gráfica
𝑓(𝑥) = −𝑥 3
1
𝑓(𝑥) = 𝑥 4
2
3
𝑓(𝑥) = − 𝑥 6
5
𝑓(𝑥) = −𝑎𝑥 8 ; 𝑎 > 0
𝑓(𝑥) =
1
𝑥5 ; 𝑏 > 𝑐
𝑏−𝑐
𝑓(𝑥) = √2 𝑥 2𝑛
𝑓(𝑥) = −
√2 2𝑛+1
𝑥
2
2-
Dadas las funciones 𝑓(𝑥) = 𝑎𝑥 𝑛 y 𝑔(𝑥) = 𝑏𝑥 𝑛 , con 𝑎, 𝑏 ∈ ℝ+ − {0}. ¿Es correcto afirmar con seguridad
que si 𝑎 > 𝑏, la gráfica de la función 𝑓(𝑥) = 𝑎𝑥 𝑛 estará más cerca del eje de las ordenadas que la gráfica
de la función 𝑔(𝑥) = 𝑏𝑥 𝑛 ? Justifique.
34-
Grafique la función 𝑓(𝑥) = √𝑥 − 5 y determine su dominio y recorrido.
Complete la siguiente tabla en donde podrá sintetizar el comportamiento de la gráfica de la función
potencia 𝑓(𝑥) = 𝑎𝑥 𝑛 según los valores del coeficiente “a” y el exponente “n”.
Si “a” es:
Positivo
y “n” es:
Impar
Entonces la forma de la gráfica de la función potencia es:
Página 1