Ejercicios de velocidad

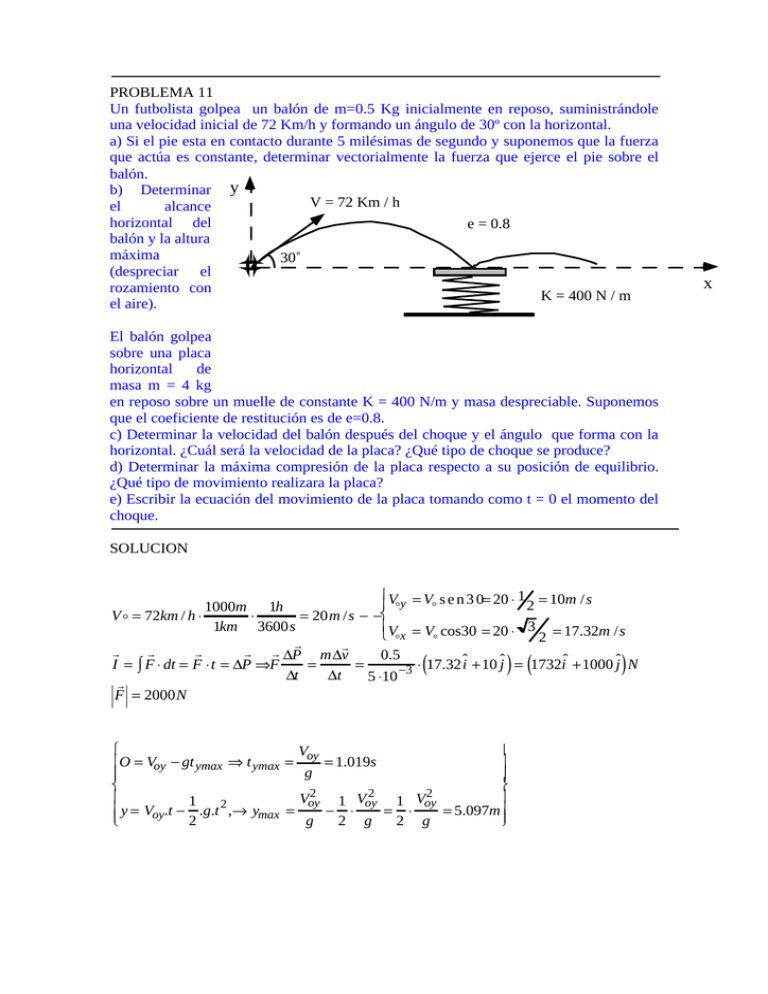
PROBLEMA 11
Un futbolista golpea un balón de m=0.5 Kg inicialmente en reposo, suministrándole
una velocidad inicial de 72 Km/h y formando un ángulo de 30º con la horizontal.
a) Si el pie esta en contacto durante 5 milésimas de segundo y suponemos que la fuerza
que actúa es constante, determinar vectorialmente la fuerza que ejerce el pie sobre el
balón.
b) Determinar y
V = 72 Km / h
el
alcance
horizontal del
e = 0.8
balón y la altura
máxima
30˚
(despreciar el
rozamiento con
K = 400 N / m
el aire).
El balón golpea
sobre una placa
horizontal
de
masa m = 4 kg
en reposo sobre un muelle de constante K = 400 N/m y masa despreciable. Suponemos
que el coeficiente de restitución es de e=0.8.
c) Determinar la velocidad del balón después del choque y el ángulo que forma con la
horizontal. ¿Cuál será la velocidad de la placa? ¿Qué tipo de choque se produce?
d) Determinar la máxima compresión de la placa respecto a su posición de equilibrio.
¿Qué tipo de movimiento realizara la placa?
e) Escribir la ecuación del movimiento de la placa tomando como t = 0 el momento del
choque.
SOLUCION

1
 Voy = Vo s e n 3 0= 20 ⋅ 2 = 10m /s
1000m 1h
Vo = 72km / h ⋅
⋅
= 20m /s − −
1km 3600s
 V = V cos30 = 20 ⋅ 3 = 17.32m /s
 ox
o
2
r
r
r
r
r
r r ∆P m∆v
0.5
I = ∫ F ⋅ dt = F ⋅t = ∆P ⇒F
=
=
⋅ 17.32 iˆ +10 jˆ = 1732iˆ +1000 jˆ N
−3
∆t
∆t
5 ⋅10
r
F = 2000 N
(
) (


V
O = Voy − gt ymax ⇒ t ymax = oy = 1.019s

g




2
2
2


V
V
V
1
1
1
oy
oy
oy
 y = Voy.t − .g.t 2 ,→ ymax =

−
⋅
=
⋅
=
5.097m


2
g
2 g
2 g
)
x


2.Voy
1
2
0 = Voy .txmax − ⋅ g⋅ t xmax
⇒ txmax =
= 2.038s 
2
g




2Vox .Voy


= 35.31m
 xmax = Vox .t max =


g

Choque central oblicuo. Es inelástico, ya que la energía no se conserva.
A=bola
conservación del momento: m AV Ay + m BVBy = m AV ´ Ay + m BV ´ By
B=placa
coeficiente de restitución: e = −
( VBy′ − VAy′ )
(VBy − VAy )
⇒ − eVAy = VAy
′ − VBy
′
La componente x de la velocidad permanece constante. Al suponer despreciable
el rozamiento del aire, la velocidad con la que llega a la placa es la misma que la de
salida, pero con la componente y cambiada de signo.
VAx = 17.32m/ s

Velocidad antes del choque 
 VAy = −10m / s 
(
)
0.5( −10) = 0.5VAy
′ + 4VBy
′ ⇒ −5 = 0.5 VBy
′ + 8 + 4VBy
′ ⇒ −9 = 4.5VBy
′ ⇒ VBy
′ = −2m/ s
−0.8( −10) = VAy
′ − VBy
′ ⇒ VAy
′ = VBy
′ + 8 ⇒ VAy
′ = 6m / s
V ´ A = 18.33m / s
tg A =
VAy
′
VAx
′
⇒ A = 19.11º
Aplicamos el principio de conservación de E entre A y B.
1
1
1
1
1
2
K.y02 + m.g.y max + mV 2 = K (y0 + ymax ) = K.y02 + K.y 2max + K.y0 .ymax ⇒
214444424442443 1
2 44
2
42444
3 2
A
B
mg
además en el equilibrio mg = K.y0 ⇒ y0 =
K
1
1
mg
m.g.ymax + mV 2 = K.y 2max + K
y
⇒ ymax =
2
2
K max
mV 2
16
=
= 0.2m
K
400
Realiza un movimiento armónico simple entorno a la posición de equilibrio con una
amplitud A=0.2m
La frecuencia angular será W =
K
=
m
400
= 10rad / s ; partiendo de la ecuación
4
 y = A.sen(Wt + Φ1) 
 como para t = 0 parte de la posición de equilibrio y = 0
general 
 y = A.cos(Wt + Φ2 ) 
 Φ = 0,

sen Φ1 = 0   1

⇒ 
⇒ 
3  además y empieza tomando valores negativos
cosΦ2 = 0 Φ2 = , 

2 2 
Φ1 = 


 ⇒ y = 0.2sen(10t + )
y = 0.2 cos(10t + )
o
⇒
2
 Φ2 = 

2