Programación Lineal y Entera

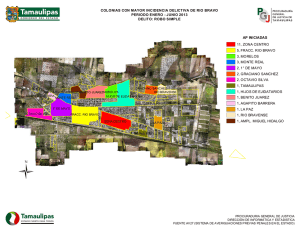
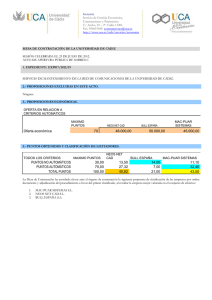
Programación Lineal y Entera
Balbina Virginia Casas Méndez
Casos prácticos con AMPL
MÁSTER EN TÉCNICAS ESTADÍSTICAS
Curso 2010/11
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Caso 1: Problema del Transporte
Un modelo para el Problema del Transporte
Un modelo AMPL para el Problema del Transporte
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Caso 1: Problema del Transporte
Un modelo para el Problema del Transporte
Un modelo AMPL para el Problema del Transporte
Enlaces en INTERNET
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Caso 1: Problema del Transporte
Enlaces en INTERNET
Lenguaje AMPL
AMPL es un lenguaje de modelado algebraico para
programación matemática: un lenguaje capaz de expresar en
notación algebraica problemas de optimización tales como los
problemas de programación lineal y entera.
La gran potencia del lenguaje AMPL está en separar el
modelo en sí por un lado y por otro los datos particulares del
problema concreto.
Los modelos AMPL involucran variables, restricciones y
objetivos, expresados con la ayuda de conjuntos y
parámetros. A todos se les llama elementos del modelo.
La llamada a AMPL normalmente causa la entrada en un
entorno de comandos, donde los comandos pueden ser
introducidos interactivamente. Las declaraciones del modelo y
las instrucciones de introducción de datos son también
aceptados como comandos.
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Caso 1: Problema del Transporte
Enlaces en INTERNET
KNITRO es un software para resolver problemas de
optimización matemática a gran escala. KNITRO está
especializado en optimización no lineal, pero también
resuelve problemas de programación lineal, problemas de
programación cuadrática y sistemas de ecuaciones no lineales.
Puede resolver también problemas con variables que toman
valores enteros.
Los problemas de optimización deben ser presentados en
forma matemática. Los problemas pueden ser escritos en C,
C++, Fortran, o Java, en cuyo caso KNITRO se llama como
una rutina software para resolver el problema.
Una a menudo sencilla aproximación es desarrollar el
problema de optimización en un lenguaje de modelado
algebraico (AML) como AIMMS, AMPL, GAMS, Mathematica,
etc. KNITRO se llama como un “solver" desde dentro de algún
entorno o servidor.
KNITRO ofrece tres algoritmos para resolver problemas de
optimización. Dos son de los denominados de punto interior y
uno es de los denominados de conjuntos activos.
Los métodos de punto interior siguen un camino a través del
interior de la región factible mientras que los métodos de
conjuntos activos tienden a permanecer en la frontera.
KNITRO proporciona ambos tipos de algoritmos para mayor
flexibilidad en la resolución de problemas y permite pasar de
uno a otro durante el proceso de obtención de la solución.
Proporciona una opción de “multistart" para promover el
cálculo del óptimo global y utiliza algoritmos de “branch and
bound" ante la presencia de variables enteras.
KNITRO, acrónimo de “Nonlinear Interior point Trust Region
Optimization" (la “K" es muda) fue creado en 2001 en
Northwestern por R. Waltz, J. Nocedal, T. Plantenga y R. Byrd.
Está comercializado por Ziena Optimization, Inc.
Introducción
El lenguaje AMPL
Optimizadores: KNITRO
El servidor NEOS
Caso 1: Problema del Transporte
Enlaces en INTERNET
Podemos acceder a este servidor libre en la dirección:
http://www-neos.mcs.anl.gov/
Los problemas de optimización se resuelven automáticamente.
El usuario debe proporcionar una definición del problema
(modelo, datos concretos y comandos a ejecutar en ficheros
de texto) y toda la información adicional requerida por el
“solver" de optimización se determina automáticamente. Los
resultados son enviados a la dirección de correo electrónico
proporcionada por el usuario.
Es necesario escoger un “solver" según el tipo de problema de
optimización que se quiera resolver y en caso de duda se
puede consultar el “Optimization Tree" de la guía de NEOS. La
elección del “solver" también depende del lenguaje utilizado
para definir el problema de optimización.
Introducción
Caso 1: Problema del Transporte
Un modelo para el Problema del Transporte
Un modelo AMPL para el Problema del Transporte
Enlaces en INTERNET
Un ejemplo de problema del transporte: resolución
informática (Parlar, 2000; Fourer y otros, 2002)
Ejemplo. Gastos de envío de esquíes. Para ilustrar este
modelo vamos a considerar el problema de SunSno, una
empresa multinacional con tres factorías en (1) Jasper,
Canadá, (2) Seoul, Korea, and (3) Toronto, Canadá. SunSno
transporta esquíes a cuatro empresas propietarias de
almacenes en (1) Frankfurt, Alemania, (2) New York, USA, (3)
París, Francia, y (4) Yokohama, Japón.
=
Las capacidades de producción semanales, ai , i 1; 2; 3 de
las m 3 factorías y las demandas semanales, bj ,
j 1; 2; 3; 4 de los n 4 almacenes están dados en la
siguiente tabla donde también indicamos los costes por unidad
de transporte cij , i 1; 2; 3 y j 1; 2; 3; 4.
=
=
=
=
=
Desde# n A!
Frankfurt
NY
París
Jasper
Seoul
Toronto
DEMANDA
19
15
11
150
7
21
3
100
13
18
12
200
Yokohama
8
6
20
150
SUMINISTRO
100
300
200
600
Para resolver este problema como uno de programación lineal,
definimos las variables Xij como el número de unidades
transportadas desde la factoría i al almacén j para las factorías
i 1; ; m y los almacenes j 1; ; n.
=
=
De esta forma, el modelo de programación lineal del problema
del transporte toma la siguiente forma:
Min Z
18X23
= 19X11 + 7X12 + 13X13 + 8X14 + 15X21 + 21X22 +
+ 6X24 + 11X31 + 3X32 + 12X33 + 20X34
sujeto a
+ X12 + X13 + X14 = 100 (Capacidad de Jasper)
X21 + X22 + X23 + X24 = 300 (Capacidad de Seoul)
X31 + X32 + X33 + X34 = 200 (Capacidad de Toronto)
X11 + X21 + X31 = 150 (Demanda de Frankfurt)
X12 + X22 + X32 = 100 (Demanda de New York)
X13 + X23 + X33 = 200 (Demanda de París)
X14 + X24 + X34 = 150 (Demanda de Yokohoma)
X11
Todo Xij
0:
Introducción
Caso 1: Problema del Transporte
Un modelo para el Problema del Transporte
Un modelo AMPL para el Problema del Transporte
Enlaces en INTERNET
El modelo del Transporte (transp_mod.txt)
#
#
set ORIG; orígenes
set DEST; destinos
param capacidad fORIGg >= 0; cantidades en orígenes
param demanda fDESTg >= 0; cantidades en destinos
check:
sum fi in ORIGg capacidad[i] = sum fj in DESTg
demanda[j];
param coste fORIG,DESTg >= 0; coste unitario
var Trans fORIG,DESTg >= 0; unidades a ser transportadas
minimize Coste_Total:
sum fi in ORIG, j in DESTg coste[i,j] * Trans[i,j];
subject to Capacidad fi in ORIGg:
sum fj in DESTg Trans[i,j] = capacidad[i];
subject to Demanda fj in DESTg:
sum fi in ORIGg Trans[i,j] = demanda[j];
#
#
#
#
Datos para el modelo del Transporte (transp_dat.txt)
# definimos los conjuntos “ORIG" y “DEST" y los parámetros
“capacidad" y “demanda"
param: ORIG: capacidad :=
JASPER 100
SEOUL 300
TORONTO 200 ;
param: DEST: demanda :=
FRANKFURT 150
NEWYORK 100
PARIS 200
YOKOHAMA 150 ;
param coste:
FRANKFURT
JASPER
19
SEOUL
15
TORONTO
11
NEWYORK
7
21
3
PARIS
13
18
12
YOKOHAMA :=
8
6
20 ;
Comandos para el modelo del Transporte
(transp_run.txt)
#Ejemplo del problema del transporte
solve;
display Trans, Coste_Total;
Resultados para el modelo del Transporte
NEOS Server Version 5.0
Host : vieta.mcs.anl.gov
1 linear objective;
KNITRO 6.0.0:
Objective goal: Minimize
Number of variables: 12
bounded below: 12
Number of constraints: 7
linear equalities: 7
No start point provided – KNITRO computing one.
KNITRO changing algorithm from AUTO to 1.
Total program time (secs) = 0.00352
6 iterations; 7 function evaluations
Trans :=
JASPER FRANKFURT 0
JASPER NEWYORK 0
JASPER PARIS 100
JASPER YOKOHAMA 0
SEOUL FRANKFURT 150
SEOUL NEWYORK 0
SEOUL PARIS 0
SEOUL YOKOHAMA 150
TORONTO FRANKFURT 0
TORONTO NEWYORK 100
TORONTO PARIS 100
TORONTO YOKOHAMA 0;
Coste_Total = 5950
Referencias Bibliográficas
I
FOURER, R. / GAY, D. M. / KERNIGHAM, B. W. (2002):
“AMPL: A modeling language for Mathematical
Programming". Ed. Duxbury Press.
I
HILLIER, F. / LIEBERMAN, G. (2005): “Introduction to
operations research". Ed. McGraw-Hill.
I
NOCEDAL, J. / WRIGHT, S. J. (2006): “Numerical
Optimization", 2nd Edition. Ed. Springer.
I
PARLAR, M. (2000): “Interactive operations research with
Maple. Methods and models". Ed. Birkhäuser.
Enlaces en INTERNET
I
Libro y software AMPL:
http://www.ampl.com
I
KNITRO: An Integrated Package for Nonlinear
Optimization. R.H. Byrd, J. Nocedal, R.A. Waltz (2006)
(PDF):
http://www.ziena.com/papers/integratedpackage.pdf
I
Plataforma NEOS:
http://neos.mcs.anl.gov/neos/solvers/index.html
I
Apuntes:
http://destio.us.es/calvo/ampl2a.pdf
I
Grupo de trabajo en Google grupos:
http://groups.google.com/group/ampl