Clase11_Codigos_de_Linea

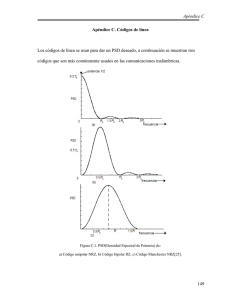
Sistemas de Comunicación
Clase 11: Introducción Sistemas de
Comunicación Digitales – Espectro PAM
Códigos de Línea
Objetivo

Introducción sistemas de comunicación digitales

Modelado de la señal

Códigos de Línea
Sistemas de Comunicación Digital


Objetivo: Enviar un mensaje digital: secuencia de símbolos
(‘0’ ‘1’ ‘2’ ‘2’….) a una cadencia de r bits/s a través de un
canal analógico.
Un Sistema de Comunicación Digital (SCD) trasmite durante
un intervalo finito T una señal analógica elegida de un
conjunto finito de señales posibles, dependiendo del símbolo a
trasmitir.
‘0’ ‘1’ ‘2’
TX SCD
T
Sistemas de Comunicación Digital
‘0’
‘1’
‘2’
Mensaje: ‘0’ ‘1’ ‘2’ ‘2’
Señal :
Banda Base
‘0’
‘1’
Mensaje: ‘0’ ‘1’ ‘2’ ‘2’
‘2’
Señal :
Pasabanda
Trasmisor- SCD
Fuente
de Datos
Codificación
de fuente
(huffman)
Codificación
de canal
(gray)
‘A’
1
000
‘B’
01
011
‘C’
011
101
‘D’
010
110
Código M-ario
Ej: caracteres teclado
Codificación
de línea
Longitud media mínima Bit de pariedad
Elimina redundancia
Agrega redundancia,
Inmunidad ruido
canal
Adecuado a
características de
canal analógico
Comunicaciones Digitales vs Analógicas
Regeneración: Posibilidad de recuperar el mensaje sin
degradación a pesar de su trasmisión en canal ruidoso.
Pulso
original
Pulsos
degradados
en el canal
Pulso
regenerado
Ej: Regenerador Binario
‘1’
‘0’
LPF
V
Pe
En condiciones severas de ruido de canal (SNR R pobre) puedo detectar con
error. Regeneración puede introducir error con probabilidad Pe.
Repetidores Regenerativos
‘1’
TX
Canal
Regenerador
Canal
Procesan, regeneran el pulso antes que se degrade mucho y genere error
en la detección.
Diferencia entre repetidor regenerativo y analógico: En la toma de
decisión (detección) uso conocimiento a priori, conozco que se trasmitió
una de n posibles formas de pulso.
Pregunta:¿Cuándo copian del pizarrón se comportan como un repetidor
regenerativo o analógico?
SC Digital vs Analógico
Reproducción confiable: La perturbación tiene que ser muy
grande para que haya un error (cambio de estado). Ej: trasmisión
de datos Pe<10-5. Es posible trasmitir sin errores en canales con
ruido (codificando con redundancia) sujeto a restricciones de
ancho de banda y energía trasmitida.
Estabilidad: Se pueden lograr sistemas que sean más estables en
el tiempo al usar hardware con diseño especializado (dsp) en los
que la variabilidad se introduce en la codificación algorítmica y
no a través de componentes analógicos variables (resistencias,
condensadores) que pueden derivar en el tiempo con la
temperatura, etc.
SC Digital vs Analógico
Flexibilidad: Se puede cambiar (reprogramar) el algoritmo:
aumentar la redundancia, control de errores, encriptado,
ecualización simplemente cambiando el software.
Multiplexado de distintas fuentes de información: Se pueden
integrar sobre un mismo flujo de datos, información proveniente
de distintas fuentes: audio, video, datos lo que facilita la
convergencia de servicios y el diseño de los dispositivos en
forma económica.
SC Digital vs Analógico
Desventajas:
Complejidad para tareas sencillas: Pasabajos analógico: circuito
RC, pasabajos digital: A/D, DSP, D/A, filtro antialiasing.
Necesidad de Sincronismo TX-RX: Muestreo en instante
óptimo.
Desventajas/Ventaja: Requerimiento de ancho de banda:
PCM binario n bits: requiere BT=nW (n=8).
TV Digital con MPEG: logra trasmitir 4 canales digitales con
calidad standard en el ancho de banda de un canal analógico
(6MHz)
Modelado de la Señal Digital
‘0’
Mensaje:
‘1’
‘0’
‘1’
‘1’
‘1’
‘0’
Señal TX :
Expresión analítica de la Señal Digital :
x(t) 

a
k  
k
pk (t  kT  t d ) con t d  U 0, T 
1
ak  a0 , a1....aM 1  y r 
T
En cada intervalo de duración T se envía un pulso de
duración T con forma pk (t) y amplitud ak .
Caso particular: M-ario unipolar con forma
de pulso p(t) (PAM digital).
p (t ) : fijo vario amplitud según símbolo a TX
p0(t)  p1(t)  p(t)
a0  a1 binario polar
ak  0, A,2 A..........( M  1) A M - ario unipolar
Toma la forma de una señal PAM digital :
x(t) 

a
k  
k
pk(t  kT  t d )
Modulación Amplitud de Pulso (PAM)
ak
ak: valores continuos (PAM analógica) o discretos (PAM digital)
Descripción analítica de la señal PAM
xPAM t    ak pt  kTs  t d 
k
con t d : U 0, Td  retardo aleatorio
 xk  : muestras de la señal - PAM analogica

ak  
 1,1 : onda binaria aleatoria - PAM digital

PAM
p(ttd)
a
k
Secuencia
randómica
estacionaria
sentido
amplio
p(t): pulso
conformador
determinítico td
retardo
aleatorio
U[0,Ts]
xPAM(t
)
Proceso
estacionario
en sentido
amplio
En estas hipótesis RxPAM τ  es determinítica
GxPAM  f  
P( f )
2
Ts

 j 2fkTs


R
k
e
con Ra k   Rx kTs 
 a

GxPAM  f   P ( f ) Ga  f 
2
Espectro PAM
Caso particular : Símbolos no correlacionados
 a 2  ma 2 k  0
Ra k   E(a j .a j  k )   2
ma
k 0

k 
Ra k e
  a  ma  e
  f  


Tb 
k  
k  
k   

1
2
2
2
2
G xPAM  f    a r P ( f )  (ma r )  P (kr )   f  kr  con r 
Tb
k  

 j 2fkTb
2
2

 j 2fkTb
ma
2
a 
Tb
2

Ej : Espectro de onda binaria aleatoria depende forma del pulso, de la
estadística de la secuencia ( a , ma ) y de la duración de los bits Tb .
PAM Digital
p(t-td)
ak
Secuencia
randómica
estacionaria
sentido amplio
Gx  f  
P( f )
2
x (t)
p(t): pulso
conformador
determinítico td
Proceso
estacionario
en sentido
amplio
retardo aleatorio U[0,Ts]
Ga  f 
1
con Ga  f  
Ts

 R k e

a
Sup : Símbolos no correlacionados :
Gx  f    a r P ( f )  ma r 
2
2
2

 P(nr )   f  kr 
k  
2
 j 2fkTs
Códigos de línea
ak
p(t-td)
x (t)
Gx  f    a r P ( f )  ma r 
2
2
2

 P(nr )   f  kr 
2
k  
Espectro depende del pulso conformador y de la codificación.
Modificando estos parámetros puedo generar distintos códigos
de línea (distintos formátos para enviar datos).
Unipolar NRZ
Mensaje:
0
1
0
Unipolar NRZ:
1
1
1
0
+A
0
Sup : Fuente de símbolos binarios equiprobables 0,1
no correlacionados y codificamos con a0  0, a1  A,
pulso rectangular de duración T.
2
A
Ra 0  E ak ak    ak pak   A2 p( A)  0 p(0) 
2
k
2
A
A2
A2
2
2
2
ma  E ak   Ap ( A)  0 p(0) 
ma 
 a  Ra 0  ma 
2
4
4
Unipolar NRZ
Mensaje:
0
1
0
1
1
1
0
Unipolar NRZ:
t
p(t )     P(f)  Tsinc 2 fT
T 
2
TA2
A
k

2
2
2
Gx ( f ) 
sinc fT  2  T sinc k  f  
4
4T k
T

2
TA2
A
Gx ( f ) 
sinc 2 fT 
 0
4
4
+A
0
Unipolar NRZ
Mensaje:
Unipolar NRZ:
0
1
0
1
1
1
0
+A
0
 Tiene δ en 0 (continua ma≠0)
 Alto contenido bajas frecuencias
BT≈1/T (criterio primer cruce x 0)
BT≈1/2T (criterio práctico)
 No tiene información de reloj
Códigos de línea- Características Deseables

Requiera menor ancho de banda de trasmisión.

Lleve información de sincronismo en la señal

No tenga continua (mayor eficiencia en el uso de la
potencia, menor Pe para la misma ST ).

Espectro adecuado a las características del canal.
Ej: NRZ no es adecuado para líneas telefónicas: alternan
polaridad, mala respuesta a bajas frecuencias.
Polar NRZ:
Mensaje:
0
Polar NRZ:
1
0
1
1
1
0
+A/2
-A/2
TA2
Gx ( f ) 
sinc 2 fT
2
Mejor eficiencia en el uso de
la potencia que el unipolar.
Unipolar RZ:
Mensaje:
0
1
0
1
1
1
0
Unipolar RZ:
2
TA 2
fT
A
Gx ( f ) 
sinc 2

4
2 16
+A
0
k 
k
 sinc 2   f  T 
2
 Requiero el doble del ancho
de banda que Unipolar
NRZ.
 Lleva información de reloj.
 Problema de perdida de
sincronismo ante cadena
larga de ceros.
Bipolar Alternate Mark Inversion (AMI):
Mensaje:
0
1
Bipolar -AMI:
0
1
1
1
0
+A
0
-A
Los 0 se trasmiten con nivel 0 y los unos en forma alternada con +A y-A.
Gana inmunidad frente a la inversión de polaridad en líneas telefónicas.
Para analizar el comportamiento espectral se puede modelar como un
código ternario con tres niveles: +A,0,-A con probabilidades ¼, ½ , ¼.
 A2 / 2 k  0
 2
Ra k    A / 2 k  1
0
k2

TA2
Gx ( f ) 
sinc 2 fTsen 2 (fT )
2
Bipolar Alternate Mark Inversion (AMI):
Mensaje:
Bipolar -AMI:
0
1
0
1
1
1
0
+A
0
-A
 No tiene continua.
 Se puede recuperar reloj rectificando.
 BT≈1/T
 Bajo contenido espectral en bajas
frecuencias.
 Sensible a pérdida de sincronismo ante
cadenas largas de ceros.
 No transparente (depende de la estadística
de la fuente de datos)
HDBn- High density bipolar: No permite cadenas de más de n ceros seguidos,
sustituye el 0 n+1 por el código correspondiente a 1 pero con polaridad opuesta
a la que le tocaría al 1.
Manchester
1
0
1
0
1
1
1
1
1
0
+A
0
-A
 t T / 4   t T / 4 
p (t )   
  

 T /2   T /2 
TA 2
2
2 fT
Gx ( f ) 
sinc ft sen
4
2
Transición en cada bit - sincronismo