Document

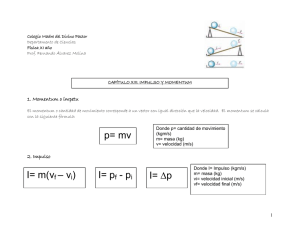
Movimiento Circular
r
r ∆v
a=
∆t
aceleración
cambio por unidad de tiempo que
experimenta el vector velocidad
existe aceleración si cambia dirección de la velocidad
Objeto moviéndose en trayectoria circular con rapidez constante v
Cambia continuamente la dirección de la velocidad
En cada punto de la trayectoria la dirección de la velocidad es la de la
tangente a la curva
L = v∆t
A
L
B
h
h: distancia de “caída” hacia el centro
∆AOB es rectángulo
(R + h )2 = R 2 + L2
R 2 + h 2 + 2hR = R 2 + L2
R
h 2 + 2hR = L2
R
∆t muy chico
O
h 2 << 2hR
h 2 + 2hR = (v∆t )
2
1v2  2
h =   ∆t
2 R 
h=
Caída libre
tenemos
1
2
g∆t 2
1v2  2
h =   ∆t
2 R 
ac ≡
v2
v2
R
juega un rol análogo a g
aceleración centrípeta
R
Movimiento Circular Uniforme
τ: período
tiempo de una vuelta completa a la circunferencia
v=
2πR
τ
ac =
4 π 2R
τ2
Objeto de masa m con rapidez v en trayectoria circular de radio R
experimenta fuerza centrípeta
Fc = mac =
mv 2
R
EJEMPLO
Un trineo de 50 kg, que se encuentra sobre una superficie plana de hielo, está
unido por una cuerda de 5 m de largo a un punto fijo, en torno al cual gira con
rapidez constante, realizando cuatro vueltas completas en un minuto.
¿Cuál es la fuerza que ejerce la cuerda sobre el trineo?
T: tensión de la cuerda
Fc: fuerza centrípeta
4 vueltas/minuto
v = cte
τ=
60
4
T = Fc = mac
[s] = 15 [s]
R = 5 [m]
ac =
Fc = 50 ⋅ 0.877 = 43.86 [N]
con
ac =
4 ⋅ 3.14 2 ⋅ 5
15
2
4 π 2R
τ2
[
= 0.877 m s 2
]
EJEMPLO
¿Cuál es la máxima rapidez con que se puede mover un automóvil al tomar una
curva plana de radio 40m sin derrapar, si el coeficiente de roce estático entre los
neumáticos y el pavimento es 0.6?
Máxima rapidez se obtiene cuando la fuerza de roce estático es máxima
Fc = FR max
v = µgR
Fc = mac = m
v2
R
FR max = µmg
m
v2
R
= µmg
¡no depende de la masa de automóvil!
v = 0.6 ⋅ 9.8 ⋅ 40 [m s] = 15.33 [m s ]
v = 55.2 km/h
¿por qué se usan curvas con peralte?
Otra mirada a la 2ª Ley de Newton
F = ma
F =m
∆v
F=
∆t
F=0
F=
∆p = 0
∆t
∆p
∆t
2ª Ley de Newton
p = cte
m = cte
en general
puede cambiar m o v o ambas
p: cantidad de movimiento o momentum lineal
nueva magnitud física
p ≡ mv
∆ (mv )
v = cte
1ª Ley de Newton
si la fuerza neta sobre un objeto es cero,
se conserva la cantidad de movimiento
Si el momentum cambia en ∆p en un
intervalo de tiempo ∆t, la fuerza media es
F =
∆p
∆t
EJEMPLO
Un jugador de fútbol patea un penal. El pié del jugador y la pelota permanecen
en contacto durante 5·10-3 s. Como resultado la pelota, de masa 0.8 kg,
adquiere una velocidad de 100 km/h. ¿Cual es la fuerza media que ejerce el pié
del jugador sobre la pelota?
Pelota inicialmente en reposo y movimiento en 1-D
F =
∆p
∆t
=
m∆v
∆t
∆v = 100 km/h = 27.78 m/s
∆t = 5·10-3 s
F =
m∆v
∆t
=
0.8 [kg] ⋅ 27.78 [m/s ]
5 ⋅ 10 −3 [s ]
= 4444 .8 [N]
¡equivalente a sostener una masa de ≈ 453 kg!
EJEMPLO
Una persona tipo cae desde un segundo piso. Estime la fuerza media a que
está sometida la persona para los casos:
a) caída sin consecuencias, en que la persona hace contacto con el suelo
primero con sus pies y amortigua la caída flectando sus rodillas, hasta quedar
tendida sobre la superficie.
b) caída con consecuencias, en que el cuerpo de la persona hace contacto de
espaldas con el suelo.
a)
Supongamos que cae desde h = 3 m, que la masa es 70 kg y que la
distancia pié-rodilla es d = 0.45 m
v s = 2g (h − d )
vs: velocidad al empezar a frenar
Ecuaciones que describen el frenado
fuerza media de frenado
1
y = d − af t 2
2
v = v s − af t
F = maf =
mv s2
2d
F = 3887.7 [N]
vs = 7.07 m/s
af =
v s2
2d
tiempo de frenado
tf =
vs
af
=
2d
vs
t f = 0.127 [s]
¡Para las piernas equivale a soportar una masa de ≈ 397 kg durante 0.127 s!
b)
supongamos que como resultado del impacto del cuerpo horizontalmente
sobre el suelo, éste experimenta una compresión de 2 cm, por lo que la
distancia de frenado es ahora d = 0.02 m
v s = 2gh = 7.67 [m/s ]
velocidad al llegar al suelo
F = maf =
fuerza media de frenado
mv s2
2d
F = 102950 .6 [N]
tiempo de frenado
tf =
vs
af
=
2d
vs
t f = 0.005 [s]
¡equivale a soportar una masa de ≈ 10500 kg durante 5 milésimas de segundo!
1a Ley de Newton y la conservación de la energía mecánica
1a Ley de Newton: si la fuerza total externa que actúa sobre un sistema
físico es cero, entonces el momentum total del sistema se conserva
Fext = 0 ⇒ ∆p = pf − pi = 0 ⇒ pf = pi
Si las fuerzas de interacción al interior del sistema son conservativas y no hay
cambio en la energía potencial, entonces la energía cinética total del sistema
se conserva
∆K T = K f − K i = 0 ⇒ K f = K i
Físicas de colisiones (choques)
Colisión entre partícula
alfa y núcleo de átomo
de Sodio
M ≈ 10-26 kg
L ≈ 10-10 m
Colisión entre bolas
de billar
M ≈ 10-1 kg
L ≈ 10-1 m
Colisión entre galaxias
M ≈ 1040 kg
L ≈ 1040 m
colisiones
v1
m1
v2
m2
Antes de la colisión, las masas se mueven con velocidades v1 y v2
Después de la colisión, las masas se mueven con velocidades u1 y u2
Problema en 1-D
carácter vectorial lo absorbemos en el signo
No hay fuerzas externas
se conserva el momentum lineal
Colisión elástica
se conserva la energía mecánica
m1v 1 + m2v 2 = m1u1 + m2u 2
Conservación de momentum
1
1
1
1
m1v 12 + m2v 22 = m1u12 + m2u 22
2
2
2
2
Conservación de energía
I) Caso particular: m1 = m2 = m
v 1 + v 2 = u1 + u2
v 1 − u1 = u 2 − v 2
v 12 + v 22 = u12 + u 22
v 12 − u12 = u 22 − v 22
(v1 − u1 )(v1 + u1 ) = (u2 − v 2 )(u2 + v 2 )
v 1 + u1 = u 2 + v 2
u2 = v1
u1 = v 2
se invierten las velocidades
m1v 1 = m1u1 + m2u2
II) Caso particular: v2 = 0
m1v 12 = m1u12 + m2u 22
m22 2
2
2
m1v 1 = m1u1 +
u 2 + 2m2u1u 2
m1
 m 
0 = m2  1 − 2 u 22 − 2m2u1u 2

m1 

(m1 − m2 )u2 = 2m1u1
u2 =
m1v 1 = m1u1 + m2
2m1
m1 − m2
III) Caso particular: m1 << m2
2m1
m1 − m2
u1 =
u1
u2 =
u1
m1 − m2
m1 + m2
2m1
m1 + m2
v1
v1
u1 = −v 1
u2 = 0
antes
después
v
−v
u1 = v 1
IV) Caso particular: m1 >> m2
u 2 = 2v 1
v1 = v
u 2 x = 2v
EJEMPLO
Una bola de masa 2 kg baja por una rampa
de 2.5 m de altura sin experimentar roce.
En el extremo inferior de la rampa
experimenta una colisión elástica con una
caja de masa 5.0 kg, que se encuentra en
reposo. a) ¿Cual será la velocidad de la
caja inmediatamente después de la
colisión? b) ¿Que ocurre con la bola
después de la colisión?
2.5 m
solución
a) conservación de la energía mecánica
vb, en h = 0
v b = 2gh = 2 ⋅ 9.8 ⋅ 2.5= 7[ m s ]
vb ≠ 0, vc = 0
Colisión corresponde a caso II)
ub =
uc =
mb − mc
mb + mc
2 mb
mb + mc
vb =
vb =
2−5
2+5
2⋅2
2+5
⋅ 7 [m s ] = −3 [m s]
⋅ 7 [m s] = 4 [m s]
b) Luego de la colisión, la bola sube por la rampa, con velocidad inicial 3 m/s.
bola sube a altura h*
conservación de la energía mecánica
h* =
1
2g
u b2 =
mgh * =
1
2 ⋅ 9 .8
1
2
mub2
3 2 [m] = 0.459 [m]
EJEMPLO
Dos masas, de 2 kg y 3 kg, están unidas por un
resorte de constante elástica 120 N/m y
descansan sobre una superficie sin roce.
Inicialmente el sistema está en reposo y el
resorte está comprimido una distancia de 5 cm.
Si el sistema es liberado, ¿con qué velocidad
se mueven las masas?
k
m1
m2
m1 = 2 kg
m2 = 3 kg
solución
0 = m1v 1 + m2v 2
Conservación de momentum
1
Conservación de energía
2
2
 m1  2
2
 v 1 = kx 2
m1v 1 + m2 
m 
 2
v1 =
km2
x
m1 (m1 + m2 )
v1 =
kx 2 =
1
1
m1v 12 + m2v 22
2
2
v2 = −
m1
m2
v1
 m1 + m2 

m1v 12 = kx 2
 m

2


120 ⋅ 3
2 ⋅ (2 + 3 )
⋅ 0.05 = 0.3 [m s ]
v 2 = −0.2 [m s ]
EJEMPLO
Una bala de calibre 0.30 tiene una masa de 7.2 g y una velocidad de salida de
601 m/s relativa al cañón del rifle, cuya masa es 2.8 kg. Al disparar, el rifle,
sostenido sin firmeza, retrocede a 1.85 m/s relativo al suelo. ¿cuál es el
momentum de los gases de la detonación que salen por el cañón?
solución
0 = pr + pb + pg
Conservación de momentum
0 = mr v r + mbv b + pg
Signo de vr es opuesto a signo de vb
pg = − (− mr v r + mbv b ) = − (− 2.8 ⋅ 1.85 + 0.0072 ⋅ 601) = 0.8528 [N⋅ m s ]
EJEMPLO
Un vagón de 20000 kg viaja sin roce ni impulso sobre una superficie horizontal.
Llueve verticalmente y el vagón acumula agua. Si inicialmente está vacío y se
mueve a 4 m/s, ¿Cuál será su velocidad cuando acumule 2000 l de agua?
solución
No hay fuerza externa
se conserva el momentum
mv v i = (mv + ma )v f
vf =
mv
mv + ma
vi
vf =
pi = pf
20000
20000 + 2000
⋅ 4 = 3.64 [m s ]