Capítulo

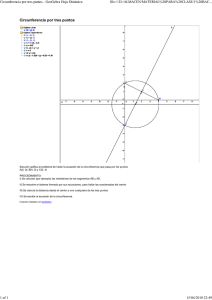
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Capítulo
4
LA CIRCUNFERENCIA
Encontrar la ecuación de la circunferencia sabiendo que sus extremos de
un diámetro son los puntos A = (− 2,3 ) y B = (4,−1) .
Solución:
C = (h,k ) es punto medio de AB
!



Luego :
h=1
k =1
! C = (1,1)
r=
AB
2
=
52
2
! r 2 = 13
ˆ C : (x − h)2 + (y − k )2 = r 2
(x − 1)2 + (y − 1)2 = 13
C : x 2 + y 2 + 12x − 12y + 36 = 0
27
Capítulo 4. LA CIRCUNFERENCIA
Obtener la ecuación de la circunferencia tangente a los dos ejes, radio 6,
en el segundo cuadrante.
Solución:
Del gráfico, se deduce que
C = (h,k ) = (− 6,6 ) es el centro
de la circunferencia
y su radio r = 6.
ˆ C : (x − h)2 + (y − k )2 = r 2
(x + 6)2 + (y − 6)2 = 36
C : x 2 + y 2 + 12x − 12y + 36 = 0
Dada la ecuación de la circunferencia 3 x 2 + 3 y 2 + 4 y − 7 = 0 , encontrar
el centro y el radio.
Solución:
Completando cuadrados :
! 3x 2 + 3 y 2 + 4y − 7 = 0
4
4
4

3 x 2 + 3 y 2 + y +  = 7 +
3
9
3

2
2
25

3x 2 + 3 y +  =
3
3


2
2
25

x2 +  y +  =
3
9

28
ˆ
d donde : h = 0 , k = −
; De
2
5

C =  0,−  ; r =
3
3


2
3
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
Hallar la ecuación de la circunferencia cuyo centro es el punto C = (− 4,−1)
y que es tangente a la recta: 3 x + 2y − 12 = 0 .
Solución:
r = Distancia de C a
Sea :
‹ : 3x + 2y − 12 = 0
Luego :
! r=
=
=
(3)(− 4) + (2)(− 1) − 12
3 2 + 22
− 12 − 2 − 12
13
− 26
13
=
26
13
! r 2 = 52
ˆ C : (x − h)2 + (y − k )2 = r 2
Reemplazando :
C : (x + 4 )2 + (y + 1)2 = 52
Hallar la ecuación de la circunferencia que pasa por los puntos A = (4,0 ) ,
B = (0,3 ) y C = (− 2, − 2) .
Solución:
Sea
C : x 2 + y 2 + Dx + Ey + F = 0 → ⊗
!
A = (4,0 ) ∈
C ! 16 + 4 D+ F = 0 → #
!
B = (0,3 ) ∈
C ! 9 + 3E + F = 0 → "
!
C = (− 2, − 2) ∈
Luego, de
C ! − 2D − 2E + F = 8 → !
# ," y ! :
D=−
19
5
132
; E=
; F=−
13
13
13
29
Capítulo 4. LA CIRCUNFERENCIA
En
⊗:
ˆ C:
x 2 + y2 −
19
5
132
=0
x+
y−
3
13
13
C : 13x 2 + 13y 2 − 19x + 5y − 132 = 0
Hallar la ecuación de la circunferencia de radio 10, tangente en el eje X,
cuyo centro está sobre la recta x = 2y .
Solución:
! Primer caso
‹ : x = 2 y pero C = (h1,10) ∈ ‹ ! h1 = 20 ; C = (20,10)
C : (x − h1)2 + (y − k1)2 = r 2
(x − 20)2 + (y − 10)2 = 100
30
x 2 + y 2 − 40x − 20y + 400 = 0
PROBLEMAS DE GEOMETRÍA ANALÍTICA PLANA
! Segundo caso
‹ : x = 2 y pero C = (h2,−10) ∈ ‹ ! h2 = −20 ; C = (− 20,−10)
C : (x − h2 )2 + (y − k 2 )2 = r 2
(x + 20)2 + (y + 10)2 = 100
x 2 + y 2 + 40x + 20y + 400 = 0
La ecuación de una circunferencia es x 2 + y 2 = 50 . El punto medio de
una cuerda de esta circunferencia es el punto P = (− 2,4 ) . Hallar la ecuación
de la cuerda.
Solución:
Sea
y
‹2 la recta que contiene a la cuerda referida
‹1 la recta que pasa por el punto P y el centro de la circunferencia.
! Pendiente de
‹1 : m‹1 =
4−0
= −2
−2−0
Luego :
‹1 ⊥ ‹2 "! m‹1 ⋅ m‹ 2 = −1
"!
(− 2)⋅ m‹ 2
"! m‹ =
2
= −1
1
2
Luego :
!
‹ 2 : y − 4 = (x + 2)
1
2
‹ 2 : x − 2y + 10 = 0
31
Capítulo 4. LA CIRCUNFERENCIA
Encontrar la ecuación de la circunferencia con centro en C = (4, 4 3 ) y
que pasa por Q = (− 1,− 4 3 ) .
Solución:
De los datos, tenemos :
C : (x − h)2 + (y − k )2 = r 2
(x − 4)2 + (y − 4 3)2 = r 2
!
ˆ
Q = (− 1,− 4 3 ) ∈
2
289
4 4
C ! (− 1 − 4)2 +  − −  = r 2 ! r 2 =
 3
3
2
4
289
C : (x − 4)2 +  y −  =

3
9
Hallar el área del círculo cuya ecuación es:
9 x 2 + 9 y 2 + 72 x − 12 y + 103 = 0
Solución:
Tenemos la ecuación de la circunferencia :
C : 9x 2 + 9y 2 + 72x − 12y + 103 = 0
Despejando el término independiente y completando cuadrados
!
C : 9x 2 + 9y 2 + 72x − 12y = −103
(
)
4
4

9 x 2 + 8x + 16 + 9  y 2 − y +  = −103 + 144 + 4
9
3

2
2

9 (x + 4 )2 + 9  y −  = 45
3


(x + 4)2 +  y − 2 

32
ˆ
A = πr2 = π × 5
3
2
=5
"!
Donde : r 2 = 5
A = 5 πu 2
9