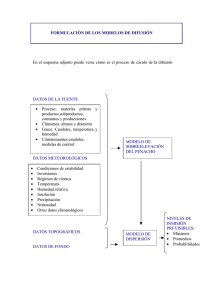
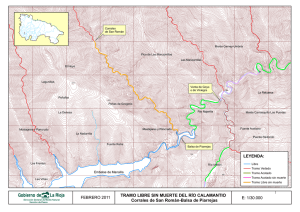
Descargar

CUADERNOS DEL CURIHAM (Revista de Estudios sobre la Cuestión Hidroambiental)
Volumen Nro. 16 – Año 2010
CURIHAM : Centro Universitario Rosario de Investigaciones Hidroambientales
Facultad de Ciencias Exactas, Ingeniería y Agrimensura. Universidad Nacional de Rosario
Director: Dr. Ing. Gerardo Adrián Riccardi
Riobamba 245 bis, 2000 Rosario (Santa Fe), Argentina. Telefax 54 (0341) 480 8541
E_mail: [email protected]. Sitio web: http://www.fceia.unr.edu.ar/curiham
CONSEJO EDITORIAL
Dr. Ing. Pedro Abel Basile: Editor responsable revista Cuadernos del CURIHAM.
Msc. Ing. Adelma Mancinelli: Editora asociada.
Dr. Ing. Hernán Stenta: Jefe de edición.
Msc. Ing. Carlos Scuderi; Msc. Inga. Marina García: Asistentes de Edición
CONSEJO REVISOR
Gabriel Caamaño Nelli, Centro de Investigaciones Hídricas Región Semiárida, Conicet, Villa Carlos Paz, Córdoba.
caamañ[email protected]
Alfredo Trento, Facultad de Ingeniería y Ciencias Hídricas, Ciudad Universitaria, Universidad Nacional del Litoral.
[email protected]
José Vargas, Universidad de Concepción, Chile.
[email protected]
Virginia Pacini , Centro de Ing. Sanitaria, Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario.
[email protected]
José Rodríguez, Departamento de Hidráulica, Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario.
[email protected]
Victor Lallana, Facultad de Ciencias Agropecuarias, Universidad Nacional de Entre Ríos.
[email protected]
Javier Heredia, Instituto Geológico y Minero de España, Madrid.
[email protected]
Luis Vives, Instituto de Hidrología de Llanura, UNCPBA.
[email protected]
Alicia Ronco, Centro de Investigaciones del Medio Ambiente, Facultad de Ciencias Exactas, Universidad Nacional de La Plata.
[email protected]
Erik Zimmermann, CURIHAM, Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario.
[email protected]
Armando Brizuela, Facultad de Ciencias Agropecuarias, Universidad Nacional de Entre Ríos.
[email protected]
Mónica Blarasín, Depto. de Geología, Facultad de Ciencias Exactas, Físico-Químicas y Naturales, Universidad Nacional de Río Cuarto.
[email protected]
Leticia Rodríguez, Facultad de Ingeniería y Ciencias Hídricas, Universidad Nacional del Litoral.
[email protected]
Pablo Miguel Jacovkis, Instituto de Cálculo, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires.
[email protected]
Leopoldo Génova, Facultad de Ciencias Agrarias y Forestales, Universidad Nacional de La Plata.
[email protected]
Objetivos de la Revista
El Cuaderno del CURIHAM es una publicación semestral del Centro Universitario Rosario de Investigaciones Hidroambientales,
Facultad de Ciencias Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario. La revista está dedicada a la divulgación de
trabajos de investigación básica y aplicada, como así también innovaciones tecnológicas en el campo concerniente a la disciplina
hidroambiental. Asimismo, esta publicación puede incluir resultados de investigaciones de campo, estudios interdisciplinarios como así
también trabajos acerca de estado del arte en la temática. El CURIHAM invita a la contribución de trabajos para ser incluidos en
próximas publicaciones. Las temáticas comprendidas son: Hidráulica Fundamental, Fluvial e Hidrodinámica; Hidrología Superficial y
Subterránea; Hidrología Urbana; Estocástica; Planeamiento y Manejo de Recursos Hídricos; Evaluación Ambiental; Contaminación y
Calidad de aguas; Política y Legislación de Aguas; Gerenciamiento Hidroambiental Regional; Obras Hidráulicas, Métodos y Técnicas
Constructivas; y todos aquellos temas relacionados con las ciencias hidroambientales. Los artículos estarán sujetos a revisión a cargo del
Consejo Revisor. Se solicita que los trabajos publicados no hayan sido enviados para publicación ni publicados en otras revistas
científicas y/o tecnológicas.
Copyright
Todos los derechos reservados. Ninguna parte de esta publicación podrá ser reimpresa, reproducida o utilizada de cualquier forma o por
medio electrónico, mecánico u otro medio conocido o por inventarse, sin expresa autorización del Consejo Editorial.
ISSN 1514-2906
Catálogo LATINDEX Nº 1715
INDICE
PUBLICACIONES
Efectos de la Base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales. Caso
de Estudio: Río Baconao.
Anders Pérez Brugal, Juan F. Weber y Yaismil R. Castellanos………………...…………………… 01
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre Tramo del Río Paraná.
Marina L. Garcia, Pedro A. Basile y Gerardo A. Riccardi…………………….........……………….. 13
Tratamiento del Frente Abrupto de Infiltración para el Caso de Profundidad de Inundación
Variable. Soluciones implícita y explicita.
Sergio Masuelli y Daniel Barrera…………………………...………………...……………………… 33
Estudio de Columnas Reactivas para la Remoción de Arsénico mediante el empleo de la
Técnica ZVI.
Juan M. Triszcz, Luciana Chippano, Andrés Gordon, Andrés Porta y Fernando García Einschlag…. 43
Integración de Cuencas de Drenaje en Áreas de Llanura durante la última Centuria. El Caso
del Arroyo Las Lajas, Córdoba, Argentina.
Nelso Doffo, Susana Degiovanni y Mónica Villegas……………………..………………………….. 49
NOTA TÉCNICA
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos.
Juan F. Weber, Héctor I. Paoli y Laureana Apestegui…………………………...…………………… 59
CUADERNOS del CURIHAM, Vol. 16, Año 2010
EFECTOS DE LA BASE CARTOGRÁFICA EN LA SIMULACIÓN HIDRÁULICA DE LAS
INUNDACIONES FLUVIALES. CASO DE ESTUDIO: RÍO BACONAO
Anders Pérez Brugal(1), Juan F. Weber(2), Yaismil R. Castellanos3
(1)
Universidad de Oriente. Facultad de Construcciones. Sede Mella. Departamento de Ingeniería Hidráulica.
Ave. Las Américas, s/n, CP 90900, Santiago de Cuba. e-mail: [email protected]
(2)
Laboratorio de Hidráulica, Departamento de Ingeniería Civil, Facultad Regional Córdoba, Universidad
Tecnológica Nacional. Maestro M. López esq. Cruz Roja Argentina. Ciudad Universitaria - CP
(X5016ZAA). Córdoba. Argentina. e-mail: [email protected]
(3)
GeoCuba Oriente Sur, agencia Catastro, Santiago de Cuba
RESUMEN
En la investigación se analizó el efecto de la cartografía en los resultados de la simulación hidráulica de
inundaciones con HEC-RAS. Se crearon cinco Modelos Digitales del Terreno derivados de fuentes
diferentes: cuatro, a partir de cartografía vectorial de curvas de nivel a varias escalas, y uno, obtenido de un
levantamiento con GPS en conjunto con una Estación Total. Este último se estableció como punto de
comparación para determinar los errores que impone el uso de dichos planos en la representación del cauce y
las llanuras de inundación y revelar su influencia en los resultados de la simulación. Finalmente, en
dependencia del plano utilizado, se obtuvieron divergencias de 2.88 hasta 18.82 m de altura al representar un
mismo punto en el terreno, lo que influyó de manera significativa en el cálculo de altura de la lámina de agua
y en la estimación del área inundada, ya que se encontraron errores de 1.6 hasta 2.6 m y de 0.039 hasta 0.283
Km2 respectivamente, lo que demuestra que la cartografía con que se modela el terreno determina en gran
medida los resultados de la simulación.
Palabras clave: HEC-RAS, Simulación Hidráulica, Inundaciones, Modelos Digitales del Terreno, SIG.
ABSTRACT
This research examines the effect of mapping in the results of hydraulic simulation with HEC-RAS software.
Five Digital Terrain Models were created from different sources: four from vector mapping contours at
various scales, and one obtained from a survey with GPS in conjunction with a Total Station. The latter was
established as a baseline to determine the errors imposed by the use of such cartography in the representation
of the main channel and floodplains and reveal their influence on the results of the simulation. Finally,
depending on the map used, the differences to represent the same point on the ground were from 2.88 to
18.82 m in height, which significantly influence the calculation of water surface elevation and flooded area,
with errors founded 1.6 to 2.6 m and 0.039-0.283 km2 respectively. It shows that mapping largely determines
the outcome of the simulation.
Keywords: HEC-RAS, Hydraulic Simulation, Floods, Digital Terrain Models, GIS.
1
Efectos de la base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales
variado para flujo permanente e impermanente en
una red completa de canales abiertos, ya sean
naturales o artificiales. En el caso de trabajar con el
régimen permanente, el perfil de flujo es calculado
de una sección a otra por la aplicación iterativa de la
ecuación de energía mediante el denominado
método del paso estándar. Pero si el estudio que se
va a realizar necesita modelar flujo en régimen
impermanente, el programa resuelve las ecuaciones
de Saint-Venant completas mediante el método de
diferencias finitas implícitas. Para ello utiliza el
esquema de Preissmann. Dicha solución se resuelve
iterativamente con el uso de la técnica de NewtonRaphson (Brunner, 2008).
INTRODUCCIÓN
Las inundaciones, eventos naturales y recurrentes
para un río, se producen cuando lluvias intensas o
continuas sobrepasan la capacidad de retención e
infiltración del suelo, el volumen máximo de
transporte del río es superado y el cauce principal se
desborda e inunda los terrenos cercanos a los
propios cursos de agua. Para la implementación de
medidas que permitan mitigar sus devastadores
efectos es necesario calcular los niveles de agua, los
caudales y velocidades del flujo en cada una de las
secciones de cálculo definidas a lo largo de los
cauces considerados. Se pueden distinguir diversos
métodos de cálculo que pueden ir desde el uso de
ecuaciones del régimen uniforme hasta las
ecuaciones del régimen variado. Para llevarlos a
cabo, se presentan dos situaciones: si se conoce la
cota de la superficie libre del agua, se determina el
caudal; o viceversa dado el caudal se determina el
tirante real del flujo.
Por otra parte, muchos de estos modelos se han
desarrollado con el apoyo en algunos Sistemas de
Información Geográfica (SIG) debido a la gran
potencia que poseen los Modelos Digitales del
Terreno (MDT) para representar el relieve.
Esta posibilidad abrió el camino para la
modificación de los modelos matemáticos de
simulación hidráulica en la incorporación de nuevas
capacidades estrechamente relacionadas con la
información espacial. Como parte de este esfuerzo
surge la aplicación HEC–GeoRAS implementada
sobre el popular SIG ArcView. Su utilización
permite el cálculo automatizado de buena parte de
los parámetros necesarios para la operación del
modelo matemático HEC–RAS; así se gana una
mayor precisión al trabajar con una resolución
espacial mucho más elevada que la que podría
obtenerse mediante la introducción manual de los
datos del terreno.
La Hidráulica de Canales clásica desde sus inicios se
basó en la aproximación unidimensional al problema
del flujo en conducciones libres, lo cual es bastante
razonable en la medida en que las dimensiones
transversales a la dirección del flujo sean
despreciables frente a la escala longitudinal. León
(2000), Chow (2004) y Weber (2003) coinciden en
que para muchas aplicaciones prácticas las
variaciones espaciales de la velocidad pueden
resolverse simplificando el campo de velocidades a
un campo unidireccional y en otros casos
bidimensional, lo cual permite que se empleen
formas más simples de las ecuaciones básicas del
flujo con acierto. No obstante, Weber (2003) asevera
que en el caso de canales con planicies de
inundación, la aproximación unidimensional se
puede ver seriamente limitada debido a que
normalmente estas zonas presentan mayor
resistencia al flujo por tener profundidades bajas,
presencia de vegetación, etc. De todos modos,
numerosos modelos matemáticos unidimensionales
han surgido intentando representar el flujo en estas
condiciones, y en la gran mayoría de los proyectos
de simulaciones fluviales que se llevan a cabo hoy
día en todo el mundo, se utiliza este tipo de modelos.
El registro de la información referente a elevaciones
de una zona se ha realizado frecuentemente
mediante el uso de modelos analógicos tales como
los mapas y planos, situación que en los últimos
tiempos ha variado con la introducción de modelos
de naturaleza digital y en particular los MDT. En
estos, el almacenamiento de la información es de
tipo puramente numérico, lo que hace posible el
desarrollo de un análisis más detallado y profundo
del relieve en cada ámbito de estudio.
Históricamente, según Fernández y Geler (2004),
Felicísimo (1994) y Olaya (2004), estos modelos se
han dividido básicamente en dos grupos en función
de la concepción básica de la representación de los
datos: vectoriales y raster. La principal característica
del modelo vectorial es el almacenamiento de
coordenadas en dos o tres dimensiones con un
Entre los más utilizados en la práctica a nivel
internacional están: Mike-11, Sobek, WES, Dambrk,
HEC-RAS, etc. Este último probablemente sea el
más empleado en la actualidad. Con este sistema se
puede calcular el perfil de la superficie de agua en
régimen gradualmente variado o rápidamente
2
CUADERNOS del CURIHAM, Vol. 16, Año 2010
formato de números decimales de alta precisión.
Estas coordenadas son la base para tipos de datos
más complejos como son: puntos, líneas, polígonos,
etc. Dicha estructura permite una gran flexibilidad
en el manejo de la información debido a que esta
puede tener distintas formas y características con
menores limitaciones que en el caso raster.
admite datos adicionales como puntos de máxima
cota o de depresiones y líneas de ruptura que
permiten representar los elementos característicos
del terreno como márgenes, cauces, afluentes,
además de construcciones como carreteras y diques
que influyen de forma decisiva en el
comportamiento hidráulico del río modelado.
El modelo raster representa los datos por medio de
una matriz de celdas que conforman una malla en
dos direcciones, en la que cada celda contiene un
atributo. Los datos en formato raster son muy
simples y su consumo de memoria es proporcional
solo al tamaño de la matriz y no a la diversidad y
distribución de los datos dentro de ella, lo que los
hace adecuados para representar características que
varían suavemente en el espacio.
La captura de la información hipsométrica
constituye el paso inicial para transformar la realidad
geográfica en una estructura digital de datos a través
de la construcción de un MDT. Este proceso
involucra diferentes métodos: directos e indirectos.
En Cuba y en los países del tercer mundo o en vías
de desarrollo se trabaja, por lo general, a través de la
digitalización directa debido a los elevados precios
de las tecnologías más avanzadas que suponen los
restantes métodos. De la misma forma, en la realidad
cubana, los planos utilizados en la modelación de
inundaciones están sujetos al uso de cartografía
vectorial de curvas de nivel a escalas 1:10000,
1:25000, 1:50000 y 1:100000 ya que estas son las
más comunes en el país.
Por otro lado, Olaya (2004) plantea que el
inconveniente principal del modelo raster reside en la
discretización del espacio a la que da lugar,
responsable directa de una pérdida de precisión, la
cual debe ser asumida desde un primer momento a la
hora de trabajar bajo este modelo de almacenamiento.
En los trabajos desarrollados por Chavarri (2004),
Oleagordia et. al. (2005), Carrasco et. al. (2004),
Etxeberria (2004), Rodríguez y González (2008),
Etxeberria et. al. (2002) y Cárdenas (2000) se
evidencia la utilización a nivel internacional de otras
escalas; de ellas, las más usadas son: 1:100, 1:1000,
1:2000 y 1:5000. No obstante en las publicaciones
de Oleagordia et. al. (2001), Cruz et. al. (2005) y
Treviño y Ortiz (2004) se emplean planos 1: 10000.
La amplia búsqueda bibliográfica realizada en
relación con el tema, indica que es muy poco
frecuente el uso de escalas más pequeñas que la
anterior en trabajos que requieran llegar a resultados
con un alto nivel de precisión. Esto se debe,
principalmente, a que la exactitud y precisión de los
MDT están determinadas por el modo en que han
sido obtenidos los datos; así pues, a mayor escala,
mayor precisión del modelo del terreno.
Ambos tipos de modelos presentan variantes que
permitieron la evolución a nuevas estructuras de
organización de los datos, donde las más
utilizadas son las mallas de celdas regulares
(GRID) y la Red Irregular de Triángulos (TIN),
(Fernández y Geler, 2004).
Numerosos estudios han demostrado que la
descripción vectorial es más apropiada para
representar variables discretas que, por su
naturaleza, están limitadas por fronteras lineales
claras, mientras las descripciones raster se adaptan
mejor a la representación espacial de variables
continuas, así como para otras con una naturaleza
estadística o probabilística. En este sentido, Casa et.
al. (2005) revelan a partir del trabajo realizado por
Bonham-Carter en 1996, que el uso de mallas
regulares para la representación de un modelo del
terreno no es el adecuado para el análisis hidráulico
de conducciones naturales debido a que este modo
de representación del terreno no permite definir con
detalle áreas con relieve complicado al no poder
variar la resolución.
Diversas investigaciones abordan el efecto de la
resolución espacial en modelos de simulación de
inundación como los de Werner (2001), Bates y De
Roo (2000), Marks y Bates (2000), Hardy et. al.
(1999), Horritt y Bates (2001), Omer et. al. (2003) y
Horritt (2000); pero sin dudas el que mejor caracteriza
el efecto de la resolución espacial en modelos de
inundación es el realizado por Casa et. al. (2005). En
él se manifiesta que la influencia de la topografía,
tanto del cauce como de la llanura de inundación,
constituye el factor limitante más importante en la
De este modo, los TIN resultan más acertados dado
que consiguen una mejor representación de la
geometría del río al permitir el ajuste de la densidad
de la red a la cantidad de variación de los datos
según Bates et. al. (1996). Igualmente un TIN
3
Efectos de la base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales
modelación hidráulica y su representación como
variable de entrada al modelo determina en gran
medida la hidráulica de la crecida modelada y la
extensión del área inundada. Es, por tanto, necesario,
llevar a cabo un análisis de la influencia de diversas
bases cartográficas en la simulación hidráulica de
inundaciones a partir del uso de las escalas de trabajo
más frecuentes en Cuba.
MATERIALES Y MÉTODOS
Descripción del área de estudio
La investigación se desarrolló en el tramo del río
Baconao comprendido entre el afluente el Indio y la
estación hidrométrica Trucucú. La cuenca que
tributa al río, se localiza al este de la ciudad de
Santiago de Cuba, en la vertiente norte de la Sierra
de la Gran Piedra. Limita al norte y al este con la
cuenca del río Guantánamo; al noroeste, con la
cuenca del río Guaninicún; al oeste, con la cuenca
del río San Juan y al sur, con el río La Anita,
afluente del propio Baconao (Figura 1).
Figura 1. Ubicación del tramo de río en estudio.
Se escogió esta zona, por la disponibilidad de
información hidrometeorológica y física con que
cuenta, al poseer una de las dos estaciones
hidrométricas que existen en la provincia Santiago de
Cuba. La información extraída, a partir de dicha
estación, garantiza el sistema de datos necesarios para
una adecuada simulación de la inundación, pues
facilita, entre otras cosas, conocer valores reales de
caudales y niveles del agua que circulan por el río.
Toda esta información, necesaria para los propósitos
académicos del presente estudio, fue suministrada por
el Instituto Nacional de Recursos Hidráulicos (INRH).
Figura 2. Nivel máximo del agua en la estación hidrométrica
Trucucú, durante el paso del ciclón Flora.
Modelación y exportación del terreno
El tramo de río en estudio, presenta una longitud de
642 m con una pendiente media del cauce de 0.0018
m/m. El cierre de la estación se encuentra ubicado en
las coordenadas Norte: 152.1 y Este: 637.7; hasta este
punto la cuenca presenta una superficie de 167.8 km2,
perímetro de 84.68 km y una pendiente media de 343
‰. El tramo de río exhibe una topografía empinada,
donde se define, a simple vista, el límite entre el cauce
principal y las llanuras de inundación. El caudal
máximo registrado en dicha estación, ocurrió el 4 de
julio de 1963, durante el paso del ciclón Flora, con un
valor de 1109 m3/s, y elevó el nivel del agua a una
altura de 6.7 m como se muestra en la Figura 2.
En el análisis del flujo en conducciones libres, el
primer paso a dar está encaminado a obtener con
precisión la geometría del río y las llanuras de
inundación a partir de un TIN. Para facilitar el
trabajo se generó con ArcView 3.3 y su extensión
3d Analyst un total de cuatro TIN de la zona de
estudio. Para ello se utilizaron como fuente de
datos las escalas: 1:100000, 1:50000, 1:25000 y
1:10000 (Figuras 3, 4, 5 y 6). Estas se obtuvieron
en la empresa GeoCuba Oriente Sur a través de la
agencia Catastro.
4
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Para establecer la precisión de los cuatro modelos del
terreno y determinar su influencia en los resultados de
la simulación, se construyó un quinto TIN a partir de
los puntos obtenidos con un levantamiento de alta
resolución por posicionamiento global (GPS) en
conjunto con una Estación Total del tramo de río en
estudio (Figura 7).
Figura 3. Curvas de nivel del plano 1:10000 y MDT.
Figura 7. Puntos medidos con el GPS y la Estación Total, y
Modelo Digital del Terreno construido a partir de ellos.
La captura de los puntos se basó en el levantamiento
sistemático de los perfiles transversales de interés,
espaciados en función de los cambios en la
geomorfología del río.
Figura 4. Curvas de nivel del plano 1: 25000 y MDT.
Se tomaron los puntos de fuerte cambio de pendiente,
los bancos de arena encontrados en el cauce, los
cambios en la forma de la sección transversal del
cauce, etc. El fondo del río fue medido de manera
directa debido a que se realizó la medición en el
período seco y este presentaba un nivel de agua muy
bajo. En algunas zonas el levantamiento se vio
afectado por las dificultades del terreno, la vegetación
que impedía la visibilidad de los satélites y la gran
inversión de tiempo que se necesitó. Como alternativa
se complementó el levantamiento con la ayuda de una
Estación Total Leyca tps 805, con un alcance de
1500/2000 m y una precisión 10 mm ppm + 2 mm.
Figura 5. Curvas de nivel del plano 1:50000 y MDT.
Simulación y representación de la inundación
Luego de delimitar las secciones transversales del
río se determinó el perfil de la superficie de agua
a lo largo del río a través de la simulación
hidráulica con el HEC-RAS. Una de las
cuestiones transcendentales para obtener una
buena estimación del mismo es el establecimiento
de condiciones de contorno apropiadas, ya que la
localización de estas está gobernada por el estado
del flujo y su inadecuada colocación impondrá un
estado del flujo incorrecto.
Figura 6. Curvas de nivel del plano 1:100000 y MDT.
5
Efectos de la base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales
El HEC-RAS admite tres zonas para establecer las
condiciones de contorno: 1) Aguas arriba, cuando se
prevé la existencia de un flujo supercrítico. En este
tipo de flujo las fuerzas inerciales predominan sobre
las de gravedad y se describe usualmente como
rápido o torrencial. 2) Aguas abajo, cuando se prevé
la existencia de un flujo subcrítico. En este estado
del flujo el papel desempeñado por las fuerzas
gravitacionales es más pronunciado, por tanto el
flujo tiene una velocidad baja y a menudo se
describe como de corriente lenta. 3) En los extremos
aguas arriba y aguas abajo, si se prevén cambios de
régimen, es decir, si el canal o río a estudiar tiene
tramos en régimen subcrítico y otros en supercrítico.
poseer una elevada precisión. El error de cada MDT se
calculó hallando la diferencia entre los valores tomados
como puntos de control y los interpolados en los TIN
construidos con ArcView que se muestran en las
Figuras 3, 4, 5 y 6. En total se compararon 467 puntos,
cuyos resultados se exhiben en la Tabla 2.
En el río se cuenta con una estación hidrométrica, a
través de la cual se obtuvo la relación de los
caudales máximos y altura de la lámina del agua al
1%, 5% y 20% de probabilidad (Tabla 1). Con estos
datos se estableció en esa sección del río la
condición de contorno correspondiente a nivel de
agua conocido (Known W.S.) y se simuló el perfil
de la superficie del agua en régimen permanente.
Figura 8. Gráfico de la zona inundada y la altura del agua,
para un caudal correspondiente al 20% de probabilidad,
empleando el TIN del levantamiento con GPS y Estación Total.
Tabla 1. Relación de los caudales máximos y
altura de la lámina del agua.
Probabilidad
Caudal
Nivel
p (%)
1
5
20
Q (m3/s)
1025
714
436
y (m)
6.45
5.52
4.06
Una vez determinado el perfil del flujo en las secciones
transversales, se delimitaron las zonas inundadas con
ArcView. Este realiza una superposición de la altura
que alcanza la superficie del agua sobre el terreno y una
operación de resta de alturas que tiene como finalidad
delimitar la extensión de la mancha de inundación. A
continuación se muestran gráficamente algunos
resultados de la simulación, en los que se evidencia las
diferencias existentes en los resultados con tan solo
variar el TIN (Figuras 8 a 12).
Figura 9. Gráfico de la zona inundada y la altura del agua,
para un caudal correspondiente al 20% de probabilidad,
empleando el TIN del plano 1:10000.
ANÁLISIS Y DISCUSIÓN DE RESULTADOS
Para evaluar la precisión de los modelos cartográficos
construidos a partir de la cartografía vectorial de curvas
de nivel, se utilizaron como puntos de control los
medidos a través del levantamiento con GPS en
conjunto con una Estación Total porque, como se
explicó anteriormente, este se considera el más
representativo de la geometría del cauce y las llanuras
de inundación, al encontrarse adecuadamente
distribuidos los puntos por toda la zona de estudio y
Figura 10. Gráfico de la zona inundada y la altura del agua,
para un caudal correspondiente al 20% de probabilidad,
empleando el TIN del plano 1:25000.
6
CUADERNOS del CURIHAM, Vol. 16, Año 2010
próxima al río tiene valor de altura (zmín = 140 m),
menor que la encontrada en planos más precisos
como el 1:10000 y 1:25000, en los que los valores
de z mínimos fueron 145 y 150 m respectivamente.
La presencia de esta curva deja muchas dudas acerca
de la calidad de la información que contiene el plano
1:50000, no solo por tener un valor de z inferior al
de otros planos más precisos, sino también, porque
es el único plano que contiene en el tramo de río
analizado una curva que corta al río y es
precisamente la que se está analizando, todo lo cual
rompe con la semejanza que presentan los otros
planos en el trazado de sus curvas, lo que puede
estar dado, entre otras causas, por un error cometido
en la construcción de dicha cartografía. Estos
aspectos influyeron de manera significativa en que el
TIN del plano 1:50000 alcanzara errores en z
inferiores a los que podrían esperarse.
Figura 11. Gráfico de la zona inundada y la altura del agua,
para un caudal correspondiente al 20% de probabilidad,
empleando el TIN del plano 1:50000.
Llama la atención que, al calcular el EMC, en cada
uno de los planos se obtuvo una apreciable
desigualdad de precisión en relación con la
establecida por GeoCuba como norma. Ante esta
situación imprevista se consideró necesario obtener
la diferencia de precisión que deberían mostrar los
planos con respecto a la real (Tabla 3).
Tabla 3. Comparación de la precisión en z.
Escala
Figura 12. Gráfico de la zona inundada y la altura del agua,
para un caudal correspondiente al 20% de probabilidad,
empleando el TIN del plano 1:100000.
1: 10 000
1: 25 000
1: 50 000
1: 100 000
Tabla 2. Estadísticos de los errores (m) de los diferentes
Modelos Digitales del Terreno.
GeoCuba
1.67 m
3.33 m
6.67 m
13.3 m
Precisión en z
calculada
5.46 m
9.22 m
2.88 m
18.82 m
diferencia
+3.79 m
+5.89 m
-3.79 m
+5.52 m
Cartográficos
10 000
25 000
Puntos de control
Error Máximo
Error Mínimo
Error Medio
467
10.63
0.11
5.20
467
12.77
0.02
8.75
50000
467
10.73
0.01
2.10
100 000
467
22.77
0.11
18.46
Error Medio
Cuadrático
5.46
9.22
2.88
18.82
En la comparación anterior se observa claramente
que ninguno de los mapas presenta la precisión que
deberían poseer, y que alcanza la mayor desigualdad
al utilizar los planos 1:25000 y 1:100000, pues con
ellos se lograron valores de 5.89 y 5.52 m
respectivamente. Sin embargo, al recurrir a los
planos
1:10000
y
1:50000
se
obtuvo
coincidentemente la misma diferencia de precisión,
con un valor de 3.79 m. Una vez más se corrobora el
hecho de que la utilización del 1:50000 conduce a
resultados ilógicos, pues es en el único caso en el
que se obtiene mayor precisión que la establecida
por GeoCuba (3.79 m por encima).
Como consecuencia se obtuvo la precisión en z de
todos los planos y, como era de esperarse, esta fue
disminuyendo a medida que lo hizo la escala.
Resalta el hecho de que al emplearse el plano
1:50000 no se cumple esta tendencia, si se tiene en
cuenta que con este se obtuvo un error medio
cuadrático (EMC) de 2.88 m, mientras que con la
utilización de los otros planos de mayor precisión
(1:10000 y 1:25000) se alcanzaron valores de 5.46 y
9.22 m respectivamente. Esta desigualdad se debe a
que en el plano 1:50000 la curva de nivel más
En sentido general se evidenció la manifestación de
grandes diferencias entre los TIN como
consecuencia del cambio de escala. Esto se debe a
que están compuestos por una serie de puntos con
7
Efectos de la base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales
valores x, y, z y un conjunto de arcos que los unen
para formar los triángulos, por lo que a medida que
disminuye la escala, aumenta la equidistancia y la
distancia entre las curvas de nivel. Toda esta
situación conlleva a un aumento significativo de la
distancia entre los puntos así como de sus valores de
altura, de esta manera queda cada vez menos
detallada la topografía del cauce y las llanuras, lo
que se pone en evidencia principalmente, en un
aumento significativo del ancho del cauce y de la
altura con respecto a la real. La Figura 13 resulta
representativa para mostrar el efecto de los
diferentes modelos en una sección transversal
cualquiera del tramo, y pone de manifiesto que las
desigualdades entre las superficies van a influir de
manera significativa en los resultados de la
simulación hidráulica.
adecuado entre todos para representar el terreno en
proyectos que no requieran tanta precisión.
Influencia de la precisión de los planos en el
cálculo de la altura del agua y el área de
inundación
Para determinar la influencia que ejerce la pérdida
de precisión de los planos en el cálculo de la altura
del agua y del área de inundación, se tomó como
patrón de comparación el TIN construido con los
puntos tomados en el terreno y, como consecuencia,
se obtuvieron los valores de elevación de la lámina
de agua con respecto al nivel medio del mar y al
fondo del río, los perfiles de la altura del agua y los
gráficos de las zonas inundadas en cada plano. Con
estos valores se calcularon las desigualdades al
emplear la cartografía vectorial de curvas de nivel
para representar el terreno (Figuras 14 y 15).
163
161
159
157
155
153
151
149
147
145
GPS
143
10 000
141
25 000
139
50 000
137
100 000
135
0
10
20
30
40
50
60
70
80
90
100
110
120
130
Figura 13. Geometría de la sección transversal 1.299
representada por los distintos planos.
Figura 14. Error Medio Cuadrático (m) en la determinación
de la altura del agua con respecto al nivel medio del Mar.
Teniendo en cuenta esta situación, se pone de
manifiesto que las desigualdades entre las
superficies del terreno van a influir de manera
significativa en los resultados de la simulación
hidráulica, por lo que los autores consideran que los
errores que impone el uso de dichas cartografías en
los resultados de la simulación, no pueden admitirse
en proyectos que necesiten un alto nivel de
precisión, pues aunque estaría trabajándose del lado
de la seguridad, al sobreestimarse los resultados, se
incurriría en grandes gastos si se fuera a proyectar
una obra o en la movilización innecesaria de
recursos humanos y materiales que se verían
afectados. Todo ello evidentemente descarta esos
planos como base cartográfica para realizar
proyectos a nivel de ingeniería de detalle. Se
considera, además, que el 1:10000 es el único
Figura 15. Error Medio Cuadrático (m) en la determinación
de la altura del agua con respecto al fondo del río.
8
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Como puede observarse, al recurrir al MDT del
plano 1:10000 se alcanzó un EMC de 6.96 m en la
altura de la lámina de agua con respecto al nivel
medio
del
mar.
Este
se
incrementa
considerablemente a medida que se trabaja con
planos de menor escala hasta obtener un valor
máximo de 22.1 m con el empleo del plano
1:100000. Una vez más esta tendencia no se
manifestó al utilizar el cartográfico 1:50000, pues se
obtuvo un EMC igual a 2.18 m, resultado que los
autores consideran inconcebible puesto que es
menor al alcanzado con el empleo del plano
1:10000, lo cual puede deberse a los errores
cometidos en la construcción del plano 1:50000
como se explicó anteriormente.
Finalmente, con el objetivo de hallar el error que se
comete en el cálculo del área inundada al utilizar
cualquiera de los planos provenientes de la cartografía
vectorial de curvas de nivel, se tomó como muestra un
total de 467 puntos. De esta manera se procedió a
establecer una comparación entre las zonas inundadas
calculadas con el empleo del TIN construido a partir
del levantamiento con GPS y Estación Total con las
obtenidas a partir del empleo de los planos 1:10000,
1:25000, 1:50000 y 1:100000.
Una vez más se pone de manifiesto que el 1:10000
es el más adecuado de todos (1:25000, 1:50000 y
1:100000) para representar el terreno, pues con su
uso la diferencia del área inundada con respecto al
valor real fue la menor, se alcanzó un valor de
0.016 Km2, mientras que con la utilización de las
restantes cartografías, incluyendo el 1:50000, estas
desigualdades aumentaron considerablemente hasta
llegar a un valor máximo de 0.230 Km2, en el caso
del MDT menos preciso (Figura 16).
Por otro lado, si se analiza el error en la altura que
alcanza el agua sin tener en cuenta el que introduce
la cota del terreno se llega a resultados muy
interesantes, pues aproximadamente se introduce el
mismo error a pesar de utilizarse planos diferentes,
pues se obtuvieron diferencias que oscilan entre 1.6
y 2.6 m; lo que revela que cuando se trabaje con uno
de estos planos se estará introduciendo, como
promedio, dichos errores en la simulación y por
tanto, se puede afirmar que sus resultados dependen
en gran medida de la cartografía de partida con que
se modela el terreno. No obstante, es necesario
resaltar que la menor diferencia obtenida se produjo,
como en las demás ocasiones, al emplear el
cartográfico 1:10000.
Una vez efectuado el cálculo de la elevación de la
lámina de agua se crea de manera automática con
ArcView un mapa del área inundada. Como
resultado del cálculo del área de inundación se
puede apreciar que a medida que disminuye la
precisión del MDT ocurre un aumento significativo
del área inundada debido a que con la disminución
de la escala del plano aumenta el ancho del cauce.
Es por esta razón que la menor área inundada se
obtuvo al utilizar el levantamiento con GPS y
Estación Total y la mayor al emplear el plano
1:100000 como se muestra en la Tabla 4.
Figura 16. Error Medio (Km2) en el cálculo
del área de inundación.
No obstante, es importante señalar que a pesar de que
la menor diferencia obtenida en el cálculo del área
inundada se haya alcanzado con el uso del
cartográfico 1:10000, resalta el hecho de que la
desigualdad es considerable, sobre todo si se tiene en
cuenta que el tramo de río en estudio es bastante corto
pues sólo es de 642 m. Por otro lado es importante
aclarar que este tramo presenta una topografía muy
abrupta, aspecto que favorece el aumento de las
diferencias debido a que en este tipo de planos el
cauce y las llanuras de inundación quedan apenas
representados en profundidad y extensión, y por tanto,
el agua ocupa desproporcionadamente más espacio de
la llanura de inundación como se puede apreciar en
las Figuras 7, 8, 9, 10 y 11.
Tabla 4. Área de inundación (Km2) para caudales con
probabilidades al 20, 5 y 1%.
Q
(m3/s)
436
714
1022
GPS
0.039
0.048
0.053
10 000
0.056
0.065
0.070
Cartografía
25 000 50 000
0.098
0.087
0.109
0.100
0.116
0.108
100 000
0.269
0.277
0.283
9
Efectos de la base Cartográfica en la Simulación Hidráulica de las Inundaciones Fluviales
con el empleo de TIN a menores escalas, se observa
que aumentan las desigualdades a medida que
disminuye la escala, sin importar el caudal que se
emplee. Se encontraron divergencias de 0.017 Km2
al utilizar el modelo cartográfico 1:10000 mientras
que con las cartografías elaboradas a partir de
escalas más pequeñas, estas desigualdades
aumentaron considerablemente hasta llegar a un
valor máximo de 0.21 Km2 en el caso del 1:100000.
CONCLUSIONES
Se calculó la diferencia existente entre los valores
de altura de cada uno de los obtenidos a partir de
los planos: 1:10000, 1:25000, 1:50000 y 1:100000,
y el levantamiento hecho con GPS y Estación
Total. Se obtuvo un EMC de 5.46 m cuando se
empleó el 1:10000. Dicha desigualdad fue
aumentando simultáneamente con la utilización de
planos de menor escala hasta llegar a un máximo de
18.82 m de altura con el 1:100000. Esta tendencia
no se evidenció con el 1:50000 pues se alcanzó el
menor EMC (2.88 m).
REFERENCIAS BIBLIOGRÁFICAS
Bates, P.B., Anderson, D.A, Price, D.A., Hardy,
R.J., Smith, C.N. 1996. Análisis and Development
of Hydraulic Models for Floodplain Flows. En:
Anderson, D.A, Walling, D.E. and Bates, P.B.
eds. Floodplain Proceses, John Wiley & Sons Ltd.
Bates, P.B., y De Roo, A.P.J. 2000. A simple rasterbased model for flood inundation simulation.
Journal of Hydrology, 236, pp.54-77.
Brunner, G. 2008. HEC-RAS, River Analysis
System. Hydraulic reference manual. Versión 4.0,
EE.UU. 411pp.
Cárdenas, A. 2000. Aplicación de Sistemas de
Información Geográfica para el modelamiento de
zonas con riesgo de inundación. Caso Estudio Río
Lurin. Inédito (13 páginas).
Carrasco, S., Pérez, R., Sánchez, M. 2004.
Inundaciones en Jimaní, Río Soliette. Diagnóstico
del Problema. Inédito (103 páginas).
Casa, A.; Benito, G. et al. 2005. Efectos de las Fuentes
Cartográficas en los resultados de la modelación
hidráulica de crecidas. Inédito (12 páginas).
Chavarri, E. A. 2004. Modelos matemáticos en
hidrología. Tesis de Maestría en Recursos
Hídricos, Escuela de Postgrado, Universidad
Nacional Agraria La Molina.
Chow, V. T. 2004. Hidráulica de los canales
abiertos. Editorial Nomos S. A. Santafé de
Bogotá, Colombia.
Cruz, E. y otros 2005. Inundaciones Fluviales.
Mapas de Amenazas. Recomendaciones Técnicas
para su elaboración, Managua, Nicaragua. Inédito
(71 páginas).
Etxeberria, P., Brazaola, A., Edeso, J. M. 2002.:
Cartografia de peligro de inundación mediante
Sistemas de Información Geográfica y modelos
Hidrológicos e Hidráulicos, Santander, España.
Inédito (9 páginas).
Etxeberria, P. 2004. Metodología para la creación de
cartografía de peligros naturales en Gipuzkoa.
Aplicación al valle de Oiartzun. Tesis doctoral,
Universidad del País Vasco.
La tendencia a que el EMC aumente con la
disminución de la escala no se evidencia con el uso
del plano 1:50000. Esto se debe a que la curva de
nivel más próxima al río tiene valor de altura menor
a la encontrada en planos con mayor precisión como
el 1:10000 y 1:25000, lo que puede estar dado por un
error cometido en la construcción de dicha
cartografía y/o de cambios en la topografía de la
zona con el paso del tiempo, todo lo cual influye de
manera significativa en los resultados mostrados, al
alcanzarse errores inferiores a los que podrían
esperarse con el uso de ese plano.
Los resultados de la modelación hidráulica dependen
en gran medida de la cartografía de partida con que
se modela el terreno, pues se ha obtenido un EMC de
6.96 m en la determinación de la altura de la lámina
de agua con respecto al nivel medio del mar al
recurrir al modelo cartográfico 1:10000, el cual se
incrementa a 7.29 m al aumentar el caudal en la
simulación. Por otro lado se evidencia que dicho
error aumentó considerablemente cuando se trabajó
con los planos de menor escala, hasta llegar a un
EMC máximo de 22.1 m con el uso del 1:100000.
Una vez más esta tendencia no se manifestó con el
uso del 1:50000 al alcanzar un valor de 2.16 m.
Al analizar el error en la altura que alcanza el agua
sin tener en cuenta el que introduce la cota del
terreno, se evidencia que aproximadamente se
produce el mismo error en la simulación a pesar de
utilizarse planos diferentes, pues se alcanzaron
valores que oscilan entre 1.6 y 2.6 m de diferencia,
lo que revela que cuando se trabaje con uno de estos
planos se estará introduciendo, como promedio,
dichos errores en la simulación.
Al comparar el área inundada obtenida con el TIN
creado a partir del levantamiento con GPS y
Estación Total, con las áreas inundadas alcanzadas
10
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Oleagordia, I., Rodríguez, R., Navarro, J. 2005. Estudio
Hidrologico del río Arlanzón a su paso por el
Término Municipal de Burgos. Inédito (9 páginas).
Omer, C.R., Nelson, E.J. y Zundel, A.K. 2003.
Impact of varied data resolution on Hydraulic
Modeling and Floodplain Delineation. Journal of
the American Water Resources Association, pp.
467-475.
Rodríguez, E. A., González, R. A. 2008. Propuesta
metodológica para la generación de mapas de
inundación y clasificación de zonas de amenaza.
Caso de estudio en la parte baja del río Las
Ceibas. Inédito (25 páginas).
Treviño, A., Ortiz, S. 2004. Metodología para la
modelación distribuida de la Escorrentía
Superficial y la delimitación de zonas inundables
en ramblas y ríos-rambla mediterráneos. Inédito
(18 páginas).
Weber, J. F. 2003. Modelación integrada uni y
bidimensional de flujo en planicies de
inundación. Maestría en Ciencias de la Ingeniería
– Mención en Recursos Hídricos, Universidad
Nacional de Córdoba, Facultad de Ciencias
Exactas, Físicas y Naturales.
Werner, M.G.F. 2001. Impact of grid size in GIS
based flood extent mapping using a 1D flow
model. Phys.Chem.Earth (B), Vol. 26, No 7-8,
pp.517-522.
Fernández, R., Geler, T. 2004. Modelo Digital de
Elevación de la Zona Emergida del Ecosistema
Sabana Camagüey, Cuba, /s.e/ (14 páginas).
Felicísimo, A. 1994. Modelos Digitales de Terreno.
Introducción y aplicación en las ciencias
ambientales. U. Oriente, Santiago de Cuba.
Hardy, R.J., Bates, P.D. y Anderson, M.G. 1999.
The importance of spatial resolution in hydraulic
models for floodplain environments. Journal of
Hydrology, 216, pp. 124-136.
Horritt, M.S. 2000. Development of physically
based meshes for two -dimensional models of
meandering channel flow. International Journal
for Numerical Methods in Engineering, 47, pp.
2019-2037.
Horritt, M.S., Bates, P.D. 2001. Effects of spatial
resolution on a raster based model of flood flow.
Journal of Hydrology, 253, pp. 239-249.
León A y Estopiñan A 1989. Hidráulica de Canales.
Editorial Pueblo y Educación. Cuba.
León A. 2000. Hidráulica de las conducciones libres.
Editorial Pueblo y Educación. Cuba.
Marks, K., Bates, P. 2000. Integration of high
resolution topographic data with floodplain flow
models. Hydrological Processes, 14, pp. 2109-2122.
Olaya, V. 2004. Hidrología Computacional y
Modelos Digitales de Terreno. Edición 0.95.
licencia Creative Common Attribution Share–
alike. Madrid.
Oleagordia, I., Rodríguez, R., Navarro, J., Del
Castillo, V. 2001. Estudio Hidrológico del Río
Arlanzón a su paso por el Término Municipal de
Burgos. Inédito (9 páginas).
Artículo recibido el 05/2010 y aprobado para su
publicación el 09/2010.
11
CUADERNOS del CURIHAM, Vol. 16, Año 2010
ANÁLISIS DE PENDIENTES HIDROMÉTRICAS EN GRANDES CRECIDAS SOBRE TRAMO
DEL RÍO PARANÁ
Marina L. Garcia(1), Pedro A. Basile(1), Gerardo A. Riccardi(1),(2)
(1)
Dto. Hidráulica y Centro Universitario Rosario de Investigaciones Hidroambientales, Facultad de Ciencias
Exactas, Ingeniería y Agrimensura, Universidad Nacional de Rosario,
(2)
Consejo de Investigaciones de la Universidad Nacional de Rosario
Riobamba 245 bis, (2000) Rosario, Santa Fe, Argentina.
E-mail: [email protected]
RESUMEN
En este trabajo se presenta un estudio sobre el comportamiento hidráulico de un tramo del sistema cauceplanicie aluvial del Río Paraná, desde Diamante hasta Ramallo, involucrando una longitud de 200 km
aproximadamente. En el tramo se observa que el flujo encauzado en el curso principal, sobre margen derecha, es separado del escurrimiento en el valle de inundación mediante albardones naturales hasta aguas abajo
de Rosario. El objetivo del trabajo es analizar el comportamiento del río en grandes crecidas a partir de registros de niveles hidrométricos y caudales sobre el cauce principal. Los resultados son importantes para la
realización de calibraciones de modelos aplicados en este tramo, y como antecedente para ríos con configuraciones similares. Se calcularon pendientes longitudinales de la superficie libre por tramos y se contrastaron
gráficas de pendientes-caudales-alturas. Cuando los caudales aumentan, manteniéndose menores a 25000
m³/s (flujo encauzado), se incrementan niveles hidrométricos y pendientes en todo el tramo. En cambio, al
superar 25000 m³/s (anegamiento en el valle), el nivel hidrométrico en Rosario crece, pero más rápidamente
se incrementa en San Nicolás por el retorno de flujo al cauce principal desde el valle, causando pendientes
menores. Con caudales máximos, esta situación es más evidente. Se observa que en la interacción cauceplanicie el aumento del caudal no necesariamente implica un incremento de la pendiente hidráulica en el
cauce, sino que depende de la configuración integral cauce-planicie y de la situación hídrica antecedente
aguas abajo.
Palabras clave: Río Paraná, grandes ríos de llanura, registros en grandes crecidas.
ABSTRACT
In this work a study on the hydraulic behavior of a river-floodplain reach of the Paraná River, from Diamante
to Ramallo is presented. The studied reach has a length of 200 Km approximately. In the reach it is observed
that the stream flow channeled into the main course is separated from the runoff in the floodplain by natural
levees up to downstream of Rosario. The study aims to analyze the hydraulic behavior of the river during
large floods from water levels and discharge measurements performed in the main stream. The results are
important for the calibration of mathematical models used in the reach, and as background for rivers with
similar configurations. Longitudinal water surface slopes were calculated and slope-discharge-water level
relationships were analyzed. It is observed that when the discharge is increased, keeping less than 25000 m³/s
(channeled flow), the water level and slopes are correspondingly augmented in the entire river reach. In contrast, exceeding 25000 m³/s (inundated floodplain), the water level in Rosario grows, but increases faster in
San Nicolás due to the return of flow from the valley to the main channel, causing a lowering in water surface slopes between Rosario and San Nicolás. That behaviour is much more evident for maximum discharges
during very large floods. It is observed that, in the channel-floodplain interaction, increasing the discharge
does not necessarily imply an increase in water surface slopes in the main channel, but depends on the integral morphological configuration of channel-floodplain system and the state of the system downstream previous to the incoming floods flows.
Keywords: Paraná River, large lowland rivers, large flood records.
13
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
las escalas existentes de los puertos del tramo mencionado. La configuración del río es tal que, aguas
arriba de Diamante, el cauce principal se presenta
recostado netamente sobre la margen izquierda y
valle de inundación con cursos y espejos de agua
interiores, y a partir de esta localidad hacia aguas
abajo cruza el cauce principal todo el valle y se
recuesta sobre la margen santafesina a la altura de
las ciudades de Maciel y Oliveros. A partir de esa
zona, la planicie aluvial se desarrolla sobre la margen izquierda del río y el ancho del mismo varía
entre 40-60 Km, mientras que, el ancho del cauce
principal varía entre 0,5-3 Km aproximadamente.
En la Figura 1 se puede visualizar el área en estudio y los cursos de aguas principales.
INTRODUCCIÓN
El estudio de procesos hidrodinámicos en crecidas
de grandes ríos de llanura, de conformación tipo
cauce-planicie, es importante para evaluar el anegamiento en sus valles, consecuencias y problemas
hidroambientales asociados. El Río Paraná es uno
de los principales cursos de agua en el territorio
argentino, formado en su tramo inferior por un
cauce principal y valle de inundación lateral. Aquí
se analiza el comportamiento hidrodinámico del
mismo en grandes crecidas ocurridas, desde la
ciudad de Diamante (Km 533 de la vía navegable)
aguas arriba a Ramallo (Km 325) aguas abajo; a
partir de los registros de alturas limnimétricas en
Figura 1. Área en estudio del Río Paraná, desde Diamante a Ramallo.
14
CUADERNOS del CURIHAM, Vol. 16, Año 2010
principal, especialmente, para la zona en estudio,
cuando éste cruza toda la planicie hacia la margen
santafecina. Según Zapata (1999), el desborde de
margen izquierda se produce en varias ubicaciones a
lo largo del albardón, el agua desborda lateralmente
en una especie de vertedero que se presenta en la
depresión o ausencia del albardón, y así ingresa al
valle, adquiriendo una dirección definida de penetración. Las ubicaciones de esos desbordes se corresponden con nacientes de arroyos y riachos de existencia permanente: Espinillo, Paranacito-Victoria,
Barrancoso, Careaga, San Lorenzo, ParanacitoRosario. Las trayectorias líquidas, en su mayor parte, se alinean con las direcciones medias de los cursos permanentes, aunque se producen algunas desviaciones bien definidas que no tienen contrapartida
en aguas bajas: desde el Barrancoso hacia los Timbó
(afluentes del Paranacito-Victoria), desde los Timbó
hacia el área de drenaje que confluye a La Camiseta,
desde el San Lorenzo al Barrancoso, etc. La mayor
concentración de corrientes, a la altura de Rosario,
se da en la zona comprendida entre el ParanacitoVictoria y la barranca entrerriana. Estos cursos más
–en menor medida– las precipitaciones en la zona,
son los que alimentan las lagunas.
El régimen del Paraná es principalmente gobernado
por los aportes provenientes de aguas arriba, los
afluentes laterales incrementan en poco porcentaje el
caudal total. La principal entrada de volumen de agua
en la zona en estudio, es a través del cauce principal
del río, y es éste el que recoge y distribuye el fluido
en todo lo que conforma el valle de inundación.
En el tramo en estudio, el agua que ingresa a la planicie, lo hace a través de cursos de agua menores originarios en el cruce del cauce principal, presentándose
dos principales escurrimientos: encauzado sobre la
margen derecha y sobre el valle (a través de cursos,
bajos y lagunas interconectados). Éstos se presentan
separados por crestas angostas –denominadas albardones– que existen hasta aguas abajo de Rosario.
Interiormente por el valle, existe una red de cursos, de
menores magnitudes que el cauce principal, pero de
distintas y variadas jerarquías. Los mismos pueden ser
permanentes o transitorios, tienen trazas zigzagueantes que se van moldeando y modificando a través del
tiempo según la dinámica hídrica que se presente. La
planicie en el tramo en estudio, cuenta por lo menos
con una decena de cursos de agua interiores importantes, con escurrimiento predominantemente NO-SE,
que son los que alimentan principalmente de flujo al
valle. También aquí se pueden presentar en las márgenes de los mismos albardones menores, producto de
las deposiciones de sedimentos en los desbordes.
Algunos de los cursos de agua en sus recorridos unen
sus trazas y forman uno nuevo aguas abajo, o por lo
contrario, pueden presentarse bifurcaciones y dar
origen a nuevos cursos. La mayoría de ellos, sobre
aguas abajo del tramo estudiado, descargan sus aguas
sobre el Río Pavón, curso de importancia que atraviesa el valle desde la margen santafecina a la entrerriana. Algunos otros cursos comienzan en el cauce principal para luego de un corto recorrido retornar al de
origen, desarrollándose éstos en la zona cercana a los
albardones divisorios de los dos escurrimientos generales antes citados.
El aporte del sistema del río Coronda, que penetra
desde la margen derecha del cauce principal del
Paraná, se concentra a la altura de Oliveros, y aguas
abajo de Diamante se produce un desborde del cauce
principal del Paraná, sobre margen derecha, que se
reencauza antes de alcanzar Oliveros.
Durante las crecidas, los ingresos entre los albardones a los cursos se incrementan considerablemente,
y –según sea la magnitud de la creciente– pueden
llegar a desbordar los mismos, situación que da hasta
aguas abajo de Rosario, en que ya los mismos no se
presentan. Los cursos de agua aumentan su carga y
también desbordan, comienzan a incrementar el
volumen de agua de lagunas cercanas aledañas a los
cursos y a interconectarse las depresiones, que al
aumentar la cota del pelo de agua presente en ellas,
pueden iniciar un escurrimiento interlagunar. Las
que podían haber estado inicialmente aisladas, con la
crecida, usualmente quedan formando parte de la red
de escurrimiento a través del valle.
A su vez el valle contiene grandes y variadas depresiones lagunares, así como bajos que surgen de cauces y curvas o meandros abandonados por sus cursos
al moldear los mismos otros nuevos en su recorrido
dinámico. Algunos pueden ser aislados, o ser el
origen de cursos de agua menores.
Al presentarse una crecida, el río sale de su cauce
principal y pierde capacidad de transporte, formando
en ambas márgenes los albardones. Los sedimentos
del flujo que ingresa a la planicie aluvial, con el
tiempo tienden a reducir el relieve local, ya que
decantan al bajar la velocidad y por la vegetación
En épocas de aguas bajas, el flujo es encauzado y se
identifican lagunas que pueden conectarse con los
mismos. El valle se “carga” de agua principalmente
a través de los cursos que tienen origen en el cauce
15
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
fundamentalmente en grandes crecidas, que son las
que provocan cambios morfológicos importantes en
los valles aluviales.
presente que los fija, así es como rellenan lagunas y
pantanos, y también se depositan en albardones y
otros relieves (Rocca et. al., 1973). El estudio de las
crecidas es importante, ya que la magnitud de éstas y
la permanencia están vinculadas a las modificaciones topográficas que se producen en el valle, al generarse cambios en los procesos de sedimentación
(Asselman et. al., 1995).
MATERIALES Y MÉTODOS
Se recopilaron registros limnimétricos de las escalas de los puertos de: San Nicolás (SN) en el Km
353 de la vía navegable, Rosario (R) en el Km 416,
Puerto San Martín (PSM) en el Km 448 y Diamante (D) en el Km 533, y caudales en Puerto San
Martín (informados –ley H-Q– y aforados). Para
ordenar el estudio de los registros, se plantean los
siguientes tramos, que pueden visualizarse en la
Figura 2 siguiente:
Respecto a la vegetación que se presenta en el valle
y su relación con la morfología y escurrimiento, la
trama de lechos permanentes y temporarios, que
divaga con niveles energéticos bajos, crea espacios
donde se generan ecosistemas de evolución dependiente e influenciada por la dinámica que tiene la
planicie. Sobre los albardones laterales del cauce
principal, constituidos de granulometría más gruesa,
se desarrolla vegetación arbórea y arbustiva. En
cambio en el valle, donde se depositan los sedimentos más finos en las áreas más alejadas de los cauces,
se generan ecosistemas más simples, de vegetación
arbustiva, pajonales y pastizales. Los gradientes de
vegetación que se presentan, entonces, tienen directa
relación con la disposición sedimentaria, así como
también con la permanencia del agua sobre estos
terrenos aluvionales (Zapata, 1999).
Diamante-Puerto San Martín (D-PSM): es en
donde el cauce principal cruza todo el valle de inundación, desde el comienzo en la costa entrerriana a
la santafecina a la altura de Oliveros. El tramo es de
85 Km de longitud aproximadamente con orientación leve NE-SO, la planicie aluvial pasa de estar en
la margen derecha aguas arriba de Diamante, a la
izquierda aguas abajo de este tramo. Aquí se originan la mayoría de los cursos de agua interiores a la
planicie. En todo el tramo existen albardones costeros de la margen izquierda, y la margen derecha está
constituida también por albardones hasta que el
cauce principal encuentra la costa santafecina, en
donde pasa a ser barranca de gran altura.
Durante las crecidas, en el cauce principal, el nivel
del pelo de agua lógicamente se eleva a lo largo de
todo el tramo en cuestión, pudiendo anegar parte o
por completo las islas y zonas bajas que forman
parte del mismo. Según los desbordes que se presenten –en función de la situación– y el caudal que
fluya, el pelo de agua va a tener distintas pendientes longitudinales.
Puerto San Martín-Rosario (PSM-R): este tramo
conserva las características anteriores, el cauce
principal tiene sobre la margen izquierda albardones que lo separan del valle de inundación, donde
además se originan varios cursos interiores a éste, y
la margen derecha constituida por barranca. La
longitud es de aproximadamente 32 Km, con orientación leve NO-SE.
El objeto del presente trabajo es analizar el comportamiento del río en grandes crecidas, a partir de
registros limnimétricos y caudales sobre el cauce
principal. Los que serán tenidos en cuenta, son
aquellos anteriores a la Conexión física RosarioVictoria, para independizar los resultados de esta
obra significativa en el tramo estudiado. Se podrá
vislumbrar sobre el comportamiento no uniforme
del río, e intentar establecer dependencias de los
registros de distintos factores que afectan a su
comportamiento. Los resultados serán importantes
para calibraciones de modelos aplicados en este
tramo –como el de simulación de escurrimiento
hidrodinámico cuasi-2D implementado y aplicado
en Garcia et al (2008)–, así como también de antecedente para ríos con configuraciones similares,
Rosario-San Nicolás (R-SN): el cauce principal
sobre la margen derecha sigue siendo con barrancas, pero en dos oportunidades, la barranca no se
presenta tan neta como lo hacía aguas arriba, a la
altura de Villa Constitución y de San Nicolás se
encuentra distante del mismo a través de isletas. La
margen izquierda ya no cuenta con los albardones
que dividían el cauce principal con la planicie y
hay una interconexión de flujos más directa. El
tramo es de 63 Km aproximadamente, sigue con
orientación NO-SE.
16
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 2. Tramos en estudio del cauce principal del Río Paraná.
- Puerto San Martín (PSM): frente a la ciudad del
mismo nombre, sobre el cauce principal. Existen
aforos realizados entre el 14/05/1980 y el
10/12/2009 (no se cuenta con aforos de los años
1990; 1991 y 1992). Los datos oficiales de los
valores de caudales, los otorga la Subsecretaría de
Recursos Hídricos de la Nación (SSRH), que se
obtienen a partir de una ley H-Q propia. La misma
está evaluada a partir de los registros existentes de
alturas locales, y responde a una ley definida hasta
el 31/08/2000, a partir de allí se evidencia la aplicación de otra ley H-Q para calcular los caudales
en la sección de PSM. La relación entre alturas
registradas y caudales utilizada se puede visualizar
en la Figura 3 inferior, conjuntamente con los valores de los aforos realizados. Éstos últimos tienen
dispersión respecto a las curvas de las leyes H-Q,
difieren en aproximadamente un metro de los que
podría llegar a ser el caudal; o para una misma
lectura de la escala, el caudal podría variar en
Caudales
Los aforos de caudales sobre este tramo del Río
Paraná no son habituales, de hecho, aunque la importancia del río probablemente lo justifique, no
existe una sección de aforo permanente. Se han
realizado aforos esporádicos en el cauce principal y
muy ocasionalmente en el valle aluvial, sobre la
transecta Rosario-Victoria. Los aforos para los que
se cuentan con datos son los siguientes:
- Diamante: frente a la ciudad, se supone que sobre
el cauce principal, de fechas 02/07/1920 (aguas
medias) y 22/08/1925 (aguas bajas). Por la fecha de
estos aforos no son considerados, ya que posiblemente la configuración del río en este lugar haya
cambiado. Además son anteriores a los comienzos
de la década del ‘70, donde se construyeron las
grandes presas en el tramo superior del Paraná, que
hacen a la serie de datos anteriores no homogénea.
17
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
aproximadamente 5000 m³/s, pero si se traza una
línea de tendencia logarítmica, ésta se aproxima
bastante bien a la curva H-Q utilizada hasta septiembre del 2000.
Figura 3. Gráfica H-Q de la Subsecretaría de Recursos Hídricos de la Nación y Aforos,
en el cauce principal frente a Puerto San Martín.
A partir de los registros de alturas y los caudales aforados entre 14/05/1980 y 22/04/1997, se puede obtener
una ecuación polinómica de 6º grado para vincular las
alturas locales de Puerto San Martín y el caudal del
cauce principal frente a esa misma localidad:
Q = 0,296 H − 5,502 H + 42,969 H
6
5
y otra debida a las crecidas desfasadas del río Paraguay (repunte del pejerrey por la presencia del Pantanal) y/o a las crecidas cortas y abruptas del río
Iguazú, que se dan a partir de julio.
El rango de caudales registrado, para el cauce principal del Río Paraná frente a Puerto San Martín, es
de 7000 a 32500 m³/s aproximadamente. El módulo
del río se considera de aproximadamente 17500 m³/s
(para el período 1970-2008, el módulo resulta de
17586 m³/s). Particularmente, cuando se presenta la
situación de caudales mayores a 25000 m³/s se evidencia anegamiento de gran parte del valle, ya que
en varios lugares desde Diamante a Rosario se superan las cotas de los albardones costeros que separan
el cauce principal de la planicie. Por lo tanto, la
presencia de agua en el valle ya no sólo es a través
de los cursos interiores, que pueden llegar incluso a
tener desbordes al aumentar sus tirantes, sino que
además, hay ingreso de agua en forma de desborde
del cauce principal. A partir de este valor singular de
caudales, la dinámica general de la zona en estudio
tiene modificaciones. La misma se puede apreciar
esquemáticamente en la Figura 4 a continuación.
4
− 159,417 H 3 + 421,176 H 2 + 2512,421H
+ 4730,817
(1)
Siendo:
Q: caudal en la sección del cauce principal frente a
Puerto San Martín, en m³/s,
H: altura local en PSM, en m.
Para los posteriores análisis se tomarán los caudales
que se informan oficialmente, ya que la curva H-Q
presenta un ajuste aceptable de los valores aforados.
El régimen hidrológico del río en este tramo del
Paraná Inferior se presenta usualmente con dos crecidas anuales, una que corresponde a los aportes del
Alto Paraná entre los meses de marzo, abril y mayo,
18
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 4. Esquema de la dinámica general de escurrimiento de la zona en estudio.
Desde la zona aguas abajo de Rosario, el cauce principal ya deja de tener la presencia de albardones que
encaucen netamente el agua en éste, y puede haber un
intercambio más franco de flujo entre aquél y el valle
aluvial. Dependiendo de los niveles de agua presente
según la situación, la planicie puede descargar sobre el
cauce principal recargándolo y aumentado su tirante, o
bien suceder exactamente lo contrario.
mienzo de la década del ‘70, ya que se presenta un
cambio en la tendencia central de las series (Paoli et.
al., 2000), período éste, en el que la cuenca Del Plata
experimentó marcados cambios en el uso del suelo,
en especial deforestación, y que además comenzaron
a operar una serie de presas en el propio Río Paraná,
que podrían formar parte de las causas de mayores
escurrimientos, que hacen que la serie homogénea a
analizar a partir de dicha fecha.
Con los caudales considerados (los que otorga la
SSRH) y los registros limnimétricos para cada año
hidrológico analizado, se van a exponer las pendientes longitudinales de los distintos tramos. A priori,
se puede esperar que las pendientes tengan similares
variaciones, con respecto al caudal sobre el cauce
principal. Los resultados esperables son que las
pendientes sean cada vez menores hacia aguas abajo,
contemporáneamente en los tramos analizados. Se
verá más adelante que no se puede asegurar esta
suposición, ya que para diferentes crecidas, el río
tiene distintos comportamientos, especialmente en el
tramo aguas abajo, por la particularidad de la configuración topográfica presente.
Adicionalmente, se analiza el tramo en el período
anterior al 2003, en que finaliza la construcción de
la Conexión física Rosario-Victoria, para independizar los resultados de esta obra significativa en el
tramo estudiado. La presencia de la misma podría
traer aparejado una serie de cambios en los procesos morfológicos naturales del río, que podrían
provocar una redistribución de los caudales en una
zona de influencia aguas arriba y aguas abajo de
ella (FICH, 2004). Es de importancia si aquí existiesen cambios, ya que hacia aguas abajo es donde
se puede presentar intercambio de flujo entre valle
y cauce principal.
Las crecidas analizadas fueron las de los años 19821983; 1992; 1997-1998, que fueron tres eventos
extraordinarios (aquellas en que los máximos anuales superaron los 30000 m³/s), siendo las de mayor
relevancia en el período a analizar. Para éste, se
tomaron en cuenta aquellos años posteriores al co-
En la Figura 5 se grafican los caudales obtenidos
de la SSRH para las crecidas a considerar. Se indica allí mismo los períodos en que los aumentos y/o
disminución de caudales fueron de consideración,
para asociarlos posteriormente a los registros de
alturas limnimétricas.
19
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
Figura 5. Hidrogramas anuales en la sección del cauce principal frente a PSM,
correspondiente a las crecidas de 1982-1983; 1992 y 1997-1998.
Los años hidrológicos 1982-1983 se los puede
analizar en conjunto, ambos conforman la crecida
del Río Paraná que tuvo mayor permanencia de
agua altas. Lo particular de ésta es el cambio considerable de la rugosidad frente al escurrimiento, ya
que la vegetación presente muere o se ve afectada
luego de un cierto tiempo con presencia de agua.
En 1982, si bien los caudales registrados están por
encima del módulo del río (17500 m³/s), al final del
primer año se experimenta un descenso rápido (casi
4000 m³/s en 14 días) e inmediatamente se produce
un incremento considerable (aumento de casi
13300 m³/s en menos de 3 meses, tasa promedio de
229,25 m³/s/día), que hace que más de la primera
mitad de 1983 tenga caudales por encima de los
25000 m³/s, implicando el anegamiento de la mayoría del valle, para luego disminuir en la segunda
mitad de dicho año, manteniendo los caudales superiores al módulo.
medio, tasa de crecimiento de 148,4 m³/s/día),
para luego volver a disminuir en aproximadamente igual proporción (100,6 m³/s/día) a los mismos
valores cercanos al módulo. El período en que se
superan los 25000 m³/s y vuelve a disminuir, es de
casi 2 meses, que comprándolo con el tiempo que
permanece el agua encima de ese valor en 198283 (8 meses aproximadamente), la crecida es denominada de tipo rápida. Nuevamente casi al final
del año se produce un leve aumento del caudal,
pero no llega a ser significante.
Los años continuos hidrológicos 1997-1998 se
caracterizaron por ser de aguas altas, en particular
el ’97 fue de aguas medias-altas al principio, con
una crecida rápida que llega a los 27200 m³/s y con
marcados crecimiento (7700 m³/s en 2 meses, tasa
de 120,3 m³/s/día) y descenso (13500 m³/s en 2,5
meses, tasa de 179,7 m³/s/día) de caudales. Luego
se da la mayor crecida en registros históricos de
niveles de agua del Paraná en el ’98, cuando el
caudal sobre el cauce principal fue de 32283 m³/s.
El escenario para el comienzo de este año particular fue con bastante presencia de agua, que ha influenciado en gran medida a que se registren los
máximos niveles. Los caudales en esta crecida se
En 1992 lo que sucede en el río puede denominarse como crecida rápida. En el principio del año los
caudales que se computaban estaban dentro del
rango de aguas medias, pero cerca de mitad de
año se produce una crecida con un rápido incremento de caudales (casi 12000 m³/s en 2 meses y
20
CUADERNOS del CURIHAM, Vol. 16, Año 2010
mantuvieron por encima de los 25000 m³/s algo
más de 6 meses, pero siendo éstos de importancia,
el período fue menor a 2 meses. El descenso que se
produce luego del pico de la crecida es muy marcado, ya que desciende en 100 días (3,3 meses)
aproximadamente 14000 m³/s, tasa de decrecimiento de 133,6 m³/s/día.
Alturas limnimétricas
En la Figura 6 siguiente se pueden visualizar los
registros limnimétricos en cada escala estudiada
(todas las cotas del pelo de agua fueron llevadas a
cotas del IGN para su comparación), para los años
de las crecidas citadas.
Figura 6. Registros limnimétricos y caudales del cauce principal del Río Paraná, en las escalas de: Diamante, Pto. San Martín,
Rosario y San Nicolás; para las crecidas de 1982-83; 1992 y 1997-98.
Como puede apreciarse, los rangos de variación
del pelo de agua para cada escala, en forma
aproximada fue de 4 metros, que en cada caso
fueron los siguientes:
-
cos; no obstante, los caudales fluviales no han sido
tan extremos como en crecidas anteriores. Esto se
evidencia, por ejemplo, en que los niveles máximos
registrados durante la crecida de 1998 en Diamante
no son los máximos históricos, como sucede en
Rosario, sino que se ubican en el cuarto lugar en la
serie, detrás de las crecidas de 1992, 1983 y 1905.
Estas diferencias se asignan al diferente desarrollo
de la vegetación sobre el valle de inundación y al
albardón del cauce principal del Paraná, que producen una resistencia hidráulica distinta (Serman &
asociados S.A., 1999).
Diamante: de cota 9,53 mIGN a 13,56m IGN
Pto. San Martín: de cota 6,46 mIGN a 10,43 mIGN
Rosario: de cota 5,66 mIGN a 9,48 mIGN
San Nicolás: de cota 3,99 mIGN a 8,22 mIGN
Se observa que las máximas alturas se producen en
general en el año 1998, y las segundas en 1992. Si
bien el valor de 1992 es el segundo ocurrido en la
historia registrada, su permanencia y volumen es
mucho menor de los que se producen en la crecida
de 1983, que es lo que le da relevancia a la misma.
En el caso de 1998, hay un prolongado período de
crecida moderada estacionaria, seguidas de un pico
cuya magnitud excede varios de los registros históri-
El área en estudio forma parte del Paraná Inferior,
donde suele citarse que aguas abajo de Ramallo hay
influencia de la marea del Océano Atlántico. Para
estimar si la misma afecta a nuestra zona, se contrastan las distintas alturas limnimétricas registradas, las
cuales se representan en la Figura 7.
21
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
Figura 7. Registros limnimétricos confrontados de a pares contiguos, de las escalas de Diamante, Pto. San Martín, Rosario y San
Nicolás, de los años 1982-1983-1992-1997-1998.
aguas arriba de PSM y de 3,6x10-5 para aguas abajo
de Rosario (Rentería et. al., 2009), cuyos rangos
quedan contenidos en el que aquí resulta, siendo los
extremos cercanos a los valores citados.
Las gráficas tienen tendencia mayoritariamente
recta, representan las relaciones cuasi lineales entre
los distintos registros contiguos. El contraste entre
las alturas de San Nicolás y Rosario es el que presenta mayor divergencia de la recta, con dispersión
menor a un metro. Por las relaciones que aquí se
muestran, no habría influencia notable de la marea.
La correlación entre las alturas de Diamante y Pto.
San Martín, a partir de determinado valor, comienza a tener mayor dispersión, que puede vincularse
con el hecho que para aguas altas del Paraná, el
aporte del Río Coronda, que tiene lugar aguas arriba de Pto. San Martín en el Km 460 de la vía navegable, puede incrementarse.
A continuación se presenta en la Figura 8 las gráficas de las pendientes calculadas en cada tramo (DPSM, PSM-R y R-SN), para las distintas crecidas.
Para el tramo D-PSM, las pendientes han variado
en el entorno de 2,96 a 4,33 x10-5, estando la mayoría de los registros dentro de los 3,25 a 4,00x10-5.
Se han registrado algunas pendientes que escapan
de dicho rango más acotado, pero son valores puntualizados para los cuales los caudales tuvieron
ascensos y/o descensos abruptos en un corto tiempo. No se evidencian grandes variaciones de la
pendiente con los cambios de caudales en crecidas,
y usualmente tienen la misma tendencia de crecimiento/descenso que éstos.
Pendientes limnimétricas
A partir de los registros en las escalas de los puertos
mencionados y para los años de las crecidas citadas,
se calculan las pendientes limnimétricas de los tramos definidos con las longitudes que indican la
ubicación de cada escala en la vía navegable. Las
pendientes, en general, se encuentran en el rango de
1,6x10-5 a 4,3x10-5 aproximadamente. Dentro de la
zona en estudio, para la definición de cotas de obras
de toma sobre el cauce principal del río (frente a
Timbúes y a Fighiera), se han indicado como referentes pendientes longitudinales mínimas de
2,0x10-5 y máximas del orden 4,0x10-5 para el tramo
En el tramo PSM-R, las pendientes registradas varían dentro de un rango más amplio que el anterior, de
2,19 a 4,19 x10-5, siendo la mayor densidad de registros ubicados entre los valores 2,60 a 3,60x10-5.
Aquí las pendientes que escapan por fuera de este
rango más limitado son de mayor frecuencia, pero
nuevamente coinciden con caudales muy bajos o
aumento repentino de los mismos.
22
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 8. Gráficas de pendientes longitudinales en los tramos D-PSM, PSM-R y R-SN y caudales en PSM, para las crecidas de
1982-1983; 1992 y 1997-1998.
En el tramo R-SN, las pendientes longitudinales
registradas varían de 1,56 a 3,75x10-5, siendo un
rango más estrecho –con la mayoría de los registros–
de 1,75 a 3,50x10-5, que al no ser mucho menor se
pone de manifiesto mayor variabilidad de los valores. Casi no hay registros por fuera de los rangos
definidos, únicamente en casos extremos de las
crecidas (picos y final del ’83).
Análisis por Crecidas
A partir de las pendientes limnimétricas calculadas,
se analizará cada crecida por separado, para evaluar
las singularidades presentes.
Crecida 1982-1983
La misma se caracterizó por aguas altas en el Río
Paraná y de una importante permanencia. Se puede
apreciar en detalle en la Figura 9 a continuación.
Ésta es singular por el período en que reside el
agua en el valle, produciendo un cambio considerable en la rugosidad frente al escurrimiento, ya
que la vegetación presente muere o se ve afectada
luego de un tiempo considerable de estar sumergida, como fueron los casi 8 meses que duraron los
caudales sobre 25000 m³/s.
Por los rangos expresados anteriormente, se cumple
con lo previsto que hacia aguas abajo en el curso
principal, las pendientes longitudinales son cada vez
menores. Se evidencia también mayor variabilidad
en el mismo sentido, manifestando hacia aguas arriba que el curso es mucho más definido; hacia aguas
abajo, hay mayor cantidad de factores que afectan el
nivel del agua sobre el cauce principal, lo que podría
provocar los rangos más amplios en las pendientes.
23
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
En cuanto a las pendientes, se ve una relativa estabilidad aguas arriba (D-PSM), y que acompañan
las variaciones de caudales, especialmente en
1982. En primera mitad de 1983, es notable la
dispersión entre las tres pendientes analizadas,
existe una fuerte disminución de la de aguas abajo
(R-SN), y que se refleja –en menor medida– en la
pendiente de PSM-R. Esto puede deberse a que al
estar el valle con importante volumen de agua
–que ingresó desde finales de 1982–, se produce
un regreso desde la planicie al cauce principal,
aguas abajo de Rosario, cuando los bordos ya no
condicionan la interconexión hidráulica entre cauce principal y valle aluvial.
Figura 9. Gráficas de pendientes longitudinales en los tramos D-PSM, PSM-R y R-SN y caudales en PSM, para la crecida de 1982-1983.
Así, aguas abajo de Rosario, los niveles se incrementan en la escala de San Nicolás por tener una doble
concurrencia de agua –desde el valle y cauce principal– y dan como resultado pendientes longitudinales
muy bajas para esta situación, la cual se esquematiza
en la Figura 10. Al finalizar la crecida y cuando disminuyen los caudales sobre comienzos de agosto del
‘83, se tienden a reestablecer las pendientes habituales, siendo notable la recuperación de la de R-SN
cuando el caudal baja de los 25000 m³/s.
variación de los caudales presentes. Con el leve ascenso de los mismos sobre fin de año también aumentan estas pendientes, pero no de forma considerable.
Es de destacar el comportamiento disímil de la pendiente R-SN, ya que antes del pico de la crecida, al
superar el caudal los 25000 m³/s, ésta cae en forma
abrupta, a valores muy bajos durante el pico, luego
presenta oscilación y al descender los caudales –en
especial de 25000 m³/s– asciende hasta igualar a las de
los otros tramos. Esta disparidad entre las pendientes
puede llegar a responder a que al aumentar los caudales, el tramo aguas abajo no responda rápidamente en el
sistema y tenga una inercia hídrica al escurrimiento que
hace que se acumule agua en este tramo, hasta tanto se
logre una adecuada evacuación aguas abajo del lugar
estudiado. Puede ser además que se repita lo supuesto
durante la crecida de 1982-83, que al existir una interconexión franca entre el valle y curso principal aguas
abajo de Rosario, parte del flujo retorne desde la planicie, incrementando considerablemente los registros de
niveles de agua en esta zona.
Crecida 1992
En cuanto a esta crecida, ver Figura 11, las pendientes
de D-PSM no tienen mayores variaciones, elevándose
ligeramente durante la crecida y nuevamente al final
del año con el aumento leve de caudales. Las pendientes PSM-R responden a la crecida primero con aumento y luego un rápido descenso a partir de superar
los caudales el valor singular de 25000 m³/s; posteriormente ya pasado el pico de la crecida y con caudales en descenso lento, se presenta una elevación puntual de las pendientes que parece no responder a la
24
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 10. Esquemas de la dinámica general de la zona en estudio a) escurrimientos en aguas medias,
b) escurrimientos en crecida importante.
Figura 11. Gráficas de pendientes longitudinales en los tramos D-PSM, PSM-R y R-SN y caudales en PSM, para la crecida de 1992.
25
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
de aguas medias-altas, con la clásica crecida en marzo y
luego al año siguiente se da la mayor crecida en registros de niveles de agua históricos del Paraná en Rosario.
Crecida 1997-1998
Los años hidrológicos 1997-1998 se caracterizaron por
ser de aguas altas, ver Figura 12, en particular el ’97 fue
Figura 12. Gráficas de pendientes longitudinales en los tramos D-PSM, PSM-R y R-SN y caudales en PSM,
para la crecida de 1997-1998.
En 1997 las pendientes de los tramos estudiados
acompañan bastante bien las variaciones de caudales registrados, notando como singular que la pendiente de R-SN resulta levemente por encima de la
de PSM-R. Hacia fines de 1997 el caudal comienza
su crecimiento y llega a mantenerse casi por 4
meses en el valor de 25000 m³/s, donde se manifiesta un decrecimiento en las pendientes de los
tramos aguas abajo PSM-R y R-SN; posteriormente
comienza un nuevo incremento hasta el pico de la
crecida, donde se superan ampliamente los 25000
m³/s y las pendientes caen abruptamente, especialmente la de R-SN.
de los caudales), pero no tan significativas. Una vez
pasado el pico, al bajar el caudal hasta valores cercanos al módulo del río, las pendientes se restituyen
a las usuales; y en la crecida tardía en ese mismo año
al final, se tiende a repetir la situación anterior, pero
con la particularidad que la pendiente de PSM-R
tiene un mayor descenso, y la de D-PSM se eleva
casi al final del año (aún cuando los caudales siguieron disminuyendo).
A modo de ilustración, se presentan en la Figura 13
siguiente, combinaciones de imágenes satelitales
(obtenidas de la página del U. S. Geological Survey), inmediatamente posteriores a las crecidas que
se analizan, donde se refleja la gran proporción de
zona anegada sobre el valle. Las distintas calidades
en las imágenes responden a la evolución en el correr de los años de las imágenes multiespectrales que
brindan los satélites.
Se vuelve a repetir lo visto para las crecidas anteriores, las pendientes hacia aguas abajo decaen, más
pronunciadamente cuando el gradiente de caudales
se incrementa en forma notable. La pendiente de DPSM tiene variaciones (siempre acompañando a las
26
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 13. Imágenes Landsat TM combinadas, bandas 4-3-2. Superior Izquierda: 226-083 (22/07/1983) y 227-082 (29/07/1983);
Superior Derecha: 226-083 (23/08/1992) y 227-082 (14/08/1992); Inferior: 226-083 (08/08/1998) y 227-082 (30/07/1998).
caudales. Las pendientes presentes en el tramo DPSM son medianamente uniformes, no parece
haber una fuerte dependencia entre las mismas y
los caudales, con una dispersión un tanto más amplia en aguas medias-altas.
RESULTADOS
Para analizar algún tipo de vinculación entre las
pendientes limnimétricas que se presentan en los
distintos tramos y los caudales sobre el cauce principal, se realiza una gráfica integral que contraste
ambos parámetros, Figura 14 siguiente.
Las pendientes PSM-R tienen una variación similar
a las de R-SN respecto a los caudales, hasta el
módulo del río acompañan la tendencia de crecimiento, pero disminuyen cuando se presentan caudales elevados –en especial mayores de 25000
Se puede observar que en aguas medias, las pendientes limnimétricas sobre el cauce principal siguen la misma tendencia de crecimiento que los
27
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
m³/s–, dando una variación en forma de V, con
pico cercano al módulo. Este comportamiento es
más pronunciado para el tramo R-SN, registrándose
para caudales altos valores muy bajos de pendientes longitudinales (con bastante diferencia de los
del tramo aguas arriba).
Figura 14. Gráficas de pendientes longitudinales en los tramos D-PSM, PSM-R y R-SN versus caudales en PSM,
para las crecidas de 1982-83; 1992 y 1997-98.
Las pendientes longitudinales dependen principalmente de la configuración integral cauce principal-planicie. Cuando los caudales aumentan y
son menores a 25000 m³/s (flujo encauzado), se
incrementan los tirantes y pendientes en el cauce.
En cambio, cuando el caudal aumenta superando
dicho valor, el tirante en Rosario crece, pero más
rápidamente se incrementa en San Nicolás por el
retorno de flujo al cauce principal desde el valle,
donde ya no se presenta la separación física neta
(albardones) del flujo, causando pendientes longi-
tudinales menores. Con caudales máximos, esta
situación es más evidente.
Un esquema de lo recientemente expresado se presenta en la Tabla 1. Debajo en la Figura 15 se muestra la combinación de dos imágenes satelitales Landsat procesadas digitalmente, para la crecida de 1998,
que reflejan las líneas generales de escurrimiento,
especialmente sobre el valle, junto a un zoom de la
posible zona donde se produce el retorno del flujo
desde el valle al cauce principal.
Tabla 1. Variaciones en los parámetros más significativos durante una crecida, en la zona de estudio del Río Paraná.
Condición de Tirantes
Condición de Pendientes
longitudinales
Q en Cauce
Principal en PSM
Características del Flujo
sobre CP
Intercambio de
Flujo CP-PI
Pto. San
Martín
Rosario
San
Nicolás
D-PSM
PSM-R
R-SN
< 25000m³/s
encauzado
NO
↑
↑
↑
---
↑
↑
> 25000m³/s
retorno de flujo desde PI
SI
↑
↑
↑↑
↑
↓
↓↓
Referencias: CP: Cauce Principal
PI: Planicie de Inundación
↑: aumento
↑↑: aumento de mayor incremento
↓: disminución
↓↓: disminución de mayor intensidad
---: sin variación significativa
28
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 15.- Combinación de Imágenes Landsat TM 227-082 (05/06/1998) y 226-083 (04/05/1998) procesadas digitalmente,
para visualización de trayectorias líquidas.
Para visualizar en conjunto la relación presente entre
caudales, cotas del pelo de agua y pendientes longitudinales sobre el cauce principal, se estudian estos
valores de la serie 1970-2007 y se presenta la Figura
16. En la misma se contrastan las pendientes longitudinales PSM-R y los caudales informados por la
SSRH en PSM, en función de las cotas del pelo de
agua presentes en cada día, en la escala de PSM. Se
exponen conjuntamente los valores de aforos disponibles (períodos 1980-1989 y 1993-2007) frente a PSM.
cuando las alturas son mayores, la variación llega a
ser de 1,5x10-5. De esta comparación se puede concluir que al intentar considerar un caudal sobre el
cauce principal, con cierto valor de rugosidad y un
tirante, la pendiente longitudinal consecuente
–teniendo en cuenta flujo uniforme– sería de un
valor determinado, no habiendo en la realidad una
relación biunívoca. Esto hace suponer que los cálculos que puedan llegar a realizarse utilizando la ecuación de continuidad y de flujo uniforme, que muy a
menudo se supone en corrientes naturales (Chow,
1959), son simplemente estimativas.
De acuerdo a lo anteriormente expresado y de lo
expuesto en esta gráfica, no se presenta una pendiente claramente definida para un mismo tirante y caudal, de los cuales se ha visto que los aforos responden con bastante aproximación al valor que surge de
la curva H-Q definida. Para un valor determinado de
altura de agua, las pendientes que se presentan están
dentro de un rango aproximado de 1,00x10-5; y
En resumen, no puede establecerse una vinculación
directa entre caudales y pendientes registradas, dada
la dependencia de las condiciones topográficas locales y de la situación hídrica sobre el valle de inundación, que condicionan la descarga del sistema. Además la topografía dependerá del momento en que se
29
Análisis de Pendientes Hidrométricas en Grandes Crecidas sobre tramo del Río Paraná
la analice, pues las condiciones antecedentes de ésta
influyen en la misma y en el escurrimiento del flujo.
se cuenta con mayor cantidad de datos, en el tramo
estudiado. No existen registros –ni de lectura de
escalas, ni de caudales– fidedignos y de una cantidad
significativa sobre los cursos interiores y/o lagunas
del valle de inundación.
Hay que recordar que este análisis se realiza con los
registros existentes sobre el cauce principal, del que
Figura 16. Gráficas de pendientes longitudinales en el tramo PSM-R, caudales registrados y aforados en PSM
versus cotas del pelo de agua en PSM, período 1970-2007.
tiene encauzado en el cauce principal y no establece
intercambios francos con el volumen que escurre por
el valle, las pendientes mantienen igual tendencia de
variación que el caudal, y se aproximan a las pendientes del fondo del curso de agua.
CONCLUSIONES
Se han analizado los registros de alturas limnimétricas
y caudales de un tramo importante del Río Paraná,
desde el Km 325 al 533 de la vía navegable. Los registros de las escalas analizadas fueron los de los puertos
de: Diamante, Puerto San Martín, Rosario y San Nicolás. Los caudales calculados y aforados corresponden al
cauce principal a la altura de Puerto San Martín.
Si en cambio, el caudal supera los 25000 m³/s, aguas
abajo de Rosario se pueden producir retornos importantes desde el valle al cauce principal, elevando el
pelo de agua en mayor proporción aguas abajo,
ocasionando pendientes menores que aguas arriba
por la situación local en la configuración presente.
Cuando los caudales son elevados y de alta permanencia, esta situación es más evidente.
Se han contrastado los caudales aforados y los calculados a través de una relación H-Q establecida en el
PSM por la SSRH, dando resultados satisfactorios la
curva planteada.
Las pendientes longitudinales sobre el cauce principal, a partir de los registros en las escalas de los puertos, se encuentran en el rango de 1,60x10-5 a 4,30x10-5
aproximadamente, según el tramo y fecha considerados. De lo analizado se ha visto que las pendientes
longitudinales dependen en gran medida de la configuración topográfica integral cauce-planicie y del
caudal presente en las crecidas, ya que si éste es en
aumento, pero inferior a 25000 m³/s, el flujo se man-
Se concluye que los aumentos de caudales no producen necesariamente incremento de tirantes, según
sean las pendientes presentes, dependientes de la
topográfica y la situación hídrica aguas abajo que
condiciona la descarga del sistema, y según también
de las condiciones antecedentes.
Este estudio es importante para establecer el tipo de
relaciones entre alturas y caudales que puede llegar a
30
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Paraná para el diseño de obra de toma de
acueductos”. Congreso Nacional del Agua 2009,
Trelew, Chubut, Argentina.
Rocca, E.; Vasallo, M. R.; Lopresti, A. (1973)
Referencias hidrogeológica del Río Paraná frente a
Rosario y su relación con la historia del pótamo.
Publicaciones Universitarias, Facultad de Ciencias
Exactas, Ingeniería y Agrimensura, Universidad
Nacional de Rosario, Argentina.
Serman & asociados S. A. (1999) “Estudio de la
distribución y las luces de los puentes en la planicie
inundable”. Informe de Puentes del Litoral S.A.,
Convenio Gobierno Nacional – Provincias de Santa
Fe y Entre Ríos para la obra Conexión Física
Rosario-Victoria. Argentina.
U.S. Geological Survey, página de Internet:
http://edcsns17.cr.usgs.gov/NewEarthExplorer
Zapata, C. (1999) “Estudio de la dinámica hídrica
del Río Paraná en la transecta Rosario-Victoria”.
Informe de Puentes del Litoral S.A., Convenio
Gobierno Nacional – Provincias de Santa Fe y
Entre Ríos para la obra Conexión Física RosarioVictoria. Argentina.
presentarse en los lugares citados, especialmente
para la calibración de modelos aplicados en este
tramo. También es un antecedente para el análisis de
otros grandes ríos de llanura con configuraciones
similares de cauce-planicie.
REFERENCIAS BIBLIOGRÁFICAS
Chow, V. T. (1959). Open channel hydraulics.
McGraw-Hill, New York.
FICH (2004). “Estudios Hidráulicos y Morfológicos
Zona Isla La Invernada. Río Paraná”. Subsecretaría
de Puertos y Vías Navegables. Facultad de
Ingeniería y Ciencias Hídricas, Universidad
Nacional del Litoral, Santa Fe, Argentina.
Garcia, M.; Basile, P.; Riccardi, G.; Stenta, H.
(2008) “Modelación hidrodinámica cuasi-2D a
gran escala espacial de un tramo del Río Paraná”.
XXIII Congreso Latinoamericano de Hidráulica
2008, Cartagena de Indias, Colombia.
Paoli, C.; Schreider, M. (2000) El río Paraná en su
tramo medio. Tomo 1. UNL editora. ISBN 987508-120-5. Santa Fe, Argentina.
Rentería, J. P.; Garcia, M.; Forestieri, C.;
Avellaneda, D.; Orsolini, H.; Aguiar, R. (2009)
“Estudio estadístico de niveles en el sistema Río
Artículo recibido el 10/2010 y aprobado para su
publicación el 12/2010.
31
CUADERNOS del CURIHAM, Vol. 16, Año 2010
TRATAMIENTO DEL FRENTE ABRUPTO DE INFILTRACIÓN PARA EL CASO DE
PROFUNDIDAD DE INUNDACIÓN VARIABLE. SOLUCIONES IMPLÍCITA Y EXPLÍCITA
Sergio Masuelli(1) y Daniel Barrera(2)
(1)
Instituto de Altos Estudios Espaciales “Mario Gulich”, CETT/CONAE
Ruta C45, Km 8, CP 5187. Falda del Carmen. Córdoba
(2)
CONICET/Departamento de Ingeniería Agrícola y Uso de la Tierra. Facultad de Agronomía. UBA
e-mail: [email protected]
RESUMEN
La formulación teórica del proceso de infiltración según el modelo de frente abrupto (Green-Ampt) se ha
extendido a condiciones de profundidad de anegamiento decreciente en un sistema aislado. Las ecuaciones
implícitas obtenidas relacionan la tasa de infiltración y el espesor del anegamiento al tiempo. Mediante la
definición de variables adimensionales de profundidad de inundación s y tiempo x se obtuvo la ecuación
ds/dx, la cual es función de un único parámetro descriptivo γ, en el cual se combinan todas las variables que
caracterizan las condiciones dinámicas iniciales del proceso de infiltración; éste parámetro define la forma de
la curva de infiltración dada por la ecuación adimensional hallada. Luego se obtuvo una función paramétrica
explícita s(x), la cual depende de un único parámetro a, el cual a su vez es función de γ. Dicho parámetro
posee cuatro coeficientes constantes válidos para un rango amplio de propiedades y condiciones del suelo
que se observan en la naturaleza. Mediante simulaciones numéricas se demostró que la función paramétrica
propuesta genera tasas de infiltración y volúmenes infiltrados similares a los que se obtienen partiendo de la
ecuación de Darcy en el esquema de Green-Ampt.
Palabras clave: Frente de mojado de Green-Ampt, profundidad de anegamiento variable, variables
adimensionales.
ABSTRACT
The “sharp wetting front” infiltration model has been developed for conditions of decreasing ponding depth
in an isolated system. The implicit dimensionless equations obtained relate the infiltration rate and the
flooding depth to time. By defining dimensionless variables of flooding depth s and time x the equation ds/dx
was obtained, which is a function of only one descriptive parameter γ; in it, all the variables describing the
initial dynamic conditions are included. This parameter determines the shape of the curve given by the
dimensionless infiltration equation combining the variables s and x. Afterwards a parametric explicit
expression s(x) depending on one parameter a has been obtained; a in turn depends on γ and has four generic
constant coefficients valid for a wide range of physical soil properties and conditions occurring in nature. By
means of numeric simulations using a wide range of values for the soil parameters and different initial
flooding depths, it is proved that the proposed explicit parametric function generates similar infiltration rates
and cumulative storages to those that are obtained starting from Darcy’s equation in the extended GreenAmpt scheme.
Keywords: Green-Ampt wetting front scheme, variable ponding depth, dimensionless variables.
33
Tratamiento del Frente Abrupto de Infiltración para el caso de profundidad de inundación variable
cumple sólo si la capa inundante es menor que
1cm. Con estas suposiciones obtuvieron una
ecuación implícita del volumen total infiltrado F en
función del tiempo; esta ecuación es no lineal en F
y debe ser resuelta por aproximaciones sucesivas o
por métodos iterativos. En el caso especial de
intensidad de lluvia constante, conocida y menor
que la tasa potencial de infiltración, lo cual implica
que no se ha producido el encharcamiento, se
obtiene una ecuación explícita para F que permite
calcularla directamente (Smith y Parlange, 1978).
INTRODUCCIÓN
Las experiencias en laboratorio han comprobado que
la infiltración en un suelo no saturado es alta al
principio del proceso y luego declina gradualmente
con el tiempo. Hay excepciones a este patrón general
debidas, por ejemplo, a la rotura de costras en la
superficie del terreno o a la disminución de la
hidrofobia en algunas clases de suelos; estas
situaciones especiales no son tratadas en este trabajo.
La tasa de infiltración expresa la velocidad de
penetración del agua a través de la superficie del
suelo; si ésta se encharca, la infiltración ocurre a su
tasa potencial o máxima posible. La mayoría de las
ecuaciones de infiltración describen la evolución
temporal de dicha tasa.
El modelo de Green-Ampt ha sido objeto de gran
desarrollo en física del suelo e hidrología debido a su
simplicidad y buen desempeño en gran variedad de
problemas. Su solución está de acuerdo con el modelo
más general de difusión de Richards (1931). Las
ecuaciones implícitas en el tiempo para la tasa de
infiltración f y su valor acumulado F deben resolverse
con un método iterativo, pues las funciones
requeridas f(t) y F(t) no están disponibles (Warrick et
al., 2005). Salvucci y Entekhabi (1994) obtuvieron,
por integración de la ecuación de Darcy y un posterior
desarrollo en serie de tiempo y truncado, expresiones
explícitas para estas dos variables.
Green y Ampt (1911) propusieron un modelo
simplificado del proceso de infiltración que contiene
una física realista y a la vez permite obtener una
solución analítica. Proveyeron así la primera
ecuación basada físicamente que describe la
infiltración del agua en el suelo. Introdujeron el
concepto de “frente abrupto de mojado” como una
superficie frontal horizontal que avanza hacia abajo
dejando tras de sí una franja de suelo ya mojada, con
tenor de humedad uniforme en la vertical y
constante en el tiempo, a saturación o a un valor
muy cercano a ésta; por debajo del frente el suelo
permanece con un tenor volumétrico de humedad
uniforme e igual a la humedad inicial θi ; esta
El objetivo de este trabajo es obtener una
parametrización de la infiltración en el suelo sujeto a
anegamiento, que permita generalizar la ecuación de
Darcy en el esquema de Green y Ampt para el
decrecimiento de la altura de inundación a medida
que se infiltra, a partir de cualquier valor inicial. Se
trata de obtener una expresión simple y explícita del
volumen infiltrado y de la tasa de infiltración en
cualquier instante de tiempo, en función del déficit
de saturación ∆θ y la conductividad hidráulica del
suelo mojado Ke (Van Genuchten, 1980) para
distintas condiciones iniciales de anegamiento y
humedad y potencial capilar en el suelo. Se
profundiza el desarrollo hecho anteriormente
(Masuelli y Barrera, 2010).
suposición implica que no existe difusión de
humedad (Philip, 1957). El frente de mojado es una
frontera plana y abrupta donde existe una
discontinuidad en el perfil vertical de humedad y de
la succión capilar; ésta también permanece constante
en el frente de mojado, independientemente de la
posición del mismo y del tiempo transcurrido; este
esquema da resultados satisfactorios cuando el suelo
está inicialmente seco, y en particular en los suelos
de textura gruesa, los cuales exhiben un frente de
mojado abrupto (Hillel, 1971). Se asume además
que en todo el perfil de suelo la porosidad y la
conductividad hidráulica son uniformes (MorelSeytoux y Khanji, 1974).
DESCRIPCIÓN TEÓRICA DEL PROCESO DE
INFILTRACIÓN
EN
EL
ESQUEMA
PROPUESTO
La cantidad ∆θ, dada por la diferencia (η-θi) entre la
porosidad efectiva η y la humedad volumétrica
inicial θi, expresa el volumen relativo de poros a ser
llenado por agua tras el paso del frente de mojado, a
menos de una fracción despreciable correspondiente
al volumen remanente de aire, pues el frente de
A fin de simplificar el desarrollo teórico, Green y
Ampt limitaron su análisis al caso en que la
contribución del potencial hidrostático puede
despreciarse (Eagleson, 1970); esto ocurre si la
capa de anegamiento es mucho menor en valor
absoluto que el nivel de potencial capilar, lo cual se
34
CUADERNOS del CURIHAM, Vol. 16, Año 2010
mojado deja tras de sí pequeñas burbujas de aire
atrapadas en la matriz porosa. La conductividad
efectiva del suelo mojado Ke también llamada
“conductividad hidráulica a re-saturación”, es una
fracción de la conductividad K del suelo saturado,
debido a que la presencia de tales burbujas retrasa el
movimiento del agua. Según Vieux (2004)
usualmente se toma Ke=1/2K. Al nivel del potencial
capilar en el frente de mojado la denominamos ψf y
lo expresamos en cm ya que se trata de unidades de
energía por unidad de peso. A su valor con signo
positivo lo denominamos nivel de succión. Éste
favorece el movimiento del agua hacia abajo, hacia
la región del suelo con mayor succión debido a su
menor contenido de humedad.
1. Suelo incompresible y homogéneo, lo cual
implica que η es constante en el tiempo y
uniforme en el perfil.
2. Humedad volumétrica inicial θi uniforme en todo
el perfil. El déficit de saturación ∆θ es constante
y uniforme.
3. Potencial capilar en el frente de mojado ψf
uniforme en todo el perfil y constante en el tiempo.
4. Conductividad hidráulica efectiva del suelo
mojado Ke uniforme en la vertical y constante
en el tiempo.
5. Al comienzo de la infiltración existen una capa
acuosa de altura h0 anegando la superficie y una
lámina de suelo mojado contigua a la superficie
de espesor infinitesimal, en la cual es válida la
ecuación de Darcy, seguida de una franja
profunda de suelo no saturado. El esquema
también admite la preexistencia de una franja de
suelo mojado contigua a la superficie, como si el
proceso se hubiera iniciado con anterioridad al
instante considerado como inicial.
Por simplicidad en la notación, en adelante se utiliza
K en lugar de Ke. Se parte del esquema de Green y
Ampt para infiltración (Figura 1) en el que se asume
que se trata de un suelo inicialmente subsaturado,
con las siguientes características:
Figura 1. Frente de mojado de Green-Ampt.
Partimos de la ecuación de Darcy en forma similar
al desarrollo mostrado por Chow et al. (1994) para el
cálculo del movimiento dentro de la aproximación
de Green-Ampt, considerando los potenciales de
presión hidrostática, de gravedad y de capilaridad.
Denominamos L al espesor de la capa de suelo
saturado detrás del frente de mojado, el cual
aumenta hacia abajo, y hacemos el cambio de
variable zf = -L. Asimismo, denominamos ψ = -ψf
de tal modo que ψ es positivo. De esta manera, la
caída de potencial al pasar del nivel z=0 (superficie)
al nivel z=-zf (en el frente de mojado) es:
∆h = h + L +ψ
Consideramos además que:
L(0) = 0, h(0) = h0 ⇒ L =
(3)
En este último paso hemos asumido, al igual que
Green y Ampt, que la profundidad de agua infiltrada
(h0 – h) resulta en que una franja de suelo de
profundidad L ha incrementado su humedad en la
cantidad ∆θ, lo cual implica suponer que no existe
escurrimiento lateral (ya sea superficial o subsuperficial) ni evapotranspiración.
(1)
Si definimos α = 1-∆θ > 0 y reemplazamos en (2)
se tiene:
Entonces la ecuación de Darcy se expresa:
dh
∂h
 h + L +ψ 
= −K
= −K 

dt
∂z
L


h0 − h
∆θ
 h − α h + (1 − α )ψ 
dh
= −K  0

dt
h0 − h


(2)
35
(4)
Tratamiento del Frente Abrupto de Infiltración para el caso de profundidad de inundación variable
Hemos presentado hasta aquí el desarrollo de GreenAmpt que expresa el proceso de infiltración para un
frente de mojado abrupto. A continuación proponemos
un nuevo tratamiento de la ecuación (4) que a
diferencia del método de Green-Ampt no desprecia la
capa acuosa. Por el contrario, permite considerar el
proceso con una capa inundante decreciente a medida
que se infiltra en un sistema aislado, es decir, sin
entradas o salidas laterales ni verticales (sin
precipitación ni evapotranspiración); ésta es la
innovación principal en el esquema que proponemos.
h / h0
∫
1
x=−
x=
x=
γ=
α
1 − ∆θ
=
χ  ∆θ ⋅ψ 
1 +


h0

t


(7)
γ −1
γ
1
γ
x0 =
∫
1
ds
−
1−γ s
h / h0
∫
1

ds 


h / h0
∫
1
ds
1
−
1−γ s γ
h / h0
∫
ds
1
2
h / h0
( (γ − 1) ln (1 − γ s ) − γ s )
1
γ −1  1− γ s  1− s
ln
+
γ 2   1 − γ 
γ 
(9)
1− γ
γ
2
ln (1 − γ ) +
1
γ
(10)
En la Figura 2 se muestran los valores de x0 para
todos los valores posibles de γ, es decir entre 0 y 1.
Según la ecuación (10) el límite inferior de γ, que
corresponde a un suelo inicialmente seco, se
corresponde con un valor de x0 igual a 0.5, que es el
mínimo tiempo posible en que puede completarse la
infiltración. Este valor es igual a la mitad del
correspondiente al caso de suelo inicialmente
saturado (γ=1).
Al combinar las ecuaciones (5), (6) y (7) obtenemos:
 1− s 
ds
1−γ s 
= −
 ⇔ dx = −ds 

dx
 1− s 
1−γ s 
h / h0
Esta es la ecuación que se buscaba, pero observamos
que no es posible obtener una expresión de s(x)
mediante despejes. Antes de buscar una forma
paramétrica para dicha expresión, podemos calcular
el x para el cual s=0, que corresponde al instante en
el cual se acaba el agua en superficie pues toda se ha
infiltrado. Llamamos a este valor x0:
(6)



1
ds  1
 1
−1 = 
γ  1 − γ s  γ 
h / h0
1  γ −1
h/h 
ln (1 − γ s ) 1 − s 1 0 

γ γ

x=
Definimos ahora la variable x para adimensionalizar
el tiempo, y la variable γ:
 1 ∆θ ⋅ψ
K ⋅χ
⋅t = K  +
h
h0
h02
 0
∫
Obtenemos finalmente:
(5)
x=
h / h0
Por lo tanto tenemos:
Definimos la variable adimensional s=h/h0 que
expresa la profundidad de anegamiento h relativa a
su valor inicial. De modo similar hacemos β=K / h0
y χ=1+ψ ∆θ / h0 y obtenemos:
ds
 χ −αs 
= −β 

dt
 1− s 
s ds
=
1−γ s
(8)
En la ecuación diferencial obtenida, toda la
información referida al tipo de suelo y su condición
inicial está condensada en la variable γ y en el reescalamiento temporal en x. La variable γ puede
tomar valores entre 0 (cuando el potencial capilar es
mucho mayor que los otros) y 1 (cuando el suelo
está completamente saturado).
Integrando la ecuación (8) obtenemos:
x=−
h / h0
∫
1
ds
1− s
=−
1−γ s
h / h0
∫
1
ds
+
1−γ s
h / h0
∫
1
s ds
1−γ s
Figura 2. Duración adimensional del proceso de infiltración
en función de γ.
Resolvemos la segunda integral:
36
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Analicemos ahora las características funcionales y el
significado físico del parámetro γ (ecuación 7). Es
conveniente tratar a γ como función de ∆θ y del
cociente de potenciales ψ/h0, ya que si éste
permanece constante γ es solo función del ∆θ inicial,
independientemente de los valores de h0 y ψ. La
Figura 3 muestra las isolíneas de γ en el plano h0 vs
ψ para dos condiciones iniciales de humedad: un
suelo inicialmente muy seco y otro medianamente
húmedo; dichas isolíneas son rectas cuya pendiente
es función de ∆θ. Cuanto más seco está el suelo más
altos son los valores de γ.
variación en el valor de γ, es más uniforme en todo
el rango de alturas iniciales de la capa inundante
cuanto mayor es el valor de succión en el frente de
mojado, o sea cuanto más fina es la textura del
suelo. Ambas curvas tienden asintóticamente al
límite superior (1-∆θ) cuando la profundidad h0
tiende a infinito. En el ejemplo de la Figura 5 dicho
valor umbral es igual a 0.58.
Figura 4. Isolíneas de γ en el plano ψ/h0 vs ∆θ.
Figura 3. Isolíneas de γ en el plano h0 vs ψ para dos
condiciones iniciales de humedad: un suelo inicialmente muy
seco y otro medianamente húmedo.
En la Figura 4 se muestran las isolíneas de γ en el
plano ψ/h0 vs ∆θ. Se puede observar que para suelos
casi saturados el valor de γ es alto,
independientemente del cociente ψ/h0 excepto para
valores muy pequeños de éste. En cambio, para
suelos secos el valor de γ depende fuertemente de
dicho cociente, y solo toma valores mayores que 0.6
para valores del cociente entre potenciales cercanos
a la unidad o aún menores, lo cual implica que la
capa inicial de inundación debe tener una
profundidad apreciable, al menos unos 5 cm en el
caso de suelos arenosos y diez veces superior en el
caso de arcillas.
Figura 5. γ(h0) para un suelo inicialmente muy seco y dos
valores de succión típicos de suelos de textura gruesa y fina.
Para comprender mejor el significado físico de γ es
conveniente modificar la ecuación (7) y escribir:
En la Figura 5 se muestra la función γ(h0) para un
suelo inicialmente muy seco (∆θ=0.42) y en donde
el potencial de succión frontal ψ actúa como
parámetro, para dos valores típicos (5 cm y 50 cm)
que a ese déficit de saturación tienen los suelos
limo-arenoso y arcilloso respectivamente. La
γ =
37
h0 (1 − ∆θ )
h0 + ∆θ ⋅ψ
=
α h0
h0 + ∆θ ⋅ψ
(11)
Tratamiento del Frente Abrupto de Infiltración para el caso de profundidad de inundación variable
En el miembro de la derecha, el numerador es el
producto de α –la fracción de volumen de suelo no
disponible para infiltración– por h0 –la capa de agua
a ser infiltrada–. O sea, el numerador expresa el
grado de dificultad para que el proceso se complete.
A su vez, el denominador contiene en dos términos
las condiciones iniciales que favorecen el
movimiento del agua hacia abajo: h0 y psi, los
potenciales que junto con el gravitatorio aceleran la
infiltración, y la fracción de volumen poroso
disponible dt. Cuanto mayores son estos términos,
más rápidamente se completa el proceso. En la
expresión de γ, tanto un mayor numerador como un
menor denominador causan un retardo en completar
la infiltración de la capa de agua inundante. Vemos
que γ es un número fundamental adimensional que
contiene todas las condiciones iniciales extrínsecas
que afectan la dinámica del proceso. Es interesante
notar que la conductividad hidráulica, condición
intrínseca por ser una propiedad del suelo y el agua
y que es el otro factor que afecta el proceso, solo
está contenido en el tiempo adimensional x.
Otro caso de interés es γ ≈ 0, lo cual se verifica
cuando el suelo está muy seco y ψ es mucho mayor
que h0. Desarrollando la ecuación (9) en el límite
para γ tendiendo a cero tenemos:
2
s = 1− 2 x
(12)
x
s( x) = 1 −  
b
Por otra parte, para γ ≈ 1 lo cual corresponde a la
saturación, desarrollando el primer término de (9) y
tomando de la teoría de límites que el límite cuando
x tiende a 0 de (x ln x) es 0, tenemos:
x = 1− s ⇔ s = 1− x
γ −1 1− γ s  1
ln 
 + (1 − s ) − x
γ2
 1−γ  γ
(15)
a
(16)
Es de observar que tanto a como b, los cuales
dependerán de γ, son iguales a x0 para sus valores
extremos. De este análisis surge como natural que el
parámetro b sea directamente igual a x0 que es la raíz
de s y por lo tanto proponemos la función de ajuste:
(13)
 x
s ( x) = 1 −  
 x0 
Para obtener s(x) dado x podemos pensar al
problema como uno de optimización; la función y su
derivada a las cuales hay que hallarle las raíces para
cada x son, a partir de (9):
f ( s) =
s −1
1−γ s
El ajuste más obvio sería usar una combinación
lineal de las expresiones (12) y (13), que expresan
los comportamientos para valores extremos de γ,
asignando a ambos términos coeficientes de peso
complementarios; pero hemos preferido la siguiente
expresión por una cuestión de simplicidad funcional:
2
⇔
f '( s ) =
Figura 6. s vs x para distintos valores de γ. La recta
corresponde a γ =1 (suelo saturado) y la curva de la izquierda
a γ =0 (suelo seco).
Obtención de una función paramétrica s(x)
(1 − s )
γ −1 1
1
γ −1+1−γ s
( −γ ) − = −
γ 2 1−γ s
γ
γ (1 − γ s )
Se ve que para f(s) = 0 los valores en los extremos
son (x = 0, s = 1) y (x = x0 , s = 0). Por lo tanto, si
se generan N puntos distribuidos convenientemente,
podemos para cada punto xi hallar las raíces si de la
ecuación (14) mediante iteraciones. Mediante el
método de Newton-Raphson se obtuvieron las
curvas s(x) para distintos valores de γ (de 0,1 a 1 en
intervalos de 0,1) que se muestran en la Figura 6; la
recta de pendiente unitaria corresponde a la
saturación, o sea γ = 1.
SOLUCIÓN EXPLÍCITA DE LA ECUACIÓN
DE INFILTRACIÓN
x=
f '( s ) =
a
(17)
Hemos comprobado que los ajustes son similares a
los obtenidos con la combinación lineal mencionada.
El parámetro a fue calculado para distintos valores
de γ (21 valores entre 0 y 1) y se verificó que, en
(14)
38
CUADERNOS del CURIHAM, Vol. 16, Año 2010
todos los casos y para cualquier valor de x, el error
entre la función original derivada de la ecuación (9)
y el ajuste propuesto (ecuación 17) fue de un 7%
como máximo. Las mayores discrepancias se hallan
para los x más grandes, lo que habla muy bien de la
calidad del ajuste teniendo en cuenta que para esos
valores la función está tendiendo a cero y por lo
tanto el error relativo para cualquier ajuste en
general es muy difícil de controlar.
de h y de su derivada, obtenidas a partir de la
ecuación implícita y por la parametrización.
Previamente se calcularon los valores de γ según
(7), para 3 alturas iniciales distintas y 3 tipos de
suelo diferentes. Para los déficit de saturación ∆θ se
eligieron los valores dados por Chow et. al. (1994)
como porosidad efectiva y la mitad de tal valor para:
arena magrosa, marga limosa y arcilla limosa. Los
resultados mostraron que γ puede tomar cualquier
valor entre 0 y 1 para todos los tipos de suelo
dependiendo de sus condiciones iniciales.
Dado que, como fuera mencionado, x0 tiene los
mismos valores que a en los extremos el ajuste el
ajuste se realizó para x0-a para minimizar los
errores. Así, el ajuste de a versus γ resulta:
 a γ + a2 γ 2 
a(γ ) = x0 −  1
2
 1 + a3 γ + a4 γ 
En la Tabla 1 se muestran para 5 de los casos
anteriores (que notamos con la letra N) y 3 tiempos
distintos los valores de h y de su derivada respecto
del tiempo, es decir la tasa de infiltración, obtenidos
por cálculo directo (ecuación 4) y por la
parametrización propuesta.
(18)
con:
a1= 0,05339671
a2=-0,05339299


a3=-1,32447855
a4= 0,34984288
Llamamos cálculo directo a la resolución numérica de
la ecuación (9). Los tiempos fueron elegidos de modo
de cubrir las tres regiones de s(x), es decir cercano a
0, cercano a x0 e intermedio. Como puede observarse
en la Tabla 1 la función paramétrica es muy
satisfactoria para suelos y condiciones iniciales tan
diversas. Tal como ya se mencionara anteriormente
las mayores discrepancias relativas se observan para
tiempos grandes, lo cual implica que el espesor de
agua remanente sobre la superficie es muy baja.
(19)
En la Figura 7 se muestra cómo ajusta la
parametrización obtenida a los valores de s(x)
calculados a partir de (9). El caso que se muestra
corresponde a un valor de γ = 0,3029,
correspondiente a un suelo tipo arena margosa según
la tabla 4.3.1 de Chow et al. (1994), con
∆θ = 0,4; ψ = 6,13cm; y h0 = 2,5cm.
Todo el cálculo precedente sirve para calcular la
función h(t) para todo tipo de situaciones, pero
partiendo de la condición de que no hay una franja
saturada en el subsuelo contigua a la superficie. Si
éste fuera el caso habría que calcular primero h0,
luego s y x correspondientes al tiempo inicial
usando la ecuación (9).
CONCLUSIONES
En el marco del estudio de las transferencias de masa
implicadas en el balance hidrológico en la superficie
del suelo, se avanzó en la formulación teórica del
proceso de infiltración. Se ha logrado extender la
formulación teórica del proceso de infiltración en el
suelo según el modelo de “frente abrupto de mojado”
de Green-Ampt, al caso de profundidad decreciente
de la capa de agua que anega el suelo. Esta situación
ocurre con cierta frecuencia en las depresiones del
terreno luego de una lluvia intensa. En las grandes
llanuras, como en el caso de las llanuras pampeana y
chaqueña, las depresiones inundadas suelen ser de
Figura 7. Descenso de la altura de inundación en función del
tiempo hasta que la infiltración se completa, expresado en la
forma adimensional s(x). Ajuste para γ=0,3029. Los puntos son
valores de s calculados a partir de (9); en línea llena valores
obtenidos mediante la función paramétrica.
Validación
para
hidrodinámicas
diferentes
condiciones
Para verificar la bondad de la función propuesta se
han comparado para distintas situaciones los valores
39
Tratamiento del Frente Abrupto de Infiltración para el caso de profundidad de inundación variable
gran extensión debido a la baja pendiente general del
terreno. En estas condiciones, la capa inundante va
disminuyendo su profundidad o altura a medida que
el agua se infiltra.
Tabla 1. Comparación entre las alturas h y la tasa de infiltración para distintos casos (N) según el cálculo directo aplicando
Darcy (ecuación 3) y a partir de la parametrización obtenida.
Caso
1
1
1
5
5
5
9
9
9
13
13
13
18
18
18
Tiempo
[h]
0,00013
0,00065
0,00120
0,01500
0,07500
0,13500
0,84970
4,24840
7,64710
0,00160
0,00800
0,01440
12,3609
61,8046
111,248
h Darcy
[mm]
0,69
0,29
0,05
7,15
3,23
0,58
70,7
31,6
5,67
0,68
0,29
0,05
73,0
33,8
6,20
h Param
[mm]
0,69
0,29
0,05
7,19
3,18
0,56
71,1
31,2
5,52
0,68
0,29
0,05
73,7
33,1
5,92
Error
%
0,04
-0,11
-0,22
0,64
-1,59
-3,36
0,49
-1,28
-2,68
0,01
-0,02
-0,04
0,93
-2,10
-4,47
dh/dt Darcy
[mm/h]
-2394,7
-1076,3
-805,5
-176,3
-86,6
-69,2
-32,5
-15,6
-12,3
-196,6
-88,0
-65,7
-2,0
-1,0
-0,8
dh/dt Param
[mm/h]
-2397,9
-1077,0
-804,0
-180,0
-87,5
-67,2
-33,0
-15,7
-12,0
-196,7
-88,0
-65,6
-2,0
-1,0
-0,8
Error
%
0,13
0,07
-0,19
2,09
1,07
-2,83
1,64
0,85
-2,26
0,03
0,01
-0,04
2,88
1,47
-3,80
Adicionalmente, la ecuación implícita obtenida x (s)
permite derivar el tiempo transcurrido xο hasta que
la capa de agua sobre el suelo se infiltra totalmente;
en esta ecuación, xο depende sólo del parámetro γ,
mostrando la funcionalidad que relaciona ambas
variables. Philip (1992) obtuvo una ecuación
equivalente pero más compleja en la cual el tiempo
que corresponde a xο depende de los cuatro
parámetros incluidos en γ y x.
El desarrollo teórico presentado constituye un
avance significativo con respecto a la ecuación
derivada por Philip (1992), la cual está expresada en
forma dimensional y depende de los cuatro
parámetros
trabajados
aquí:
conductividad
hidráulica; succión capilar en el frente de mojado;
déficit de humedad volumétrica inicial; y
profundidad
de
anegamiento.
En
nuestra
formulación se describe el mismo proceso con una
ecuación adimensional en espacio y tiempo, la cual
contiene un único parámetro descriptivo γ que
engloba las condiciones dinámicas iniciales.
Por otra parte, hemos propuesto una solución
paramétrica explícita s(x) para aproximar la
solución de la ecuación implícita obtenida que
describe el proceso de infiltración. Se ha mostrado
que la solución propuesta se ajusta bien a la solución
de la ecuación implícita que se obtiene por métodos
numéricos, para una gama amplia de valores de los
parámetros K, ψ, ∆θ y h0 que cubren las condiciones
presentes en la naturaleza. La ecuación obtenida s(x)
depende únicamente del parámetro descriptivo γ.
Proponemos denominar a γ “parámetro de retardo
de la infiltración”. En él se combinan todos los
parámetros que caracterizan las condiciones
dinámicas iniciales del proceso de infiltración; éste
parámetro expresa el grado de dificultad que el
proceso de infiltración tendrá para un suelo dado en
función de las condiciones iniciales, y define la
forma de la curva de infiltración.
Además, se ha mostrado el papel clave de las
relaciones K/h0 y (ψ ∆θ/h0) para expresar el tiempo
como una variable adimensional.
A su vez, la conductividad hidráulica K, que
caracteriza las propiedades hidráulicas intrínsecas
del suelo y el fluido, aparece solamente en la
expresión adimensional del tiempo, como un
parámetro que caracteriza la expansión o
contracción del tiempo adimensionalizado x. De
esta forma se demostró que la conductividad
hidráulica no tiene influencia en la forma de la
curva de infiltración, la cual queda determinada por
el parámetro γ.
AGRADECIMIENTOS
El presente trabajo tuvo el apoyo institucional de la
Comisión Nacional de Actividades Espaciales
(CONAE), el Consejo Nacional de Investigaciones
Científicas y Técnicas (CONICET) y la Universidad
40
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Philip, J.R. 1992. Falling head ponded infiltration.
Water Resources Research, 28, 2147-2148.
Richards, L. A. 1931. Capillary conduction of liquids
through porous mediums. Physics, 1, 318-333.
Salvucci, G.D. y Entekhabi, D. 1994. Explicit
expressions for Green-Ampt (delta function
diffusivity) infiltration rate and cumulative storage.
Water Resources Research, 30, 2661-2663.
Smith, R.E. y Parlange, J.Y. 1978. A parameterefficient infiltration model. Water Resources
Research, 14, 533-538.
Van Genuchten, M. Th. 1980. A closed-form
equation for predicting the hydraulic conductivity
of unsaturated soils. Soil Science Society of
America Journal, 44, 892-898.
Vieux, B.E. 2004. Distributed hydrologic modeling
using GIS. Kluwer Academic Press, Dordrecht.
Warrick, A. W., D. Zerihun, C. A. Sanchez y A.
Furman 2005. Infiltration under Variable Ponding
Depths of Water. Journal of Irrigation and
Drainage Engineering, 131(4), 358-363.
de Buenos Aires, y se financió parcialmente con
fondos del proyecto UBACYT G036.
REFERENCIAS BIBLIOGRÁFICAS
Chow, V.T., Maidment, D.R. y Mays, L.W. 1994.
Hidrología
aplicada.
McGraw-Hill
Interamericana, Bogotá.
Eagleson, P.S. 1970. Dynamic Hydrology. McGrawHill, New York.
Green, W.H. y Ampt, G.A. 1911. Studies on soil
physics. 1. The flow of air and water sthrough
soils. Journal of Agricultural Soils, 4, 1-24.
Hillel, D. 1971. Soil and Water. Academic Press,
New York.
Masuelli, S. y Barrera, D., 2010. Una extensión del
modelo de Green-Ampt a condiciones de
inundación de profundidad variable en llanuras,
con solución paramétrica. En: Varni M., Entraigas
I. y Vives L. (eds) Hacia la Gestión Integral de los
Recursos Hídricos en Zonas de Llanura, 287-293.
Morel-Seytoux, H.J. y Khanji, J. 1974. Derivation of
an equation of infiltration. Water Resources
Research, 10, 795-800.
Philip, J.R. 1957. The theory of infiltration. 1: The
infiltration equation and its solution. Soil Science,
83, 345-357.
Artículo recibido el 11/2010 y aprobado para su
publicación el 12/2010.
41
CUADERNOS del CURIHAM, Vol. 16, Año 2010
ESTUDIO DE COLUMNAS REACTIVAS PARA LA REMOCIÓN DE ARSÉNICO
MEDIANTE EL EMPLEO DE LA TÉCNICA ZVI
Juan M. Triszcz(1), Luciana Chippano(1), Andrés Gordon(1), Andrés Porta (1-2) y Fernando García Einschlag(3)
(1)
Laboratorio de Ingeniería Sanitaria, Dpto. de Hidráulica, Facultad de Ingeniería (UNLP).
Calle 115 Nº 742 La Plata, Buenos Aires, Argentina.
(2)
División Química Analítica, Dpto. de Química, Facultad de Ciencias Exactas (UNLP).
47 y 115 La Plata, Buenos Aires, Argentina.
(3)
Instituto de Investigaciones Fisicoquímica Teóricas y Aplicadas (INIFTA), Dpto. de Química, Facultad de
Ciencias Exactas (UNLP). Calle 64 Diag. 113 La Plata, Buenos Aires, Argentina.
e-mail: [email protected]
RESUMEN
La remoción de As en agua puede lograrse mediante el empleo de la técnica hierro cero Valente o ZVI (zero
valent iron). El proceso se basa en la oxidación de hierro metálico a especies insolubles de Fe(II) y/o Fe(III),
que dependiendo de las condiciones del medio, generan rápidamente mezclas de oxi/hidróxidos de hierro.
Estas partículas juegan un papel fundamental en el secuestro del contaminante mediante mecanismos de
adsorción y/o co-precipitación. Posteriormente las partículas producidas deben ser removidas de la fase acuosa para restablecer las características higiénico-sanitarias de las aguas. En el presente trabajo se muestran los
estudios realizados sobre columnas reactivas destinadas a la remoción del contaminante en forma continua.
Palabras clave: ZVI, arsénico, saneamiento ambiental.
ABSTRACT
Arsenic removal can be achieved by using the zero-valent iron methodology (ZVI). This simple technique is
based on the oxidation of metallic iron that yields insoluble species containing Fe(II) and/or Fe(III), mainly
oxi/hydroxides. The formed particles play a fundamental role since irreversibly uptake arsenic species
through adsorption and/or co-precipitation processes. In order to restore the physicochemical and potability
features of the treated water, the formed particles have to be removed from the aqueous phase. The present
work shows the results obtained with ZVI-permeable reactive barriers for the removal of the pollutant in
continuous systems.
Key words: ZVI, arsenic, environmental clean-up.
43
Estudio de Columnas Reactivas para la Remoción de Arsénico Mediante el Empleo de la Técnica ZVI
INTRODUCCIÓN
El arsénico (As) es un contaminante presente en
aguas subterráneas ampliamente distribuido en
muchas regiones de nuestro país (Castro de Esperanza y Wong, 2004) donde los niveles superan
significativamente los valores recomendables por
el Código Alimentario Argentino (CAA) y la
Organización Mundial de la Salud (OMS). En
particular en la provincia de Buenos Aires varias
localidades presentan índices de contaminación de
As superiores a los tolerados (Nicolli et al., 1989).
Su origen se atribuye principalmente a la presencia de cenizas volcánicas, que fueron transportadas antiguamente desde diferentes zonas por acción eólica hasta su depósito en los suelos.
En los últimos años, la técnica denominada “Hierro
Cero-Valente” (ZVI, Zero-Valent Iron) ha recibido
especial atención como una de las tecnologías innovadoras para la remoción de contaminantes
(Matheson y Tratnyek, 1994; Agrawal et al., 2002).
Recientemente, se ha encontrado que esta técnica
es capaz de remover compuestos arsenicales en
aguas (Lackovic et al., 2000; Melitas et al., 2002).
Este procedimiento se basa en complejos mecanismos fisicoquímicos de adsorción y/o coprecipitación, íntimamente relacionados con los
productos de corrosión generados por la oxidación
del hierro metálico (Hug y Leupin, 2003).
En las primeras etapas ocurre la oxidación del
hierro metálico a Fe(II). Este paso puede ocurrir
por las reacciones 1 y 2 que se muestran mas adelante. En presencia de oxígeno disuelto (OD), el
hierro en estado ferroso es rápidamente oxidado a
la especie Fe(III) mediante la reacción 4. Posteriormente, el Fe(III) generado puede reaccionar
con la superficie de ZVI originando Fe(II) mediante la reacción 3 (ésta reacción reviste particular importancia en medios con bajas concentraciones de oxígeno disuelto) o bien formar lentamente
fases coloidales debido a la insolubilidad de las
especies de Fe(III) para valores de pH entre 5 y 9
típicos de aguas naturales, reacciones 5 y 6. Las
especies formadas en las reacciones relevantes
mencionadas conllevan a la captación del arsénico
mediante la reacción 7.
En particular, se ha encontrado que la metodología ZVI es capaz de remover compuestos arseni-
44
cales y presenta una relación eficiencia/costo muy
favorable para su empleo en la remediación de
aguas de consumo.
Estudios previos realizados en condiciones batch
han mostrado que la presencia de OD, la superficie
de Fe-metálico expuesta y la presencia de sales en
la matriz acuosa son las variables que mayor influencia presentan en la cinética de producción del
agente precipitante (Triszcz et al., 2009).
Fe(0) + 2 H2O → Fe(II) + H2 + 2 HO-
(1)
Fe(0) + H2O + ½ O2 → Fe(II) + 2 HO-
(2)
Fe(0) + 2 Fe(III) → 3 Fe(II)
(3)
Fe(II) + ½ H2O + ¼ O2 → Fe(III) + HO-
(4)
Fe(III) + 3 H2O → Fe(HO)3 + 3 H+
(5)
Fe(II) + CO32-/HO- → Pptados ferrosos
(6)
As(III/V) + ≡FeOH → ≡FeOH.As(III/V)
(7)
Teniendo en cuenta que en el rango de valores de
pH estudiados la oxidación de Fe(II) a Fe(III)
mediada por OD es relativamente rápida para las
escalas de tiempo analizadas, puede considerarse
que la etapa limitante del proceso de formación
del agente precipitante es la representada por las
reacciones 1 y 2. Por lo tanto, las dependencias
observadas para la velocidad de oxidación, con la
superficie de contacto de Fe0 y con la conductividad de las aguas empleadas, estarían directamente
relacionadas con el proceso heterogéneo inicial de
corrosión electroquímica.
Sin embargo, la gran mayoría de los estudios
realizados en sistemas continuos se ha enfocado
solamente en el análisis de las concentraciones de
As en el efluente de las columnas sin mencionar el
efecto de su presencia cuando se evalúa el desempeño de las mismas.
El objetivo del presente trabajo ha sido mostrar
que la presencia de diferentes especies de As
(As(III) o As(V)) influyen sobre la tasa de corrosión del material de ZVI. Desde el punto de vista
operacional (prototipo, planta de tratamiento) es
un factor que debe tenerse en cuenta cuando se
evalúen parámetros de diseño.
CUADERNOS del CURIHAM, Vol. 16, Año 2010
METODOLOGIA
Materiales
Las aguas empleadas en los diferentes ensayos
fueron caracterizadas según medidas de pH, conductividad, turbidez, cloruros, dureza, alcalinidad, sulfatos, fluoruros, amonio, nitratos, nitritos,
hierro, arsénico, sodio y potasio (datos no mostrados). Como material de ZVI de partida se ha
seleccionado lana de acero comercial (área específica = 2.02 ± 0.09 m2/g), sin tratamiento previo.
Soluciones stock de As(V) y As(III) de 1 mg/ml
fueron preparadas, respectivamente, por disolución directa de Na2HAsO4 (Merck) y As2O3 (Fluka) en medio alcalino.
Evaluación en escala de laboratorio de la actividad de las barreras permeables activas
Estos experimentos se realizaron a 17±1 ºC usando
tubos de vidrios rellenos con lana de acero. Los
parámetros monitoreados fueron: pH, OD y potencial de oxido-reducción (ORP). En todos los casos
la lectura de los parámetros se realizó para diferentes caudales de alimentación y luego de la estabilización del sistema de monitoreo.
Análisis de las etapas de remoción de As en un
prototipo a escala piloto
Estos ensayos fueron realizados empleando la columna descripta anteriormente y acoplando a la salida
de la misma un dispositivo de filtración para eliminar
partículas en suspensión (Figura 1) (Triszcz et al.,
2008a). Las medidas se extendieron por espacio de 3
semanas realizando 2 muestreos diarios para la cuantificación de pH de salida, Fe(III)-Total y As-Total.
Se realizaron ajustes periódicos del caudal mediante
operaciones de purga una vez por día. Con el objeto
de evaluar la eficiencia del proceso se realizaron
análisis fisicoquímicos completos sobre el agua del
tanque de alimentación y el agua tratada colectada en
el tanque de almacenamiento.
Análisis
La metodología empleada consistió en analizar los
perfiles de Fe(III)-Total y As-Total mediante determinaciones colorimétricas.
Los perfiles de Fe(III)-Total fueron cuantificados
empleando KSCN (6M) en medio ácido y midiendo
absorción a λ = 540 nm (Oliveros et al., 2004)
mediante el empleo de un espectrofotómetro
(ChromTech UV-1800). Para la determinación de
As-Total se utilizó el método espectrofotométrico
45
de Gutzeit (Standard Methods for the Examination
of Waste and Wastewater, 1998) basado en la reducción de As(V/III) a un compuesto volátil: arsina
(AsH3), que posteriormente reacciona con el compuesto dietilditiocarbamato de plata (DDC) formando un producto coloreado que se cuantifica por
fotometría a λ = 530 nm. Asimismo, se utilizaron
tiras reactivas (Merckoquant®) para monitorear la
carga de As en las distintas etapas del proceso. Los
parámetros pH, conductividad, ORP y OD se obtuvieron por potenciometría.
Agua a tratar
Material Activo
(ZVI = Fe0)
Corrosión
Generación
[Fe(III)]
Sedimentación
Filtración
Agua Tratada
Adsorción & Co-precipitación
Figura 1. Esquema del montaje empleado para el tratamiento
de aguas arsenicales.
RESULTADOS
Estudios preliminares, realizados en nuestro laboratorio y en condiciones batch, mostraron que en
presencia de aire se obtienen velocidades de corrosión y porcentajes de remoción del contaminante
significativamente mayores que en su ausencia
(Triszcz et al., 2007a y 2007b). Este hecho puede
justificarse debido a que la presencia de OD aumenta las velocidades asociadas a las reacciones (2, 4, 5
y 7). Asimismo, los perfiles de pH, ORP y
Fe(III)Total evaluados en ausencia o en presencia de
(As(III) o As(V)) muestran una disminución del
ORP y un aumento del pH asociados a la formación
de Fe(II) y HO-.
Por otra parte se observó que el incremento en las
concentraciones iniciales de As(III) o As(V) incide
sobre la velocidad de corrosión del ZVI (Triszcz et
al., 2008b). Debido a la complejidad de las dependencias encontradas en estos ensayos, actualmente
se están realizando estudios complementarios con el
objeto de esclarecer el efecto de la concentración
inicial de arsénico sobre el desempeño de la técnica.
Estudio de Columnas Reactivas para la Remoción de Arsénico Mediante el Empleo de la Técnica ZVI
Puede observarse que, para bajos caudales, la concentración de oxígeno disuelto a la salida de la columna es despreciable. Asimismo se observan altos
valores de pH y bajos potenciales redox. Este comportamiento está relacionado con la formación de
cantidades importantes de iones Fe(II) y HO- debidos a la corrosión del ZVI que permanecen en solución debido a la baja tasa de producción de Fe(III)
en ausencia de oxígeno disuelto.
4
Oxígeno Disuelto (ppm)
Con el fin de evaluar el impacto del contaminante,
empleando As(III) o As(V) ambos de concentración
700 ppb, sobre el comportamiento de las barreras
reactivas se realizaron ensayos en ausencia de As y
en presencia. En estos ensayos se analizó la evolución de los parámetros pH, OD y ORP para diferentes caudales de trabajo. Los perfiles obtenidos,
empleando una masa de ZVI de 20 g, se muestran
en las Figuras 3a, 3b y 3c, respectivamente.
Por otro lado, a medida que se incrementa el caudal
de trabajo, está claro que la concentración de OD, el
pH y el ORP tienden a sus valores de entrada. Sin
embargo, se observan diferencias significativas en
los perfiles obtenidos en presencia de As. En particular, los perfiles obtenidos en presencia de As(III)
evidencian una inhibición importante de la actividad
de las columnas respecto a lo observado en ausencia
del contaminante.
3
2
1
0
0
50
100
150
200
250
300
350
Q (mL/min)
Figura 3a. Monitoreo del OD para diferentes caudales. (●)
Sin arsénico, (▼) As(III) = 700 ppb, (■) As(V) = 700 ppb.
8.5
Libre de Arsénico
Presencia de As(III)
Presencia de As(V)
8.0
pH
Estudios de actividad de las barreras permeables
reactivas
El análisis del comportamiento de las columnas rellenas con ZVI muestran claramente que la masa de
hierro metálico empleada y el caudal de trabajo son
variables que influyen notablemente en la concentración de OD en el efluente (Figura 2). Puede observarse una clara disminución del oxígeno disuelto a la
salida de la columna a medida que se reincrementa la
carga de material activo en la columna. Asimismo, el
análisis de las curvas obtenidas para diferentes caudales de trabajo muestra una dependencia más pronunciada de la concentración de oxígeno disuelto en el
efluente para bajos tiempos de residencia en la columna (altos caudales de trabajo).
7.5
6
Q= 10 mL/min
Q= 25 mL/min
Q= 100 mL/min
Q= 330 mL/min
5
7.0
O D (ppm )
4
0
3
50
100
150
200
250
300
350
Q (ml/min)
Figura 3b. Monitoreo del pH para diferentes caudales. (●)
Sin arsénico, (▼) As(III) = 700 ppb, (■) As(V) = 700 ppb.
2
1
0
10
15
20
25
30
35
40
ZVI (g)
Figura 2. Oxígeno disuelto en el efluente en función de la
masa de ZVI para diferentes caudales de trabajo.
46
Asimismo, puede observarse (Figuras 3b y 3c) un
caudal crítico cercano a 50 mL/min donde existe un
drástico comportamiento cuando se analiza el pH y
ORP hecho directamente relacionado con la presencia de las diferentes especies del contaminante.
CUADERNOS del CURIHAM, Vol. 16, Año 2010
total en el efluente del sistema.
-100
Cabe destacar que durante los ensayos realizados se
encontraron variaciones en el caudal debidas a la
obstrucción parcial de la salida de la columna como
consecuencia la acumulación de partículas de óxidos de hierro. Por este motivo, se realizaron ajustes
regulares del caudal para estandarizar el monitoreo
del sistema.
ORP (mV)
-200
-300
-400
-500
0
50
100
150
200
250
300
350
Q (mL/min)
Figura 3c. Monitoreo del ORP para diferentes caudales. (●)
Sin arsénico, (▼) As(III) = 700 ppb, (■) As(V) = 700 ppb.
100
Los resultados de las Figuras 4a y 4b muestran que
pequeñas fluctuaciones en las concentraciones de
hierro a la salida de la columna no afectan la eficiencia de remoción del contaminante por parte del
prototipo completo ya que las concentraciones totales de As en el tanque de almacenamiento siempre
se mantuvieron debajo del límite máximo recomendado por la OMS y el CAA (10 ppb).
Caudales
Cabe destacar que las concentraciones de As-Total
encontradas en el efluentes guardan relación inversa
con las concentraciones de Fe(III)-Total a la salida
de la columna. Sin embargo, mediante estos estudios pudo verificarse que el contaminante presente
en fase acuosa pudo ser removido exitosamente a
pesar de las complicaciones operativas por taponamiento de la columna.
Caudal (L/día)
80
60
40
20
0
0
5
10
15
CONCLUSIONES
20
Tiempo (días)
Figura 4a. Fluctuaciones del caudal en función del tiempo de
operación, (caudal medio aprox. 40 L/día).
7.5
25
[As]Total (Efluente)
6.0
20
4.5
15
3.0
10
1.5
5
0.0
[As]Total (ppb)
[Fe(III)] Total (ppm)
[Fe(III)]T Salida de la Columna
Los estudios realizados en nuestro laboratorio sobre
sistemas continuos muestran una buena correlación
con resultados previos realizados en sistemas batch
y confirman que la presencia de oxígeno disuelto, la
superficie de Fe-metálico expuesta y la conductividad de la matriz acuosa son las variables que mayor
influencia presentan en la cinética de producción del
agente precipitante (Triszcz et al., 2009).
En el presente trabajo hemos verificado que las
velocidades de corrosión del hierro cero valente en
sistemas continuos dependen significativamente de
la presencia de As en las aguas a tratar.
0
0
5
10
15
20
Tiempo (días)
Fig. 4b. Perfiles de [Fe(III)-Total] a la salida de la columna y
de [As-Total] en el efluente.
Pruebas de remoción de As
En la etapa final del trabajo se evaluó el desempeño
de un prototipo completo para la remoción de As
mediante el análisis del contenido de Fe(III)Total a la
salida de la columna y de la concentración de As-
47
En condiciones de déficit relativo de oxígeno en el
interior de la columna la proporción de Fe(III) en el
efluente disminuye debido a una menor contribución
de la reacción 4 y a una mayor contribución de la
reacción 3. Por otra parte, aunque el mecanismo de
inhibición de la corrosión por la presencia de especies de As aun no ha sido esclarecido, los resultados
muestran una fuerte interacción entre especies de
hierro y de arsénico cuyos efectos sobre la corrosión
Estudio de Columnas Reactivas para la Remoción de Arsénico Mediante el Empleo de la Técnica ZVI
del ZVI y la remoción de As deben ser considerados
en el diseño de técnicas de tratamiento eficientes.
Los resultados obtenidos en las pruebas de remoción a mediano plazo sugieren la factibilidad de
implementación de sistemas continuos basados en
ZVI para la remediación de aguas contaminadas con
As. En particular, la lana de acero comercial presenta ventajas respecto de otras fuentes de hierro metálico debido a su bajo costo, amplia disponibilidad y
a su importante relación área/volumen.
AGRADECIMIENTOS
Los autores agradecen a la Universidad Nacional de
La Plata, quien financió la presente investigación.
FSGE y AP son miembros de la carrera de investigador del CONICET y CIC PBA, respectivamente.
REFERENCIAS BIBLIOGRÁFICAS
Agrawal, A.; Ferguson, W. J. y Gardner, B. O. 2002.
Effect of carbonate species on the kinetics of dechlorination of 1,1,1-trichloroethane by zero-valent
iron. Environ. Sci. Technol. (36): 4326-4333.
Castro de Esperanza, M. L. y Wong, M. 2004. Remoción de arsénico a nivel domiciliario, HDT –
CEPISNO74:http://www.cepis.opsoms.org/bvsair/
e/hdt/hdt74.pdf.
Hug, S. J. y Leupin, O. 2003. Iron catalyzed oxidation of As(III) by oxygen and by hydrogen peroxide: pH-dependent formation of oxidants in the
Fenton reaction. Environ. Sci. Technol.,
(37):2734-2742.
Lackovic, J. A.; Nikolaidis, N. P. y Dobbs, G. M.
2000. Inorganic arsenic removal by zero-valent
iron. Environ. Sci. Technol. (17): 29-39.
Matheson, L. J. y Tratnyek, P. G. 1994. Reductive
dehalogenation of chlorinated methanes by iron
metal. Environ. Sci. Technol., (28):2045-2053.
Melitas, N.; Wang, J. P.; Conklin, M.; O’Day, P. y
Farrell, J. 2002. Understanding soluble arsenate
48
removal kinetics by zerovalent iron. Environ. Sci.
Technol., (36):2074-2081.
Nicolli, H. B.; Suriano, J. M.; Gomez Peral, M. A.;
Ferpozzi, L. H. y Balean, O. 1989. Groundwater
contamination with arsenic and other trace – element in an area of the Pampa, Argentina. Applied
Geol. Water Sci., (14): 3-16.
Oliveros, E.; Braun, A. M.; Bossmann, S. H.; Lang,
J.; Duran de Bazua, C.; Shahin, N. y Ríos Enrique,
M. 2004. Optimization of the heterogeneous Fenton-Oxidation of the model pollutant 2,4-Xylidine
using the optimal experimental design methodology. Solar Energy. 77: 491-502.
Standard Methods for the Examination of Waste and
Wastewater. 1998. 20th Edition, Method 3500-AsB, pp. 3-60/3-61.
Triszcz, J. M.; Rosales, E. M.; Tagliero, C. A. y García Einschlag, F. S. 2007ª. Abatimiento de As en
aguas de consumo mediante el empleo de la técnica
ZVI. Ingenieria Sanitaria y Ambiental, 91: 50-54.
Triszcz, J. M.; Luchessi, N.; Sosa, M.; Rosales, E.M.
y García Einschlag, F. S. 2007b. Estudio de parámetros relevantes para el abatimiento de As con
hierro cero valente. Ingeniería Sanitaria y Ambiental, 93: 64-69.
Triszcz, J. M.; Luchessi, N. y García Einschlag, F. S.
2008a. Tratamiento de aguas arsenicales mediante
el empleo de la técnica ZVI. Ingeniería Sanitaria y
Ambiental, 99: 52-57.
Triszcz, J. M.; Chippano, L.; Zuliani, D. N.; Rava,
R.; Bernardelli, C. E.; Casagrande R. T. y García
Einschlag, F. S. 2008b. Corrosión de hierro cerovalente en presencia de concentraciones crecientes
de As. XXVII Congreso Argentino de Química,
Tucumán, Argentina.
Triszcz, J. M.; Porta, A. y García Einschlag, F. S.
2009. Effect of operating conditions on iron corrosion rates in zero-valent iron systems for arsenic
removal. Chem. Eng. J., (150):431-439.
Articulo recibido el 12/2010 y aprobado para su
publicación el 03/2011.
CUADERNOS del CURIHAM, Vol. 16, Año 2010
INTEGRACIÓN DE CUENCAS DE DRENAJE EN ÁREAS DE LLANURA DURANTE LA ÚLTIMA
CENTURIA. EL CASO DEL ARROYO LAS LAJAS, CÓRDOBA, ARGENTINA
Nelso Doffo; Susana Degiovanni y Mónica Villegas
Dpto. de Geología - Fac. Cs. Exac. Fco.-Qcas. y Nat. - Universidad Nacional de Río Cuarto - Ruta Nac. 36 Km. 601 / (CP X5804BYA). Río Cuarto, Córdoba, Argentina.
[email protected]
RESUMEN
En la última centuria, la integración de cuencas serranas con otras de llanura tuvo fuertes implicancias ambientales. En este trabajo se analiza la evolución morfohidrológica del arroyo Las Lajas (procesos-causastendencias), utilizando indicadores morfológicos-morfométricos del canal y valle, extraídos de cartografía de
diferentes años y relevamiento actual. A principios del siglo XX, el arroyo, con nacientes serrana, semipermanente, descargaba en una depresión periserrana, integrándose al arroyo Santa Catalina durante la década del 50.
Por retroceso y coalescencia de cabeceras de canales efímeros y discontinuos, evolucionó de régimen semipermanente-endorreico, con predominio de inundación-sedimentación, a permanente-exorreico (régimen dominante) donde prevalece la erosión-transporte. La migración de cabeceras se asocia a ciclos húmedos (1953-1968,
1972-actualidad) y canalizaciones. La longitud de canal, profundidad del valle, desbordes y cabeceras de retroceso, resultaron indicadores sensibles de los procesos de ajuste. Las obras de mitigación controlan los procesos
naturales, reduciendo el peligro de erosión y estabilizando el canal.
Palabras clave: arroyos, integración, evolución.
ABSTRACT
Integration between mountain and plain basins had strong environmental consequences in the last century. This
paper analyses morphohydrological evolution of Las Lajas stream (processes-cause-tendency) by using morphological and morphometric indicators for channel and valley obtained from old cartography and present surveys. In early XX century, the stream began in the mountains, was semipermanent, and ended in a depressed
area. In 50´s decade, it joined Santa Catalina stream, by backward erosion and coalescence of multiple headcuts
of ephemeral and discontinuous courses. The stream evolved from semipermanent and endoreic regime with
flooding-sedimentation processes to permanent-exoreic regime with transport processes. Headcuts migrations
are related to humid periods (1953-1968, 1972- present time) and channelizations. Channel length, valley
depth, flooding, and backward headcuts were most sensitive indicators. Control structures control adjustment
process by stabilizing the stream and reducing erosion hazard.
Keywords: stream, integration, evolution.
49
Integración de Cuencas de Drenaje en Áreas de Llanura durante la Última Centuria. El Caso del Arroyo Las Lajas, Córdoba, Argentina
(540 km2), afluente del arroyo Santa Catalina, que
desagua en los Bañados del Tigre Muerto (Figura 1).
INTRODUCCIÓN
Es conocida la respuesta que manifiestan los sistemas
naturales a cambios ambientales, ya sean naturales o
antrópicos. Entre ellos, los sistemas fluviales, principalmente los canales aluviales, suelen experimentar
diferentes procesos de ajuste debido a modificaciones
en sus variables de control, como caudal, cantidad y
tipo de sedimentos y gradiente. Estas alteraciones
inciden sobre la geometría de la sección transversal,
perfil longitudinal y patrón del canal, por lo que estos
parámetros morfológicos resultan diagnósticos de
cambios en la dinámica del canal (erosión o agradación). El modo con que un canal responde a cambios
en sus variables de control no es uniforme y depende
de su sensibilidad, concebida por Downs y Gregory
(1993) como la relación entre fuerzas de perturbación
versus fuerzas de resistencia. Así, se pueden diferenciar tramos con distinto comportamiento morfodinámico y consecuentemente diferentes grados de estabilidad. (Schumm, 1969, 1977, 2005; Gregory, 2006;
Macklin y Lewin, 2008).
El clima de la región es Mesotermal SubhúmedoHúmedo, con temperaturas medias del orden de 16,5
ºC y precipitaciones medias anuales que varían desde
939,4 mm, en proximidades de las sierras a 856,3 mm
hacia el SE, en todos los casos concentradas en primavera-verano (75-80 %). Las precipitaciones muestran
una tendencia lineal de carácter ascendente desde el
año 1972, muy marcada a partir de 1998 (hasta 200
mm de incremento - Doffo, 2007) y una alternancia de
ciclos húmedos y secos temporalmente coincidentes en
varias series (Vollenwaider – Moldes - Ea. Las Rosas
– Tomaselli - Meinero). Entre los húmedos se destacan
los períodos comprendidos entre los años 1912-1933,
1953-1968, 1972-actualidad y, entre los secos, 18961911, 1934-1954 y 1969-1971 (Doffo y Bonorino,
2008; Degiovanni et al, 2009).
El arroyo Las Lajas (Figura 1) desarrolla su cuenca
alta sobre rocas de basamento ígneo-metamórfico
precámbrico a paleozoico inferior del extremo
meridional de las Sierras de Comechingones (Sas.
Pampeanas), mientras que en su cuenca media y
baja drena secuencias cuaternarias de la Llanura
Pampeana, con diferente grado de diagénesis. En
el sector pedemontano, el relieve es fuertemente
ondulado debido a la presencia de bloques de basamento cercanos a la superficie apenas cubiertos
por depósitos de antiguas bajadas y materiales
loessoides. Hacia el Este, se reconoce una llanura
fluvio-eólica, con paleocanales cubiertos por depósitos eólicos holocenos que, transicionalmente, se
interdigita con la planicie eólica pampeana, caracterizada por mantos loéssicos y formas medanosas
con distinto grado de disipación y actividad (Doffo, 2007). El área presenta una tectónica de bloques asociados a fallas regionales, entre los que se
destacan la depresión del arroyo Chico y el alto
Santa Catalina-Golf, los cuales controlan la morfodinámica de este curso (Figura 1) y la depresión
de La Olla con menor expresión topográfica. Varias de estas estructuras tienen probada actividad
neotectónica y sísmica reciente, como la falla de
las Lagunas (Sagripanti, 2006), que se reconoce en
el tramo medio de la cuenca.
En el Sur de la provincia de Córdoba son numerosas
las contribuciones que abordan distintos aspectos
morfodinámicos de los cursos de la región, todos
ellos en vías de ajuste, y los problemas ambientales
que de ellos se derivan (Blarasin et al., 1994; Degiovanni et. al., 2005; Degiovanni, 2008). En particular, los ajustes experimentados por el arroyo Las
Lajas, durante la segunda mitad del siglo XX, han
traído consecuencias nocivas para la infraestructura
instalada, al destruir dos puentes carreteros y uno
ferroviario, aislar importantes sectores rurales, sepultar con sedimentos suelos productivos en su
cuenca baja y contribuir a la colmatación de la depresión de Tigre Muerto, área receptora de carácter
regional (Doffo, 2007).
Los cambios operados presentan una marcada variabilidad en espacio y tiempo, dependiendo no sólo de
la posición en la cuenca, sino del contexto geológicogeomorfológico, régimen climático y actividades
humanas. En este trabajo se trata de reconstruir la
evolución morfohidrológica y la integración de la red
de drenaje de la cuenca del arroyo Las Lajas durante
la última centuria y caracterizar los procesos de ajuste, sus causas y tendencias.
En su recorrido (aproximadamente 100 km) este
curso salva un desnivel de 850 m (cota 1250-400
m.s.n.m), de los cuales, 400 m corresponden al tramo
extraserrano (60 km) donde exhibe un gradiente
promedio de 0,6% e importantes variantes morfológicas en su faja fluvial extraserrana.
Características generales del área de estudio
El área de estudio se sitúa en el Dpto. Río Cuarto, al
Sudeste de la provincia de Córdoba, y comprende el
tramo extraserrano de la cuenca del arroyo Las Lajas
50
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 1. Mapas de ubicación y geomorfológico de la cuenca del Aº Las Lajas, Provincia de Córdoba.
Doffo (2007) describe un canal sinuoso, areno gravoso, con tendencia a la agradación hasta el salto La
Carolina (14 m), frente de retroceso que señala el
inicio de un tramo muy incidido (hasta 20 m), con
un nivel de terraza, canal de variada sinuosidad y
sección transversal que desarrolla una importante
llanura de inundación en un valle profundo, donde
son muy relevantes los procesos de evolución de
laderas, gravitatorios e hídricos. Aguas abajo, en la
depresión del arroyo Chico, la faja fluvial se estrecha y se reduce sólo al canal exhibiendo un único
frente de retroceso activo (2 m). El último tramo
(sector bloque Santa Catalina-Golf) corresponde a
un canal meándriforme que divaga en un valle evolucionado con 3 niveles de terrazas presumiblemente sintectónicas (Doffo y Bonorino, 2006).
Hidrología superficial
El arroyo Las Lajas, de orden 5, es el único
colector y sólo recibe al arroyo Chico en la depresión homónima. Posee régimen permanente
en cuenca alta, temporario en la zona periserrana
y nuevamente permanente en cuenca media y
baja. El sector serrano comprende solamente el
8% del área drenada, no obstante define el carácter torrencial que caracteriza a este curso, que
evacua caudales mínimos de 0,2-1 m3 /s y alcanza, en crecidas estivales extraordinarias, valores
superiores a los 150 m3 /s. Los eventos de mayor
efectividad geomorfológica fueron las crecidas
de 1912, 1918, 1928, 1979, 1983, 1985, (Degiovanni, 2008).
51
Integración de Cuencas de Drenaje en Áreas de Llanura durante la Última Centuria. El Caso del Arroyo Las Lajas, Córdoba, Argentina
mapa hidrográfico y mapa catastral de la provincia
de Córdoba elaborados por Brackebusch (1883),
Ríos y Achaval (1906) y Dirección Provincial de
Catastro (1924), respectivamente; hojas topográficas del Instituto Geográfico Militar escala
1:250.000 (1953) y 1:50.000 (1963); fotografías
aéreas a diversas escalas correspondientes a los años
1963, 1970, 1989 e imágenes satelitales en soporte
digital de diferentes años.
Intervenciones humanas
Todo el sector extraserrano forma parte del agroecosistema pampeano el cual, en los pasados 50
años, ha experimentado importantes cambios en el
uso del suelo (mecanización-monocultivo-siembra
directa) cuya consecuencia es el aumento en la
escorrentía superficial (Becker, 2006), con marcada
incidencia en el régimen hidrológico del arroyo.
Siguiendo la expansión de la frontera agrícola e
incremento del cultivo de soja, se realizaron intervenciones directas en el curso que alteraron su morfología (longitud de canal, pendiente, sección transversal), sedimentológicos (disponibilidad de material) e hidrológicos (caudal por trasvases). Entre las
de mayor impacto se destacan:
Los parámetros seleccionados son medidos, utilizando metodología convencional, en 4 tramos de
canal, los cuales fueron definidos con criterio
geológico y morfohidrológico tomando como
punto de partida la cartografía de fines de siglo
XIX. Las características de los mismos se detallan más adelante.
1- Canalización del área de desbordes del arroyo
Las Lajas en la depresión del arroyo Chico, a mediados de la década del ’50, hacia el arroyo homónimo y finalmente hacia el Santa Catalina. Para la
misma época y por razones similares comenzó el
drenaje artificial de los Bañados del Tigre Muerto,
nivel de base regional.
La profundización del canal surgió de la comparación
de las cotas del canal extraídas de las hojas topográficas (escala 1:50.000, IGM, 1963) con las obtenidas
con GPS referencial en 2003 (Doffo, 2007).
El análisis de los mecanismos de extensión e integración de canales se apoyó en los criterios de Bull
(1997) para canales efímeros y discontinuos, análogos
a cursos profundos y perennes de Packard (1974).
2- Canalización del arroyo Chico hacia el arroyo
Las Lajas, en sector puente ruta Nac. 35, por la
obstrucción que se generara por la crecida de este
último en 1979 y recanalización 4 km aguas arriba
en el 2005, por severos problemas erosivos.
EVOLUCIÓN MORFOHIDROLÓGICA
3- Control de cabecera de retroceso en salto La
Carolina obra inaugurada en 2008, esta intervención
no se efectuó en el frente natural, sino en una traza
de bypass al curso original.
Análisis de los procesos involucrados
Se definieron 4 sectores de la actual cuenca (Figura
2) para efectuar el seguimiento de los indicadores
seleccionados (Tabla 1).
4- La puesta en funcionamiento (2007) de la Presa
Las Lajas situada en el sector serrano, regula los
caudales provenientes de la cuenca alta.
1) Sector planicie fluvio eólica, entre el sector serrano y la depresión tectónica de La Olla (antigua zona
de descarga). Régimen semipermanente dominante.
2) Tramos de canal discontinuos, localizados en
paleocanales de la planicie fluvio-eólica, que se
extienden desde la depresión de la Olla hasta la del
Chico. Régimen efímero.
3) El sistema de drenaje en la depresión del arroyo
Chico. Régimen permanente.
4) Tramo que discurre por el bloque de Santa Catalina-Golf, de régimen permanente.
METODOLOGIA
Para alcanzar los objetivos propuestos se analiza la
variabilidad de diferentes aspectos del canal, como:
longitud, diseño en planta, sinuosidad, ancho, profundidad, presencia de cabeceras de retroceso y
algunos rasgos del valle, entre ellos, dimensiones,
desbordes, áreas sedimentadas, llanura de inundación, niveles de terrazas, etc., a partir de documentación cartográfica y fotografías aéreas de diferentes
años, complementando con relevamiento de campo
en los últimos años. Se utilizaron: el plano general,
Finalmente se relacionan los cambios morfológicos
e hidrológicos observados con las variables de control (naturales y antrópicas) y se establecen las tendencias de cambios.
52
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Figura 2. Comparación de distintos estadios evolutivos para los cuatro tramos definidos en el Arroyo Las Lajas entre 1883 y 2010.
Tabla 1. Variabilidad de los indicadores morfohidrológicos entre 1883-2010, para cada tramo de canal.
Sector
de la
cuenca
Indicadores morfohidrológicos
Longitud (km)
Años
1883-1924
1963
1970
1989
2010
18
15
Variable
2-7
Poco profundo
15
Variable
2-7
Más profundo
1 - tramo
final
14,2
Variable
2-7
Más profundo
1 - tramo
final
14,2
Variable
2-7
Más profundo
S =1,10
S = 1,10
S = 1,17
S = 1,13
1-Tercio
superior
Importantes,
finales del
tramo
Permanentetemporario
1-Tercio
superior
Moderados
sector medio
Permanentetemporario
1-Tramo
completo
Confinados
a espiras de
meandros
Permanentetemporario
1-Tramo
completo
Confinados a
espiras de
meandros
Permanentetemporario
Cuenca serrana –media alta
Ancho (m)
Profundidad de valle
(m)
Cabeceras de retroceso
Diseño de canalSinuosidad (S)
Terrazas
Desbordes-derrames
Régimen
Canal bien
definido
(Cañada de
la Paja,
Cañada de
Las Lajas)
con zona de
descarga en
la depresión
de La Olla
Permanentetemporario
-
53
-
Integración de Cuencas de Drenaje en Áreas de Llanura durante la Última Centuria. El Caso del Arroyo Las Lajas, Córdoba, Argentina
Tabla 1. Variabilidad de los indicadores morfohidrológicos entre 1883-2010, para cada tramo de canal (continuación).
Sector
de la
cuenca
Indicadores morfohidrológicos
Años
1883-1924
Longitud (km)
Sector medio
Ancho medio canal
(m)
Profundidad de valle
(m)
Cabeceras de retroceso
Diseño de canal
Terrazas
Desbordes-derrames
Bajos inundables, parcialmente
conectados,
que desaguaban en eventos importantes en la
depresión del
Chico
Sector Alto Estructural
Santa Catalina
Sector Depresión del arroyo Chico
Régimen Dominante
1963
1970
1989
2010
13
(tramo con
canal)
15,5
(tramo con
canal)
36,30
(tramo casi
completo)
37,30
(tramo completo)
8 -12
8 -16
7 -16
8 -16
6 extremos
3 centro
7 extremos
3 centro
5
4
15-22
(tramo
completo)
1
(16 m)
S = 1,18
1
15-22
(tramo completo)
1
(16 m)
S = 1,20
1
-
-
Secuencia
frentes retroceso-canal
recto-derrames
entrelazado
Efímerotemporario
Secuencia
de tramos
agradacióndegradación
Efímerotemporario
Permanente
Permanente
14
(incremento
por canalización)
18
(extensión
aguas arriba)
18
(desconexión Aº
Chico,
1979)
18
(conexión
artificial Aº
Chico, 2007)
Ancho medio canal
(m)
5-7
5-7
5-7
5-7
Profund. de valle (m)
3-5
6
6
-
No
1,01
-
Permanente
8,6
6 -7
profundo
1,01
Moderada
área
Permanente
8,6
6 -7
> profund
1-(2,5 m),
tramo final
1,05
Sólo en
1979
Permanente
8,6
6 -7
> profund
-
-
-
-
1,40
2
en espiras de
meandro
Permanente
1,40
2
en espiras
de meandro
Permanente
1,40
2
en espiras
de meandro
Permanente
1,38
2
en espiras de
meandro
Permanente
Longitud (km)
Cabeceras de retroceso
Sinuosidad (S)
Terrazas
Desbordes–derrames
Régimen
Longitud (km)
Ancho med canal (m)
Profun de valle
Cabeceras de retroceso
Diseño de canal (S)
Terrazas
11
(estimado de
cartografía
antigua)
Aº Corralito
(ant. a Las
Lajas) que
confluye en
el arroyo
Santa Catalina
Desbordes–derrames
Régimen
Permanente
Extensa área
En el primer sector los cambios fueron mínimos
(Figura 2) tanto en el diseño en planta como sección transversal del canal y sólo se ha registrado
un proceso de incisión moderado a partir de mediados de la década del ’60, que implicó la progresiva desaparición de los sectores de desbordes
(Figura 2c). El régimen hidrológico se mantiene
semipermanente por lo que el tramo preserva su
15
(tercio sup. e
inferior)
1 - desplazó
1,5 km ag.arr.
1,08
Permanente
8,5
6 -7
> profund
carácter agradacional, sólo algo más confinado al
canal y llanura de inundación, ambientes estabilizados por una abundante vegetación ribereña. La
longitud de canal con estas características se
redujo a expensas de la migración de ondas de
erosión remontante, desde la depresión de la Olla
hasta el frente de retroceso del salto La Carolina
(Figuras 2c y d).
54
CUADERNOS del CURIHAM, Vol. 16, Año 2010
El sector intermedio es el de mayor variabilidad. La
sucesión de canales discontinuos y efímeros precedidos por cinco frentes de retroceso de altura intermedia (Figura 2b), evolucionó por medio de coalescencia de estas cabeceras (Bull, 1997; Figura 3), a
un único canal profundizado (10 a 15 m) y sinuoso
(1,20), donde desaparecieron, a excepción de un
reducido sector, los canales someros y las áreas de
derrames asociadas. Este proceso de incisión, muy
marcado ya en las fotografías de 1989 (Figura 2c),
generó un valle profundo, con barrancas de hasta 22
m, cuya evolución (caídas, vuelcos, sufusión y erosión hídrica), constituyen una nueva e importante
fuente de sedimentos y promueven procesos de
agradación y posterior estabilización de las márgenes del valle. Otra consecuencia relevante de la
profundización es la extensión aguas arriba del
régimen permanente por aporte freático (Figuras 2c
y d), lo cual promueve el desarrollo de vegetación
en márgenes y llanura de inundación, aumentando
la rugosidad hidráulica y promoviendo la agradación en la llanura de inundación. Tras el paso de la
onda de retroceso mayor el canal incrementó su
sinuosidad levemente, se generó un nivel de terraza
y en la actualidad discurre en un valle ensanchado
con marcada estabilidad morfológica.
ceso, con algunos cambios de ritmo, continúa en la
actualidad, ya que la desconexión por aluvionamiento con el arroyo Chico en 1979 y posterior
canalización, nunca implicó cambios en el nivel de
referencia del arroyo Santa Catalina. La sinuosidad
se mantiene baja (1,01; 1,05 y 1,08) y el segmento
de canal cambió de somero, dominado por desbordes y sedimentación, a un canal moderadamente
profundizado, confinando los episodios de crecidas
a la faja fluvial (Figuras 2c y d).
ANÁLISIS DE LAS CAUSAS
Confrontando la magnitud y distribución espaciotemporal de los procesos de integración analizados,
con las variaciones climáticas registradas en el siglo
pasado y las intervenciones humanas en la red de
drenaje que se llevaron a cabo durante ese período,
revela notoriamente que los cambios morfohidrológicos descriptos se vinculan fundamentalmente a
modificaciones del perfil longitudinal (conexiones
por canalizaciones), como el incremento de caudal.
Las intervenciones antrópicas en las áreas de interfluvios y, fundamentalmente, las directas en el curso
han iniciado y/o potenciado los procesos de ajuste
en el sistema fluvial. Las sucesivas alteraciones de
la cota del lecho y del nivel de base en la depresión
del arroyo Chico y Tigre Muerto, sumadas a conexiones menores en la antigua Cañada de la Paja,
han incrementado el gradiente del perfil longitudinal y disparado ondas de erosión retrocedente.
Relaciones entre potencia y resistencia de canal
Pendien
te
prom ed
io
de fondo
El aumento del caudal está marcadamente relacionado a ciclos húmedos donde las precipitaciones,
muy superiores a la media, generan importantes
excesos hídricos y un marcado ascenso del nivel
freático. Los períodos húmedos 1953-1968 y 1972actualidad son los más relevantes por la magnitud
de los cambios asociados. El primero de ellos,
debido a la magnitud de las áreas afectadas por
desbordes, motivó la conexión artificial con el
arroyo Chico-Santa Catalina y el segundo, especialmente las crecidas de 1979, 1983 y 1985, ocasionó la máxima tasa de incisión y erosión retrocedente de la centuria, provocando los mayores cambios morfo-hidrológicos.
de v alle
Puntos de intersección
Figura 3. Diagrama en planta y perfil longitudinal de secuencia de patrones de canal efímeros y discontinuos (Bull, 1997).
En la depresión del arroyo Chico, la dinámica del
canal manifiesta cambios muy importantes, ya que
este sector pasó de ambiente receptor de sedimentos
a uno con dominio de transporte. Los sucesivos
ciclos de desbordes y sedimentación provenientes
de la integración hidrológica en eventos de tormentas importantes de la cuenca de Las Lajas (naciente
serrana) con la Cañada de la Paja (Figura 2a) y
posterior canalización (década del 50) con el arroyo
Chico-Santa Catalina, aceleró la migración de una
onda de erosión retrocedente (Figura 2b). Este pro-
A pesar que la región registra actividad tectónica
cuaternaria (Sagripanti, 2006), esta no resulta relevante para explicar los procesos de ajuste detectados, no obstante condiciona el carácter y localización de los procesos fluviales (depresión del arroyo
Chico y bloque Santa Catalina-Golf).
55
Integración de Cuencas de Drenaje en Áreas de Llanura durante la Última Centuria. El Caso del Arroyo Las Lajas, Córdoba, Argentina
longitud de canal, caudal líquido y sólido y morfología del canal.
Tendencias de cambio
Si bien el arroyo Las Lajas es un curso en vías de
ajuste, con dos cabeceras de retroceso activas localizadas en cuenca media y baja, es posible señalar
diferentes grados de peligro de incisión, inestabilidad de laderas y posterior divagación.
No obstante, dos obras mitigan esta tendencia. La
más importante es la presa Las Lajas, que actúa
como reguladora de caudales de crecida y disminuye marcadamente la amenaza, ya que los eventos
de mayor peligrosidad se asocian a crecidas generadas por lluvias serranas. En segundo término, la
realización de una obra de control de erosión en la
cabecera de retroceso mayor, situada próxima al
paraje La Carolina, también disminuye la susceptibilidad del sitio y por lo tanto la peligrosidad. La
efectividad de esta obra está reforzada por la construcción de la presa Las Lajas, ya que la cabecera
natural (15 m) está desprotegida y si la derivación
del canal fuera superada en un evento de crecida
importante ésta se activaría. No se esperan mayores
cambios en el Sector 1.
La extensión del canal se efectuó por crecimiento
aguas abajo y erosión retrocedente de canales
discontinuos localizados en bajos, correspondientes a paleocanales del Pleistoceno. Las tasas de
retroceso son variables, no sólo en función del
caudal, sino de la litología.
Los indicadores morfométricos que mejor describen
el proceso son la profundidad del valle, los rasgos
de desbordes y las cabeceras de retroceso, mientras
que la sinuosidad exhibe una escasa variabilidad, en
algunos tramos por variaciones mínimas en los
factores de control (Sector 1) y en otros, por permanecer los canales aún desajustados (Sector 3).
El proceso de ajuste natural está controlado por
obras de mitigación por lo que el peligro de erosión
está muy atenuado y se observa una tendencia a la
estabilización de las condiciones actuales.
Se supone que el frente de retroceso situado aguas
arriba de la Ruta 35, continúe activo ya que el arroyo Las Lajas tiene un área de aporte considerable en
la zona de llanura, pero por su escasa magnitud (2
m) se le asigna baja peligrosidad (Sector 3). Por su
parte, no son esperables nuevas ondas de incisión a
partir del arroyo Santa Catalina, ya que desde 2004,
está en operación la Presa Tigre Muerto en su zona
de descarga, por lo que en el Sector 4 no se prevén
mayores cambios.
REFERENCIAS BIBLIOGRÁFICAS
Brackebuch, L. 1883. Plano general de la provincia
de Córdoba. Ed. Dpto. Topográfico de la provincia
de Córdoba.
Becker, A. 2006. Evaluación del proceso de degradación de suelos por erosión hídrica en una subcuenca
representativa de la región pedemontana del suroeste
de la provincia de Córdoba, Argentina. Tesis Doctoral Facultad de Ciencias Exactas Fco-Qcas y Naturales. Universidad Nacional de Río Cuarto (Inédita).
Blarasin M., Degiovanni, S., Cantú, M., Eric, C.,
Cabrera, A., Villegas, M., Doffo, N., Becker, A.,
Cisneros, J., Gonzalez, J. y Cholaky, C. 1994. Diagnóstico global del funcionamiento hídrico de las
cuencas que afectan las trazas de la Ruta Nac. 7, entre Laboulaye y Villa Mercedes, y la Ruta Nac. 8,
entre Canals y Villa Mercedes. Convenio U.N.R.C. y
Empresa Caminos del Oeste S.A. Inédito.
Bull, W. 1997. Discontinuous ephemeral streams.
Geomorphology 19, 227-276.
Degiovanni, S. 2008. Análisis geoambiental del
comportamiento de los sistemas fluviales del Sur
de Córdoba, en especial del Aº Achiras-del Gato,
como base para su gestión sustentable. Tesis Doctoral. UNRC. Inédito.
Degiovanni, S., Villegas M. y Doffo N. 2005. Monitoreo del comportamiento del río Cuarto en un tramo del curso medio sometido a fuerte presión antrópica. Aguas superficiales y subterráneas en el
Los sectores de valle ya ajustados del Sector 2,
presentan un grado de estabilidad elevado, los taludes están evolucionados y se ha desarrollado una
extensa llanura de inundación.
CONCLUSIONES
Aunque no fueron analizados en este trabajo, hay
antecedentes (Doffo, 2007) que indican que la red
serrana no presenta mayores cambios, a pesar de
existir registros de incisión en la última centuria. En
contraposición, para el mismo período, las modificaciones son muy notorias en el área de llanura, en
respuesta principalmente a variaciones en el régimen de precipitaciones y actividad humana. Como
resultado dos cuencas de drenaje (Las Lajas-Cañada
de la Paja y Corralito-Arroyo Chico) se integraron
en una cuenca única, incrementando área drenada,
56
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Gregory, K.J. 2006. The human role in changing
river channels. Geomorphology, 79(3-4): 172-191.
Macklin, M. y Lewin, J. 2008. Alluvial responses to
the changing Earth system. Journal of Earth surface processes and landforms. (p 1374-1395) Published Online: Jul 25 2008 5:24AM.
Packard, F. 1974. The Hidraulic Geometry of a Discontiuous Ephemral Stream on a Bajada near Tucson, Arizona. Univ. Arizona, Ph.D. Thesis. En
Komar, 1989. Floods: Hydrological, Sedimentological and Geomorphogical Implications. Edited
by Beven and P. Carling. John Wiley & Sons.
Ríos, J. y Achaval, F. 1906. Mapa Hidrográfico,
cuenca superior de los ríos Tercero y Cuarto. En
Geografía de la provincia de Córdoba. Gobierno de
la provincia de Córdoba.
Sagripanti, G. 2006. Neotectónica y peligro sísmico
de la región de Sampacho, Dpto Río Cuarto, prov.
Cba. Tesis Doctoral Facultad de Ciencias Exactas,
Físico-Químicas y Naturales. Universidad Nacional de Río Cuarto. (Inédita).
Schumm S. 1969. River Metamorphosis. ASCE
J.Hydraul. Div. 95(1):255-273.
Schumm S. 1977. The Fluvial System. Ed. John
Wiley & Sons, New York-London.
Schumm S. 2005. River variability and complexity.
Cambridge University Press, New York.
sur de Córdoba: una perspectiva geoambiental. En
Blarasin, M., Degiovanni, S., Cabrera, A. y Villegas, M. (Ed.) Aguas Superficiales y subterráneas
en el sur de Córdoba. Una perspectiva geoambiental. Universidad Nacional de Río Cuarto.
Degiovanni, S., Doffo N. y Villegas, M. 2009. Rejuvenecimiento de la red de drenaje del Sur de Córdoba como consecuencia del cambio climático durante la última centuria. En: Sayago y Collantes
(Eds), Geomorfología y Cambio Climático-. INGEMA (UNTuc)- I (Cap. 6):79-96. MAGNA Ediciones, Tucumán.
Dirección Provincial de Catastro de la Provincia
de Córdoba. 1924. Carta Catastral del Territorio
de la Provincia.
Doffo, N. 2007. Alteraciones en el régimen hidrológico de la cuenca del arroyo Las Lajas, Cba: causas
naturales y antrópicas, umbrales de resistencia al
cambio. Tesis Doctoral Facultad de Ciencias Exactas, Universidad Nacional de Río Cuarto (Inédita).
Doffo N. y González Bonorino, G. 2006. Evidencias
de ajustes por tectonismo en los cauces de los arroyos Las Lajas y Santa Catalina, Dpto Río Cuarto,
Córdoba. En: J. Sanabria y G. Argüello (Eds), Actas III Cong. Cuaternario y Geomorfología, UNC,
I, 367-375.
Doffo N. y González Bonorino, G. 2008. Modificaciones morfohidrológicas en el tramo medio del
arroyo Las Lajas, Departamento de Río Cuarto,
Córdoba, como respuesta a cambios climáticos.
XVII Congreso Geológico Argentino. Jujuy. III,
1202-1203.
Downs, P. W. y Gregory, K.J. 1993. The sensitivity
of River Channels in the Landscape System. Ed.
John Wiley & Sons.
Artículo recibido el 12/2010 y aprobado para su
publicación el 03/2011.
57
CUADERNOS del CURIHAM, Vol. 16, Año 2010
DESEMPEÑO DE UN MICROSIMULADOR DE LLUVIA PORTÁTIL PARA ESTUDIOS
HIDROLÓGICOS
Juan F. Weber, Héctor I. Paoli, Laureana Apestegui
Laboratorio de Hidráulica, Departamento de Ingeniería Civil, Facultad Regional Córdoba,
Universidad Tecnológica Nacional.
Maestro M. López esq. Cruz Roja Argentina. Ciudad Universitaria-CP(X5016ZAA). Córdoba – Argentina.
e-mail: [email protected]
RESUMEN
En este trabajo se presenta un microsimulador de lluvia portátil íntegramente diseñado, construido y
calibrado en el Laboratorio de Hidráulica (UTN Facultad Regional Córdoba). Este equipo, que es
completamente desarmable y define una parcela de ensayo de 1 m², tiene como finalidad la medición in situ
de diversos parámetros hidrológicos. El conjunto de formadores de gotas, construido con 289 agujas
hipodérmicas (diámetro 0.8 mm), se alimenta de una batea con carga variable (entre 10 y 20 cm), que permite
intensidades entre los 65 y 120 mm/h, la altura de caída es de 1.85 m y su diámetro medio de 5.2 mm. Si bien
se contaba con una estimación inicial de la relación buscada, fue necesario una calibración sobre el prototipo
para tener en cuenta las condiciones reales de operación. Las mediciones fueron realizadas utilizando 5
pluviómetros distribuidos en la parcela de estudio, con 10 observaciones por carga, para un total de 7 cargas,
lo que totalizó un universo de 350 datos experimentales. Luego de un cuidadoso análisis estadístico, fue
posible ajustar una curva potencial entre carga e intensidad, con una incertidumbre de ±3 mm/h,
aproximándose en un 86% los valores teóricos esperados. Los primeros ensayos de campo realizados
muestran resultados satisfactorios, en comparación con la técnica del infiltrómetro de doble anillo utilizada
hasta el presente en este Laboratorio.
Palabras clave: infiltración, mediciones hidrologicas, simuladores de lluvia.
ABSTRACT
This work presents a portable rainfall micro-simulator entirely designed, constructed and calibrated in the
Hydraulics Laboratory (UTN Facultad Regional Córdoba). This apparatus is completely disassembled and
defines a test plot of 1 m². It aims at the in situ measurement of various hydrological parameters. All the
drop-formers, built with 289 needles (diameter 0.8 mm), feeding on a tray with variable hydraulic head h (10
to 20 cm), which allows intensities i between 65 and 120 mm/h. Fall height of drops is 1.85 m, and its
average diameter of 5.2 mm. Although there were initial estimates of the i-h relationship, a calibration was
needed on the prototype to reflect actual operating conditions. Measurements were made using 5 raingauges
distributed in the test plot, with 10 observations per hydraulic head, for a total of 7 heads, which amounted
350 experimental data. After careful statistical analysis it was possible to fit a potential curve between head
and intensity, with an uncertainty of ±3 mm/hour, about 86% to the theoretical values expected. First in-situ
experimental observations were successful, compared with double-ring infiltrometer technique widely used
in this Laboratory.
Keywords: infiltration, hydrologic measurements, rainfall simulators.
59
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
que tratan de simular la lluvia natural (Pla Sentis,
1981; Rostagno y Garayzar, 1995). El mayor de
estos problemas recae sobre la reproducción de gotas
que se asemejen a las de una lluvia natural.
INTRODUCCION
Uno de los procesos hidrológicos de importancia en
la modelación de eventos hidrológicos es la
infiltración. La determinación in situ de los
parámetros de un modelo de infiltración, se puede
realizar a través de dos tipos de mediciones: las
globales, que plantean un balance a nivel de cuenca,
lo cual exige disponer de instrumental espacialmente
distribuido en la misma y las puntuales, en las cuales
se estiman parámetros en sitios específicos. Entre
estas últimas se cuentan los ensayos del infiltrómetro
de doble anillo y los microsimuladores de lluvia.
Los simuladores de lluvia son instrumentos de
investigación diseñados para aplicar agua de forma
similar a los episodios tormentosos naturales. Son
útiles para obtener datos de erosión, infiltración,
escorrentía superficial y transporte de sedimentos.
No obstante, las características de la lluvia natural
deben ser simuladas de forma adecuada, los datos
obtenidos deben ser analizados cuidadosamente y se
debe efectuar una buena interpretación de los
resultados para obtener información fiable en las
condiciones para las que ha sido aplicable la lluvia
(Benito et al., 2001).
En el ámbito del Laboratorio de Hidráulica,
Universidad Tecnológica Nacional, Facultad
Regional Córdoba (UTN-FRC), se han llevado a
cabo numerosas mediciones a través del dispositivo
conocido como infiltrómetro de doble anillo (Weber
et al., 2005).
En este trabajo se presentan las características del
microsimulador de lluvia desarrollado en el ámbito
del Laboratorio de Hidráulica, UTN-FRC, en el
marco de un Proyecto de Investigación y Desarrollo.
Est equipo servirá para la determinación in situ de
parámetros hidrológicos tales como infiltración,
intercepción vegetal, producción de sedimentos, etc.
Este ensayo tiene la ventaja de ser de fácil
implementación, pero presenta tres limitaciones
importantes, a saber: i) el ensayo es de carácter
puntual, esto es, el área involucrada es muy pequeña
y por lo tanto los errores en la extrapolación a
superficies del orden de magnitud de una cuenca son
muy importantes; ii) el ensayo está limitado a la
condición
de
encharcamiento
superficial
permanente, lo cual limita la aplicabilidad de los
parámetros a calibrar y iii) el dispositivo no
representa fielmente la entrada hidrológica del
sistema, esto es, la precipitación, dado que lo que se
hace es mantener una lámina de agua constante en la
superficie del suelo.
EL SIMULADOR DE LLUVIA
Se describe a continuación el proceso seguido en el
diseño y construcción del equipo bajo análisis. Para
mayor detalle, se puede consultar la referencia
(Weber et al., 2009).
Antecedentes locales
Uno de los antecedentes que más se consideró a la
hora de diseñar el simulador de lluvia fue el
precedente local de un instrumento diseñado por
Irurtia y Mon (1994); a partir de un modelo de
Kamphorst (1987).
El microsimulador de lluvia tiene la ventaja de
reproducir con más fidelidad el fenómeno de la
precipitación. Numerosos autores (Marelli, 1989)
muestran la importancia del impacto de las gotas
en la microcapa superior del suelo en el balance
hídrico, además del efecto evidente sobre la
erosión superficial.
Este microsimulador de lluvia fue luego modificado
por Aoki y Sereno (1999) y se encuentra
actualmente en uso en la Facultad de Agronomía de
la Universidad Nacional de Córdoba. En su forma
básica el microsimulador es un prisma cuadrado de
1.5 m de altura y de 0.25 m de base. La estructura es
de hierro en ángulo, que sostiene las paredes de
acrílico transparente que actúan como rompeviento.
El peso total del aparato es de 8 kg. En la parte
superior se apoya sobre una caja porta gotero de
acrílico, en cuya base se encuentran 49 tubos
plásticos formadores de gotas. Esta caja tiene una
Por otra parte, en este tipo de dispositivos es posible
simular una precipitación de intensidad variable en
el tiempo, incluso una precipitación discontinua. La
necesidad de reproducir bajo condiciones
controladas los efectos de la precipitación, y en
especial el impacto de las gotas de lluvia sobre las
propiedades físicas del suelo superficial, y las
consecuencias que ello provoca en la infiltración,
escorrentía y erosión, condujeron desde hace años al
desarrollo de diferentes mecanismos e instrumentos
60
CUADERNOS del CURIHAM, Vol. 16, Año 2010
alimentación de agua, proveniente de un reservorio
colocado en una de las aristas de la estructura. El
reservorio está graduado en milímetros de lámina de
agua aplicados en la microparcela, para simplificar
la lectura durante la medición.
excesivos en relación a los objetivos para los cuales
fue diseñado el simulador.
i (mm/h)
Formadores de gotas
El formador utilizado se compone de una aguja
hipodérmica introducida en tubo rígido, el cual se
obtiene de cortar su propio estuche, al ras de dicha
aguja (Figura 1). Los formadores ensayados
correspondieron a un mismo diámetro de la aguja,
0.8 mm y tres longitudes diferentes: 25.4 mm, 38.1
mm, 50.8 mm, las que corresponden a 1, 1 ½ y 2
pulgadas respectivamente.
2
1,8
1,6
1,4
1,2
1
0,8
0,6
0,4
0,2
0
F1
F2
F3
1
10
h (cm)
100
Figura 2. Intensidad de lluvia por formador – resultados
experimentales.
El simulador de lluvia
El equipo (Figuras 3 y 4) consta básicamente de una
estructura metálica, de caño de acero de sección
cuadrada, formando un prisma cuadrado de 2 m de
altura y 1 m de lado. Este prisma se forma a través
de cuatro columnas y cerrado por medio de cortinas
rompevientos. Las columnas sostienen el sistema de
alimentación de agua que esta compuesto por dos
tanques, uno de alimentación solamente y el otro de
alimentación y regulación de intensidad.
Figura 1. Formadores de gotas analizados.
Se realizó una serie de mediciones de laboratorio
para determinar el comportamiento hidráulico de
estos formadores (Paoli y Rojas, 2006). En base a
esta información se decidió colocar un total de 289
formadores, distribuidos en 17 filas por 17 columnas
y separados a una distancia de 5.30 cm entre ejes,
cubriendo de esta manera cada formador un área
aproximada de 28.10 cm² sobre la base de una batea
de 96 cm x 96 cm de lado. El tipo de formador
seleccionado fue el Nº 3, correspondiente a la aguja
de 2 pulgadas, ya que fue el que presentó las
menores intensidades (Figura 2).
Esta elección se basó en que las intensidades
logradas con los formadores más cortos y con un
número de 289 formadores alcanzaron, para el
formador Nº 1, i = 167 mm/h y para el formador Nº
2, i = 149 mm/h, valores que se consideraron
Figura 3. Simulador de lluvia – vista axonométrica.
La regulación de la intensidad se produce a través de
un flotante (Achutegui et al., 1996). Debajo del
sistema de alimentación de agua se encuentra la
61
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
batea con los 289 formadores de gota, que producen
la lluvia simulada. La base de este prisma esta
constituida por un marco cuadrado de hierro, de 1 m
de lado y 0.10 m de altura, con vertederos en sus
cuatro lados y canales para el transporte del agua
escurrida. Este marco de hierro, en su posición de
trabajo es clavado en el suelo, constituyendo así las
paredes límites de la parcela de medición (Figura 4).
El peso total del equipo armado es de 110.60 Kg, el
peso del fluido puede llegar hasta los 100 Kg.
- el sistema de lluvia simulada: consta de la batea
con los 289 formadores de gota, los cuales pueden
ser reemplazados inmediatamente ante cualquier
desperfecto en campaña.
- el sistema de puesta en régimen: conformado por
una bandeja intermedia, cuya finalidad es evitar que
durante el periodo de puesta en régimen del sistema
(del orden de 15 minutos) se altere el contenido de
humedad inicial del suelo (Figura 5).
- la parcela de medición y sistema de recolección del
escurrimiento superficial: la parcela de medición
queda definida por el marco de hierro hincado
(Figura 6), que posee salidas laterales por donde
fluye el escurrimiento superficial, que es capturado
por canales y conducido finalmente a los vasos de
medición.
Las partes componentes del microsimulador de
lluvia son:
- la estructura metálica: constituida por columnas,
vigas tipo 1 (rigidización estructural) y tipo 2
(soporte para los tanques de alimentación), conjunto
tensor y mamparas rompeviento. Las partes
metálicas se hallan unidas entre sí por bulones y
tuercas permitiendo así el rápido montaje y
desmontaje de la estructura.
Montaje y desmontaje del equipo
Una vez finalizada la construcción del simulador,
se realizó una experiencia de campo (denominada
Ensayo 0) con el objeto de poner a punto el
armado, operación y desarmado del equipo. En
este Ensayo 0 se detectaron algunas deficiencias
en el equipo que fueron subsanadas y además se
midieron los tiempos de armado, puesta en
régimen y desarmado, como así también el
consumo de agua, valores de fundamental
importancia para la planificación de futuras
mediciones en campaña.
- el sistema de alimentación: conformado por los
tanques alimentador 1 (reserva) y alimentador 2
(generación de carga), filtro de agua y conjunto flotante.
Figura 5. Puesta en régimen del simulador de lluvia.
Se indican a continuación en forma sucinta los pasos
necesarios para el montaje y desmontaje del
simulador de lluvia:
Figura 4. Simulador de lluvia en campaña.
62
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Montaje:
−
Preparación del Terreno
−
Instalación de la parcela de medición y
nivelación de la misma (Figura 6).
−
Sellado de los bordes de la parcela de medición
−
Colocación de columnas
−
Instalación de batea con formadores de gota
(Figura 7).
−
Colocación de vigas tipo Nº1 y tipo Nº2
−
Ajuste de bulones y fijación de la estructura
−
Colocación de ángulos guías y de bandeja
intermedia
−
Instalación de tanques alimentadores Nº1 y Nº2
−
Conexión de mangueras y accesorios
−
Conexión del filtro de agua (Figura 8).
−
Colocación de los canales de transporte de agua
−
Colocación de los puntos de medición
−
Colocación de mamparas rompevientos y
tensores (Figura 4).
Desmontaje:
− Desconexión de mangueras y sacado del filtro
− Remoción de tensores, mamparas rompevientos,
y ángulos guías
− Desajuste parcial de los bulones de la estructura
− Retiro de vigas tipo Nº1 y tipo Nº2
− Retiro de la batea con formadores de gotas
− Retiro de columnas
− Extracción de la parcela de medición
Figura 7. Estructura armada, con batea y bandeja instaladas.
Figura 8. Tanques de alimentación y filtro de agua.
Funcionamiento
Una vez montado el equipo en el terreno se está en
condiciones de comenzar el ensayo, lo cual se
realizará en los siguientes pasos.
Figura 6. Parcela de medición instalada en campaña.
63
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
Tareas Preliminares
Tareas de Medición
−
Llenado de tanques: en primer lugar, se debe
llenar con agua el tanque alimentador Nº1,
habiendo controlado antes que todas las
válvulas de conexión se encuentren cerradas.
−
Posicionamiento del flotante: se tendrá en
cuenta con qué intensidad de lluvia se quiere
realizar el ensayo y luego se posicionará la regla
graduada con la que cuenta el conjunto flotante.
−
Apertura de válvula de conexión entre tanques
alimentadores: se abre la válvula que conecta
los tanques alimentadores y se espera a que el
flotante cierre el paso de agua. Con esto, se
asegura un volumen de agua suficiente como
para abrir las válvulas de conexión entre tanque
alimentador Nº2 y batea, lo que facilitará la
purga completa del sistema. Cabe destacar que
durante este proceso se irá recargando el tanque
alimentador Nº1.
Será necesario contar con por lo menos dos
probetas graduadas en cada punto de medición. En
la planilla correspondiente se escribirán las
sucesivas hora inicial y final que tarda en llenarse
un volumen fijo seleccionado para los vasos
graduados. Acumulando los volúmenes en ambos
vasos se obtiene el escurrimiento superficial
acumulado, por diferenciación con respecto al
tiempo se obtiene la tasa de escurrimiento
superficial,
por diferencia con la intensidad
simulada, finalmente, la tasa de infiltración.
−
−
−
−
TAREAS DE CALIBRACIÓN
La calibración del simulador de lluvia tuvo los
siguientes objetivos principales (Paoli, 2009):
Apertura de válvulas entre tanque alimentador
Nº2 y batea: se comienza con la apertura de las
válvulas que conectan estas dos partes
componentes del simulador de lluvia.
Regulación de la carga: mientras la batea se va
cargando de agua se controla el piezómetro de
ésta, el cual se encuentra graduado con una
escala en centímetros. Cuando se llegue a la
carga elegida se regula el paso de agua a través
del conjunto flotante, con la regla deslizable
dispuesta para tal fin, hasta obtener que la
misma no sufra variaciones importantes.
Verificación de funcionamiento de los
formadores de gota: antes de extraer la bandeja
y dar por comenzado el ensayo se debe verificar
que todos los goteros se encuentren funcionando
correctamente, siendo los problemas típicos las
obstrucciones debido a burbujas y la formación
de gotas de pequeño tamaño.
−
Verificar que la intensidad de lluvia sea
homogénea en toda el área precipitada.
−
Estudiar el comportamiento general del equipo.
−
Determinar una curva de intensidad de lluvia
para cada altura de carga sobre los formadores
de gotas, junto a un intervalo de incerteza y su
probabilidad de ocurrencia.
−
Determinar la escala de apreciación del
instrumento.
−
Comparar las intensidades de lluvia reales
obtenidas con el simulador de lluvia, con las
estimadas para los 289 goteros que componen
el equipo.
Materiales
Para determinar la homogeneidad e intensidad
media de lluvia se utilizaron cinco probetas
graduadas de 1000 ml, con divisiones de 10 ml
cada una. En su parte superior se añadió un
embudo de 32 cm de diámetro exterior y 31 cm de
diámetro interior (Figura 9).
Extracción de bandeja intermedia: por último, si
la carga en el piezómetro se mantuvo constante
durante 10 o 15 minutos y si se han verificado y
corregido todos los formadores de gotas, ya se
puede proceder a retirar la bandeja intermedia.
Este conjunto probeta–embudo, al que de ahora en
más se denominará pluviómetro, justifica sus
características en la capacidad de captar un número
64
CUADERNOS del CURIHAM, Vol. 16, Año 2010
representativo de gotas, con un área pequeña para la
medición del volumen de agua precipitada,
reduciendo de ese modo el error de apreciación en
los volúmenes.
datos para cada carga analizada. Esto representa un
total de 350 datos obtenidos.
Procedimiento de ensayo
Los cinco pluviómetros se ubicaron dispuestos
como lo indica la Figura 10, uno en cada esquina
y el último en el centro, para lograr cubrir la
mayor parte del área precipitada. Esta posición
teórica se replanteó en laboratorio por medio de
una plomada. Los pluviómetros recibieron las
denominaciones AB, BC, CD, DA y el último de
éstos correspondiente a la posición central fue
llamado CENTRO.
Figura 10. Distribución de pluviómetros
Se midió el tiempo que tardó en llenarse un
volumen fijo de 850 ml en cada pluviómetro para
las diferentes cargas sobre formadores estudiadas.
Estas fueron 11 cm, 13 cm, 15 cm, 17.5 cm, 20 cm,
22.5 cm y 25 cm.
Es importante destacar que durante los ensayos
también se filmó la variación de la presión dentro de
la batea con formadores de gotas. Para ello, se
utilizó una cámara digital que registró la variación
de nivel en el piezómetro.
Análisis preliminar de la información
Con el volumen fijo en las probetas (V = 850 ml), el
diámetro del embudo (D = 31 cm) y el tiempo de
llenado, se calculó la intensidad de la precipitación:
i=
V
At
(1)
siendo A el área de la boca del embudo. Se analizó
la estacionariedad de la intensidad generada para
carga constante, obteniéndose gráficas como la de la
Figura 12 (en el ejemplo para h = 25 cm), graficando
la intensidad de lluvia registrada en función del
tiempo acumulado de ensayo. Se puede apreciar que
en el pluviómetro BC se obtuvieron intensidades
levemente superiores a las medidas en los restantes,
presentándose este comportamiento para todas las
cargas excepto la de 13 cm en donde las intensidades
son similares para todos los pluviómetros y la de 15
cm en donde el pluviómetro AB produjo
intensidades menores al resto.
Figura 9. Pluviómetro utilizado para la calibración.
Por otro lado, se graficaron los histogramas de
intensidades
obtenidas
para
cada
carga,
obteniéndose representaciones como la Figura 13
(nuevamente como ejemplo, para h = 25 cm). Puede
observarse un sesgo importante que impide asumir
una distribución de probabilidades normal. Este
Cada uno de los puntos fue medido simultáneamente
durante un funcionamiento continuo del simulador
de lluvia de aproximadamente 2 hs por ensayo
(Figura 11), obteniéndose de esta manera diez datos
por pluviómetro y una muestra total de cincuenta
65
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
comportamiento se repitió para todas las cargas, con
coeficientes de asimetría entre -0.68 y 0.81.
Si bien en principio podría suponerse que el
pluviómetro BC está produciendo resultados
anómalos y por tanto no debería considerarse parte
de una muestra homogénea de datos, se puede
demostrar estadísticamente que la eliminación sin
más de los datos recogidos en el pluviómetro BC no
puede corregir la dispersión producida por el ingreso
de alguna porción de formador (por más o por
menos) en el área de captación de los pluviómetros
cuando se consideran la totalidad de los datos. En
efecto, se realizó una comparación entre los datos
obtenidos para cada carga considerando el
pluviómetro BC y prescindiendo del mismo. Se
utilizó la prueba t de Student aplicada a dos muestras
independientes. De esta forma fue posible
comprobar si existen o no diferencias entre ambos
tratamientos de datos.
La hipótesis nula (H0), se formuló tomando a la
media como parámetro de comparación para ambos
casos considerados. Así, si el p-valor obtenido es
menor a 0.05 se concluye que existen diferencias
entre los datos con el pluviómetro BC y sin tener en
cuenta los valores del mismo.
Figura 11. Simulador de lluvia durante la calibración.
Intensidad por Pluviómetro vs Tiempo
Carga 25 cm
135
En primer lugar se obtuvieron los p-valor para cada
carga en particular y se encontraron diferencias
solamente en los casos correspondientes a las cargas
25 cm y 22.5 cm (Tabla 1).
Intensidad (mm/h)
130
Tabla 1. Resultados prueba t de Student.
125
120
115
AB
BC
CD
DA
CENTRO
110
carga (cm)
p-valor
105
25.0
0.0251
100
22.5
0.0376
20.0
0.0559
17.5
0.1338
15.0
0.7107
13.0
0.3375
11.0
0.1742
0
500
1000
1500
2000
2500
3000
3500
Tiempo (seg)
Figura 12. Intensidad en los pluviómetros – h = 25 cm.
Incluso, se adimensionalizaron los valores de cada
serie en función de su media, generando de ese
modo una única serie adimensional de 350 valores,
para la cual también el histograma generado
presentó una asimetría de 0.21 (Figura 14).
Luego tomando la totalidad de los datos (350) y
comparándolos con los 280 finales (después de la
eliminación de los datos de BC) se obtuvo un pvalor igual a 0.5024, con lo que se podría inferir que
ambos
tratamientos
pueden
considerarse
equivalentes ya que no es estadísticamente
discernible la diferencia.
A partir de estos resultados se pudo establecer un
intervalo de incerteza (alrededor de los valores
medios) del orden de ±9 mm/h. Surgió entonces la
necesidad de conocer qué fracción de esta incerteza
fue debida al error asociado al propio simulador y
cuál debida al procedimiento de medición utilizado.
66
CUADERNOS del CURIHAM, Vol. 16, Año 2010
del nivel en el piezómetro), las cuales provocan (a
partir de la aplicación de la relación teórica de la
Figura 2) los valores y rangos de intensidad
indicados en la Tabla 2, los que caen por debajo de
±3 mm/h. Estas oscilaciones tendrían como
principal causa el sistema de alimentación
discontinuo a través de flotante.
Histograma
Carga 25 cm
18
16
14
Frecuencia
12
10
8
6
4
131 - 134
128 - 131
125 - 128
122 - 125
119 - 122
116 - 119
113 - 116
110 - 113
0
Diferencia esperada en la medicicón
2
Intensidades (mm/h)
Figura 13. Histograma de intensidades – h = 25 cm.
19
17
15
13
11
9
7
5
5
7
9
11
13
15
17
19
Rango de datos medidos
Figura 15. Errores de posicionamiento y rangos observados.
En base a lo anterior, se asumió que el intervalo ± 3
mm/h es un rango adecuado de incerteza y por tanto
los errores que cayeron por fuera de él deben ser
asociados a los errores propios de los instrumentos y
procedimientos de calibración utilizados y no al
propio simulador. Por tanto, se procedió a eliminar
de la serie aquellos valores atípicos fuera del
intervalo de incerteza indicado, reduciendo de este
modo el conjunto de 350 a 323 datos. Se considera
que dicha reducción no es significativa y que aún se
conserva una cantidad suficiente de información
experimental que respalda el ajuste de una curva de
calibración.
Figura 14. Histograma de intensidades adimensionales.
Análisis final de la información
Pudo detectarse que un error en el
posicionamiento de los pluviómetros (Figura 10)
de ±5 mm provoca una variación en el número de
formadores de gota captados entre 23 y 25 (Paoli,
2009). A partir de las intensidades teóricas sobre
un formador (Figura 2) se obtuvieron diferencias
de intensidad entre 7 mm/h (para h = 11 cm) y 13
mm/h (para h = 25 cm) de considerar 23 a 25
formadores. Si se analizan los rangos de
intensidades medidas para las mismas cargas, de
8.3 mm/h y 19.2 mm/h respectivamente, puede
detectarse la correlación representada en la Figura
15. En éstas puede observarse que el punto
correspondiente a una carga h = 25 cm es un valor
anómalo en la serie ya que cae fuera del intervalo
de incerteza asumido en ±3 mm/h (graficado con
líneas de trazos en la Figura 15).
Tabla 2. Variación en intensidad (mm/h) debida a oscilaciones
de carga.
Variación de carga
h (mm)
- 5 mm
+ 5 mm
Este intervalo de incertidumbre puede justificarse
además, considerando una variación hipotética de
la carga en la batea de ±5 mm (compatible con las
observaciones realizadas a través de filmaciones
11.0
-2.54
2.53
13.0
-2.50
2.49
15.0
-2.46
2.45
17.5
-2.40
2.39
20.0
-2.35
2.34
22.5
-2.30
2.29
25.0
-2.25
2.24
Realizada esta eliminación de datos atípicos, se
volvió a representar un histograma de intensidades
67
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
estandarizadas (equivalente al de la Figura 14)
obteniéndose la Figura 16.
122
Intensidad (mm/h)
120
Puede apreciarse que la distribución de
probabilidades se acerca mucho más a la
distribución normal (coeficiente de asimetría 0.13). Incluso, si se vuelve a representar la
información de la Figura 15, se observa que ahora
todos los valores caen dentro del intervalo de
incerteza establecido (Figura 17).
118
AB
BC
CD
DA
CENTRO
3 mm/h
-3 mm/h
116
114
112
110
0
500
2000 2500 3000
3500
Tiempo (seg)
Como ejemplo, se muestra la intensidad registrada
en los pluviómetros en función el tiempo, para la
carga h = 25 cm, generada a partir de la serie
reducida (Figura 18). En esta gráfica, equivalente a
la Figura 12, ya no se observa un comportamiento
diferenciado de algún pluviómetro en particular
(todos los valores están dentro del intervalo de
incerteza de ±3 mm/h alrededor de la media), lo cual
indica que la reducción de la serie habría eliminado
los errores sistemáticos introducidos por el
procedimiento de medición implementado.
Figura 18. Intensidad en los pluviómetros – h = 25 cm – serie
reducida.
RESULTADOS
Finalmente, con la intensidad media para cada
carga estudiada y su error asociado se puede
obtener una línea de tendencias sobre estos puntos
que determinará la curva de calibración del
simulador de lluvia.
En la Figura 19 se puede observar la curva
intensidad de lluvia – altura de carga, que responde a
una regresión potencial (línea continua). Como
envolventes de la curva media, se observan dos
curvas límites de intervalos de confianza del 99.07
% y el 90.71 % de probabilidad, lo cual surge de
aplicar una distribución normal estándar a partir de
la serie reducida (para la cual se asumió válida la
hipótesis de normalidad). Estos valores se traducen
en ±3 mm/h y 2.11 mm/h, respectivamente. La
función empírica así obtenida fue:
Figura 16. Histograma de intensidades adimensionales – serie
reducida.
i = 15,15h 0,63
Diferencia esperada en la medicicón
1000 1500
(2)
19
en donde i es la intensidad en mm/h y h es la carga
sobre el formador en cm. Siendo posible medir
fácilmente esta carga en el piezómetro instalado
sobre la batea, la ecuación (2) en conjunto con la
Figura 19 representan una herramienta muy valiosa
para la estimación in situ de la intensidad de lluvia
producida por el simulador sin necesidad de realizar
mediciones directas de la misma.
17
15
13
11
9
Si se comparan las intensidades obtenidas sobre el
equipo completo en funcionamiento, con aquéllas
esperadas a partir del estudio de laboratorio de los
formadores de gotas, se aprecia una leve
disminución de las intensidades producidas, que
aproximadamente mantienen una relación lineal, con
7
5
5
7
9
11
13
15
17
19
Rango de datos corregidos
Figura 17. Errores de posicionamiento y rangos observados –
serie reducida.
68
CUADERNOS del CURIHAM, Vol. 16, Año 2010
un factor de proporcionalidad de 0.86, según se
aprecia en la Figura 20.
prefiriéndose determinar a posteriori la relación
empírica hallada (ecuación 2).
130
APLICACIÓN
120
El equipo fue utilizado en dos ensayos in situ, de
carácter preliminar, realizados en la zona de Ciudad
Universitaria, Córdoba. En estos ensayos se fijó
como objetivo la medición (indirecta) de la
capacidad de infiltración del suelo, a través de la
cuantificación del escurrimiento superficial. El
registro de los volúmenes erogados fue manual, a
través de dos operadores.
i (mm/h)
110
100
90
80
70
60
10
12
14
16
18
20
22
24
26
Los ensayos se relizaron bajo dos intensidades
extremas: 69 mm/h y 117 mm/h. La curva de
escurrimiento
superficial
se
obtuvo
por
superposición de las obtenidas en cada punto de
descarga. A partir de éstas y por diferencia con las
intensidades generadas, se obtiene la curva de
infiltración y finalmente, por diferenciación de esta
última, la tasa de infiltración en función del tiempo.
Las curvas obtenidas corresponden a la Figura 21 (i
= 69 mm/h) y Figura 22 (i = 117 mm/h).
h (cm)
Figura 19. Relación carga – intensidad obtenida.
145
i exp. (mm/h)
135
125
115
105
95
85
A partir de esta información, se ajustaron los
parámetros del modelo de infiltración de Horton:
75
65
65
75
85
95
105
115
125
135
145
f (t ) = f b + ( f 0 − f b )e − kt
i teórica (mm/h)
Figura 20. Intensidades reales versus teóricas.
(3)
en la cual f(t) es la tasa de infiltración variable en el
tiempo, fb es la tasa de infiltración base, f0 la tasa de
infiltración inicial (estas tres medidas en mm/h) y k
es un factor de forma (en h-1).
El rango de incertidumbre así obtenido (±3 mm/h) y
el efecto de grupo anteriormente descripto podrían
explicarse en base a una combinación de las
siguientes causas:
100
tasa de infiltración ( mm/h)
- son inevitables las obstrucciones parciales o totales
de las agujas que conforman los formadores, debido
principalmente a la aparición de burbujas que
quedan alojadas en el interior de las agujas.
- la carga h actuante no se mantiene perfectamente
constante, debido a que la alimentación del tanque
inferior se produce por pulsos (sistema de flotantes),
dando origen a una variación periódica de la carga.
Incluso, es posible interpretar el error sistemático por
defecto debido a que el flotante establece una cota
superior para la carga. Si bien hubiera sido posible
desarrollar un sistema de alimentación continua y
desborde que hubiera permitido ajustar la carga
generada, la complicación operativa que esto hubiera
implicado en campaña hizo desistir de esa idea,
80
60
40
20
0
0
0,25
0,5
0,75
1
1,25
1,5
1,75
2
Tiempo (h)
Figura 21. Tasa de infiltración – intensidad 69 mm/h.
En la Tabla 3 se muestran los valores calibrados de
los parámetros del modelo de Horton (ecuación 3)
69
Desempeño de un Microsimulador de Lluvia Portátil para Estudios Hidrológicos
ajustados por un procedimiento de optimización no
lineal. En las Figuras 21 y 22 pueden verse
superpuestas a los puntos experimentales las curvas
del modelo de Horton (ecuación 3) para los
parámetros calibrados de la Tabla 3. Estos valores
coinciden, en líneas generales, con los obtenidos
previamente en la zona con el infiltrómetro de doble
anillo (Weber et al., 2005).
series observadas, y en base a un criterio heurístico
que ha mostrado su verosimilitud, corregir los
valores afectados por errores sistemáticos en las
mediciones realizadas.
- La normalidad de la distribución de valores así
obtenidos mostraría en principio la ausencia de
errores sistemáticos propios en el simulador de lluvia.
- Como valor agregado, ha sido posible estimar un
intervalo de confianza de ±3 mm/h con una
probabilidad asociada del 99%, lo cual permite acotar
la incidencia de la incertidumbre en la lluvia simulada
sobre los resultados experimentales a obtener.
tasa deinfiltración ( mm/h)
250
200
150
- Las pruebas preliminares realizadas en campaña
han permitido por un lado, ajustar la metodología de
montaje y desmontaje del equipo y por otro,
generaron información experimental a la cual fue
ajustada el modelo de Horton, obteniéndose valores
razonables para sus parámetros.
100
50
0
0
0,25
0,5
0,75
1
1,25
1,5
1,75
Tiempo (h)
Figura 22. Tasa de infiltración – intensidad 117 mm/h.
- Futuras mejoras del equipo actualmente en marcha
(adquisición electrónica de mediciones, aleatoriedad
en la posición de impacto de las gotas, ampliación
del rango de intensidades a generar) contribuirán a
aumentar la calidad de las observaciones a realizar.
Tabla 3. Parámetros ajustados del modelo de Horton.
parámetro
i = 69 mm/h
i = 117 mm/h
f0 (mm/h)
90.8
225.5
fb (mm/h)
33.3
40.1
k (1/h)
6.5
47.3
AGRADECIMIENTOS
Los autores del presente trabajo quieren manifestar
su agradecimiento a la Secretaría de Ciencia y
Tecnología, Universidad Tecnológica Nacional por
el financiamiento recibido a través del proyecto de
I+D consolidado 25E117.
CONCLUSIONES
Se han presentado los resultados de las tareas de
calibración realizadas sobre el simulador de lluvia
portátil diseñado y construido en el Laboratorio de
Hidráulica,
Facultad
Regional
Córdoba,
Universidad Tecnológica Nacional. Se destacan las
siguientes conclusiones:
REFERENCIAS BIBLIOGRÁFICAS
Achutegui A., Abreu X., Páez M.L. 1996. Diseño y
Evaluación de un Simulador de Lluvias Tipo Gotero con Efecto Vibratorio. Venesuelos , 4:24-28.
Aoki A.M. y Sereno R. 1999. Modificaciones de un
Microsimulador de Lluvia. Investigación Agrícola, vol 19 Nº 1 y 2, 47-51.
Benito E.; de Blas, E.; Santiago, J.L. y Varela, M.E
2001. Descripción y Puesta a Punto de un Simulador de Lluvia de Campo para Estudios de Escorrentía Superficial y Erosión del Suelo. Cuadernos
Laboratorio Xeolóxico de Laxe nº 26.
Irurtia C.B., Mon R. 1994. Microsimulador de Lluvia para Determinar Infiltración a Campo. Publicación Nº 176. Instituto de Suelos, Castelar, Bue-
- Ha sido posible a través de un procedimiento
relativamente sencillo y de bajo costo la
determinación de una relación funcional entre la
carga hidráulica sobre los formadores y la intensidad
de lluvia producida.
- La relación así determinada tiene gran valor
práctico en la actividad del experimentalista, ya que
le permite definir en campo la intensidad requerida a
la lluvia simulada.
- En base a un análisis estadístico ha sido posible
detectar los valores anómalos (outliers) de las
70
CUADERNOS del CURIHAM, Vol. 16, Año 2010
Rostagno, C.M., Garayzar, D. 1995. Diseño de un
Simulador de Lluvia para Estudios de Infiltración y Erosión de Suelos. Ciencia del Suelo, 13,
41 - 43.
Weber J., Urbano J., Stuyck E., Azelart D., Martinez
N. 2005. Caracterización de los Parámetros del
Modelo de Infiltración de Horton en Suelos de la
Ciudad de Córdoba. Cuadernos del Curiham, vol
11 Nº 1, 29-38.
Weber, J. F., Paoli, H., Apestegui, L. 2009. Diseño,
construcción y puesta a punto de un microsimulador de lluvia portátil para estudios hidrológicos.
XXII Congreso Nacional del Agua - CONAGUA
2009 – Trelew.
nos Aires, República Argentina. Pp. 18.
Kamphorst, A. 1987. A Small Rainfall Simulator for
the Determination of Soil Erodibility. Netherlands
Journal of Agricultural Science, 35, 407 - 415.
Marelli H. J. 1989. La Erosión Hídrica. Proyecto:
Alternativas Mejoradas Conservacionistas de
Producción Agrícola Ganadera en el Sur de
Córdoba. Publicación técnica Nº1. INTA, Estación Experimental Agropecuaria Marco Juarez,
Córdoba, Argentina.
Paoli, H. I., Rojas, J. A. 2006. Estudio Hidráulico,
Teórico y Experimental, sobre Formadores de Gotas. JEI 2006, Mendoza.
Paoli, H. I. 2009. Diseño, construcción y puesta a
punto de un simulador de lluvia portátil para la determinación in situ de parámetros hidrológicos.
Trabajo final de Ingeniería Civil – U.T.N. – F.R.C.
Pla Sentis, I. 1981. Simuladores de Lluvia Para el
Estudio de Relaciones Suelo Agua Bajo Agricultura de Secano en los Trópicos. Rev. Fac. Agron.
12 (1-2): 81-93. Maracay, Venezuela.
Articulo recibido el 03/2010 y aprobado para su
publicación el 06/2010.
71
CUADERNOS del CURIHAM, Vol. 16, Año 2010
tablas, fotos, mapas, etc deberán estar en Times New
Roman 8 PT, en negrita y centrado.
Los gráficos deben estar pegados en el texto como
imagen de metarchivo mejorado.
Las tablas deben estar con bordes delimitados con
línea continua.
INSTRUCCIONES PARA AUTORES
1.
2.
3.
4.
5.
6.
7.
8.
9.
Los artículos serán sometidos a arbitraje por un Consejo
Revisor. Los artículos publicados no serán devueltos y
aquellos no publicados estarán a disposición del autor.
El artículo deberá ser escrito preferentemente en su forma
definitiva en español, portugués o inglés.
Primera Página: Resumen no mayor a 200 palabras, en su
forma definitiva y en ingles. Palabras claves en ambos
idiomas
Máximo 54 líneas por Columna.
Ultima Página: Bibliografía citada, ordenada alfabéticamente,
ver instrucciones abajo.
No utilizar pie de página, las referencias pueden ser colocadas
al final del artículo, antes de la bibliografía.
Microsoft Word del paquete de Office 97, a espacio simple, y
doble cuando intervengan fórmulas.
Cada artículo no deberá exceder de 25 páginas, incluyendo
fotos, figuras, mapas, tablas, gráficos, etc.
Los originales deben enviarse de acuerdo a las siguientes
instrucciones de presentación:
a.
-
-
Formato de página
Tamaño del papel: A4 (210 mm x 297 mm).
Márgenes: Superior: 4 cm; Inferior: 3.7 cm ; Izquierdo:
3 cm; Derecho: 2.5 cm; Encabezado 3 cm; Pie de
Página: 2.3 cm.
2 Columnas de ancho: 7,5 cm con espacio de 0,5 cm.
b.
-
Formato del texto
Fuente: Times New Roman
Estilo: Normal
Tamaño: 10 PT.
c.
-
Estructura del texto
Como norma general, el artículo estará encabezado por
su título, representativo del contenido en Mayúsculas y
negrita con alineación centrada.
Los párrafos del texto deberán contar con alineación
justificada y comenzarán sin tabulado o sangrado.
los títulos del texto se ajustarán al siguiente formato:
-
Titulo primario, deberá escribirse en mayúsculas y
negrita dejando dos líneas en blanco por arriba y una
por debajo.
Título Secundario, deberá escribirse en minúsculas y
negrita dejando una línea en blanco por arriba y una
por debajo.
Título Terciario y sucesivos, deberán escribirse en
minúsculas y negrita dejando una línea en blanco por
arriba y ninguna por debajo.
e.
Formato de las ecuaciones:
-
Las ecuaciones deben numerarse consecutivamente tal
como sean citadas en el texto, con números arábigos y
deben ser referenciadas mediante su número solamente,
ej. (3). Deben dejarse espacios arriba y debajo de cada
ecuación.
f.
Referencias bibliográficas:
-
Las referencias deben incluirse en el siguiente orden:
apellido de autor, iniciales, fecha, titulo del artículo con
primera letra en mayúscula, nombre de la publicación o
journal en itálica, volumen (Numero), rango de
páginas. Si es un libro, editorial y lugar de publicación.
Se dan ejemplos a continuación.
-
Artículo de Journal:
Otto R. 2001. Estimating groundwater recharge rates in
southeastern Holstein region, northern Germany.
Hydrogeology Journal, 9(5), 498-511.
-
Capítulo de libro:
Berner R. 1981. Kinetics of weathering and diagenesis.
In: Lasaga A and Kirkpatrick R. (eds.) Kinetics of
Geochemical Processes, Reviews in Mineralogy, Vol.
8, BookCrafters, Inc., Chelsea, Michigan, 111-134.
-
Libro:
Draper NR, and Smith H. 1981. Applied Regression
Analysis, 2nd. edn. John Wiley & Sons, New York.
-
Artículos de Congresos o Simposios:
Atwood DF, and Barker C. 1989. The effect of Perth´s
perturbation on groundwater quality: A comparison
with case histories in the USA. In: Proc. Swan Coastal
Plain Groundwater Management Conference, 177-190.
-
Las referencias deben ser listadas en orden alfabético
por nombre de autor y con crecientes fechas de
publicación, con la adición de una “a” o “b” a la fecha
cuando sea necesario. En el texto, la referencia se hará
con el apellido del autor seguido por la fecha de
publicación, ej. Smith y Rodriguez (1928a)…
Cuando en la referencia participen más de dos autores
debería citarse en el texto como: Jones et al. (1994).
d.
-
-
-
Formato de Gráficos , Tablas, Fotos, Mapas, etc
Los gráficos, tablas, fotos y mapas deberán adaptarse al
espacio disponible respetando 1 ó 2 columnas en su
ancho. Deben estar en blanco y negro o Escala de
Grises con contrastes bien definidos. Enumerar las
figuras en el orden en cual se hacen referencias en el
texto, ej. Figura 1, Figura 2, etc.
Las tablas, al igual que los gráficos deben estar sujetas
y respetando tamaños a 1 ó 2 columnas en su ancho.
Tipografía de las tablas Times New Roman 9 PT.
Deben estar en blanco y negro o Escala de Grises con
contrastes bien definidos.
Los enunciados, nombres y numeración de los gráficos,
10.
Impresión de la totalidad del artículo (1 copia A4).
11.
Los autores deben remitir un (1) original de sus
contribuciones, además de una copia del archivo de texto en
diskette de 3,5" (Microsoft Word del paquete de Office 97).
12.
Ante cualquier consulta comuníquese a
[email protected]
CUADERNOS del CURIHAM, Vol. 16, Año 2010
13.
Los trabajos y toda correspondencia mediante correo postal
y/o electrónico deberán ser remitidos a:
Editor Responsable Cuadernos del CURIHAM
Dr. Ing. Pedro Abel Basile
CURIHAM (Centro Universitario Rosario de
Investigaciones Hidroambientales.)
Facultad de Cs. Exactas, Ingenieria y Agrimensura.
Universidad Nacional de Rosario
Riobamba 245 bis
2000 ROSARIO (SF) . ARGENTINA
[email protected]
Telefax: 54 (0341) 480 8541
Suscripción:
La suscripción a la revista será anual. El monto de la misma, sin
incluir envíos, es de treinta pesos ($ 30,00) y de cincuenta pesos
($ 50,00) con envío incluido dentro de Argentina. Para el exterior el
monto es de treinta dólares (US$ 30,00) sin incluir envíos y de
cincuenta dólares (US$ 50,00) para envíos fuera del país. La
suscripción podrá realizarse personalmente en:
-
la sede de la Fundación Facultad de Ingeniería Rosario, sito en
Avda. Pellegrini 250, 1er. piso, 2000 Rosario; Argentina, Te.
54 341 4486782; Fax 54 341 4802654, o
-
en la Sede del CURIHAM , Riobamba 245 bis, 2000 Rosario,
Argentina, TeleFax 54 341 4808541.
La suscripción a distancia podrá llevarse a cabo mediante
transferencia bancaria a: Cuenta Corriente nº: 333800000040391.
Banco Macro S.A. Sucursal 338 - Barrio Martin. Av. de la
Libertad 169. (2000). Rosario. Santa Fe.
CBU: 2850338530000000403916
Se ruega para cualquiera de las modalidades de suscripción
completar la correspondiente ficha. La misma deberá ser enviada
por duplicado a: Sede de la Fundación Facultad de Ingeniería
Rosario y a Sede del CURIHAM mediante envío postal o envío
electrónico.
FICHA DE SUSCRIPCION CUADERNO DEL CURIHAM AÑO 2011
Apellido y Nombres:
Ocupación, título o cargo:
Instituto, Empresa u Organismo:
Dirección:
Teléfono:
Fax:
E_mail:
FICHA DE SUSCRIPCION CUADERNO DEL CURIHAM AÑO 2011
Apellido y Nombres:
Ocupación, título o cargo:
Instituto, Empresa u Organismo:
Dirección:
Teléfono:
Fax:
E_mail:
FICHA DE SUSCRIPCION CUADERNO DEL CURIHAM AÑO 2011
Apellido y Nombres:
Ocupación, título o cargo:
Instituto, Empresa u Organismo:
Dirección:
Teléfono:
E_mail:
Fax:
CUADERNOS DEL CURIHAM
REVISTA DE ESTUDIOS SOBRE LA CUESTION HIDROAMBIENTAL
Volumen 16 – Año 2010
Páginas tipiadas provistas por autores
UNR EDITORA
EDITORIAL DE LA UNIVERSIDAD NACIONAL DE ROSARIO
Secretaría de Extensión Universitaria
Urquiza 2050 – S2000AOB – Rosario – Santa Fe – República Argentina
www.unreditora.unr.edu.ar / [email protected]
Edición de 200 ejemplares
JULIO 2011