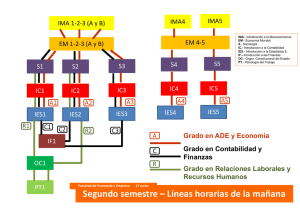
Metodología de integración orientada (1)

c Luis Ismael Minchala Avila, 2011
Metodologı́a de integración orientada a las técnicas
de visión estereoscópica e iluminación estructurada
para obtener atributos 3D en la inspección de
objetos
por
Ing. Luis Ismael Minchala Avila
Tesis
Presentada al Programa de Graduados de la
División de Mecatrónica y Tecnologı́as de la Información
como requisito parcial para obtener el grado académico de
Maestro en Ciencias
especialidad en
Automatización
Instituto Tecnológico y de Estudios Superiores de Monterrey
Campus Monterrey
Mayo de 2011
Instituto Tecnológico y de Estudios Superiores de
Monterrey
Campus Monterrey
División de Mecatrónica y Tecnologı́as de la Información
Programa de Graduados
Los miembros del comité de tesis recomendamos que la presente tesis de Luis Ismael
Minchala Avila sea aceptada como requisito parcial para obtener el grado académico
de Maestro en Ciencias, especialidad en:
Automatización
Comité de tesis:
Dr. Luis Eduardo Garza Castañón
Asesor de la tesis
MSc. Luis Rosas Cobos
Dr. Francisco Palomera Palacios
Sinodal
Sinodal
Dr. Gerardo Castañón Avila
Director del Programa de Graduados
Mayo de 2011
El buen ejemplo, la honestidad y la perseverancia son un legado que se los debo a mis
formadores, quienes con amor y comprensión han sabido enrumbarnos a nosotros, sus
hijos, por el camino del bien. Gracias Papi y Mami por ser mi infinita fuente de
inspiración, a ustedes va dedicado éste trabajo con el que culmino una importante
etapa de formación profesional.
Reconocimientos
La consecución no solo de éste trabajo, sino de una productiva estancia en México se las debo a muchas personas valiosas que tuve la oportunidad de conocer en el
ITESM. Quiero agradecer de manera especial al Dr. Luis Eduardo Garza Castañón por
su intenso apoyo en la fase de investigación, adicionalmente me es grato reconocer el
importante aporte de los miembros del comité de tesis: Dr. Francisco Palomera Palacios
y MSc. Luis Rosas Cobos.
A los grandes amigos que he conocido en México les debo un agradecimiento
especial, ya que permitieron que el perı́odo de estudios de maestrı́a además de ser
enriquecedor en conocimiento, sea un espacio de crecimiento personal; y sobre todo
gracias a esa increı́ble persona que me supo apoyar a pesar de la distancia que nos
separa, Alejandra.
Luis Ismael Minchala Avila
Instituto Tecnológico y de Estudios Superiores de Monterrey
Mayo 2011
v
Metodologı́a de integración orientada a las técnicas
de visión estereoscópica e iluminación estructurada
para obtener atributos 3D en la inspección de
objetos
Luis Ismael Minchala Avila, M.C.
Instituto Tecnológico y de Estudios Superiores de Monterrey, 2011
Asesor de la tesis: Dr. Luis Eduardo Garza Castañón
Resumen
El control de calidad al final de las lı́neas de manufactura es un punto neurálgico en el
proceso de fabricación de un producto, más aún si se considera que mayoritariamente se
realiza de manera manual. Disminuir los errores de estimación en mediciones de distancias y formas, además de aumentar el número de piezas inspeccionadas por unidad de
tiempo en una lı́nea de producción es el objetivo de muchos trabajos de investigación,
por lo que en el desarrollo de esta tesis se propone una metodologı́a que permita implementar un sistema de inspección tridimensional en una lı́nea de manufactura.
En esta tesis se plantea la captura de información relacionada con la geometrı́a
de los objetos y a través de sus caracterı́sticas tridimensionales emitir un reporte con
información de distancias y formas dentro de rangos establecidos de tolerancia propios
del sistema de visión, que permitan decidir si éstos continúan el proceso de fabricación
o deben ser redireccionados para su reparación o desecho. Las soluciones actuales a esta
problematica se enfocan principalmente en inspeccionar los objetos en 2D, mientras que
las soluciones de tres dimensiones son extremadamente costosas y se basan en técnicas
de visión estereoscópica o iluminación estructurada por separado, teniendo como base
la triangulación para generar información del espacio tridimensional. En este trabajo
de investigación las dos técnicas anteriores se fusionan para establecer un enfoque de
sensor 3D, que analiza en detalle las caracterı́sticas tridimensionales de los productos
y las partes que lo componen. Los resultados se cuantifican a través de las diferentes
respuestas que nos brinda un prototipo construido para desarrollar esta metodologı́a,
compuesto por dos cámaras para visión estereoscópica y un haz de luz estructurado.
La integración de las técnicas de visión estereoscópica e iluminación estructurada,
que es el principal aporte de éste trabajo de investigación, considera la simplificación
del problema de correspondencia de puntos que presentan el par de imágenes estéreo, a
través del análisis del patrón de luz estructurado que se encuentra proyectado sobre el
objeto bajo análisis, lo que permite reducir la complejidad de los algoritmos y mejorar
los tiempos de procesamiento en el software.
vii
Índice general
Reconocimientos
V
Resumen
VI
Índice de tablas
XI
Índice de figuras
XII
Lista de sı́mbolos
XIV
Capı́tulo 1. Introducción
1.1. Introducción . . . . . . . . . . . . . .
1.2. Definición del Problema y Motivación
1.3. Meta . . . . . . . . . . . . . . . . . .
1.4. Objetivos . . . . . . . . . . . . . . .
1.5. Hipótesis . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Capı́tulo 2. Fundamentos de visión estereoscópica e iluminación estructurada para el cálculo de posición de objetos en el espacio
2.1. Aspectos generales de una configuración estereoscópica . . . . . . . . .
2.2. Herramientas matemáticas para localización espacial . . . . . . . . . .
2.2.1. Representación de la posición . . . . . . . . . . . . . . . . . . .
2.2.2. Representación de la orientación . . . . . . . . . . . . . . . . . .
2.2.3. Coordenadas y matrices homogéneas . . . . . . . . . . . . . . .
2.3. Modelo de la cámara . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3.1. Matriz de transformación para perspectiva . . . . . . . . . . . .
2.3.2. Proyección ortogonal y de perspectiva débil . . . . . . . . . . .
2.3.3. Estimación de puntos 3D utilizando sistemas de visión artificial
2.4. Estimación de la matriz de calibración con un enfoque práctico . . . . .
2.4.1. Ejemplo de calibración de dos cámaras y cálculo de posición 3D
2.5. Iluminación estructurada . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1. Triangulación Activa . . . . . . . . . . . . . . . . . . . . . . . .
viii
1
1
3
4
5
6
7
7
10
10
11
15
16
17
20
21
22
24
25
26
2.5.2. Iluminación estructurada . . . . . . . . . . . . . . . . . . . . . .
2.6. Trabajos relacionados . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.7. Aporte al conocimiento . . . . . . . . . . . . . . . . . . . . . . . . . . .
Capı́tulo 3. Construcción y calibración de un prototipo para pruebas
experimentales
3.1. Diseño y construcción del prototipo . . . . . . . . . . . . . . . . . . . .
3.1.1. Cámaras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1.2. Proyector luz estructurada . . . . . . . . . . . . . . . . . . . . .
3.1.3. Circuito de control y comunicación con la PC . . . . . . . . . .
3.2. Ventajas de la configuración estereoscópica con iluminación estructurada
3.3. Calibración del sistema de visión . . . . . . . . . . . . . . . . . . . . .
3.3.1. Adquisición de las imágenes . . . . . . . . . . . . . . . . . . . .
3.3.2. Pre-procesamiento de las imágenes . . . . . . . . . . . . . . . .
3.3.3. Barrido del ángulo del láser . . . . . . . . . . . . . . . . . . . .
3.3.4. Correspondencia de puntos . . . . . . . . . . . . . . . . . . . . .
3.3.5. Cálculo de las matrices de calibración . . . . . . . . . . . . . . .
3.4. Validación de la calibración del sistema . . . . . . . . . . . . . . . . . .
Capı́tulo 4. Desarrollo de una metodologı́a para inspección de objetos
con visión estereoscópica e iluminación estructurada
4.1. Evaluación del desempeño del prototipo . . . . . . . . . . . . . . . . .
4.1.1. Precisión del sistema . . . . . . . . . . . . . . . . . . . . . . . .
4.1.2. Pruebas de precisión sobre un objeto de manufactura . . . . . .
4.1.3. Operación bajo diferentes condiciones de iluminación . . . . . .
4.2. Metodologı́a utilizada en el desarrollo del proyecto . . . . . . . . . . . .
4.3. Metodologı́a para la integración de visión estéreo e iluminación estructurada para la inspección de objetos y adquirir atributos 3D . . . . . .
4.3.1. Selección de los componentes del sistema . . . . . . . . . . . . .
4.3.2. Configuración del ambiente de trabajo . . . . . . . . . . . . . .
4.3.3. Desarrollo y pruebas de algoritmos de Pre-procesamiento de imágenes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.4. Validación de la calibración del sistema . . . . . . . . . . . . . .
4.3.5. Decodificación de información tridimensional . . . . . . . . . . .
28
30
32
34
34
36
38
39
40
43
43
44
46
47
49
52
58
58
58
63
65
66
68
70
71
72
74
74
Capı́tulo 5. Conclusiones y trabajos futuros
5.1. Conclusiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2. Trabajos futuros . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
76
76
78
Apéndice A. Algoritmo de calibración en Matlab
79
ix
Apéndice B. Programación Basic del microcontrolador
82
Bibliografı́a
85
x
Índice de tablas
2.1. Datos de dos cámaras distintas y de puntos en el espacio. . . . . . . . .
2.2. Resultados obtenidos con el software implementado en Mathscript de
LabVIEW y/o Matlab. . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.1. Heurı́sticas para la localización de los puntos de inflexión. . . . . . . . .
3.2. Puntos de calibración en el espacio y coordenadas en el par de imágenes
estéreo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Resultados de la validación de la calibración del sistema. . . . . . . . .
4.1. Resultados de la medición de distancias sobre el rectángulo de prueba. .
4.2. Resultados de la medición de distancias sobre la pieza de la figura 4.2. .
4.3. Resultados de la medición de distancias sobre la pieza manufactura de
la figura 4.4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xi
25
26
50
55
56
60
62
65
Índice de figuras
2.1.
2.2.
2.3.
2.4.
Configuración de un par de cámaras en el espacio. . . . . . . . . . . . .
Configuración estereo con una cámara y un proyector de luz. . . . . . .
Representación de un vector en un sistema coordenado cartesiano derecho.
Representación de un vector en un sistema de coordenadas polares y
cilı́ndricas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5. Representación de un vector en un sistema de coordenadas esféricas. . .
2.6. Orientación de un sistema móvil OU V con relación a uno fijo OXY . . .
2.7. Rotación del sistema OU V W con respecto a los ejes OX, OY y OZ. .
2.8. Transformación de perspectiva. . . . . . . . . . . . . . . . . . . . . . .
2.9. Transformación de perspectiva. El sensor de la cámara está en el centro
de la proyección. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.10. Comparación de proyecciones: perspectiva y ortogonal. . . . . . . . . .
2.11. Arquitectura de un sistema de triangulación activa básico. . . . . . . .
2.12. Patrón de franjas codificado y proyectado sobre un objeto cilı́ndrico. . .
2.13. Proyección de un patrón tipo rejilla sobre objetos 3D [15] . . . . . . . .
2.14. Concepto de Iluminación Estructurada. . . . . . . . . . . . . . . . . . .
2.15. Sistema propuesto en [6] . . . . . . . . . . . . . . . . . . . . . . . . . .
2.16. Sistema propuesto en [21] . . . . . . . . . . . . . . . . . . . . . . . . .
2.17. Arquitectura del sistema propuesto en [11] . . . . . . . . . . . . . . . .
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
Disposición de las cámaras y el patrón de iluminación en el prototipo. .
Arquitectura del sistema de visión 3D prototipo. . . . . . . . . . . . . .
Sistema prototipo implementado. . . . . . . . . . . . . . . . . . . . . .
Comparación USB - IEEE 1394. . . . . . . . . . . . . . . . . . . . . . .
Proyector de luz estructurada. . . . . . . . . . . . . . . . . . . . . . . .
Circuito de control y comunicación. . . . . . . . . . . . . . . . . . . . .
PCB del circuito de control y comunicación. . . . . . . . . . . . . . . .
Problema de correspondencia analizado con correlación cruzada. . . . .
Simplificación del problema de correspondencia a través de la redundancia del sistema de visión. . . . . . . . . . . . . . . . . . . . . . . . . . .
3.10. Diagrama de flujo del algoritmo de calibración. . . . . . . . . . . . . . .
xii
8
9
10
11
12
13
14
17
18
20
27
27
28
29
30
31
32
35
36
37
39
40
41
42
43
44
45
3.11. Adquisición de imágenes en LabVIEW. . . . . . . . . . . . . . . . . . .
3.12. Preprocesamiento de las imágenes. . . . . . . . . . . . . . . . . . . . .
3.13. Esqueletización de la imagen preprocesada. . . . . . . . . . . . . . . . .
3.14. Conectividad entre pı́xeles. . . . . . . . . . . . . . . . . . . . . . . . . .
3.15. Formaciones de las submatrices 5 × 5 y 3 × 3 para el criterio de las
heurı́sticas. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.16. Diseño del patrón de calibración. . . . . . . . . . . . . . . . . . . . . .
3.17. Puntos de calibración en la pieza. . . . . . . . . . . . . . . . . . . . . .
3.18. HMI implementado en LabVIEW para el proceso de calibración. . . . .
3.19. Dispersión del error en las mediciones de distancia realizadas sobre el
objeto patrón. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.
4.2.
4.3.
4.4.
4.5.
Objeto de prueba para mediciones longitudinales. . . . . . . . . . . . .
Medición del ancho de una pieza tridimensional. . . . . . . . . . . . . .
Reconstrucción del patrón de calibración en 3D. . . . . . . . . . . . . .
Objeto de manufactura utilizado para comprobar la precisión del sistema.
Preprocesamiento fallido de la imagen. Sistema funcionando en un ambiente con demasiada luz. . . . . . . . . . . . . . . . . . . . . . . . . .
4.6. Preprocesamiento exitoso sobre una de las imágenes capturadas del par
estéreo. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7. Pasos seguidos a lo largo del camino de investigación. . . . . . . . . . .
4.8. Metodologı́a para la integración de las técnicas de visión estereoscópica
e iluminación estructurada para inpección de objetos en 3D. . . . . . .
4.9. Selección del lente de la resolución y el lente de la cámara. . . . . . . .
4.10. Niveles de procesamiento en aplicaciones que involucran imágenes digitales.
4.11. Decodificación de puntos de inflexión. . . . . . . . . . . . . . . . . . . .
xiii
46
46
48
49
51
52
53
54
57
59
61
63
64
66
66
67
69
70
73
75
Lista de sı́mbolos
Sı́mbolo
W
P
W
P 1O
r
θ
φ
T
I
P
I
CW
F
C Π(f )
c0 , . . . , c 4
r0 , . . . , r4
∼ ∼
c∼
0 , c1 , c2
r0∼ , r1∼ , r2∼
Abreviaturas
FOV
fl
IEEE 1394
IIDC
Punto en el espacio con coordenadas (W Px ,W Py ,W Pz )
Rayo de proyección entre W P y el centro coordenado de la cámara 1
Distancia medida en un sistema coordenado cartesiano desde el origen
hasta la punta del vector con coordenadas (W Px ,W Py ,W Pz )
Ángulo formado por el eje de las abscisas en un sistema coordenado
cartesiano y la proyección de un vector v, en el plano xy
Ángulo formado por el eje z y un vector v en el espacio
Matriz de transformación homogénea
Punto del espacio proyectado en la cámara, con coordenadas (r, c)
Matriz de transformación de coordenadas espaciales a coordenadas de la
imagen (r, c), luego de la adquisición
Matriz de transformación para perspectiva
Columnas de una submatriz de 5 × 5 de la imagen original para aplicar
las heurı́sticas que permiten encontrar los puntos de inflexión
Renglones de una submatriz de 5 × 5 de la imagen original para aplicar
las heurı́sticas que permiten encontrar los puntos de inflexión
Columnas de una submatriz de 5 × 5 de la imagen original para aplicar
las heurı́sticas que permiten encontrar los puntos de inflexión
Renglones de una submatriz de 3 × 3 de la imagen original para aplicar
las heurı́sticas que permiten encontrar los puntos de inflexión
Field of View, ó campo de visión.
Focal length
Bus de comunicación estándar para cámaras digitales
Industrial and Instrumentation specification for Digital Cameras
xiv
Capı́tulo 1
Introducción
1.1.
Introducción
La geometrı́a de un objeto es invariante con respecto a rotaciones, suciedad e incluso condiciones de iluminación. Además, la forma de un objeto es la caracterı́stica
que normalmente es requerida en los propósitos de inspección de calidad. La mayorı́a
de técnicas actuales para control de calidad utilizando visión artificial, basan su funcionamiento en imágenes adquiridas por una sola cámara y un exhaustivo procesamiento
de las mismas en una PC o en un procesador con una aplicación de visión artificial embebida corriendo en tiempo real, que comunica la decisión de la inspección realizada
sobre el objeto al sistema (normalmente de control) para que éste realice la clasificación
de manera adecuada. A pesar de que la iluminación juega un rol fundamental en las
aplicaciones de visión artificial 2D, el objetivo fundamental en estas aplicaciones es homogeneizar la cantidad de luz sobre los objetos a analizar, eliminar reflejos y sombras,
etc. Los atributos que se pueden obtener del procesamiento de imágenes 2D tienen que
ver principalmente con mediciones de longitudes, diámetros, determinación de color y
textura [25]. Resulta, sin embargo, muy complicado obtener información de la forma
de los objetos con una sola imagen de los mismos, por lo que la construcción de una
representación 3D a partir de imágenes 2D serı́a una aproximación con muchos detalles
perdidos [14].
En el momento, en el que detalles de la forma de los objetos se vuelven importantes, ganan un significante protagonismo las técnicas de procesamiento de más de
una imagen del mismo objeto capturadas con más de una cámara, y a través de una
configuración particular de las mismas (por ejemplo, visión estereoscópica) es posible
decodificar detalles 3D de partes claves del producto para su posterior procesamiento.
Existe sin embargo, otro enfoque, que al igual que la visión estereoscópica, basa el análisis de las caracterı́sticas de forma de los objetos en cálculos a partir de triangulaciones,
desde un punto de iluminación y una cámara apuntando el objeto en cuestión. En este
caso además de la cámara existe un haz de luz estructurado, proyectando un patrón
1
especı́fico de iluminación: punto, lı́nea, rejilla, etc. Gracias a esta técnica es posible
capturar caracterı́sticas 3D con una sola cámara [15].
Los sistemas de inspección visual 3D son en la actualidad bastante especializados y por tanto relativamente costosos, considerando que muchas empresas del sector
industrial que requieren solucionar problemas relacionados con inspección automática
prefieren continuar trabajando en modo manual en lugar de invertir en un sistema de
visión 3D. Estos sistemas, por otra parte, basan su principio de operación en técnicas
de visión estereoscópica o iluminación estructurada por separado. Existen, sin embargo
una gran variedad de técnicas para adquirir modelos de objetos 3D, con un variado
rango de costos de hardware y diferentes niveles de precisión y detalle en la geometrı́a
de los modelos capturados como se menciona en [4, 6, 10, 11, 22]. Durante el desarrollo
de esta investigación se trabajará en el concepto de un sensor 3D que basará su funcionamiento en la combinación de las técnicas de visión estereoscópica e iluminación
estructurada, a través del análisis de imágenes estereo adquiridas por cámaras de idénticas caracterı́sticas y la alineación de las imágenes proyectando patrones conocidos en
los objetos a analizar, emitidos por un sistema de iluminación estructurado.
El énfasis en la información 3D de un objeto se justifica porque representa el detalle
de la forma geométrica de éste y por tanto posee mucho más valor que la información
2D que representa las variaciones locales de reflectividad solamente [23]. El concepto de
sensor 3D va de la mano con el concepto de triangulación activa [30], en donde existe
una fuente de luz estructurada que ilumina el objeto. La ventaja de utilizar iluminación
estructurada radica en el uso de un patrón de luz conocido, como por ejemplo un punto
láser proyectado en la superficie a analizar, o también una lı́nea, una rejilla o un patrón
senoidal con frecuencia variable para lograr una triangulación de fase [15].
Los trabajos desarrollados en [6, 10, 11, 13, 18, 22] utilizan variadas técnicas de
adquisición de caracterı́sticas tridimensionales, utilizando principalmente visión esteréo
o iluminación estructurada por separado, a excepción de [18] que contempla combinar
las dos técnicas para la reconstrucción del relieve facial. El presente trabajo, por otro
lado tiene por meta el procesamiento de las imágenes del par estéreo para adquirir los
atributos 3D, simplificando el problema de correspondencia de puntos a través de la
búsqueda del patrón de iluminación estructurada (lı́nea) en el objeto bajo análisis en las
dos imágenes de manera simultánea utilizando procesamiento multihilo (multithread)
en LabVIEW.
Los resultados de la investigación, se cuantificarán a través de las diferentes respuestas que nos brinde un prototipo construido para desarrollar una metodologı́a que
permita obtener atributos de objetos en 3D utilizando la fusión de las técnicas de ilumi2
nación estructurada y visión estereoscópica. Este prototipo utilizará una configuración
de dos cámaras dispuestas en formato estéreo, un haz de luz estructurado para resaltar
las caracterı́sticas 3D del objeto y que a su vez servirá como patrón conocido en el par de
imágenes estéreo para simplificar el problema de correspondencia. La implementación
de los algoritmos de visión artificial, triangulación, calibración de cámaras, interpolación, ingenierı́a inversa, etc., se realizarán en la plataforma de desarrollo LabVIEW
2009.
1.2.
Definición del Problema y Motivación
El control de calidad al final de una lı́nea de producción se lleva a cabo de diversas
maneras:
Manual. Un operador al final de una lı́nea de producción se encarga de analizar
detalladamente las caracterı́sticas, forma, dimensiones, etc., del producto y decide
si éste debe continuar o no con el proceso de fabricación.
Muestra aleatoria [20]. Se elige una muestra del total de un lote de producción
y se aprueba o no el lote completo para su distribución en base a la cantidad
de objetos que hayan pasado la inspección. Es posible notar que a pesar de que
los métodos estadı́sticos normalmente son confiables, existirán de todas maneras
productos defectuosos en el mercado.
Semiautomática. Un operador inspecciona el producto asistido por algún sistema
automático.
Automática. Se encuentran difundidas técnicas de visión 2D para reconocimiento
de patrones, análisis de color, textura, etc.
No se realiza.
Uno de los principales problemas en los procesos de control de calidad tiene que
ver con los tiempos de inspección y la precisión con la que éste pueda realizarse. En
la actualidad existen numerosos sistemas de visión 2D que solucionan parte de los procesos de inspección para control de calidad, sin embargo no cubren áreas especı́ficas,
como la automotriz por ejemplo, en la que se requiere un análisis detallado de las piezas
(altos y bajos relieves, agujeros, etc.) que se usarán en ensambles completos de vehı́culos y que por supuesto no pueden fallar, de manera que no se ponga en riesgo la vida
del usuario. Es posible por tanto, notar que una parte importante en un proceso de
producción tiene que ver con la inspección de objetos al final de una lı́nea de producción.
3
La inspección de la forma de los objetos, de manera particular está vinculada
con el campo de aplicaciones de visión artificial 3D e ingenierı́a inversa [15]. El método activo sin contacto más ampliamente usado en el campo de visión 3D es el de los
sistemas de iluminación estructurada. Estos sistemas están compuestos comúnmente
por una cámara y un proyector de luz estructurada [23]. Sin embargo el costo de estas aplicaciones han limitado su expansión a nivel industrial, por lo que una solución
de costo moderado y que pueda inspeccionar objetos en tiempos mucho menores que
lo que lo harı́a un operador de manera manual tendrá muy buena acogida en el mercado.
A pesar de que el estado del arte actual en visión 3D permite la adquisición de
una gran variedad de objetos; operadores eficientes y procedimientos con tiempos de
retardo más bajos siguen siendo una meta de investigación en los trabajos que se están
llevando a cabo, como por ejemplo: “A Simple, Low Cost, 3D Scanning System Using
the Laser Light-Sectioning Method ” [6] y “3D real time camera” [13], por citar un par de
trabajos de investigación realizados en esta área. De allı́, se han encontrado varias áreas
de mejora para la adquisición de modelos 3D, identificados en [4], como se menciona a
continuación:
Planificar métodos para adquisición de datos.
Captura confiable y procesamiento robusto de información para un gran número
de clases de objetos, ambientes, y objetos con superficies particulares.
Automatización de todos los procedimientos, para minimizar la interacción del
usuario con el sistema.
Retroalimentación en tiempo real de la superficie adquirida.
Métodos para evaluar la precisión global del modelo.
Adicionalmente y no menos importante, resulta interesante mencionar que el campo de los sistemas de visión 3D, no sólo es posible aplicarlos a nivel industrial para
procesos automáticos, como los de control de calidad que es el caso especı́fico de este
trabajo de investigación, sino que también se puede encontrar una enorme área de
aplicación práctica en la robótica móvil y la robótica industrial, por lo que el aporte
cientı́fico, que este trabajo brinde será de gran utilidad para los estudiantes, profesionales e investigadores involucrados o que deseen involucrarse en el campo de aplicaciones
de visión artificial.
1.3.
Meta
La meta de este trabajo de tesis es desarrollar una metodologı́a para la integración
de las técnicas de visión estereoscópica e iluminación estructurada en el campo de in4
spección de objetos para adquirir caracterı́sticas 3D. Esta metodologı́a se aplica a un
prototipo desarrollado en la etapa de investigación y que consta de dos cámaras de
idénticas caracterı́sticas, un haz de luz estructurado y objetos conocidos construidos
con alta precisión (patrones de calibración) de forma que permitan calibrar el sistema
y además comprobar su exactitud. El software que despliega los resultados de las mediciones 3D se implementará con LabVIEW como plataforma de desarrollo.
1.4.
Objetivos
El objetivo general de este trabajo de investigación es alcanzar la meta establecida en la sección 1.3, para lo cual adicionalmente se requiere cumplir con los siguientes
objetivos particulares:
Construir un prototipo que incluya dos cámaras y un sistema de iluminación
estructurada para evaluar resultados con diferentes objetos.
Evaluar el desempeño en la adquisición de atributos 3D, de sistemas de iluminación estructurada basados en patrones de punto y lı́nea.
Implementar un Interfaz Hombre Máquina (HMI) para la interacción del usuario
con el sistema. Las utilerı́as con las que el HMI debe contar son las siguientes:
• Una ventana de visualización del proceso de captura de imágenes en tiempo
real.
• Panel de control para calibración de cámaras, control del ángulo del haz de
luz estructurada y ejecución y paro de la aplicación.
• Una ventana flotante que presente los datos del perfil del objeto en 3D.
• Salida en un archivo de texto con los resultados de la medición 3D.
Desarrollar una metodologı́a de calibración de cámaras en formato estereo, al igual
que el patrón de iluminación estructurado. Esta metodologı́a debe contemplar el
desarrollo de las siguientes actividades:
• Hallar matrices de calibración individuales para las cámaras y el haz de luz.
• Combinar las matrices de calibración individuales para ajustar el sistema de
adquisición 3D de forma que sea posible adquirir atributos de la geometrı́a
de objetos.
• Desarrollar y utilizar algoritmos de autocalibración de LabVIEW.
5
1.5.
Hipótesis
La combinación de sistemas de iluminación estructurada y visión estereoscópica
son eficientes para adquirir la geometrı́a tridimensional de objetos de manufactura para
implementar procesos de inspección automáticos que permitan tomar decisiones de control de calidad en lı́neas de producción.
La tesis busca responder además, las siguientes preguntas de investigación:
¿Puede un sistema de triangulación activa monitorear la forma de los objetos en
tiempo real?
¿La precisión del sistema de inspección 3D de bajo costo se adaptará a los requerimientos de la industria?
¿Será posible utilizar cámaras de diferentes especificaciones y lograr una calibración óptima del sistema completo?
6
Capı́tulo 2
Fundamentos de visión estereoscópica e iluminación
estructurada para el cálculo de posición de objetos
en el espacio
Presentar la relación cuantativa entre imágenes 2D y sus estructuras 3D del mundo real, a través de las matemáticas e ingenierı́a involucradas es el principal objetivo
de este capı́tulo. En la sección 2.1 se encuentra el detalle de una configuración estéreo
general. La sección 2.2 detalla sistemas coordenados para representar posición y orientación, a la vez que se presentan los conceptos de coordenadas homogéneas y matrices
de transformación homogéneas. La sección 2.3 presenta la modelación matemática de
cámaras para adquisición de imágenes, y la forma en la que utilizando configuración
estereoscópica es posible calcular la posición tridimensional de puntos definidos en el
espacio. La sección 2.4 presenta en detalle el cálculo de matrices de calibración de dos
cámaras distintas y la estimación de puntos en el espacio utilizando estas matrices y
Matlab como herramienta de desarrollo. Las caracterı́sticas técnicas y de diseño de iluminación estructurada se presentan en la sección 2.5. Finalmente la sección 2.6 contiene
breves descripciones de aplicaciones e investigaciones relacionadas al área de inspección
tridimensional utilizando técnicas de visión estéreo o iluminación estructurada.
2.1.
Aspectos generales de una configuración estereoscópica
En la figura 2.1 se ilustra la configuración general de dos cámaras observando el
mismo espacio tridimensional. A menudo, en el manejo de gráficos por computadora el
uso de un sistema coordenado derecho resulta lo más común, con el eje Z correspondiente al rayo que deja el lente de la cámara hacia el campo de visión (FOV – Field of
View) [14].
De la figura 2.1, se puede notar que las dos cámaras observan un mismo espacio
de trabajo, siendo éste el espacio tridimensional con su propio sistema de coordenadas
7
Figura 2.1: Configuración de un par de cámaras en el espacio.
W adjunto a él. Intuitivamente, resulta sencillo notar que la localización del punto
W
P = W Px ,W Py ,W Pz en el espacio de trabajo puede ser obtenido simplemente determinando la intersección de los dos rayos de las imágenes W P 1 O y W P 2 O.
Para poder realizar la configuración estéreo general ilustrado en la figura 2.1, se
deben considerar los siguientes aspectos:
Debemos conocer la posición de la cámara C1 en el espacio de trabajo W y algunas
de las caracterı́sticas internas de la cámara, como la distancia focal.
De manera similar, debemos conocer la posición de la cámara C2 en el espacio de
trabajo W y sus parámetros internos.
Es necesario identificar la correspondencia del punto 3D,
de las imágenes (1 P, 2 P ).
W
P con los puntos 2D
Se requiere de alguna formulación que calcule W P de los dos rayos de las imágenes
W
P 1 O y W P 2 O.
8
Antes de entrar en el detalle de los puntos citados, se describen a continuación
variantes a la configuración estereo general presentanda en la figura 2.1:
La configuración mostrada en la figura 2.1 consiste de dos cámaras calibradas a
las coordenadas del espacio de trabajo. Las coordenadas de un punto 3D son calculadas a través de la intersección de dos rayos de las imágenes correspondientes
a los puntos en ellas.
Una de las cámaras puede ser reemplazada por un proyector el cual ilumina
una o más puntos de la superficie utilizando un haz de luz o un patrón especial
(Iluminación Estructurada). El proyector puede ser calibrado de idéntica manera
a una cámara, como se ilustra en la figura 2.2 [14].
El conocimiento previo del modelo del objeto puede reemplazar una de las cámaras.
En muchos casos la información del modelo del objeto agrega suficiente información que permite decodificar información tridimensional a partir de una sola
imagen.
Figura 2.2: Configuración estereo con una cámara y un proyector de luz.
9
2.2.
Herramientas matemáticas para localización espacial
En la sección 2.1 se resaltó la importancia de hallar una formulación matemática
que permita calcular W P de los dos rayos de las imágenes W P 1 O y W P 2 O. Las
herramientas matemáticas de localización espacial que se presentan en esta sección son
de aplicación general, siendo los campos de aplicación principales los de visión 3D,
robótica y realidad virtual.
2.2.1.
Representación de la posición
La localización de un cuerpo rı́gido en el espacio precisa de especificar tanto su
posición como su orientación. Ambas deben ser establecidas en relación a un sistema
de referencia definido. En un plano bidimensional, la posición de un cuerpo rı́gido
está ligada a dos grados de libertad y, por tanto, la posición del cuerpo quedará definida
por dos componentes independientes. En el caso de espacio tridimensional será necesario
emplear tres componentes.
Coordenadas cartesianas
Si se trabaja en un plano, con un sistema coordenado OXY Z de referencia asociado, un punto p vendrá expresado por las componentes (x, y, z) correspondientes a
los ejes coordenados del sistema OXY Z, como se ilustra en la figura 2.3.
Figura 2.3: Representación de un vector en un sistema coordenado cartesiano derecho.
10
Coordenadas polares y cilı́ndricas
Para un plano, es posible también caracterizar la localización de un punto p de un
vector utilizando como referencia la distancia desde el origen del sistema coordenado
hasta el punto de interés y el ángulo que forma el rayo trazado desde el origen hasta
el punto p, y el eje x. Para el caso tridimensional se aumenta la coordenada z para
caracterizar la localización del punto p. Esta situación se ilustra en la figura 2.4.
Figura 2.4: Representación de un vector en un sistema de coordenadas polares y cilı́ndricas.
Coordenadas esféricas
Es posible también utilizar coordenadas esféricas para realizar la localización de un
vector en un espacio tridimensional. Considerando el sistema de referencia OXY Z, un
vector cualquiera p tendrá como coordenadas esféricas (r, θ, φ), donde r es la distancia
medida desde el origen hasta el extremo del vector p; la componente θ es el ángulo
formado por la proyección del vector en el plano OXY y el eje OX, y finalmente la
componente φ es el ángulo formado por el vector p y el eje OZ, como se ilustra en la
figura 2.5.
2.2.2.
Representación de la orientación
Un punto en el espacio queda completamente definido a través de los datos de su
posición. Sin embargo, en el caso de un sólido rı́gido, se requiere conocer adicionalmente
11
Figura 2.5: Representación de un vector en un sistema de coordenadas esféricas.
su orientación con respecto al sistema de referencia.
Una orientación en el espacio tridimensional viene definida por tres grados de libertad o tres componentes linealmente independientes. Para poder describir de forma
sencilla la orientación de un objeto respecto a un sistema de referencia, es habitual
asignar solidariamente al objeto un nuevo sistema, y después estudiar la relación espacial existente entre los dos sistemas, el de referencia fijo y el nuevo. Para simplificar
este análisis, se utilizan las matrices de rotación.
Matrices de rotación
Considérese un sistema OXY de referencia fija y un sistema móvil OU V solidario
al objeto cuya orientación es de interés. Un vector p del plano se puede representar
como:
p = pu iu + pv jv
(2.1)
Adicionalmente, se presentan las siguientes igualdades:
px = ix p
py = j y p
(2.2)
Realizando la sustitución de la expresión 2.1 en la ecuación 2.2, se obtiene:
px
py
=R
12
pu
pv
(2.3)
Donde:
R=
ix iu ix jv
jy iu jy jv
es la matriz de rotación, que define la orientación del sistema OU V con respecto
al sistema OXY , y que sirve para transformar las coordenadas de un vector en un
sistema a las del otro. En el caso de un sistema de dos dimensiones, la orientación viene
definida por un único parámetro independiente, como se ilustra en la figura 2.6.
Figura 2.6: Orientación de un sistema móvil OU V con relación a uno fijo OXY .
Para el caso tridimensional el razonamiento es similar. Supóngase ahora que los
sistemas OXY Z y OU V W son coincidentes en el origen. Un vector p del espacio podrı́a
estar referido, como se estudió en la sección 2.2.1, a cualquiera de los dos sistemas de
la siguiente manera:
puvw = [pu , pv , pw ]T = pu iu + pv jv + pw kw
(2.4)
pxyz = [px , py , pz ]T = px ix + py jy + pz kz
(2.5)
Y de manera similar al caso bidimensional, es posible establecer la siguiente equivalencia:




px
pu
 py  = R  pv 
pz
pz
Donde:
13
(2.6)

ix iu ix jv ix kw
R =  jy iu jy jv jy kw 
kz iu kz jv kz kw

es la matriz de rotación que define la orientación del sistema OU V W con respecto
al sistema OXY Z. Resulta de gran utilidad establecer la expresión de matrices de
rotación que relacionen giros sobre un eje únicamente, como se ilustra en la figura 2.7.
Figura 2.7: Rotación del sistema OU V W con respecto a los ejes OX, OY y OZ.
Las matrices de rotación pueden componerse para expresar la aplicación continua de varias rotaciones [2]. Es importante considerar el orden en que se realizan las
rotaciones, pues el producto de matrices no es conmutativo.
14
2.2.3.
Coordenadas y matrices homogéneas
Para representar de manera conjunta la posición y la orientación de un sólido
en el espacio, se introducen las coordenadas homogéneas. Un elemento de un espacio
n-dimensional, se encuentra representando en coordenadas homogéneas por n+1 dimensiones, de tal forma que un vector p(x, y, z) vendrá representado por p(wx, wy, wz, w),
donde w tiene un valor arbitrario y representa un factor de escala.
A partir de la definición de las coordenadas homogéneas surge inmediatamente el
concepto de matriz de transformación homogénea. Se define como matriz de transformación homogénea, T a una matriz de dimensión 4×4 que representa la transformación
de un vector de un sistema de coordenadas a otro.
T=
R3×3 p3×1
f1×3 w1×1
(2.7)
Donde, R3×3 representa una matriz de rotación como las que se presentaron en la
sección 2.2.2, p3×1 por otro lado es un vector de posición en coordenadas cartesianas
similar a los presentados en la sección 2.2.1, f1×3 indica la transformación de perspectiva, que se detalla más adelante para el caso de cámaras en configuración estéreo, y
w1×1 se usará como herramienta de escalamiento global.
La ecuación 2.7 puede ser utilizada para representar la orientación y la posición
de un sistema O0 U V W resultado de rotar y trasladar el sistema original OXY Z según
R3×3 y p3×1 respectivamente. Asimismo, esta matriz puede servir para conocer las
coordenadas (rx , ry , rz ) del vector r en el sistema OXY Z a partir de sus coordenadas
(ru, rv, rz) en el sistema O0 U V W :




ru
rx




 rv 
 ry 
(2.8)
 = T


 rz 
 rz 
1
1
La principal ventaja de las matrices homogéneas reside en su capacidad de representación conjunta de posición y orientación. Esta representación se realiza utilizando
al mismo tiempo la matriz de rotación R3×3 y el vector de traslación p3×1 en una misma matriz de transformación homogénea [2]. Se debe considerar sin embargo, el orden
de las transformaciones puesto que se pueden producir resultados diferentes.
Una aplicación de gran utilidad en nuestros propósitos de visión 3D, que las matrices de transformación homogéneas nos ofrecen es la transformación de perspectiva.
Supóngase un lente situado sobre el plano OXZ cuya distancia focal es f situado sobre
15
el eje OY, como se ilustra en la figura 2.8. Es posible comprobar que el punto r(x, y, z)
se ve en el plano del lente como un punto r0 (x0 , y 0 , z 0 ) cuyas coordenadas vienen dadas
por la siguiente expresión:
x
1−
x0 =
y
f
y0 = y
z
1−
z0 =
y
f
(2.9)
Es posible representar esta transformación
matriz de transformación homogénea del tipo:
 

1 0 0
x0
 0   0 1 0
 y  
 0 =
 z   0 0 1
0 − f1 0
1
2.3.
de perspectiva, utilizando una sola
0
0
0
1





x
y
z
1





(2.10)
Modelo de la cámara
En la ecuación 2.11 se presenta el modelo algebráico utilizado para calibrar sistemas de visión con imágenes en perspectiva. A lo largo de esta sección nos dedicaremos
a determinar los componentes de la matriz IW C a partir de configuraciones fijas del sistema de visión.
I
P =
s I Pr
 s I Pc  =
s

I
W
P
WC

W

I
WC




Px
W
Py
W
Pz
1






s I Pr
c11 c12 c13 c14

 s I Pc  =  c21 c22 c23 c24  


s
c31 c32 c33 c34

W



W
Px
W
Py
W
Pz
1





(2.11)
El objetivo de la ecuación 2.11 es proyectar un punto del espacio tridimensional
T
T
P = W Px ,W Py ,W Pz a un punto de la imagen I P = I Pr ,I Pc , .
16
Figura 2.8: Transformación de perspectiva.
2.3.1.
Matriz de transformación para perspectiva
En la figura 2.8 se ilustra la problemática general de perspectiva en un sistema
de visión. El conjunto de ecuaciones 2.12 presenta el álgebra de la transformación de
T
perspectiva. Las coordenadas de la imagen F Px , F Py , se encuentran en las mismas
unidades que las coordenadas del espacio tridimensional, y no en pı́xeles. La transformación a pı́xeles se desarrolla en detalle más adelante.
f
CP
z
f
= C
Pz
F
Px =
C
Px
F
Py
C
Py
(2.12)
Una transformación de perspectiva sencilla se ilustra en la figura 2.9, que a su vez
se define únicamente en términos del parámetro f , la distancia focal. La matriz FC Π(f )
se presenta en la ecuación 2.13 en su forma de 4 × 4 elementos, de forma que se pueda
combinar con otras matrices de transformación. Nótese que la matriz tiene rango 3, y
17
no 4, por lo que no es invertible.
P = FC Π(f ) C P


1 0 0
s F Px
 F

 0 1 0
 s Py 

 F
 = 
 s Pz 
 0 0 1
0 0 f1
s
F

0
0
0
0
 








s C Px
s C Py
s C Pz
1





(2.13)
Figura 2.9: Transformación de perspectiva. El sensor de la cámara está en el centro de
la proyección.
Una transformación alternativa puede definirse colocando el origen de la cámara
en el centro de la imagen de manera que F Pz = 0, a diferencia de lo que se muestra en
la figura 2.9 en la que F Pz = f . La matriz de proyección, por tanto quedarı́a modificada
de la siguiente manera:
F
P = FC Π(f ) C P


1 0 0
s F Px
 F

 0 1 0
 s Py 

 F
 = 
 s Pz 
 0 0 0
0 0 f1
s

0
0
0
0
 








s C Px
s C Py
s C Pz
1





(2.14)
El caso más general, involucra la no coincidencia del sistema coordenado general
W y el de la cámara C. Una rotación y traslación son necesarias para convertir el punto
18
del mundo W P a las coordenadas de la cámara C P . Tres parámetros de rotación y tres
de traslación se requieren para lograr esto:
C
C





C
Px
C
Py
C
Pz
1
P = T (tx , ty , tz ) R (α, β, γ)
W
P
W
C
P
W TR (α, β, γ, tx , ty , tz )
P =






 = 



r11 r12 r13 tx

r21 r22 r23 ty 

r31 r32 r33 tz 
0
0
0 1
(2.15)
Es posible por tanto, combinar las transformaciones para modelar el cambio de
coordenadas de W a C, seguido de una transformación de perspectiva. La tercera fila
de la matriz se descarta puesto que únicamente se obtendrá el valor constante para
F
Pz . F P está en el plano de la imagen por lo que una transformación de escalamiento
será necesaria para convertir a las coordenadas de pı́xeles de I P .
F
P =
F
P =
F
C
CΠ P
F
C
W
P
C Π W TR (α, β, γ, tx , ty , tz )

s F Px
d11 d12 d13 d14

 s F Py  =  d21 d22 d23 d24  


s
d31 d32 d33 d34




W
Px
W
Py
W
Pz
1





(2.16)
La transformación de números reales a pı́xeles, incluyendo la dirección opuesta del
eje vertical está dada por:
 


 
1
0
0 − dy
sr
s F Px
 1

I
P =  s c  =  dx
(2.17)
0 0   s F Py 
s
s
0
0 1
siendo dx y dy el tamaño vertical y horizontal, respectivamente, de capa pı́xel en la imagen, pero en unidades del mundo real. El resultado final para la matriz de calibración de
la cámara que transforma los puntos 3D en coordenadas de pı́xeles de imagen está dada
por:
I
W
F
C
Π
TR
(α,
β,
γ,
t
,
t
,
t
)
P
S
x
y
z
C
W
F


W
 I



Px
c11 c12 c13 c14
s Pr
 W

Py 
 s I Pc  =  c21 c22 c23 c24  
 W

 Pz 
s
c31 c32 c33 1
1
P =
I
19
(2.18)
Resulta muchas veces complicado ejecutar este cálculo con precisión suficiente,
puesto que en la práctica se requieren medir ángulos y distancias, por lo que muchas
veces es recomendable y preferible utilizar un procedimiento definido para calibración
de la cámara, como se detalla más adelante en este capı́tulo.
2.3.2.
Proyección ortogonal y de perspectiva débil
Si simplificamos el problema de proyección de la sección 2.3.1, proyectando cada
punto del mundo, W , paralelamente al eje óptico y directamente sobre el plano de
la imagen, obtendremos una situación similar a la que se ilustra en la figura 2.10. La
proyección ortogonal se puede observar como una proyección de perspectiva considerando una distancia focal, f , igual a infinito.
Figura 2.10: Comparación de proyecciones: perspectiva y ortogonal.
F
P =
F
C
C Π(∞) P

F
Px
F
Py
=
1 0 0 0
0 1 0 0
20




C
Px
C
Py
C
Pz
1





(2.19)
A menudo, una transformación de perspectiva puede ser aproximada por una
de perspectiva ortogonal a través de un escalamiento uniforme en el plano real de
la imagen. Proyectar un punto lejano en la coordenada z y aplicar un escalamiento
uniforme ha sido llamado perspectiva débil. Un factor de escala adecuado se encuentra
por la relación de la distancia del objeto, W Pz , y la distancia focal, f , de la cámara
a través de la expresión s = WfPz . La transformación de perspectiva, queda por tanto
representada como sigue:
F
P =
F
C
C Π(s) P

2.3.3.
F
Px
F
Py
=
s 0 0 0
0 s 0 0




C
Px
C
Py
C
Pz
1





(2.20)
Estimación de puntos 3D utilizando sistemas de visión
artificial
En la figura 2.1 se ilustra la configuración general estéreo de dos cámaras. Resulta
sencillo allı́ observar que el punto W P puede ser estimado de la intersección de los dos
rayos que salen de los centros de proyección de las cámaras. Por tanto, si utilizamos
las matrices de calibración de perspectiva estudiadas en las secciones anteriores, para
dos cámaras, podremos estimar las coordenadas reales tridimensionales de un punto
en el espacio, [x, y, z] a partir de las coordenadas de imagen obtenidas con las cámaras
previamente calibradas, [r1 , c1 ] y [r2 , c2 ].
Tomando como referencia la ecuación de calibración de una camara, presentada
en la expresión 2.11, podemos plantear un sistema de ecuaciones para la estimación de
un punto en el espacio, con un procedimiento similar al que se muestra a continuación:





x
y
z
1

s r1
b11 b12 b13 b14
 

 s c1  =  b21 b22 b23 b24  
 
 
s
b31 b32 b33 1
 




x
t r1
c11 c12 c13 c14
 
y 
 t c1  =  c21 c22 c23 c24  
 
 z 
t
c31 c32 c33 1
1
(2.21)
Las variables desconocidas son las coordenadas del punto en el espacio, [x, y, z], y
21
si eliminamos las coordenadas homogéneas s y t de las ecuaciones anteriores, es posible
plantear el siguiente sistema lineal de ecuaciones:
r1 = (b11 − b31 r1 ) x + (b12 − b32 r1 ) y + (b13 − b33 r1 ) z + b14
c1 = (b21 − b31 c1 ) x + (b22 − b32 c1 ) y + (b23 − b33 c1 ) z + b24
r2 = (c11 − c31 r2 ) x + (c12 − c32 r2 ) y + (c13 − c33 r2 ) z + c14
c2 = (c21 − c31 c2 ) x + (c22 − c32 c2 ) y + (c23 − c33 c2 ) z + c24
(2.22)
Errores de aproximación en los modelos de las cámaras y el truncamiento de
coordenadas continuas a pı́xeles, pueden producir inconsistencia en la solución de las
ecuaciones 2.22. Una solución apropiada planteada en [14], menciona calcular la distancia más corta entre los rayos de las imágenes hacia el punto en el espacio tridimensional.
Si la distancia de este segmento es lo suficientemente pequeña, se asigna el punto medio
como el punto de intersección de los rayos de la imagen, [x, y, z].
2.4.
Estimación de la matriz de calibración con un
enfoque práctico
Se presenta a continuación la manera de encontrar los elementos de la matriz de
calibración presentada en la ecuación 2.11, utilizando un enfoque práctico. El campo
de visión de la cámara y el enfoque deben permanecer fijos y, con el uso de un patrón
de calibración, con dimensiones conocidas, procedemos a plantear un problema de optimización para ajustar los parámetros de calibración de nuestra cámara.
Se toma un juego de coordenadas I Pj , W Pj , donde I Pj = [I Pr , I Pc ] es la coordenada del pı́xel en la imagen donde se visualiza el punto 3D W Pj = [W Px , W Py , W Pz ].
En [14] recomiendan un mı́nimo de 6 puntos para una calibración adecuada, siendo 25
o más lo ideal para mejorar el proceso de optimización a través de mı́nimos cuadrados.
De manera similar a la que utilizamos para eliminar el factor de escala en las
ecuaciones 2.22, definimos dos ecuaciones que modelan la geometrı́a del rayo de una de
las cámaras (ecuación 2.23). Cabe destacar en este punto, que este análisis y el método
en si, puede ser aplicado a otra cámara con una ubicación diferente, y una vez obtenidas
las matrices de calibración de las cámaras es posible proceder a los cálculos de posición
de objetos en el espacio, como se mencionó en la sección 2.3.3.
22
uj = (c11 − c31 uj ) xj + (c12 − c32 uj ) yj + (c13 − c33 uj ) zj + c14
vj = (c21 − c31 vj ) xj + (c22 − c32 vj ) yj + (c23 − c33 vj ) zj + c24
T
[xj , yj , zj ]T = W Pj = W Px ,W Py ,W Pz
T
[uj , vj ]T = I Pj = I Pr ,I Pc
(2.23)
Reescribiendo la ecuación 2.23 en forma matricial, generamos la siguiente ecuación
vectorial-matricial:

xj yj zj 1 0 0 0 0 −xj uj −yj uj
0 0 0 0 xj yj zj 1 −xj vj −yj vj








−zj uj 


−zj vj








c11
c12
c13
c14
c21
c22
c23
c24
c31
c32
c33








 
u
j
=

vj








(2.24)
En virtud de que se pueden tener varios rayos desde el centro de la imagen a
diferentes puntos en el espacio y generar siempre para cada rayo el conjunto de ecuaciones planteadas en la expresión 2.23, es posible obtener 2n ecuaciones diferentes a
partir de n puntos de calibración. Se puede utilizar notación matricial para reescrbir
nuevamente la expresión 2.23 de la siguiente forma, considerando n puntos de calibración:
A2n×11 x11×1 = b2n×1
(2.25)
Resulta sencillo notar, analizando brevemente la expresión 2.25 que existen 11
incógnitas y más de 12 ecuaciones, por lo que el sistema es redundante y nuestro problema se vuelve principalmente de optimización. En la sección 2.3.3 se mencionó que las
ecuaciones de los rayos de las cámaras apuntando hacia un punto no siempre tendrán
solución, y en virtud de que nuestro análisis partió de las ecuaciones en esa sección
planteadas, existe una gran posibilidad de que el sistema de ecuaciones 2.25 no sea
consistente. Se trata por tanto, de hallar la solución que más se acerque a una solución real del sistema, en caso de que fuera consistente. En [12], se detalla el proceso de
proyección ortogonal y la minimización del error en el cálculo de sistemas de ecuaciones
23
inconsistentes a través del algortimo de mı́nimos cuadrados, que es justamente lo que
utilizaremos en nuestra aplicación práctica. El proceso de proyección ortogonal y minimización del error para la estimación de la solución de un sistema como el presentado
en la expresión 2.25, trata de proyectar el vector al cual queremos representar en el
espacio columna de nuestra matriz de coeficientes a través de la ortogonalización del
mismo en este espacio generado. A pesar de la complejidad aparente del criterio, la
aplicación del algoritmo para dar solución a nuestro problema y lograr los resultados
esperados es muchı́simo más simple de lo que aparenta.
A continuación se presenta el algoritmo de solución del sistema de ecuaciones 2.25
a través de mı́nimos cuadrados:
A2n×11 x11×1 = b2n×1
AT11×2n A2n×11 x11×1 = AT11×2n b2n×1
−1 T
x11×1 = AT11×2n A2n×11
A11×2n b2n×1
(2.26)
Si utilizamos Matlab o LabVIEW como herramienta de desarrollo para implementar el método de mı́nimos cuadrados para la solución del sistema de ecuaciones 2.25,
basta utilizar el comando x = A\B. A continuación se presenta un ejemplo de calibración de dos cámaras diferentes y el cálculo de posición 3D utilizando la teorı́a hasta
aquı́ presentada.
2.4.1.
Ejemplo de calibración de dos cámaras y cálculo de posición 3D
En la tabla 2.1 se presenta un conjunto de datos que representan varios puntos
3D, en milı́metros, y las coordenadas correspondientes en el par de imágenes estéreo,
imagen 1 e imagen 2 capturadas por dos cámaras distintas. En el Anexo 1 se presenta
el detalle de la solución de este ejemplo utilizando el Mathscript de LabVIEW 2009, y
los resultados generados por el sistema se analizan en esta sección. El Mathscript de
LabVIEW 2009 posee una estructura idéntica a la que el Matlab ofrece, en lo que a
creación de archivos se refiere, por lo que el código del Anexo 1 podrı́a ejecutarse sin
problema también en ésta platafoma.
Los resultados de calcular los puntos en el espacio partiendo de los datos del par
de imágenes estéreo, y luego de haber hallado las matrices de calibración del sistema
C1 y C2 , como se detalla en la sección 2.4, se presentan en la tabla 2.2. Las columnas
8, 9 y 10 muestran el error generado en la estimación del punto en el espacio, al que se
hace referencia en la columna correspondiente; resulta sencillo notar que a pesar de que
24
Punto
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Puntos del Espacio
W
W
W
x
y
z
0.0
0.0
0.0
0.0
15.24
0.0
27.94 15.24
0.0
27.94
0.0
0.0
20.955 0.0
-11.43
6.985
0.0
-11.43
13.97
0.0
-8.89
13.97 15.24 -8.89
0.0
0.0
-1.905
27.94
0.0
-1.905
5.08
0.0
0.0
5.08 15.24
0.0
22.86 15.24
0.0
22.86
0.0
0.0
20.955 0.0 -4.5974
6.985
0.0 -4.5974
Imagen 1
1
1
u
v
167 65
96 127
97 545
171 517
352 406
347 186
311 294
226 337
198 65
203 518
170 143
96 198
97 465
173 432
245 403
242 181
Imagen 2
2
u
v
274
168
196
42
96
431
154
577
366
488
430
291
358
387
Oculto Oculto
303
169
186
577
248
248
176
116
114
363
176
507
259
482
318
283
2
Tabla 2.1: Datos de dos cámaras distintas y de puntos en el espacio.
el método de calibración utilizado es eficiente y que la estimación del error se realiza
sobre los mismos puntos utilizados en la calibración del sistema pueden existir errores
de hasta 0,1721 mm, lo que nos indica como primer resultado experimental previo a
la implementación práctica que el error de estimación de los puntos en el espacio con
una configuración estereoscópica será mayor que cero. En la sección 3.4 se presentan los
resultados de precisión del sistema experimental utilizando el mismo enfoque de éste
ejemplo.
2.5.
Iluminación estructurada
La mayorı́a de los problemas de inspección industrial, ingenierı́a inversa y realidad virtual requieren información sobre la forma geométrica de los objetos en el espacio
tridimensional [15]. Los sensores ópticos 3D trabajan con fuentes de luz, lentes, fotodiodos y cámaras de video para brindar información de la geometrı́a de un objeto, de
manera tan precisa como las limitaciones fı́sicas de los componentes del sistema lo permitan. Una práctica bastante común en visión 3D es proyectar un patrón conocido en
la superficie del objeto a analizar y observar este patrón (triangulación activa). Para
interpretar la informacion 3D del objeto, se requieren conocimientos y experiencia en
25
Punto
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
W
x
0.0
0.0
27.94
27.94
20.955
6.985
13.97
13.97
0.0
27.94
5.08
5.08
22.86
22.86
20.955
6.985
W
W
y
z
0.0
0.0
15.24
0.0
15.24
0.0
0.0
0.0
0.0
-11.43
0.0
-11.43
0.0
-8.89
15.24 -8.89
0.0
-1.905
0.0
-1.905
0.0
0.0
15.24
0.0
15.24
0.0
0.0
0.0
0.0 -4.5974
0.0 -4.5974
W
W
W
x̂
ŷ
ẑ
0.03
0.01
-0.06
0.064
15.3
-0.004
28.0025 15.2133 -0.0264
27.9305 -0.0560 0.1092
20.9312 -0.1350 -11.3525
6.9849 -0.0767 -11.4174
13.9697 0.1721 -8.9953
NA
NA
NA
-0.0871 -0.0176 -1.8402
27.9481 0.0190 -1.8732
5.0787 -0.1223 0.0311
4.9993 15.1702 0.0697
22.8131 15.2639 -0.0581
22.8549 0.0149 -0.0686
20.9308 0.1052 -4.6476
7.0941 0.0804 -4.6368
ex
-0.03
-0.06
-0.0640
0.0095
0.0238
0.0001
0.0003
NA
0.0871
-0.0081
0.00311
0.0807
0.0469
0.0051
0.0242
-0.1091
ey
ez
-0.01
0.06
-0.0631 -0.0049
0.0267
0.0264
0.0560 -0.1092
0.1350 -0.0775
0.0767 -0.0126
-0.1721 0.1053
NA
NA
0.0176 -0.0648
-0.0190 -0.0318
0.1223 -0.00311
0.0698 -0.0697
-0.0239 0.0581
-0.0149 0.0686
-0.1052 0.0502
-0.804
0.0394
Tabla 2.2: Resultados obtenidos con el software implementado en Mathscript de LabVIEW y/o Matlab.
el manejo de imágenes bidimensionales y adquisición de imágenes.
2.5.1.
Triangulación Activa
La triangulación, en geometrı́a, es el uso de triángulos para determinar posiciones
de puntos, medidas de distancias o áreas de figuras. La aplicación práctica de este principio matemático, para la obtención de la información geométrica mediante triangulación
activa por proyección de luz estructurada, consiste en lo siguiente:
Un patrón es proyectado sobre el objeto bajo prueba, en una “dirección de iluminación” especı́fica, y es observado desde una diferente “dirección de observación”.
El ángulo formado entre las dos direcciones es llamado ángulo de triangulación
φ, figura 2.11.
El patrón puede ser un punto de un láser, para medición de distancias locales,
ó un patron de franjas, para una medición completa de la forma del campo de
visión adquirido, como se ilustra en la figura 2.12. De la ubicación del patrón
en la imagen, a través de triangulación se evalúa la distancia del detalle sobre el
objeto, que queremos resaltar y decodificar. Un cambio en la distancia hacia el
objeto se codificarı́a como un desplazamiento lateral del patrón. Proyectar una
26
Figura 2.11: Arquitectura de un sistema de triangulación activa básico.
lı́nea sobre la superficie del objeto brinda la posibilidad de observar un perfil de
la superficie. Para adquirir la superficie completa, harı́a falta un ’scan’ de la lı́nea
láser sobre el objeto.
Figura 2.12: Patrón de franjas codificado y proyectado sobre un objeto cilı́ndrico.
La técnica de triangulación por medición de fase (pmt), por otro lado proyecta un
patrón tipo rejilla sobre el objeto o un patrón sinusoidal con diferentes desplazamientos
de fase. A través del uso de está técnica es posible adquirir la forma de la superficie de
un objeto sin un ’scan’, debido a que en el caso de un patrón tipo rejilla, por ejemplo,
en un objeto curvado la cámara captarı́a lı́neas de rejillas curvadas también. Asimismo,
si el patrón posee una diferencia de fase, con por lo menos tres exposiciones de éste es
posible derivar la distancia de capa punto del objeto (figura 2.13).
27
Figura 2.13: Proyección de un patrón tipo rejilla sobre objetos 3D [15]
2.5.2.
Iluminación estructurada
La iluminación tiene un papel fundamental en un sistema de visión artificial,
puesto que ayuda a simplificar considerablemente el análisis e interpretación de las escenas. Al implementar una buena iluminación, se consigue una buena formación de la
imagen a adquirir, y esto facilita su procesamiento. Por el contrario, una mala iluminación puede aumentar complejidad a los algoritmos de procesamiento.
El problema en visión artificial es ubicar correctamente la iluminación, los sensores
y los cuerpos a examinar para resaltar las caracterı́sticas visuales de los objetos.
La iluminación estructurada, particularmente utiliza la proyección de patrones de
luz especı́ficos, como puntos, franjas o rejillas sobre la superficie de trabajo. En función
de cómo se deforme este patrón de luz es posible detectar las singularidades de la pieza
y/o objeto bajo análisis. Por tanto, el término iluminación estructurada se define como
la proyección de un patrón de luz simple o codificado sobre la escena iluminada [24]. Este
método de iluminación posee dos ventajas importantes con respecto a metodologı́as de
iluminación tradicionales para 2D:
Establece un patrón de luz conocido sobre la superficie de trabajo y las diferencias
con este patrón indican la presencia de un objeto, simplificándose ası́ el problema
de detección de un objeto.
Analizando la forma en que el patrón de luz es distorsionado, es posible obtener
información de las caracterı́sticas tridimensionales del objeto (figura 2.14).
Los métodos tradicionales de luz estructurada para el sensado de profundidad, por
28
Figura 2.14: Concepto de Iluminación Estructurada.
lo general, están basados en la introducción de información geométrica en la técnica de
iluminación a fin de facilitar la extracción de la profundidad de la escena de análisis.
Una de estas técnicas consiste en la proyección de una lı́nea sencilla de luz sobre la
escena y la imagen bidimensional es adquirida por medio de una cámara digitalizadora
que se encuentra a un ángulo de toma adecuado.
La información de profundidad se adquiere del desplazamiento relativo de los diferentes puntos de la lı́nea de luz. Una particularidad del método de lı́nea sencilla es
la necesidad de procesar múltiples imágenes para reconstruir la escena completa. La
totalidad de la escena puede cubrirse ya sea moviendo la fuente de luz o bien, dejando
el sistema de iluminación fijo y recorrer la escena. Una variación de este método de
luz estructurada consiste en la proyección de múltiples lı́neas sobre la escena con una
regularidad o un patrón definido. Lo anterior es logrado mediante el uso de una rejilla
de difracción diseñada para el caso. La técnica de múltiples lı́neas tiene la ventaja ob29
via de requerir en principio una sola imagen para lograr la reconstrucción de la escena
completa. Esta ventaja, en términos computacionales, representa una simplificación en
el manejo de los “buffers” o memoria RAM. Sin embargo, la complejidad de los algoritmos de reconstrucción aumenta considerablemente pues es necesario resolver ciertas
dificultades inherentes al método, entre las cuales destaca la posible confusión entre las
diferentes lı́neas. El principio de extracción de profundidad mediante el desplazamiento
relativo de puntos de luz conduce al diseño de algoritmos demasiado complejos para
poder aspirar a su implantación en tiempo real [26].
2.6.
Trabajos relacionados
A continuación se presentan algunas referencias de trabajos de investigación relacionados con el campo de adquisición y análisis de imágenes 3D.
El uso de sistemas de escaneo tridimensional para adquirir caracterı́sticas externas
de un objeto arbitrario posee muchas aplicaciones en el campo industrial, por lo que el
trabajo presentado en [6] se enfoca en analizar objetos con formas geométricas sencillas
como: cilindros, rectángulos, etc. El sistema propuesto utiliza un haz de luz estructurada
de la fábrica StockerYale tipo lı́nea con un costo de USD 2500 (el laser únicamente) una
tarjeta NI PCI-1411 y una cámara TM-200 CCD de alta resolución. La técnica utilizada
es la de escaneo progresivo del laser a través del objeto y capturas consecutivas de la
cámara (Light Sectioning [17]) para resolver las caracterı́sticas 3D en software a través
de un programa escrito en Matlab.
Figura 2.15: Sistema propuesto en [6]
30
En [13] se detalle el esfuerzo de un grupo de investigadores por generar un concepto de cámara tridimensional utilizando como patrón de iluminación señales senoidales
consecutivas con fases distintas, de forma que sea posible implementar la técnica de triangulación por medición de fase (pmt), para ello emplean un proyector de alta definición
(Ferroelectric Crystal Display - FLC) muy costoso. Gracias a la proyección perfecta de
patrones senoidales con intervalos de tiempo entre cada patrón de tan solo 3µs y un
procesamiento de la imagen en computadoras dedicadas es posible presentar la información 3D de las escenas en tiempo real.
La medición de perfiles en piezas de manufactura es el principal objetivo del sistema propuesto en [21]. El objeto es rotado en frente de un sistema de iluminación
estructurado: proyección de luz estructurada tipo lı́nea y una cámara que observa el
objeto en un ángulo diferente, llamado ángulo de triangulación. Para la reconstrucción
de la geometrı́a del objeto se implementa en Matlab una aproximación por mı́nimos
cuadrados a través de un cı́rculo cuya curvatura es estimada en función de las distancias
calculadas por el sistema.
Figura 2.16: Sistema propuesto en [21]
Por otro lado, en [11] se describe la técnica utilizada para adquirir la superficie
completa de un objeto en una escena sin la necesidad de rotar o mover el sistema
y/o el objeto. La configuración del sistema es novedosa y propone utilizar una cámara
de alta resolución, un proyector de luz estructurada DLP que emita una secuencia de
luz codificada en código Gray, y el tercer elemento para completar el sistema consiste
de un arreglo de espejos que permita tener capturas de diferentes ángulos del objeto
bajo análisis, como se ilustra en la figura 2.17. La ventaja inmediata que este sistema
31
presenta es la supresión de múltiples capturas de la imagen para su reconstrucción
tridimensional.
Figura 2.17: Arquitectura del sistema propuesto en [11]
2.7.
Aporte al conocimiento
En la sección anterior se presentan brevemente trabajos relacionados con la temática
de inspección de objetos utilizando los enfoques de visión estereoscópica e iluminación
estructurada. En virtud de que existe gran cantidad de literatura formal y trabajos
realizado en éstas áreas, con resultados y metodologı́as diferentes, se han identificado
las siguientes contribuciones, no mencionadas, ni tratadas en ningún trabajo citado en
ésta investigación, que el presente trabajo de tesis aborda:
Metodologı́a de integración de dos técnicas de visión 3D: visión estereoscópica e
iluminación estructurada. Se estudia con detalle ésta metodologı́a en la sección
4.3.
Sencillez en la calibración del sistema y en la implementación práctica de los
algoritmos. En la sección 2.4 se presentó el algoritmo de calibración de las cámaras
y un ejemplo práctico.
32
No se requieren proyectores de luz estructurada costosos, ni patrones de luz estructurada complejos como rejillas ó franjas, ni codificación a través de triangulación
por medición de fase (pmt). Éstos resultados se abordan con mayor profundidad
en el capı́tulo 4.
La redundancia que el sistema ofrece al estar compuesto por tres diferentes sitemas
de visión 3D asegura continuidad en la operación en una lı́nea de producción, en
caso de que uno de los componentes falle. Las ventajas que la redundancia del
sistema ofrece se presentan en la sección 3.2.
Simplificación del problema de correspondencia de imágenes en imágenes capturadas por el sistema de visión estereoscópico.
33
Capı́tulo 3
Construcción y calibración de un prototipo para
pruebas experimentales
En el capı́tulo anterior se expusieron los conceptos relacionados con visión estereoscópica e iluminación estructurada desde un enfoque enteramente matemático. El
objetivo principal de éste capı́tulo, es detallar la aplicación de las matemáticas e ingenierı́a involucradas en sistemas de visión 3D a través de pruebas experimentales de
calibración en un sistema prototipo cuyo diseño y construcción se discuten más adelante. La sección 3.1 presenta el diseño y construcción del prototipo para las pruebas
experimentales que se desarrollan a lo largo de éste trabajo de investigación. La justificación de la arquitectura elegida y sus ventajas se exponen en la sección 3.2. La tercera
sección está dedicada al problema de calibración del sistema y el Pre-procesamiento de
las imágenes del par estéreo. Finalmente la sección 3.4 presenta los diferentes resultados
de precisión alcanzados en la calibración a través de pruebas de medición realizadas sobre los mismos objetos utilizados en el proceso de cálculo de las matrices de calibración
de las cámaras.
3.1.
Diseño y construcción del prototipo
La arquitectura elegida para obtener los atributos espaciales de un objeto, se
bosqueja en la figura 3.1. Resulta sencillo notar allı́ que el sistema de visión 3D planteado es un sistema redundante. Las razones por la que se asevera que el sistema es redundante, tienen que ver con el hecho de que se forman simultáneamente 3 diferentes
sistemas de visión artificial para obtener atributos 3D, mismos que se detallan a continuación:
Sistema de iluminación estructurada con una cámara. Utilizando cualquiera de
las dos cámaras que se muestran en la figura 3.1, y el proyector del patrón de luz
estructurada es posible construir un sistema de visión 3D basándose en los conceptos de triangulación activa que se detallan en la sección 2.5.1, y cuya aplicación
se comenta en [16] y [21]. Ejemplos de calibración de éste sistema se presentan
en [9].
34
Figura 3.1: Disposición de las cámaras y el patrón de iluminación en el prototipo.
Sistema de visión estéreo. Claramente se puede obsevar que usando las dos cámaras
del sistema de la figura 3.1 y el procesamiento de las dos imágenes en un computador, será posible adquirir la geometrı́a de un objeto situado en el espacio de
trabajo (área calibrada [31]). Se vuelve, sin embargo relativamente compleja la
correspondencia de puntos entre las imágenes adquiridas por cada cámara para
aplicar los conceptos del capı́tulo anterior, relacionados con la ubicación de puntos y/o patrones en el par de imágenes estéreo. Fácilmente podemos suponer que
el esfuerzo computacional se incrementa debido al procesamiento adicional para
solucionar el problema de correspondencia en las imágenes, lo cual no aplica en
el primer sistema, descrito anteriormente. En [1] se detallan las limitaciones de
los sistemas de visión estéreo, al igual que sus ventajas.
Sistema de visión estéreo + iluminación estructurada. Se debe precisamente a
éste sistema la configuración de la figura 3.1, cuya justificación se menciona en
detalle en la sección 3.2.
La ubicación de las cámaras no está sujeta a restricciones de ningún tipo, más bien
se pretende situarles de forma que se cubra la mayor cantidad de volumen del objeto
bajo análisis. El proyector de luz estructurada, sin embargo se propone ubicarlo en el
plano yz, forma que el procesamiento posterior de las imágenes resulte menos complejo.
En la figura 3.2 se ilustra la configuración del sistema prototipo.
La implementación del sistema bosquejado en la figura 3.2 se muestra en la figura
3.3. Los componentes principales del sistema se describen en las siguientes secciones.
35
Figura 3.2: Arquitectura del sistema de visión 3D prototipo.
3.1.1.
Cámaras
Las cámaras que se eligieron para el desarrollo del proyecto son de la firma Unibrain, modelo Fire-i Digital Camera. Las especificaciones principales son las siguientes:
Tipo de dispositivo: IIDC FireWire Digital Camera
Interfase: FireWire, 2 puertos (6 pines)
Velocidad: 400M bps
R Wfine 1/4” CCD
Tipo de sensor: SONY
Escaneo: Progresivo
Resolución: (H x V) 640 × 480
Distancia focal: 4,65 mm
36
Figura 3.3: Sistema prototipo implementado.
Ángulo horizontal de visión: 42◦
Ángulo vertical de visión: 32◦
Color: Monocromática - RBG 24 bits
A pesar de que en sistemas de visión estéreo se recomienda utilizar cámaras idénticas para facilitar los cálculos de las matrices de calibración, la metodologı́a que se desarrolla a lo largo de éste trabajo, no propone esa restricción principalmente debido a
la estimación de las matrices de calibración a través de un criterio de minimización del
error, como se detalla en la sección 2.4. La elección de un bus de comunicación IEEE
1394 en lugar de uno USB en las cámaras a utilizar tiene que ver con los siguientes
aspectos:
Velocidad de transferencia efectiva: A pesar de que la especificación de USB 2.0
permite alcanzar un ancho de banda de hasta 480 Mbps [8], el encabezado del
protocolo de comunicación resta velocidad a la transmisión de datos de los dispositivos, además de ser un bus compartido dentro del PC. Por otro lado, la
37
especificación IEEE 1394a asegura una transferencia efectiva de 400 Mbps, lo
cual permite una transferencia de hasta 100 cuadros por segundo en imágenes
con una resolución de 640 × 480.
Estandarización del interfase: A pesar de que existen muchos puertos USB disponibles en una PC, es uno de los buses menos estandarizados dentro del campo
de adquisición de imágenes. Cada fabricante ha implementado su propio diseño
de hardware y software, lo que significa que muchas veces se requiere de un driver especı́fico para conectar la cámara con la PC. Por otro lado, hace muchos
años la Asociación de Intercambio 1394 formó un grupo que defina especificaciones de cámaras cuyo bus de comunicación sea IEEE 1394. El resultado de
ésta asociación es el estándar IIDC (Industrial and Instrumentation specification
for Digital Cameras), con muchos dispositivos de hardware para disparo e iluminación con comunicación a éste bus, ademas de la especificación completa de
comunicación de cámaras IEEE 1394a/b.
Uso del CPU: IEEE 1394 no requiere de un frame grabber, lo que significa que el
estandar confı́a en el CPU para la transferencia de imágenes hacia la memoria. En
USB, además de relegar la tarea de transferencia de imágenes hacia la memoria al
CPU, se requieren software utilitarios corriendo en segundo plano como el caso de
DirectShow, lo cual por supuesto genera mayor demanda de uso del procesador.
Disponibilidad de las cámaras: A pesar de que encontrar cámaras USB es muy
sencillo, la mayorı́a de aplicaciones de visión artificial a nivel industrial requieren
un rendimiento superior al que la electrónica de consumo puede ofrecer. IEEE
1394 ha sido un estandar industrial en cámaras para aplicaciones industriales por
más de 5 años. Actualmente se pueden encontrar cámaras infrarrojas, linescan,
de alta resolución, y de alta velocidad con bus de comunicación IEEE 1394.
En la figura 3.4 se puede apreciar la ventaja que supone desarrollar el sistema de
visión 3D con cámaras estandarizadas IIDC sobre cámaras con comunicación USB.
3.1.2.
Proyector luz estructurada
A pesar de la diversidad de patrones de iluminación estructurada que se pueden
encontrar en el mercado, para el desarrollo de este proyecto, en virtud de que se ha
diseñado una arquitectura redundante de visión estéreo + iluminación estructurada, se
eligió como proyector de iluminación estructurada un láser de lı́nea, con las siguientes
especificaciones:
Voltaje de operación: 3V
38
Figura 3.4: Comparación USB - IEEE 1394.
Corriente de operación: 300mA
Potencia del LED: 5mW − 532nm
Ángulo de generación: 110◦
En la figura 3.5 se muestra el aspecto fı́sico del generador de lı́nea láser. Esta lı́nea
se proyecta sobre los objetos bajo análisis para aplicar las técnicas de triangulación
activa y visión estereoscópica con correspondencia de puntos generada a través del
patrón de luz estructurada sobre el objeto.
3.1.3.
Circuito de control y comunicación con la PC
En base a las especificaciones de operación de las cámaras y del láser de lı́nea,
además de las necesidades del sistema de visión 3D, se propone un circuito que sea
capaz de manejar la corriente de los láseres de lı́nea, controlar un servomotor sobre el
que se monta el láser para barrer la lı́nea generada sobre el objeto bajo análisis. Cabe
destacar en este punto que se vuelve un requisito permitir que la PC controle desde
el software de aplicación el encendido/apagado de los láseres y el ángulo de giro del
motor que a su vez tiene montado el proyector de lı́neas sobre su eje. Para alcanzar éste
39
Figura 3.5: Proyector de luz estructurada.
propósito, se dota al circuito de control un interfase RS-232 para que a través del puerto
serie de la PC se envı́en las instrucciones pertinentes al circuito microcontrolado. En las
figuras 3.6 y 3.7 se ilustran los circuitos de control y el diseño de la tarjeta electrónica.
3.2.
Ventajas de la configuración estereoscópica con
iluminación estructurada
El aspecto que guarda mayor complejidad en un sistema de visión estéreo no se
encuentra en el cálculo de la profundidad, sino en la determinación de las correspondencias utilizadas en éste cálculo. En caso de que alguna correspondencia esté incorrecta,
el cálculo de las coordenadas en el espacio será incorrecto también [14]. Las técnicas
más utilizadas para el establecimiento de correspondencias, son las que se detallan a
continuación:
Correlación cruzada. Parte de la suposición de que para un punto P1 en una
imagen I1 (la primera imagen del par estéreo), existirá una región fija en la imagen I2 (la segunda imagen del par estéreo) en la cual se localizará el punto P2
que corresponde al punto P1 . La técnica de búsqueda, utiliza el operador de
correlación cruzada a los vecindarios cercanos a P2 , hasta que se encuentre el
pı́xel que maximice la respuesta a ésta operación, que será el correspondiente a
40
Figura 3.6: Circuito de control y comunicación.
su par P1 . En la figura 3.8 se ilustra el análisis de correlación cruzada en un par
de imágenes estéreo.
Emparejamiento simbólico y restricciones relacionales. Se debe realizar
la búsqueda de una caracterı́stica en una imagen que se relacione con alguna
caracterı́stica en la otra imagen. Las caracterı́sticas que tı́picamente se utilizan
son cruces, segmentos de lı́nea, o regiones. La técnica de búsqueda, normalmente
se basa en el etiquetamiento de imágenes binarias, de forma que sea más sencillo
relacionar caracterı́sticas sin consumir demasiado tiempo del procesador.
Uno de los problemas tı́picos en sistemas de visión estéreo, se da cuando no es
posible detectar las caracterı́sticas de la primera imagen, en la segunda. Algunas caracterı́sticas pueden simplemente no estar presentes, debido a la ubicación de las cámaras.
Ocurre por ejemplo que, algunas caracterı́sticas serán visibles en una imagen, pero en
la otra estarán ocultas.
La configuración del sistema de visión 3D presentada en la figura 3.1, por tanto
tiene la ventaja de proyectar un patrón de iluminación conocido sobre el objeto, lo
cual permitirá simplificar el problema de correspondencia puesto que el procesamiento
de las imágenes será sobre lı́neas ubicadas y orientadas de manera distinta en cada
imagen, como se ilustra en la figura 3.9. Claramente se puede notar que en las dos
41
Figura 3.7: PCB del circuito de control y comunicación.
imágenes (Izquierda y Derecha), se encuentra presente la lı́nea proyectada por el láser
sobre el objeto a analizar. Adicionalmente, resulta importante destacar que el hecho de
procesar únicamente lı́neas en las dos imágenes, reducirá significativamente el tiempo
de procesamiento.
El problema de correspondencia para esta aplicación, se reduce por tanto a la
búsqueda de “puntos de quiebre” en las lı́neas de cada imagen, que en la práctica
representan cambios en la orientación de la superficie sobre la que está siendo proyectada
la lı́nea del láser, y que a la postre nos brindará la información necesaria para la
reconstrucción tridimensional del objeto bajo análisis.
42
Figura 3.8: Problema de correspondencia analizado con correlación cruzada.
3.3.
Calibración del sistema de visión
El proceso de calibración del sistema de visión consiste en utilizar una pieza (objeto) con dimensiones conocidas en el espacio, y a través del conocimiento de las coordenadas bidimensionales (u, v) en cada imagen, y utilizando el proceso detallado en la
sección 2.4, se encuentran matrices de calibración para cada una de las cámaras del
sistema, con las que es posible calcular las coordenadas de los puntos del objeto en
el espacio. En [7] se detalla el procedimiento de calibración de un sistema de visión
estéreo. Previo al proceso de calibración, resulta importante pre-procesar las imágenes,
justamente con el objetivo de reducir la complejidad del problema de correspondencia,
de forma que se obtengan como imágenes resultado únicamente las lı́neas que el laser
proyecta sobre el objeto a analizar.
En la figura 3.10 se ilustra un diagrama de flujo del proceso de calibración y
Pre-procesamiento de las imágenes, cuyos pasos se detallan en las secciones siguientes.
3.3.1.
Adquisición de las imágenes
La plataforma de software en la que se desarrolla el presente trabajo de investigación es LabVIEW 2009 de la firma National Instruments. Se utilizan dos cámaras con
formato de comunicación IEEE 1394a, cuyas caracterı́sticas técnicas se describen en la
subsección 3.1.1. El detalle de programación en LabVIEW para adquirir las imágenes
desde las cámaras se presenta en la figura 3.11, de donde es posible resaltar cuatro
43
Figura 3.9: Simplificación del problema de correspondencia a través de la redundancia
del sistema de visión.
pasos básicos:
Crear espacio de memoria. Las imágenes que están siendo adquiridas por las
cámaras se colocan en la memoria RAM de la computadora a través del bloque
“IMAQ Create”. Se recomienda manejar con cuidado la cantidad de espacios
de memoria que se creen a lo largo del desarrollo de la aplicación puesto que se
podrı́an generar cargas excesivas de memoria, y por ende problemas en depuración
y tiempos de ejecución.
Adquirir la imagen. Una vez que la sesión con la cámara ha sido abierta, la
función “Grab” se encarga de realizar adquisición continua de las imágenes, a la
velocidad que la cámara ha sido configurada. En esta aplicación la velocidad de
transferencia de imágenes es de 30 fps (cuadros por segundo).
Mostrar imagen en pantalla. La opción de despliegue de imágenes es opcional.
Por ejemplo, en el caso de éste sistema el objetivo es adquirir la información de la
geometrı́a del objeto bajo análisis y no interesan el par de imágenes estereo, sin
embargo en la etapa de desarrollo se vuelve fundamental desplegar las imágenes
en pantalla para corroborar el resultado de ciertos algoritmos.
Cerrar sesión. Al momento en que la aplicación se detenga se deben cerrar las
sesiones de las cámaras, de forma que en la siguiente oportunidad en que éste
recurso (cámaras) sea llamado se encuentre disponible, asimismo es recomendable
destruir los espacios de memoria RAM generados.
3.3.2.
Pre-procesamiento de las imágenes
La etapa de Pre-procesamiento del par de imágenes estéreo, es quizás una de
las que se debe realizar con mayor cuidado, ya que los resultados posteriores depen44
Figura 3.10: Diagrama de flujo del algoritmo de calibración.
derán fuertemente del desempeño que aquı́ se obtenga. El par de imágenes adquiridas
utilizarán los mismos algoritmos de Pre-procesamiento, por lo que se describirán los
algoritmos utilizados en una de las dos imágenes.
El objetivo de ésta etapa es básicamente segmentar la información de la imagen
adquirida de forma que se obtenga como resultado únicamente la lı́nea que el láser
proyecta sobre el objeto, como se ilustra en la figura 3.12. Para lograr éste resultado,
como se puede suponer, es necesario binarizar la imagen utilizando como lı́mites de
umbralización, valores que se aproximen a la intensidad luminosa de los pı́xeles que
forman la lı́nea láser proyectada sobre el objeto a analizar. Posteriormente, en virtud
de que algunos pı́xeles que no pertenecen a la lı́nea laser proyectada sobre el objeto
45
Figura 3.11: Adquisición de imágenes en LabVIEW.
también están presentes en la imagen luego de haber sido binarizada, se utiliza un
filtro que elimine los clústeres de pı́xeles de la imagen con áreas menores a 3 pı́xeles,
a través del uso de la herramienta morfológica de erosión y luego la de dilatación, con
un elemento estructurante de tamaño 3 × 3.
Figura 3.12: Preprocesamiento de las imágenes.
3.3.3.
Barrido del ángulo del láser
La proyección de una lı́nea láser sobre el objeto que se encuentra bajo análisis
permite, a través del procesamiento del par de imágenes estéreo, resaltar las carac46
terı́sticas geométricas de éste. Sin embargo, la proyección de ésta lı́nea resalta una
pequeña porción de la totalidad del volumen, y para cubrir la geometrı́a completa que
se encuentra disponible en las imágenes de la configuración estereoscópica, I1 e I2 , se
proponen algunos métodos entre los que se destacan dos sencillos:
1. Se propone mover el objeto longitudinalmente a lo largo de una distancia, y1
constante medida desde el eje y del sistema (la elección del eje y se debe a la
manera en la que se ubicó el sistema coordenado de referencia fijo); y
2. Otra solución, que es precisamente la que se propone en éste trabajo, considera la
no movilidad del objeto, y en consecuencia la rotación del ángulo de proyección
del láser de lı́nea de forma que cubra la totalidad del cuerpo del objeto bajo
inspección.
La modificación del ángulo de proyección del láser se logra rotando el eje del
servomotor, al cual se encuentra acoplado el proyector de luz estructurada, generándose
ası́ el barrido láser. En el anexo 2 se detalla la programación en Microcode utilizando
lenguaje Basic del microcontrolador, que se dedica al control del encendido y apagado de
los láseres y se encarga de gestionar la comunicación (RS232) entre la tarjeta electrónica
y la PC.
3.3.4.
Correspondencia de puntos
La complejidad y los métodos que tradicionalmente se utilizan para solucionar el
problema de correspondencia en visión estereoscópica se analizaron en la sección 3.2.
La proyección de un patrón conocido sobre el objeto que será objeto de análisis, simplifica notablemente el problema de hallar la correspondencia de puntos en el par de
imágenes estéreo, y por otra parte, el pre-procesamiento de las imágenes se reduce a
la búsqueda de imágenes que den como resultado lı́neas con geometrı́as relacionadas
directamente con la forma de los objetos, como se aprecia en la figura 3.12. Resulta
por tanto sencillo notar que la correspondencia de puntos del par de imágenes estéreo
para el cálculo de coordenadas tridimensionales se simplifica a la búsqueda de puntos
de inflexión en las lı́neas láser proyectadas sobre el objeto, en cada imagen. A pesar de
que el procedimiento aparenta ser sencillo, se requieren de heurı́sticas bien elaboradas
para alcanzar precisión en la estimación de los puntos de inflexión en el par de imágenes
estéreo.
Para simplificar la búsqueda de los mencionados puntos, primeramente se aplicó el
algoritmo de esqueletización de la imagen pre-procesada, de forma que el espesor de las
lı́neas se reduzca a un pı́xel de ancho y ası́ resulta aún más factible el procesamiento
por análisis de conectividad. En la figura 3.13 se presenta el resultado de aplicar el
47
algoritmo de esqueletización a la imagen pre-procesada. Claramente se pueden notar,
analizando la figura 3.13, que existen puntos de inflexión en la lı́nea, además de puntos
de bifurcación, de inicio y fin. Un detalle importante a considerar, sobre todo al momento de calibrar el sistema, tiene que ver con el resultado de la esqueletización, puesto
que el algoritmo merma en un pı́xel la longitud del segmento de lı́nea en cada lado, lo
que podrı́a generar imprecisiones al momento de realizar las mediciones en el espacio,
por lo que se recomienda incluir esta reducción al momento de generar las matrices de
calibración del sistema.
Figura 3.13: Esqueletización de la imagen preprocesada.
Conectividad entre pı́xeles
Cuando se habla de pı́xeles conectados entre sı́ o yuxtapuestos, es necesario precisar el tipo de conexión o conectividad que se acepta como válida. En principio, un pı́xel
de una malla rectangular puede estar conectado con los ocho pı́xeles que le rodean en un
espacio plano o solamente con los cuatro más cercanos, como se ilustra en la figura 3.14.
El algoritmo de búsqueda de los puntos de inflexión por tanto analizará las conectividades entre los vecinos de los pı́xeles que forman parte de la lı́nea obtenida luego de
la “esqueletización”, y en donde se cumplan las heurı́sticas detalladas en la tabla 3.1.
Es requisito almacenar las coordenadas de los puntos en una posición definida de un
vector, de forma que al aplicar el mismo algoritmo en la otra imagen del par estéreo se
obtenga los puntos de inflexión en las mismas posiciones del vector almacenado en la
primera imagen, solucionándose ası́ el problema de correspondencia, para seguidamente
dar paso a los cálculos de la geometrı́a en el espacio del objeto.
48
Figura 3.14: Conectividad entre pı́xeles.
Heurı́sticas 5 × 5
xi = [(r1 = 0) ∨ (r1 = 0)] ∧ [(c3 = 0) ∨ (c1 = 0)]
(3.1)
Heurı́sticas 3 × 3
yi = [(r1∼ = 1) ∧ (r2∼ ≥ 2) ∧ (c∼
1 = 3)] ∧ [(c3 = 0) ∨ (c1 = 0)] ∧ [(r3 ≥ 2) ∨ (r4 ≥ 2)]
(3.2)
En la figura 3.15 se ilustran las formaciones de las submatrices 5 × 5 y 3 × 3 para
el criterio de las heurı́sticas que se detallan en la tabla 3.1.
3.3.5.
Cálculo de las matrices de calibración
El algoritmo utilizado en la sección 2.4.1, para estimar matrices de calibración a
partir de una tabla de datos con coordenadas espaciales conocidas y la correspondencia
de puntos en el par de imágenes estéreo se aplica de manera idéntica para calibrar el
sistema real. La diferencia principal con los datos utilizados en el ejemplo desarrollado
en la sección 2.4.1, radica en que los puntos de calibración que se utilizan para el sistema prototipo se toman de una pieza construida con precisión en una maquina CNC,
49
Columna (c)
c0
c1 c∼
0
c2 c∼
1
c3 c∼
2
c4
10 s (5 × 5) 10 s (3 × 3) Operación Lógica
0
xi ∨ y i
2
1
xi ∨ y i
4
3
xi ∨ y i
0
0
xi ∨ y i
0
0
xi ∨ y i
Fila (r)
r0
r1 r0∼
r2 r1∼
r3 r2∼
r4
10 s (5 × 5) 10 s (3 × 3) Operación Lógica
1
xi ∨ y i
1
1
xi ∨ y i
1
1
xi ∨ y i
2
2
xi ∨ y i
1
xi ∨ y i
Tabla 3.1: Heurı́sticas para la localización de los puntos de inflexión.
cuyo diseño se ilustra en la figura 3.16.
La geometrı́a del patron de calibración, que se aprecia en la figura 3.16, se debe
a las variaciones en las pendientes de los segmentos de recta que forman parte de las
aristas de éste, permitiéndo ası́ la generación de una cantidad considerable de puntos de
calibración a través del movimiento del ángulo de proyección del láser de lı́nea (patrón
de iluminación estructurada). Para capturar los puntos de calibración a utilizar en el
algortimo de minimización del error para la estimación de las matrices del sistema, se
eligieron puntos especı́ficos en la pieza de la figura 3.16. En la práctica, se obtienen estos
puntos luego de procesar las lı́neas que el proyector de luz estructurada genera sobre
el patrón de calibración a través del algoritmo de estimación de los puntos de inflexión
desarrollado anteriormente, cuyo detalle se explica en la sección 3.3.4, de forma que se
obtenga un vector con las correspondencias de los puntos en el par de imágenes estéreo
y las coordenadas reales de la pieza en el espacio, considerando un sistema coordenado
fijo.
La correspondencia de puntos y las coordenadas tridimensionales de los puntos de
calibración se muestran en la tabla 3.2.
El resultado de aplicar el algoritmo implementado en la sección 2.4 se resume
en las matrices de calibración estimadas C1 y C2 , correpondientes a la calibración
geométrica espacial de las cámaras izquierda y derecha, respectivamente. Las matrices
50
Figura 3.15: Formaciones de las submatrices 5 × 5 y 3 × 3 para el criterio de las heurı́sticas.
de calibración C1 y C2 se utilizarán más adelante para el cálculo de las coordenadas en
el espacio de puntos especı́ficos a través del procesamiento de la información del par
de imágenes estéreo, ası́ como de distancias e información relevante de la geometrı́a del
objeto bajo prueba.

0.5260 -3.6640 -2.6531 514.7103
=  -1.0930 -1.1390 -2.7945 382.6006 
0.0014 -0.0040 -0.0058 1.000000


0.2495 -3.7308 -2.0109 520.2729
=  -1.0692 -1.3172 -2.5344 374.2948 
0.0014 -0.0044 -0.0053 1.000000

C1
C2
51
(3.3)
(3.4)
Figura 3.16: Diseño del patrón de calibración.
3.4.
Validación de la calibración del sistema
Para validar la calibración del sistema y sobre todo emitir un criterio de precisión, utilizamos el mismo patrón que en la etapa de calibración, descrito en la sección
3.3.5, cuyo detalle se presenta en la figura 3.17. La interfaz hombre-máquina (HMI)
implementado en LabVIEW para las pruebas de calibración y medición de distancias
se ilustra en la figura 3.18, en donde resulta sencillo notar que a través de la determinación de los puntos de inflexión de las imágenes estéreo previamente preprocesadas,
mismos que se hallan utilizando el algoritmo detallado en la sección 3.3.4, es posible
formar la matriz de puntos que se presenta en la tabla 3.2.
52
Figura 3.17: Puntos de calibración en la pieza.
Para verificar la precisión y validar la calibración del sistema, es necesario realizar
mediciones sobre el objeto patrón en los mismos puntos en los que se capturaron para
el cálculo de las matrices; luego se deben contrastar las distancias medidas con las
reales del patrón de calibración y ası́ poder estimar un error de medición promedio
y la desviación estándar del mismo, herramientas que utilizaremos como medidas de
variabilidad para emitir un criterio de precisión del sistema de visión 3D. Los resultados
de éstas pruebas se ilustran en la tabla 3.3.
Los datos presentados en la tabla 3.3 permiten calcular cantidades de la estadı́stica descriptiva tı́picas, como la variabilidad del error a través de su media aritmética y
desviación estándar, cuyos valores son µ = 0,3361mm y σ = 1,1301mm. La disperción
de los datos del error, su relación con su media aritmética (µ) y la desviación estándar
(σ) se ilustran en la figura 3.19. Resulta sencillo concluir a partir de los resultados de
la tabla 3.3 y la gráfica 3.19 que la precisión del sistema en medición de distancias se
aproxima a ≈ ±1 mm. La precisión anteriormente definida a través de las medidas
53
Figura 3.18: HMI implementado en LabVIEW para el proceso de calibración.
de variabilidad del error, nos permitirá más adelante analizar el desempeño del sistema cuando se sometan objetos diferentes al de calibración a pruebas similares a las
realizadas en este punto.
54
Punto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
w
Px
0.00
53.00
1.84
51.16
3.68
49.32
5.52
47.48
7.36
45.64
9.20
43.80
11.04
41.96
12.28
40.72
13.52
39.48
14.76
38.24
16.01
36.99
17.25
35.75
18.49
34.51
19.73
33.27
20.97
32.03
22.21
30.79
23.45
29.55
w
Py
0.00
0.00
5.00
5.00
10.00
10.00
15.00
15.00
20.00
20.00
25.00
25.00
30.00
30.00
33.00
33.00
36.37
36.37
39.74
39.74
43.12
43.12
46.49
46.49
49.86
49.86
53.23
53.23
56.60
56.60
59.97
59.97
63.34
63.34
w
Pz
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
46.00
42.31
42.31
38.62
38.62
34.92
34.92
31.23
31.23
27.24
27.24
23.85
23.85
20.15
20.15
16.46
16.46
12.77
12.77
9.08
9.08
1
IC
535.00
521.00
529.00
515.00
514.00
500.00
500.00
492.00
485.00
477.00
470.00
467.00
464.00
457.00
452.00
447.00
440.00
437.00
431.00
429.00
422.00
421.00
415.00
414.00
405.00
405.00
397.00
396.00
389.00
390.00
380.00
379.00
373.00
372.00
1
IR
348.00
238.00
347.00
251.00
342.00
247.00
339.00
250.00
335.00
255.00
331.00
258.00
332.00
261.00
334.00
269.00
336.00
279.00
339.00
287.00
341.00
295.00
346.00
302.00
348.00
311.00
351.00
320.00
353.00
326.00
357.00
336.00
359.00
343.00
2
IC
562.00
528.00
558.00
524.00
542.00
514.00
538.00
507.00
520.00
494.00
508.00
487.00
495.00
479.00
487.00
469.00
474.00
458.00
463.00
449.00
449.00
440.00
439.00
430.00
427.00
420.00
419.00
411.00
407.00
402.00
400.00
390.00
383.00
383.00
2
IR
342.00
239.00
339.00
241.00
332.00
245.00
335.00
247.00
328.00
252.00
324.00
253.00
317.00
255.00
324.00
263.00
327.00
271.00
329.00
278.00
332.00
285.00
332.00
293.00
334.00
301.00
340.00
308.00
340.00
315.00
348.00
323.00
346.00
330.00
Tabla 3.2: Puntos de calibración en el espacio y coordenadas en el par de imágenes
estéreo.
55
Punto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
1
IR
609
568
602
562
591
553
575
545
570
538
529
526
539
519
533
516
517
502
504
490
490
485
480
470
470
462
462
454
449
444
442
437
432
429
1
IC
328
229
327
232
324
235
320
238
320
241
258
245
309
247
310
250
317
261
317
269
322
277
325
288
329
296
331
303
333
311
337
317
340
324
2
IR
604
592
596
587
582
576
556
563
556
553
538
540
532
532
524
523
510
509
500
500
493
494
480
482
472
474
465
466
455
457
449
450
442
350
2
IC
346
236
342
238
338
242
331
246
331
248
328
254
325
325
324
259
330
270
331
279
334
286
338
297
340
306
342
311
345
320
347
325
442
333
Distancia Medida (mm) Distancia Real (mm)
52.235
53.00
Error
-0.765
51.937
49.32
2.617
47.421
45.64
1.7814
41.966
41.96
0.0064
39.421
38.28
1.141
34.121
34.60
-0.478
29.140
30.92
-1.78
27.335
28.44
-1.105
25.197
25.96
-0.763
23.558
23.48
0.078
21.271
20.98
0.291
18.881
18.50
0.381
16.211
16.02
0.191
14.55
13.54
1.01
11.554
11.06
0.494
10.270
8.58
1.69
7.0243
6.10
0.9243
Media Aritmética del Error 0.3361
Desviación Estándar del Error 1.1301
Tabla 3.3: Resultados de la validación de la calibración del sistema.
56
Figura 3.19: Dispersión del error en las mediciones de distancia realizadas sobre el
objeto patrón.
57
Capı́tulo 4
Desarrollo de una metodologı́a para inspección de
objetos con visión estereoscópica e iluminación
estructurada
El desarrollo de un sistema experimental y una evaluación superficial de resultados
en su funcionamiento fueron objeto de estudio del capı́tulo anterior. Sin embargo, la
meta de investigación de ésta tesis es la de establecer una metodologı́a para implementar sistemas de inspección tridimensional a nivel industrial que permitan solucionar
problemas relacionados al control de calidad en lı́neas de manufactura, y es justamente
por ello que en el desarrollo de éste capı́tulo se encuentran los resultados de diferentes
pruebas del sistema, con los cuales se establece una correcta secuencia de pasos para
la solución de problemas de inspección 3D. En la sección 4.1 se aborda con detalle la
evaluación del desempeño del sistema experimental con objetos diferentes al utilizado
en la calibración y diferentes condiciones de iluminación. En la sección 4.2 se desarrolla y explica la metodologı́a utilizada a lo largo de éste trabajo de investigación, para
presentar finalmente en la última sección el método que permite alcanzar los objetivos
de inspección tridimensional a nivel industrial.
4.1.
4.1.1.
Evaluación del desempeño del prototipo
Precisión del sistema
La medición de distancias en el espacio es uno de los aspectos de mayor utilidad
a nivel industrial en procesos de control de calidad asistidos por sistemas de visión
artificial 2D y 3D, por lo que es menester conocer la precisión del sistema propuesto en
el capı́tulo anterior para realizar mediciones sobre objetos con caracterı́sticas diversas.
La evaluación de la precisión en las mediciones realizadas por el prototipo de la figura
3.3 se realiza utilizando 2 objetos diferentes, de forma que sea posible contrastar los
resultados aquı́ obtenidos entre sı́ mismos y con los de la sección 3.4. El primer objeto
con el que se realiza la evaluación del desempeño y prueba de precisión es un rectángulo
sencillo de dimensiones 50 × 56 × 20 mm, como se ilustra en la figura 4.1.
58
Para completar la geometrı́a del objeto con el haz de luz estructurada, como se
detalló en la subsección 3.3.3, se realiza el barrido del ángulo del láser a lo largo de
la cara superior del rectángulo cuya dimensión real es de 49,6 mm. En la tabla 4.1 se
muestran los resultados de 7 capturas de lı́neas láser proyectadas en diferentes posiciones
del objeto, mismas que se detallan en la figura 4.1, que dan como resultado 14 puntos, 2
por cada recta, con los cuáles se realizan las mediciones de distancias correspondientes
y cálculos del error en esa medición.
Figura 4.1: Objeto de prueba para mediciones longitudinales.
El análisis del error de las mediciones que se presentan en la tabla 4.1, nos entrega como resultado una media aritmética, µ = −0,393 y una desviación estándar,
σ = 1,385 mm, a partir de lo cual podemos concluir que la precisión aproximada del
sistema será de 1,385 mm y que las mediciones estarán dentro de un rango de error
59
Punto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
IR
586
554
567
536
552
524
536
505
517
489
494
467
469
467
1
IC
357
270
359
270
361
269
365
271
364
272
369
274
372
274
2
IR
596
585
578
565
558
551
534
532
517
513
487
485
457
485
2
IC
376
278
380
278
381
278
379
279
382
279
381
281
383
281
Distancia Medida (mm) Distancia Real (mm)
50.143
49.6
Error
0.543
49.594
49.6
-0.006
49.230
49.6
-0.37
51.241
49.6
1.641
48.852
49.6
-0.748
47.12
49.6
-2.48
47.899
49.6
-1.701
Media Aritmética del Error -0.393
Desviación Estándar del Error 1.385
Tabla 4.1: Resultados de la medición de distancias sobre el rectángulo de prueba.
de ±1,3 mm, lo cual es bastante cercano al resultado obtenido en la sección 3.4. La
geometrı́a de éste primer objeto de prueba es muy sencilla, sin embargo ha permitido
confirmar la confiabilidad del sistema al menos en mediciones de la superficie de un
sólido.
En la figura 4.2 se muestra la geometrı́a del segundo objeto utilizado para comprobar la precisión del sistema. La prueba que se realiza en esta oportunidad consiste
en la medición del ancho de la pieza en varios puntos de ésta a través del barrido del
láser a lo largo de su superficie, cuya medida real es de 28,33 mm. De manera parecida
al caso anterior, se resumen los resultados de las mediciones en la tabla 4.2. A pesar de
que en ésta etapa de validación no estamos decodificando mayormente la información
tridimensional del sistema, puesto que nos hemos concentrado en mediciones de distancias, la geometrı́a de éste segundo objeto de prueba permite confirmar la robustez
del sistema calibrado puesto que presenta pendientes y cambios de alturas, lo que no
sucedı́a en el primer experimento con el objeto de la figura 4.1.
El análisis del error de las mediciones que se presentan en la tabla 4.2, nos entrega como resultado una media aritmética, µ = −0,59 y una desviación estándar,
σ = 1,226 mm. A pesar de que la desviación estándar se parece mucho a los resultados
obtenidos en la sección 3.4 y los de la tabla 4.1, la media aritmética es mucho más
60
Figura 4.2: Medición del ancho de una pieza tridimensional.
alta que en los casos anteriores, divergiendo esta vez considerablemente de cero. La
desviación de los resultados se puede atribuir a que estamos utilizando una pieza de
mayor longitud a la que se uso en la calibración del sistema y que abarca un área no
calibrada, lo cual se puede observar en el resultado de las mediciones 9, 11 y 13 de la
tabla 4.2 que corresponde a los puntos más lejanos del origen del sistema coordenado
del sistema cuya coordenada en y alcanza valores cercanos a los 78 mm y la elevación
en z es de 50 mm, mientras que para ese valor coordenado en y el patrón de calibración tenı́a elevaciones en z cercanas a cero. La observación más importante que este
resultado nos arroja, radica en que para optimizar los resultados de precisión sobre un
objeto, se recomienda fuertemente calibrar el sistema con un objeto patrón de idéntica
geometrı́a a los de una lı́nea de producción, en la que este sistema se podrı́a instalar.
61
Punto
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
IR
612
590
599
327
585
562
570
551
543
526
456
442
454
423
1
IC
327
271
578
272
330
271
338
278
351
293
335
275
340
276
2
IR
608
602
593
591
577
568
561
557
538
535
424
434
404
410
2
IC
345
281
344
281
346
281
353
288
367
303
342
280
344
281
Distancia Medida (mm) Distancia Real (mm)
28.126
28.33
Error
-0.204
28.84
28.33
0.51
27.151
28.33
-1.179
26.982
28.33
-1.348
26.872
28.33
-1.458
26.41
28.33
-1.92
29.794
28.33
1.464
Media Aritmética del Error
Desviación Estándar del Error
-0.59
1.226
Tabla 4.2: Resultados de la medición de distancias sobre la pieza de la figura 4.2.
Resulta importante destacar, que ha pesar de que el sistema es capaz de detectar
todos los puntos de inflexión producidos en el quiebre del láser producto de la geometrı́a
del objeto bajo análisis, la decodificación de la información tridimensional se realiza en
función del ángulo de proyección del patrón de iluminación estructurada (lı́nea laser),
que en éste sistema no es fijo y además es desconocido. Es posible realizar una notable
observación a partir del análisis de los resultados de las mediciones de las dos piezas
utilizadas para la evaluación de la precisión del sistema, y radica en el hecho de que
la eficiencia máxima en éste sistema se consigue aplicando mediciones sobre objetos
idénticos al usado como patrón de calibración. Adicionalmente, para facilitar la interpretación de la información tridimensional se recomienda fijar en un ángulo conocido
la proyección del haz de luz estructurada y recorrer el objeto a lo largo de algún eje
del sistema coordenado fijo. En la figura 4.3 se ilustra una representación de los puntos
en el espacio correspondientes al objeto de calibración (patrón), de la que se puede
destacar la forma que los puntos en el espacio tornean, que como era de esperarse se
parece mucho a la de la figura 3.16.
Claramente se puede observar que existen variaciones en los puntos estimados
pertenecientes a las aristas del objeto, que estarán dentro del rango de tolerancia determinado en la sección 3.4. La reconstrucción visual en 3D están fuera del alcance de
62
Figura 4.3: Reconstrucción del patrón de calibración en 3D.
éste trabajo de investigación, sin embargo en [3, 5, 18, 19] se presentan varias técnicas
para éste propósito.
4.1.2.
Pruebas de precisión sobre un objeto de manufactura
Además de desarrollar una metodologı́a para la medición de objetos en el espacio
a través de la combinación de las técnicas de visión estéreo e iluminación estructurada,
es de particular interés en el desarrollo de esta tesis el comprobar la precisión del sistema en la determinación de distancias en objetos de manufactura, por lo que en este
punto se muestran los resultados de aplicar mediciones y estimaciones de los puntos en
el espacio correspondientes a tres objetos con una geometrı́a como la que se muestra
en la figura 4.4.
En la tabla 4.3 se muestran los resultados de ésta prueba experimental para 3
diferentes objetos con la geometrı́a de la figura 4.4. Es decir, a través de ésta prueba
se pretende simular los resultados que arrojarı́a un sistema instalado en una lı́nea de
manufactura.
Los resultados presentados en la tabla 4.3 muestran pequeños errores en la determinación de las longitudes l1 y l2 sobre las tres diferentes piezas. Analizando con
cuidado los resultados, es posible rescatar los siguientes aspectos importantes:
63
Figura 4.4: Objeto de manufactura utilizado para comprobar la precisión del sistema.
Precisión del sistema. A pesar de que el sistema no fue calibrado para trabajar
exclusivamente con ésta pieza, la calibración realizada en la sección 3.3.5 nos ha
permitido obtener mediciones con errores mucho menores a 1mm, excepto en el
primer resultado de la tabla, cuyo error en la medición de l2 es mayor a 1mm
puede atribuirse a ruido sobre la medición. Adicionalmente, en las condiciones
de operación del sistema actuales, se puede notar que existe un incremento en
la imprecisión cuando se requieren medir pequeñas distancias, y esto se debe
justamente a la resolución de las cámaras con las que estamos trabajando.
Precisión de las mediciones manuales. En la figura 4.4 se presentan las dimensiones de diseño de la pieza utilizada para las pruebas experimentales, cuyas medidas difieren ligeramente a las utilizadas en la tabla 4.3, puesto que se tomaron
manualmente utilizando un calibrador. La ventaja de utilizar un sistema de inspección automático resalta notablemente en este punto, puesto que la realización
de ésta operación de medición tomo muchı́simo más tiempo que la determinación
de distancias hecha de manera automática por el sistema.
64
Pieza
1
2
3
l1 medida l2 medida l1 real l2 real Error l1
24.099
9.6967
23.9
7.8
0.199
23.187
7.253
23.9
7.8
-0.713
23.325
NA
23.9
7.8
-0.575
24.682
8.3944
24.01
8.1
0.672
24.89
8.8968
24.01
8.1
0.88
24.53
NA
24.01
8.1
0.52
24.011
7.315
23.9
7.78
0.111
23.173
7.901
23.9
7.78
-0.727
24.533
NA
23.9
7.78
0.633
Error l2
1.8967
-0.547
NA
0.2944
0.7968
NA
-0.465
0.121
NA
Tabla 4.3: Resultados de la medición de distancias sobre la pieza manufactura de la
figura 4.4.
4.1.3.
Operación bajo diferentes condiciones de iluminación
A pesar de que el objetivo en esta ocasión es el de obtener atributos tridimensionales de un objeto bajo prueba, la condición de iluminación más favorable para el
sistema prototipo construido, es aquella en la que existe ausencia de luz sobre la escena,
de forma que sea posible únicamente capturar la lı́nea láser del proyector del haz de luz
estructurada con sus correspondientes deformaciones debidas a la geometrı́a del objeto.
En la figura 4.5 se muestra la imagen de la captura de la escena de trabajo de una de
las cámaras y su correspondiente preprocesamiento, de donde se puede observar que
el preprocesamiento no puede cumplir con el propósito de obtener como caracterı́stica
final de la imagen únicamente la lı́nea láser proyectada sobre el objeto bajo análisis.
Para lograr ese propósito, deberı́a utilizarse un láser de mayor potencia y de un color
que resalte en el ambiente, de forma que a través de procesamiento de la imagen en
color la segmentación sea un éxito.
Si por otro lado, las condiciones de iluminación son más favorables al sistema, es
decir existe poca luz en el ambiente o ausencia de ella, el preprocesamiento se vuelve
más eficiente y existe menos propensión a errores. En la figura 4.6 se ilustra el resultado de procesar una imagen en un ambiente de poca iluminación, que como se
puede observar, se ajusta a los requerimientos de los algoritmos y la metodologı́a hasta
aquı́ implementada en éste trabajo. Se recomienda por tanto, utilizar el sistema en
ambientes donde no exista iluminación natural y la lı́nea láser del proyector de luz
estructurada resalte sobre cualquier otra reflectancia del objeto bajo prueba. Debemos
recordar que el objetivo de la iluminación estructurada en nuestro caso puntual es el de
resaltar atributos tridimensionales, y no estamos interesados en aumentar el contraste
65
Figura 4.5: Preprocesamiento fallido de la imagen. Sistema funcionando en un ambiente
con demasiada luz.
de la escena capturada, como en el caso del procesamiento de imágenes en 2D.
Figura 4.6: Preprocesamiento exitoso sobre una de las imágenes capturadas del par
estéreo.
4.2.
Metodologı́a utilizada en el desarrollo del proyecto
La continua revisión del estado del arte en el procesamiento de imágenes en 3D,
y el estudio de técnicas similares a las que han sido presentadas en éste trabajo de investigación, condujeron el desarrollo de nuestra aplicación de sensor tridimensional por
etapas en principio desconocidas que fueron a su vez desencadenando nuevas opciones
para continuar la búsqueda del objetivo principal de esta tesis. En la figura 4.7 se presenta un bosquejo de los pasos que se siguieron durante el desarrollo de los algoritmos,
prototipo, formulación matemática y el HMI (Human Machine Interface), que como
se puede notar, a pesar de haber estado someramente establecidos, fueron objeto de
66
continuos cambios y actualizaciones que dieron como resultado la metodologı́a que se
presenta en la sección siguiente.
Figura 4.7: Pasos seguidos a lo largo del camino de investigación.
Resulta sencillo notar de la figura 4.7 que la problemática empieza con la elección
del sistema tridimensional a usar, presentándose las siguientes opciones: Sistema de
visión estereoscópica, Sistema de visión tridimensional con iluminación estructurada y
una cámara, y finalmente la opción elegida para éste trabajo que fue la combinación de
las dos técnicas mencionadas anteriormente, cuyo detalle y ventajas se describen en la
sección 3.2. Vale la pena destacar que a pesar de que existe gran cantidad de literatura
relacionada con sistemas de visión tridimensional, son mı́nimas las aportaciones de sistemas como el propuesto en éste trabajo. La calibración del sistema, por otro lado, se
puede realizar de diversas maneras y depende del sistema elegido en la etapa anterior,
no obstante es fundamental realizar bien éste paso puesto que la precisión global del
sistema depende mucho del éxito con el que se estimen las matrices C1 y C2 . Proba67
blemente el diagrama de transición de estados no expresa con claridad la problemática
que la implementación práctica presentó, sin embargo resulta fundamental contar con
un algoritmo de Pre-procesamiento de las imágenes funcionando correctamente previo
a la calibración del sistema, puesto que la precisión en la adquisición de los puntos en el
espacio para la estimación de las matrices de calibración está sujeta a diversos factores
como: condiciones de iluminación, distancia de trabajo, ubicación de las cámaras en el
espacio y la resolución de las cámaras.
Una vez que el sistema ha sido correctamente calibrado, se podrı́a decir que el
50 % del trabajo está hecho, constituyendo la otra mitad la elaboración de los algoritmos de decodificación tridimensional, desarrollo y refinamiento de algoritmos de
preprocesamiento de las imágenes y la presentación de la información 3D. La etapa que
mayores contratiempos presentó en éste trabajo fue la elaboración de los algoritmos de
decodificación tridimensional que consistió en segmentar la información de las imágenes
de forma que únicamente se obtengan en vectores las coordenadas de los puntos de inflexión del par de imágenes estéreo, para a continuación presentar una colección de
puntos en el espacio que tornean la forma del objeto bajo análisis, además de mostrar
el detalle de las mediciones longitudinales de las piezas bajo inspección.
El caos de pasos que se persiguieron y se han detallado hasta aquı́, se aclaran y
definen metodológicamente en la siguiente sección.
4.3.
Metodologı́a para la integración de visión estéreo
e iluminación estructurada para la inspección
de objetos y adquirir atributos 3D
Metodologı́a es una palabra compuesta por tres vocablos griegos: metà (“más
allá”), odòs (“camino”) y logos (“estudio”), cuyo concepto hace referencia a los métodos de investigación que permiten lograr ciertos objetivos en una ciencia. Se proponen,
por tanto en la figura 4.8 la secuencia ordenada de pasos que se deben seguir para la
integración de las técnicas de visión estereoscópica e iluminación estructurada para la
inspección de objetos en 3D.
En las secciones siguientes se detallan los pasos propuestos en ésta metodologı́a y
los resultados que se deberı́an esperar en cada etapa.
68
Figura 4.8: Metodologı́a para la integración de las técnicas de visión estereoscópica e
iluminación estructurada para inpección de objetos en 3D.
69
4.3.1.
Selección de los componentes del sistema
En función del ambiente en el que sistema se encontrará operando, la precisión
que se busque y el presupuesto del proyecto, se deben seleccionar los componentes
que formarán parte del sistema de visión tridimensional. El equipamiento principal
está compuesto por los siguientes elementos:
2 Cámaras. Se utilizan para la configuración estéreo y no hace falta que sean
idénticas, sin embargo es muy recomendable contar con cámaras de caracterı́sticas
similares. Uno de los aspectos importantes en la elección de las cámaras, tiene
que ver con el formato de comunicación, cuya discusión se presentó en la sección
3.1.1. La segunda consideración relevante al momento de elegir las cámaras es la
resolución, que está involucrada directamente con la precisión que se espera que
el sistema ostente, para lo cual se propone la siguiente estimación sencilla, en la
que se involucra también la distancia focal, como parámetro de libre elección.
Figura 4.9: Selección del lente de la resolución y el lente de la cámara.
Fl = 4,65mm D = 200mm SS = 2,4mm
D
200
F OV = SS
= 2,4
Fl
4,65
F OV = 103,22mm
Resolucion = 640 × 480 pixeles
F OVvertical = 103mm
T amanoP ixel =
103
= 0,21mm
480
70
De manera sencilla podemos deducir que mientras mayor sea la resolución, el
tamaño de los pı́xeles será menor y por tanto la precisión del sistema mejorará,
asimismo se puede notar que existe una fuerte influencia de la distancia de trabajo
y la distancia focal, por lo que se recomienda elegir con cuidado éstos parámetros
para maximizar la eficiencia del sistema final.
Proyector de luz estructurada. En virtud de que se pretende simplificar el problema de correspondencia en el par de imágenes estéreo, se recomienda utilizar
un láser de lı́nea con una potencia de al menos 5mW , y de un color que permita asimismo sintetizar el preprocesamiento de las imágenes, es decir que ofrezca
suficiente contraste sobre la superficie del objeto bajo análisis.
Software. Éste elemento del sistema es de libre elección y el proyectista deberı́a
optar por la opción en la que se sienta más cómodo desarrollando, o en su defecto
existen plataformas comerciales que no requieren programación sino únicamente
configuraciones por pasos, como el caso del NI Vision Builder for Automated
Inspection de National Instruments. Sin embargo, existen requerimientos mı́nimos
que el software elegido debe cumplir:
1. Comunicación con cámaras de diferentes formatos, y en nuestro caso puntual
por lo menos IEEE 1394.
2. Calcular distancias en el objeto a través de manipulaciones matriciales y
operaciones matemáticas, probablemente esto se desarrolları́a dentro de un
script.
3. Integración con otros dispositivos, puesto que una aplicación de visión es
con frecuencia una parte de un sistema de control mucho más grande.
4.3.2.
Configuración del ambiente de trabajo
Difı́cilmente un ingeniero de aplicación puede elegir la problemática en la que
desea trabajar, y por ende el ambiente de trabajo tampoco. Por tanto, la configuración
del ambiente de trabajo más bien se relaciona con los siguientes aspectos:
Ubicación de los componentes del sistema. En la sección anterior se detallaron
los componentes mı́nimos necesarios para la implementación de una cámara 3D.
La disposición de las cámaras y el proyector de luz estructurada tiene un fuerte
impacto en la complejidad de los algoritmos, por lo cual se recomienda considerar
las siguientes recomendaciones:
1. Definir un sistema coordenado derecho dentro del campo de visión de las
cámaras.
71
2. La ubicación de las cámaras debe favorecer la adquisición de la geometrı́a de
los objetos, por tanto el criterio de emplazamiento de éstas debe contemplar
el no generar oclusiones de una imagen con respecto a la otra.
3. El proyector de luz estructurada preferentemente deberı́a generar lı́neas láser
paralelas a alguno de los ejes del plano en el que la pieza reposa.
4. Definir la zona en la que el objeto será ubicado para el análisis, y ası́ realizar
las pruebas de calibración en esa área, figura 3.1.
La iluminación del ambiente preferentemente deberı́a ser tenue para una mejor y
mayor distinción del haz de luz sobre la superficie del objeto y el ambiente propiamente, sin embargo esta recomendación está sujeta a la potencia del proyector de
luz estructurada y a su color. Asimismo, es recomendable evitar ambientes con
exceso de impurezas como polvo, debido a que en un plazo extendido afectarı́a la
visibilidad de las cámaras por las partı́culas que se podrı́an depositar sobre los
lentes. En caso de que el ambiente sea de caracterı́sticas no favorables, deberı́a
programarse una limpieza perı́odica sobre los lentes de las cámaras y el proyector
de luz estructurada.
4.3.3.
Desarrollo y pruebas de algoritmos de Pre-procesamiento
de imágenes
No existe un acuerdo general entre autores que especifique en donde termina el
área del procesamiento digital de imágenes y otras áreas empiezan, tales como el análisis
de imágenes y visión por computadora. Muchas veces se realiza esta distinción definiendo al procesamiento digital de imágenes como una disciplina en la cual el ingreso y la
salida del sistema son imágenes [25]. Por otro lado, los campos de visión por computadora pretenden emular la visión humana, incluyendo procesos de aprendizaje y toma
de decisiones, por lo que conviene definir niveles de procesamiento para ubicar nuestros
diferentes algoritmos en este contexto. En la figura 4.10 se ilustran los niveles de procesamiento en aplicaciones que involucran imágenes digitales.
Los algoritmos de Pre-procesamiento de imágenes, que tienen como propósito simplificar la información del par de imágenes estéreo de forma que el resultado de éstas
operaciones sea únicamente la lı́nea láser proyectada sobre la superficie del objeto bajo
prueba, como se ilustra en la figura 4.6, se ubican por tanto en los niveles de procesamiento de bajo nivel para el mejoramiento de la imagen y también en el nivel de
procesamiento de nivel medio para segmetar la imagen. Para el desarrollo de los algoritmos de preprocesamiento de las imágenes se recomiendan las siguientes técnicas:
Procesamiento de Bajo Nivel. Necesariamente se debe realizar un ajuste de contraste para que el lı́nea láser proyectada sobre el objeto bajo prueba sea lo que
72
Figura 4.10: Niveles de procesamiento en aplicaciones que involucran imágenes digitales.
más resalte en la imagen. Adicionalmente, es muy recomendable realizar un enmascaramiento de la región de interés (ROI - Region of Interest) a través de
operaciones lógicas.
Procesamiento de Nivel Medio. La idea en éste punto es segmentar la imagen
“mejorada” a través del procesamiento de bajo nivel. Las operaciones recomendadas son principalmente:
• Binarización. Con éste método es posible convertir una imagen de varios
niveles de gris a una nueva con solo dos, de tal forma que los objetos quedan
separados del fondo, siendo el interés separar la lı́nea láser proyectada sobre
el objeto.
1 → Ta ≤ f (x, y) ≤ Tb
g (x, y) =
(4.1)
0 → C.C.
El problema está en encontrar los valores de gris a tomar como umbrales para
aplicar la ecuación 4.1, por lo que la configuración del ambiente y la elección
de los componentes del sistema serán decisivos en la reducción del ruido en
la imagen adquirida y permitirán disminuir la complejidad del algoritmo.
• Esqueletización. Se pretende reducir a un pı́xel de grosor las lı́neas láser
capturadas por las cámaras para que la búsqueda de los puntos de inflexión
73
más adelante sea más sencillo.
El resultado del preprocesamiento de las imágenes deberı́a ser parecido al que se
ilustra en la figura 4.6 y evitar obtener resultados como el que se muestra en la figura
4.5.
4.3.4.
Validación de la calibración del sistema
Uno de los puntos neurálgicos que determinan el desempeño global del sistema
radica en la calibración de éste. Existen varios enfoques para éste propósito ([28, 29]),
sin embargo se propone utilizar el método estudiado en la sección 2.4 y ejecutado en la
sección 3.3. La idea básica es utilizar un objeto con dimensiones conocidas que tenga
suficiente variabilidad en el espacio, de forma que la captura de los puntos que forman
parte de su geometrı́a permitan estimar matrices de calibración que trabajen bien en
al menos el espacio en el que los objetos bajo prueba se situarán. La literatura formal
[14] menciona que por lo menos se deben utilizar 6 puntos en el espacio con sus correspondientes ubicaciones en las imágenes del par estéreo, sin embargo trabajos como los
realizados en [9] utilizan incluso 150 puntos. En la calibración realizada en éste trabajo
de investigación se utilizaron 34 puntos, obteniendo un resultado relativamente bueno,
considerando la resolución de las cámaras, con precisión en las mediciones próxima a
1mm.
La validación de la calibración deberı́a hacerse cotejando los datos en el espacio
reales del objeto de calibración, con los estimados por el sistema a través de las matrices
de calibración previamente estimadas. En [27] se presenta un amplio análisis sobre el
problema asociado con la calibración geométrica de las cámaras a través la aplicación
del diseño de experimentos.
4.3.5.
Decodificación de información tridimensional
Una vez que la calibración del sistema nos ha brindado resultado adecuados, el
siguiente paso consiste en interpretar la información que podemos capturar del espacio
a través del sistema de adquisición (cámaras en configuración estéreo + proyector de
luz estructurada). Considerando que las imágenes a procesar serán parecidas a las que
se ilustra en la figura 4.6, el objetivo ahora será el de encontrar los puntos de inflexión
de las lı́neas láser proyectadas sobre el objeto bajo inspección. En virtud de que éstos
puntos de inflexión se presentan en las dos imágenes, el problema de correspondencia
de visión estereoscópica queda resuelto y lo que se deberı́a hacer a continuación es
calcular los puntos en el espacio pertenecientes a los puntos de intéres que nuestros
algoritmos calculen. En la figura 4.11 se presenta el esquema de lo que el algoritmo de
74
decodificación 3D en primera instancia deberı́a realizar.
Figura 4.11: Decodificación de puntos de inflexión.
Una vez que los puntos en el espacio han sido estimados, resulta sencillo calcular
distancias utilizando la formula de Euler. En la sección 3.3.4 se detalla el algoritmo de
decodificación tridimensional implementado en éste trabajo de investigación.
75
Capı́tulo 5
Conclusiones y trabajos futuros
En esta última parte de éste trabajo se presentan las conclusiones más relevantes
del proceso de investigación, algunas reflexiones sobre los resultados, y una breve descripción de futuras investigaciones y alcances acerca de cámaras tridimensionales para
inspección en lı́neas de manufactura. La sección 5.1 presenta las conclusiones de la tesis,
y la sección 5.2 menciona las próximas investigaciones en sistemas de visión 3D.
5.1.
Conclusiones
Los resultados presentados a lo largo de ésta travesı́a investigativa han sido alentadores en el aspecto de aplicaciones potenciales que se podrı́an beneficiar de la metodologı́a
que se describe en la sección 4.3, identificándose principalmente las siguientes áreas de
oportunidad:
Asistencia y/o decisión autónoma en el control de calidad, a través de inspección
sin contacto en lı́neas de manufactura.
Clasificación de productos con geometrı́as distintas en lı́neas de producción.
Ingenierı́a inversa.
Robótica móvil.
Complemento para aplicaciones de realidad aumentada y realidad virtual.
La precisión del sistema en la medición de distancias y estimación de puntos en
el espacio tiene relación directa con la resolución de la cámara que se utilice en la aplicación, como se detalla en la sección 4.3.1. Utilizando una cámara con una resolución
mayor a la utilizada en nuestro proyecto (640 × 480), definitivamente incrementará la
precisión en las mediciones y estimación de los puntos del objeto en el espacio. Existe
sin embargo, la posibilidad de compensar esta limitación de hardware a través de una
correcta ubicación de los elementos del sistema de visión artificial, de forma que por
ejemplo el objeto bajo prueba abarque por completo el campo de visión de la cámara
76
(FOV - Field of View). La precisión del sistema de visión también puede variarse a
través de la modificación del lente de la cámara, por lo que una cámara industrial que
posea la montura C-mount para lentes, podrı́a experimentar diferentes precisiones a
través del reemplazo de un lente por otro de mayor ó menor distancia focal. Por tanto,
a través de la modificación de la distancia focal, el tamaño de los pı́xeles en unidades
métricas se verá modificado también, por lo que la elección y ubicación de todos los
componentes del sistema debe realizarse de manera cuidadosa.
A pesar de las limitaciones de hardware, restringidas principalmente por el presupuesto del proyecto, la precisión alcanzada es aceptable (aproximadamente ≈ ±1 mm),
en la figura 3.19 se ilustra la disperción del error en la medición de distancias realizada
sobre el objeto patrón y en donde es posible apreciar los lı́mites dentro de los cuáles se
ubica el error. Sin embargo, al utilizar objetos pequeños para el análisis de dimensiones
y puntos en el espacio y ubicaciones fijas para las cámaras y el patrón de luz estructurada, la precisión no fue superior debido a que los objetos ocupaban una pequeña
área del FOV.
El haber elegido cámaras cuya comunicación estándar es IEEE 1394, y especificaciones IIDC, garantiza que esta aplicación pueda adaptarse a cámaras con especificaciones más robustas y de capacidades mayores, de forma que su integración a aplicaciones industriales sea más sencilla.
Uno de los grandes problemas de visión estereoscópica, que tiene que ver con la
correspondencia de puntos en las imágenes, fue resuelto a través de la proyección de
un patrón de iluminación conocido (una lı́nea láser) sobre el objeto bajo análisis, simplificando el procesamiento a la búsqueda de puntos en las lı́neas proyectadas en el par
de imágenes estéreo, capturadas por las cámaras, en los que se detecten cambios de
pendiente sobre la tendencia global de la lı́nea, que son los atributos que justamente
guardan el detalle tridimensional de las imágenes. Este fue el método utilizado para
fusionar los técnicas de visión estereoscópica e iluminación estructurada.
El tiempo de procesamiento de una lı́nea láser proyectada sobre el objeto bajo
análisis, con la cual se podrı́a medir sin contacto distancias de la pieza, es de 0,25 segundos. Resulta sencillo por tanto notar, que un ‘scan’ completo de una pieza con 20
lı́neas tardarı́a alrededor de 5 segundos, lo cual por supuesto mejora notablemente el
tiempo de medición sobre una pieza para verificar sus dimensiones en una lı́nea de producción, comparado con el caso de que se lo realice de manera manual. Cabe destacar
en este punto que las caracterı́sticas del computador con el que se está trabajando son
las siguientes: Procesado Intel(R) Core(TM)2 Duo CPU P8600 @ 2.40GHz, memoria
RAM 2.00 GB y sistema operativo Windows 7 de 64 bits, por lo que un computador
77
de prestaciones mayores asegurarı́a mejores tiempos de respuesta también.
La metodologı́a de calibración de las cámaras y el haz de luz estructurado no
restringe el uso de cámaras idénticas, sin embargo se recomienda fuertemente utilizar
por lo menos cámaras de caracterı́sticas similares. La propuesta de calibración de las
cámaras presentada en la sección 2.4 no demanda el conocimiento de las caracterı́sticas internas de las cámaras como distancia focal, tamaño del lente, etc., por lo que
fácilmente se pueden utilizar diferentes modelos de cámaras.
5.2.
Trabajos futuros
Uno de los grandes atractivos de los sistemas de visión tridimensional se encuentra
en las formas en que la información capturada y procesada por el sistema es presentada
al usuario. En el presente trabajo de investigación, el enfoque fue la adquisición de la
información y el desarrollo de una metodologı́a principalmente, sin embargo el paso
siguiente que esta investigación debe dar por su propia inercia, será la presentación de
la colección de los puntos en el espacio en forma sólida a través de técnicas de ingenierı́a
inversa.
Adicionalmente, y por otro lado, se realizarán esfuerzos por parte de los involucrados en este proyecto por instalar un sistema de caracterı́sticas similares al prototipo
desarrollado, en una lı́nea de manufactura, y ası́ confirmar los resultados e incluso soñar
con la comercialización masiva de sistemas de este tipo y/o de servicios a empresas de
manufactura.
78
Apéndice A
Algoritmo de calibración en Matlab
Se presenta a continuación el código implementado en Matlab para la solución
del ejemplo de la subsección 2.4.1. Resulta importante destacar que al ser un código de
estructura tipo fichero *.m, puede ejecutarse también en ambientes como Mathematica,
LabVIEW Mathscript, Mapple, etc.
%************************* - Cálculo de posición 3D - *************************
%** Autor: Ismael Minchala A.
**
%** Fecha: 12/09/2010
**
%**
**
%**
A partir de datos de varios puntos en el espacio, y el conocimiento
**
%**
de las coordenadas de cada uno de los puntos en dos imágenes distin**
%**
tas se calculan las matrices de calibración para cada cámara (C1,C2)
**
%**
y luego se utilizan éstas matrices para estimar otro punto en el
**
%**
espacio tridimensional.
**
%******************************************************************************
clc
clear all
%Limpiar pantalla
%Borrar todas las variables
%**************************** - Matriz de Datos - *****************************
M = [0 0 0 167 65 274 168; 0 15.24 0 96 127 196 42;
27.94 15.24 0 97 545 96 431; 27.94 0 0 171 517 154 577;
20.955 0 -11.43 352 406 366 488; 6.985 0 -11.43 347 186 430 291;
13.97 0 -8.89 311 294 358 387; 13.97 15.24 -8.89 226 337 0 0;
0 0 -1.905 198 65 303 169; 27.94 0 -1.905 203 518 186 577;
5.08 0 0 170 143 248 248; 5.08 15.24 0 96 198 176 116;
22.86 15.24 0 97 465 114 363; 22.86 0 0 173 432 176 507;
20.955 0 -4.5974 245 403 259 482; 6.985 0 -4.5974 242 181 318 283];
%******************************************************************************
[r c] = size(M);
%Dimensiones de M
79
%*************************** - Matrices de Puntos - ***************************
for j = 1:r
WP(j,:) = M(j,1:3);
%Matriz de puntos 3D
IP1(j,:) = M(j,4:5);
%Matriz de puntos Cámara 1
IP2(j,:) = M(j,6:7);
%Matriz de puntos Cámara 2
end
%******************************************************************************
%************************ - Matrices de Coeficientes - ************************
for j = 1:r
a = 2*j - 1;
A1(a:a+1,:) = [WP(j,1) WP(j,2) WP(j,3) 1 0 0 0 0 -WP(j,1)*IP1(j,1)
-WP(j,2)*IP1(j,1) -WP(j,3)*IP1(j,1); 0 0 0 0 WP(j,1)
WP(j,2) WP(j,3) 1 -WP(j,1)*IP1(j,2) -WP(j,2)*IP1(j,2) -WP(j,3)*IP1(j,2)];
A2(a:a+1,:) = [WP(j,1) WP(j,2) WP(j,3) 1 0 0 0 0 -WP(j,1)*IP2(j,1)
-WP(j,2)*IP2(j,1) -WP(j,3)*IP2(j,1); 0 0 0 0 WP(j,1)
WP(j,2) WP(j,3) 1 -WP(j,1)*IP2(j,2) -WP(j,2)*IP2(j,2) -WP(j,3)*IP2(j,2)];
b1(a:a+1,1) = IP1(j,:)’;
b2(a:a+1,1) = IP2(j,:)’;
end
A2 = [A2(1:14,:);A2(17:32,:)];
b2 = [b2(1:14,:);b2(17:32,:)];
%******************************************************************************
%**** - Estimación de las matrices de calibración por mı́nimos cuadrados - *****
c1 = A1\b1;
c2 = A2\b2;
C1 = [c1(1) c1(2) c1(3) c1(4); c1(5) c1(6) c1(7) c1(8); c1(9) c1(10) c1(11) 1];
C2 = [c2(1) c2(2) c2(3) c2(4); c2(5) c2(6) c2(7) c2(8); c2(9) c2(10) c2(11) 1];
%******************************************************************************
%************************** - Estimación de errores - *************************
for j = 1:r
T1 = C1*[WP(j,1) WP(j,2) WP(j,3) 1]’;
80
T2 = C2*[WP(j,1) WP(j,2) WP(j,3) 1]’;
IPE1(j,:) = [T1(1)/T1(3) T1(2)/T1(3)];
IPE2(j,:) = [T2(1)/T2(3) T2(2)/T2(3)];
end
E1 = IP1 - IPE1;
E2 = IP2 - IPE2;
E2 = [E2(1:7,:);E2(9:16,:)];
%******************************************************************************
%*********** - Cálculo de coordenadas 3D con datos de las cámaras - ***********
for j = 1:r
A = [C1(1,1)-C1(3,1)*IP1(j,1)
C1(2,1)-C1(3,1)*IP1(j,2)
C2(1,1)-C2(3,1)*IP2(j,1)
C2(2,1)-C2(3,1)*IP2(j,2)
C1(1,2)-C1(3,2)*IP1(j,1)
C1(2,2)-C1(3,2)*IP1(j,2)
C2(1,2)-C2(3,2)*IP2(j,1)
C2(2,2)-C2(3,2)*IP2(j,2)
C1(1,3)-C1(3,3)*IP1(j,1);
C1(2,3)-C1(3,3)*IP1(j,2);
C2(1,3)-C2(3,3)*IP2(j,1);
C2(2,3)-C2(3,3)*IP2(j,2);];
b = [IP1(j,1)-C1(1,4); IP1(j,2)-C1(2,4); IP2(j,1)-C2(1,4); IP2(j,2)-C2(2,4);];
WPE(j,:) = (A\b)’;
end
%******************************************************************************
81
Apéndice B
Programación Basic del microcontrolador
Se presenta a continuación el código implementado en Microcode Studio Plus 4.0.0.0 en
lenguaje Basic para la programación del archivo de salida hexadecimal que se descarga en un
microcontrolador PIC16F876A que controla el encendido y apagado de láseres conectados en
el puerto B, además de controlar el ángulo de giro de un servomotor a través de instrucciones
que recibe de un computador mediante comunicación RS-232.
’*********************************************************************
’* Name
: Control_Laser
*
’* Author : Ismael Minchala A.
*
’* Notice : Copyright (c) 2011 ITEMS
*
’*
: All Rights Reserved
*
’* Date
: 30/01/2011
*
’* Version : 2.1
*
’* Notes
: Control de ángulo de un servomotor a través del
*
’*
: incremento/decremento del ancho de pulso, cuya se~
nal
*
’*
: de comando proviene de una PC con comunicación serial. *
’*
: Se permite también el encendido y apagado de dos
*
’*
: láseres conectados al puerto B.
*
’*********************************************************************
’******************* - Inicialización del Sistema - ******************
INCLUDE
"modedefs.bas"
’ Librerı́a para la comunicación serial
DEFINE
OSC
4
’ Frecuencia del Oscilador 4MHz
DATO
VAR
BYTE
’ Variable almacenamiento comm serial
I
VAR
BYTE
’ Variable de lazo For
PULSO
VAR
WORD
’ Variable de control PWM
PULSO = 1690
’ Se inicializa en 90
TRISB = 0
’ Todo el PORTB como salidas
PORTB = $FF
PAUSE
1000
’ Pulso de Prueba, sistema Vivo
82
PORTB = 0
for I = 1 to 10
’ Prueba de generación PWM
HIGH
PORTB.3
PAUSEUS PULSO
’ Pulso define ángulo giro del motor
LOW
PORTB.3
PAUSE
20
next i
’*********************************************************************
’************************ - Lazo de Control - ************************
INICIO:
’ Etiqueta
SERIN PORTC.7,T2400,Dato
’ Escribe la info recibida en Dato
IF DATO = 65 then
PORTB = $01
ENDIF
’ Si Recibe "A"
’ Encender láser 1
IF DATO = 66 THEN
PORTB = $02
ENDIF
’ Si Recibe "B"
’ Encender láser 2
IF DATO = 67 THEN
PORTB = $00
ENDIF
’ Si Recibe "C"
’ Apaga todo el puerto B
if DATO = 68 then
for I = 1 to 1
PULSO = PULSO + 1
HIGH
PORTB.3
PAUSEUS PULSO
LOW
PORTB.3
PAUSE
10
NEXT I
ENDIF
’ Si Recibe "D"
if DATO = 69 then
for I = 1 to 1
PULSO = PULSO - 1
HIGH
PORTB.3
PAUSEUS PULSO
LOW
PORTB.3
’ Incrementar ángulo del motor
’ Si Recibe "E"
’ Decrementar ángulo del motor
83
PAUSE
NEXT I
ENDIF
10
Goto INICIO
END
’*********************************************************************
84
Bibliografı́a
[1] M. Bansal, A. Jain, T. Camus, and A. Das. Towards a practical stereo vision sensor. In
Computer Vision and Pattern Recognition - Workshops, 2005. CVPR Workshops. IEEE
Computer Society Conference on, page 63, 2005.
[2] PEÑÍN Luis BARRIENTOS Antonio. Fundamentos de Robótica - Segunda Edición. Mc
Graw Hill, España, 2007.
[3] F. Bernardini, I.M. Martin, and H. Rushmeier. High-quality texture reconstruction from
multiple scans. Visualization and Computer Graphics, IEEE Transactions on, 7(4):318
–332, 2001.
[4] Rushmeier H. Bernardiniand F. The 3D model acquisition pipeline. Computer Graphics
Forum, vol.21, no.2,pp.149-172, 2002.
[5] P.J. Besl and H.D. McKay. A method for registration of 3-d shapes. Pattern Analysis
and Machine Intelligence, IEEE Transactions on, 14(2):239 –256, February 1992.
[6] B.D. Bradley, A.D.C. Chan, and M.J.D. Hayes. A simple, low cost, 3d scanning system
using the laser light-sectioning method. In Instrumentation and Measurement Technology
Conference Proceedings, 2008. IMTC 2008. IEEE, pages 299 - 304, pages 299 – 304, May
2008.
[7] C. Chen and A. Kak. Modeling and calibration of a structured light scanner for 3-d robot
vision. In Robotics and Automation. Proceedings. 1987 IEEE International Conference
on, volume 4, pages 807 – 815, March 1987.
[8] Intel Lucent Microsoft NEC Philips Compaq, Hewlett-Packard. Universal Serial Bus
Specification. USB Org, USA, 2009.
[9] Haihua Cui, Ning Dai, Tianran Yuan, Xiaosheng Cheng, and Wenhe Liao. Calibration algorithm for structured light 3d vision measuring system. In Image and Signal Processing,
2008. CISP ’08. Congress on, volume 2, pages 324 –328, May 2008.
[10] R. Szeliski D. Scharstein. High-accuracy stereo depth maps using structured light. In
Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and
Pattern Recognition, pages 195–202, 2003.
85
[11] Daniel Crispell Douglas Lanman and Gabriel Taubin. Surround structured lighting for
full object scanning. In Sixth International Conference on 3-D Digital Imaging and
Modeling, pages 107–116, 2007.
[12] URESTI Eduardo. Mı́nimos cuadrados. Departamento de matemáticas, CCIR/ITESM,
México, 2009.
[13] Häusler G. and Hernanz B. 3d real time camera. In Fringe ’97, 3rd International
Workshop on Automatic Processing of Fringe Pattern, pages 237–246, 1997.
[14] SHAPIRO Linda – STOCKMAN George. Computer Vision. Prentice Hall, USA, 2001.
[15] GIROD Bern. – GREINER Günther. – NIEMANN Heinrich. Principles of 3D Image
Analysis and Synthesis. Kluwer Academic Publishers21, USA, 2002.
[16] Kwangik Hyun and L.A. Gerhardt. The use of laser structured light for 3d surface
measurement and inspection. In Computer Integrated Manufacturing and Automation
Technology, 1994., Proceedings of the Fourth International Conference on, pages 215
–221, October 1994.
[17] S.K. Case J.A. Jalkio, R.C. Kim. Three dimensional inspection using multistripe structured light. Optical Engineering, vol.24, pp. 966-974, 1985.
[18] G. Brockmann H. Baurecht K. Schwenzer-Zimmerer N. A. Papadopulos M. A. Papadopoulos R. Sader E. Biemer L. Kovacs*, A. Zimmermann and H. F. Zeilhofer. Accuracy and precision of the three-dimensional assessment of the facial surface using a 3-d
laser scanner. In IEEE TRANSACTIONS ON MEDICAL IMAGING, volume 25, pages
742–754, june 2006.
[19] Lijun Li, Yingjie Ke, and Kaiyong Jiang. Surface reconstruction based on computer
stereo vision using structured light projection. In Intelligent Human-Machine Systems
and Cybernetics, 2009. IHMSC ’09. International Conference on, volume 2, pages 451
–454, 2009.
[20] WALPOLE MYERS. Probabilidad y Estadı́stica para Ingenieros, Sexta Edición. Prentice
Hall, México, 1999.
[21] P.; Ofner R. O’Leary, P.; Schalk. Instrumentation and Analysis-Methods for the Measurement of Profiles using Light Sectioning. Instrumentation and Measurement Technology
Conference, 2006. IMTC 2006. Proceedings of the IEEE , vol., no., pp.1108-1113, 24-27
April 2006.
[22] G.N.; Kak A.C. Park, J.; DeSouza. Dual-beam structured-light scanning for 3-d object
modeling. In 3-D Digital Imaging and Modeling, 2001. Proceedings. Third International
Conference on, pages 65–72, 2001.
[23] K. Schluns R. Klette and A. Koschan. Computer Vision: Three-Dimensional Data from
Images. Springer-Verlag, 1998.
86
[24] M. Ribo and M. Brandner. State of the art on vision-based structured light systems
for 3d measurements. In Robotic Sensors: Robotic and Sensor Environments, 2005.
International Workshop on, 30 2005.
[25] GONZALEZ Rafael – WOODS Richard. Digital Image Processing, Second Edition. Prentice Hall, USA, 2002.
[26] COLLADO Rubén. Adquisición tridimensional de piezas industriales mediante técnicas
de luz estructurada. Universidad Politécnica de Madrid, España, 2007.
[27] P. Swapna, N. Krouglicof, and R. Gosine. The question of accuracy with geometric camera calibration. In Electrical and Computer Engineering, 2009. CCECE ’09. Canadian
Conference on, pages 541 –546, May 2009.
[28] Defeng Wu, Zi Ma, Aiguo Li, Wenbiao Wang, and Xiang Wu. A novel approach to
calibrate a structured light vision sensor in a robot based 3d measurement system. In
Modelling, Identification and Control (ICMIC), The 2010 International Conference on,
pages 298 –303, 2010.
[29] Qiaoyu Xu, Dong Ye, Rensheng Che, and Yan Huang. Accurate camera calibration
with new minimizing function. In Robotics and Biomimetics, 2006. ROBIO ’06. IEEE
International Conference on, pages 779 –784, 2006.
[30] FAUGERAS O. ZHANG Z. 3D Dynamic Scene Analysis. Springer-Verlag, Sophia Antiopolis, France, 1992.
[31] Gao Zhi, Zhong Sidong, Zhang Wei, and Zhu Yunyi. A high-precision calibration technique for laser measurement instrument and stereo vision sensors. In Electronic Measurement and Instruments, 2007. ICEMI ’07. 8th International Conference on, pages
214–217, 2007.
87