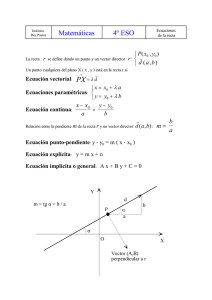
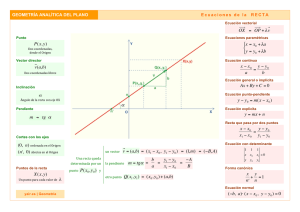
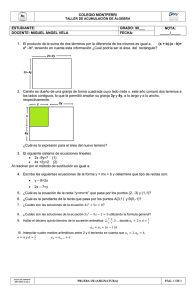
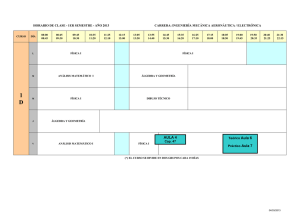
λ - Centro Concertado Juan XXIII Cartuja

BLOQUE TEMÁTICO II:
ÁLGEBRA LINEAL
Y
GEOMETRÍA
ALGEBRA
TEMA 1 Sistemas de ecuaciones lineales
TEMA 2 Matrices
TEMA 3 Determinantes
TEMA 4 Resolución de sistemas mediante
determinantes
GEOMETRÍA
TEMA 5 Vectores en el espacio
TEMA 6 Puntos, rectas y planos en el espacio
TEMA 7 Problemas métricos
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
1
1.- SISTEMAS DE ECUACIONES LINEALES
1ª. Sistemas de ecuaciones lineales. Clasificación
2ª. Interpretación geométrica de los sistemas de ecuaciones
lineales
3ª. Sistemas de ecuaciones equivalentes
4ª. Sistemas escalonados. Método de Gauss
5ª. Planteamiento de problemas
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
2
1ª.- Sistemas de ecuaciones lineales. Clasificación
Ecuaciones lineales: son ecuaciones polinómicas de primer grado con una o
varias incógnitas. Por ejemplo:

3x  2y  1 es una ecuación lineal con dos incógnitas.
o Representa una recta en el plano.
o Cada solución de la ecuación es una pareja de números (x, y) que
verifican (hacen cierta) la ecuación.
o Cada ecuación tiene infinitas soluciones, que son los infinitos puntos
del plano por los que pasa la recta.
o Los pares (1, 1), (3, 4)… son algunas de las infinitas soluciones de esa
ecuación.

x  2y  z  7 es una ecuación lineal con tres incógnitas.
o Representa un plano en el espacio.
o Cada solución de la ecuación es una terna de números (x, y, z) que
verifican (hacen cierta) la ecuación.
o Cada ecuación tiene infinitas soluciones, que son los infinitos puntos
del espacio por los que pasa el plano.
o Las ternas (9, 1, 0), (6, 0, 1)… son algunas de las infinitas soluciones
de la ecuación.

Los sistemas de ecuaciones lineales, están formados por varias ecuaciones
lineales de las que queremos saber las soluciones comunes.
a11x1
a21x1

am 1x1
 a12x 2    a1n xn  b1 
 a22x 2    a2n xn  b2 
        
 am 2x 2    amn xn  bm 
Sistema de “m” ecuaciones lineales con “n” incógnitas
Donde:
a11, …, aij son números reales llamados coeficientes del sistema
b1, …, bm son números reales llamados términos independientes y
x1, …, xn son las incógnitas del sistema.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
3
o Si todos los términos independientes son nulos, el sistema se llama
homogéneo.
a11x1
a21x1

am1x1
 a12x 2    a1n xn  0 
 a22x2    a2n xn  0 
       
 am 2x 2    amn xn  0 
Sistema homogéneo de “m” ecuaciones lineales con “n” incógnitas
o Resolver un sistema de ecuaciones lineales consiste en hallar la
solución o las soluciones comunes a todas las ecuaciones que forman
el sistema.
o La solución de un sistema de m ecuaciones con n incógnitas es un
conjunto de n números reales que verifican a la vez las m ecuaciones.
o Si la solución es única, decimos que el sistema es compatible
determinado; compatible indeterminado, si existen infinitas
soluciones, e incompatible, si no existiera ninguna.
o Los sistemas homogéneos, son todos compatibles, teniendo siempre
como una de sus soluciones, la solución x1 = 0, x2 = 0,…, xn = 0,
solución que se denomina trivial.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
4
2ª.- Interpretación geométrica de los sistemas de
ecuaciones lineales.
Los sistemas de n ecuaciones lineales con dos incógnitas,
representan n rectas en el plano: la solución nos informará de si existe o no, un
punto común a ellas, y cuál es dicho punto. Es decir, discutir y resolver un sistema
de ecuaciones con dos incógnitas nos permitirá conocer la posición relativa de las
rectas que representa.
Dos rectas que se
Tres rectas que se
cortan en un punto (SCD)
cortan en un punto(SCD)
Dos rectas paralelas
Dos rectas iguales
(SCI)
Tres rectas que se cortan dos a dos
No se cortan en ningún punto (SI)
No tienen ningún punto en común (SI)
Los sistemas de n ecuaciones lineales con tres incógnitas,
representan n planos en el espacio: la solución nos informará de si existen o no,
puntos comunes a ellos. Es decir, discutir y resolver un sistema de ecuaciones con
tres incógnitas nos permitirá conocer la posición relativa de los planos que
representan.
Tres planos que se
cortan en un punto (SCD)
Matemáticas II Álgebra lineal y Geometría
Cuatro planos que se
cortan en un punto (SCD)
CURSO 2014/15
Tres planos que se
cortan en una recta (SCI)
5
Cuatro planos que se cortan dos a dos
Tres planos que se cortan dos a dos
No tienen ningún punto en común (SI)
No tienen ningún punto en común (SI)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
6
3ª.- Sistemas de ecuaciones equivalentes
Dos sistemas de ecuaciones se dicen que son equivalentes si tienen las
mismas soluciones.
Para obtener un sistema de ecuaciones equivalente a uno dado inicialmente
se pueden aplicar cualquiera de las siguientes operaciones válidas:
OPERACIONES VALIDAS
1ª.- Multiplicar o dividir los dos miembros de una de las ecuaciones del
sistema por un nº distinto de cero.
2ª.- Sustituir una de las ecuaciones del sistema por una combinación
lineal de ella con otra.
3ª.- Añadir al sistema una nueva ecuación que sea una combinación
lineal de las otras.
4º.- Suprimir en el sistema una ecuación que sea combinación lineal de
las otras.
Ejemplo 1 – 1º
Observa como se van obteniendo sistemas equivalentes a los dados
inicialmente aplicando las transformaciones válidas:
a)
2x  y  5 
2x  y  5 
2x  y  5 


4x  2y  2  2ª:( 2) 2x  y  1 1ª 2ª
2y  6 
b)
2x  y  5  1ª .2 4x  2y  10 
4x  2y  10 
4x  2y  2 
4x  2y  2  1ª 2ª
4y  12 
c)
x  y  z  11 
x  y  z  11 
x  y  z  11 



x  y  z  7  1ª 2ª .( 1)  1ª 2ª 2y  2z  4 
2y  2z  4 
1ª .2  3 ª
2x  3y  3 
5y  2z  25  2ª .( 5)  3 ª .2
6z  30 
d)
x  y  z  11

x y z  7
e)
1ª 2ª .2
x  y  z  11 

x y z  7 
3x  y  z  25 
x  y  z  11 

x  y  z  11

x y z  7 

x y z  7

3x  y  z  25  3 ª  1ª 2ª .2

Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
7
Ejercicio 1 – 1º
Explica por qué son equivalentes los siguientes pares de sistemas:
a)
x  y  5
2x  y  7 
x  y z  5 

c)
x y
7 
2x  2y  z  12
x y  5
3x
 12 
x y

z  2

 7

b)
d)
x  y z  5 
z2 
x y
 7  x  y  7 
x  y  z  11

x  2y  z  7
x  y  z  11

y
 4
Ejercicio 1 – 2º
Comprueba que el par (1, - 4) es solución del sistema siguiente:
4x  y  8 

x  y  3 
17x  5y  3 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
8
4ª.- Sistemas escalonados. Método de Gauss
Discutir un sistema es analizar cuántas soluciones posee: una, infinitas o
ninguna. La discusión se hace de modo independiente a la búsqueda de la solución
y previamente a la misma.
Observa los siguientes sistemas:
x  3y  z  7 

5y  z  6 
3z  12 
2x  3y  14 
5y  10 
A estos sistemas se les llama escalonados y son muy fáciles de resolver porque
podemos obtener sucesivamente los valores de las incógnitas de abajo hacia arriba.
Pero, ¿cómo cómo se puede transformar un sistema cualesquiera en otro
escalonado?. La respuesta está en la aplicación de las transformaciones validas en
un sistema de ecuaciones, que hemos estudiado en la 3ª pregunta de este tema,
para obtener otro sistema equivalente.
El método de Gauss consiste en transformar un sistema de ecuaciones en
otro equivalente que sea escalonado, es decir, en el que cada ecuación tiene una
incógnita menos que la anterior:
ax  by  cz  d 

b ' y  c 'z  d ' 
c '' z  d '' 
El sistema escalonado final proporciona los datos necesarios para determinar
de qué tipo es el sistema de partida:
 Si c´´= 0 y d´´≠ 0, resulta una igualdad del tipo 0 = k (ecuación absurda)
con k ≠ 0, entonces el sistema es incompatible y no tiene solución.
 Si c´´≠ 0, sea cual sea el valor de d´´, el sistema es compatible
determinado y tiene una solución única. La resolución de la ecuación es
inmediata; en la tercera ecuación calculamos el valor de z, llevamos este
valor de z a la segunda ecuación y obtenemos el valor de y, y con ambos
valores calculamos el valor de x en la primera ecuación.
 Si c´´= d´´= 0, resulta una igualdad del tipo 0 = 0 (ecuación trivial que
podemos eliminar), en cuyo caso el sistema es compatible indeterminado
y tiene infinitas soluciones.
Resulta, así, un sistema con dos ecuaciones (una ecuación es
combinación lineal de las otras) y tres incógnitas, pues el sistema es
equivalente al sistema:
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
9
ax  by  cz  d 
b ' y  c ' z  d ' 
Para resolver este sistema, elegimos una de las dos incógnitas en la
ecuación que tiene dos (la y o la z) para asignarle un parámetro (una letra):
p.e. z = λ.
Decimos entonces que la incógnita z se ha parametrizado, siendo λ el
parámetro.
El parámetro puede tomar cualquier valor real. Para cada valor del
parámetro existe una solución del sistema.
Ejemplo 1 – 2º
Resuelve por el método de Gauss los siguientes sistemas de ecuaciones
lineales. Clasifícalos e interprétalos geométricamente:
a)
2x  y  5 
2x  y  5 

4x  2y  2  1ª.( 2) 2ª
 4y  12   y  3
2x  3  5  x  1
SOLUC: Es un sistema compatible determinado (SCD).
La solución es única y está formada por la pareja de números x = 1 y = 3
Se trata de dos rectas secantes del , es decir, dos rectas que se cortan en un punto cuyas coordenadas son (1,3)
IMPORTANTE I: La aplicación del método de Gauss puede hacerse mas cómoda si,
prescindiendo de las incógnitas, nos limitamos a utilizar sólo los coeficientes y los
términos independientes.
Veámoslo en el ejemplo anterior:
2 1 5 
1ª
 4 2 2   1ª:( 2)2ª


b)
2x  y  5  2x  3  5  x  1
2 1 5 

  4y  12  y  3
0

4

12


2x 5y 3z  4 

x 2y z  3  
5x y 7z  11
 2 5 3 4 


 1 2 1 3 
 5 1 7 11


 2 5 3 4 
 2 5 3 4 
 2 5 3
1ª
1ª
4 






1

2
1
3

1ª 2ª .2

0

1
1

2

2ª

0

1
1

2 





 5 1 7 11 1ª .( 5 )  3ª .2
 0 27 1 2  2ª .27  3ª
 0 0 26 52 






(3ª) 26z = -52 ; z = -2
(2ª) –y + z = -2 : -y + (-2) = -2 ; y = 0
(1ª) 2x – 5y +3z = 4 ; 2x - 5.0 + 3.(-2) = 4 ; x = 5
SOLUC: Es un sistema compatible determinado (SCD).
La solución es única y está formada por la terna de números x = 5 y = 0 z = -2
Se trata de tres planos en el espacio que se cortan en un único punto cuyas coordenadas son (5,0,-2)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
10
IMPORTANTE II: La aplicación del método de Gauss puede hacerse aún más
cómoda si alguna de las ecuaciones tiene coeficiente 1 en la incógnita x. Si
ponemos esta ecuación en primer lugar las transformaciones del sistema en
sistemas equivalentes es menos engorrosa.
Veámoslo en el ejemplo anterior:
2x 5 y 3z  4  x 2y z  3 


x 2y z  3   2x 5y 3z  4  
5x  y 7z  11 5x  y 7z  11
 1 2 1 3 


 2 5 3 4 
 5 1 7 11


 1 2 1 3 
 1 2 1 3 
 2 5 3
1ª
1ª
4 






  0 1 1 2   z  2
 2 5 3 4   1ª .( 2)  2ª .   0 1 1 2   2ª
 5 1 7 11 1ª .( 5)  3ª
 0 11 2 4  2ª .11  3ª
 0 0 13 26 






y 0
x 5
IMPORTANTE III: Si en todas las ecuaciones del sistema los coeficientes de x son
distinto de 1, podríamos buscar una ecuación que tuviera coeficiente 1 en y ó en z,
ponerla en primer lugar y cambiar el orden de las incógnitas (el mismo orden en
todas las ecuaciones).
c)
x 3y 7z  10 

5x y
z  8  
x 4y 10z  11
 1 3 7
10 


8 
 5 1 1
 1 4 10 11


 1 3 7
 1 3 7
 1 3 7
10 
1ª
10 
1ª
10 






8   1ª .( 5)  2ª   0 14 34 42   2ª
  0 14 34 42  
 5 1 1
 1 4 10 11
 0 7 17
0 0
1ª 3ª
21  2ª 3 ª .2
0
0 




La 3ª ecuación obtenida es la ecuación trivial 0 = 0. Esto ha sido así porque en el sistema
equivalente, anterior a la última transformación, las ecuaciones 2ª y 3ª eran equivalentes (ya que son
proporcionales entre sí). Por tanto podemos eliminar una de ellas del sistema. Pasaremos la incógnita
z al segundo miembro llamándole λ. El sistema quedaría:
x 3y 7z  10 

14y 34z  42
2ª:2
x 3y 7z  10  z λ x 3y  10 7λ 

7y 17z  21
7y  21 17λ 
Y a continuación resolvemos el sistema de ecuaciones en función del parámetro λ:
2 1  17λ
17λ
 3 
7
7
(2ª)
y 
(1ª)
x  3 y  10  7 λ 
x 3
 21  17 λ
 10  7 λ 
7
x 
7  2λ
2λ
 1
7
7
SOLUC: Es un sistema compatible indeterminado (SCI).
La solución NO es única. Tiene infinitas soluciones y están formadas por la terna de números que cumplen:
x
7  2λ
2λ
 1
7
7
y 
21  17λ
17λ
 3 
7
7
z λ
Para cada valor que le demos a λ obtenemos una de las infinitas soluciones del sistema
Se trata de tres planos en el espacio que se cortan en una recta. Las coordenadas de cada punto de la recta
2λ
17λ
(1 , 3 
,λ )
7
7
es una solución del sistema.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
11
d)
x 3y 2z  7 

2x y 15z  3  
x 8y 21z  11
 1 3 2 7 


 2 1 15 3 
 1 8 21 11


 1 3 2 7 
 1 3 2 7 
 1 3 2 7 
1ª
1ª






2

1
15
3

1ª .( 2)  2ª  0
5
19

11

2ª





 0 5 19 11 
 1 8 21 11
 0 5 19 4  2ª 3ª
 0 0 0 7 
1ª 3ª






La 3ª ecuación obtenida es la ecuación 0x + 0y + 0z = -7, que no tiene solución. Podíamos habernos
dado cuenta antes de hacer la última transformación ya que la 2ª y la 3ª ecuación son contradictorias.
SOLUC: Es un sistema incompatible (SI).
Se trata de tres planos en el espacio que no se cortan en un mismo punto.
e)
3x 2y  6 

x y  1 
3x 2y  0 
3 2 6


 1 1 1
3 2 0 


Podemos observar que la 1ª y 3ª ecuación son contradictorias. Por tanto, el sistema es incompatible.
Podemos comprobarlo también aplicando el método de Gauss.
3x 2y  6 

y  3 
0x 0y  6 
3 2 6
3 2 6
1ª




 1 1 1   1ª 2ª .3   0 1 3  
 3 2 0  1ª 3ª  0 0 6 




La tercera ecuación no se puede cumplir nunca. El sistema no tiene solución.
SOLUC: Es un sistema incompatible (SI).
Se trata de tres rectas del plano que no se cortan en un mismo punto.
f)
x 3y z  1 

2x y 2z  3
x 3y  1 z  z λ

2x y  3 2z 
x 3y  1 λ  1ª
2x y  3 2λ  1ª .2  2ª
x  1 λ  3y  x  2  λ
x 3y  1 λ 
 y  1
5y  5

SOLUC: Es un sistema compatible indeterminado (SCI).
La solución NO es única. Tiene infinitas soluciones y están formadas por la terna de números que cumplen:
x  2  λ
y 1
z λ
Para cada valor que le demos a λ obtenemos una de las infinitas soluciones del sistema
Se trata de tres planos en el espacio que se cortan en una recta. Las coordenadas de cada punto de la recta
es una solución del sistema.
(2  λ,1, λ )
g)
2x 4y 6z  2
x 2y 3z  1
Las dos ecuaciones son equivalentes, ya que son proporcionales. Se trata del mismo plano.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
12
SOLUC: Es un sistema compatible indeterminado (SCI).
Las dos ecuaciones representan al mismo plano en el espacio.
h)
x 2y z  3 
3x 6y 3z  1
Las dos ecuaciones son incompatibles, ya que si x + 2y – z = 3, tendría que ser 3x + 6y – 3z = 9.
SOLUC: Es un sistema incompatible (SI).
Se trata de dos planos en el espacio que son paralelos.
i) Considera el sistema de ecuaciones del apartado f (que es un SCI):
x 3y z  1 
2x y 2z  3 
i1) ¿Cómo ha de ser la ecuación que hay que añadirle al sistema para que
siga siendo compatible indeterminado?
Podemos añadir cualquier ecuación que sea combinación lineal de las dos que forman el sistema, es decir, cualquier
ecuación de la forma:
α.1ª + β.2ª
siendo α y β números reales.
Por ejemplo (α = 1 y β = 1):
3x + 4y - 3z = -2
i2) ¿Cómo ha de ser la ecuación que hay que añadirle al sistema para que
sea incompatible?
Podemos añadir cualquier ecuación cuyo primer miembro sea combinación lineal de los dos primeros miembros de
las dos que forman el sistema pero, cuyo segundo miembro NO lo sea.
Por ejemplo (α = 1 y β = 1):
3x + 4y - 3z = 5
Ejercicio 1 – 3º
Resuelve por el método de Gauss, clasifica e interpreta los siguientes sistemas de
ecuaciones lineales:
a)
x  y  z  11 

x y z 7 
2x  3y  3 
c)
x  y  z  3

2x  y
 3
4x  2y
 1
e)
x 
x  9y  5z  33 
2

x  3y  z  9  Sol . : y  72 λ
z λ
x  y  z  5 
b)
Sol.: (9,- 7, 5)
d)
Sol.: S.I.
3λ
Matemáticas II Álgebra lineal y Geometría
f)
2x  5y  1

x  6y  8 
7x  2y  12
Sol.: (2,-1)
2x  y  z  4 

x  y  2z  2
3x  y  3z  7 
Sol.: (1, 1, 1)
2x  y
 3 
x  2λ

x  2y  5z  4  Sol . : y  1  2λ
z λ
3x  2y  z  4 
CURSO 2014/15
13
x
x
 y  z  5

g )  2x  3y  7z  0 Sol.: (3, -2, 0)
5x
 7y  z  1
i)
h)
x  y  z  1
x  1  3λ

3x  2y  z  1 Sol . : y  2  4λ
z λ
5x  3y  3z  1
j)
2y  1

2x y  3 
5x  y  8 
Sol.: S.I.
3x  2y  z  1

5x  3y  3z  3
x  y  z  0
Sol.: (3/2, -2,1/2)
SOLUC:
a)
SCD. Se trata de tres planos que se cortan en un punto de coordenadas (9, -7, -5)
b)
SCD. Se trata de tres rectas en el plano que se cortan en un punto de coordenadas (2, -1)
c)
SI. Se trata de tres planos que se cortan dos a dos pero no existe un punto en común a los tres
d)
SCD. Se trata de tres planos que se cortan en un punto de coordenadas (1, 1, 1)
e)
SCI. Se trata de tres planos cuya intersección es una recta. Las coordenadas de cada punto de la recta es una
solución del sistema y vienen dadas por la expresión:
(
3  λ 7  λ
,
,λ )
2
2
f)
SCI. Se trata de tres planos cuya intersección es una recta. Las coordenadas de cada punto de la recta es una
solución del sistema y vienen dadas por la expresión: (2  λ,1  2λ, λ )
g)
SCD. Se trata de tres planos que se cortan en un punto de coordenadas (3, -2, 0)
h)
SI. Se trata de tres rectas del plano que se cortan dos a dos pero las tres rectas no comparten un punto en común.
i)
SCI. Se trata de tres planos cuya intersección es una recta. Las coordenadas de cada punto de la recta es una
solución del sistema y vienen dadas por la expresión: (  1  3λ ,2  4 λ, λ )
j)
SCD. Se trata de tres planos que se cortan en un punto de coordenadas (3/2, -2, 1/2)
5ª.- Planteamiento y resolución de problemas
En la resolución de problemas los sistemas se emplean con mucha
frecuencia. Para el correcto planteamiento de estos problemas hay que:
1º. Identificar las incógnitas. Darles nombre (x, y, z) son los más usuales).
2º. Establecer las relaciones entre ellas.
3º. Escribir el sistema de ecuaciones. Expresarlo en su forma estándar:
incógnitas ordenadas y términos independientes en los segundos
miembros de las ecuaciones.
Una vez realizados estos pasos, resolveremos el sistema.
Hay problemas contextualizados que se resolverán mediante un sistema de
ecuaciones de dos o tres incógnitas y otros problemas cuya resolución se basa en
encontrar una combinación lineal de las ecuaciones planteadas
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
14
Ejemplo 1 – 3º
Por dos artículos del tipo A, tres del tipo B y uno del tipo C pagamos 680 €. Por
un artículo del tipo A, dos del tipo B y dos del tipo C pagamos 450 €. ¿Cuánto
pagaremos por tres artículos del tipo A y cuatro del tipo B?
Ejemplo 1 – 4º
Un almacenista compra 5 estanterías, 3 mesas y 2 sillas y paga por ello 1600
€. Al mes siguiente paga 1100 € por tres estanterías, 2 mesas y 4 sillas. ¿Cuánto
pagará por 7 estanterías y 4 mesas?
Ejercicio 1 – 4º a 22º
4º.- Si la altura de Carlos aumenta el triple de la diferencia de las alturas de
Antonio y Juan, Carlos sería igual de alto que Juan. Las alturas de los tres suman
515 centímetros. Ocho veces la altura de Antonio equivale a nueve veces la de
Carlos. Halla las tres alturas.
5º.- Cuántas naranjas, manzanas y plátanos hay en un frutero sabiendo que:
 Si hubiese 2 manzanas más, habría igual número de manzanas que de
naranjas y plátanos juntos.
 Si hubiese 12 naranjas más, el número de éstas doblaría a la suma del
número de manzanas y plátanos.
 El doble de la cantidad de plátanos más el número de manzanas es igual al
triple de naranjas menos uno.
6º.- Un fabricante tiene una producción semanal de 42 unidades con los que
abastece a tres clientes: en una semana, el primer cliente solicitó tantas unidades
como el segundo y el tercero juntos. El segundo pidió un 20 % más que la suma de
la mitad de lo que pidió el primero y la tercera parte de lo que pidió el tercero.
¿Cuánto pidió cada uno de los clientes?
7º.- Una autoescuela tiene 3 sucursales. El número de matriculados es de 352.
Los matriculados en la tercera son la cuarta parte de los matriculados en la primera.
La diferencia entre los de la primera y la segunda es inferior en 2 unidades al doble
de los matriculados en la tercera. ¿Cuántos hay matriculados en cada sucursal?
8º.- Se desea mezclar un producto de 55 € el kilo con otro de 40 € el kilo, de
modo que la mezcla resulte a 45 € el kilo. ¿Cuántos kilos de cada clase deben
mezclarse para obtener 300 kilos de mezcla?
9º.- Una alumna ha realizado dos exámenes de una misma asignatura. La nota
media de ambos exámenes ha sido de 5 puntos. Si en el primero obtuvo una
calificación superior en 1,5 puntos a la obtenida en el segundo examen, ¿cuál fue la
nota de cada examen?
10º.- Cierta clase de pintura se distribuye en tres tipos de envases: A, B y C.
Cada envase del tipo A contiene 250 g y cuesta 2 €; el envase B contiene 500 g y
cuesta 4 €; el envase C contiene 1 kg y cuesta 6 €. Un pintor ha pagado 30 € por 8
envases que contienen un total de 4 kg de pintura. Plantea y resuelve el sistema de
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
15
ecuaciones que resolvería el problema de saber el número de envases que ha
comprado.
11º.- En una competición participan 50 atletas entre infantiles, cadetes y
juveniles. El doble del número de infantiles, por una parte, excede en una unidad al
número de cadetes y, por otra, coincide con el quíntuplo de juveniles. Calcula el
número de atletas de cada edad.
12º.- Halla dos números sabiendo que al dividir el mayor entre el menor
obtenemos 7 de cociente y 2 de resto, y que la diferencia entre el triple del mayor y
el menor es 106.
13º.- En una mesa de una cafetería se sirvieron 4 cafés, 2 refrescos y 1 té,
cobrando por ello 10,8 €. En otra mesa se pagaron 12,8 € por 3 cafés, 3 refrescos y
2 tés. En la barra, donde el precio es un 10 % más barato, tres amigos tomaron 1
café, 1 refresco y 1 té pagando 4,2 €. ¿Qué cuesta cada bebida?
14º.- Un grupo de 30 alumnos de 2º de bachillerato realiza una votación para
determinar el destino de una excursión. El número de alumnos que prefiere Baleares
triplica al número de los que prefieren París. El 40 % de los que prefieren Canarias
coincide con la quinta parte de la suma de los que prefieren los otros dos lugares.
Halla el número de votos de cada destino.
15º.- Una tienda ha obtenido 3748,8 € por la venta de 220 unidades entre productos
A, B y C. Sabiendo que el producto A cuesta 20 €, que los productos B y C son un 8 % y un
30 % más baratos que A, respectivamente, y que la suma de las unidades de B y C es el
triple que las unidades de A, halla el número de unidades vendidas de cada producto.
16º.- Los animales de un laboratorio deben recibir una dieta con 10 g de proteínas y 3
g de grasas. Se dispone de dos tipos de alimentos: el tipo A aporta un 5 % de proteínas y
un 3 % de grasas; y el tipo B aporta un 10 % de proteínas y un 1 % de grasa. ¿Cuántos
gramos de cada alimento hay que suministrar a cada animal para que la dieta sea la
correcta?
17º.- Un cliente compra 5 unidades de un producto A, 4 unidades de B y 3
unidades de C, pagando 4500 €. Otro cliente compra 2 unidades de A y 2 de C,
pagando 2000 €. Un tercer cliente compra en otra tienda que tiene los precios un 10
% más caros, 3 unidades de A y una de B, pagando 1512,5 €. ¿Qué vale cada
producto en la primera tienda?
18º.- En una estantería de una biblioteca hay novelas, libros de teatro y libros
de poesía. Hay tantas novelas como libros de teatro y poesía juntos, y el número de
libros de poesía es el triple que el de teatro. En total hay 176 libros en la estantería.
¿Cuántos hay de cada tipo?
19º.- Con dos clases de producto de 900 €/kg y 1200 €/kg se quiere obtener
una mezcla de 1000 €/kg. Hallar la cantidad que hay que mezclar de cada clase de
producto para obtener 30 kg de mezcla.
20º.- Hallar un número de 3 cifras sabiendo que suman 9, y que si al número
dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198 y
que además la cifra de las decenas es media aritmética de las otras dos.
21º.- La suma de las tres cifras de un número es 14. La cifra de las unidades es
igual a la suma de las cifras de las decenas y centenas. Si al número se le suma
270, resultan invertidas las cifras de las decenas y las centenas. Halla el número.
22º.- En la bolsa A y en la bolsa B hay un total de 80 bolas. Si pasamos 10
bolas de la bolsa B a la bolsa A, el número de bolas de la bolsa A es 3 veces el
número de bolas de la bolsa B. ¿Cuántas bolas hay en cada bolsa?
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
16
2. MATRICES
1ª. Concepto de matriz
2ª. Tipos de matrices
3ª. Operaciones con matrices y propiedades:
3.1. Suma de matrices
3.2. Producto de un nº por una matriz
3.3. Producto de una matriz fila por una matriz
columna
3.4. Producto de matrices. Matriz inversa
4ª. Cálculo de la matriz inversa por el método de Gauss
5ª. Potencia enésima de una matriz
6ª. Rango de una matriz
7ª. Cálculo del rango de una matriz por el método de Gauss
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
17
1ª.- Concepto de matriz
Una matriz es un conjunto de números ordenados en filas y columnas.
Se escribe del siguiente modo:
 a 11 a 12 a 13  a 1n 


a 21 a 22 a 23  a 2n 

A


a a a  a 
mn 
 m1 m 2 m 3
Esto es una matriz de “m” filas y “n” columnas
Cada uno de estos números, aij , se llama elemento de la matriz. El subíndice nos
indica su posición, siendo i el número de su fila, y j el de su columna.
Así, el elemento a45, indica que ocupa la cuarta fila de la quinta columna.
El número de filas y columnas de una matriz recibe el nombre de dimensión
y se representa por m  n. Si m = n se dice que la matriz es una matriz cuadrada
de orden n.
 15 6 2 
La matriz A  
 tiene dimensión 2x3 (dim (A) = 2  3) y tiene 2 · 3 = 6
 0 18 9 
elementos.
Dos matrices, A y B, son iguales cuando tienen la misma dimensión y
coinciden elemento a elemento, es decir, aij = bij.
3 x  7 4 
3 8 4 
Las matrices A  
 y B 
 son iguales si x – 7 = 8, es
8
2 1
2 1 8
decir, si x = 15.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
18
2ª.- Tipos de matrices
 Matriz traspuesta. Dada una matriz A, de dimensión m  n, se llama
traspuesta de A, y se representa por At, a la matriz que se obtiene
cambiando filas por columnas y que tendrá dimensión n  m:
4 2
 4 1 9
t


si A  
 entonces A   1 5 
 2 5 3
9 3
Propiedades:
a ) (A t ) t  A
b ) (A  B ) t  A t  B t
c ) (k  A) t  k  A t
d ) (A  B ) t  B t  A t
 Matriz nula es aquella en la que todos sus elementos son 0.
 Matriz rectangular es aquella que tiene un número de filas distinto al
número de columnas (no es cuadrada):
 4 1 9
A 

 2 5 3
 Matriz fila es aquella que tiene sólo una fila:
A  1 3 5 7 
2 
 
 Matriz columna es aquella que tiene sólo una columna: A   3 
8
 
 Matriz opuesta Dada una matriz A se define su opuesta –A como
aquella matriz formada por los elemento opuestos a los elementos de A
 Matriz cuadrada es aquella que tiene igual número de filas que de
columnas:
3 5 7 
A  2 9 6 


8 1 3 
En las matrices cuadradas podemos definir dos diagonales. La línea
formada por los elementos aij tales que i = j (a11, a22, …, a nn) se denomina
diagonal principal de la matriz. La diagonal secundaria está formada
por los elementos aij tales que i + j= n + 1.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
19
3 5 7


A 2 9 6
8 1 3


3 5 7


A 2 9 6
8 1 3


Diagonal principal
Diagonal secundaria
 Matriz simétrica es aquella matriz cuadrada que verifica que cada
elemento aij coincide con el elemento aji: aij = aji (i≠j)
3 5 4
A   5 9 6  , vemos como a12 = a21 = 5; a13= a31 = 4; a23 = a32 = 6


4 6 1 
Observa que toda matriz simétrica coincide con su traspuesta: A = At
 Matriz antisimétrica es toda matriz cuadrada tal que aij = - aji (i≠j)
 3 5 7 
A   5 9 2 


 7 2 1 
 Matriz triangular es aquella matriz cuadrada cuyos elementos
situados por encima o por debajo de la diagonal principal, son nulos:
 1 7 4
A  0 6 5


0 0 3
4 0 0
B   1 3 0


9 8 7
Triangular superior
Triangular inferior
 Matriz diagonal es una matriz cuadrada que tiene todos sus
elementos nulos, excepto los de la diagonal principal:
 1 0 0
A  0 6 0


0 0 3
 Matriz escalar es una matriz diagonal con los elementos iguales:
7 0
A

0 7
 Matriz unidad, o identidad es una matriz escalar con los elementos
iguales a 1. La matriz unidad de orden n se designa por In ; p. e. I2
indicará la matriz identidad de orden 2:
 1 0
I2  

0 1 
Matemáticas II Álgebra lineal y Geometría
 1 0 0
I3   0 1 0 


0 0 1 
CURSO 2014/15
20
Ejemplo 2 – 1º
Dadas las matrices:
 1 0 0
A   0 2 0 ,


0 0 3
a)
b)
c)
d)
1 
B   4 ,
 
0
 1  2
C 
,
1 
 0
3 1 
D   4 2


 5 3
y
4 2 3 1 
E  2 1 0 2


3 0 2 0
Indica la dimensión y escribe la traspuesta de cada una.
¿Cuáles son matrices cuadradas? Indica su diagonal principal.
¿Hay alguna que sea simétrica? ¿Y triangular?
Escribe la matriz –A, es decir, la matriz opuesta de A.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
21
3ª.- Operaciones con matrices
3.1. Suma y diferencia de matrices. Propiedades
Para que dos matrices A y B puedan sumarse, han de tener la misma
dimensión. En este caso la matriz suma S  A  B , se obtiene sumando los
elementos de ambas matrices que ocupan la misma posición: sij = aij + bij.
 3  2   3
 0 5   8

 
3 1
 4 2


 5 3

 2
 0

 1
1   0 1 

2   8 7 
1  1 2 
2   4 4 
 

4 6 7
Propiedades:
1.
2.
3.
4.
Asociativa: A + (B + C) = (A + B) + C
Conmutativa: A + B = B + A
Existe elemento neutro: la matriz nula: A + 0 = A
Existe elemento simétrico: la matriz opuesta: A + (-A) = 0
La existencia de la matriz opuesta nos permite definir la diferencia de
matrices:
A  B  A  ( B )
Ejemplo 2 – 2º
a)
3 2
A   1 0 ,


4 1 
Dadas las matrices:
 1 0 
B   2 1 


 4 3
y
 1 7 
C   2 0  ,


 0 3 
calcula: A + B, A – C y A – B + C
b)
Calcula a, b, c para que se cumpla la igualdad:
b
2  2 a  b 4  1 a 2
3  a


 4
c  1 6   1  c
2
0   2 0 6 

Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
22
3.2. Producto de matrices por un número real
Dado un número cualquiera k, y una matriz A, llamamos matriz producto k · A,
a la matriz obtenida al multiplicar k por cada elemento de la matriz A.
1   1 5

2   40
 3
5
 8
5
1 0 
Propiedades:
1.
2.
3.
4.
Asociativa: k·(h·A) = (k·h)·A
Distributiva respecto a la suma de matrices: k·(A + B) = k·A + k·B
Distributiva respecto a la suma de nº reales: (k + h)·A = k·A + h·A
Existe elemento neutro: A · 1 = A
Ejemplo 2 – 3º
a) Dadas las matrices del ejemplo 2, calcula: 2A – 3B – C
b) Hallar la matriz X en la siguiente ecuación:
 2 1
3X  4  
 3 0
4   3

1   0
1 2
2 2 
Ejercicio 2 – 1º
Comprueba las propiedades 2 y 3 del producto de números por matrices, siendo:
 3 5 1 
 7 2 1 
k 3 h 6 A 
 ; B   4 6 8
2

3
0




Soluc:

a) Propiedad 2ª 3(A  B )  3A  3B   30
18

9 0 
9 24 
 27
b) Propiedad 3ª 9A 6A 3A 
45 9 

 18 27 0 
Ejercicio 2 – 2º
 1
Dadas las matrices: A  
 2
a) A + B – C
2
;
3 
 0 3
B 

 1 2
b) A - 2B + 3C
y
 1 3 
C 
 , calcula:
 0 2 
Ejercicio 2 – 3º
Halla la matriz A que satisface la igualdad:
 1 5 6  1
3

 2 8 4   2
0
7
4
A
3 
Ejercicio 2 – 4º
 1 1
 1
Si A  
yB 

0 1
 0
0
, halla una matriz X que verifique la ecuación:
2 
2X  4 A  B
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
23
3.3. Producto
escalar de una matriz fila por una matriz
columna
Es un número que obtenemos multiplicando cada elemento aij por cada
elemento bji y sumando los resultados obtenidos, es decir:
a
11
a 12 a 13

 b11 


  b 21   a 11  b11  a 12  b21  a 13  b31
 b 31 


Para poder definir el producto escalar, el número de columnas de la primera
debe coincidir con el número de filas de la segunda.
 3
Por ejemplo: 3 1  4    2   3  3  1   2     4   0  9  2  0  7
 
 0
3.4. Producto de matrices. Matriz inversa
El producto de la matriz A = (aij) de dimensión m  n por la matriz B = (bij) de
dimensión n  q es otra matriz P = (pij) de dimensión m  q, tal que cada elemento pij
se obtiene multiplicando escalarmente la fila i de la primera matriz por la columna j
de la segunda:
P  A B
 (m  q )  (m  n )  (n  q )
El elemento p23 se obtiene multiplicando los elementos de la 2ª fila de A por
los de la 3ª columna de B y sumando los resultados.

    b13        


a
a
a     b23       p 23  
 21 22 23  



    b33        
Para poder multiplicar dos matrices es necesario que el número de
columnas de la primera coincida con el número de filas de la segunda.
Ejemplo 2 – 4º
 1 1 
a) Dadas las matrices: A   2 3 


 5 0
y
 0 2
B 
 4 3
3
, calcula A · B.
1 
 x 1
z
1


b) Sean las matrices: A  2x 1 ; B    ; X   2z


 z
y 

 x 1 
los valores de x, y, z para los que se cumple A  B  X  Y .
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15




y
 1 
Y   0  . Halla


1 3
24
Ejercicio 2 – 5º
Dadas las matrices:
 1 1 
 0 2
A   2 3 ; B  


 4 3
 5 0
a) A · C
3
1 
 4 1 
C 
 , calcula:
 0 3
y
b) C · B
c) C · C.
Ejercicio 2 – 6º
Efectúa todos los posibles productos de dos matrices que se pueden realizar entre
las siguientes matrices:
 1
A 
 2
2
5
3
1 
7 0 
 1 1 
B 

 0 1 
 3 4 
 2 7 1 5
C   6 3 0 0


 2 5 1 0 
y
 1 1 1 
D  0 5 2 


 2 3 3 
Ejercicio 2 – 7º
 1 1 
Dadas las matrices A  

3 2
 1 3
B 
 comprueba que verifican que
 2 1 
y
t
A.B 
 B t .At
Ejercicio 2 – 8º
 1 2 
Comprueba que la matriz A  
 verifica:
 3 1 
2
A  I 
 6I
Siendo I la matriz unidad de orden 2.
Ejercicio 2 – 9º
Determina los valores de x e y que cumplen la igualdad:
 1 1   x   1 x   3 
 3 2   y    y 1   2 

  
 
Si una matriz A es de dimensión 4  3 y otra B es de dimensión 3  2,
podremos hacer el producto A · B pero no el producto B · A.
Si una matriz A es de dimensión 4  3 y otra B es de dimensión 3  4,
podremos hacer tanto el producto A · B como el producto B · A, pero mientras que el
primero tiene dimensión 4  4, el segundo tiene dimensión 3  3.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
25
Cuando se cumple que A  B  B  A , se dice que A y B conmutan.
Propiedades:
1. Asociativa: A · (B · C) = (A · B) · C
2. En general el producto no es conmutativo: A · B ≠ B · A
3. Distributiva respecto a la suma:
A · (B + C) = A · B + A · C
(B + C) · A = B · A + C · A
4. Elemento unidad: Si A es una matriz de orden n, se verifica que:
A . In = In .A = A
siendo In la matriz unidad del mismo orden de A.
5. Elemento simétrico: se representa por A-1 y se conoce como matriz
inversa. (sólo existe para matrices cuadradas)
No siempre existe, pero si existe se verifica que: A  A 1  A 1  A  I
Una matriz cuadrada es regular o inversible cuando tiene inversa, si no, se
dice que es singular.
Ejercicio 2 – 10º
Comprueba la primera propiedad distributiva del producto de matrices para:
 1 4
A  0 5


 1 6
 1
B 
 3
5
0
6 7 
9 2 
 4 1
C 
 0 1
6 0
5 5 
 15 2 68 19 
SOLUC:  15 5 70 15 


 21 0 96 25 
Ejercicio 2 – 11º
Comprueba la segunda propiedad distributiva del producto de matrices para:
 1 
2
A 
 5 
3
 1
B 
 3
5
0
6 7 
9 2 
 4 1
C 
 0 1
6 0
5 5 
SOLUC:
 24 
 60 


Ejercicio 2 – 12º
Comprueba que la matriz B es la matriz inversa de A siendo:
 1 2 1
A  0 1 0 ,


 2 0 3
Matemáticas II Álgebra lineal y Geometría
 3 6 1 
B   0 1 0


 2 4 1 
CURSO 2014/15
26
Ejercicio 2 – 13º
 1 1 
Si la matriz A  
 , prueba cual de las siguientes matrices es su inversa:
0 2 
3 / 2 3 / 2
M 

1/2 1/ 2
 1 1 / 2
N 

 0 1 / 2
Ejercicio 2 – 14º
Determina la matriz X que verifique la igualdad 3X  I  A  B  A 2 siendo
 1 1 2 
 1 0 2 


A  2 0 3 , B   2 1 1  e I la matriz unidad de orden 3.




 3 1 2
 3 2 1 
Ejercicio 2 – 15º
Calcula los valores de a y b que satisfagan cada una de las siguientes igualdades:
 1 a  a b  0 0
a) 

 

2 b   3 4   0 0 
 a b   5 9   1 0 
b) 


 
 1 5   1 a   0 1 
4ª.- Cálculo de la matriz inversa por el método de
Gauss
Si una matriz A tiene inversa (A-1), podemos calcularla por el método de
Gauss o, como veremos en el próximo tema, mediante la matriz de adjuntos.
Para calcular la matriz inversa A-1 colocamos a la izquierda a la matriz A, y a
su derecha a la matriz unidad I. A continuación sometemos a la matriz A y a la matriz
unidad I a las mismas transformaciones que sometíamos a un sistema de
ecuaciones lineales por el método de Gauss. Las transformaciones tienen que ser
tales que aparezca la matriz unidad I a izquierda. A la derecha habrá aparecido una
nueva matriz que será la inversa de la matriz A.
Si durante el proceso aparece a la izquierda una fila de ceros, la matriz A no
tiene inversa (A no es inversible)
Ejemplo 2 – 5º
Halla, si existe, la matriz inversa de las siguientes matrices:
 3 5
a) A  

 4 8
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
27
 3 5 1 0 1ª.4 12 20 4 0 1ª 12 20
4 8 0 1   2ª.3  12 24 0 3  2ª1ª   0 4





La matriz inversa de A vale:
4
4
0 1ª2ª.5 12 0 24 15 1ª/12  1 0


 
3 2ª  0 4 4 3  2ª/4 0 1
2 5/4
1 3/4 
 2 5 / 4 
A 1  

 1 3 / 4 
Puedes comprobar que A.A-1 = I
 1 2 1 
b) A  3 0 4


0 4 1 
 1 2 1
3 0 4

0 4 1
3
1ª 3ª .4
 2ª   0

3ª
0
 1 2 1
1 0 0
1ª
1

0 1 0  2ª 1ª .3   0 6 1 3


0 0 1 
3ª
0
0 4 1
0 0 24 9 12  1ª : 3  1
2 0
3 1 1   2ª : 2   0


0 1
6 2 3  3ª  0
0 0  1ª .3  2ª  3 0 4
0 1 0


1 0  2ª 3ª  0 2 0
3 1 1  



0 1  3ª .3  2ª .2  0 0 1
6 2 3 
0 0
8
3
4 
1 0 3 / 2 1 / 2 1 / 2 

0 1
6
2
3 
La matriz inversa de A vale:
A
1
 8
3
4 

 3 / 2 1 / 2 1 / 2 


2
3 
 6
Puedes comprobar que A.A-1 = I
 2 1 0 
c) A  0 1 4 


 3 2 2 
 2 1 0
0 1 4

 3 2 2
 1
1ª
 2ª   0

3ª 2ª .2
0
1 0 0  1ª .(2)  3ª  1 0 2
0 1 0 
2ª
0 1 4


0 0 1
3ª
 3 2 2
0 2
2 0 1 
1 4
3 1 0 

0 0
12 2 4 
 1 0 2
2 0 1 
1ª

3 1 0  2ª   0 1 4


0 0 1  3ª 1ª .3  0 2 8
2 0 1 
3 1 0  

6 0 4 
La matriz A NO tiene inversa ya que en la parte izquierda ha aparecido una fila de
ceros (la tercera fila)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
28
Ejercicio 2 – 16º
Calcular la
1
es: A   0

0
inversa de la siguiente matriz diagonal y comprueba que en realidad lo
0 0
2 0

0 3
Ejercicio 2 – 17º
Calcula, si existe, la matriz inversa de cada una de las siguientes matices y
comprueba que en realidad lo es:
a)
 1 1
A

 0 1
Soluc: A 1   1
0

1 
1 
1 2
B 

3 4 
b)
 2
1 
B 1  

 3 / 2 1 / 2 
c)
C
 1 2
C 

 2 4 
1
Ejercicio 2 – 18º
Calcula, si existe, la matriz inversa de cada una de las siguientes matices y
comprueba que en realidad lo es:
a)
Soluc:
 1 2 3
A   4 5 6


7 8 9
 A 1
 1 2 3
B  0 1 2


 1 2 4
b)
 0 2 1 
B 1   2
1 2 



1
0
1 

C
1
Matemáticas II Álgebra lineal y Geometría
c)
1 1 3
C  1 2 1 


2 0 0 
 0
0
1/2 
  1 / 5 3 / 5
1 / 5 


 2 / 5  1 / 5  1 / 10 
CURSO 2014/15
29
5ª.- Potencia enésima de una matriz
Para hallarla, calcularemos las primeras potencias y buscaremos una relación
existente entre los elementos obtenidos y el exponente de la potencia calculada.
Ejemplo 2 – 6º
1
a) Dada la matriz A  
0
1
b) Dada la matriz A   1

1
Soluc:
1
, calcular A500.
1 
Soluc: A   1 500 
0 1 


1 1
1 1  , calcular An(siendo n un nº natural).

1 1
 3n 1 3n 1 3n 1 
A   3n 1 3n 1 3n 1 
 3n 1 3n 1 3n 1 


n
Ejercicio 2 – 19º
a 1 
50
a) Dada la matriz A  
 , calcular A .
0
a


0 2  1
b) Dada la matriz A   0 0 1 


0 0 0 
calcular A30
1 1/7 1/ 7
c) Calcula A y B siendo: A   0 1
0 


1 
0 0
n
n
y
 1 0
B 

0 3
 4
5  1

d) Dada la matriz M   3  4 1  calcula M128


 3  4 0 
1 a
e) Calcula A22 – 12A2 +2A, siendo A  

0 1 
f) Dada la matriz
 0

A  1
1

3
4
3
4 

 5
4 
f1) Calcula A3.
f2) Calcula razonadamente A100
Soluc: a) A5
0
128
d) M
a 5 0

 0
2
=M
5 0a 4 9 
a 5 0 
50
e) A =   9
 0

b)
A3
0 
 9 
Matemáticas II Álgebra lineal y Geometría
0
 0 0 0
  0 0 0


 0 0 0
3
f) A = -I3
c)
100
A
 1 m / 7 m / 7
An   0
1
0 


0
0
1 

y
1 0 
Bn  
n 
0 3 
= -A
CURSO 2014/15
30
6ª.- Rango de una matriz
Consideremos las matrices siguientes:
 5 1 
 2 3 5 
6 3 
 1 2 
 1 2 
 2 3 1 4 
 1 2 1 
A 
B

C

D

E




2 4 
1 0 4 5
1

17


 3 6 






1 5 6 

 11 2 
En la matriz A las dos filas son proporcionales, ya que 2ª = (-3).1ª. Se dice las
dos filas son linealmente dependientes (LD).
En la matriz B las dos filas no son proporcionales. Se dice que las dos filas
son linealmente independientes (LI).
En la matriz C las dos filas no son proporcionales, es decir, las dos filas son
LI.
En la matriz D las dos primeras filas no son proporcionales y por tanto son LI.
La tercera fila tampoco es proporcional ni a la primera ni a la segunda pero, la
tercera fila se puede poner como una combinación lineal de las dos primeras:
3ª = 1ª.5 – 2ª.4
Se dice que la tercera fila es LD de las dos primeras
Lo mismo ocurre con la cuarta fila, es LD de las dos primeras, puesto que se puede
poner como la siguiente combinación lineal:
4ª = 1ª + 2ª
En la matriz E las dos primeras filas son LI, ya que no son proporcionales. Sin
embargo la tercera fila es LD de las dos primeras, puesto que se puede poner
mediante la siguiente combinación lineal:
3ª = 1ª – 2ª
Llamamos rango de una matriz A, al nº de filas que son linealmente
independientes.
Según el razonamiento anterior, las matrices B, C, D y E anteriores tienen rango 2 y
la matriz A tiene rango 1.
Pero ¿ocurre lo mismo con las columnas? La respuesta es que sí. Podemos
observarlo en cada una de las matrices anteriores:
En la matriz A, se cumple que las dos columnas son proporcionales, ya que
C2 = (-2).C1. Por tanto las dos columnas son LD.
En la matriz B, las dos columnas son LI, puesto que no son proporcionales.
En la matriz C, las dos primeras columnas son LI pero, la tercera columna y la
cuarta son LD de las dos primeras al poder expresarse como:
C3 = 4.C1 - 3.C2
Matemáticas II Álgebra lineal y Geometría
C4 = 5.C1 - 2.C2
CURSO 2014/15
31
En la matriz D, las dos columnas son LI al no ser proporcionales.
En la matriz E, las dos primeras columnas son LI al no ser proporcionales
pero, la tercera columna es LD de las dos primeras, ya que se puede expresar
mediante la combinación lineal siguiente:
C3 = (-1).C1 + (-1).C2
El siguiente teorema (sin demostración) asegura que no es posible que en
una matriz el nº de filas LI sea distinto al nº de columnas:
TEOREMA
En una matriz, el nº de filas LI coincide con el nº de columnas LI.
Según esto el RANGO DE UNA MATRIZ es el nº de líneas (filas o columnas)
LI.
Las propiedades del rango de una matriz son las siguientes:
PR0PIEDADES DEL RANGO DE UNA MATRIZ
Si en una matriz A se intercambian dos filas o dos columnas, se obtiene una
matriz del mismo rango.
Si una línea de una matriz A está formada por ceros, el rango de la matriz A
es igual al de la matriz que se obtiene de suprimir dicha línea de ceros.
Si en una matriz A, una línea es combinación lineal de otras líneas paralelas
de la misma matriz, el rango de la matriz A coincide con el de la matriz que se
obtiene al suprimir dicha línea.
Si en una matriz A, multiplicamos (o dividimos) todos los elementos de una
línea por un mismo nº, el rango de la matriz resultante el mismo que el de la
matriz A inicial.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
32
7ª.- Cálculo del rango de una matriz por el método
de Gauss-Jordan
Para hallar el rango de una matriz A por el método de Gauss-Jordan, aplicamos
a la matriz las mismas transformaciones que aplicábamos a un sistema de
ecuaciones lineales para hacerlo escalonado. El rango de la matriz A coincide con el
nº de filas distintas de 0 en la matriz escalonada obtenida.
Ejemplo 2 – 7º
Halla el rango de las siguientes matrices. Si no lo ves directamente, hazlo por el
método de Gauss:
 1 1 1 
A2 1 0


 1 3 1 
a)
 1 1
 2 1

 1 3
1 
0  

1 
1ª
2 ª  1 ª .2
3ª 1ª
1
 0

0
1
1
4
1 
2  

2 
1ª
2ª
3 ª  2 ª .4
1
 0

0
1
1
0
1 
2 

6 
El rango de la matriz A es 3, puesto que las tres filas son LI
 1 1 1 
B  2 1 0 


1 0 1 
b)
1
2

1
1
1
0
1
0  

1 
1ª
2 ª  1 ª .2
3 ª 1 ª
1
 0

0
1
1
1
1 
2  

2 
1ª
2ª
3ª 2ª
1
 0

0
1 1 
1 2 

0
0 
El rango de la matriz B es 2, puesto que las dos primeras filas son LI pero, la tercera fila es LD de las
dos primeras (en efecto: 3ª = 1ª.(-1) + 2ª)
c)
 1 1 1 1 
C   2 1 0 1


 1 3 1 1 
IMPORTANTE: Antes de comenzar, tienes que ser consciente que el rango de la matriz C a lo sumo
puede ser 3: recuerda que el rango de una matriz es el nº de líneas LI, y por tanto no puede tener 4
filas LI, ya que la matriz C sólo tiene 3 filas.
 1 1 1 1 
 2 1 0 1 


 1 3 1 1 
1ª
2ª  1ª .2
3ª  1ª
 1 1 1 1 
  0 1 2 1  


 0 4 2 2 
1ª
2ª
3ª  2 ª.4
 1 1 1 1 
  0  1 2 1 


 0 0 6 2 
El rango de la matriz C es 3, puesto que las tres filas son LI
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
33
Ejercicio 2 – 20º
Halla el rango de las siguientes matrices. Si no lo ves directamente, hazlo por el
método de Gauss
a)
 1 2 3 4 
B 

 2 4 6 8 
d)
1 2 3
D  2 4 0 


3 6 0 
Soluc: rango(A) = 2 rango(B) = 2
b)
e)
 1 3 0
B 

 1 0 0 
 1 0 3 0
E  0 2 0 3


0 1 0 1 
rango(C) = 1
Matemáticas II Álgebra lineal y Geometría
rango(D) = 2
 1 2 3 
c ) C   2 4 6 


 12 24 36 
0 0 1 
f ) F   1 0 0


0 1 0
rango(E) = 3
CURSO 2014/15
rango(F) = 3
34
3.-DETERMINANTES
1ª. Determinante de una matriz
2ª. Matriz complementaria de un elemento
3ª. Menor complementario y adjunto de un elemento
4ª. Matriz de adjuntos
5ª. Propiedades de los determinantes
6ª. Matrices regulares y matrices singulares. Cálculo de la matriz
inversa a partir de la matriz de adjuntos
7ª. Ecuaciones matriciales
8ª. Expresión matricial de un sistema de ecuaciones lineales
9ª. Cálculo del rango de una matriz mediante determinantes
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
35
1ª.- Determinante de una matriz
El determinante de una matriz cuadrada A, es un número real que se obtiene
a partir de los elementos de dicha matriz.
Se representa por A o por det(A).
1.1
Determinante de una matriz cuadrada de orden 2
El determinante de una matriz cuadrada de orden 2 es un número que se
obtiene del siguiente modo:
A 
a 11 a 12
 a 11  a 22  a 12  a 21
a 21 a 22
Como puedes observar es el nº que se obtiene de multiplicar los dos elementos de la
diagonal principal y restarle el producto de los dos elementos de su diagonal
secundaria.
Ejemplo 3 – 1º
Hallar el valor de los siguientes determinantes:
a)
3 2
5 4
b)
7 4
8 11
Ejemplo 3 – 2º
Calcula el valor de a que anula el siguiente determinante:
5
a
3 a 8
Ejercicio 3 – 1º
Hallar el valor de los siguientes determinantes:
a)
4 2
8 5
1.2
b)
2 3
5 4
c)
5
3
0
8
d)
17 16
9 10
Determinante de una matriz cuadrada de orden 3
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
36
El determinante de una matriz cuadrada de orden 3 es un número que se
obtiene utilizando un procedimiento llamado regla de Sarrus:
a 11 a 12 a 13
A  a 21 a 22 a 23  a 11a 22a 33  a 12a 23a 31  a 13a 21a 32  a 13a 22a 31  a 12a 21a 33  a 11a 23a 32 
a 31 a 32 a 33
Ejemplo 3 – 3º
Hallar el valor de los siguientes determinantes:
3 2 5
a ) 1 4 3
7 2 8
b)
3 2
1
5 4 0
2 1 3
Ejemplo 3 – 4º
1 x 1
Resuelve la ecuación: 0 1 x  3
1 0 x
(Sol.: 2, -1)
Ejercicio 3 – 2º
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
37
Hallar el valor de los siguientes determinantes:
a)
1 2
4 5
3 2
3
6
1
2 2 2
b) 1 2 1
1 3 2
5 3
1
c) 2 0 4
2 5 4
Ejercicio 3 – 3º
Resolver las ecuaciones:
1
a) 0
4
2 1
3 2  1
a 5
1
1
2
b) x  1
0
x  3  1  7x
1
x 2
4
2ª.- Matriz complementaria de un elemento
Dada una matriz cuadrada A, definimos la matriz complementaria del
elemento aij, a la submatriz que se obtiene al eliminar la fila i y la columna j. Se
representa por Mij.
P.e. la matriz complementaria M23 de a23 en una matriz A de tercer orden es:
 a 11 a 12 a 13 
A   a 21 a 22 a 23 
a a

 31 32 a 33 
a a 
M23   11 12 
 a 31 a 32 
Ejemplo 3 – 5º
 1 3 2 6 
 2 0 3 1
Dada la matriz A  
 calcula las matrices complementarias de los
0
4
2

1


 5 1 1 2 
elementos a11, a21, a31 y a34.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
38
3ª.- Menor complementario y adjunto de un elemento
Se llama MENOR COMPLEMENTARIO del elemento aij de la matriz A, y lo
representamos por
ij,
al determinante de la matriz complementaria a dicho
elemento, es decir, al determinante de la submatriz cuadrada, que se obtiene al
suprimir la fila i y la columna j.
 ij  Mij
Se llama ADJUNTO del elemento aij de la matriz A, y lo representamos por Aij
al menor complementario de ese elemento precedido del signo + o –, según que la
suma i + j de los subíndices sea par o impar, respectivamente. Podemos expresarlo
del siguiente modo:
i j
Aij   1 
 ij
Ejemplo 3 – 6º
Calcula los menores complementarios y los adjuntos de todos los elementos de las
siguientes matrices
 2 2 
a) P  

 5 4 
α 11   4
M en o res
co m plem en tario s
 5 1
b) M   4 2

 1 2
α 12  5
α 21   2
ad jun tos
α22  2
A11   4
A12   5
A2 1  2
A2 2  2
7
3 ,

1
Menores complementarios:
α 11 
2 3
 2.1  3.(  2)  8
2 1
α 21 
1 7
  1.  7.(  2)  13
2 1
α 31 
1 7
  1.3  7.2   17
2 3
α 12 
α 22 
α 32 
4 3
 4.1  3.1  1
1 1
α 13 
4 2
 4.(  2)  2.1   10
1 2
5 7
 5.1  7.1   2
1 1
α 23 
5 1
 5.(  2)  (  1)   9
1 2
5 7
 5.3  7.4   13
4 3
α 33 
5 1
 2.5  (  1).4  14
4 2
i+j
Adjuntos: Aij = (-1) .αij
A11 = 8
A21 = -13
A31 = -17
Matemáticas II Álgebra lineal y Geometría
A12 = -1
A22 = -2
A13 = -10
A23 = 9
A32 = 13
A33 = 14
CURSO 2014/15
39
Ejercicio 3 – 4º
Halla los menores complementarios y los adjuntos de los elementos a21, a33 y a13 de
 1 2 0
la matriz: N   3 1 4 


 0 1 3 
4ª.- Matriz adjunta
Dada una matriz A, si cada elemento se sustituye por su adjunto, obtenemos
una nueva matriz que recibe el nombre de matriz adjunta. Se representa por Adj A
Ejemplo 3 – 7º
3 4 8
Calcula la matriz adjunta de A   2 1 0 


9 3 2
Ejercicio 3 – 5º
Halla las matrices adjuntas de las siguientes matrices:
 1 3
A 

0 5
Matemáticas II Álgebra lineal y Geometría
1 3 2
B  6 5 4


9 7 8 
CURSO 2014/15
40
5ª.- Propiedades de los determinantes
Aunque en las siguientes propiedades sólo aparecen matrices cuadradas de orden 2 o 3, las
propiedades que se describen a continuación las cumplen las matrices cuadradas de cualquier orden.
1ª.- El determinante de una matriz cuadrada es igual al de su transpuesta.
A  AT
Puedes comprobarlo fácilmente para matrices cuadradas de orden 2 y de orden 3.
a
b
c
d

a
c
b
d
a1
a2
a3
a1
b1
c1
b1
c1
b2
c2
b3  a 2
c3
a3
b2
b3
c2
c3
Esta propiedad nos permite hablar, en una matriz cuadrada y en el contexto de
determinantes,, indistintamente de filas o de columnas (a las que llamaremos líneas)
Si una matriz cuadrada tiene una línea cualesquiera (fila o columna) de ceros, su
determinante vale cero.
2ª.-
a
0
b a

0 c
a1
0
c1
0
0
0
a2
0
c2
a3
a1
0  b1
c3
c1
a2
b2
c2
0
0 0
0
Esta propiedad es fácil de demostrar puesto que los elementos de una cualquiera de sus
líneas intervienen en todos los productos que hay que realizar para calcular el determinante
de una matriz.
Esta propiedad también se puede demostrar aplicando la propiedad nº 11
3º.- Si en una matriz cuadrada se permuta una línea por otra paralela, su determinante cambia de
signo.
a
c
a
c
b
b

d
d
b
c
 
d
a
a
c
d
b
a1
b1
a2
b2
a3
b1
b3   a1
b2
a2
b3
a3
c1
c2
c3
c2
c3
a1
a2
a3
c1
c2
c3
b1
b2
b3  a1
a2
a3
c1
c2
c3
b2
b3
c1
b1
Observa que si el nº de permutaciones es par, habrá un nº par de veces de cambio de signo y por
tanto el determinante será igual. Sin embargo, si el nº de permutaciones es impar, habrá un nº impar
de veces de cambio de signo y, por tanto el determinante habrá cambiado de signo.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
41
4ª.- Si una matriz cuadrada tiene dos líneas paralelas iguales su determinante es cero.
Puedes comprobarlo fácilmente para una matriz de orden 2 o 3.
5ª.- Si multiplicamos por un mismo nº todos los elementos de una línea cualquiera de una
matriz cuadrada, su determinante queda multiplicado por ese mismo nº.
a
c
b a

d
c
b
a

d
c
 a1
 b1
 c1
a2
b2
a3
a1
b3   b1
c2
c3
b
d
a2
 b2
c1
a3
a1
 b3   b1
c2
c3
c1
a2
b2
a3
b3
c2
c3
Observa que si multiplicas a una matriz cuadrada por un nº, entonces el determinante de la
n . A
matriz obtenida sería:
a
c
b
a
 2
d
c
donde n es el orden de la matriz A.
 a1
 b1
 c1
b
d
a2
 b2
c2
a3
a1
 b3  3 b1
 c3
c1
a2
b2
c2
a3
b3
c3
6ª.- Como consecuencia de la propiedad anterior, si una matriz cuadrada tiene dos líneas
proporcionales, entonces su determinante vale cero.
a1
a b
a b

0
a b
a b
a2
a3
a1 a2
a1 a2 a3   a1 a2
c1
c2
c3
c1 c2
a3
a3  0
c3
7ª.- El determinante de una matriz cuadrada se puede descomponer como suma / resta de dos
determinantes del modo siguiente:
a  a'
b
c  c'
d

a1
a 2  a 2'
b1
c1
'
2
'
2
b2  b
c2  c
a
b
c d
a3
a'
b
c'
d
a1
a2

b3  b1
c3
c1
Matemáticas II Álgebra lineal y Geometría
b2
c2
a1
a 2'
a3
b3  b1
c3
c1
'
2
'
2
b3
c3
a3
b
c
CURSO 2014/15
42
8ª.- Esta propiedad es una consecuencia de la anterior y dice: si a línea de una matriz cuadrada le
sumamos o restamos otra línea paralela multiplicada por un nº, o una combinación lineal de las líneas
paralelas, su determinante no varía.
a  b
c  d
b
d
propiedad 7 ª

a1
b1
c1
a 2   a1
b2   b1
c2   c1
a1
b1
c1
a 2  a1  a3
b2  b1  b3
c2  c1  c3
a
c
a3 a1
7ª
b3  b1
c3 c1
a3
b3
c3
b b

d d
a2
b2
c2
b
d
a3 a1
b3  b1
c3 c1
7 ª dosveces

a1
b1
c1
a2
b2
c2
a
c
b
b

d
d
a3 a1
5ª
b3  b1
c3 c1
a2
b2
c2
propiedad 5 ª

 a1
 b1
 c1
a3 a1
b3  b1
c3 c1
a1
b1
c1
b
d
propiedad 4 ª

a3
a1
b3   b1
c3
c1
a3 a1
b3  b1
c3 c1
a3
b3
c3
a1
b1
c1
a
c
b
d
a3 a1
4ª
b3  b1
c3 c1
a2
b2
c2
a3
b3
c3
a3
a1
5ª y 4 ª
b3  b1
c3
c1
a2
b2
c2
a3
b3
c3
9ª.- Si una matriz cuadrada tiene una línea que es combinación lineal de las demás paralelas,
entonces su determinante es cero. Recíprocamente, si el determinante de una matriz cuadrada es
cero, entonces tiene una línea que es combinación lineal de las otras paralelas.
a2  a3 a2 a3
a2 a2 a3 a3 a2 a3 a2 a2 a3
a3 a2 a3
7ª dosveces
5ª
4ª
b2  b3 b2 b3  b2 b2 b3  b3 b2 b3  b2 b2 b3   b3 b2 b3  0
c2  c3 c2 c3
c2 c2 c3 c3 c2 c3
c2 c2 c3
c3 c2 c3
10ª.- El determinante del producto de dos matrices cuadradas es igual al producto de sus
determinantes:
A.B  A. B
De esta propiedad se pueden deducir dos importantes consecuencias:
10.1.- Permite relacionar el determinante de una matriz cuadrada con el determinante de su
-1
inversa, si la tuviera: por definición de matriz inversa (A.A = I) y, teniendo en cuenta que el
determinante de la matriz unidad es 1 (│I│= 1):
A.A1 I 1
Pero según la propiedad 10ª sobre el determinante de un producto de dos matrices:
A. A 1  A . A
1
Igualando ambas expresiones obtenemos la relación buscada:
A . A 1  1  A 1 
1
A
10.2.- Calcular el determinante de la potencia de una matriz cuadrada:
A n  A. A. A.... A  A . A . A ..... A  A
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
n
43
11ª.- Si a los elementos de una línea de una matriz cuadrada los multiplicamos por sus
correspondientes adjuntos y sumamos los resultados, obtenemos el determinante de la matriz.
En el ejemplo siguiente, el determinante se está calculando mediante los adjuntos de la
primera columna:
a 11
a 12
a 13
a 21
a 22
a 23  a 11 . A11  a 21 . A 21  a 31 . A 31  a 11 .
a 31
a 32
a 33
a 22
a 23
a 32
a 33
 a 21 .(  1)
a 12
a 13
a 32
a 33
 a 31 .
a 12
a 13
a 22
a 23
Observa que si desarrollas por la línea que mas ceros tenga, el cálculo se facilita.
Esta propiedad sirve para calcular el determinante de una matriz de orden n, mediante
determinantes de orden n-1.Por ejemplo, el determinante de una matriz de orden 3, mediante
determinantes de orden 2, o un determinante de orden 4, mediante determinantes de orden 3.
Esta propiedad sirve también para demostrar la propiedad 2ª, para ello bastaría con
desarrollar el determinante mediante los adjuntos de la línea de ceros.
12ª.- Si a los elementos de una línea cualesquiera de una matriz cuadrada los multiplicamos por los
adjuntos de una línea paralela y sumamos los resultados, el resultado de esta suma es cero.
Ejemplo 3 – 8º
 3 2 5 
Dada la matriz N   1 7 3 


 4 1 0
a) Calcula su determinante aplicando la regla de Sarrus. (Soluc: -168)
b) Calcula su determinante aplicando la propiedad nº 11, por ejemplo,
desarrollando por los adjuntos de la primera columna (comprueba que sale el mismo
resultado).
c) Haz lo mismo pero mediante los adjunto de la 3ª fila.
d) Comprueba que N  N t
e) Calcula N 1
f) Calcula 2N
Ejemplo 3 – 9º
Dadas las matrices A y B de dimensión 3 y A  3 B  2 , Calcular:
pro pie d ad 1 0.1
a) A  1

b) B t .A
c) A .B

1
t

t

d) 2A
p e o p ie d a d 1
Bt . A
B . A  3 .2  6

p r o p ie d a d 1

c A .B 1
1
1

3
A
p r o p ie d a d 1 0


b) B t .A
a) A 1
p r o p ie d a d 1 0
A .B
1

p r o p ie d a d 1 0 .1
A .B
1

A .
1
1
3
 3. 
2
2
B
propiedad 5
d) 2A

23 A  23.3  24
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
44
Ejemplo 3 – 10º
Prueba sin desarrollar, sólo aplicando las propiedades de los determinantes, que el
 7 4 74 
determinante de la matriz A   1 6 16  vale 0.


 9 3 93 
A 
7
1
9
4 74 7 4 70  4
6 16  1 6 10  6
3 93 9 3 90  3
propiedad 7

7
1
9
4 70 7 4 4 propiedad 5
7 4 7 7 4 4
6 10  1 6 6
 10. 1 6 1  1 6 6
3 90 9 3 3
9 3 9 9 3 3
propiedad 4

10.0  0  0
También podría haberse visto que la tercera columna es una combinación lineal de las dos primeras
(propiedad 9):
C3 = 10.C1 + C2
Ejemplo 3 – 11º
x y z
2 5 0  1 , calcula aplicando las propiedades de los
1 1 1
Sabiendo que
determinantes
3x  2 3y  5 3z
x
y
z
x 4 y 4 z 4
2
5
0 7 ª 3x 3y 3z
2 5 0
2 5 0
3x  2 3y  5 3z 7ª 3x
3y
3z
3x 3y 3z
x
y
z  x
y
z  x
y
z  x
y
z  x
y
z  x y z  x y z 
x 4 y 4 z 4 x 4 y 4 z 4 x 4 y 4 z 4
x
y
z
4 4 4
x y z
4 4 4
2 5 0 3ª
x y z
 0  0  0  4 x y z  4 2 5 0  4.1  4
1 1 1
1 1 1
4ªy 5ª
Ejercicio 3 – 6º a 11º
6º.-Justifica sin desarrollar (sólo aplicando las propiedades de los determinantes): a)
3 1 7
4 1
7
b) 2 9
0 0 0 0
1 0
1 11 4
8 2 14
c)
7 4 1
2 9 7 0
27 94 71
d)
45 11 10
4 1 1 0
5 1 0
x y z
7º.- Teniendo en cuenta que 5 0 3  1
1 1 1
3x 3y 3z
a) 1
1
1
5 0 3
b)
5x 5y 5z
1
0 3/5
1
1
1
, calcula los determinantes siguientes:
x
y
z
c) 2x  5 2y 2z  3  1
x 1 y 1 z 1
Soluc: a) -3 b) 1 c) 1
1 m
8º.- Considera la matriz A  
 , cuyo determinante vale -13. Calcula:
n p 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
45
n p
1 m
a)
Soluc: a) 13
b) -468
c) -52
b) | 6A|
c)
1 4m
n 4p
d) |A-1|
d) -1/13
a b c
9º.- Sabiendo que p q r  7 , calcula razonadamente:
x y z
Soluc: a) 7
b) -21
a)
c a b
r p q
z x y
c)
a  2x b  2y c  2z
p
q
r
2x  p 2y  q 2z  r
c) 14
3a
3b
3c
b) a  p b  q c  r
x  a y  b z  c
b c  b 5a
d) q r  q 5p
y z  y 5x
d) -35
10º.- Libro: pág. 95 ejercicios 4, 5 y 6.
11º.- Libro: pág. 95 ejercicios 7 y 8.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
46
6ª.- Matrices regulares y matrices singulares. Cálculo de la
matriz inversa a partir de la matriz de adjuntos
Una matriz de orden n se dice que es REGULAR O INVERSIBLE si su
determinante es distinto de 0, es decir:
A es regular
|A| 0
Una matriz de orden n se dice que es SINGULAR si su determinante vale o,
es decir:
A es singular
|A| 0
Recordemos del tema anterior que dada una matriz cuadrada A, su matriz
inversa, A-1, será aquella que verifica que:
A  A 1  A 1  A  I
No todas las matrices cuadradas tienen inversa. Para que una matriz
cuadrada A tenga inversa, la matriz tiene que ser regular, es decir, su determinante
tiene que ser distinto de 0
A 1

A 0
En el tema anterior calculamos la inversa de una matriz mediante el método de
Gauss. En este tema podemos calcular la matriz inversa, si existe, mediante
determinantes.
Para calcularla utilizaremos la siguiente expresión:
(Adj A )t
1
t
A  .(Adj A ) 
A
A
1
Atendiendo a la expresión anterior, los pasos a seguir para calcular la matriz
inversa de una matriz A serían los siguientes:
1. Calculamos el determinante de la matriz A, |A|. Si este fuese 0 la
matriz no tendría inversa por ser singular.
2. Calculamos la matriz adjunta (Adj A): para lo cual tenemos que
calcular los menores complementarios de la matriz A, y luego sus
adjuntos.
3. Escribimos la transpuesta de matriz adjunta (Adj A)t
4. Multiplicamos la matriz adjunta transpuesta por la inversa del
determinante de la matriz A (1/|A|). Esto equivale a dividir cada
elemento de la matriz adjunta transpuesta por el determinante de A.
IMPORTANTE: Puedes comprobar tú mismo si te has equivocado o no. Para ello
basta con verificar que se cumple que:
Matemáticas II Álgebra lineal y Geometría
A  A 1  I
CURSO 2014/15
47
Ejemplo 3 – 12º
Calcula, si existe, la matriz inversa de las siguientes matrices:
 2 2 
a) P  

 5 4 
1. Primero comprobamos si la matriz P tiene o no tiene inversa, es decir si es regular o no:
P 
2 2
 (  8)  (  10)  2
5 4
La matriz P sí tiene inversa.
2. Calculamos la matriz adjunta:
α 11   4
M en o res
co m plem en tario s
α 12  5
α 21   2
ad jun tos
α22  2
A11   4
A12   5
A2 1  2
A2 2  2
 4 5 
AdjP  

 2 2 
3. Escribimos la transpuesta de la adjunta:
 4 2 
(AdjP )t  

 5 2 
4. Hallamos la inversa dividiendo por el determinante de P
P 1 
1
1  4 2   2 1 
(AdjP )t  

2  5 2   5 / 2 1 
P
5. Podemos comprobar que en efecto P-1 sí es la matriz inversa de P.
 5 1
b) M   4 2

 1 2
7
3 ,

1
1. Primero comprobamos si la matriz M tiene o no tiene inversa, es decir si es regular o no:
M 
5 1
4
2
1 2
7
3  (10  3  56)  (14  30  4)   29
1
La matriz M sí tiene inversa.
2. Calculamos la matriz adjunta:
Menores complementarios:
α 11 
2 3
 2.1  3.(  2)  8
2 1
α 21 
1 7
  1.  7.(  2)  13
2 1
α 31 
1 7
  1.3  7.2   17
2 3
α 12 
α 22 
α 32 
4 3
 4.1  3.1  1
1 1
α 13 
4 2
 4.(  2)  2.1   10
1 2
5 7
 5.1  7.1   2
1 1
α 23 
5 1
 5.(  2)  (  1)   9
1 2
5 7
 5.3  7.4   13
4 3
α 33 
5 1
 2.5  (  1).4  14
4 2
Adjuntos: Aij = (-1)i+j.αij
A11 = 8
Matemáticas II Álgebra lineal y Geometría
A12 = -1
A13 = -10
CURSO 2014/15
48
A21 = -13
A22 = -2
A31 = -17
A23 = 9
A32 = 13
A33 = 14
Matriz adjunta
 8
AdjM   13

 17
1 10 
2
9

13 14 
3. Escribimos la transpuesta de la adjunta:
 8 13 17 
(AdjM )t   1 2 13 


9 14 
 10
4. Hallamos la inversa dividiendo por el determinante de M
M 1


 8 13 17  
1
1 
t

(AdjM ) 
1 2 13   

29  10
M
9 14  




8
29
1
29
10
29
13 17 

29 29 
2 13 
29 29 
9 14 
29 29 
5. Podemos comprobar que en efecto M-1 sí es la matriz inversa.
Ejercicio 3 – 12º
Halla, si existen, las matrices inversas de las siguientes matrices:
1 2 1
B  0 1 0


2 0 3
 3 0
A

 5 2 
Soluc: A 1   1 / 3 0 
5 / 6 1 / 2


 3 6 1 
B 1   0 1 0 


 2 4 1 
C
1
2 1 0
C  0 1 3


2 1 1 
 1 1 / 2 3 / 2 
3
1
3 



1
0
1 

Ejercicio 3 – 13º
Halla, si existen, las matrices inversas de las siguientes matrices:
 1 1 1 
B   1 0 3 


 2 5 3 
 2 1 
A

 1 2 
Soluc: A 1   2 / 3  1 / 3 
 1 / 3 2 / 3 


 15 8 3 
B 1   9 5 2 


 5 3 1
C
1
3 0 1 
C  0 2 0


4 2 1 
 1 1 1 
  0 1/2 0 


3 3 
4
Ejercicio 3 – 14º
 1 1 t
Considera la matriz: A   t 0 1  , halla los valores de t para los cuales A no


 6 1 0 
tiene inversa. (Sol.: Si t =  5 la matriz A no tiene inversa, ya que su determinante vale cero para estos valores de t)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
49
Ejercicio 3 – 15º
x
Considera la matriz: A   0

x
1 0
1 3

1 1
a) halla los valores de x para los cuales A sí tiene inversa.
b) Calcula, si es posible, A-1 para x = 2.
-1
Soluc: a) Existe A para todos los valores de x distintos de 0.
b)

A1  


1 1/2 3/2
3
1
3

1
0
1
7ª.- Ecuaciones matriciales
Son ecuaciones en las que la incógnita es una matriz. Antes de empezar a
operar con las matrices dadas conviene despejar la matriz incógnita.
Para resolverlas aplicaremos la propiedad de la matriz inversa:
A · A-1 = A-1 · A = In
Así lograremos que el coeficiente de la matriz incógnita sea la unidad con lo que
tendremos despejada la incógnita como en cualquier otra ecuación.
IMPORTANTE:
Puesto que el producto de matrices no es conmutativo, a la hora de multiplicar
una matriz por otra conviene observar si ha de hacerse por la derecha o por la
izquierda.
Observa que si A no tiene matriz inversa, el proceso indicado no puede
hacerse. En tal caso, la ecuación propuesta puede no tener solución, o, por el
contrario, tener infinitas soluciones.
Ejemplo 3 – 13º
Despeja la matriz X en las siguientes igualdades:
a) AX = B
IMPORTANTE:
No podemos despejar la matriz X, pasando la matriz A al segundo miembro dividiendo (la
división de dos matrices no está definida)
A.X  B
 X 
B
OPERACIÓN IMPOSIBLE
A
Suponiendo que la matriz A tiene inversa, multiplicaremos por la derecha a los dos miembros de la
igualdad por A-1
A-1.(AX) = A-1.B
Aplicando la propiedad asociativa del producto de matrices en el primer miembro:
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
50
(A-1.A)X = A-1.B
y teniendo en cuenta la definición de matriz inversa, y que la matriz Identidad es el elemento neutro
del producto de matrices:
I.X = A-1.B
X = A-1.B
b) XA + B = C
Podemos proceder del siguiente modo:
XA + B = C  XA = C – B 
-1
(XA).A = (C – B).A
-1
 X.(A.A-1) = (C – B).A-1 
 X.I = (C – B).A-1  X = (C – B).A-1
Si queremos, podemos aplicar al segundo miembro de la ecuación obtenida la propiedad
distibutiva del producto del matrices: (C – B).A-1 = C.A-1 – B.A-1
c) AXB = C
AXB = C

-1
-1

A .(AXB) = A .C
-1

(XB) = A .C

X.I = (A .C).B
-1
-1
-1
-1

(XB).B = (A .C).B

X = (A .C).B
-1
-1
-1
-1

-1

(A .A)(XB) = A .C
-1
I(XB) = A .C
-1
X.(B.B ) = (A .C).B
-1


-1
d) 2X - AX = B
Aplicamos la propiedad distributiva para sacar como factor común a la matriz X, teniendo en cuenta el
orden de las matrices en el producto
(2I – A).X = B
IMPORTANTE:
Observa que 2X = 2I.X. Si no fuese así, al sacar factor común, nos habría quedado:
(2 – A).X = B
pero la operación (2 – A) no está permitida, ya que es la resta entre un nº real y una matriz.
-1
-1
(2I – A) .[(2I – A).X] = (2I – A) .B
[(2I – A)-1.(2I – A)].X = (2I – A)-1.B
I.X = (2I – A)-1.B
X = (2I – A)-1.B
Ejercicio 3 – 16º
Despeja la matriz X en las siguientes igualdades:
a) XA = B
b) XA = B + I 2
c) XA + B = 2C
d) AX + BX = C
e) AX = BX + C
f) AX – X = C
g) XAB - XC = 2C
h) XAB = C
Ejemplo 3 – 14º
Resuelve la ecuación matricial AX + B = C, siendo
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
51
0 1 3
2 1
 1 1 




A  1 1 0 , B  1 0 y C   0 1 






2 0 0
 3 4
 1 2 
Observa, en primer lugar, que la matriz X que buscamos es una matriz 3x2.
Despejemos la matriz X:
AX + B = C  AX = C - B  A-1.(AX) = A-1.(C – B)  IX = A-1.(C – B) 
X = A-1.(C – B)
-1
Para obtener la matriz X, necesitamos calcular la matriz A y la matriz C –B, y a continuación hacer el
-1
producto A .(C – B).
 0
0
1/2 
A 1   0
1
1 / 2 


 1 / 3 1 / 3 1 / 6 
 1 2 
C B   1
1 



2

6

 0
0
1 / 2   1 2    1  3 
X  A 1 .(C  B )   0
1
1 / 2  .  1
1 2 4 

 
 

 1 / 3  1 / 3 1 / 6   2 6    1 2 
Ejercicio 3 – 17º a 21º
17º.- Resuelve la ecuación matricial AX – B = C, siendo
 1 1
1 1 0 
0 1 1 
A 
, B 
y C 



 0 1
1 2 1 
 1 1 3
1 1 
18º.- Dadas las matrices: A  
,
3 4
las ecuaciones matriciales:
a) XA = B + I2
2 1 
B  
 y
1 1
b) BXA = 2C
1 2 
C  
 , resolver
1 3 
c) AX - BX = C
19º.- Resolver la ecuación BX = C, siendo:
1 0 0
2 0 1 
B  2 1 0  , C   1 3 0 




1 0 1 
0 0 1 
20º.- Hallar la matriz X tal que AX = B + 2C, siendo:
 1 0 0
A  0 2 0 ,


 1 0 3
 1
B  0

 9
0 1 
0 0

3 3 
y
1 1 1 
C  2 3 0 


3 4 5 
21º.- Resuelve la ecuación AX + B = 2C
 2 0
A
,
 1 1 
 3
B 
 1
1
2
Matemáticas II Álgebra lineal y Geometría
0
1 
y
 4 1
C 
 0 0
CURSO 2014/15
2
1 
52
8ª.- Expresión matricial de un sistema de ecuaciones
lineales
Dado el siguiente sistema de tres ecuaciones lineales con tres incognitas:
a 11x  a 12y  a 13z  b1 

a 21x  a 22y  a 23z  b2 
a 31x  a 32y  a 33z  b3 
 a 11 a 12 a 13  x   b1 
puede expresarse matricialmente así:  a 21 a 22 a 23  y    b2 
 a a a  z   
 31 32 33    b3 
es decir, C  X  B , siendo C
la matriz de los coeficientes, X
la matriz de las
incógnitas y B la matriz de los términos independientes.
Si C es una matriz regular o inversible, en la ecuación matricial C·X = B se
puede despejar X multiplicando por la izquierda en ambos miembros por la matriz
inversa C -1, obteniendo:
C -1·C·X = C -1·B que es equivalente a X  C
1
B
Si el determinante de la matriz C es 0 quiere decir que no tiene matriz inversa,
por lo tanto el sistema no es compatible determinado.
IMPORTANTE:
Lo mismo puede decirse de un sistema de dos ecuaciones lineales con dos
incógnitas, y en general, de cualquier sistema de ecuaciones lineales en el que el nº
de ecuaciones sea igual al nº de incógnitas.
Ejemplo 3 – 22º
Expresa en forma matricial y resuelve el sistema:
 1 1 1 
A   1 0 3 


 2 5 3 
Matriz de coeficientes
x  y  z  1 

x
 3z  18 
2x  5y  3z  52 
x 
X  y 
 
z 
Matriz de incógnitas
 1 
C   18 


 52 
Matriz de términos independientes
El sistema expresado en forma matricial sería:
 1 1 1   x
 1 0 3   y


 2 5 3   z
  1 
   18 
 

  52 
es decir A.X = C
Si la matriz A tiene inversa, podemos despejar la matriz X del siguiente modo:
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
53
AX = C 
-1
-1
A .(AX) = A C 
-1
IX = A .C

-1
X = A .C
 15 8 3 
Puesto que la matriz A tiene inversa y vale: A 1   9 5 2  , obtendremos:


 5 3 1
 15 8 3   1   3 
X  A 1 .C   9 5 2  .  18     5 

 
  
 5 3 1   52   7 
Es decir, x = 3 y = -5 z = 7. Se trata de un SCD y geométricamente representa a tres planos en el
espacio que se cortan en un punto de coordenadas (3, -5, 7)
Ejercicio 3 – 17º
Expresa matricialmente los siguientes sistemas, resuélvelos, clasifícalos e
interprétalos geométricamente:
x  y  z  3

a ) 2x  y  z  2 
x  y  z  1 
b)
2x  y  7 
x  2y  11
Soluc: a) SCD. x = 1; y = 1; z = 1. Se trata de tres planos en el espacio que se cortan en un punto de coordenadas (1, 1, 1)
b) SCD. x = 1; y = -5. Se trata de dos rectas secantes en el plano. El punto de intersección es (1, -5)
9ª.- Cálculo del rango de una matriz mediante
determinantes.
9.1 Submatriz y menor de una matriz
Dada una matriz A de dimensión mxn, se llama SUBMATRIZ de la matriz A, a
cualquier matriz que se obtenga de ella suprimiendo ciertas filas y ciertas columnas.
 1 2 1 0 
En la matriz A   3 1 1 5  si suprimimos la primera fila y la tercera


 1 0 2 1 
 3 1 5
columna, obtenemos la matriz B  
 de dimensión 2x3 que es una submatriz
 1 0 1 
de A.
Si suprimimos la tercera fila y la tercera y cuarta columnas, obtenemos la
 1 2 
matriz C  
 que es una submatriz cuadrada de orden 2 de la matriz A.
3 1 
En consecuencia, las submatrices de una matriz A, podrán ser rectangulares
o cuadradas dependiendo de las filas o columnas que suprimamos en la matriz.
Llamamos MENOR de orden h de una matriz A, al determinante de una
submatriz cuadrada de dimensión hxh de la matriz A. Si dicha submatriz está
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
54
formada por las h primeras filas y las h primeras columnas de la matriz A, el menor
se llama MENOR PRINCIPAL de la matriz A.
En
C 
el
ejemplo
anterior
de
la
submatriz
C,
su
determinante
es
1 2
 1  ( 2).3  7 , es un menor principal de orden 2 y vale 7.,
3 1
9.2 Cálculo del rango de una matriz mediante determinantes
Recordemos que el RANGO de una matriz representa el NÚMERO DE
LÍNEAS (FILAS O COLUMNAS) LI.
Si el determinante de una matriz cuadrada es 0, las filas o columnas son
linealmente dependientes. Teniendo en cuenta esta propiedad, podemos decir que:
TEOREMA
El rango de una matriz A , rango (A) , es el número que expresa el orden del
mayor menor no nulo de dicha matriz. Un matriz tiene rango h cuando existe al
menos un menor de orden h distinto de cero, y todos los menores de órdenes
superiores a h, son nulos.
Las siguientes propiedades del rango de una matriz nos facilitarán su cálculo:
 Si en una matriz A intercambiamos dos filas o dos columnas, el rango de la
nueva matriz coincide con el de la matriz A.
 Si una línea de la matriz A esta formada por ceros, el rango de A es igual al
rango de la matriz que se obtiene de suprimir dicha línea.
 Si una línea es proporcional a otra paralela o es combinación lineal de otras
líneas paralelas, el rango de A es igual al rango de la matriz que se obtiene al
suprimir dicha línea.
A continuación, se describe un procedimiento para obtener el rango de una
matriz cualquiera:
1. Observamos si hay alguna línea de ceros y la eliminamos. Igualmente
observamos si hay alguna línea proporcional a otra o que sea
combinación lineal de otras paralelas y también la eliminamos.
2. Observamos si existe algún menor de orden uno diferente de cero:
 Si todos son cero, rango (A) = 0 y hemos acabado.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
55
 Si alguno de ellos es diferente de cero, rango (A)  1 y pasamos a la
etapa siguiente.
3. Calculamos los posibles menores de orden dos que se obtienen orlando
el menor anterior (orlar = añadir una fila y una columna al menor de orden
1 diferente de cero):
 Si todos son cero, rango (A) = 1 y hemos acabado.
 Si alguno de ellos es diferente de cero, rango (A)  2 y pasamos a la
etapa siguiente.
4. Calculamos los posibles menores de orden tres que se obtienen orlando
el menor anterior:
 Si todos son cero, rango (A) = 2 y hemos acabado.
 Si alguno de ellos es diferente de cero, rango (A)  3 y pasamos a la
etapa siguiente.
5. En general, continuaríamos con el proceso hasta obtener un menor de
orden h distinto de cero. En este caso, el rango será h.
Ejemplo 3 – 23º
 1 3 2 0 
Calcula el rango de la matriz: A   2 1 3 1 


 0 7 7 1 
En primer lugar tenemos que destacar que el máximo rango de esta matriz puede ser 3. Veamos cuál
es.
1.
Observamos que C3 = C1 + C2 , por tanto podemos eliminarla, es decir:
 1 3 2
r an go ( A )  ra n go  2
1
3

7
7
 0
2.
0
 1   ra n go

1 
1
2

0
3 0 
1 1 

7 1 
Observamos si existe algún menor de orden uno diferente de cero. Puesto que a 11 = 1:
|1| = 1  0
Ya hemos encontrado un menor de orden uno diferente de cero, luego rango (A)  1 .
3.
Calculamos los posibles menores de orden dos que se obtienen orlando el menor
anterior:
1 3
70
2 1
Ya hemos encontrado un menor de orden dos diferente de cero, luego rango (A)  2 .
4.
Calculamos los posibles menores de orden tres que al haber eliminado una columna sólo
nos queda uno:
1 3 0
2 1 1  0
0 7 1
No hay ningún menor de orden tres distinto de 0, luego rango (A) = 2 .
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
56
Ejemplo 3 – 24º
2 1 0 
Estudia el rango de la matriz A   1 1 2  en función del parámetro a.


3 1 a 
En primer lugar hallamos el determinante de la matriz A para ver que valores del parámetro a lo
anulan.
2 1 0
A  1 1 2  (2a  6  0)  (0  4  a )  a  2
3 1 a
|A| = 0 
a–2=0  a=2
Conclusión:
Si a ≠ 2  |A| ≠ 0  rang A = 3
Si a = 2  |A| = 0  rang A < 3 Pero como hay un menor de orden 2 distinto de cero
2 1
 1  0 , rang A = 2
1 1
Ejemplo 3 – 25º
1 a
a 2
1 

Estudia el rango de la matriz A  1 2a
a 4
3  en función del


2
2
 a a 2a  2a  4 2a  2 
parámetro a.
Démonos cuenta que el rango de la matriz como máximo puede valer 3. Veámoslo.
1 a
a 2
Hallamos el menor principal de orden 3 1 2a
a 4
 a 3  4a
2
2
a a 2a  2a  4
Este menor vale cero para a = 2, -2 y 0

Si a ≠ 2 ó a ≠ -2 ó a ≠ 0, ya hay un menor de orden 3 distinto de 0 y por tanto rango A = 3

Si a = 0
 1 0 2 1 
A   1 0 4 3 


 0 0 4 2 
1 2
 2  0
1 4


rangoA  2;

 1 2 1 
rangoA  rango  1  4 3 


 0 4 2 
1 2 1
1 4 3  4  0
0 4 2

rangoA  3
Si a = 2
1 2 0 1
A   1 4 2 3 


2 4 0 6 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
57
1 2
20
1 4

1 2 1
1 4 3 8 0
2 4 6
rangoA  2;


rangoA  3
Si a = -2
 1 2 4 1 
A   1 4 6 3 


8 2 
 2 4
1 2
 2  0
1 4

1 2 4
1 2 1
1 4 1
1 4 6  1 4 3  1 6 3  0
2 4
8
2 4 2
2 8 2
rangoA  2;

rangoA  2
Ejercicio 3 – 18º
Estudia el rango de las siguientes matrices en función del parámetro que aparece en
ellas:
a)
 a
1 0
A   1 2a 2 


 1 1 2 
b)
 2 1 k 
B  k 3 4 


 3 1 2 
Soluc: a) Si a = 0, rango A = 2; Si a = ½, rango A = 2;
b) Si k = 1, rango B = 2; Si k = -8, rango B = 2;
c) Si m = 1, rango C = 2; Si m = -1, rango C = 2;
1 1 1 
C   1 m 1 


1 1 m 
c)
Si a ≠ 0 y a ≠ ½, rango A = 3
Si k ≠ 1 y k ≠ -8, rango B = 3
Si m ≠ 1 y m ≠ -1, rango C = 3
Ejercicio 3 – 19º
Estudia el rango de las siguientes matrices en función del parámetro que aparece en
ellas:
a)
1 2 3 a 
A  2 4 6 8 


 3 6 9 12 
b)
 b 1
1 
B 

 1 b 2b  1 
c)
 c  2 1  2c 1 
C 
c
2c 
 c
Soluc: a) Si a = 4, rango A = 1; Si a ≠ 4, rango A = 2
b) Si b = 1, rango B = 1; Si b = -1, rango B = 2;
c) Si c = 0, rango C = 1; Si c = 1, rango C = 2;
Matemáticas II Álgebra lineal y Geometría
Si b ≠ 1 y b ≠ -1, rango B = 2
Si c ≠ 0 y c ≠ 1, rango C = 2
CURSO 2014/15
58
4.-RESOLUCIÓN DE SISTEMAS DE
ECUACIONES LINEALES MEDIANTE
DETERMINANTES
1ª. Matriz de coeficientes y matriz ampliada
2ª. Compatibilidad de un sistema de ecuaciones. Teorema
de Rouché-Fröbenius
3ª. Método de Cramer
4ª. Sistemas de ecuaciones homogéneos
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
59
1ª.- Matriz de coeficientes y matriz ampliada
Recordemos que un sistema de ecuaciones lineales, están formados por
varias ecuaciones lineales de las que queremos saber las soluciones comunes, y
puede escribirse de la forma:
a11x1
a21x1

am 1x1
 a12x 2    a1n xn  b1 
 a22x 2    a2n xn  b2 
        
 am 2x 2    amn xn  bm 
Sistema de “m” ecuaciones lineales con “n” incógnitas
Donde:
a11, …, aij son números reales llamados coeficientes del sistema
b1, …, bm son números reales llamados términos independientes y
x1, …, xn son las incógnitas del sistema.
Llamamos matriz de coeficientes a la matriz formada por los coeficientes
de las incógnitas, y llamamos matriz ampliada a la matriz foermada tanto por los
coeficientes de las incógnitas como por los términos independientes:
 a11 a12
a
a
A   21 22
 ... ...
a
 m 1 am 2
... a1n 
... a2n 

... ... 
... amn 
 a11 a12
a
a
A ´   21 22
 ... ...
a
 m 1 am 2
Matriz de coeficientes
Por ejemplo, si el sistema es:
Matriz de coeficientes
x


Matriz ampliada
2x  y  3
, las matrices de coeficientes y ampliada son:
x  5y  0 
 2 1
A 

 1 5 
Si el sistema fuese: x
... a1n b1 
... a2n b2 

... ... ... 
... amn bm 
 2 1 3 
A´ 

 1 5 0 
Matriz ampliada
y  z  1

y  z  2  , las matrices de coeficientes y ampliada son:
3y  2z  0 
1 1 1 
A   1 1 1 


 0 3 2 
Matriz de coeficientes
Matemáticas II Álgebra lineal y Geometría
 1 1 1 1
A´  1 1 1 2 


 0 3 2 0 
Matriz ampliada
CURSO 2014/15
60
2ª.- Compatibilidad de un sistema de ecuaciones
lineales. Teorema de Rouché-Fröbenius
Estudiando el rango de la matriz de coeficientes y de la matriz ampliada,
podemos conocer si un sistema es compatible o no lo es, y si es compatible, saber si
es determinado o indeterminado.
TEOREMA DE ROUCHÉ-FRÖBENIUS
El teorema de Rouché-Fröbenius afirma que la condición necesaria y
suficiente para que un sistema de m ecuaciones lineales con n incógnitas sea
compatible (tenga solución) es que el rango de la matriz de coeficientes, A, coincida
con el rango de la matriz ampliada A´, es decir:
El sistema es compatible  rango (A) = rango (A´)
Este teorema permite la discusión y clasificación de un sistema lineal de
ecuaciones antes de su resolución.
Cuando estudiamos el rango de la matriz A y A´, puede ocurrir:
- Si rango (A) ≠ rango (A’), el sistema es incompatible, no tiene
solución.
- Si rango (A) = rango (A´) pueden ocurrir dos cosas:
rango (A) = rango (A´) = nº de incógnitas, el sistema es
compatible determinado, es decir, tiene solución única.
rango (A) = rango (A´) < nº de incógnitas, el sistema es
compatible indeterminado, es decir, tiene infinitas soluciones que vendrán
dadas en función de un parámetro, λ, si el rango es una unidad inferior al
nº de incógnitas, de dos parámetros, λ y µ, si el rango es dos unidades
inferior a nº de incógnitas, etc.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
61
Ejemplo 4 – 1º
Discute, clasifica e interpreta los siguientes sistemas:
a)
x  y  7

2x  3y  4 
2x  y  0 

1 1 
A   2 3 


2 1 
1 1 7
A´  2 3 4 


2 1 0 
Estudiemos los rangos de la matriz de coeficientes y de la matriz ampliada:
Rango de A:
Como existe un menor de orden dos distinto de cero 1 1  5  0 , rango A = 2
2 3
Rango de A´:
Por la misma razón que
orden tres:
1 1
A´  2 3
2 1
antes, rango A´ ≥ 2. Para ver si es 3, estudiamos el menor de
7
4  60  0 
0
rango A´= 3
Conclusión: rango A = 2 ≠ rango A´= 3, por tanto es un SI, es decir, se trata de tres rectas del plano
que se cortan dos a dos, no hay un punto en común a las tres rectas.
b)
2x  3y  z  4 

x  2y
 5
3y  z  1 

 2 3 1 
A  1 2 0 


0 3 1 
 2 3 1 4 
A´  1 2 0 5 


0 3 1 1 
Estudiemos los rangos de la matriz de coeficientes y de la matriz ampliada:
Rango de A:
Como existe un menor de orden dos distinto de cero 2 3  1  0 , rango A ≥ 2.
1 2
Para ver si el
2
A 1
0
rango de A es 3, estudiemos su determinante:
3 1
rango A = 3
2 0  2  0 
3 1
Rango de A´:
El rango de A´ también es 3
Conclusión: rango A = 3 = rango A´, por tanto es un SCD, es decir, se trata de tres planos que se
cortan en un punto. Para hallar dicho punto resolveríamos el sistema.
c)
x  2y  z  0 

x  y
 1 
x  4y  3z  4 

 1 2 1 
A   1 1 0 


 1 4 3 
 1 2 1 0 
A´  1 1 0 1 


 1 4 3 4 
Estudiemos los rangos de la matriz de coeficientes y de la matriz ampliada:
Rango de A:
Como existe un menor de orden dos distinto de cero 1 2  1  0 , rango A ≥ 2.
1 1
Para ver si el rango de A es 3, estudiemos su determinante:
1 2 1
rango A = 2
A  1 1 0  0 
1 4 3
Rango de A´:
Para ver si el rango de A´ es tres, estudiamos los otros menores de orden tres:
1 2 0
rango A´ = 3

1 1 1  2  0
1 4 4
Conclusión: rango A = 2 ≠ rango A´= 3, por tanto es un SI, es decir, se trata de tres planos que se
cortan dos a dos, no hay un punto en común a los tres planos.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
62
d)
x  2y  z  0 

x  y
 1 
x  4y  3z  2 

 1 2 1 
A   1 1 0 


 1 4 3 
 1 2 1 0 
A´  1 1 0 1 


 1 4 3 2 
Estudiemos los rangos de la matriz de coeficientes y de la matriz ampliada:
Rango de A:
Como existe un menor de orden dos distinto de cero 1 2  1  0 , rango A ≥ 2.
1 1
Para ver si el rango de A es 3, estudiemos su determinante:
1 2 1
rango A = 2
A  1 1 0  0 
1 4 3
Rango de A´:
Para ver si el rango de A´ es tres, estudiamos los otros menores de orden tres:
1 2 0 1 1 0
rango A´ = 2

1 1 1  1 0 1  0
1 4 2 1 3 2
Conclusión: rango A = 2 = rango A´, por tanto es un SCI, es decir, se trata de tres planos que se
cortan en una recta, Si queremos obtener el conjunto de soluciones resolvemos el sistema.
Ejercicio 4 – 2º
Discute, clasifica e
parámetro.
ax  y
x  ay
x  y
interpreta el siguiente sistema en función de los valores del
 z  1

 z  1
 az  1 

a 1 1 
A 1 a 1


1 1 a
a 1 1 1
A´  1 a 1 1 


 1 1 a 1
Hallamos el determinante de A y vemos para que valores de a se hace cero o distinto de cero:
a 1 1
A  1 a 1  a 3  3a  2
1 1 a

Si a ≠ 1 y a ≠ -2, A  0
a 3  3a  2  0
( a  1) 2 ( a  2)  0
a  1 a  2
 rango A = 3 = rango A`= nº de incógnitas  SCD,
se trata de tres planos que se cortan en un punto.
1 1 1 
1 1 1 1
 Si a = 1 A   1 1 1  A´  1 1 1 1   rango A = 1 = rango A`< nº de incógnitas




1 1 1 
1 1 1 1
 SCI, se trata del mismo plano.
 2 1
 2 1 1 1 
1 
 Si a = -2 A   1  2 1  A´  1 2 1 1 




1 2 
 1
 1 1 2 1 
El rango de A = 2, puesto que hay un menor de orden dos distinto de cero.
El rango de A´= 3, puesto que hay un menor de orden tres distinto de cero:
2 1 1
1 2 1  9  0
1
1 1
Conclusión: rango A = 2 ≠ rango A´= 3, por tanto es un SI, es decir, se trata de tres planos que se
cortan dos a dos, es decir, no hay ningún punto en común a los tres planos.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
63
Ejercicio 4 – 1º
Aplica el teorema de Rouché para averiguar si los siguientes sistemas son
compatibles o incompatibles:
x  y  z  3
x  y  1


a) x
 z  2
b ) 3x  y  1 
2x  y  2z  5 
x  2y  5 
c)
x  y  3z  1 

3x  2y  z  3 
x  y  z  4 
d)
x  3y  7z  10 

5x  y  z  8 
x  4y  10z  5 
(Sol.: SCI; SI; SCD; SI)
Ejercicio 4 – 2º
Discute, clasifica e interpreta los siguientes sistemas en función de los valores del
parámetro correspondiente.
a)
x  y  7

kx  y  11
x  4y  K 
c)
2x  my  6z  0 
x  3y  mz  0 
b)
x  y  az  0 

ax  y
 12
x  4y  6z  0 
x 
d)
y
 1 

my
 z  0 
x  (m  1)y  mz  m  1
Sol.: a) Consejo: estudia directamente el rango de la ampliada. Si K ≠ 2 y k ≠ -31, rango A = 2 ≠ rango A´= 3 SI.
Si K = 2, rango A = rango A´= 2 SCD; Si K = -31, rango A = rango A´= 2 SCD
b) Si a ≠ 2 y a ≠ -3/4, SCD; Si a = 2, SI; Si a = -3/4, SI
c) SCI para cualquier valor de m
d) Si m ≠ 0 y m ≠ 1, SCD; si m = 0, SCI;
si m = 1, SI
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
64
3ª.- Método de Cramer
Se dice que un sistema de ecuaciones lineales A.X = B, es un SISTEMA DE
CRAMER, si el nº de ecuaciones es igual al nº de incógnitas, y además |A| ≠ 0.
a11x1
a21x1
...
an 1x1
 a12x2
 a21x2
 ...
 an 2x2




...
...
...
...
 a1n xn
 a2n xn
 ...
 ann xn




b1 
b2 
... 
bn 
Puede demostrarse que la solución del sistema viene dada por las expresiones:
x1 
b1 a12
b2 a22
... ...
bn an 2
...
...
...
...
a1n
a2n
...
ann
x2 
A
a11
a21
...
an 1
b1
b2
...
bn
...
...
...
...
a1n
a2n
...
ann
A
....
a11 a12
a21 a22
... ...
an 1 an 2
xn 
...
...
...
...
b1
b2
...
bn
A
Observa que el numerador aparece el determinante de la matriz que resulta de
sustituir en la matriz A, a la columna de los coeficientes de la incógnita que vamos a
calcular, por los términos independientes del sistema.
Ejemplo 4 – 3º
Resuelve por Cramer los sistemas:
x  y  z  6

a ) x  y  z  4
x  y  z  0 
Veamos que es un sistema de Cramer, es decir, veamos que |A| ≠ 0
1 1 1
A  1 1 1  4  0
1 1 1
Calculemos la solución:
x 
6
4
0
1
1
1
1
1
1
A

8
 2
4
y 
1
1
1
6
4
0
A
1
1
1

4
 1
4
z 
1
1
1
1
1
1
A
6
4
0

12
 3
4
Se trata de tres planos que se cortan en un punto de coordenadas (2, 1, 3)
b)
2x  y  1
3x  2y  3 
Veamos que es un sistema de Cramer:
Hallemos la solución:
x 
1 1
3 2
A
A 
2 1
10
3 2
1
 1
1
y 
2 1
3 3
A

3
3
1
Se trata de dos rectas que se cortan en un punto de coordenadas (1, 3)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
65
En los ejemplos anteriores hemos aplicado la regla de Cramer a sistemas compatibles
determinados, pero también se puede aplicarse a sistemas compatibles indeterminados. Veámoslo en
el siguiente sistema:
3x  2y  z  2 

2x  5y  3z  15 
11x  y
 21 
Discutamos el sistema:
Rango de A:
3 2 1
A  2 5 3  0
11 1 0

 3 2 1 
A   2 5 3 


 11 1 0 
 3 2 1 2 
A`  2 5 3 15 


 11 1 0 21 
3 2
 19  0
2 5
rango A < 3;

rango A = 2
Rango de A´:
3 2 1
3 2 2
3 1 2
2 5 3  2 5 15  2 3 15  0 Todos los menores de orden tres valen 0
11 1 0
11 1 21 11 0 21
 rango A´= 2
Puesto que rango A = rango A´= 2 < nº de incógnitas, se trata de un SCI, es decir, el
sistema tiene infinitas soluciones. Se trata de tres planos que se cortan en una recta,
siendo cada solución del sistema una terna de números que corresponde con las
coordenadas de un punto de esa recta.
Para resolverlo, podemos quedarnos con las dos primeras ecuaciones, puesto
3 2
 19 es distinto de cero, eliminando la 3ª que es una
que el menor
2 5
combinación lineal de las otras dos.
3x  2y  z  2 
2x  5y  3z  15
Llamamos z = λ, y pasamos al 2º miembro, de modo que nos queda un sistema de
dos ecuaciones con dos incógnitas que podemos resolver por Cramer, ya que el
determinante de la matriz de coeficientes es distinto de 0. Como el término
independiente esta dado en función de λ, las soluciones vendrán dadas en función
de este parámetro.
 3 2 
 3 2 2  λ 
3x  2y  2  λ 
A
A´ 


2x  5y  15  3λ 
2
5


 2 5 15  3λ 
Aplicando la regla de Cramer al sistema:

2  λ 2
15  3λ 5
(2  λ).5  ( 2).(15  3λ ) 40  λ 
x 


19
19 
A
40  λ
41  11λ
;Y 
;z  λ
x 
3 2λ
19
19

2 15  3λ 3.(15  3λ )  (2  λ).2 41  11λ 
y 



19
19
A

Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
66
Ejercicio 4 – 3º
Resuelve por Cramer los siguientes sistemas:
a)
x  2y  3z  1 

2x  y  4z  2 
3x  4y  z  3
Soluc: a) (1, 0, 0)
b) (1, 1, 1)
b)
x  y  z  3

2x  y  z  2 
x  y  z  1 
c)
2x  y  1 
x  3y  4 
c) (1, -1)
Ejercicio 4 – 4º
Discute y resuelve por Cramer, si es posible, los siguientes sistemas:
a)
x  y  3z  1 

3x  y  2z  3
 2y  7z  0
uc: a) SCI ((2+λ)/2, 7λ/2, λ)
b) SI
b)
x  y  3z  1 

3x  y  2z  3 
 2y  7z  10
c)
3x  4y  4 

2x  6y  23 Sol
2x  3y  1 
c) SI
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
67
4ª.- Sistemas de ecuaciones homogéneos
Un sistema de ecuaciones lineales se dice que es un SISTEMA
HOMOGÉNEO, cuando todos los términos independientes valen 0.
a11x1
a21x1
...
an 1x1
 a12x2
 a21x2
 ...
 an 2x2




...
...
...
...
 a1n xn
 a2n xn
 ...
 ann xn




0
0 
...
0 
En notación matricial sería A.X = 0
Un sistema homogéneo tiene las siguientes PROPIEDADES:
Siempre es compatible, ya que siempre tiene la solución (0, 0, …, 0),
denominada SOLUCIÓN TRIVIAL O NULA.
El rango de A y el rango de A´ siempre coinciden.
Para que el sistema tenga otras soluciones distinta de la trivial, es
necesario y suficiente que el rango de A sea menor que el nº de incógnitas,
es decir, que |A| = 0.
Ejemplo 4 – 4º
x  y  z  0

Resolver el siguiente sistema homogéneo: x  2y  3z  0
2x  3y  4z  0
a) POR GAUSS:
 1 1 1 0
 1 1 1 0
1 1
1ª
1ª
 1 2 3 0   2ª 1ª   0 1 2 0   2ª   0 1





 2 3 4 0  3ª 1ª .2  0 1 2 0  3ª 2ª  0 0
Es un SCI puesto que nos queda un sistema
pasamos al segundo miembro y resolvemos:
x  y  z  0
y  2z  0

x  y  λ 
y  2λ 
1 0
2 0

0 0 

 1 1 1 0
 0 1 2 0



x  y  z  0
y  2z  0
de dos ecuaciones con tres incógnitas. Hacemos z = λ,

x  2λ  λ 
y  2λ
z λ
x λ
b) POR ROUCHÉ-FRÖBENIUS:
1 1 1
1 1
 1  0  rango A = 2 = rango A´< nº de incógnitas  SCI
A  1 2 3  0  rango A < 3
1 2
2 3 4
Nos quedamos con las dos primeras ecuaciones y hacemos z = λ.
x  y  z  0
x  y  λ 

x  2y  3z  0 
x  2y  3λ 
Sistema que podemos resolver por Cramer ( ó por reducción, ó por igualación, ó por sustitución, ó por
Gauss):
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
68
x 
λ 1
3λ 2
A
2λ  (3λ)

λ
1
y 
1 λ
1 3λ

A
3λ  ( λ)
 2λ
1

(λ, 2λ, λ)
Ejemplo 4 – 5º
Estudia y resuelve el siguiente sistema homogéneo en función del parámetro k:
(1  k )x 
y
 0

x
 (1  k )y 
z
 0
y
 (1  k )z  0
Por ser un sistema homogéneo, tiene al menos la solución trivial x = 0, y = 0, z = 0.
Para que tenga otras soluciones, el rango de la matriz de coeficientes tiene que ser menor de 3, es
decir, el determinante de la matriz de coeficientes tiene que ser 0. Veamos la expresión del
determinante de la matriz A.
A 
1k
1
0
1
1k
1  k 3  3k 2  k  1
0
1
1k

(k  1)( k 2  2k  1)  0

Si k  1 y k  1  2 y k  1  2
solución trivial (0, 0, 0).

Si K = 1
0 1 0
A  1 0 1


0 1 0

x

Si k  1  2


y

A 0

 z

0 1
 1  0
1 0

 2 1
0 

 
A 1  2 1 
 0
1  2



y 0
x  λ
z λ
z λ
 0
 0 
rango A = 3 = rango A’


k 1
k 1 2
K 1 2

|A| ≠ 0
 k 3  3k 2  k  1  0

rango A = 2 = rango A´

SCD con la


SCI
(  λ, 0, λ )
 2
1
10 
1
 2
rango A = 2 = rango A´
SCI


 2x
x




y
2y
Si k  1  2
 z

 0 

 0 
z λ

 2 1 0


A 1 2 1 
 0 1 2


 2x
x
y
2y


 0 

  λ 

2
1
1
10 
2
2x
x


y
2y

x λ
y  2λ
z λ

( λ , 2λ , λ )
rango A = 2 = rango A´

SCI

2x
x


y
2y
 z
 0 

 0 
z λ

Matemáticas II Álgebra lineal y Geometría
 0 

  λ 

CURSO 2014/15
x λ
y   2λ
z λ

( λ ,  2λ , λ )
69
Ejercicio 4 – 5º
Resolver los siguientes sistemas homogéneos:
3x  5y  z  0
x  y  z  0
x  y  z  0


a ) x  2y  z  0 b) x  y  3z  0 c) x  y  2z  0
x  y
 0
x  5y  9z  0
2x  4y  z  0
Soluc: a) SCD: (0, 0, 0)
b) SCI: (-λ, -2λ, λ)
c) SCI: (3λ/2, λ/2, λ)
Ejercicio 4 – 6º
Discute y resuelve el sistema hogéneo siguiente en función del parámetro a:
ax  y
 0

 y  2az  0
x  ay
 0
Soluc: Si a ≠ 0, SCD con la solución trivial (0, 0, 0)
Si a = 0, SCI: (0, 0, λ)
IMPORTANTE:
Desde este momento, si has asimilado bien los contenidos de algebra,
puedes hacer todos los ejercicios nº 3 de los exámenes de selectividad de ambas
opciones, salvo los que contengan preguntas de vectores que lo aprenderás en el
tema siguiente.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
70
5.- VECTORES EN EL ESPACIO
1ª. Vectores en el espacio (R3)
2ª. Definición geométrica de suma y resta de vectores.
Propiedades
3ª. Definición geométrica de producto de un escalar por un
vector. Propiedades
4ª. Vectores unitarios
5ª. Espacio vectorial R3
6ª. Combinación lineal de vectores
7ª. Dependencia e independencia lineal de vectores
8ª. Base de un espacio vectorial
9ª. Coordenadas de un vector respecto a una base
10ª. Definición analítica de suma y resta de vectores, y de
producto de un escalar por un vector
11ª. Producto escalar de vectores. Propiedades
12ª. Producto vectorial de vectores. Propiedades
13ª. Interpretación geométrica del producto vectorial
14ª. Producto mixto de vectores. Interpretación geométrica
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
71
1ª.- Vectores en el espacio (R3)
Las características de los vectores en el espacio (R3), así como sus
propiedades, son idénticas a las de los vectores en el plano (R2), que ya se
estudiaron el año pasado tanto en Matemáticas como en Física.

Un vector AB , es una flecha con origen en el punto A y extremo en el punto
B, que tiene las siguientes características:

Módulo: la distancia del punto A al punto B. Se representa por |AB |
Dirección: es la dirección de la recta que une los puntos A y B.
Sentido: el que va del origen al extremo.
B
A
Cuando dos vectores tienen la misma dirección, el mismo módulo, pero son de

sentidos opuestos, se dicen que son VECTORES OPUESTOS. Los vectores AB y



BA son vectores opuestos, es decir: AB = - BA
Dos vectores son iguales cuando tienen la misma dirección, sentido y
módulo.
A
A’
B
B’
A’’
B’’
Y se dice de ellos que son VECTORES EQUIPOLENTES
Se dice que un VECTOR ES UNITARIO, si su módulo vale la unidad

u

es unitario
Matemáticas II Álgebra lineal y Geometría
 |u | 1
CURSO 2014/15
72
2ª.- Suma y resta geométrica de vectores


Para sumar geométricamente dos vectores u y v , se sitúa uno de ellos a
continuación del otro, y se une el origen del primero con el extremo del último:


u+v



u
u+v

v
Puedes observar que cuando los vectores que sumas no tienen la misma dirección,


su suma coincide con la diagonal del paralelogramo que forman u y v :



Para restar geométricamente dos vectores u - v , se le suma a u el opuesto

de v y se procede a realizar la suma como se ha explicado.




u - v = u + (-v )





-v
v
u -v
u





u
u-v
u
v


v
v


Observa como en este caso el vector u - v , es el vector que une el extremo del
segundo con el extremo del primero.


u
u-v


v
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
73
PROPIEDADES:

1ª. ASOCIATIVA:





u  (v  w )  (u  v )  w




2ª. CONMUTATIVA:
u v  v  u
3ª. ELEMENTO NEUTRO:
u  0  0 u  u



4ª. ELEMENTO OPUESTO:
Matemáticas II Álgebra lineal y Geometría





u  (u )  0
CURSO 2014/15
74
3ª.- Definición geométrica de producto de un escalar
por un vector
Se llama producto de un escalar por un vector, al producto de un nº real k,


por un vector u . Se representa por k. u , y el resultado es un nuevo vector que tiene
las siguientes características:

Dirección: la misma que u .


Sentido: el mismo que u , si el escalar es positivo y, contrario a u , si el
escalar es negativo.



Módulo: el valor absoluto del escalar por el módulo de u : |k .u ||k |.| u |


ku (K >1)
ku (0<K<1)

u


ku (K< -1)
ku (-1<K<0)
PROPIEDADES:

1ª. ASOCIATIVA:

a .(b.u )  (a .b).u
2ª. DISTRIBUTIVA RESPECTO A LA SUMA DE ESCALARES:



(a  b).u  a .u  b.u
3ª. DISTRIBUTIVA RESPECTO A LA SUMA DE VECTORES:




a .(u v )  a .u  a.v

4ª. ELEMENTO NEUTRO:
Matemáticas II Álgebra lineal y Geometría

1.u  u
CURSO 2014/15
75
4ª.- Vectores unitarios
Un vector es unitario cuando su módulo vale la unidad.

Si un vector v no es unitario, el producto de un escalar por un vector nos
permite hallar dos vectores unitarios de la misma dirección que él: uno en el mismo
sentido y otro en sentido contrario.

Para ello, basta con multiplicar al vector v por el escalar inversa de su módulo
o por el opuesto de la inversa de su módulo, respectivamente.


Si | v | 1

1
.v 

|v |

v

ó

1

|v |


.v 
|v |
.v  

|v |

tienen de módulo la unidad
|v |


1
v

| v | 1
v

|v |



1
.v  

|v |
Matemáticas II Álgebra lineal y Geometría
v

|v |
CURSO 2014/15
76
5ª.- Espacio vectorial R3
En la pregunta nº 2 de este tema hemos definido una ley de composición
interna en R3, la suma de vectores, que podemos representar así:
R 3xR 3  R 3
 

u ,v

 u v
Y que cumple las siguientes propiedades:

1ª. ASOCIATIVA:





u  (v  w )  u  (v  w )




2ª. CONMUTATIVA:
u v  v  u
3ª. ELEMENTO NEUTRO:
u  0  0 u  u








u  (u )  0
4ª. ELEMENTO OPUESTO:
En la pregunta nº 3 hemos definido una ley de composición externa en R3,
el producto de un escalar por un vector, que puede representarse así:
RxR 3  R 3


k ,u
 k .u
Y cumple las siguientes propiedades:

1ª. ASOCIATIVA:

a .(b.u )  (a .b).u
2ª. DISTRIBUTIVA RESPECTO A LA SUMA DE ESCALARES:



(a  b).u  a .u  b.u
3ª. DISTRIBUTIVA RESPECTO A LA SUMA DE VECTORES:




a .(u v )  a .u  a.v

4ª. ELEMENTO NEUTRO:

1.u  u
Con esta ley de composición interna y sus propiedades, y con esta ley de
composición externa y sus propiedades, se dice que R3 ES UN ESPACIO
VECTORIAL.
Lo mismo podría decirse del conjunto de vectores del plano, es decir, de R2.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
77
6ª.- Combinación lineal de vectores



Supongamos un conjunto de n vectores u 1 , u 2 , ..., u n , y un conjunto de n nº
reales, a1 , a2 ,..., an . Llamamos COMBINACIÓN LINEAL DE LOS n VECTORES a
la expresión:



a1 u1  a2 u2  ...  an un
Es decir, a la suma de los resultados de multiplicar a cada vector por un escalar.

Por ejemplo, la expresión


3 u  2v  w es una de las infinitas combinaciones

 
lineales posibles que se pueden hacer con los vectores u,v y w .
7ª.- Dependencia e independencia lineal de vectores
Se dice que varios vectores son LINEALMENTE DEPENDIENTES (LD), si
alguno de ellos se puede poner como combinación de los demás. Cuando ninguno
de ellos se puede poner como combinación lineal de los demás se dice de ellos que
son LINEALMENTE INDEPENDIENTES (LI).
Por ejemplo:
Dos vectores de la misma dirección siempre son LD porque uno de ellos se
puede expresar como el producto del otro pon un apropiado nº real. Pero, dos
vectores de distinta dirección siempre son LI porque ninguno de ellos se puede
expresar como el producto del otro pon un apropiado nº real:




v  k.u
v


u
u



u y v LI
u y v LD




(v  k.u)

Tres vectores u, v y w coplanarios siempre son LD porque cualquiera de
los tres se puede poner como combinación lineal de los otros dos.


b.v


w  a.u  b.v

v
Matemáticas II Álgebra lineal y Geometría


u
a.u
CURSO 2014/15
78



Tres vectores u, v y w no coplanarios son LI porque ninguno de los tres se
puede poner como combinación lineal de los otros dos.

v

u

w

Pero cualquier otro vector t del espacio se puede poner como combinación
lineal de ellos

β.v




t  α .u  βv
.  μ .w


μ .w
α.u
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
79
8ª.- Base de un espacio vectorial
Se llama BASE DE UN ESPACIO VECTORIAL, al mínimo nº de vectores LI
que generan a todos los demás vectores mediante combinación lineal de ellos.
En el plano, R2, una base está formada por dos vectores cualesquiera de
distinta dirección, ya que cualquier otro vector del plano se podrá expresar como una
combinación lineal de ellos.
En el espacio, R3, una base la formarían cualesquiera tres vectores no
coplanarios, ya que cualquier otro vector del espacio se puede poner como
combinación lineal de ellos tres.
Si los vectores de la base son perpendiculares entre sí, se dice que forman
una BASE ORTOGONAL. Si además de ser perpendiculares, los vectores de la
base son unitarios, se dice que LA BASE ES ORTONORMAL.


En el plano, R2, una base ortonormal está formada por los vectores i y j ,
denominada BASE CANÓNICA DE R2, que son vectores unitarios en la dirección
positiva de los ejes X e Y respectivamente. Esto significa que cualquier vector del
plano se puede generar mediante combinación lineal de los vectores de la base
  
B  i , j 




En el espacio, R3, una base ortonormal está formada por los vectores i , j y

k , denominada BASE CANÓNICA DE R3, que son vectores unitarios en la dirección
positiva de los ejes X, Y y Z respectivamente. Esto significa que cualquier vector del
espacio se puede generar mediante combinación lineal de los vectores de la base
   
B  i , j , k 


y
y


j
j



i
k
i
x
x
z
BASE CANÓNICA DE R2
Matemáticas II Álgebra lineal y Geometría
BASE CANÓNICA DE R3
CURSO 2014/15
80
9ª.- Coordenadas de un vector respecto a una base
   
Dada una base cualesquiera de de R3, B  v , w ,t  , sabemos que



cualquier vector u del espacio se puede expresar como combinación lineal de los
vectores de la base B, es decir:




u  a .v  b .w  c .t
A los nº reales a, b y c se les denomina COORDENADAS DEL VECTOR
RESPECTO A LA BASE B, y se expresa:




u  a .v  b.w  c .t  (a, b,c )
   
Y como siempre vamos a trabajar con la base canónica, B   i , j , k  ,


cualquier vector quedaría de la forma:




u  a . i  b. j  c.k  (a, b,c )  (ux ,uy ,uz )
OBSERVACIÓN:
Las coordenadas de los vectores de la base canónica serían:




i  1. i  0. j  0.k  (1,0,0)




j  0. i  1. j  0.k  (0,1,0)




k  0. i  0. j  1.k  (0,0,1)
Si de un vector conocemos su origen A y su extremo B, las coordenadas del
vector se obtienen restando al extremo el origen

AB = coordenadas del extremo – coordenadas del origen

AB = B – A = (x2, y2, z2) - (x1, y1, z1) = (x2 – x1, y2 – y1, z2 –z1) =



= (x2 – x1,) i +( y2 – y1 ) j  ( z2 – z1 )k
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
81
10ª.- Definición analítica de suma y resta de vectores
y de producto de un escalar por un vector.


Si tenemos dos vectores u y v , cuyas coordenadas respecto a la base
canónica son:



u  (ux ,uy ,uz )  ux i  uy j  uz k



v  (vx ,vy ,vz ) vx i vy j vz k


y


Se define la suma analítica de los vectores u y v , como es vector que se
obtiene de sumar las coordenadas semejantes:



uv  (ux ,uy ,uz ) (vx ,vy ,vz )  (ux vx ,uy vy ,uz vz )  (ux vx )i (uy vy )j (uz vz )k
 


Se define la resta analítica de los vectores u y v , como es vector que se obtiene de
restar a las coordenadas del primero, las coordenadas semejantes del segundo:
 



u v  (ux ,uy ,uz )  (vx ,vy ,vz )  (ux vx ,uy vy ,uz vz )  (ux vx )i  (uy vy )j  (uz vz )k

Se define el producto de un escalar k por un vector u , como el vector que se obtiene
de multiplicar cada una de sus coordenadas por el escalar:




k .u  k .(ux ,uy ,uz )  (k .ux ,k .uy ,k .uz )  k .ux i  k .uy j  k .uz k
Ejemplo 5 – 1º




Considera los vectores u , v , w
canónica son:
t , cuyas coordenadas respecto a la base
y




u  (1, 2,0)
v  (0, 1,3)
w  (1,0, 5)
t  (1,1,0)



a) Comprueba que los vectores u , v y w forman una base de R3.




b) Expresa al vector t como combinación lineal de u , v y w .




c) Calcula 2 u + 3v - w - 3t
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
82
11ª.- Producto escalar de dos vectores. Propiedades.
11.1 Definición geométrica

 

El producto escalar de dos vectores u y v, que se representa por u.v , es
un escalar que se obtiene de multiplicar los módulos de ambos vectores por el
coseno del ángulo que forman:


 
u. v | u |. | v |.cos(u ,v )
 
11.2 Definición analítica

 

El producto escalar de dos vectores u y v, que se representa por u.v , es
un escalar que se obtiene de multiplicar las coordenadas semejantes de ambos
vectores y sumar los resultados:
 
u .v  (ux ,uy ,uz ).(vx ,vy ,vz )  ux .vx  uy .vy  uz .vz
De la definición de producto escalar podemos deducir las siguientes
consecuencias:

El producto escalar de dos vectores puede ser positivo, negativo o cero,
dependiendo del valor del coseno del ángulo que forman:
o Si el ángulo que forman los vectores es agudo (coseno +), el producto
escalar es positivo, si el ángulo es obtuso (coseno -), el producto
escalar es negativo.
o Si los vectores son perpendiculares, el producto escalar es 0, puesto
que cos 90º = 0. Esta propiedad sirve como CRITERIO DE
PERPENDICULARIDAD ENTRE DOS VECTORES.



v
v
v



u
u
u
 
 
 
u .v  0
u .v  0
u .v  0
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
83

Si multiplicamos escalarmente al vector por sí mismo, obtenemos una
expresión que nos permite calcular el módulo del vector a partir de sus
coordenadas:


 


u .u | u | . | u | .cos(u , u ) | u |2 cos 0º | u |2
 


 
| u | u .u
Y si sustituimos el producto escalar por su expresión analítica:

 
|u | u .u  ux2  uy2 ,uz2
Obtenemos que el módulo de un vector es igual a la raíz cuadrada de la suma de los
cuadrados de sus coordenadas.

Si despejamos el coseno en la definición geométrica, obtenemos la
expresión:
 
 
cos(u ,v ) 
u. v

ux .vx  uy .vy  uz .vz


ux2  uy2 ,uz2 . vx2  vy2  vz2
| u |.| v |
De modo que si conocemos las coordenadas de los vectores, podemos conocer el
ángulo que forman.
Propiedades del producto escalar:
Y cumple las siguientes propiedades:
 
 
u .v  v .u
1ª. CONMUTATIVA:
 
 


k .(u .v )  (k .u ).v  u .(k .v )
2ª. ASOCIATIVA:



 
 
u .(v  w )  u .v  u .w
3ª. DISTRIBUTIVA:
Ejemplo 5 - 2º



Considera los vectores u  (3, 1,5) , v  (4,7,11) y w  (2,k ,3) .

 
i. Calcula u.v

b) Halla el ángulo que forman u y v


c) Halla el valor de k para que v y w sean perpendiculares.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
84
12ª.- Producto
Propiedades.
vectorial
de
dos
vectores.
Definición geométrica:




El producto vectorial de dos vectores u y v, que se representa por u v o bien
 
por u x v , es un nuevo vector que tiene las siguientes características:
Módulo: es el producto del módulo de los vectores que se multiplican por el
seno del ángulo que forman ambos vectores
 


 
| u  v || u |. | v |.sen (u ,v )


Dirección: perpendicular a u y v, es decir, perpendicular al plano que


determinan u y v.
Sentido: el de avance de un tornillo al girar el primer vector hacia el
segundo por el camino mas corto.


u v

v

u




v  u = - u v
Definición analítica:
La expresión analítica del vector que resulta de un producto vectorial entre
dos vectores se obtiene hallando el siguiente determinante:

i
 
u v  ux
vx

j
uy
vy

k



uz  uy .vz  uz .vy i  uz .vx  ux .vz  j  ux .vy uy .vx k
vz

Matemáticas II Álgebra lineal y Geometría


CURSO 2014/15

85
De la definición geométrica del producto vectorial podemos deducir las siguientes
propiedades:



Si los vectores u y v tienen la misma dirección, su producto vectorial es
nulo, ya que los vectores formarían entre sí un ángulo de 0º o 180º, y en
ambos casos el seno vale 0.

Si los vectores son perpendiculares su producto vectorial es máximo, ya que


los vectores u y v formarían 90º y su seno vale 1.

El producto vectorial de dos vectores no es conmutativo, como puede verse
en el dibujo:




v  u = - u v

De la propiedad anterior puede deducirse que el producto vectorial, en
general tampoco es asociativo, es decir:






(v  u)  w  v  (u  w )

Sí se cumple la propiedad distributiva del producto vectorial respecto a la
suma de vectores, es decir:







v  (u  w )  v  u  v  w
Ejemplo 5 – 3º


Considera los vectores u  (3, 5,1) y v  (4,7,6) .


a) Calcula el producto vectorial uv


b) Comprueba que el resultado obtenido es perpendicular a u y v
Soluc: (-37, -14, 41)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
86
13ª.- Interpretación geométrica del producto
vectorial y aplicaciones
LA INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO VECTORIAL es
que el módulo del producto vectorial de dos vectores coincide con el área del
paralelogramo que forman dichos vectores

v


Área | u  v |

u


Área del parale log ramo | u  v |
Por tanto si nos dan tres puntos A, B y C, no alineados, podemos calcular el
área del triángulo que tiene por vértices dichos puntos:
B

1 
Área  | AB  AC|
2

AB

AC
A
C

1
1 
Área del triángulo  Área del parale log ramo  | AB  AC |
2
2
Ejemplo 5 – 4º


Considera los vectores u  (3, 5,1) y v  (4,7,6) . Calcula el área del paralelogramo


que forman los vectores u y v
Soluc:
3 2 4 6 u2
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
87
14ª.- Producto mixto de vectores. Interpretación
geométrica del producto mixto



Se llama producto mixto de los vectores u v y w , y se designa por
  
[ u ,v , w ], al nº que se obtiene al realizar la siguiente operación:
ux uy uz
[u ,v ,w ]  u .(v  w )  v x v y v z
wx w y wz
  



OBSERVACIÓN:
Podemos observar que si cambiamos el orden de los vectores en el
producto mixto, cambia, a lo sumo, el signo del resultado (recuerda lo que ocurre con
el determinante de una matriz si permutamos dos líneas, propiedad 3ª).
LA INTERPRETACIÓN GEOMÉTRICA DEL PRODUCTO MIXTO es que su valor
absoluto, coincide con el volumen del paralelepípedo formado por dichos vectores:


w
w


v
v


u
u
  



|[u ,v ,w ]|| u .(v  w )| Volumen del paralelepípedo
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
88
Si nos piden el volumen del tetraedro del que conocemos sus cuatro
vértices A, B, C y D, podemos darnos cuentas que es la sexta parte del volumen del



paralelepípedo que forman los vectores AB AC Y AD
B
B


AB
AB


C AC


AD
A
AC
C
A AD
D
D
1
1  
Volumen del tetraedro  Volumen del paralelepípedo  |[u,v ,w]|
6
6
Ejemplo 5 – 5º



Considera los vectores u  (5,1,7) , v  (4,7,3) y w  (1,0,4) .
  
a) Calcula el producto mixto [u,v ,w ]
b) Calcula el volumen del paralelepípedo que forman los tres vectores.
c) Calcula el volumen del tetraedro formado por los tres vectores.
Soluc: a) -202
3
b) 202 u
3
c) 101/3 u
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
89
Ejercicios 5 – 1º a 8º
1º.- Comprueba el valor de los siguientes productos escalares:
 
 
 
 
 
 
i .i
i .j
i .k
j .j
j .k
k .k
a)
Aplicando la definición geométrica.
b)
Aplicando la definición analítica.
Soluc: 1, 0, 0, 1, 0 y 1
2º.- Comprueba los siguientes productos vectoriales:



i i


i j


i k


ji

a)
Aplicando la definición geométrica.
b)
Aplicando la definición analítica.
Soluc:


0,
k,

 j,

 k,



0,
i,
j,



j j




k i

k j


k k

i,

3º.- Considera los vectores u , v , w
canónica son:

j k
0

y t , cuyas coordenadas respecto a la base




u  (1, 5,2)
v  (3,4, 1)
w  (6,3, 5)
t  (24, 26, 6)



a) Comprueba que los vectores u , v y w forman una base de R3.




b) Expresa al vector t como combinación lineal de u , v y w .




Soluc: t  6 u  2 v  4 w


4º.- Considera los vectores u  (3, 4,12) y v  (5, 2, 6) . Calcular:

 
a)

b) |u | y |v |
u.v
c) El ángulo que forman los vectores.
d) Comprueba que los vectores


u
v
y

|u|

son unitarios.

|v |

e) Un vector perpendicular a u y v . Calcular:
Soluc: a) -49
b)
13 y
65
c) 117º 52’
e)
Matemáticas II Álgebra lineal y Geometría



4 8i  7 8 j  14 k
CURSO 2014/15
90



5º.- Halla el valor de m para que los vectores u  (1,2, 1) , v  (0,1,2) y w  (1,m,3) no
formen una base de R3.
Soluc: m = -1


6º.- Dados los vectores u  (3, 4,0) , v  (m,0,7) :


a) Halla m para que los vectores u y v sean perpendiculares.



b) Halla un vector w perpendicular a u y v



c) Halla tres vectores unitarios u' , v' y w' de la misma dirección,



respectivamente, que u , v y w



d) ¿Forman una base ortonormal los vectores u' , v' y w'?

Soluc: a) m = 0 b) w  (  2 8,  2 1, 0 ) c) 
3 4
u' ( ,
, 0)
5
5

v '  ( 0, 0, 1)

4  3
w' (
,
, 0)
5
5
7º.- Halla el área del triángulo de vértices A = (-5, 2, 1), B =(1, 7, 5) y C = (-1, 0, 4)
Soluc:
A 
1
2
2
1557 u
8º.- Calcula el volumen del tetraedro que tiene de vértices A = (3, 5, 7), B =(1, 0, -1)
C = (7, -1, 4) y D = (11, 4, -6). Soluc: V = 107 u 3
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
91
6.-
RECTAS Y PLANOS EN EL ESPACIO
1ª. Coordenadas de un vector
2ª. Puntos alineados
3ª. Punto medio de un segmento
4ª. Simétrico de un punto respecto a otro
5ª. Ecuaciones de la recta en el espacio
6ª. Posiciones relativas de dos rectas
7ª. Ecuaciones del plano
8ª. Ecuaciones de los ejes de coordenadas y de los planos
9ª. Posiciones relativas de una recta y un plano
10ª. Posiciones relativas de dos planos
11ª. Haz de planos que contiene a una recta
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
92
1ª.- Coordenadas de un vector
Si tenemos dos puntos P = (x1, y1, z1) y Q = (x2, y2, z2), las coordenada del

vector que une P y Q, vector PQ , se obtienen restando a las coordenadas del
extremo las coordenadas del origen.

PQ = coordenadas del extremo – coordenadas del origen

PQ = (x2, y2, z2) - (x1, y1, z1) = (x2 – x1, y2 – y1, z2 –z1)


Observa que el vector PQ y el vector QP son VECTORES OPUESTOS ya
que tienen coordenadas opuestas, es decir, son vectores de la misma dirección, del


mismo módulo pero de sentidos contrarios. Los vectores PQ y QP son vectores LD
puesto que son proporcionales:


PQ = - QP
Q
Q


PQ
QP
P
P
Ejemplo 6 - 1º
a)
Calcula las coordenadas del vector que tiene de origen el punto A = (1, -1,
3), y por extremo el punto B = (3, -2, 0)

AB  B  A  (3,  2, 0)  (1,  1, 3)  (2,  1,  3)
b)
Las coordenadas de un vector son (2, -2, 4). Sabiendo que su origen es el
punto P = (5, ½, -2), halla las coordenadas de su extremo.

PQ  Q  P

(2,  2, 4)  Q  (5, 1 ,  2)
2
Matemáticas II Álgebra lineal y Geometría

Q  (2,  2, 4)  (5, 1 ,  2)  (7,  3 ,2)
2
2
CURSO 2014/15
93
2ª.- Puntos alineados
Tres puntos P = (x1, y1, z1), Q = (x2, y2, z2) y R = (x3, y3, z3) estarán


alineados, siempre que los vectores PQ y PR tengan la misma dirección, es decir,
sean proporcionales (LD).
R
R


PR
PR
Q
Q


PQ
PQ
P
P
Puntos alineados
Puntos no alineados
vectores LD
vectores LI
También podemos observar que si tres puntos están alineados, los tres puntos
tienen que pertenecer a la misma recta.
Ejemplo 6 - 2º
Comprueba si los puntos A = (5, -1, -4), B = (3, 3, 2) y C = (2, 5, 5) están
alineados o no.


Calculemos las coordenadas de los vectores AB y AC y veamos si son proporcionales, es decir, si
los vectores tienen la misma dirección, o sea, si son LD.


AB  B  A  (3,3,2)  (5, 1, 4)  ( 2, 4,6) 


AC  C  A  (2,5,5)  (5, 1, 4)  (3,6,9) 



AB 
2 
AC
3

Las coordenadas de los vectores AB y AC son proporcionales, es decir, son vectores de la misma
dirección (LD) y por tanto los puntos A, B y C están alineados
Ejemplo 6 - 3º
Averigua los valores de m y n para que los puntos A = (4, -1, 3), B = (3, 5, 1)
y C = (0, m, n) estén alineados.


Para que los puntos A, B y C estén alineados, los vectores AB y AC tienen que ser de la misma
dirección (LD), y por tanto las coordenadas de dichos vectores tienen que ser proporcionales.
Calculemos las coordenadas de dichos vectores y obliguemos a que sean proporcionales:





AC  C  A  (0, m, n )  (4, 1,3)  ( 4, m  1, n  3) 
AB  B  A  (3,5,1)  (4, 1,3)  ( 1,6, 2)
m = 23 y n = -5
Matemáticas II Álgebra lineal y Geometría

1
6
2


4 m  1 n  3

1
6

4 m 1
1
2

4 n 3
C = (0, 23, -5)
CURSO 2014/15
94
3ª.- Punto medio de un segmento
Si tenemos un segmento de extremos P = (x1, y1, z1) y Q = (x2, y2, z2), las
coordenadas de su punto medio MPQ = (Mx, My, Mz), se pueden obtener si tenemos
en cuenta la siguiente relación:
Q = (x2, y2, z2)

PQ
MPQ = (Mx, My, Mz)

PMPQ
P = (x1, y1, z1)

1  1
PMPQ  MPQ  P  PQ  (Q-P)
2
2
Despejando MPQ de la expresión anterior, obtenemos la expresión de las
coordenadas del punto medio de un segmento:
 x x y  y z z 
1
1
MPQ  (Q-P)  P  (Q  P )   1 2 , 1 2 , 1 2 
2
2
2
2 
 2
Es decir, la media aritmética de las coordenadas de sus extremos.
IMPORTANTE:
Del mismo modo se procedería para calcular las coordenadas de los puntos
que dividen a un segmento en tres partes iguales, etc.
Ejemplo 6 - 4º
a) Calcula el punto medio del segmento qe tiene por extremos los puntos:
A = (5, -1, -4) y B = (3, 3, 2).
 a  b ay  by a  b
x
z
MAB   x
,
, z
 2
2
2

  5  3 1  3 4  2 

,
,
   4,1, 1 
  2
2
2


b) El punto medio de un segmento vale M = (2, -1, 0). Sabiendo que uno de
sus extremos es el punto P = (5, -1, -4), calcula las coordenadas del otro extremo del
segmento.
 p  q py  qy p  q
x
z
MPQ   x
,
, z
 2
2
2


 5  q 1  qy 4  q
x
z
   2, 1,0   
,
,

 2
2
2


Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15





Q   1, 1, 4
95
Ejemplo 6 - 5º
Los extremos de un segmento son A = (5, -1, -4) y B = (3, 3, 2). Halla los
puntos que dividen al segmento AB en tres partes iguales.
B
M2
M1
A

1
3

En el esquema puede observarse que: AM1  AB

1 
AM1  AB
3

M1  A 
1
B  A
3

 13 1

1
1
2
1
2
B  A  A  B  A  3,3,2   5.  1, 4   , , 2

3
3
3
3
3
3 3 
M1 
El punto M2, lo podemos calcular de dos formas:

2
3

 Teniendo en cuenta que AM2  AB
 Teniendo en cuenta que M2 es el punto medio del segmento M1B
En ambos casos se obtendría: M2 = (11/3, 5/3,0)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
96
4ª.- Simétrico de un punto respecto a otro
Si tenemos un punto P = (px, py, pz) y nos piden que calculemos el punto P’
simétrico a P respecto A = (ax, ay, az), podemos observar en el dibujo que el punto P’
que nos piden forma con P un segmento cuyo punto medio es el punto A
P = (px, py, pz)
A = (ax, ay, az)
P’ = (p’x, p’y, p’z)
Por tanto, si aplicamos como se calcula el punto de un segmento, se cumple que:

 p  p' py  p'y p  p' 
x
z
ax ,ay ,az  x
,
, z

 2

2
2



Y despejando se obtendrían las coordenadas de P’.
Ejemplo 6 - 6º
Halla el punto P’, simétrico al punto P = (7, 4, -2), respecto al punto Q = (3, -11, 7).
Teniendo en cuenta que el punto Q es punto medio del segmento PP’ , podemos escribir:
P = (7, 4, -2)
Q = (3, -11, 7)
P’ = (p’x, p’y, p’z)
7  p 'x
2
4  p 'y
11 
2
2  p 'z
7
2
3
Q=
P P'
2

 7  p ' 4  p 'y 2  p '
x
z
,
,
2
2
2

3, 11,7   






p 'x  1
p 'y  26
p 'z  16
P’ = (-1, -26, 16)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
97
Ejercicios 6 – 1º a 5º
1º.- Calcula a y b para que los puntos P = (7, -1, a), Q =(8, 6, 3) y R =(10, b, 9),
estén alineados.
Soluc: a = 0 b =0 20
2º.- Dados los puntos A = (-3, 5, 11) y B = (3, 5, -1)
i. Halla el punto medio del segmento AB.
ii. Halla el punto simétrico de B respecto de A.
Soluc: a) MAB = (0, 5, 5)
b) B’ = (-9, 5, 23)
3º.- Hallar los puntos M y N que dividen al segmento de extremos A = (7, -2, 11) y B
= (10, 7, 5), en tres partes iguales.
Soluc: M = (8, 1, 9)
N = (9, 4, 7)
4º.- Los tres vértices consecutivos de un paralelogramo son A = (1, 3, -4), B = (2, 6,
7) y C=(5, -1, 2). Halla las coordenadas del cuarto vértice D.
Soluc: D = (4, -4, -9)
5º.- Los tres vértices consecutivos de un paralelogramo son A = (1, 3, -1), B = (2, 0,
2) y C = (4, -1, -3). Halla las coordenadas del cuarto vértice D y del centro del
paralelogramo.
Soluc: D = (3, 2, -6) y centro = (5/2, 1, -2)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
98
5ª.- Ecuaciones de una recta en el espacio.
Para escribir las diferentes expresiones de la ecuación de una recta r en el
espacio, necesitamos un punto cualquiera P = (x0, y0, z0) de la recta y un vector

cualquiera u = (ux, uy, uz) paralelo a dicha recta llamado VECTOR DIRECTOR O
VECTOR DIRECCIÓN.

u = (ux, uy, uz)
.
P = (x0, y0, z0)
r
IMPORTANTE:
1º.- Como punto P, sirve cualquier punto de la recta.
2º.- No hay un único vector director de la recta, hay infinitos, y todos ellos
son proporcionales entre sí (LD). Por esta razón siempre podremos elegir, de entre
todos ellos, a aquel vector que tenga las coordenadas más sencillas.
3º.- A veces, sólo nos dan dos puntos A y B de la recta. En este caso

nosotros siempre podemos hallar como vector director de la recta al vector AB ó
cualquiera proporcional a él, y como punto P a uno de los dos puntos: A ó B.
B
.

A.
AB =B - A
r
Una recta puede describirse mediante diferentes ecuaciones. Nosotros
vamos a estudiar cuatro:

Ecuación vectorial

Ecuaciones paramétricas

Ecuación en forma continua

Ecuación implícita
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
99

Ecuación vectorial
Supongamos una recta r de la que sabemos que pasa por el punto P =(x0, y0, z0) y

tiene como vector director a u (ux ,uy ,uz )
Un punto genérico (x, y, z) de la recta r, lo podemos calcular mediante la expresión:
x, y,z   x , y ,z   λ.(u ,u ,u )
0
0
0
x
y
Ecuación vectorial
z
λ representa a un nº real, de modo que si vamos dándole diferentes valores a λ,
obtenemos las coordenadas de los sucesivos puntos de la recta.

Ecuaciones paramétricas
La ecuación vectorial de la recta r, da lugar a tres ecuaciones numéricas:
x  x 0  λ .u x
y  y 0  λ .u y
z  z 0  λ .u z






Ecuaciones paramétricas
Ecuación en forma continua
Despejando el parámetro λ en cada una de las ecuaciones paramétricas e
igualando, obtenemos la siguiente doble igualdad:
x  x0
y  y0
z  z0


ux
uy
uz
Ecuación continua
IMPORTANTE:
Si alguna de las coordenadas del vector director es nula, la forma continua de la
recta se nos presentaría con algún cero en el denominador. Tal expresión no es
correcta aritméticamente, pero puede admitirse como expresión simbólica cuyos
denominadores nos indican las coordenadas del vector director.

Ecuación en forma implícita
Si en la forma continua de una recta, tomamos las igualdades dos a dos y
agrupamos todo en el primer miembro, obtenemos dos ecuaciones de la forma:
ax
a 'x
 by
 b 'y
 cz
 c 'z
 d  0

 d '  0
Ecuación implícita
Observa que la forma implícita no es más que la intersección de dos planos.
La forma que adopta cada ecuación para una misma recta, depende del punto P y
del vector director utilizados.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
100
Ejemplo 6 - 7º
De una recta se sabe que pasa por el punto P = (1, 2, -2) y que es paralela al vector

u  (2, 5,0) . Hallar las distintas formas de las ecuaciones de la recta.
recta

Forma vectorial:
r
 punto P  (1,2, 2)


dirección u  (2, 5,0)
x,y,z   1,2, 2)  λ.(2, 5,0)
x  1  2λ 

y  2  5λ 
z  2  0 λ 

Ecuaciones paramétricas:

Ecuación en forma continua:

Ecuación en forma implícita:
x 1 y 2


2
5 
y  2 z  2

5
0 
x 1 y 2 z 2


2
5
0

5x  2y
 9  0
z  2  0
Ejemplo 6 - 8º
La recta r pasa por el punto P = (1,2,-1) y es paralela a la recta s, cuyas ecuaciones
x  2  λ

paramétricas son: y 
2λ  . Halla todas las formas de la recta r.
z  1  λ 
De la recta r sabemos un punto P = (1, 2, -1). También sabemos que es paralela a la recta s, y por
tanto el vector director de la recta s sirve como vector director de la recta r, es decir:
recta
r
 punto P  (1,2, 1)


dirección
u
 (1,2,1)

Ya puedes continuar tú sólo.
Ejemplo 6 - 9º
La ecuación en forma implícita de una recta r es:
a)
x  2y  z  1  0
2x  y  z  1  0
¿Pertenece el punto P = (1, 0, 0) a la recta r?
Para que el punto P pertenezca a la recta, tiene que verificar su ecuación.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
101
Como vemos el punto P verifica la primera ecuación, pero no la segunda y, por tanto, P no
pertenece a la recta
b)
Halla sus ecuaciones paramétricas.
Para pasar de la forma implícita a las paramétricas, hacemos z = λ, pasamos al segundo miembro y
resolvemos el sistema
1  λ 

5
 3  3λ 
y 

5

z λ


X 
x
2x
 2y
 y
 z
 z
z λ
 1  0
 1  0 
x
2x

 2y
 y
 1  λ
  1  λ 

Las soluciones obtenidas son las ecuaciones paramétricas de la recta, que podemos escribir:
1  λ 

5
 3  3 λ 
y 

5

z λ


X 
c)

x

y

z

1
1 

λ
5
5 
3
3 

λ
5
5 
0  λ 

Calcula dos vectores directores de r.
En las ecuaciones paramétricas, podemos leer directamente las coordenadas de un vector director
de la recta:

u  (
1 3
, ,1) .
5 5
Cualquier otro vector proporcional a él, también tiene la misma dirección, y por tanto serviría como
vector director de r. Por ejemplo


v  5u  (
1 3
, , 1 )  ( 1, 3 , 5 )
5 5
que sería más cómodo de utilizar.
d)
Calcula dos puntos por los que pasa la recta r.
En las ecuaciones paramétricas, también podemos leer directamente un punto de la recta:
P = (-1/5, -3/5, 0).
Para calcular cualquier otro punto, bastaría con dar un valor real cualesquiera a λ. Por ejemplo λ = 1 y
obtendríamos las coordenadas del punto:
Q = (0, 0, 1)
OBSERVACIÓN: Date cuenta se podrían reescribir las ecuaciones paramétricas de la recta r,

utilizando el punto Q = (0, 0, 1) y como dirección de la recta el vector v  ( 1, 3 , 5 )
x
y
z
Matemáticas II Álgebra lineal y Geometría



0
0
1



λ 

3λ 
5 λ 
CURSO 2014/15
102
6ª.- Posiciones relativas de dos rectas en el espacio
Dadas dos rectas r y s en el espacio, cada una de ellas definidas por un
punto y su vector dirección:
recta
r
 punto P  (px , py , pz )



dirección
u
 (ux ,uy ,uz )

recta
s
 punto Q  (qx ,qy ,qz )



dirección
v
 (vx ,vy ,vz )

Las posiciones relativas entre ellas pueden ser las siguientes:
PARALELAS
Misma dirección
Ningún punto en común
COINCIDENTES
Misma dirección
Todos los puntos en común
SECANTES
SE CRUZAN
Distinta dirección
Distinta dirección
Un punto en común
Ningún punto en común
Para averiguar la posición relativa entre dos rectas empezaremos
comprobando si sus vectores directores son paralelos, es decir, si son LD. Para ello
basta con ver si sus coordenadas son proporcionales.
Si los vectores directores son paralelos, las rectas r y s o son paralelas o
son coincidentes. Para averiguar cuál de las dos situaciones es, tomamos, por
ejemplo, el punto P de la recta r y comprobamos si pertenece o no a la recta s. Si
pertenece, las rectas son coincidentes, si no pertenece las rectas son paralelas.
Si los vectores directores no son paralelos, las rectas r y s o se cortan
(secantes) o se cruzan. Para averiguar cuál de las dos situaciones es, se forma el

vector P Q y se comprueba si es coplanario (LD) o no (LI) con los vectores



directores de las rectas r y s. Si los vectores u v y P Q son LD, entonces las
rectas son secantes, es decir, se cortan en un punto. Si los tres vectores son LI, las
rectas se cruzan.
RECUERDA que para averiguar si tres vectores son o no son LI, debemos
comprobar si el determinante de la matriz formada con las coordenadas de los tres
vectores es o no es cero.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
103
Ejercicios 6 – 6º a 12º
6º.- Halla las ecuaciones paramétricas de las rectas que pasan por los puntos:
a)
A = (2, 0, 5) y B = (-1, 4 6)
b)
M = (5, 1, 7) y N = (9, -3, -1)
7º.- Obtén las ecuaciones paramétricas, continua e implícitas de la recta que pasa

por el punto P = (0, 1, -3) y es paralela al vector u  ( 1 ,  5 , 0 )
Soluc:
x
y
z

λ 

 1  5λ 

 3
y 1
x
z 3


1
5
0
5x  y
8º.- Comprobar si alguno de los siguientes puntos A = (3, 2, -1)
C = (1, 5, 0) D = (2, 8, -1) pertenece a la recta r de ecuaciones:
 1  0
z  3  0 
B = (-2, 17, -1)
x  3  λ

y  2  3λ

z  1
Soluc: A y B Si
C y D No
9º.- Estudiar las posiciones relativas de las siguientes parejas de rectas y, en al caso
de que corte, halla el punto de intersección:
a)
b)
c)
d)
r
x  3  5λ

y  2  λ
z  5  λ 
r
x  2  3λ

y  3  5λ
z 
λ 
r
x  2  3λ

y  3  5λ
z 
λ 
r
x  3  5λ

y  2  3λ
z  4  λ 
Soluc: a) paralelas
b) se cruzan
s
s
x  1  10μ

y  4  2μ 
z 
2μ 
s
x  1  μ

y 
μ

z  5
s
x  1  μ

y 
2μ 

z  5
x  2y  z  1  0
2x  y  z  1  0
c) se cortan en el punto (-13, 28, 5) d) se cruzan
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
104
10º.- Comprueba que los puntos A = (1, -2, 1), B = (2, 3, 0) y C = (-1, 0, 4) no están
alineados. Hazlo de dos formas:

b)

Comprobando que los vectores AB y AC no tienen la misma dirección.
a)
Comprobando que uno de los puntos no pertenece a la recta que pasa por
los otros dos.
11º.- Determina la ecuación de la recta que, siendo paralela a la recta t, pasa por el
punto de intersección de las rectas r y s.
r
Soluc:
x
y
z



x  2  λ

y  3  λ
z  6  λ
1
2
7



s

x  1

y 
μ
z  9  μ 
t
x  8  β

y  5  β :
z  6  2β
λ 

λ 
2 λ 
12º.- Halla la ecuación de una recta r que pasa por el punto P = (5, 5, 1) y es
perpendicular a s
Soluc:
x
y
z
 5
 5
 1
s
x  1  2λ

y  3  λ

z  5
 λ 

 2λ 
 3 λ 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
105
7ª.- Ecuaciones de un plano
Para escribir las diferentes expresiones de la ecuación de un plano π,
necesitamos un punto cualquiera P = (x0, y0, z0) del plano la recta y dos vectores


cualesquiera, u = (ux, uy, uz) y v = (vx, vy, vz), paralelos al plano y LI entre sí,
llamados VECTORES DIRECTORES O VECTORES DIRECCIÓN.
π
IMPORTANTE:
1º.- Como punto P, sirve cualquier punto del plano.
2º.- No hay una única pareja de vectores directores del plano, hay infinitas
parejas, basta con que sean paralelos al plano y de distinta dirección (LI). Por esta
razón siempre podremos elegir, de entre todos ellas, a aquella pareja de vectores
que tengan las coordenadas más sencillas.
3º.- A veces, sólo nos dan un vector director y dos puntos A y B del plano.
En este caso nosotros podemos hallar como el otro vector director del plano al vector

AB ó cualquiera proporcional a él, y como punto P a uno de los dos puntos A ó B.

B AB
π

A
u
Es importante darse cuenta que los puntos A y B deben de formar un vector
de distinta dirección al dado
4º.- Otras veces, solo nos dan tres puntos A, B y C del plano no alineados.


En este caso podemos utilizar a los vectores AB y AC , o cualesquiera
proporcionales a ellos, como directores del plano, y a uno de los tres puntos como
punto característico del plano
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
106
Un plano puede describirse mediante diferentes ecuaciones. Nosotros
vamos a estudiar tres:

Ecuación vectorial
Supongamos un plano π del la que sabemos que pasa por el punto P =(x0,


y0, z0) y tiene como vectores directores a u (ux ,uy ,uz ) y u (vx ,vy ,vz )
Un punto genérico (x, y, z) del plano πr, lo podemos calcular mediante la expresión:
x, y,z    x , y ,z   λ.(u ,u ,u )  μ.(v ,v ,v )
0
0
0
x
y
z
x
y
z
Ecuación vectorial
λ y µ representan a sendos números reales, de modo que si vamos dándole
diferentes valores a λ y µ, obtenemos las coordenadas de los sucesivos puntos del
plano.

Ecuaciones paramétricas
La ecuación vectorial de la recta r, da lugar a tres ecuaciones numéricas:
x  x 0  λ .u x  μv x 

y  y 0  λ .u y  μv y 
z  z 0  λ .u z  μv z 

Ecuaciones paramétricas
Ecuación en forma implícita
Despejando los parámetros λ y µ en las ecuaciones paramétricas
obtenemos una expresión del tipo:
ax  by  cz  d  0
Ecuación implícita
IMPORTANTE:
1º.- La forma que adopta la ecuación implícita de un plano siempre es la
misma, independientemente del punto y de los vectores directores utilizados.
2º.- Los coeficientes de las incógnitas de la ecuación implícita de un plano,

son las coordenadas de un vector n = (a, b, c) perpendicular a dicho plano y
denominado VECTOR NORMAL DEL PLANO

n = (a, b, c)
Π: ax + by +cz +d = 0
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
107
Ejemplo 6 - 10º
El plano π pasa por los puntos A = (2, 3, 5) B = (3, 5, 8) y C = (3, 6, 10). Hallar las
distintas formas de las ecuaciones del plano.

punto P  (2,3,5)



u

AB
 B  A  (1,2,3)
dirección



v  AC  C  A  (1,3,5)

π
plano
 x , y , z   2,3,5)   λ.(1,2,3)  μ .(1,3,5)

Forma vectorial:

Ecuaciones paramétricas:

Ecuación en forma implícita:
 2  λ  μ 

 3  2λ  3μ 
 5  3 λ  5 μ 
x
y
z
La forma implícita podemos averiguarla de dos formas diferentes:
1ª.- A partir de las ecuaciones paramétricas, considerando que se trata de un sistema de tres
ecuaciones con dos incógnitas, λ y µ,
λ
2λ
3λ
 μ
 3μ
 5μ
 x
 y
 z
 2

 3
 5 
1 1 x  2
A'  2 3 y  3 


3 5 z  5 
1 1
A  2 3 


3 5 

Como el sistema es compatible, según Rouché-Fröbenius, el rango de la matriz de coeficientes
coincide con el de la ampliada. Pero, como la matriz A tiene que tener rango 2, entonces el
determinante de la matriz ampliada tiene que ser 0 (si no fuese así, la matriz A’ tendría de rango 3). Al
hacer 0 el determinante de A’ obtenemos la ecuación implícita del plano
A 0
1 1 x 2
2 3 y 3  0
3 5 z 5


x  2y  z  1  0
2ª.- A partir de un vector normal del plano, que podemos hallar si hacemos el producto vectorial de
dos vectores directores del plano:



i
n  u  v  1
1
j
2
3
k



3  i  2 j  k  ( 1,  2 , 1 )
5



La ecuación implícita del plano que buscamos tendrá la forma:
x  2y  z  d  0
El valor de d se obtiene teniendo en cuenta que el punto P = (2, 3, 5) es del plano y por tanto debe de
verificar la ecuación anterior:
2  2 .3  5  d  0

1 d  0

d  1
Obteniéndose la misma ecuación implícita del plano que por el primer método:
x  2y  z  1  0
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
108
Ejemplo 6 - 11º
a) Halla la ecuación implícita de un plano π que pasa por el punto P =
(3,0,1) y es paralelo al plano π’ de ecuación x  2y  z  1  0
Como el plano π que buscamos es paralelo al plano π’, entonces el vector normal del plano π’ sirve

como vector normal del plano π:

nπ  nπ '
π
P

nπ
π’
'
Por tanto la ecuación del plano que buscamos tiene la forma: x  2y  z  d  0 , y como el
punto P = (3,0,1) es de dicho plano, tiene que verificar la ecuación anterior. Así obtenemos el valor de
d.
3  2 .0  1  d  0

d  2
La ecuación del plano π que pasa por el punto P = (3,0,1) y es paralelo al plano π’ es:
x  2y  z  2  0
b) Halla las ecuaciones paramétricas del plano π
Para hallar las ecuaciones paramétricas de un plano escrito en forma implícita, hacemos y = λ y z =
µ, y despejamos x:
x  2y  z  2  0 

y λ
 x  2λ  μ  2  0

z μ

x  2  2λ  μ
Quedando las ecuaciones paramétricas siguientes:
x
y
z
 2  2λ  μ 

 0  λ  0μ 
 0  0 λ  μ 

En dónde se está utilizando como punto a P = (2, 0, 0) y como vectores directores a u = (-2, 1, 0) y

v = (1, 0, 1).
OBSERVACIÓN:
Puedes comprobar, en las paramétricas, que el punto P = (3, 0, 1) es del plano π.
Si quieres obtener otros puntos del plano, basta con que le des valores a λ y a µ.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
109
8ª.- Ecuaciones de los ejes de coordenadas y
planos
y
x
z
Observa que todos los puntos del PLANO XY tienen de coordenadas (x, y, 0), es
decir, su tercera coordenada siempre es nula z = 0. Esta es la ecuación implícita del
plano XY.
Observa que todos los puntos del PLANO XZ tienen de coordenadas (x, 0, z), es
decir, su segunda coordenada siempre es nula y = 0. Esta es la ecuación implícita
del plano XZ.
Observa que todos los puntos del PLANO YZ tienen de coordenadas (0, y, z), es
decir, su primera coordenada siempre es nula x = 0. Esta es la ecuación implícita
del plano YZ.
Observa que el EJE X es la intersección del plano XZ con el plano XY, es decir del
plano de ecuación y = 0 con el de ecuación z = 0. Es lógico puesto que todos los
puntos del eje x son de la forma (x, 0, 0).
Observa que el EJE Y es la intersección del plano XY con el plano YZ, es decir del
plano de ecuación x = 0 con el de ecuación z = 0. Es lógico puesto que todos los
puntos del eje y son de la forma (0, y, 0).
Observa que el EJE Z es la intersección del plano YZ con el plano XZ, es decir del
plano de ecuación x = 0 con el de ecuación y = 0. Es lógico puesto que todos los
puntos del eje x son de la forma (0, 0, z).
ECUACIÓN IMPLICITA
PLANOS
EJES DE COORDENADAS
XY
XZ
YZ
EJE X
EJE Y
EJE Z
z=0
y=0
x=0
y  0
z  0 
x  0
z  0 
x  0
y  0 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
110
9ª.- Posiciones relativas de plano y recta
La posición relativa entre una recta r y un plano π puede ser la siguiente:





nπ
nπ
ur
nπ
ur

ur
CONTENIDA EN EL PLANO
Todos los punto de r son de π
PARALELA AL PLANO
r y π no tienen puntos comunes
RECTA SECANTE AL PLANO
r y π tienen solo un punto en común
Para averiguar la posición relativa entre una recta y un plano podemos
proceder de tres formas:

1ª.- Una de ellas consiste en identificar a un vector director de la recta, u r , y



a un vector normal del plano π, n π , y multiplicarlos escalarmente u r . n π .


Si el producto escalar u r . n π vale 0, la recta está contenida en el plano o
es paralela a él. Para averiguar cuál de las dos situaciones es, bastaría con ver si un
punto cualquiera de la recta satisface la ecuación del plano. Si la satisface, la recta
está contenida en el plano, y si no, la recta es paralela al plano.


Si el producto escalar u r . n π no vale cero, entonces la recta corta al plano
en un punto.
2ª.- Otra forma de averiguarlo es identificar a un vector director de la recta, y
a dos directores del plano. A continuación comprobamos si los tres vectores son LD
o LI.
Si el vector director de la recta r y los dos vectores directores del plano π
son LD, la recta, o está contenida en el plano, o es paralela a él. Si un punto
cualquiera de la recta r satisface la ecuación del plano π, la recta está contenida en
el plano. En caso contrario la recta es paralela al plano.
Si el vector director de la recta r y los dos vectores directores del plano π
son LI, la recta r es secante al plano π.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
111
3ª.- Otra forma de averiguarlo es escribir en forma implícita a la recta y al
plano y discutir el sistema de tres ecuaciones con tres incógnitas.
a1x
a2x
a3x
 b1 y
 b2 y
 b3 y
 c1z
 c 2z
 c 3z
 d1  0 

 d2  0 
 d 3  0 

 a 1 b1 c 1 
A   a 2 b2 c 2 


 a 3 b3 c 3 
 a 1 b1 c 1 d 1 
A '   a 2 b2 c 2 d 2 


 a 3 b3 c 3 d 3 
OBSERVACIÓN:
En realidad la cuarta columna de la matriz A’, sería opuesta a la que hay escrita,
pero recuerda que el rango de una matriz no cambia si multiplicas a una de sus
líneas por un nº.
Si rango A = rango A’ = 3  SCD  una sola solución  r corta a π en un punto
Si rango A = rango A’ = 2  SCI  infinitas soluciones  r contenida en π
Si rango A ≠ rango A’
 SI
Matemáticas II Álgebra lineal y Geometría
 ninguna solución  r paralela a π
CURSO 2014/15
112
10ª.- Posiciones relativas de dos planos
La posición relativa entre dos planos π y π’ puede ser la siguiente:


nπ
nπ
'
COINCIDENTES
PARALELOS
Son el mismo plano
no tienen puntos comunes
SECANTES
se cortan en una recta
Para averiguar la posición relativa entre dos planos podemos proceder de
tres formas:
1ª.- Una de ellas consiste en identificar a un vector normal a cada plano π y


π’, n π y n π ' , y ver si tienen la misma dirección o no.


Si las coordenadas de n π y n π ' son proporcionales, los vectores son LD, es
decir, tienen la misma dirección, y por tanto los planos π y π’, o son coincidentes, o
son paralelos. Para averiguar cuál de las dos situaciones es, bastaría con ver si un
punto cualquiera de uno de los planos satisface la ecuación del otro. Si la satisface,
los planos son coincidentes, y si no, los planos son paralelos.


Si las coordenadas de n π y n π ' no son proporcionales, los vectores son LI,
es decir, tienen distinta dirección, y por tanto los planos π y π’ son secantes.
2ª.- Otra forma de averiguarlo es escribir la ecuación implícita de cada plano
y ver la proporcionalidad entre los coeficientes de cada ecuación.
π 
π '
a1 x
a2x
 b1 y
 b2 y
 c1 z
 c2z
 d1
 d2
 0
 0
Si
a1
b
c
d
 1  1  1
a2
b2
c2
d2

planos paralelos.
Si
a1
b
c
d
 1  1  1
a2
b2
c2
d2

planos coincidentes
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
113
3ª.- Otra forma de averiguarlo es escribir en forma implícita a los dos planos y
discutir el sistema de dos ecuaciones con tres incógnitas.
a1x
a2x
 b1 y
 b2 y
 c1z
 c 2z
 d1
 d2
 0
 0 

 a b1 c1 
A  1

 a 2 b2 c 2 
 a b1 c 1 d 1 
A'   1

 a 2 b2 c 2 d 2 
OBSERVACIÓN:
En realidad la cuarta columna de la matriz A’, sería opuesta a la que hay escrita,
pero recuerda que el rango de una matriz no cambia si multiplicas a una de sus
líneas por un nº.
Si rango A = rango A’ = 2 < nº de incógnitas  SCI  infinitas soluciones 
π corta a π’ en una recta
Si rango A = rango A’ = 1 < nº de incógnitas  SCI  infinitas soluciones 
π y π’ son el mismo plano
Si rango A ≠ rango A’
 SI
Matemáticas II Álgebra lineal y Geometría
 ninguna solución  π y π’ son paralelos
CURSO 2014/15
114
11ª.- Haz de planos que contienen a una recta
Se llama haz de planos de eje la recta r, al conjunto de todos los planos
que contienen a la recta r:
¿Cómo hallar una expresión para el haz de planos que contienen a la recta r?
Supongamos que la recta r está dada en implícita:
 ax  by  cz  d  0
r :
a 'x  b'y  c'z  d '  0
Según la tercera operación válida para obtener un sistema de ecuaciones
equivalentes (tema 1º, 3ª pregunta), si añadimos una tercera ecuación que sea
combinación lineal de las dos ecuaciones dadas, el sistema formado por las tres
ecuaciones sería equivalente y, por tanto, la ecuación añadida también contiene a la
recta r:
α .(ax  by  cz  d )  β .(a 'x  b 'y  c 'z  d ')  0
Si dividimos por α (también podemos hacerlo por α), obtenemos:
(ax  by  cz  d ) 
β
.(a 'x  b 'y  c 'z  d ')  0
α
Si llamamos λ = α/β, la ecuación del haz de planos que contienen a la recta r, en
función de un solo parámetro, es:
(ax  by  cz  d )  λ.(a 'x  b 'y  c 'z  d ')  0
Ejemplo 6 - 12º
a)
Halla la ecuación del haz de planos que contiene a la recta r de ecuaciones:
x  y  z  2  0
r :
2y  z  1  0

La ecuación del haz de planos que contienen a la recta r es:
( x  y  z  2)  λ .(2y  z  1)  0
Matemáticas II Álgebra lineal y Geometría

x  (  1  2λ ) y  (1  λ )z  (2  λ )  0
CURSO 2014/15
115
b)
De todos los planos que contienen a la recta r, halla el que pasa por el punto
(0,1,-1)
Si pasa por el punto P = (0,.1, -1), la ecuación del haz de planos que contienen a la recta r debe de
cumplirse para este punto, es decir:
0  ( 1  2λ ).1  (1  λ ).( 1)  (2  λ )  0

 1  2λ  1  λ  2  λ  0

λ0
Y por tanto el plano pedido tiene de ecuación:
x y z 2 0
Ejercicios 6 – 13º a 19 º
13º.- Un plano pasa por los puntos P = (1, 7, -2), Q = (4, 5, 0) y R = (6, 3, 8). Hallar:
a)
Las ecuaciones paramétricas.
b)
La ecuación implícita a partir de las ecuaciones paramétricas.
c)
La ecuación implícita utilizando el vector normal del plano.
Soluc: a)
x  4  3λ  μ 

y  5  2λ  μ 
z 
2λ  4μ 
b)
y c)
6 x  10 y  z  7 4  0
14º.- Dado el punto P = (2, -1, 3), hallar la ecuación implícita del plano π que:
a)
Contiene al punto P y es paralelo al plano π’ de ecuación 2x  3y  z  4  0
b)
Contiene a P y es perpendicular a la recta r
Soluc: a) 2x + 3y – z + 2 = 0
x 3
z 2
y 
2
1
b) 2x + y – z = 0
15º.- Estudia la posición relativa de los siguientes planos y rectas y, si se cortan,
hallar el punto o los puntos de corte:
a)
c)
π  x  3y  4z  11  0
π' 4x  12y  16z  40  0
π
2x  3y  z  4  0
Matemáticas II Álgebra lineal y Geometría
r
b)
π x  y  z  4  0
π' 2x  y  z  1  0
x  3  2λ

y  1  λ
z  4  6λ
CURSO 2014/15
116
Soluc: a) son planos paralelos
b) se cortan en una recta de ecuaciones

x  1
 c) La recta corta al plano en el punto
y  3  λ
z 
λ
(21/13,4/13,106/13)
16º.- Considera el plano π
x  y  z  1  0
x  2y  z
 0
2x  y  az  b  0 y la recta r
a)
Determina a y b para que el plano π contenga a la recta r.
b)
Determina a y b para que la recta y el plano sean paralelos.
c)
Determina para que valores de a y b la recta corta al plano.
d)
Halla el punto de corte entre la recta y el plano para a = 0 y b = 7.
Soluc: a) a = 4 y b = 3 b) a = 4 y b ≠ 3
c) a ≠ 4 y b cualquier valor
e) (5, -3, -1)
17º.- Estudia la posición relativa de los tres planos siguientes. Cuando se corten,
halla el punto o puntos de corte:
a)
x  2y  z  0 

x  y
 1  b)
 y  z  1
3x  y  z  0 

x  y  z  0
y  z  1
c)
x  y  z  2

2x  y  3z  3 
x  2y  2z  0 
Soluc: a) Tres planos que se cortan en una recta (SCI). Unas posibles ecuaciones paramétricas de la recta son:
x  2  λ 

y  1  λ
z 
λ 
b) SCD, es decir, tres planos que se cortan en el punto (-1/3, 2/3, -1/3)
no hay ningún punto en común a los tres planos.
c) SI. Tres planos que se cortan dos a dos, es decir,
18º.- Estudia la posición relativa de los tres planos siguientes en función del
parámetro m. Cuando se corten halla el punto o puntos de corte.
mx  y  z  0 

x  my  z  1
2x  y  z  0 
Soluc: Si m = 1 SI, los planos se cortan dos a dos pero no hay ningún punto en común a los tres.
Si m = 2 SCI, los planos se cortan en una recta cuyas ecuaciones paramétricas son:
x
y
z
1
1 

λ
5
5 
2
3 
 

λ
5
5 

λ 


1
1 
,
 0,

m

1
m
1

Si m ≠ 1 y m ≠ 2 SCD, los tres planos se cortan en un punto de coordenadas 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
117
19º.- a) Halla la ecuación del haz de planos que contienen a la recta r de ecuación:
x  y  z  4  0
r :
2x  y  z  1  0
b)
De todos los planos que contienen a la recta r, halla el que es paralelo a la
recta s de ecuación:
x 3 y z  2
 
0
3 3
c)
Soluc: a)
De todos los planos que contienen a la recta r, halla el que pasa por el
origen de coordenadas.
(1  2λ)x  (1  λ)y  (1  λ)z  (4  λ)  0
Matemáticas II Álgebra lineal y Geometría
b)
x 1  0
CURSO 2014/15
c)
3x  y  z  0
118
7.-
PROBLEMAS MÉTRICOS
1ª. Ángulo entre dos rectas
2ª. Ángulo entre dos planos
3ª. Ángulo entre una recta y un plano
4ª. Distancia entre dos puntos
5ª. Distancia entre un punto y una recta
6ª. Simétrico de un punto respecto a una recta
7ª.- Distancia entre un punto y un plano
8ª. Simétrico de un punto respecto a un plano
9ª.- Distancia entre una recta y un plano
10ª. Distancia entre dos planos
11ª. Distancia entre dos rectas
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
119
1ª.- Ángulo entre dos rectas


Recordemos que el producto escalar de dos vectores u y v nos permite
calcular el ángulo α que forman dichos vectores:
 
cos α 
| u .v |


| u | . |v |
Al tomar el valor absoluto del producto escalar, garantizamos que elegimos el ángulo
mas pequeño que forman los vectores.
El ángulo α que forman dos rectas r y s, es el ángulo que forman sus


respectivos vectores directores u r y u s

r
ur

cos α 

| ur .u s |


us

s
| ur | . | us |
IMPORTANTE
Si las rectas se cruzan, el ángulo entre dichas rectas se define como el ángulo que
forma una de ellas con la paralela a la otra que es secante con la primera. Por tanto,
el cálculo de dicho ángulo es idéntico al de dos rectas secantes.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
120
2ª.- Ángulo entre dos planos
El ángulo α que forman dos planos π y π’, es igual al ángulo que forman sus
vectores normales:
π’

π
nπ

nπ
'
α
α


| nπ . nπ ' |
cos α 


| nπ | . | nπ ' |
3ª.- Ángulo entre una recta y un plano
El ángulo α que forman una recta r y un plano π, es igual al ángulo
complementario que forman el vector director de la recta y el vector normal al plano:
r


nπ
ur
α
90º-α

cos(90 º  α ) 

| u r . nπ |

π

 senα
| u r | . | nπ |
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
121
Ejercicio 7 - 1º
1º.- Calcula el ángulo que forman:
x 3 y 1 z


5
3
1
las rectas r :
b)
La recta r :
c)
Los planos π : x 2y  4z  0 y π': 2x y 3  0
a) Soluc:41º 59’ 35’’
s:
2x  3y  5z  4  0
x  2y
 5  0
a)
x 3 y 1 z 1


con el plano π : 2x 5y 7z 11  0?
2
5
1
b) Soluc:35º’ c) 67º 1’ 23’’
Ejercicio 7 - 2º
a)
Calcula el ángulo que forman los planos π : z  3 y π': x y 2z  4  0
b)
Calcula el ángulo que forma el plano π : x 2y z  0 con cada uno de los
ejes de coordenadas.
c)
Halla el valor de m para que las rectas r y s formen un ángulo de 90º
r
a) 35º 15’ 52’’
x  2  5λ

y 
λ
z  2  λ 
b) :EJE X: 24º 5’ 41’’ EJE Y: 54º 44’ 8’’
s
EJE Z: 24º 5’ 41’’
x  2  λ

y 
2λ 
z 
mλ
c) m = -3’
4ª.- Distancia entre dos puntos
La distancia entre dos puntos P = (px, py, pz) y Q = (qx, qy, qz), es el módulo
del vector que une ambos puntos:
Q = (qx, qy, qz)

PQ
P = (px, py, pz)




2
2
2

  d (P,Q)  (qx  px )  (qy  py )  (qz  pz )
|PQ | |(qx  px ,qy  py ,qz  pz )|
d (P,Q) | PQ | |QP |
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
122
5ª.- Distancia entre un punto y una recta
Se llama distancia de un punto P a un recta r, a la longitud del segmento
perpendicular que va desde el punto P a la recta r, es decir la distancia del punto P a
su proyección, R, sobre la recta r.
r

d(P, r) = d(P, R) = |PR |
R
P
Para localizar al punto R, podemos proceder de cualquiera de las dos formas
siguientes:
1ª.- Hallar la ecuación del plano π que pasa por P y es perpendicular a r. A
continuación buscamos la intersección del plano π con la recta r, que es el punto R.
2ª.- A partir de las ecuaciones paramétricas de r, escribimos las
coordenadas del punto R desconocido que quedarán expresadas en función del

parámetro λ. A continuación hallamos las coordenadas del vector PR e imponemos


la condición de perpendicularidad entre los vectores PR y ur , es decir,


PR .ur  0
Obteniendo el valor de λ que nos permite identificar a R.
Ejemplo 7 – 1º
x  1  2λ

Calcula la distancia del punto P = (5, -1, 6) a la recta r de ecuaciones y 
 λ
z  5  λ 
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
123
Primer método:
Plano π que pasa por P y es perpendicular a r:
π
 P  (5, 1,6)
 
n  ur  (2, 1,1)

2x  y  z d  0 
2.5 1.(1)  6 d  0  d  3
π 2x  y  z  3  0
r
r


ur
R.

π 2x  y  z  3  0
nπ  u r
. P = (5, -1, 6)
. P = (5, -1, 6)
R
Intersección de la recta r con el plano π:
Sustituimos las coordenadas de r en la ecuación de π y obtenemos el valor de λ
2(1  2λ)  (λ )  (5  λ)  3  0

λ  1
R  (3,1, 4)



d (P , r )  d (P , R ) | PR |


PR  R  P  ( 2,2, 2) 


d (P , r )  d (P , R ) | PR | 12  2 3u
Segundo método:
El punto R buscado tiene de coordenadas R = (1 - 2λ, -λ, 5 + λ), y forma con el punto


P un vector, PR , perpendicular al vector director de la recta, ur . Por tanto el
producto escalar de estos dos vectores tiene que ser nulo

PR  R  P  (1  2λ, λ,5  λ )  (5, 1, 6)  ( 4  2λ, λ  1, 1  λ )


ur . PR  ( 2, 1,1).( 4  2λ, 5  λ, 1  λ )  0

λ  1

R  (3,1, 4)
Hemos obtenido el mismo punto que por el procedimiento anterior.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
124
6ª.- Punto simétrico a otro respecto a una recta
Se llama punto simétrico P’, de un punto P, respecto a una recta r, al punto
que se encuentra a la misma distancia de r que P y en la perpendicular a la recta r
que pasa por P, es decir, el punto P y su simétrico P’ forman un segmento cuyo
punto medio es la proyección de P sobre la recta r.
P’
r
R  MPP ' 
R = MPP’
P P'
2
P
Podemos localizar el punto R, por cualquiera de los dos métodos descritos en la
pregunta anterior, y a continuación aplicar que dicho punto es el punto medio del
segmento PP’.
Ejercicio 7 – 3º
Halla la distancia del punto P = (5, 6, 6) a la recta r = (5λ, 2 – λ, λ). Hazlo por los dos
métodos.
Solc: 5 2
u
Ejercicio 7 – 4º
Calcula las coordenadas del punto A’ que es simétrico a A = (-3, 1, -7), respecto a la
recta r = (-1 + λ, 3 + 2λ, -1 + 2λ).
Solc: A’ = (-3, -3, -3)
Ejercicio 7 – 5º
Halla las coordenadas del punto o puntos de la recta r = (λ, 3 –λ, 1 + 2λ) cuya
distancia al punto P = (1, 0, 2), vale 11 u.
Solc: Hay dos puntos A = (0, 3, 1) y B = (2, 1, 5)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
125
7ª.- Distancia de un punto a un plano
Se llama distancia de un punto P = (px, py, pz) a un plano π, a la distancia de
P a su proyección sobre el plano π.
.P
π

d(P, π) = d(P, Q) = | PQ |
Q
Para localizar el punto Q, podemos seguir cualquiera de estos tres procesos:
1º.- Hallar la ecuación de la recta r que pasa por P y es perpendicular a π, y
buscar la intersección de la recta con el plano.
2º.- A partir de las ecuaciones paramétricas del plano π, escribimos las
coordenadas del punto Q desconocido que quedarán expresadas en función de los

parámetros λ y µ. A continuación hallamos las coordenadas del vector
PQ e

imponemos la condición de perpendicularidad entre el vector PQ y los vectores


dirección del plano uπ y vπ , es decir,



PQ.uπ  0 y

PQ.vπ  0
Obteniendo los valores de λ y µ que nos permite identificar a Q.
3º.- Aplicando la siguiente fórmula:
d (P ,π ) 
Matemáticas II Álgebra lineal y Geometría
| a.px  b.py  c.pz  d |
a 2  b2  c 2
CURSO 2014/15
u
126
Ejemplo 7 – 2º
Calcula la distancia del punto P = (3, 1, 7) al plano π de ecuación x – 3y + 5z – 1 = 0
Primer método:
Recta r que pasa por P y es perpendicular a π: r
 P  (3,1,7)
 
ur  n  (1, 3,5)
x  3  λ

 y  1  3λ 
z  7  5λ
Intersección de la recta r con el plano π:
Sustituimos las coordenadas de r en la ecuación de π y obtenemos el valor de λ
( 3  λ )  3 (1  3 λ )  5 ( 7  5 λ )  1  0


d ( P , π )  d ( P , Q ) | PQ |


34 102
34 
PQ  Q  P  ( 
,
,
)
3 5 35
7 
λ  

34
35

Q  (


d ( P , π )  d ( P , Q ) | PQ |
71 137 15
,
,
)
35 35
7
40 460
3 4 35

2
35
35
u
Segundo método:
x  1  3λ  5μ 

Escribimos el plano x – 3y + 5z – 1 = 0 en paramétricas: y 
λ

z 
μ 
El punto Q buscado tiene de coordenadas Q = (1 + 3λ - 5µ, λ, µ), y forma con el punto P un vector,



PQ , perpendicular a los vectores directores del plano, uπ = (3, 1, 0) y vπ = (-5, 0, 1) . Por tanto el

producto escalar del vector PQ con cada uno de los vectores directores del plano tiene que ser nulo

P Q  Q  P  (1  3 λ  5 μ , λ , μ )  (3, 1, 7 )  (  2  3 λ  5 μ , λ  1, μ  7 )


u π . P Q  (3, 1, 0 ).(  2  3 λ  5 μ , λ  1, μ  7 )  0


10λ  15μ  7  0

 15 λ  2 6 μ  3  0

Vπ . P Q  (  5, 0, 1).(  2  3 λ  5 μ , λ  1, μ  7 )  0
Resolviendo el sistema 1 0 λ
15λ
 15μ
 2 6μ


7  , obtenemos los valores de λ = 137/35 y µ = 15/7,
 3 
que nos proporcionan el valor del punto Q = ( 7 1 , 1 3 7 , 1 5 )
35
35
7
Hemos obtenido el mismo punto Q que por el procedimiento anterior.
Tercer método:
Aplicamos la fórmula de la distancia de un punto P a un plano π:
d (P ,π ) 
| a.px  b.py  c.pz  d | |3  3.1  5.7  1| |34| 34 35



u
2
2
2
2
2
2
35
35
a  b c
1  (3)  5
Que evidentemente es mas rápida y cómoda.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
127
8ª.- Simétrico de un punto respecto a un plano
El punto simétrico a un punto P respecto a un plano π, es un punto P’, que
se encuentra del plano π a la misma distancia que P, y en la perpendicular al plano
trazada desde el punto P.
En el dibujo podemos observar que el punto P’, simétrico a P, forma un
segmento PP’ cuyo punto medio Q, es la proyección de P sobre el plano π.
π
.P
Q  MPP ' 
P P'
2
Q
. P’
Podemos localizar el punto Q por cualesquiera de los dos primeros métodos de la
pregunta anterior y aplicar que Q es el punto medio del segmento PP’ para obtener
las coordenadas de P’.
Ejercicio 7 – 6º
Calcula la distancia de los puntos P = (8, 5, -6) Q = (3, 0, 0) y R = (0, 0, 0) al plano
π : x 2y 2z 3 0. Hazlo por los tres métodos.
Soluc: d(P,π) = 11 u
d(Q,π) = 2 u
d(P,π) = 1 u
Ejercicio 7 – 7º
Halla el punto simétrico de P = (1, 0, 1) respecto al plano π : x y z 1
Soluc: P’ = (1/3, 2/3, 1/3)
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
128
9ª.- Distancia entre una recta y un plano
Lo primero que tenemos que analizar es la posición relativa entre la recta r y
el plano π, ya que, si la recta está contenida en el plano, o es secante a él, la
distancia entre la recta y el plano es 0.
Si la recta es paralela al plano, la distancia entre r y π es la distancia de
cualquier punto de la recta al plano, como se puede observar en el esquema.
.P
r
d (r,π )  d (Pr ,π)
π
10ª.- Distancia entre dos planos
Lo primero que hay que averiguar es la posición relativa de los planos π y
π’, ya que, si los planos son coincidentes o se cortan en una recta, la distancia entre
ellos es 0.
Si los planos son paralelos, la distancia entre ellos es la distancia de un
punto cualquiera de ellos, al otro.
π
.P
d (π,π ')  d (Pπ ,π ')
π’
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
129
11ª.- Distancia entre dos rectas
En primer lugar hay que averiguar la posición relativa entre ellas, ya que, si
las rectas r y s son coincidentes o secantes, la distancia entre ellas es 0.
Si las rectas son paralelas, la distancia entre ellas es la distancia de
cualquier punto de una de ellas a la otra.
r
Pr .
d (r,s )  d (Pr ,s )
s
Si las rectas se cruzan, podemos proceder de dos formas:
1ª.- Hallar el plano π, que contiene a una de las rectas y es paralelo a la
otra. La distancia de esta recta al plano π es la distancia entre ambas rectas.
2ª.- Tomar un punto R, genérico de la recta r, cuyas coordenadas
dependerán del parámetro λ; y un punto S, genérico de la recta s, cuyas

coordenadas dependerán del parámetro µ. Formamos el vector RS , cuyas
coordenadas dependerán de los dos parámetros, λ y µ. A continuación imponemos
la condición de que este vector tiene que ser perpendicular a las dos rectas, es decir:



RS .ur  0
y

RS .us  0
Obtenemos un sistema de dos ecuaciones con dos incógnitas, λ y µ. Resolviéndolo
obtenemos los valores de λ y µ, y, por tanto, los valores de las coordenadas de los
puntos R y S, cuya distancia es la distancia entre las dos rectas.
r
r
P
s
R
π
s
S
d (r,s )  d (Pr ,πs )
Matemáticas II Álgebra lineal y Geometría
d (r,s )  d (R,S)
CURSO 2014/15
130
Ejemplo 7 - 3º
Hallar la distancia entre las rectas: r = (5 + λ, -1, 8 + 2λ) y s = (4 + 3µ, 3 - µ, 5 + 4µ).
Puedes comprobar que las rectas r y s se cruzan.
Primer método:
Hallamos el plano π que contiene a r y es paralelo a s
P  (5, 1,8)

 

u

v
 (1, 0,2) 
 π
r


 
 vπ  u s  (3,  1, 4) 
π;





nπ  u r  u s  (2,2, 1)
2.5  2.( 1)  8  d  0

d 0
 π;
2x  2 y  z  d  0
2x  2y  z  0
d (s , r )  d (s ,πr )  d (Ps ,πr )  d (4,3,5),2x  2y  z  0  
|2.4  2.3  5 |
4  4 1

9
 3u
3
Segundo método:
Punto genérico de r: R = (5 + λ, -1, 8 + 2λ)
Punto genérico de s: S = (4 + 3µ, 3 - µ, 5 + 4µ)

Vector RS

RS  S  R   4  3µ , 3  µ , 5  4µ    5  λ,  1, 8  2λ   ( 1  3μ  λ, 4  μ , 3  4μ  2λ )

Buscamos el vector RS que se a perpendicular a las dos rectas, es decir:


RS . ur  ( 1  3μ  λ, 4  μ , 3  4 μ  2λ ).(1, 0, 2)  0

RS . us  ( 1  3μ  λ, 4  μ , 3  4 μ  2λ ).(3,  1, 4)  0




5λ  11μ  7  0 

11λ  26μ  19  0 

λ 3
μ 2
Sustituyendo en r y en s, obtenemos los puntos R = (8, -1, 14) y S = (10, 1, 13)

d (s , r )  d (S , R ) | SR || ( 2, 2,1) |
4  4 1  3u
Como es lógico, la misma distancia que por el procedimiento anterior.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
131
Ejercicio 7 – 8º
Calcula la distancia entre:
x 3 y 1 z 2
y el plano π: x – 3y – z + 6 = 0.


5
2
1
a)
La recta r:
b)
Los planos π: x – 5y + 2z – 19 = 0 y π’: 2x – 10y + 4z = 0
c)
La recta r = (1 - 3λ, 2 + λ, 1 – λ) y el plano π: x + 3y = 0
Soluc: a) 8 1 1 u
b) 1 9 3 0 u
c) 7 1 0 u
30
10
11
Ejercicio 7 – 9º
Calcula la distancia entre cada par de rectas:
a)
x  13  12λ

r: y  2

z  8  5λ
Soluc: a) 13 u

x 6

s : y  6  μ
z  9 
x   5λ

b) r : y  2  λ 
z 
λ 
x  5  7μ

s : y  1  5μ
z  1  5μ
b) 0
Ejercicio 7 – 10º
x  5  λ

Calcula el punto de la recta r : y  1  λ  que equidista de los puntos P = (1, 0, -1)
z  2  2λ
y Q = (2, 1, 1)
Soluc: R = (4, -2, 0)
Ejercicio 7 – 11º
Halla la ecuación de la recta s que pasa por el punto P = (2, -1, 1) y corta
x  3  λ

perpendicularmente a la recta r : y  1  2λ
Soluc:s = (2 + 8λ, -1 + 2λ, 1 - 4λ)
z 
3λ
Ejercicio 7 – 12º
x  11  4λ

Sean las rectas r : y  5  2λ
z  7  3λ
x  11  9μ

s : y  5  5μ y el plano π: 2x – 5y + 3z – 4 = 0
z  7  7μ
a)
Calcula el ángulo que forman r y s.
b)
Calcula el ángulo que forma la recta r con el plano.
c)
Halla la distancia entre los puntos de corte de r y s con el plano π.
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
132
Soluc: a) 2º 5’
b) 12º 10’ 23’’ c)
3u
Ejercicio 7 – 13º
a)
Halla el área del triángulo determinado por los puntos de corte del plano π:
3x + y + 2z – 6 = 0 con los ejes de coordenadas.
b)
Halla el volumen de la pirámide determinada por esos tres puntos y el origen
de coordenadas.
2
Soluc: a) 3 14 u
3
c) 6 u
Ejercicio 7 – 14º
Un tetraedro tiene por vértices A = (2, 1, 0), B = (3, 4, 0), C = (5, 1, 0) y D. El vétrice
D es un punto de la recta r = (1 – λ, 2 + λ, 3 + λ).
Halla las coordenadas de D para que el volumen del tetraedro se de 6 u3.
Soluc: Hay dos soluciones D = (0, 3, 4) y D = (8, -5, -4)
Ejercicio 7 – 15º

x 1
x  7  3μ


Comprueba que las rectas r : y  5  λ y s : y  5  μ  se cruzan, y halla la

z 
λ
z  7
ecuación de la recta t que corta a las dos y es perpendicular a ellas.
Soluc:
t:
x  1  λ

y  3  3λ
z  2  3λ
Matemáticas II Álgebra lineal y Geometría
CURSO 2014/15
133