Ejercicios de cada apartado

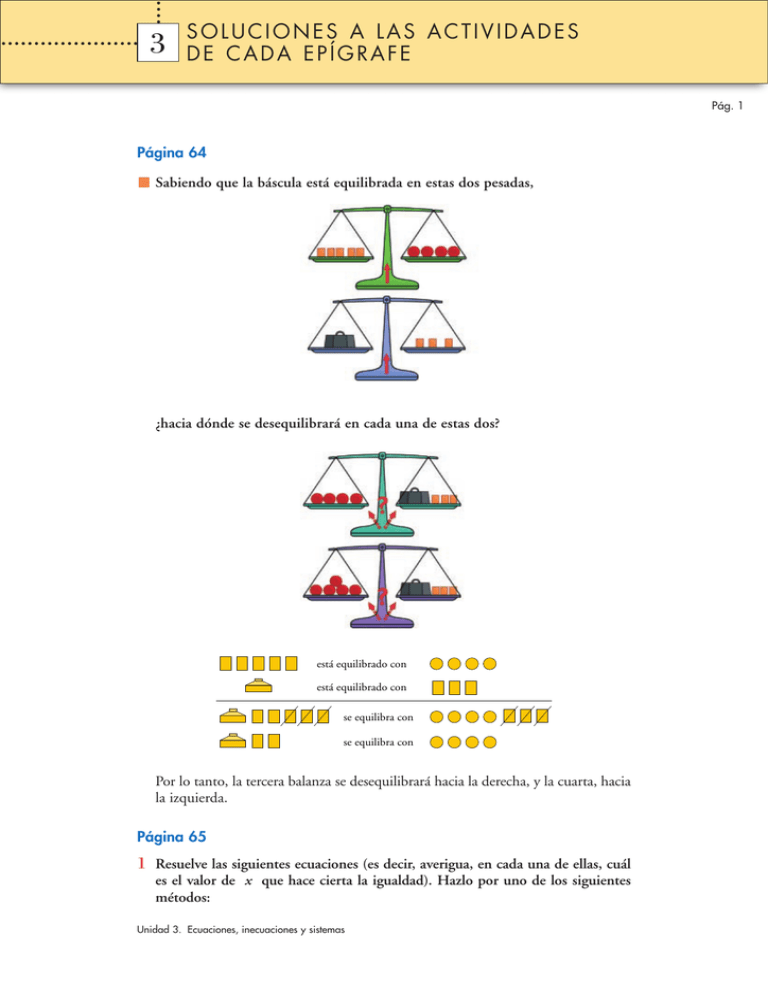
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 1
Página 64
Sabiendo que la báscula está equilibrada en estas dos pesadas,
¿hacia dónde se desequilibrará en cada una de estas dos?
está equilibrado con
está equilibrado con
se equilibra con
se equilibra con
Por lo tanto, la tercera balanza se desequilibrará hacia la derecha, y la cuarta, hacia
la izquierda.
Página 65
1 Resuelve las siguientes ecuaciones (es decir, averigua, en cada una de ellas, cuál
es el valor de x que hace cierta la igualdad). Hazlo por uno de los siguientes
métodos:
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 2
• “A ojo”, es decir, intuyendo la solución y comprobando que, efectivamente,
lo es.
• “Tanteando”, esto es, probando y acercándote cada vez más a la solución.
Puedes usar la calculadora, siempre que el cálculo vaya precedido de la
reflexión.
Aunque ya sepas cómo se resuelven sistemáticamente las ecuaciones, es decir,
aunque sepas despejar x , no apliques aquí esos conocimientos. Simplemente,
mira y tantea.
a) 3x + 7 = 73
b) 3 · (x + 7) = 240
c) √x – 11 = 4
d) (x + 1)2 = 25
e) x 3 + x = 222
f) x 5 + x = 1 000
g) (x – 3) · (x + 2) · (2x – 10) = 0
h) 1 – 1 = 1
x 3 6
i) 3x =59 049
j) 3x = 500
k) x x = 823 543
l) x x = 100
a) 3x + 7 = 73 → x = 22, ya que 3 · 22 + 7 = 66 + 7 = 73
b) 3 (x + 7) = 240, luego x + 7 = 80 → x = 73
c) √x – 11 = 4 → x = 27, por ser √27 – 11 = √16 = 4
d) (x + 1) 2 = 25 → Como 5 2 = 25 ó (–5) 2 = 25, x = 4 ó x = –6
e) x 3 + x = 222
Si x = 5, obtendríamos 5 3 + 5 = 125 + 5 = 130, que es distinto de 222.
Probamos con x = 6 → 6 3 + 6 = 216 + 6 = 222, luego la solución es x = 6.
f ) x 5 + x = 1 000
Buscamos la solución tanteando:
• Si x = 3 → 3 5 + 3 = 243 + 3 = 246 (muy lejos de 1 000)
• Si x = 4 → 4 5 + 4 = 1 024 + 4 = 1 028 (nos pasamos de 1 000)
La solución es un número comprendido entre 3 y 4.
• Si x = 3,9 → 3,9 5 + 3,9 = 902,24 + 3,9 = 906,14
La solución está entre 3,9 y 4.
• Si x = 3,97 → 3,97 5 + 3,97 = 990,14
• Si x = 3,98 → 3,98 5 + 3,98 = 1 002,63
La solución está entre 3,97 y 3,98.
Podríamos continuar probando con más cifras decimales hasta aproximarnos
más a 1 000.
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 3
g) (x – 3) · (x + 2) · (2x – 10) = 0
Si x = 3 → (3 – 3) · (3 + 2) · (6 – 10) = 0 · 5 · (–4) = 0
Si x = –2 → (–2 – 3) · (–2 + 2) · (–4 – 10) = –5 · 0 · (–14) = 0
Si x = 5 → (5 – 3) · (5 + 2) · (10 – 10) = 2 · 7 · 0 = 0
h) 1 – 1 = 1
x
3 6
→ x = 2, ya que 1 – 1 = 1
2 3 6
i) 3 x = 59 049
Tanteando se obtiene que 3 10 = 59 049, luego la solución es x = 10.
j) 3 x = 500
La solución está entre x = 5 y x = 6, ya que 3 5 = 243 y 3 6 = 729.
k) x x = 823 543
Por tanteo se obtiene que 7 7 = 823 543, luego x = 7 es la solución.
l) x x = 100
Tanteando se observa que 3 3 = 27 y 4 4 = 256, luego la solución está entre 3 y 4.
2 Inventa una ecuación similar a cada una de las anteriores y cuya solución sea
elegida por ti de antemano. Por ejemplo, para inventar una ecuación similar a
la c) cuya solución sea 16: √16 – 7 = √9 = 3. Por tanto, la ecuación que
planteo es √x – 7 = 3.
a) 3x – 26 = 70
Su solución es x = 32 (3 · 32 – 26 = 96 – 26 = 70).
b) 2 (x – 5) = 180
Su solución es x = 95 (2(95 – 5) = 2 · 90 = 180).
c) x = 28 es la solución de la ecuación √x – 3 = 5, ya que √28 – 3 = √25 = 5.
d) (x + 3) 2 = 49 es la ecuación que tiene como soluciones x = 4 y x = –10, ya
que (4 + 3) 2 = 7 2 = 49 y (–10 + 3) 2 = (–7) 2 = 49.
e) 4 3 + 4 = 68, luego x = 4 será la solución de la ecuación x 3 + x = 68.
f ) 4 4 + 4 = 260  La ecuación x 4 + x = 500 tiene como solución un número

5 4 + 5 = 630  entre 4 y 5.
g) (x + 4)(x – 2)(3x + 6) = 0 es una ecuación que tiene como soluciones x = –4,
x = 2, x = –2.
h) 1 – 1 = 2 , luego x = 7 es la solución de la ecuación 1 – 1 = 2 .
5 7 35
5 x
35
i) 5 6 = 15 625 → x = 6 es la solución de la ecuación 5 x = 15 625.
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 4
j) Como 2 9 = 512 y 2 10 = 1 024, la ecuación 2 x = 1 000 tiene como solución
un número entre 9 y 10.
k) 6 6 = 46 656, por tanto x = 6 es la solución de la ecuación x x = 46 656.
l) Como 4 4 = 256 y 5 5 = 3 125, la ecuación x x = 2 000 tiene como solución
un número entre 4 y 5.
3 Si a ≤ b, pon el signo de la desigualdad en los siguientes casos:
a) a + 5 … b + 5
b) a – 7 … b – 7
c) 3a … 3b
d) 1 a … 1 b
3
3
e) a … b
5
5
f) –2a … –2b
g) a … b
–3
–3
h) –a … –b
a) a + 5 ≤ b + 5
b) a – 7 ≤ b – 7
c) 3a ≤ 3b
d) 1 a ≤ 1 b
3
3
e) a ≤ b
5 5
f ) –2a ≥ –2b
g) a ≥ b
–3 –3
h) –a ≥ –b
Página 66
1 Resuelve:
a) 2x 2 – 50 = 0
b) 3x 2 + 5 = 0
c) 7x 2 + 5x = 0
a) 2x 2 – 50 = 0 → x 2 = 25 → x1 = 5; x2 = –5
b) 3x 2 + 5 = 0 → x 2 = –5 → No tiene solución.
3
c) 7x 2 + 5x = 0 → x(7x + 5) = 0 → x1 = 0; x2 = –5
7
2 Resuelve:
a) 10x 2 – 3x – 1 = 0
b) x 2 – 20x + 100 = 0
c) 3x 2 + 5x + 11 = 0
a) 10x 2 – 3x – 1 = 0 → x =
3 ± √ 9 + 40 3 ± 7
=
→ x1 = 1 ; x2 = – 1
20
20
2
5
b) x 2 – 20x + 100 = 0 → x =
20 ± √ 400 – 400
= 10
2
c) 3x 2 + 5x + 11 = 0 → x =
–5 ± √ 25 – 132
→ No tiene solución.
6
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 5
3 En un triángulo rectángulo, el lado mayor es 3 cm más largo que el mediano,
el cual, a su vez, es 3 cm más largo que el pequeño. ¿Cuánto miden los lados?
x → lado pequeño


x + 3 → lado mediano  (x + 6) 2 = (x + 3) 2 + x 2 → x 2 + 12x + 36 =

x + 6 → lado grande 
= x 2 + 6x + 9 + x 2
x 2 – 6x – 27 = 0 → x =
6 ± √ 36 + 108 6 ± √ 144 6 ± 12
=
=
2
2
2
x = –3 → Solución no válida, por trabajar con longitudes
Los lados miden 9 cm, 12 cm y 15 cm.
Página 68
1 Resuelve:
a) 7x 4 – 63x 2 = 0
b) 7x 4 – 112 = 0
c) 4x 4 – 5x 2 + 1 = 0
a) 7x 4 – 63x 2 = 0
Hacemos el cambio: x 2 = z; x 4 = z 2
z = 0
7z 2 – 63z = 0 → z(7z – 63) = 0 
 z = 63/7 = 9
→ x=0
→ x = ±3
Soluciones: x1 = 0; x2 = 3; x3 = –3
b) 7x 4 – 112 = 0
x 4 = 112 = 16 → x 4 = √16 → x = ±2
7
Soluciones: x1 = 2; x2 = –2
c) 4x 4 – 5x 2 + 1 = 0
Hacemos el cambio: x 2 = z; x 4 = z 2
4z 2 – 5z + 1 = 0 → z =
5 ± √ 25 – 16 5 ± 3
=
8
8
z1 = 1
z2 = 1/4
x = ±1 
1
1
 Soluciones: x1 = 1; x2 = –1; x3 = , x4 = –
x = ±1/2 
2
2
Página 69
2 Resuelve:
a) √x + 4 – √6 – x = –2
Unidad 3. Ecuaciones, inecuaciones y sistemas
b) x – √2x – 3 = 1
x1 = 9
x2 = –3
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 6
a) √x + 4 – √6 – x = –2
√x + 4 = √6 – x – 2 → Elevamos al cuadrado los dos miembros:
x + 4 = 6 – x + 4 – 4 √6 – x
→ 2x – 6 = –4 √6 – x
→ x – 3 = –2 √6 – x
Volvemos a elevar al cuadrado ambos miembros:
x 2 – 6x + 9 = 4(6 – x) → x 2 – 6x + 9 = 24 – 4x → x 2 – 2x – 15 = 0 →
→ x=
2 ± √ 4 + 60 2 ± 8
=
→ x1 = 5; x2 = –3
2
2
Comprobamos estas soluciones en la ecuación inicial:
x1 = 5 → √5 + 4 – √6 – 5 = 3 – 1 = 2 ≠ –2 → x = 5 No es solución.
x2 = –3 → √–3 + 4 – √6 + 3 = 1 – 3 = –2 → x = –3 Sí es solución.
b) x – √2x – 3 = 1
x – 1 = √2x – 3
→ Elevamos ambos miembros al cuadrado:
x 2 – 2x + 1 = 2x – 3 → x 2 – 4x + 4 = 0 → (x – 2) 2 = 0 → x = 2
Comprobamos en la ecuación inicial:
2 – √2 · 2 – 3 = 2 – 1 = 1 → x = 2 Sí es solución.
3 Resuelve:
2
b) x + 7 + x 2 – 3 x + 6 = 1
x + 3 x + 2x – 3
a) x + 1 + 1 – x = 5
x+5 x–4 2
a) x + 1 + 1 – x = 5
x+5 x–4 2
Reducimos a común denominador multiplicando los dos miembros por
(x + 5) · (x – 4)2 y quitamos los denominadores:
2(x – 4)(x + 1) + 2(x + 5)(1 – x) = 5(x + 5)(x – 4)
2x 2 – 8x + 2x – 8 + 2x – 2x 2 + 10 – 10x = 5x 2 – 20x + 25x – 100
5x 2 + 19x – 102 = 0 → x =
=
–19 ± √ 361 + 2 040 –19 ± 49
=
=
10
10
x1 = 3
–68 –34
x2 = — = —
10
5
Comprobamos las dos posibles soluciones:
3 + 1 + 1 – 3 = 4 + 2 = 1 + 2 = 5 → x = 3 sí es solución.
3+5 3–4 8 1 2
2
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 7
–34
34
—+1 1+—
5
5 = –29 + 39 = 29 – 13 = 58 – 13 = 45 =
+
–34
–9
–54
9
8
18 18 18
— + 5 –34
—–4
5
5
= 5
2
→ –34 también es solución
5
Soluciones: x1 = 3, x2 = –34
5
2
b) x + 7 + x 2 – 3x + 6 = 1
x + 3 x + 2x – 3
x + 7 + x 2 – 3x + 6 = 1
x + 3 (x – 1)(x + 3)
Multiplicamos ambos miembros por (x + 3)(x – 1):
(x + 7)(x – 1) + x 2 – 3x + 6 = (x – 1)(x + 3) →
→ x 2 + 7x – x – 7 + x 2 – 3x + 6 = x 2 + 2x – 3
x2 + x + 2 = 0 → x =
–1 ± √ 1 – 8
→ No tiene solución.
2
4 a) Invéntate una ecuación que tenga por soluciones los valores 3, –3, √7
y – √7 .
b) Escribe otra ecuación cuyas soluciones sean 5, 0, 3 y –2.
a) Creamos una ecuación a partir del producto de factores cuyas raíces sean
dichos valores:
(x – 3)(x + 3) (x – √7 )(x + √7 ) = 0 → (x 2 – 9)(x 2 – 7) = 0 →
→ x 4 – 16x 2 + 63 = 0
b) Se hace lo mismo que en el apartado a):
x(x – 5)(x – 3)(x + 2) = 0 → (x 2 – 5x)(x 2 – x – 6) = 0 →
→ x 4 – 6x 3 – x 2 + 30x = 0
5 Resuelve las siguientes ecuaciones:
a) 3x 4 – 75x 2 = 0
b) x 4 – 10x 2 + 9 = 0
c) x 4 – 9x 2 + 20 = 0
d) √4x + 5 = x + 2
e) √x + 2 = x
f) √2x – 3 – √x – 5 = 2
g) x + 2x = 3
x–1 x+1
i) 1 + 12 = 3
x x
4
h)
Unidad 3. Ecuaciones, inecuaciones y sistemas
5 + x = 3
x+2 x+3 2
j) ( √x – x + 2) · x = 0
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 8
(
)
k) x · (x + 1) · (x – 2) · x – 1 = 0
2
l) (x 2 – 9) · ( √x + 3) = 0
a) 3x 4 – 75x 2 = 0
x2 = 0
x 2 (3x 2
– 75) = 0
→ x = 0
75
3x 2 – 75 = 0 → x 2 = — → x 2 = 25 → x = ±5
3
Soluciones: x1 = 0; x2 = 5; x3 = –5
b) x 4 – 10x 2 + 9 = 0
x 2 = z → x 4 = z2
z 2 – 10z + 9 = 0 → z =
x2 = z
10 ± √ 100 – 36 10 ± 8
=
2
2
z=9
z=1
x 2 = 9 → x = ±3
x 2 = 1 → x = ±1
Soluciones: x1 = 3; x2 = –3; x3 = 1; x4 = –1
c) x 4 – 9x 2 + 20 = 0
x 2 = z → x 4 = z2
9 ± √ 81 – 80 9 ± 1
=
2
2
–
x 2 = 5 → x = ±√5
z 2 – 9z + 20 = 0 → z =
x2 = z
z=5
z=4
x 2 = 4 → x = ±2
Soluciones: x1 = √5 ; x2 = – √5 ; x3 = 2; x4 = –2
d) √4x + 5 = x + 2
Elevamos ambos miembros al cuadrado:
4x + 5 = (x + 2) 2 → 4x + 5 = x 2 + 4x + 4 → x 2 – 1 = 0 → x 2 = 1 → x = ±1
Comprobación:
—
—
x = 1 → √4 + 5 = √ 9 = 3 
 x = 1 es solución.
1+2=3

—
x = –1 → √–4 + 5 = 1 
 x = –1 es solución.
–1 + 2 = 1 
e) √x + 2 = x
√x = x – 2 → Elevamos al cuadrado ambos miembros:
x = (x – 2) 2 → x = x 2 – 4x + 4 → x 2 – 5x + 4 = 0 →
x1 = 4
5 ± √ 25 – 16 5 ± 3
→ x=
=
x2 = 1
2
2
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 9
Comprobación:
√4 + 2 = 4 → x1 = 4 es solución.
√1 + 2 = 3 ≠ 1 → x2 = 1 no es solución.
Solución: x = 4
f ) √2x – 3 – √x – 5 = 2
√2x – 3 = 2 + √x – 5 → Elevamos al cuadrado ambos miembros:
2x – 3 = (2 + √x – 5 ) 2 → 2x – 3 = 4 + x – 5 + 4 √x – 5 → x – 2 = 4 √x – 5
Volvemos a elevar al cuadrado ambos miembros:
(x – 2) 2 = 16(x – 5) → x 2 – 4x + 4 = 16x – 80 → x 2 – 20x + 84 = 0 →
x1 = 14
20 ± √ 400 – 336 20 ± 8
→ x=
=
x2 = 6
2
2
Comprobación:
x1 = 14 → √2 · 14 – 3 – √14 – 5 = 5 – 3 = 2 → x1 es solución.
x2 = 6 → √2 · 6 – 3 – √6 – 5 = 3 – 1 = 2 → x2 es solución.
g)
x + 2x = 3
x–1 x+1
Reducimos a común denominador, multiplicando por (x + 1)(x – 1) ambos
miembros:
x(x + 1) + 2x(x – 1) = 3(x + 1)(x – 1) → x 2 + x + 2x 2 – 2x = 3x 2 – 3 → x = 3
Comprobamos que la solución es válida:
3 + 6 = 3 + 3 = 6 =3
2 4 2 2 2
h)
5 + x = 3
x+2 x+3 2
Reducimos a común denominador, multiplicando por 2 · (x + 2) · (x + 3)
ambos miembros:
2 · 5(x + 3) + 2x(x + 2) = 3(x + 2)(x + 3) → 10x + 30 + 2x 2 + 4x =
= 3x 2 + 15x + 18 → x 2 + x – 12 = 0
x=
–1 ± √ 1 + 48 –1 ± 7
=
2
2
x1 = 3
x2 = –4
Comprobamos que las dos soluciones son válidas:
5 + 3 = 1 + 1 = 3 → Vale
3+2 3+3
2 2
5
+ –4 = – 5 + 4 = 3 → Vale
–4 + 2 –4 + 3
2
2
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 10
i) 1 + 12 = 3
x
4
x
Multiplicamos por 4x 2 ambos miembros:
4x + 4 = 3x 2 → 3x 2 – 4x – 4 = 0
x1 = 2
4 ± √ 16 + 48 4 ± 8
4
2
x=
=
x2 = – — = – —
2·3
6
6
3
Comprobamos que las dos soluciones son válidas:
1 + 1 = 2 + 1 = 3 → Vale
2 4 4 4 4
1 +
1
2
2
–—
–—
3
3
( )
2
= – 3 + 9 = – 6 + 9 = 3 → Vale
2 4
4 4 4
j) ( √x – x + 2)x = 0
x=0
√x – x + 2 = 0 → √x = x – 2 → x = x 2 – 4x + 4 → x 2 – 5x + 4 = 0 →
→ x=
5 ± √ 25 – 16 5 ± 3
=
2
2
x1 = 4
x2 = 1
Comprobación:
x1 = 4 → √4 – 4 + 2 = 2 – 4 + 2 = 0 → x1 sí es solución.
x2 = 1 → √1 – 1 + 2 = 1 – 1 + 2 ≠ 0 → x2 = 1 no es solución.
Soluciones: x1 = 0; x2 = 4



1
k) x(x + 1)(x – 2) x –
=0 → 
2



( )
x=0
x + 1 = 0 → x = –1
x–2=0 → x=2
1
1
x–—=0 → x=—
2
2
Soluciones: x1 = 0; x2 = –1; x3 = 2; x4 = 1
2
 x2 – 9 = 0
l) (x 2 – 9) ( √x + 3) = 0 →  —
 √x + 3 = 0
x 2 – 9 = 0 → x = ±3
√x = –3 → x = 9 → No es solución ( √9 + 3 = 3 + 3 ≠ 0).
Soluciones: x1 = 3; x2 = –3
Unidad 3. Ecuaciones, inecuaciones y sistemas
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
31
Pág. 11
Página 70
1 Resuelve aplicando dos veces el método de reducción:
 22x + 17y = 49

 31x – 26y = 119
22x – 17y = 49 

31x – 26y = 119 
1-o Multiplicamos la primera ecuación por 31, la segunda por 22 y restamos:
682x + 527y = 1 519
682x – 572y = 2 618
1 099y = –1 099 → y = –1
2-o Multiplicamos la primera ecuación por 26, la segunda por 17 y sumamos:
572x + 442y = 1 274
527x – 442y = 2 023
1 099x
= 3 297 → x = 3
Solución: x = 3, y = –1
Página 71
1 Resuelve estos sistemas:
 x – y = 15
a)  x · y = 100

x 2 + xy + y 2 = 21
b) x + y = 1

 x – y = 15
a) 
 x · y = 100
x = 15 + y
(15 + y)y = 100 → 15y + y 2 = 100 → y 2 + 15y – 100 = 0
y1 = 5
–15 ± √ 225 + 400
= –15 ± 25
y2 = –20
2
2
y1 = 5 → x1 = 20 → Solución: x1 = 20, y1 = 5
y=
y2 = –20 → x2 = –5 → Solución: x2 = –5, y2 = –20
 x 2 + xy + y 2 = 21
b) 
x + y = 1
x=1–y
(1 – y) 2 + (1 – y)y + y 2 = 21 → 1 + y 2 – 2y + y – y 2 + y 2 = 21
y1 = 5
1 ± √ 1 + 80 1 ± 9
=
y2 = –4
2
2
Si y1 = 5 → x1 = –4 → Solución: x1 = –4, y1 = 5
y 2 – y – 20 = 0 → y =
Si y2 = –4 → x2 = 5 → Solución: x2 = 5, y2 = –4
Unidad 3. Ecuaciones, inecuaciones y sistemas
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
31
Pág. 12
Página 72
2 Resuelve estos sistemas:

a) 2x2 – y – 1= 0
x – 7 = y + 2
y + 8 = x 2
x + y = 18
b) x y = y + 6x + 4
c) 
–2 ± √ 4 + 32 –2 ± 6
=
–2
–2
x1 = –2
x2 = 4

y – 2x = 0
 2x – y – 1 = 0
a)  2
x – 7 = y + 2
2x – y – 1 = 0
–x 2 + y + 9 = 0
–x 2 + 2x + 8 = 0 → x =
Si x1 = –2 → y1 = –5 → Solución: x1 = –2, y1 = –5
Si x2 = 4 → y2 = 7 → Solución: x2 = 4, y2 = 7
 x + y = 18
b) 
 xy = y + 6x + 4
x = 18 – y
(18 – y)y = y + 6(18 – y) + 4 → 18y – y 2 = y + 108 – 6y + 4
y 2 – 23y + 112 = 0 → y =
23 ± √ 529 – 448 23 ± 9
=
2
2
y1 = 16
y2 = 7
Si y1 = 16 → x1 = 2 → Solución: x1 = 2, y1 = 16
Si y2 = 7 → x2 = 11 → Solución: x2 = 11, y2 = 7
 y + 8 = x2
c) 
 y – 2x = 0
y = 2x
2x + 8 = x 2 → x 2 – 2x – 8 = 0
x=
2 ± √ 4 + 32 2 ± 6
=
2
2
x1 = 4
x2 = –2
Si x1 = 4 → y1 = 8 → Solución: x1 = 4, y1 = 8
Si x2 = –2 → y2 = –4 → Solución: x2 = –2, y2 = –4
Página 73
1 ¿Cuáles de los siguientes valores son soluciones de la inecuación x 2 – 8x < 12?
a) –5
b) 0
c) 1,1
d) 2
e) 5/2
f) 3,2
g) 5,3
h) 10
Unidad 3. Ecuaciones, inecuaciones y sistemas
31
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 13
Comprobamos si se cumple la desigualdad con cada número:
a) –5 → (–5) 2 – 8 · (–5) = 25 + 40 = 65 > 12 → –5 no es solución.
b) 0 → 02 – 8 · 0 = 0 < 12 → 0 es solución.
c) 1,1 → 1,12 – 8 · 1,1 = 1,21 – 8,8 = –7,59 < 12 → 1,1 es solución.
d) 2 → 2 2 – 8 · 2 = 4 – 16 = –12 < 12 → 2 es solución.
e) 5
2
→
()
5
2
2
– 8 · 5 = 25 – 20 = – 55 < 12 →
2
4
4
5 es solución.
2
f ) 3,2 → (3,2)2 – 8 · 3,2 = 10,24 – 25,6 = –15,36 < 12 → 3,2 es solución.
g) 5,3 → (5,3)2 – 8 · 5,3 = 28,09 – 42,4 = –14,31 < 12 → 5,3 es solución.
h) 10 → 10 2 – 8 · 10 = 100 – 80 = 20 > 12 → 10 no es solución.
2 Traduce a lenguaje algebraico:
a) El triple de un número más ocho unidades es menor que 20.
b) El número de alumnos de mi clase es menor que 35.
c) Si mi dinero aumentara al triple y me tocaran 20 € tendría, por lo menos,
110 €.
a) 3x + 8 < 20; x → número.
b) x < 35; x → número de alumnos.
c) 3x + 20 ≥ 110; x → dinero que hay inicialmente.
Unidad 3. Ecuaciones, inecuaciones y sistemas