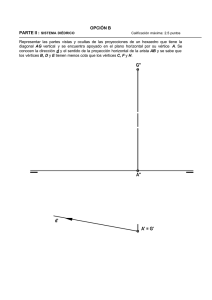
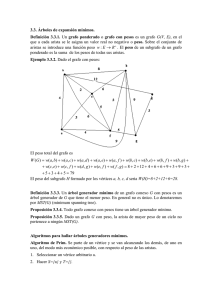
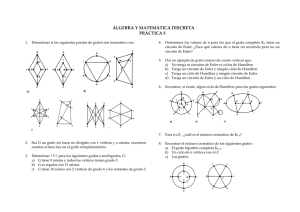
Número 50 (septiembre 2013 - mayo 2014)

 Revista Escolar de la Olimpíada Iberoamericana de Matemática
Número 50 (septiembre 2013 - mayo 2014)
ISSN – 1698-277X
ÍNDICE
Editorial en el cincuentenario, por Francisco Bellot
Artículos, Notas y lecciones de preparación de Olimpiadas (50)
Lo que se piensa bien… por Claude Villers.
Introducción a la teoría de grafos, por A. Kiselev y Ekaterina Zhukova.
La suficiencia de la equivalencia e independencia de las desigualdades de
Cauchy-Buniakowski-Schwarz y de
Bergström, por
D.M. Bătinețu‐Giurgiu y Neculai Stanciu. Problemas para los más jóvenes (50)
Problemas de la Brother
Introductory Division
Alfred
Brousseau
Mathematics
Competition,
Soluciones a los problemas PMJ48-1, PMJ48-2, PMJ48-3 y PMJ48-4, por Luis
Miguel Maraví Zavaleta, Huamachuco, Perú.
Problemas de nivel medio y de Olimpiadas (50)
Problemas de la Ronda Final de la 26ª Olimpiada de Corea del Sur (2013)
Problemas (50)
Problemas propuestos 246-255
Problemas resueltos
Problema 241
Recibidas soluciones de Daniel Lasaosa Medarde, Pamplona, España; Marcos
Martinelli, Brasilia, Brasil; y de los proponentes
Problema 242
Recibidas soluciones de Daniel Lasaosa Medarde, Pamplona, España y de los
proponentes.
Problema 243
Recibidas soluciones de Daniel Lasaosa Medarde, Pamplona, España; Marcos
Martinelli, Brasilia, Brasil y de los proponentes.
Problema 244
Recibidas soluciones de Ignacio Larrosa Cañestro, La Coruña, España; Daniel
Lasaosa Medarde, Pamplona, España; Marcos Martinelli, Brasilia, Brasil; y del
proponente.
Problema 245
Recibidas soluciones de Saturnino Campo Ruiz, Salamanca, España; Andrea
Fanchini, Cantú, Italia; Daniel Lasaosa Medarde, Pamplona, España.
El editor se complace en comunicar la recuperación de David Monk, autor del
problema 245.
Noticia de congresos, referencia de páginas web y reseña de libros
(50)
Tres necrológicas: Pawel Jarek , Leon van den Broek y Marie Hélène Deledicq,
por F. Bellot
Congreso Iberoamericano de Ciencia, Tecnología, Innovación
Educación, Buenos Aires (Argentina). 12 al 14 de noviembre de 2014
y
Divertimentos Matemáticos (50)
Los Caballeros de la Larga Búsqueda (3ª y última parte), por Víctor Buján
Delgado
Otras informaciones
Cursos de GeoGebra
Para Primaria
http://www.ibertic.org/primariageogebra/
Para Secundaria
http://www.ibertic.org/ticymatematica/
Formación Docente
Especialización en Educación Matemática (secundaria)
http://www.oei.es/cursomatematica/
Curso Programación, Creatividad y Resolución de Problemas con Scratch
http://www.ibertic.org/scratch/
Colaboración docentes alumnos
Club Iberoamericano GeoGebra
http://www.ibertic.org/clubgeogebra.php
Realizado en el marco del Instituto Iberoamericano de Enseñanza
de las Ciencias y la Matemática (IBERCIENCIA) con la colaboración
de la Consejería de Economía, Innovación, Ciencia y Empleo de la
Junta de Andalucía
EDITORIAL EN EL CINCUENTENARIO
El que la Revista Escolar de la O.I.M. llegue a su volumen número 50
justifica, en mi opinión, un editorial. Y lo primero que hay que decir son dos
palabras: gracias y perdón.
Gracias a todos los colaboradores, y lectores de la Revista. Gracias, sin
duda a la OEI, en cuyas generosas páginas web se alberga la REOIM y sin
cuyo decidido apoyo desde el primer momento no hubiera sido posible llevar
a efecto la iniciativa. Gracias a los más de treinta mil quinientos
suscriptores, que, aparte del aviso por email de que el siguiente número
está en la red, no reciben otros beneficios. Muchas gracias a todos.
En segundo lugar, el editor tiene que pedir perdón. En 2006, un persistente
vértigo provocó un impasse de varios meses en la publicación. Ahora se ha
vuelto a producir una larga interrupción, afortunadamente no por
enfermedad, sino por un exceso de trabajo (parece mentira que esto lo diga
un jubilado…): la Olimpiada Matemática Española, el Concurso Canguro
Matemático, los Seminarios de Problemas, el proyecto ESTALMAT…
Por eso presento mis excusas a los lectores de la Revista, y aprovechando
que 50 es un número redondo, en lugar de los cinco problemas propuestos
en cada número, en éste proponemos 10, e incluimos las soluciones de los
problemas del número anterior de todos los que nos las han hecho llegar.
Quisiera mencionar también a los autores de los Artículos que presentamos
en este volumen.
El Prof. Claude Villers es un veterano matemático belga, cuyo artículo fue
presentado en el Congreso de la Sociedad Belga de Profesores de
Matemáticas de expresión francesa celebrado en 2010 en Dinant, una de las
ciudades con emplazamiento más espectacular en el valle del río Meuse, y
que ha accedido amablemente a que lo traduzcamos para los lectores de la
REOIM.
Los Prof. Batinetzu-Giurgiu y Neculai Stanciu, de Rumania, nos hicieron
llegar el artículo complementario del que apareció en el vol. 49 al poco
tiempo de la publicación de éste, y han tenido que esperar pacientemente la
aparición del volumen 50.
La profesora Ekaterina Zhukova, de la Universidad de Electrotecnia de San
Petersburgo, y su colaborador A. Kiselev, de la Universidad de San
Petersburgo contribuyen con un artículo de Introducción a la teoría de
grafos que espero sea del agrado de todos los lectores, y en especial de los
jóvenes. Contiene un gran número de ejercicios, cuyas soluciones se
incluyen en la última parte de su contribución. Creo que es una excelente
muestra de la manera de enseñar en los centros rusos.
Los posibles errores son imputables al editor, naturalmente.
Las tres notas necrológicas afectan en esta ocasión a tres destacados
miembros de la Asociación Kangourou Sans Frontières que han
desaparecido entre febrero de 2013 y abril de 2014: Pawel Jarek, de
Polonia; Leon van den Broek, de Holanda, y Marie Hélène Deledicq, de
Francia. Nuestras más sinceras condolencias a sus familiares y amigos.
La OEI está ahora inmersa en la organización, el próximo mes de
noviembre, de un macro congreso en Buenos Aires sobre Ciencia,
Tecnología, Innovación y Educación Matemática en Iberoamérica. Por eso la
sección Noticia de Congresos está dedicada a este magno acontecimiento.
Y la sección de Divertimentos Matemáticos contiene el tercer y último
capítulo del relato Los Caballeros de la Larga Búsqueda, del Prof. Víctor
Buján Delgado, de Costa Rica.
Repito mis palabras iniciales: Muchísimas gracias a todos, y perdón por el
retraso en la salida de este vol. 50 de la REOIM.
Francisco Bellot Rosado
Valladolid, mayo de 2014.
Artículos, Notas y lecciones de preparación de Olimpiadas Lo que se piensa bien …. Claude Villers Dirección del autor: Rue Louis Piérard, 29 à 7022 Hyon Mail : [email protected] Este texto es el soporte de la conferencia presentada en Dinant, el miércoles 25 de agosto de 2010, en el marco del 36e congreso de la SBPMef (Société Belge des Professeurs de Mathématiques d’expression française). Las matemáticas no se aprenden : se comprenden.
Autor desconocido
1‐Introducción « Maths et mots » era el tema principal del congreso. Un tema vasto, sin duda alguna, y particularmente abierto. Puede, evidentemente, suscitar la expresión de numerosos puntos de vista yendo en sentidos diversos y encontrarse también en el origen de debates, discusiones, textos, intervenciones, … sin duda muy interesantes. Por otra parte, el tema ha sido tratado de diferentes formas en numerosas obras cuyas referencias pueden encontrarse fácilmente en Internet utilizando algún motor de búsqueda. Es bastante evidente que la matemática, tanto en su enseñanza como en sus aplicaciones y en sus investigaciones, necesita, al menos para su comunicación, el uso de diversos lenguajes, entre los cuales está el lenguaje coloquial, formado por frases constituidas a su vez por palabras, y que tiene ciertamente un lugar importante. La búsqueda de la calidad de esta comunicación y de su percepción aparecen abundantemente en las recomendaciones metodológicas que acompañan a los programas de los cursos de matemáticas, especialmente los de los dos primeros cursos de la enseñanza secundaria. En las listas de competencias a desarrollar que conciernen al lenguaje, están por ejemplo ::  Expresarse correctamente,  Formular correctamente los razonamientos,  Enunciar y redactar claramente la respuesta a la pregunta planteada o la conclusión del razonamiento elaborado,  Comprender un mensaje,  Analizar la estructura global de un texto y distinguir en él lo esencial de lo accesorio,  Traducir una información de un lenguaje a otro,  Pasar del lenguaje coloquial al algebraico o al gráfico y recíprocamente,  Dominar el vocabulario y el simbolismo,  Explicar y redactar una demostración,  Extender una regla, un enunciado o una propiedad a un dominio más amplio,  etc… 1
Todos nosotros estamos ciertamente convencidos de la necesidad de alcanzar lo mejor posible esos objetivos, pero también sabemos que no siempre es evidente conseguirlo totalmente y que, a veces, son esas « pasadas de frenada » en el nivel de la lengua utilizada las que plantean problemas a ciertos alumnos. He aquí un ejemplo vivido por mí, hace…. mucho tiempo. El ejercicio propuesto a los alumnos les pedía dibujar las flechas de la composición de dos relaciones mediante flechas de colores. La consigna a aplicar era la siguiente : « Cada vez que a una flecha verde le sigue una flecha azul, entonces se traza una flecha roja directa». La situación inicial era, por ejemplo : Un alumno ha propuesto la construcción de la derecha, justificándola porque si una flecha verde está seguid de una azul, es que la azul está detrás de la verde y no delante de ella. 2
Otro ejemplo. ¿Qué significados atribuímos a la palabra « altura » ? cuando se dice :  El área de un triángulo es igual a la mitad del producto de su base por su altura.  Las tres alturas de un triángulo se cortan en un mismo punto, llamado ortocentro del triángulo. En el primer caso, la « altura » es la longitud de un segmento (la base también). En el segundo, ¿las alturas siguen siendo segmentos ? Esos dos ejemplos ilustran bien que una misma palabra puede tener diferentes significados según el contexto en que se encuentra en el momento en que se utiliza. Sin embargo, eso puede resultar perturbador para los alumnos que nos escuchan. Conviene, por tanto, estar atentos. Vamos ahora a presentar algunas situaciones de enseñanza que ilustran las relaciones de causa a efecto que pueden existir entre las matemáticas y las palabras. En esta ocasión, se verán situaciones muy sencillas que permitan reencontrar nociones enseñadas que aclaren, quizá un nuevo día y que ofrezcan a menudo la oportunidad de abordar nociones matemáticas nuevas. 3
2 – Matemáticas sin palabras Es posible practicar ocasionalmente matemáticas sin utilizar palabras. Es el caso, por ejemplo, en algunas demostraciones. Se pueden encontrar numerosos ejemplos en un libro como « Proofs without words » de Roger B. Nelsen o en sitios de Internet. Sin embargo, deberían acompañar o seguir a esas figuras algunos comentarios orales o escritos. He aquí ejemplos de tales justificaciones sin palabras.  Suma de los ángulos de un triángulo La suma de los tres ángulos interiores de un triángulo es el ángulo llano.  Diferencia de dos cuadrados a
b
a
b
a-b
b
a
a
(a+b)(a‐b)=a²‐b² a
b
b
 El teorema de Viviani 4
h
Teorema : la suma de las distancias de un punto interior a un triángulo equilátero a los tres lados es igual a la longitud de la altura del triángulo.  El teorema de Pitágoras por Leonardo da Vinci De izquierda a derecha y de abajo a arriba.
Esta justificación es espectacular, pero hay que probar que el cuadrilátero de trazo pleno es efectivamente un cuadrado. He aquí, pues, una propuesta de demostración de la relación en cuestión.
5
BAC es un triángulo rectángulo; BAGD y CAFE son los cuadrados construídos sobre los lados del ángulo recto. F
G
E
Trazamos el segmento [GF]. |GF|=|BC| (isometría de los triángulos AGF y ABC) Trazamos [DA] y [AE]. D, A y E están alineados porque el ángulo DAE mide 45°+90°+45° es decir 180° (diagonales de cuadrados y triángulo rectángulo) A
D
B
C
Consideremos la imagen EG’F’D de DGFE por la simetría ortogonal cuyo eje es la mediatriz de [DE] . Toda simetría ortogonal conserva las longitudes, las áreas y las medidas de los ángulos en valor absoluto. Luego DGFE y EG’F’D tienen la misma área y por consiguiente los hexágonos BDGFEC y BDF’G’EC tienen también la misma área. Los puntos D, G y F’ están alineados pues los ángulos no orientados GDA y F’DA miden los dos 45° . Igualmente E, G’ y F están alineados. Se tiene también |F’G’|=|FG|. Pero|FG|=|BC|=|BF’|=|CG’|(triángulos isométricos). Luego |BF’|=|F’G’|=|G’C|=|BC|. F'
G'
E
A
D
P
B
F
F'
G'
G
E
A
D
B
C
Observemos el hexágono BDF’G’EC. Tracemos [BF’] y [CG’] El cuadrilátero BCG’F’ es un rombo pues sus cuatro lados son de la misma longitud (la de la hipotenusa del triángulo rectángulo BAC). C
Sea P un punto de la recta CB (ver la figura). DB y AC son perpendiculares a AB (cuadrado y triángulo rectángulo), luego DB//AC. Los ángulos PBD y PCA son isométricos (ángulos correspondientes formados por dos paralelas y una secante). Ahora bien, los ángulos BCA y BF’D son isométricos (triángulos isométricos). Los ángulos DBF’ y BF’D sont complementarios (triangulo rectángulo) luego los ángulos DBF’ y DBP también lo son. PBF’ es pues un ángulo recto, así como F’BC. 6
El rombo BCF’G’ tiene un ángulo recto y por tanto es un cuadrado. Comparando la segunda y cuarta figuras que tienen la misma área y haciendo abstracción de los dos triángulos rectángulos isométricos que aparecen en ellas, resulta que la suma de las áreas de los cuadrados construídos sobre los lados del ángulo recto de un triángulo rectángulo es igual al área del cuadrado construído sobre la hipotenusa. 7
3 – Matemáticas con palabras En el sentido estricto del título, es cierto que es posible encontrar matemáticas y desarrollar nociones de los programas utilizando diversos textos en los cuales las palabras o los conjuntos de palabras son considerados únicamente como simples objetos. He aquí un ejemplo sacado de El Burgués Gentilhombre de Molière que puede abrir el camino al análisis combinatorio. M. JOURDAIN. No, no, no, yo no quiero todo eso : yo no quiero más que lo que os he dicho : « Belle marquise, vos beaux yeux me font mourir d'amour. » MAESTRO DE FILOSOFÍA. Es preciso extender un poco el asunto. Los cinco términos que son: belle marquise ‐ vos beaux yeux ‐ me font – mourir ‐ d'amour, pueden ser permutados. Engendran así 120 anástrofes. He aquí 10. 1: (belle marquise vos beaux yeux me font mourir d'amour ) 2: (vos beaux yeux belle marquise me font mourir d'amour ) 3: (me font belle marquise vos beaux yeux mourir d'amour ) 4: (belle marquise me font vos beaux yeux mourir d'amour ) 5: (vos beaux yeux me font belle marquise mourir d'amour ) 6: (me font vos beaux yeux belle marquise mourir d'amour ) 7: (mourir belle marquise vos beaux yeux me font d'amour ) 8: (belle marquise mourir vos beaux yeux me font d'amour ) 9: (vos beaux yeux mourir belle marquise me font d'amour ) 10: (mourir vos beaux yeux belle marquise me font d'amour Naturalmente, queda el problema de construirlos todos de manera organizada y no anárquicamente. Ahí aparece la noción de algoritmo. Quizá es el momento de resolverlo en colaboración con el curso de informática. 8
4 – Las matemáticas después de las palabras Una lectura, una afirmación o una reflexión bien entendidas son a menudo ocasiones de establecer una búsqueda de lo que puede desembocar en algo creativo en el dominio matemático. Veamos un ejemplo. Es bien conocida la emisión « Cifras y letras » de las emisoras de TV, y en particular, su componente « La cuenta está bien ». El objetivo de este último juego consiste en formar, en un tiempo limitado, un número natural de 3 cifras (por tanto entre 100 y 999), utilizando las operaciones elementales (suma, resta, multiplicación y división exacta) sobre 6 números naturales sacados al azar de entre los números naturales siguientes: los que van de 1 a 10, que pueden aparecer dos veces cada uno, como máximo, más 25, 50, 75 y 100 , es decir 24 possibilidades en total que se pueden suponer equiprobables. 4‐1 La cuenta suele estar bien. Este es el título de un artículo que trata del juego, publicado en el número de marzo‐abril de 2010 del boletín n° 487 de l’APMEP (Association des Professeurs de Mathématiques de l’Enseignement Public (France)), firmado por Michel Lafond. El autor estudia este juego bajo diversos aspectos combinatorios y muestra de manera muy detallada que la probabilidad de hacer bien la cuenta es particularmente grande. Para ello, el autor calcula el número total de casos del juego, lo que no plantea gran dificultad si se dispone de elementos de análisis combinatorio. Ese número es C(24,6)X900 o sea 121 136 400. A continuación, mediante un cálculo detallado y bastante complejo demuestra que el número de casos que permiten obtener el resultado correcto es 113 554 259. La probabilidad en cuestión es pues 113 554 259/121 136 400 es decir 0,93740823567… 4‐2 Las palabras en cuestión En el transcurso de una emisión, los dos concursantes debían tratar de formar el número 864 o aproximarse a él lo más posible, con los números 2, 1, 5, 3, 1, 9. Ambos han respondido 540 efectuando (2+1)x(3+1)x5x9. 9
El presentador ha declarado entonces que 540 era efectivamente el máximo valor posible y sobre todo ha añadido con insistencia que ambos concursantes habían aplicado bien la siguiente regla « que no me canso de repetir ». « Si aparece un 1 entre los números extraídos, entonces el producto de otros
dos de los números extraídos sera el mayor posible si se suma el 1 al menor de
los dos números, antes de multiplicarlos ».
Efectivamente, en el caso de la situación propuesta es preferible calcular (2+1)x(3+1)x5x9 en vez de 2x3x(5+1)x(9+1) que vale solamente 360. Reacciones Una primera reacción consiste en preguntarse si la regla enunciada es correcta. Algunos ejemplos numéricos utilizando los números autorizados por el juego (e incluso otros) parecen ir en el sentido de una respuesta afirmativa. Y al mismo tiempo esas verificaciones numéricas nos empujan a abandonar el estricto dominio de los números utilizables en el juego y a generalizar la regla a los elementos del conjunto N de los números naturales. Es conveniente entonces recurrir a una demostración, es decir, utilizar variables que generalicen el estudi hecho. Sean dos naturales a y b tales que a £ b y el número 1 que se sumará a uno u otro antes de efectuar el producto. Comparemoss (a+1)b con a(b+1) es decir ab+b conc ab+a. Se tiene : ab = ab Y a £ b De ahí, ab + a £ ab + b O bien ab + b ³ ab + a lo que da validez a la regla enunciada. 10
5 – Las matemáticas antes de las palabras 5‐1 Puesta en situación a y b son dos números tales que a – ab + b = 0.
¿Qué significa esta igualdad? ¿Qué interpretación darle ?
Existen, desde luego, diferentes maneras de traducir esta espresión al lenguaje ordinario, transformándola. Así se utiliza la competencia de interpretación que da sentido a la escritura de la fórmula. a – ab + b = 0 se escribe como (a+b) – ab = 0 La diferencia entre la suma de dos números a y b y su producto es nula. a– ab + b = 0 se escribe también a+b = ab La suma de dos números a y b es igual a su producto. Se observará que esas expresiones no traducen en ningún modo una propiedad general de los números, sino una igualdad local. Esta situación ambigua podía evitarse enunciando : a y b son dos números tales que la diferencia entre su suma y su producto es nula. a y b son dos números tales que su suma es igual a su producto. 5‐2 Investigaciones Busquemos, en primer lugar, valores naturales de a y b. Se obtienen rápidamente los valores siguientes : a=b=0 dan a+b=0=ab y a=b=2 dan a+b=4=ab Otros ensayos dan lugar a casos interesantes que generan terminología matemática. Por ejemplo a=1 da 1 – b +b = 0 o sea 1=0 que es imposible. a no puede valer 1. La cuestión es ahora buscar si existen pares (a,b) de NxN distintos de (0,0) y (2,2) que verifiquen la igualdad. Eso exige un tratamiento matemático que constittuye una cierta forma de investigación. 5‐3 Búsqueda de pares (a,b) de NxN Vamos a expresar b en términos de a pero también sería posible escribir a en términos de b. Así aparecen las nociones de variable independiente y de variable dependiente. Sea pues a‐ab+b=0. a
. La ley de formación de b en términos Entonces a – b(a‐1) = 0 o bien a=b(a‐1) luego b 
a 1
de a es bastante simple. El denominador a‐1 no puede anularse pues a no puede valer 1. Volvemos a encontrar la condición hallada previamente. 11
Además se tiene b=a/(a‐1) o sea b=(a‐1+1)/(a‐1) 1 Es decir b=1+ 1/(a‐1) Para que b sea un número natural, es necesario que a – 1 divida a 1, lo que da a‐1=1 ó a‐1=‐1 de donde a=2 ó a=0. Las dos únicas parejas de naturales son pues (2,2) y (0,0). Esto confirma lo que habíamos hallado antes y responde a nuestra pregunta. 5‐4 Y en RxR? Todo valor de a, distinto de 1, proporciona un valor correspondiente para b. 5
3
1
1
, etc… ) (Ejemplos: a= 5 da b  , a= ‐3 da b  , a  da b 
6
4
4
3
Es claro que existen infinitas parejas (a,b) de números reales tales que
a‐ab+b=0 La tabla muestra algunas de ellas. a ‐2,00 ‐1,50 ‐1,00 ‐0,50 0,00 0,50 1,00 1,50 2,00 2,50 b 0,67.. 0,60 0,50 0,33.. 0,00 ‐1,00 3,00 2,00 1,67.. 1
La transformation de la fraction utilisée ici pourra être réinvestie dans la rencontre ultérieure d’autres notions (asymptote oblique, p. ex.).
12
5‐5 Representaciones gráficas a y b son ahora números reales. Podemos representar los valores de a sobre una recta dotada de una referencia (0,1) y los valores de b sobre otra recta igualmente dotada de otra referencia (0,1) como muestra el ejemplo que sigue. 1/2
0
3/4
5/4
1
B
2
3/2
A
-2
-3
5
3
2
1
0
-1
Llamaremos a esta dibujo una « gráfica segmentaria ». De hecho, la utilización de las flechas en vez de los segmentos sería lo mismo que establecer el grafo sagital de la función que relaciona los elementos de A con los de B. Naturalmente, es posible utilizar la representación de una gráfica cartesiana. He aquí una parte. y
5
4
3
2
1
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
6
7
8x
-1
-2
-3
NB : Aquí la función utilizada es y=f(x)=x/(x‐1) con x distinto de 1 en vez de b=f(a)=a/(a‐1) con a distinto de 1. De esta gráfica cartesiana se pueden hacer varias lecturas.  Cuánto más aumenta a, en valor absoluto, más se acerca b a 1. 13

Cuanto más se acerca a a 1, mayor es b. 5‐6 Y si … ? ¿Y si intentamos modificar el gráfico segmentario haciendo coincidir los puntos cuyas abscisas son 0 ? Esto es lo que da utilizando un programa de geometría dinámica. 1/2
0
5/4
1
3/4
B
2
3/2
A
5
3
2
1
0
-1
-2
-3
Se convierte en…. 2
B
3/2
5/4
1
3/4
1/2
0
-3
-2
-1
0
1
2
3
5
A
y … sorpresa : Todas las rectas que contienen los segmentos de esa gráfica parecen concurrir en un punto de coordenadas (1,1). La validez de esta conjetura ha de ser justificada, evidentemente. Volvamos a las notaciones tradicionales de los ejes. La función representada se define como f(x)=x/(x‐1). 14
Y
A'(0,a/(a-1))
B'(0 ,b/(b-1))
C'(0,c/(c-1))
O(0,0)
Una primera estrategia: A(a,0)
I
B(b,0)
C(c,0)
X
y
 1 es decire x + (a‐1)y =a o bien x+(a‐1)y‐a=0 a
a 1
Igualmente, BB’ tiene por ecuación x+(b‐1)y‐b=0 y CC’ tiene por ecuación x+(c‐1)y‐c=0 Ahora se demuestra que el sistema de esas tres ecuaciones lineales con dos incógnitas tiene la solución única x=1, y=1. Une segunda estrategia: Se escriben las ecuaciones de AA’ y de BB’; su intersección es I : (1,1), que verifican la ecuación de CC’’. Une tercera estrategia A :(a,0) y A’ :(0,a/(a‐1)) son las coordenadas de los extremos de un A'(0,a/(a-1))
segmento [AA’] de la gráfica segmentaria. AA’ tiene por ecuación: x + (a‐1)y – a = 0 O sea (x‐y) + a(y‐1) = 0 AA’ es pues un elemento de un haz de rectas que pasan todas por el O(0,0)
A(a,0)
xy0
punto definido por y  1  0 es decir (1,1).
AA’ tiene por ecuación : x

a

15
Otra estrategia que no precisa las ecuaciones de las rectas: Seat A:(a,0) e I: (1,1). La recta AI corta ae OY en A’. Pongamos A’: (0,b) y demostremos que entonces a‐
ab+b=0. ¡Aprovechemos la semejanza de triángulos ! Los triángulos A’OA y A’EI son semejantes b b 1
luego 
de donde : b=ab‐a o a‐ab+b=0. a
1
A'(0,b)
E(0,1)
O(0,0)
I(1,1)
D(1,0)
A(a,0)
5 ‐7 Algunas sugerencias de investigación.  ¿ Se pueden hacer coincidir otros puntos de la gráfica segmentaria y obtener la misma constante que antes ? ¿Cuáles ? 
Comparar la suma de dos números con su diferencia, 
Comparar la suma de dos números con su cociente, 
Comparar la diferencia de dos números con su producto 
Comparar la diferencia de dos números con su cociente, 
Comparar el producto de dos números con su cociente. 6 – A modo de conclusión. Avant donc que d'écrire, apprenez à penser. Selon que notre idée est plus ou moins obscure, L'expression la suit, ou moins nette, ou plus pure. Ce que l'on conçoit bien s'énonce clairement, Et les mots pour le dire arrivent aisément. Boileau (L’art poétique) Antes que a escribir, aprended a pensar. Según que nuestra idea sea más o menos oscura, La expresión la sigue, o menos neta, o más pura. Lo que se piensa bien, se enuncia claramente, Y las palabras para decirlo llegan fácilmente 16
Introducción a la teoría de grafos
A.Kiselev, Universidad Estatal de San Petersburgo, y Ekaterina Zhukova,
Universidad Estatal Electrotécnica de San Petersburgo
1. Introducción
Todos los lectores habrán visto problemas como los siguientes
Problema 1.1. En el país de Genovia hay 2013 ciudades. ¿Es posible conectarlas con carreteras de tal manera que salgan 3 carreteras de cada ciudad?
Problema 1.2. Demostrar que si 2013 personas asisten a una reunión y
algunas de ellos estrechan la mano con otras (pero no a si mismas), entonces al
…nal hay al menos dos personas que han estrechado la mano al mismo número
de personas.
Problema 1.3. Demostrar que si 2013 personas asisten a una reunión y todo
el mundo estrecha la mano a otros (pero no a sí mismo), entonces al …nal se han
producido 201322012 apretones de manos.
Todos estos problemas están relacionados con el concepto de grafo. Los
objetos de los que trata cada problema (ciudades, personas, etc) se llaman
vértices. Para hacer la situación más obvia, se pueden dibujar como puntos en
el plano. La representación visual del grafo puede ser útil para entender mejor
el concepto. Conectaremos vértices que estén relacionados entre sí (ciudades
unidas por carreteras, personas relacionadas entre sí por apretones de manos,
etc) por líneas llamadas aristas .Se verá un dibujo, parecido a un mapa o algo
similar.
Esta es una idea intuitiva de la noción de grafo. Vamos a dar ahora la
de…nición estricta para expresar la idea visual.
De…nición 1.1. Sea V cualquier conjunto …nito de vértices y sea VV el
conjunto de todos los subconjuntos de V que tengan 2 elementos. Entonces
E V V es el conjunto de las aristas. El par ordenado (V; E) es un grafo .
He aquí algunos ejemplos de grafos. El grafo tal que E = V V se dice que es
completo. El grafo tal que E = ? se dice grafo vacío o grafo nulo.
En lo que sigue, para hablar sobre vértices y aristas de grafos usaremos
alguna terminología intuitivamente entendible que exprese el enfoque visual.
Por ejemplo, la arista y el vértice perteneciente a ella se dirán incidentes. Dos
vértices a y b tales que fa; bg 2 E se dirá que están conectados por una arista
o que son adyacentes.
Necesitaremos la siguiente de…nición:
De…nición 1.2. El número de aristas incidentes con un vértice se llamará
grado del vértice.
Ahora echemos una mirada a algunas propiedades obvias de los grafos.
Teorema 1.1.El número de vértices de grado impar es un número par.
La suma de los grados de todos los vértices de un grafo es igual al número de
aristas multiplicado por 2 (un número efectivamente par), así que debe haber
un número par de términos impares en esta suma.
Teorema 1.2. En cualquier grafo hay dos vértices del mismo grado.
1
Consideremos la negación de la proposición: supongamos que todos los vértices del grafo tienen grados distintos. Puesto que puede haber grados desde 0
hasta n 1 (donde n es el número de vértices), pero no puede haber un vértice
de grado 0 y otro con grado n 1 en el mismo grafo, esto es una contradicción.
Teorema 1.3. Un grafo completo de n vértices tiene n(n2 1) aristas.
En efecto, cada vértice está conectado a otros n 1; pero cada vértice se
cuenta así dos veces.
Cada uno de los teoremas anteriores da la solución a los problemas de la
sección siguiente. Luego se proponen otros problemas de solución obvia.
Problema 1.4. Demostrar que si hay 2013 ciudades y cada ciudad está
conectada a todas las demás, entonces en total hay 201322012 carreteras entre
ellas.
Problema 1.5. Demostrar que si hay 2013 ciudades y cada una de ellas
está conectada por carretera con alguna de las demás, entonces hay al menos
dos ciudades de las que sale el mismo número de carreteras.
Problema 1.6. En Genovia hay 2013 ciudades. ¿Es posible conectarlas por
carretera de manera salgan 3, 5 ó 7 carreteras de cualquier ciudad?
Problema 1.7. ¿Existe un grafo con vértices de grados
4,4,4,3,3,2?
8,6,6,5,3,2,1,1?
7,3,3,3,3,2,2,1?
7,7,5,4,4,2,2,1?
7,6,4,3,4,4,1,2?
7,7,7,5,3,3,2,2?
De…nición 1.3. Un grafo con vértices que pueden ser distribuidos en dos
grupos de tal manera que ningún par de vértices del mismo grupo estén conectados por una arista se llama grafo bipartito.
Si el grafo bipartito es tal que toda arista permitida está en E (toda arista
entre vértices de grupos diferentes) se llamará grafo completo bipartito.
Teorema 1.4. En un grafo completo bipartito con n y m vértices en los
grupos hay nm aristas.
En efecto, todo vértice del primer grupo está conectado con m vértices, así
que hay nm aristas que salen del primer grupo. Obsérvese que así contamos
todas las aristas (una sola vez).
Problema 1.8. Vamos a considerar que algunos vértices del grafo son
azules y otros son verdes. Todo vértice azul está conectado a 5 vértices azules
y a 10 vértices verdes; y todo vértice verde está conectado a 9 vértices azules y
6 verdes. ¿Cuál es el color dominante en ese grafo?
Problema 1.9. En Genovia hay 100 ciudades y cuatro carreteras salen de
cada ciudad. ¿Cuántas carreteras hay en total?
Problema 1.10. ¿Existe una línea quebrada de 21 segmentos tal que interseque a cualquiera de esos segmentos
2
a) una vez?
b) dos veces?
c) tres veces?
Problema 1.11. En una clase hay 30 estudiantes. ¿Es posible que 9 de
ellos tengan (en la clase) 3 amigos cada uno, 11 tengan 4 amigos cada uno y 10
tengan 5 amigos cada uno?
Problema 1.12. El rey de Genovia tiene 19 vasallos. ¿Es posible que cada
vasallo tenga 1, 5 ó 9 vecinos?
Problema 1.13. En el reino de Genovia hay 3 carreteras que salen de cada
ciudad. ¿Es posible que haya 100 carreteras en Genovia?
Problema 1.14. Probar que el número de personas de entre la población
de Valladolid que han dado apretones de manos a un número impar de otros
residentes de Valladolid, es par.
Problema 1.15. Nueve personas juegan un torneo a una sola vuelta. En
un cierto momento solo hay dos jugadores que hayan jugado el mismo número
de partidas. Probar que, o bien hay un jugador que todavía no ha jugado, o
bien un jugador que ya ha jugado todas sus partidas.
Problema 1.16. Cada uno de los 102 estudiantes de un centro escolar
conoce al menos a otros 68 estudiantes. Probar que hay cuatro estudiantes que
tienen el mismo número de amistades.
Problema 1.17. Una matemática y su marido van a una reunión, en la que
hay un total de cuatro parejas. Como es normal, al llegar los participantes se
saludan dándose la mano (Nadie se da la mano a sí mismo o a la persona con la
que llega). Y no todo el mundo le da la mano a todos los demás. Pero cuando
la matemática pregunta a las otras 7 personas presentes a cuántas personas ha
dado la mano, recibe 7 respuestas diferentes. ¿A cuántas personas ha dado la
mano el marido de la matemática?
Problema 1.18. Juan, a su regreso de Disneylandia, dice que allí ha visto
un lago encantado con 7 islas, a cada una de las cuales llegan 1, 3 ó 5 puentes.
Es verdad que alguno de esos puentes debe llegar a la orilla del lago?
En nuestra introducción decíamos que la aproximación visual es bastante
apropiada para entender estos conceptos. En realidad, nuestra representación
visual del grafo, un dibujo, es un objeto que merece la pena estudiar por sí
mismo. Diferentes grafos a veces se pueden representar por la misma …gura,
o diferentes …guras pueden representar el mismo grafo. La siguiente de…nición
pretende dar más luz sobre este asunto.
De…nición 1.4. Dos grafos se llamarán isomorfos si sus vértices pueden ser
numerados de tal manera que los vértices con el mismo número está conectados
o no, simultáneamente, en ambos grafos.
Esto signi…ca que a veces uno puede considerar dos grafos como distintos
solo si no son isomorfos (y dos grafos isomorfos se consideran el mismo), aunque
3
se diga otra cosa en la de…nición de grafo que dimos antes. Los siguientes
problemas pretenden simpli…car la de…nición y ayudar a entenderla mejor.
Problema 1.19. Hágase una lista con todos los grafos no isomorfos con 4
vértices.
Problema 1.20. Hallar dos grafos con el mismo número de vértices de cada
grado que no sean isomorfos.
Problema 1.21. ¿Es verdad que dos grafos deben ser isomorfos, si
a) ambos tienen 10 vértices y el grado de cada uno es 9?
b) ambos tienen 8 vértices y el grado de cada uno es 3?
2. Conectividad
Como se puede observar de la Introducción, la noción de grafo puede representarse en forma visual. Dijimos que dibujar un grafo tiene algunas desventajas
relacionadas con un grafo equivalente, pero aún asi, varios conceptos y proposiciones sobre grafos en teoría de grafos provienen de la experiencia práctica,
deducidos de la intuición y obvios para las …guras.
Uno de esos conceptos es la conectividad. Ante todo, necesitamos algunas
de…niciones que son intuitivamente claras.
De…nición 2.1. Una sucesión de vértices, en la que cada dos vértices consecutivos están conectados por una arista, se llama ruta.
Visualmente, esta de…nición signi…ca que se empiezan a conectar vértices en
un cierto orden; se elige siempre el siguiente vértice de modo que sea adyacente
al anterior.
De…nición 2.2. Una ruta en la que el primer y el último vértice coinciden,
se llamará cerrada.
Si el vértice a está en la ruta, se dice que la ruta pasa por el vértice a. Si
los vértices a y b son consecutivos en la ruta, se dice que la ruta contiene a la
arista fa; bg.
De…nición 2.3. Una ruta que contiene cada arista no más de una vez, se
llama camino.
Es claro que cualquier camino es una ruta por la de…nición anterior. Pero
antes, en nuestro dibujo, se pueden conectar vértices en cualquier orden posible,
se permite usar cualquier arista dos veces, o tres, o más. Ahora sólo se puede
usar cada arista una vez. Esta es la diferencia entre ruta y camino. Tampoco
es obligatorio usar todas las aristas.
De…nición 2.4. Una ruta cerrada que además es un camino, se llama ciclo.
Si existe una ruta en la que el vértice a es el primero y el vértice b es el
último, se dice que los vértices a y b están conectados por la ruta. La misma
terminología se usa para caminos. En efecto, si los vértices están conectados
por un camino, también lo están por una ruta (es obvio que cualquier camino
es también una ruta). Se puede observar que el recíproco es también cierto: si
los vértices están conectados por la ruta, también lo están por el camino.
4
De…nición 2.5. La componente de conectividad de un vértice es un conjunto de vértices para los cuales existe un camino que los conecta con el vértice
dado.
Se debe observar que las componentes de conectividad de dos vértices diferentes o son iguales o son disjuntos. En efecto, si los consideramos conjuntamente
obtendremos que deben ser iguales en ese caso. Recordemos siempre la representación visual del grafo que introdujimos antes. Úsese para conseguir una
visualización más clara.
Problema 2.1. Se considera el "grafo del al…l": V es el conjunto de las
casillas del tablero de ajedrez y E está formado por los pares de tales casillas
tales que el al…l puede moverse de una a otra en un movimiento. ¿Cuántas
componentes de conectividad hay en este grafo?
De…nición 2.6. Un grafo con una única componente de conectividad se
llama un grafo conexo.
Hay otros grafos relacionados con el ajedrez construídos de esta manera:
"grafo del rey", "grafo de la reina", "grafo del caballo", "grafo de la torre" - y
obsérvese que todos son conexos.
Problema 2.2. Considérese el "grafo del caballo" en un tablero n n.
Hallar valores de n para los que el grafo no es conexo.
La de…nición 2.6 con…rma una vez más nuestro punto de vista intuitivo del
grafo. Un grafo es conexo si y solamente si existe un camino entre cualesquiera
vértices en él. Visualmente signi…ca que se puede trazar una línea quebrada
usando aristas como segmentos entre cualquier par de vértices. Así en este
aspecto, dos vértices cualesquiera están "conectados".
Hay una condición simple para que el grafo sea conexo, expresada en términos del número de aristas:
Teorema 2.1. Sea n el número de vértices de un grafo. Si el número de
2)
, entonces el grafo es conexo.
aristas es mayor que (n 1)(n
2
Supongamos que hay al menos dos componentes de conectividad en el grafo
dado. Sea k el número de vértices en una de las componentes, y por tanto, n k
vértices en la otra. El máximo número de aristas cuando hay dos componentes
de conectividad es cuando ambos son grafos completos. Por lo tanto, el número
de aristas en el grafo entero es k(k2 1) + (n k)(n2 k 1) que no es mayor que
(n 1)(n 2)
: Esto es una contradicción, así que el grafo es conexo.
2
También se puede observar que si hay menos de n 2 aristas en el grafo,
no es conexo. Luego cualquier grafo con n vértices debe tener al menos n 1
aristas para ser conexo. Más adelante estudiaremos algunos grafos interesantes
con exactamente n 1 aristas.
Ahora, algunos problemas relativos a la conectividad.
Problema 2.3. Un grafo tiene 100 vértices y el grado de cada vértice es
por lo menos 50. Probar que el grafo es conexo.
Problema 2.4. En un grafo conexo, el grado de 4 de los vértices es 3 y
el de los demás vértices es 4. Probar que no se puede borrar una arista de tal
manera que el grafo se dividaen dos componentes de conectividad isomorfos.
5
De…nición 2.7.Una arista tal que al borrarla aumenta el número de componentes de conectividad de un grafo se llama puente.
Problema 2.5. Hay 10 vértices en un grafo y exactamente dos de sus aristas
son puentes. ¿Cuál es el máximo número de aristas en este grafo?
Problema 2.6. ¿Es verdad que dos grafos tienen que ser isomorfos si ambos
son conexos, sin ciclos y tienen 6 aristas?
Problema 2.7. En el reino de Genovia salen 100 carreteras de cada ciudad
y se puede viajar por ellas de cualquier ciudad a otra. Se cierra una carretera por
obras de reparación. Probar que se sigue pudiendo viajar de cualquier ciudad a
cualquier otra.
3 Caminos y ciclos Eulerianos
En nuestra infancia intentábamos dibujar …guras sin levantar el lápiz del
papel. Algunas veces se podía, y otras no. Por ejemplo, no es posible dibujar
un sobre cerrado (que se ve como un rectángulo con sus diagonales) sin levantar
el lápiz del papel, pero sí se puede dibujar un sobre abierto.
He aquí el conocido problema de los puentes de Königsberg
La ciudad de Königsberg en Prusia Oriental (hoy Kaliningrado, Rusia) está
construída en ambas orillas del río Pregel, que forma dos grandes islas conectadas entre sí y con las orillas del río por medio de siete puentes. El problema
era encontrar un camino que cruzase cada puente una vez y solamente una. Las
islas no se podían alcanzar de ninguna forma que no fuera por los puentes; y
cada puente debía cruzarse por completo cada vez: no se podía dar media vuelta
al llegar a la mitad del puente. El camino no tenía por qué empezar y terminar
en el mismo sitio. Leonhard Euler demostró que el problema no tenía solución.
Veremos a continuación el criterio para saber si tal camino es posible.
De…nición 3.1.Un camino que visite cada arista exactamente una vez se
llama camino euleriano.
De…nición 3.2. Un ciclo que visite cada arista exactamente una vez se
llama ciclo euleriano.
El siguiente teorema es el criterio de existencia de un ciclo euleriano en un
grafo conexo, que fué introducido por primera vez por Euler cuando intentaba
resolver el problema de los puentes de Königsberg.
6
Teorema 3.1. Existe un ciclo euleriano en un grafo conexo si y solamente
si todos los vértices tienen grado par.
Supongamos que en el grafo existe un ciclo euleriano. Cada vez que el ciclo
visita un vértice, hay dos aristas incidentes con el vértice. Luego el grado de
cada vértice ha de ser par.
Recíproco: Supongamos que todos los vértices tienen grado par. Construyamos un ciclo A que visite cada arista solamente una vez (pero que tal
vez no visite todas las aristas del grafo).Si quedara alguna arista que el ciclo
A no visite, consideremos un vértice c que visite el ciclo A pero que no visite
alguna de las aristas incidentes con el vértice c: Es posible construir un ciclo
B que empiece y termine en c tal que A no visite ninguna de las aristas de
B. Ahora consideremos un ciclo D que sea la unión de A y B (el ciclo B está
"incluído" en el ciclo A). Obsérvese que D sigue visitando cada una de sus
aristassolamente una vez y es más largo que A. Si siguieran quedando aristas,
el proceso se puede repetir, pero no puede ser in…nito porque el conjunto de
aristas es …nito. Al …nal tenemos un ciclo euleriano.
También hay el criterio de existencia de camino euleriano en un grafo conexo
que formulamos a continuación.
Teorema 3.2. Existe un camino euleriano (pero no ciclo) en un grafo conexo
si y solamente si todos los vértices, salvo dos, tienen grado par y esos dos tienen
grado impar.
La demostración es bastante similar a la anterior. El camino euleriano empieza y termina en un vértice de grado impar.
Problema 3.1. Probar que un grafo conexo con 2n vértices de grado impar
puede trazarse sin dibujar ninguna arista más de una vez y de tal manera que
el lápiz se levante del papel exactamente n 1 veces.
Problema 3.2. Hay 100 círculos formando una …gura conexa en el plano.
Demostrar que esta …gura se puede dibujar sin levantar el lápiz del papel o
dibujando cualquier parte de cualquier círculo dos veces.
Problema 3.3. En la ciudad de Tiro hay 7 islas. Hay 3 puentes entre 2
islas, 3 puentes entre 4 islas y 4 puentes desde la última. ¿Es posible recorrer
la ciudad visitando cada puente una vez y solamente una?
Problema 3.4. Hallar valores de n tales que sea posible dibujar un polígono
de n lados con todas sus diagonales sin levantar el lápiz del papel.
Problema 3.5. a) Un trozo de cable mide 120 cm de largo. ¿Se puede usar
para formar las aristas de un cubo, que midan 10cm cada una?
b) ¿Cuál es el menor número de cortes que hay que hacer en el cable para
poder formar ese cubo?
Problema 3.6. ¿Es posible contruir una red con 5 5 nudos a partir de 5
líneas quebrads de longitud 8?
Problema 3.7. ¿Es posible construir una red de 5 5 nudos a partir de
ocho líneas quebradas de longitud 5?
7
4 Camino y ciclo hamiltoniano
En paralelo al contenido de la sección anterior, vamos a tratar ahora de los
caminos y ciclos hamiltonianos, que visitan cada vértice del grafo una vez y
solamente una.
De…nición 4.1. En un grafo, un camino que pasa por cada vértice exactamente una vez se llama hamiltoniano.
De…nición 4.2. En un grafo, un ciclo que pasa por cada vértice (excepto
uno, en el que empieza y termina) exactamente una vez, se llama hamiltoniano.
De…nición 4.3. Un grafo se llama hamiltoniano si existe un ciclo hamiltoniano en él.
No hay criterios de existencia de caminos y ciclos hamiltonianos, sino sólo
condiciones necesarias. Los enunciados correspondientes van a continuación. Su
uso práctico es casi inexistente y sus demostraciones son bastante complicadas
y no las incluiremos aquí. El lector interesado puede consultar los títulos [3] y
[4] de la Bibliografía.
Teorema 4.1. (Dirac, 1952)Un grafo con n vértices (n 3) es hamiltoniano
si cada vértice tiene grado n2 o mayor.
Teorema 4.2. (Ore, 1960) Un grafo con n vértices (n 3) es hamiltoniano
si, para cada par de vértices no adyacentes, la suma de sus grados en n o mayor.
Para formular el siguiente teorema necesitamos el concepto de clausura de un
grafo. Dado un grafo G con n vértices, la clausura de G, cl(G), se construye de
manera unívoca a partir de G, añadiendo repetidamente una nueva arista fu; vg
que conecte dos vértices no adyacentes u y v con grado(u) +grado(v) n, hasta
que no puedan encontrarse más pares con esta propiedad.
Teorema 4.3. (Bondy-Chvátal, 1972) Un grafo es hamiltoniano si y solamente si su clausura es hamiltoniana.
Problema 4.1. Dado el tablero 4 4 sin las casillas de las 4 esquinas,
¿es posible que el caballo de ajedrez visite cada casilla exactamente una vez y
vuelva?
Problema 4.2. ¿Existe un ciclo hamiltoniano en el grafo del caballo de
ajedrez en el tablero 5 5?
Problema 4.3. ¿Existe un ciclo hamiltoniano en el grafo de la torre, del
al…l, de la reina y del caballo en el tablero de ajedrez tradicional?
Problema 4.4. Se considera el siguiente grafo: sus vértices son los vértices
de un cubo y los centros de las caras; sus aristas son las diagonales (o sea, las
aristas del cubo no son aristas en este grafo). ¿Existe un ciclo hamiltoniano en
este grafo?
5 Árboles
De…nición 5.1. Un grafo conexo sin ciclos se llama un árbol.
8
De…nición 5.2. Un grafo conexo tal que todas sus aristas son puentes es
un árbol.
De…nición 5.3. Un grafo en el que existe exactamente un camino entre
cada par de vértices es un árbol.
Como hemos dado tres de…niciones diferentes del mismo objeto, debemos
probar que todas de…nen el mismo objeto, pues si no, no las podríamos utilizar:
Teorema 5.1. Las tres de…niciones de árbol son equivalentes.
Consideremos un árbol dado por la primera de…nición y probemos que cumple
la tercera. Supongamos que el grafo G no tiene ciclos. Enteonces en efecto todos
los vértices están conectados por un camino - existe al menos uno (G es conexo)
y si existieran al menos dos diferentes habría un ciclo.
Ahora tomemos un árbol según la tercera de…nición y probemos que cumple
la segunda. El grafo G es conexo por de…nición. Supongamos que G es tal que
existe exactamente un camino entre cada par de vértices. Tomemos la arista
fa; bg. Observemos que si no es un puente, existiría un camino diferente entre
los vértices a y b, ya que G sin fa; bg sigue siendo conexo. Luego toda arista es
un puente.
Finalmente, tomemos un árbol según la segunda de…nición y probemos que
cumple la primera. Supongamos que cada arista de G es un puente. Entonces
efectivamente no hay ciclos en G, porque si C fuera un ciclo entonces ninguna
arista de C sería un puente.
Ya que hemos de…nido bien la noción de árbol, usaremos en lo que sigue
cualquiera de las 3 de…niciones a nuestra conveniencia.
Veamos algunas propiedades importantes de los árboles.
Teorema 5.2. En cualquier árbol existe un vértice de grado 1.
Consideremos el camino P más largo del árbol G: Ese camino existe, porque
como entre dos vértices cualesquiera, existe siempre un camino, no puede haber
más de n(n2 1) caminos en G; que es …nito. Si hubiera varios de la máxima
longitud, elegimos uno cualquiera de ellos. Marcamos el último vértice, b; en
ese camino. Si el grado de b fuera mayor que 1, podríamos prolongar el camino
usando otra arista incidente con b: Esto contradice la hipótesis sobre la maximalidad de P:
De hecho, en´un árbol hay al menos dos vértices de grado 1. Se puede probar
fácilmente esto a partir de la demostración del teorema anterior.
Observemos que hay un grafo conexo "mínimo" - en el sentido de que tiene
el menor número de aristas para el número dado de vértices. Antes vimos que
cualquier grafo con n vértices y menos de n 1 aristas no es conexo.
Teorema 5.3. En cualquier árbol con n vértices hay n 1 aristas.
Sea m el número de aristas en el árbol G de n vértices. Por el teorema
anterior, existe un vértice a de grado 1 en G: Consideremos G1 , que va a ser G
9
sin el vértice a y sin la única arista incidente con a: Obviamente, en G1 hay n 1
vértices y m 1 aristas; sigue siendo conexo y no tiene ciclos. Así construímos
una cadena de árboles en la que cada Gk es Gk 1 sin el vértice de grado 1 y
sin la única arista incidente en él. El último, Gn 1 ; tiene sólo dos vértices y
m (n 2) aristas. Pero el único árbol (el único grafo conexo) con dos vértices
tiene solamente una arista. Por tanto m (n 2) = 1; es decir, m = n 1:
Así, es obvio que en cualquier grafo conexo con n vértices debe haber al
menos n 1 arista, como dijimos antes sin demostración.
Problema 5.1. En un país encantado hay 239 ciudades y dos ciudades cualesquiera están unidas por una carretera y solamente una. ¿Cuántas carreteras
hay allí?
Problema 5.2. El rey Guidon tiene 3 hijos. Tiene un total de 93 descendientes; algunos de ellos tienen 2 hijos y otros ni se han casado ni tienen hijos.
¿cuántos de sus descendientes no se han casado?
Problema 5.3. Tenemos 5 cajas. Dentro de algunas de ellas hay otras 5
cajas (de menor tamaño), y así sucesivamente. En total hay 12 cajas no vacías.
¿Cuántas cajas hay en total?
Problema 5.4. La diabólica reina del ajedrez edi…ca muros entre todos los
escaques del tablero. ¿Cuál es el menor número de muros que hay que derribar
para que la torre pueda visitar todos los escaques?
Problema 5.5. Una red de volleyball tiene un retículo rectangular de
dimensiones 50 600. El gamberro Xavi corta sus hilos unidad. ¿Cuál es el
máximo número de hilos unidad que puede cortar antes de que la red se rompa
en dos o más trozos?
Esta última proposición es bastante fácil de formular de manera formal y
tiene su importancia en aplicaciones de la teoría de grafos, así que merece la
pena discutirla.
Teorema 5.4. Para todo grafo G = (V; E), existe un árbol T = (V; E ) tal
que E
E: Además, si n es el número de vértices de G y N es el número
de aristas, entonces hay que borrar exactamente N n + 1 aristas de E para
obtener E :
Problema 5.6. En el reino de Genovia hay 30 ciudades. Cada una de
ellas está unida a cualquier otra por una única carretera. ¿Cuál es el máximo
número de carreteras que se pueden cerrar de manera que siga pudiéndose ir de
cualquier ciudad a cualquier otra?
Problema 5.7. Probar que en cualquier grafo conexo es posible borrar un
vértice, junto con todas las aristas que salen de él, de manera que el grafo así
obtenido siga siendo conexo.
Problema 5.8. El mapa del metro de Tiro es un grafo conexo. Demostrar
que el alcalde de Tiro puede cerrar una estación, y todas las líneas de metro que
llegan a ella desde estaciones contiguas de forma que lo que quede siga siendo
conexo.
6 Grafos binarios coloreados
10
Problema 6.1. En el valle del río Amazonas hay 5 poblados. Dos cualesquiera de ellos están conectados por senderos selváticos o por el río, pero no
por ambas cosas al mismo tiempo. Además, de entre tres poblados cualesquiera,
existe un par conectados por el río y un par conectados por sendero. Probar que
es posible completar un viaje empezando y terminando en el mismo poblado,
visitando los 5 poblados (cada uno de ellos solamente una vez) y usando solamente senderos o la ruta ‡uvial.
Problema 6.2. En el valle del río Mississippi hay 6 poblados. Dos cualesquiera de ellos están conectados por senderos o por el río, pero no por los dos
medios simultáneamente. Probar que los 6 poblados no se pueden conectar de
tal manera que entre tres cualesquiera de ellos existan dos conectados por el río
y dos conectados por senderos.
Resolveremos primero el segundo problema. Llamemos A a uno de los poblados. Existen al menos tres rutas ‡uviales o senderos desde él (porque si hubiera
menos de dos senderos o menos de 2 rutas ‡uviales, entonces A no se podría
conectar con cualquier otro poblado). Tratemos el caso de al menos 3 senderos.
Razonemos por contradicción: los poblados se conectarían como se indica en
el enunciado. Entonces, cualquier par de tres poblados conectados con A por
senderos deberían estar conectados por rutas ‡uviales, lo cual es una contradicción.
El caso de al menos 3 rutas ‡uviales se analiza de manera análoga.
Ahora vamos con el primer problema. De la solución del segundo se deduce
que debe haber exactamente dos senderos y exactamente dos rutas ‡uviales
desde cualquier poblado. Entonces se puede fácilmente deducir que es posible
completar el viaje en la forma que se indica.
Por último, de…namos la noción en cuestión: el grafo binario coloreado.
De…nición 6.1. Un grafo completo, cada una de cuyas aristas es de uno de
dos colores, se llama grafo binario coloreado.
Problema 6.3. Supongamos que seis personas son citadas, aleatoriamente,
para formar parte de un Jurado. Probar que o bien tres de ellas se conocen
mutuamente, o bien tres de ellas no se conocen mutuamente.
Problema 6.4. Supongamos que nueve personas son citadas, aleatoriamente, para formar parte de un Jurado. Se sabe que ninguna terna de ellas está
formada por personas que no se conocen entre sí. Demostrar que cuatro de ellas
se conocen mutuamente.
Problema 6.5. Supongamos que 18 personas han sido citadas, aleatoriamente, para formar parte de un Jurado. Probar que, o bien cuatro de ellas se
conocen mutuamente o bien cuatro de ellas no se conocen mutuamente.
Problema 6.6. En el reino de Genovia las ciudades están conectadas por
carretera o por tren. El ministro de Transportes introduce líneas de autobús
entre aquellos pares de ciudades que no están conectadas por tren. Probar que
11
es posible llegar a cualquier ciudad desde cualquier otra usando solamente un
tipo de transporte.
Soluciones de los problemas
1.1 a 1.6 están resueltos en el texto.
1.7. El primer grafo es fácil de dibujar. Sea V = fa; b; c; d; e; f g y
E = ffa; bg ; fa; cg ; fa; dg ; fa; eg ; fb; cg ; fb; dg ; fb:eg ; fc; dg ; fc; f g ; fe; f gg :
El segundo grafo no existe porque el máximo grado en el grafo con 8 vértices
es 7 y no puede ser 8.
El tercer grafo existe: V = fa; b; c; d; e; f; g; hg y
E = ffa; bg ; fa; cg ; fa; dg ; fa; eg ; fa; f g ; fa; gg ; fa; hg ; fb; cg ; fb:eg ; fc; dg ; fd; eg ; ff; ggg :
El cuarto grafo no existe pues dos vértices deben estar conctados con los
demás, con lo que los grados de estos demás vértices deben ser al menos 2, así
que no puede haber un vértice de grado 1.
El sexto grafo no existe por la misma razón: tres vértices han de estar
conectados con cualesquiera otros, luego los grados de estos deben ser al menos
3 y no puede haber un vértice de grado 2.
El quinto grafo no existe porque hay tres vértices de grado impar, lo que
contradice el teorema 1.3.
1.8. Olvidémonos de las aristas que conectan vértices del mismo color. Así
tenemos un grafo bipartito. Contemos sus aristas. Sea g el número de vértices
verdes y b el número de vértices azules. Por una parte, hay 9g aristas (todo
vértice verde está conectado a 9 azules); por otro lado, debe ser igual a 10b
(todo vértice azul está unido a 10 verdes). Como 9g = 10b; debe ser b menor
que g, luego predomina el color verde.
1.9. Si hay 100 ciudades y 4 carreteras llegando a cada una, hay 400 …nales
de carreteras: luego hay 200 carreteras.
1.10. a) y c). Consideremos el grafo cuyos vértices son los segmentos de la
línea quebrada y las aristas conectan aquellos pares que se intersecan mutuamente. Tenemos 21 vértices de grado 1 (en a)) o 3 (en c)). Eso contradice el
teorema 1.1.
b) Consideremos la siguiente situación: hay 21 puntos en el círculo, numerados en el sentido horario. Conectamos el punto No 1 con el No 3, el No 2 con el
No 4, ... , No 19 con el No 21, el No 20 con el No 1, el No 21 con el No 2. Se
observa fácilmente que esta es la quebrada buscada.
1.11. Si fuera posible, entonces también sería posible dibujar un grafo con 30
vértices (los estudiantes), nueve de los cuales tienen grado 3, once tienen grado
4 y diez tienen grado 5 (conectando "amistosamente" los vértices con aristas).
Sin embargo, tal grafo tendría 19 vértices con grados impares, lo que contradice
el teorema 1.3.
12
1.12. Considermos un grafo en el que los vasallos son los vértices y los que
sean vecinos se conectan por una arista. Ese grafo tendría 19 vértices de grado
impar, contradiciendo el teorema 1.3.
1.13. Sea n el número de ciudades en Genovia. Entonces hay 3n
2 carreteras.
Si fuera igual a 100, resultaría que 200 sería divisible por 3, lo cual es falso. Por
tanto no puede haber 100 carreteras en Genovia.
1.14. Es la situación del teorema 1.1 para un grafo en el que V es el conjunto
de los habitantes de Valladolid y E es el conjunto de pares de elementos de V
que han estrechado sus manos,
1.15. Si sólo hay 2 jugadores que han jugado el mismo número de partidas,
habría exactamente 8 números diferentes de partidas jugadas por los jugadores.
Pero si nadie ha jugado 0 u 8 partidas, no puede haber más de 7 números
diferentes.
1.16. Todo estudiante conoce a otros 68, 69,...,101; en total hay 33 oportunidades. Si no hay más de 3 estudiantes que tengan el mismo número de
conocidos, entonces no hay más de 99 estudiantes. Por lo tanto, debe haber al
menos 4 con el mismo número de conocidos.
1.17. Como cualesquiera 7 personas dan diferentes respuestas, esas respuestas varían de 0 a 6, porque nadie puede estrechar menos de 0 ó más de 6 manos.
Si alguna persona estrecha 6 manos, entonces la única persona que estrecha 0
manos puede ser su cónyuge. Entonces, si alguna persona estrecha 5 manos, la
única persona que estrecha 1 mano ha de ser su cónyuge. Lo mismo para 4 y 2.
Entonces, el único número disponible para el marido de la matemática es 3.
1.18. Si ningún puente conduce a la costa, entonces existiría un grafo (donde
V es el conjunto de islas y E el conjunto de puentes que las conectan) con 7
vértices de grado impar, lo que contradice el teorema 1.1.
1.19. He aquí los 11 grafos existentes
1.20. Ver la solución del siguiente problema, apartado b).
1.21. a) Tales grafos son completos, luego en efecto todos son isomór…cos.
b) Consideremos los siguientes grafos de 8 vértices. Numeramos los vértices
de 1 a 8. Las aristas de uno de los grafos conectan el vértice 1 con el 2, el 2 con
el 3, ... , el 7 con el 8 y el 8 con el 1, el 1 con el 5, el 2 con el 6, el 3 con el 7 y
el 4 con el 8.
El otro grafo consiste en dos grafos completos de vértices 1,2,3,4 y 5,6,7,8.
Ambos grafos no son isomorfos.
2.1. Es bastante obvio que ningún al…l cambia el color de los escaques; el
al…l visita escaques del mismo color. Por lo tanto, habrá dos componentes de
conectividad: "blanca" y "negra".
2.2. Se comprueba sin di…cultad que n = 2 y n = 3 da grafos no conexos
(si n = 2 no hay aristas en el grafo de 4 vértices, si n = 3 no hay ningún
cuadrado conectado con la casilla central), n = 1 y n = 4 dan grafos conexos.
Entonces es claro ampliar el tablero (n 1) (n 1) hacia la derecha y hacia
abajo (obteniendo un tablero n n) con cada nuevo escaque añadido conectado
a alguno de los anteriores.
13
2.3. Razonemos por contradicción: supongamos que hay al menos dos componentes de conectividad en el grafo. Supongamos que los vértices a y b están
en componentes diferentes. No pueden ser adyacentes a los mismos vértices,
así que debe haber al menos 51 vértices más en la primera componente y otros
tantos en la segunda. Entonces hay al menos 102 vértices en el grafo, lo que
contradice el que en el grafo haya 100.
2.4. Razonemos por contradicción: Debe haber un número par de vértices
del mismo grado. Entonces habrá 0 ó 2 vértices de grado 2. En el primer caso
hay 2 vértices de grado 3 y en el segundo 6. Luego en ambas componentes
isomorfas hay 1 (ó 3) vértices de grado 3; cualquier otro vértice tiene grado 2 ó
4, lo que contradice el Teorema 1.1.
2.5. Excluyamos ambos puentes del grafo. Entonces hay 3 componentes de
conectividad. El máximo número de aristas estará en el grafo completo de 8
vértices y 2 vértices solitarios. Esto da 28 aristas. Por tanto en total hay 30
aristas en el grafo.
2.6. Consideremos los dod grafos siguientes: uno consta de 7 vértices conectados en …la; el otro, 7 vértices de tal forma que uno de ellos esté conectado a
todos los demás. Obviamente esos dos grafos no son isomorfos.
2.7. Se requiere demostrar que ninguna arista en tal grafo es un puente,
así que su supresión no afecta a la conectividad. Razonemos por contradicción:
sea fu; vg el puente; quitándolo descompone el grafo en dos componentes de
conectividad. Pero el número de …nales de arista (…nales de carretera) en ambas
componentes es impar, lo cual es imposible.
3.1. La demostración es similar a la del teorema 3.1.
3.2. Consideremos un grafo cuyos vértices son puntos de intersección de
circunferencias y las aristas, los arcos de circunferencia entre esos puntos. El
14
grado de cada vértice es par (cada circunferencia da dos aristas a cada punto
de intersección). Entonces existe un ciclo euleriano.
3.3. Hay 4 vértices de grado impar, lo cual contradice los teoremas 3.1 y 3.2.
3.4. Es fácil observar que el grado de cada vértice es n 1; y debe ser par
por el teorema3.1. Luego es posible dibujar tal polígono, si y sólo si n es impar.
3.5. a) La longitud total del cable es igual a la suma de las longitudes de
las aristas del cubo. Luego necesitamos que exista un ciclo euleriano, pero no
puede ser que el grado de cada vértice sea 3.
b) Como hemos observado, tenemos 8 vértices de grado 3. Luego por el
problema 3.1, necesitamos 3 cortes. Es decir, podemos cortar tres trozos de 10
cm del cable.
3.6. Es claro que hay 12 nudos (los vértices del grafo) de grado 3, así que
debe haber, por lo menos, 6 líneas quebradas.
3.7. Es posible y no es difícil de dibujar.
4.1. Consideremos el tablero como el tablero de ajedrez standard usando las
letras a,b,c,d y los números 1,2,3,4. Las esquinas del tablero (que no pertenecen
al grafo) son a1,a4, d1, d4. Entonces el ciclo siguiente
d3
b2
c4
d2
b3
c1
a2
c3
b1
a3
c2
b4
d3
es un ciclo hamiltoniano.
4.2. No, ese ciclo no es hamiltoniano. Como el movimiento del caballo es
entre casillas de diferente color, todo ciclo debe tener longitud par. Pero el
tablero tiene 25 casillas, así que todo posible ciclo hamiltoniano dbería tener
longitud impar de 25. Esto es una contradicción.
4.3. El grafo del al…l, como sabemos por el problema 2.1, no es conexo, así
que no puede ser ni camino ni ciclo hamiltoniano (aunque haya ciclos hamiltonianos en las dos componentes de conectividad). Considermos el tablero etiquetado por las letras a,b,c,d,e,f,g,h y por los números 1,2,3,4,5,6,7,8. Un ciclo
hamiltoniano en el grafo de la torre o en el de la reina no son difíciles de construir
(de hecho, el mismo grafo de la torre sirve para el de la reina). El siguiente ciclo
es hamiltoniano para ambos:
a1 a2:::a8 b8:::b2 c2:::c8 d8:::d2 e2:::e8 f 8:::f 2 g2:::g8 h8:::h1 g1:::b1 a1:
El siguiente ciclo es hamiltoniano para el grafo del caballo:
a1
c2
a3
b5
a7
c8
d6
c4
e5
f7
h8
g6
h4
c1
e2
g1
f3
d2
b1
c3
a2
b4
a6
b8
d7
c5
g7
h5
g3
h1
f2
h3
g5
h7
f8
b2
d1
e3
f1
h2
g4
h6
g8
e7
e6
f5
f4
d4
d5
c6
c7
d8
g2
e4
a8
b7
e1
d3
f6
e8
b6
a5
4.4. Obsérvese que toda arista conecta vértices de tipo diferente - "vérticevértice" con "vértice-centro". Luego si existiera un camino o ciclo hamiltonianoentonces el número de "vértices-vértices" y el número de "vértices-centros"
15
a4
b3
a1:
debería ser igual o diferir en no más de 1. Pero el grafo tiene 8 vértice-vértices
y 6 vértices-centros.
5.1. El mapa de carreteras es, por de…nición, un árbol (solamente un camino
conecta cada par de ciudades-vértices.. Por lo tanto hay 238 aristas-carreteras.
5.2. El árbol genealógico de Guidon es un árbol (en el sentido de los grafos)es conexo y no hay ciclos en él. Contemos el número de sus aristas. Por un lado
son 93 (el número de vértices menos 1). Por otro lado es igual al doble de los que
tienen 2 hijos, más 3. Si x es el número de descendientes solteros, entonces el
número de los que tienen 2 hijos es 93 x y resulta entonces 2 (93 x) + 3 = 93;
de donde x = 45:
5.3. Construyamos un grafo cuyos vértices son las cajas, y sus aristas
conectan dos cajas tales que una está dentro de otra. Es útil introducir una
caja imaginaria en la que están las 5 cajas. Entonces, el grafo así construído es
un árbol. Así, podemos contar el número de aristas en este grafo. Es igual a
13 5 = 65:El número de cajas reales es igual al número de aristas (toda caja,
salvo la imaginaria, está dentro de alguna otra). Por lo tanto hay 65 cajas.
5.4. Construyamos el grafo de la torre. Al principio está vacío, porque
todo par de escaques está separado por el muro. El menor número de muros
derribados es el mismo que el de aristas en el árbol de 64 vértices, que es 63.
5.5. Consideremos esta red de volleyball como un grafo. Sus nudos son los
vértices, y las arsitas son las cuerdas. Nuestro objetivo es borrar tantas aristas
como sea posible, manteniendo el grafo conexo. borramos las aristas de una en
una, tantas como se pueda. Obsérvese que si el grafo tiene un ciclo, entonces
podemos borrar cualquiera de las aristas de este ciclo. Pero un grafo conexo sin
ciclos es un árbol - es decir, cuando hayamos obtenido un árbol, ¡no podemos
borrar ninguna más de las aristas del grafo!. Calculemos el número de aristas
en nuestro grafo en este momento …nal. El número de vértices es el mismo que
al principio - es decir, es igual a 51 601 = 30651: Por otro lado, un árbol
con tantos vértices debe tener 30651 1 = 30650 aristas. Al principio había
601 50 + 600 51 = 60650 aristas. Luego no se pueden borrar más de 30000
aristas, y es fácil ver como se puede conseguir esto.
5.6. Tenemos un grafo completo y la situación tras cerrar tantas carreteras
como se pueda la expresamos en términos de árboles. Por el teorema 5.4 sabemos
que es posible cerrar 30229 30 + 1 = 406 carreteras.
5.7. En cualquier grafo conexo hay un sub-árbol (Teorema 5.4). En el árbol
existe un vértice de grado 1 (Teorema 5.2). Podemos quitar este vértice, y lo que
queda sigue siendo un grafo conexo. Después restauramos otras aristas (excepto
las que llevan al vértice borrado), y la conectividad se mantiene.
5.8. Es la reformulación de 5.7 en términos "sociales".
6.1 a 6.2 se discutieron en la sección correspondiente.
6.3. En lenguaje formal, tenemos un grafo binario coloreado donde el color
1 es "se conocen" y el color 2 es "no se conocen"; y hay que probar la existencia
de un triángulo monocromático. Consideremos el vértice a; al menos tiene tres
aristas del mismo color (digamos color 1) incidentes con él. Sean b; c; d los tres
vértices conectados a a por esas aristas. Las aristas fb; cg ; fc; dg y fb; dg no
pueden tener el mismo color (ya que entonces tendríamos un triángulo de color
16
1). Pero así hemos obtenido un triángulo de color 2.
6.4. En lenguaje formal, tenemos un grafo binario coloreado donde el color
1 es "se conocen" y el color 2 es "no se conocen"; no hay un triángulo de color
2, y hemos de probar la existencia de un rectángulo de color 1 con diagonales.
Consideremos el vértice a.
Si existen al menos 4 aristas de color 2 (conectando a con los vértices
b; c; d; e), entonces toda arista que conecte los vértices b; c; d; e debe ser de color
1 y tenemos el problema resuelto.
Si existen al menos 6 aristas de color 1 (conectando a con otros seis vértices),
entonces consideramos el grafo con esos vértices. Hay un triángulo de color 1
(por el problema 6.3). Incluyendo a a se obtiene un rectángulo con diagonales.
El único caso que queda es el siguiente: no hay más de 3 aristas de color
2 y no más de 5 de color 1. Como el grado es igual a 8, hay exactamente 3
aristas de color 2 y exactamente 5 aristas de color 1. Si esto fuera verdad para
cualquier vértice, consideremos el grafo con aristas únicamente de color 1. Es
un grafo con 9 vértices , todos de grado 5, lo que contradice el teorema 1.1. Por
lo tanto, el primero o el segundo caso deben ser ciertos para algún vértice.
6.5. En lenguaje formal, tenemos un grafo binario coloreado donde el color
1 es "se conocen" y el color 2 es "no se conocen"; y hay que probar la existencia
de un rectángulo con diagonales, del mismo color. Consideremos el vértice a.
Hay al menos 9 aristas de un mismo color.
Por el problema 6.4 obtenemos que en el grafo construido con esos 9 vértices, o bien existe un triángulo monocromático, o bien existe un rectángulo con
diagonales del otro color. Incluyendo a el triángulo nos da un rectángulo con
diagonales.
6.6. De nuevo tenemos un grafo binario coloreado. El color 1 son las conexiones por tren y el color 2 las conexiones por autobús. Supongamos el grafo
de color 1. Si no es conexo, todos los vértices con diferentes componentes de
conectividad deben ser conectados con diferente color. Así, cada par de vértices
está conectado; bien por una arista del segundo color, o un camino de longitud
2 cruza cualquier vértice de diferente componente de conectividad.
Bibliografía
1. D. Fomin, S. Genkin, I. Itenberg. Mathematical Circles (Russian Experience). AMS, 1996.
2. O. Ore. Graphs and their uses. Random House, New York, 1963.
3. O. Ore. Theory of Graphs. AMS, Providence, Rhode Island, 1962.
4. R.J.Wilson. Introduction to Graph Theory. Oliver and Boyd, Edinburgh,
1972.
17
La suficiencia de la equivalencia e independencia de las desigualdades
de Cauchy-Buniakowski-Schwarz y de Bergström
por D.M. Bătineţu-Giurgiu, Bucharest, Romania
y Neculai Stanciu, Buzău, Romania
La desigualdad de H. Bergström:
Si n ∈ N * − {1} , x k ∈ R , y k ∈ R+* , ∀k = 1, n , entonces:
 n

 ∑ xk 
2
n
x k  k =1 
≥ n
∑
k =1 y k
∑ yk
2
(B)
k =1
La desigualdad de Cauchy-Buniakowski-Schwarz:
Si n ∈ N * − {1} , a k ∈ R , bk ∈ R , ∀k = 1, n , entonces:
2

 n

 n
 n
 ∑ a k bk  ≤  ∑ a k2  ∑ bk2 
 k =1

 k =1  k =1 
(C-B-S)
1. Probaremos que es suficiente demostrar (B) sólo para x k , y k ∈ R+* , ∀k = 1, n .
Por tanto, suponemos que (B) se verifica para x k , y k ∈ R+* , ∀k = 1, n , y demostraremos
que (B) se cumple para x k ∈ R , y k ∈ R+* , ∀k = 1, n .
a) Si x k ∈ R , ∀k = 1, n , teniendo en cuenta que:
x 2 = ( x ) , ∀x ∈ R ,
2
y
x + y ≥ x + y , ∀x, y ∈ R .
entonces:
2
n x
x k2
k
=∑
∑
k =1 y k
k =1 y k
n
2
 n

x


∑
k
(B)
k =1

 ≥
≥
n
∑ yk
k =1
2

 n


 ∑ xk 
 ≥  k =1  ,
n
n
∑ yk
∑ yk
 n
 ∑ x k
 k =1
k =1
luego (B) es cierta.
b) Si x k = 0 , ∀k = 1, n , tenemos: 0=0, que es cierto.
2
k =1
c) Si m ( m ∈ N * , m < n) de los números x1 , x 2 ,..., x n son nulos y el resto son no nulos,
podemos
suponer
(sín
pérdida
de
generalidad)
x1 , x 2 ,..., x n ∈ R+* ,
que
y x m +1 = x m + 2 = ... = x n = 0 .
En este caso se tiene:
2
2
2
 n

 m

 n

x
x
 ∑ xk 




∑
k
2
2 ( B) ∑ k
n
m
xk
x
= ∑ k ≥  k =m1  =  k =m1  ≥  k =n1  ,
∑
k =1 y k
k =1 y k
∑ yk
∑ yk
∑ yk
k =1
k =1
k =1
luego (B) queda probado también en este caso.
2. Probaremos que es suficiente demostrar (C-B-S) sólo para a k , bk ∈ R+* , ∀k = 1, n .
Supongamos que (C-B-S) se cumple para a k , bk ∈ R+* , ∀k = 1, n y demostremos que (CB-S) se cumple ∀a k , bk ∈ R, k = 1, n .
a) Si entre los números a k , bk algunos son negatives, entonces considerando que:
x 2 = ( x ) , ∀x ∈ R ,
2
y
x + y ≥ x + y , ∀x, y ∈ R ,
deducimos que:
2

 n
 n

 n

 n

 ∑ a k bk  =  ∑ a k bk  ≤  ∑ a k bk  =  ∑ a k ⋅ bk 
 k =1

 k =1

 k =1


 k =1
n
n
n
n
(C − B − S )




2 
2
≤  ∑ a k  ∑ bk  =  ∑ a k2  ∑ bk2  ,
 k =1
 k =1
  k =1  k =1 
lo que demuestra que (C-B-S) se cumple.
2
2
2
(C − B − S )
≤
b) Si entre los números a k , bk algunos son nulos, sin pérdida de la generalidad
suponemos que
a k ∈ R+* , k = 1, m , a m +1 = a m + 2 = ... = a n = 0 ,
y
bk ∈ R+* , k = 1, p , b p +1 = b p + 2 = ... = bn = 0 , donde 1 ≤ p ≤ m ≤ n ,
con lo cual:
n
p
k =1
k =1
∑ ak bk = ∑ ak bk ,
así que de aquí se obtiene:
2
 p

 n

 ∑ a k bk  =  ∑ a k bk 
 k =1

 k =1

2
 p
 p

≤  ∑ a k2  ∑ bk2  ≤
 k =1  k =1 
(C − B − S )
  n
 m
 p

 n
≤  ∑ a k2  ∑ bk2  =  ∑ a k2  ∑ bk2  .
 k =1  k =1   k =1  k =1 
Por lo tanto, cuando hablamos de la equivalencia entre las desigualdades (B) y (C-B-S)
podemos suponer que a k , bk , x k , y k ∈ R+* , ∀k = 1, n .
A continuación, probaremos que:
(B) ⇔ (C-B-S).
Demostración.
(B) ⇒ (C-B-S)
Si en la desigualdad (B) tomamos x k = a k bk e y k = bk2 , ∀k = 1, n obtenemos que:
2
 n

x


∑
k
2
n
x k  k =1 
≥ n
⇔
∑
k =1 y k
∑ yk
k =1
2
 n

a
b


2
∑
k
k
2
2
n
a k bk  k =1
 n 2  n 2   n


≥
⇒  ∑ a k  ∑ bk  ≥  ∑ a k bk  ,
∑
n
2
2
k =1 bk
 k =1  k =1   k =1

∑ bk
k =1
es decir, (C-B-S).
(C-B-S) ⇒ (B)
Si en la desigualdad (C-B-S) tomamose a k =
y k y bk =
 n 2  n 2   n

 n
 n x 2
 ∑ a k  ∑ bk  ≥  ∑ a k bk  ⇔  ∑ y k  ∑ k

 k =1  k =1   k =1
 k =1  k =1 y k
2
xk
yk
∀k = 1, n obtenemos que:
  n
x
 ≥ ∑ y k ⋅ k
yk
  k =1
2
2
n

 =  ∑ x k 

 k =1 

2
 n

 ∑ xk 
2
n
x
⇒ ∑ k ≥  k =n1  , es decir, (B).
k =1 y k
∑ yk
k =1
Observación. Ya que (C-B-S) puede demostrarse independientemente de (B) y vice
versa deducimos que (C-B-S) y (B) son mutuamente independientes.
Problemas para los más jóvenes Problemas para los más Jóvenes 50
Problemas de la "Brother Alfred Brousseau Mathematics Competition, Introductory Division"
Los problemas que presentamos a continuación proceden del libro - publicado
por Dale Seymour Publications - sobre la Competición arriba mencionada, que
se desarrolla en California.
PMJ50-1
Las dimensiones de una caja rectangular están en la proporción 2 : 3 : 5 y
su volumen es 82320 cm3 . Calcular estas dimensiones.
PMJ50-2
Formando las tablas de valores de 3n ; 7n y 4n para n = 1; 2; :::; 10 y observando las regularidades existentes, determinar la cifra de las unidades del
número 13841 + 17508 + 24617 :
PMJ50-3
Los cuatro enteros positivos a; b; c; d son tales que tomándolos por parejas en
las 6 maneras posibles, los dos números de cada pareja tienen un divisor común
mayor que uno. Además, a + b + c + d es un número primo. Hallar el conjunto
de enteros más pequeños para los que se cumplan esas dos condiciones.
PMJ50-4
Dos jugadores igualmente hábiles juegan cinco partidas, de manera que quien
gane tres partidas se llevará las apuestas. Si el jugador A gana la primera
partida, ¿cuál es la probabilidad de que se lleve las apuestas?
PMJ50-5
Un barco echa el ancla en aguas tranquilas (sin corriente). Cuatro horas más
tarde el nivel del mar ha bajado 8 pies y el barco se ha movido una distancia
horizontal de 80 pies desde el ancla. ¿Qué longitud de la cadena del ancla hay
sumergida en ese momento?
1
Problemas de nivel medio y de Olimpíadas Problemas de Nivel Medio y de Olimpiadas 50
Problemas de la Ronda …nal de la 26a Olimpiada de Corea del Sur (2013)
PO50-1
b > C
b y sea D el punto del lado AC tal que
Sea ABC un triángulo con B
b Sea I el incentro de ABC y E 6= I el segundo punto de intersección
\ = C.
ADC
de AI con la circunferencia circunscrita de CDI: Sea P el punto de intersección
de la recta BD con la recta que pasa por E y es paralela a AB: Sea J el incentro
de ABD;y A0 el simétrico de A con respecto a I:Supongamos que las dos rectas
JP y A0 C se cortan en el punto Q: Demostrar que QJ = QA0 :
PO50-2
Hallar todas las funciones f : R ! [0; +1) tales que, para todos los reales
a; b; c; d que veri…can ab + bc + cd = 0, se cumple la siguiente igualdad:
f (a
b) + f (c
PO50-3
Dado un entero positivo n
T = f(i; j) : 1
d) = f (a) + f (b + c) + f (d):
2; se de…ne el conjunto T de la siguiente manera:
i<j
n con i j jg
(i divide a j).
Para los números reales no negativos x1 ; x2 ; :::; xn tales que x1 +x2 +
1; hallar el máximo valor (en función de n) de la suma
X
xi xj
+xn =
(i;j)2T
PO50-4
Dado el triángulo ABC; sean B1 y C1 los exincentros correspondientes a los
b y C,
b respectivamente.
ángulos B
La recta B1 C1 corta a la circunferencia circunscrita de ABC en un punto
D 6= A: La perpendicular desde B1 a CA y la perpendicular desde C1 a AB se
cortan en E: Sea ! la circunferencia circunscrita a ADE: La tangente a ! en
D corta a la recta AE en F: La perpendicular desde D a AE corta a AE en G
e interseca a ! en H 6= D:La circunferencia circunscrita de HGF corta a ! en
I 6= H: Sea J el pie de la perpendicular desde D a AH:
Demostrar que AI pasa por el punto medio de DJ:
PO50-5
Sean a y b enteros positivos primos entre sí, y an ; bn sucesiones de enteros
que veri…can
p
a+b 2
2n
p
= an + bn 2:
Hallar todos los números primos p tales que existe un entero positivo n menor
o igual que p que veri…ca bn 0(mod p):
PO50-6
1
Dada una correspondencia 1-1 f : f1; 2; :::; ng ! f1; 2; :::; ng para algún
entero positivo n, se de…nen cuatro conjuntos A; B; C; D de la siguiente manera:
A =
B
=
C
=
D
=
fi j i > f (i)g
f(i; j) j i < j
f(i; j) j i < j
f (j) < f (i) o f (j) < f (i) < i < jg
f (i) < f (j) o f (i) < f (j) < i < jg
f(i; j) j i < j y f (i) > f (j)g
Si jXj representa el número de elementos del conjunto X; demostrar que
jAj + 2 jBj + jCj = jDj :
2
Problemas Problema 246, propuesto por Ma Francisca Adrover Garau y Miguel
Amengual Covas, Mallorca, España
En la …gura, el segmento CD es una semicuerda perpendicular al diámetro
AB de una circunferencia de centro O. Los respectivos centros de las circunferencias de diámetros AC y CB son los puntos O1 y O2 : Las restantes circunferencias
son tangentes exteriores entre sí y están inscritas en el ángulo curvilíneo y en el
segmento circular, tal como se indica. Si los círculos sombreados (los de ambos
extremos de la cadena de círculos) son iguales, determinar la razón AC : CB:
Problema 247, propuesto por Marcos Martinelli, Brasilia, Brasil
Si n 2 N y k 2 N tal que 1 k n + 1, se consideran los números reales
ak tales que
n+1
X
k=1
Calcular
max
a2k 6= 0:
8 n
X
>
>
>
ak ak+1
>
<
>
>
>
>
:
k=1
n+1
X
k=1
1
a2k
9
>
>
>
>
=
>
>
>
>
;
:
Problema 248, propuesto por José Luis Díaz Barrero, Barcelona,
España
Sean x1 ; x2 ; :::; xn con n 2; números reales no negativos menores que 1 y
tales que x21 +
+ x2n = 1:
Demostrar que
xn
r
x1
x1 x2 + n
1
+ xn
1
r
x2
x2 x3 + n
1
+
+ x1
r
xn
xn x1 + n
1
1:
Problema 249, propuesto por Marcel Chiritza, Bucarest, Rumania
Resolver, en el conjunto de los números reales, el sistema de ecuaciones
(9x + 9y + 9z ) (3 x + 3 y + 3 z ) = 3
3
3y+z+1 3z+x+1 = 3x + 3y + 3z
x+y+1
Problema 250, propuesto por Marcel Chiritza, Bucarest, Rumania
Sea P un punto interior al triángulo equilátero ABC, de lado 1. Si ponemos
x = P A; y = P B; z = P C; probar que
x2 + y 2 + z 2 + x2 + y 2 + z 2
1
2
= 3 x2 y 2 + y 2 z 2 + z 2 x2 :
Problema 251, propuesto por Marcel Chiritza, Bucarest, Rumania
Hallar los números reales a; b tales que
"
#
n3
+ an + b = 0:
lim
n!1 (n + 1)2
Problema 252, propuesto por Marcel Chiritza, Bucarest, Rumania
Sea ABC un triángulo. Si existe una recta que corte a los lados AB y AC en
M y N, respectivamente, de tal manera que exista una circunferencia interior,
tangente a las rectas AB, AC, BN y CM, entonces el triángulo es isósceles.
Problema 253, propuesto por Marcel Chiritza, Bucarest, Rumania
Las sucesiones (an )n 1 y (bn )n 1 se de…nen de la manera siguiente:
an
bn
=
=
n X
m
X
m=1 k=0
n X
m
X
( 1)
m
( 1)
m
m=1 k=0
n
m
m+2
n
m
(m + 2) (m + 4)
:
Determinar si son convergentes y, en su caso, hallar sus límites cuando
n ! 1:
Problema 254, propuesto por Laurentiu Modan, Bucarest, Rumania
2
Sea ABC un triángulo isósceles con b = c: Demostrar que existen in…nitos
triángulos de ese tipo, veri…cando que R < 2r, siendo R el radio de la circunferencia circunscrita y r el de la inscrita.
Problema 255, propuesto por D.M. Batinetzu-Giurgiu, Bucarest,
y Neculai Stanciu, Buzau, Rumania
Sean a 2 0; 2 ; b 2 [1; 1) ; y m; n 2 N : Calcular
Za
a
(b
sin x + tan x
dx:
m
cos x) + sin2n x
3
PROBLEMA 241, propuesto por D.M. Batinetu-Giurgiu (Bucarest)
y N. Stanciu (Buzau)
Sean s, t ∈ R, y consideremos la sucesión
{Ln (s, t)}n≥2
definida por
Ln (s, t) = (n + 1)s ·
q
n+1
t
((n + 1)!) − ns ·
q
n
t
(n!) .
Calcular
lim Ln (s, t) = L(s, t).
n→∞
Solución por Daniel Lasaosa Medarde, Universidad Pública de Navarra,
Pamplona, España
p
Definamos Mn (s, t) = ns · n (n!)t , con lo que usando notación de Landau, y la
aproximación de Stirling
1
1
ln(n!) = n ln(n) − n + ln(2πn) + O
.
2
n
Tenemos entonces que
ln (Mn (s, t)) = s ln(n) +
t
t
ln(n!) = (s + t) ln(n) − t +
ln(2πn) + O
n
2n
1
n2
.
Si s + t = 0 y s + t < 0, entonces respectivamente tenemos
lim ln (Mn (s, t)) = −t,
lim ln (Mn (s, t)) = −∞,
n→∞
n→∞
luego como Mn (s, t) tiende a una constante, igual a e−t en el primer caso e igual a
0 en el segundo caso, entonces Ln (s, t) = Mn+1 (s, t) − Mn (s, t) tiende a 0 en ambos
casos, es decir, L(s, t) = 0 siempre que s + t ≤ 0.
Supogamos que s + t = α > 0, con lo que
2
t
ln (n)
1
Mn (s, t)
α
=
n
·
1
+
ln(2πn)
+
O
·
1
+
O
=
−t
2
e
2n
n
n2
tnα−1
ln(2πn) + O nα−2 ln2 (n) .
2
Ahora bien, (n + 1)α − nα = α · nα−1 + O nα−2 , luego si α > 1, se tiene que el
término dominante en Mn+1 (s, t) − Mn (s, t) es de la forma α · nα−1 , que diverge.
Luego L(s, t) → +∞ cuando s + t > 1. Si α = 1, tenemos que
2
Mn (s, t)
t
ln (n)
=
n
+
ln(2πn)
+
O
,
e−t
2
n
= nα +
luego
2
1
ln (n)
1
Ln (s, t)
t
+O
=1+O
,
= 1 + ln 1 +
e−t
2
n
n
n
con lo que L(s, t) = e−t = es−1 cuando s + t = 1. Finalmente, si 0 < s + t = α < 1,
se tiene que
2
Mn (s, t)
t
ln (n)
α
lim
−n
= lim
ln(2πn) + O
= 0,
n→∞
n→∞ 2n1−α
e−t
n2−α
1
con lo que
L(s, t) = e−t · lim ((n + 1)α − nα ) = e−t · lim nα−1 = 0.
n→∞
n→∞
Concluı́mos por lo tanto que:
• si s + t < 1, L(s, t) = 0,
• si s + t = 1, L(s, t) = e−t = es−1 ,
• si s + t > 1, L(s, t) no existe porque Ln (s, t) diverge a +∞.
Solución al problema 241)
Marcos Francisco Ferreira Martinelli – Brasília – Brasil
PROBLEMA 242, propuesto por D.M. Batinetu-Giurgiu (Bucarest)
y N. Stanciu (Buzau)
Sea m ∈ R+ . Con las notaciones habituales para los triángulos, llamando S al
área del triángulo ABC, demostrar que se verifica la siguiente desigualdad:
√
bm+2
cm+2
4 3
am+2
+
+
≥
· S.
(b · R + c · r)m
(c · R + a · r)m
(a · R + b · r)m
(R + r)m
Solución por Daniel Lasaosa Medarde, Universidad Pública de Navarra,
Pamplona, España
Utilizamos en la solución el siguiente
2
2
2
√Lema: En todo triángulo de lados a, b, c y área S, se cumple que a + b + c ≥
4 3 · S, con igualdad si y sólo si el triángulo es equilátero.
Demostración: Ya que ambos miembros son positivos, el Lema es equivalente a
(a2 + b2 + c2 )2 ≥ 48S 2 . La fórmula de Herón para S en función de a, b, c se puede
escribir de forma equivalente como
16S 2 = 2a2 b2 + 2b2 c2 + 2c2 a2 − a4 − b4 − c4 ,
que introducida en el resultado a demostrar, reduce la tarea a probar que a4 + b4 +
c4 ≥ a2 b2 + b2 c2 + c2 a2 , claramente cierta en virtud de la desigualdad del producto
escalar, y con igualdad si y sólo si a = b = c, cqd.
Volviendo al problema propuesto, definamos f (x) = x1m , que para x, m ∈ R+ es
estrictamente convexa al ser su derivada segunda f 00 (x) = m(m+1)
> 0. Tenemos
xm+2
entonces que el miembro de la izquierda de la desigualdad a demostrar es
b·R+c·r
c·R+a·r
a·R+b·r
a2 f
+ b2 f
+ c2 f
≥
a
b
c
!
a2 b·R+c·r
+ b2 c·R+a·r
+ c2 a·R+b·r
2
2
2
a
b
c
≥ (a + b + c )f
=
a2 + b2 + c2
m 2
2
(R + r)(ab + bc + ca)
a + b2 + c2
a + b2 + c2
2
2
2
= (a + b + c )f
·
≥
=
a2 + b2 + c2
ab + bc + ca
(R + r)m
√
4 3·S
≥
,
(R + r)m
como querı́amos demostrar, y donde hemos usado la desigualdad de Jensen, el
Lema, y que a2 + b2 + c2 ≥ ab + bc + ca en virtud de la desigualdad del producto
escalar. El que el triángulo ABC sea equilátero es condición necesaria para que se
dé la igualdad, y se comprueba trivialmente que también es suficiente.
1
PROBLEMA 243, propuesto por D.M. Batinetu-Giurgiu (Bucarest)
y N. Stanciu (Buzau)
Sean A1 , A2 , . . . , An (con n ≥ 3) los vértices de un polı́gono regular; M un
punto de su circunferencia inscrita y N un punto de su circunferencia circunscrita.
Demostrar que
n
n
X
1
2π X
M Ak 4
≥
3 + cos
M Ak 2 .
4
n
N Ak 2
k=1
k=1
Solución por Daniel Lasaosa Medarde, Universidad Pública de Navarra,
Pamplona, España
Comenzamos la solución con un Lema general y dos Proposiciones particulares
a la situación descrita en el enunciado:
Lema: Sean R, r el circunradio e inradio de un polı́gono regular de n ≥ 3 lados.
Entonces, r = R cos nπ .
Demostración: Sea A1 A2 . . . An el polı́gono, y O su centro. El triángulo A1 OA2
es isósceles en O, con OA1 = OA2 = R, ∠A1 OA2 = 2π
n , y siendo r la longitud de
la altura desde O sobre A1 A2 . Como A1 A2 = 2R sin nπ , el área de A1 OA2 es
1
2π
π
π
π
= R2 sin
= R2 sin cos ,
n
2
n
n
n
de donde dividiendo ambos lados por R sin nπ se deduce inmediatamente el Lema.
Rr sin
Proposición 1: Con las definiciones del enunciado, se tiene que
n
n
X
X
N Ak 2 = 2nR2 ,
M Ak 2 = n(R2 + r2 ).
k=1
k=1
Demostración 1: Utilizaremos en esta demostración el siguiente resultado conocido: para todo ángulo δ y todo entero n ≥ 3, se tiene
X
n
n
X
2kπ
2kπ
+δ =
sin
+ δ = 0.
cos
n
n
k=1
k=1
La combinación de ambas igualdades es equivalente a la existencia de un polı́gono
regular de n lados, uno de los cuáles forma un ángulo de δ con el eje X en un
cierto sistema de coordenadas cartesianas. Sea entonces un sistema de coordenadas
cartesianas con origen en el centro del polı́gono regular y An ≡ (R, 0), con lo que
podemos escribir
2kπ
2kπ
Ak ≡ R cos
, R sin
.
n
n
Podemos entonces tomar N ≡ (R cos α, R sin α) y M ≡ (r cos β, r sin β), donde r es
el inradio del polı́gono, y α, β son ángulos cualesquiera. Tenemos entonces que
2kπ
2kπ
2kπ
N Ak 2 = 2R2 − 2R2 cos α cos
− 2R2 sin α sin
= 2R2 − 2R2 cos
−α ,
n
n
n
cuya suma para k = 1, 2, . . . , n es 2nR2 , pues la suma del segundo sumando en el
miembro de la derecha es claramente 0. De la misma forma,
2kπ
M Ak 2 = R2 + r2 − 2Rr cos
−β ,
n
cuya suma para k = 1, 2, . . . , n es n(R2 + r2 ). Queda demostrada la Proposición 1.
1
Proposición 2: En la situación descrita en el enunciado, se tiene que
n
X
n(R2 + r2 )2
M Ak 4
.
>
2R2
N Ak 2
k=1
Demostración 2: En virtud de la desigualdad del producto escalar, se tiene
! n
!
!2
n
n
X
X
X
M Ak 4
2
2
N Ak
≥
M Ak
,
N Ak 2
k=1
k=1
k=1
N Ak
con igualdad si y sólo si M
Ak es independiente de k. Sustituyendo los resultados
de la Proposición 1, nos basta con demostrar que la igualdad no puede darse. En
N Ak
efecto, supongamos que M
Ak es independiente de k, con lo que N 6= Ak para todo
k, pues en caso contrario esta cantidad serı́a 0 para un k, y no nula para el resto.
Luego sin pérdida de generalidad podemos asumir que N está en la circunferencia
circunscrita al polı́gono, en el arco An A1 que no contiene
a ningún otro vértice, y
no más cerca de A1 que de An , es decir, α ∈ 0, nπ , y N A1 ≥ N An son los dos
menores valores que puede tomar N Ak . Luego
ser los dos
M An ≤ M A1 han Nde
N A1
An
menores valores que toma M Ak , y β ∈ 0, nπ . Igualando entonces M
An = M A1 y
bajo estas condiciones, tras algo de álgebra obtenemos que ha de ser α = β = nπ ,
e introduciendo el resultado en las expresiones para N Ak y M Ak , llegamos a que
(2k−1)π
N Ak
N A1
. Pero por el Lema, esta igualdad no se
M Ak = M A1 si y sólo r = R cos
n
cumple para k = 2. Luego la desigualdad hallada es siempre estricta, quedando
demostrada la Proposición 2.
En virtud de las Proposiciones 1 y 2, e introduciendo los resultados hallados en
ella en la desigualdad propuesta en el enunciado, nos basta con demostrar que
R2 + r 2
1
2π
r2
2 π
≥
3
+
cos
=
1
+
cos
=
1
+
,
R2
2
n
n
R2
claramente cierta y con igualdad siempre, y donde hemos usado el Lema. Como la
desigualdad en la Proposición 2 es estricta, hemos probado que la desigualdad propuesta en el enunciado se cumple siempre, pero siempre estrictamente sin posibilidad
de darse la igualdad.
Solución del problema 243)
Marcos Francisco Ferreira Martinelli – Brasília - Brasil
Problema 244, propuesto por Marcel Chiritza, Bucarest:
“Sea ABC un triángulo cuyo ángulo A ≥ 90°. Sea M uno cualquiera de los
puntos interiores al triángulo tales que sus proyecciones ortogonales sobre los
lados de ABC son los vértices de un triángulo rectángulo. Demostrar que, de 7
cualesquiera de esos puntos, hay 4 que son concíclicos.”
RESOLUCIÓN:
Sean D, E y F los pies de las perpendiculares a los lados a, b y c respectivamente.
Supongamos que es el ángulo FED el que es recto. Se tiene que el ángulo FMD = 180º - B,
pues el cuadrilátero BFMD es inscrito, al ser rectos sus ángulos en F y D.
Como el cuadrilátero AFME es igualmente inscrito, los ángulos AMF y AEF son iguales. Otro
tanto ocurre con los ángulos DMC y DEC. Dado que el ángulo FED es recto, tenemos que:
90º = AEF + DEC = AMF + DMC
Entonces, para el ángulo AMC se tiene:
AMC = 360º - FMD - (AMF + DMC) = 360º - (180º - B) - 90º = B + 90º
Por tanto, el punto M se encuentra en el arco capaz, interior al triángulo, del segmento AC con
ángulo B + 90º.
Si el triángulo DEF es recto en F, el punto M deberá encontrarse en el arco capaz, interior al
triángulo, del segmento AB con amplitud C + 90º.
Finalmente el triángulo DEF no puede ser recto en D, pues el correspondiente arco capaz sería
de mas de 180º.
Por tanto los siete puntos m cualesquiera deben estar en uno u otro de estos dos arcos
capaces, y necesariamente debe haber al menos cuatro en uno de ellos.
Ignacio Larrosa Cañestro
IES Rafael Dieste
A Coruña (España)
PROBLEMA 244, propuesto por Marcel Chiritza, Bucarest
Sea ABC un triángulo cuyo ángulo A ≥ 90◦ . Sea M uno cualquiera de los puntos
interiores al triángulo tales que sus proyecciones ortogonales sobre los lados de ABC
son los vértices de un triángulo rectángulo. Demostrar que, de 7 cualesquiera de
esos puntos, hay 4 que son concı́clicos.
Solución por Daniel Lasaosa Medarde, Universidad Pública de Navarra,
Pamplona, España
Sean D, E, F las proyecciones ortogonales de M sobre BC, CA, AB. Se tiene
entonces que ∠F DE < ∠F M E = 180◦ − ∠A ≤ 90◦ , luego DEF nunca puede ser
rectángulo en D. Supongamos entonces que M es tal que DEF es rectángulo en
E. Como BDM F es cı́clico con diámetro M B por ser M D, M F respectivamente
perpendiculares a las rectas BC = BD y AB = F B, se tiene por el teorema del seno
que DF = M B sin ∠B, y de forma similar DE = M C sin ∠C, EF = M A sin ∠A.
Luego usando nuevamente el teorema del seno, M es tal que DEF es rectángulo
en E si y sólo si b2 · M B 2 = c2 · M C 2 + a2 · M A2 . De forma análoga, se tiene que
M es tal que DEF es rectángulo en F , si y sólo si c2 · M C 2 = b2 · M B 2 + a2 · M A2 .
Podemos entonces particionar el conjunto de puntos M que satisfacen la condición
del enunciado, en dos conjuntos, RE y RF , según sea DEF rectángulo respectivamente en E y en F . Demostraremos que RE , RF son, cada uno, un subconjunto
de puntos situados sobre una cierta circunferencia, con lo que quedará demostrado
el resultado pedido. En efecto, de cada 7 puntos, por el principio del palomar
hay, bien al menos 4 en RE (siendo por lo tanto esos 4 puntos concı́clicos sobre
la circunferencia que contiene a RE ), bien al menos 4 en RF (siendo nuevamente
concı́clicos). Es decir, al poder intercambiar B, C y todos los puntos definidos a
partir de ellos sin afectar al problema, nos basta con demostrar que la condición
b2 · M B 2 = c2 · M C 2 + a2 · M A2 define una circunferencia o un subconjunto de
puntos situado sobre una circunferencia.
Sea un sistema de coordenadas cartesianas con origen en el pie de la perpendicular desde A sobre BC. Se tiene entonces que B ≡ (−c cos B, 0), C ≡ (b cos C, 0) y
A ≡ (0, ha ), donde ha es la longitud de la altura desde A. Luego dado M ≡ (x, y),
se tiene
M A2 = x2 + y 2 − 2ha y + ha 2 ,
M B 2 = x2 + y 2 + 2cx cos B + c2 cos2 B,
M C 2 = x2 + y 2 − 2bx cos C + b2 cos2 C,
siendo por lo tanto, tras algo de álgebra, M ∈ RE si y sólo si
a2 + b2 − c2
= 0,
x2 + y 2 − 2abcx cos(B − C) − 4aSy + 4S 2
a2
donde S es el área de ABC, y hemos usado relaciones del triángulo fácilmente
demostrables por trigonometrı́a básica, como la fórmula de Herón para el área,
a2 + c2 − b2
4S 2 (b2 − c2 )
b2 c2 cos2 C − cos2 B =
.
a2
Nótese que esta expresión puede ponerse en la forma
b cos B + c cos C = a cos(B − C),
o
2
2
(x − x0 ) + (y − y0 ) = ρ2 ,
1
donde
x0 =
b cos(B − C)
bc (b cos B + c cos C)
=
,
2
2
2
a +c −b
2 cos B
y0 =
a2
a sin B
2aS
=
,
2
2
+c −b
2 cos B
y
bc sin2 B cos C
cos B
donde x0 , y0 , ρ dependen de ABC, pero no de la elección de M . Es decir, todos los
puntos de RE están en una circunferencia de centro (x0 , y0 ) constante, y radio ρ
constante, quedando demostrado el resultado pedido en el enunciado.
ρ2 = x0 2 + y0 2 −
Solución al problema 244)
Marcos Francisco Ferreira Martinelli – Brasília - Brasil
Problema 245.Las alturas BE y CF de un triangulo ABC se cortan en H. Las prolongaciones de FE y BC se cortan
en U. Una recta que pasa por el punto medio L de BC, paralela a la bisectriz interior de <EUB,
corta a CA, AB, HC y HB (o a sus prolongaciones, si fuera necesario) en P, Q, X, Y, respectivamente. Demostrar que las circunferencias APQ y HXY tienen radios iguales.
Solución de Saturnino Campo Ruiz, Profesor de Matemáticas jubilado, de Salamanca.
El diámetro de la circunferencia de centro , circunscrita al triángulo
El de la de centro
, circunscrita al triángulo
concluirá si los segmentos
e
es
El triángulo
.
La igualdad de ambas se
son de la misma longitud.
De otra parte sabemos que el triángulo con vértice
(por una semejanza inversa). Así pues
son,
,
y .
•
es
y los pies y de las es semejante al
y por tanto, los ángulos del triángulo
es isósceles.
Vamos a calcular el ángulo
. Por tanto también
consecuencia
•
es isósceles.
Los triángulos
y
son semejantes y congruentes
y en
Son semejantes pues tienen dos ángulos iguales,
.
Ya que
es isósceles, trazando por y paralelas a
obtenemos al cortar cada una con
el lado opuesto, sendos triángulos isósceles:
y
. Por tanto, el trapecio
es
isósceles y la paralela por a la bisectriz interior de
es la paralela media de este trapecio (la paralela media contiene los puntos medios de las dos diagonales). Resulta así que los
segmentos de igual longitud
y
quedan bisecados en dos partes iguales por el segmento
. Por tanto los triángulos
y
, son congruentes y los segmentos
e
de la
misma longitud, como queríamos demostrar.
PROBLEMA 245, propuesto por el editor en homenaje a David Monk
y deseando su recuperación.
Las alturas BE y CF de un triángulo ABC se cortan en H. Las prolongaciones
de F E y BC se cortan en U . Una recta que pasa por el punto medio L de BC,
paralela a la bisectriz interior de ∠EU B, corta a CA, AB, HC y HB (o a sus
prolongaciones, si fuera necesario) en P, Q, X, Y , respectivamente.
Demostrar que las circunferencias AP Q y HXY tienen radios iguales.
Solución por Daniel Lasaosa Medarde, Universidad Pública de Navarra,
Pamplona, España
Notemos antes de empezar que ∠P AQ = ∠A, mientras que ∠XHY = ∠BHC =
180◦ − ∠A, pues ∠HBC = 90◦ − ∠C y ∠HCB = 90◦ − ∠B. Por el teorema del
seno, el resultado pedido es equivalente a demostrar que P Q y XY tiene la misma
longitud.
Como ∠BF C = ∠CEB = 90◦ , BF EC es claramente cı́clico. Si ∠B = ∠C,
se tiene que EF k BC, y no existe el punto U , salvo ”en el infinito”; podrı́amos
entonces decir en todo caso que la bisectriz de ∠EU B es paralela a BC y a EF , con
lo que P = X = C y Q = Y = B, siendo trivialmente cierto el resultado pedido.
Consideraremos entonces en el resto del problema, sin pérdida de generalidad al
poder intercambiarlos sin afectar al problema, que ∠B > ∠C. Se tiene entonces
que U está en la semirrecta CB más allá de B, y que al ser ∠U F B = ∠AF E = ∠C,
y ∠F BU = 180◦ − ∠B, se tiene ∠EU B = ∠B − ∠C, es decir, la recta que pasa
. Al mismo
por L, P, Q, X, Y forma con la recta BC un ángulo igual a ∠B−∠C
2
tiempo, P, X están respectivamente sobre los segmentos CA, CH, pero Q, Y están
respectivamente sobre las prolongaciones de BA, BH más allá de B.
Deducimos entonces, sin más que considerar triángulos, que
∠B + ∠C
∠A
∠CP X = ∠CP L = 180◦ −
= 90◦ +
,
2
2
y como ∠P CX = 90◦ − ∠A, se tiene que ∠P XC = A2 . De forma análoga,
∠A
∠B − ∠C
= 90◦ +
,
2
2
con ∠QBY = ∠EBA = 90◦ −∠A, luego los triángulos P CX y QBY son semejantes,
y como hemos de demostrar que P Q = XY , o equivalentemente que P X = QY ,
nos basta entonces con demostrar que P C = BQ. Ahora bien, ∠CLP = ∠BLQ,
CL = BL, y ∠CP L = 180◦ − ∠BQL, luego aplicando el teorema del seno a los
triángulos CLP y BLQ, se obtiene en efecto P C = BQ, quedando concluido el
problema.
∠BQY = 180◦ − ∠BQL = ∠LBQ + ∠BLY = 180◦ − ∠B +
1
Noticia de congresos, referencia de páginas web y reseña de libros “Avanzando juntos hacia las Metas Educativas Iberoamericanas 2021” Buenos Aires, Argentina 12, 13 y 14 de noviembre 2014 En la XXIII Conferencia Iberoamericana de Educación el Secretario General de la OEI presentó a las delegaciones asistentes la convocatoria del Congreso Iberoamericano de Ciencia, Tecnología, Innovación y Educación a celebrarse en Buenos Aires, Argentina, del 12 al 14 de noviembre de 2014. Presentación En el año 2010, fue aprobado por los Ministros de Educación y, posteriormente, por los Jefes y Jefas de Estado y de Gobierno de Iberoamérica, el proyecto promovido por la OEI, Metas Educativas 2021: la educación que queremos para la generación de los Bicentenarios, que tienen por objeto elevar la calidad y la equidad educativa en la región y conseguir sociedades más libres y democráticas. En este marco y como parte constitutiva de este proyecto, la OEI ha impulsado algunas iniciativas importantes para el desarrollo de la educación, la ciencia y la tecnología en la región. Entre ellas se destaca el Instituto Iberoamericano de TIC y Educación, IBERTIC, con sede en Buenos Aires, Argentina, que haciendo hincapié en las políticas educativas de la región recupera y potencia una de las líneas históricas de trabajo de la OEI: el proyecto Ciencia, Tecnología y Sociedad (CTS). El Instituto se desarrolla en las siguientes áreas: Investigación, Formación, Evaluación y una línea de Difusión y Transferencia del Conocimiento que es un espacio en el cual se celebran conferencias con especialistas, presentaciones de resultados de estudios/investigaciones, un ciclo de talleres “De docentes para docentes” y actividades especiales. IBERTIC lleva adelante su tarea de manera articulada con el Centro de Altos Estudios de la OEI (CAEU); la Red Latinoamericana de Portales Educativos (RELPE); Virtual Educa; la Televisión Educativa Iberoamericana (TEIB) y el Portal Educativo del Ministerio de Educación de la Argentina, EDUC.AR. A finales de 2012, y siguiendo la estela de IBERTIC, la OEI puso en marcha IBERCIENCIA, el Instituto Iberoamericano de Enseñanza de las Ciencias y la Matemática, en respuesta a la petición del Consejo Directivo de la Organización de Estados Iberoamericanos para la Educación, la Ciencia y la Cultura (OEI) que señaló la importancia de fortalecer la enseñanza de las ciencias y la matemática como prioridad de los sistemas educativos. En la misma línea la OEI ha elaborado un documento de base destinado a impulsar un programa de ciencia y tecnología para el desarrollo sostenible, la equidad y la cohesión social, aplicable a escala iberoamericana. Este documento, que aspira a orientar la acción de la OEI durante los próximos años y a ofrecer un espacio de convergencia con otras organizaciones, ha sido puesto a consideración de la comunidad iberoamericana a través de la Web, habiendo sido consultado por más de un millón de lectores. Con este documento la OEI quiere dar un desarrollo especial a la Meta Educativa 9: Ampliar el Espacio Iberoamericano del Conocimiento y fortalecer la investigación científica y a todas aquellas referencias que la meta 5 tiene sobre la necesidad de fomentar las vocaciones hacia la ciencia y la ingeniería. Para cerrar este proceso participativo en ciencia, tecnología e innovación y darle al mismo tiempo un nuevo impulso, la OEI convoca al Congreso Iberoamericano de Ciencia, Tecnología, Innovación y Educación que se celebrará los días 12, 13 y 14 de noviembre de 2014 en la ciudad de Buenos Aires (Argentina) dando un espacio privilegiado a la incorporación de las TIC en cada una de las facetas educativas por lo que representará, además, un espacio de diálogo académico sobre el avance de las Metas Educativas 2021. El Congreso tiene una sección de comunicaciones libres para resultados de investigación y experiencias y esperamos que las acciones vinculadas a las Olimpíadas tenga una importante presencia que permita coordinar la cooperación entre todos los actores implicados para que en 2021 sea una realidad que haya muchos estudiantes atraídos por la matemática y la resolución de problemas. http://www.oei.es/congreso2014 TRES NECROLÓGICAS : PAWEL JAREK, LEON VAN DEN BROEK Y
MARIE HÉLÈNE DELEDICQ
Francisco Bellot
Como bastantes de nuestros lectores conocen, desde su creación el editor
de la REOIM está involucrado en el Concurso Canguro Matemático; de
hecho algunos de los países iberoamericanos participantes lo son por
iniciativa nuestra. Los años 2013 y lo que va del 2014 han sido
particularmente duros con la familia de “canguristas”, que ha perdido a tres
de sus miembros. Sirvan estas líneas de homenaje de respeto y
agradecimiento a su importante labor.
Pawel Jarek (Polonia)
Pawel Jarek (Ruda Slaska, 22 de junio de 1933 – Torún, 5 de febrero de
2013) fue, junto con varios matemáticos de Torún y Wroclaw, fundador del
Concurso Canguro Matemático en Polonia, y presidente de su Comité
Organizador entre 1992 y 1997, así como miembro del Comité Directivo de
Kangourou Sans Frontières durante los primeros años de la andadura
internacional de KSF.
Estudió Matemáticas en la Universidad “Nicolás Copérnico” de Torun, de
1950 a 1955, doctorándose en 1965 bajo la supervisión del Prof. Jerzy Los.
Trabajó en la Cátedra de Matemáticas de dicha Universidad y en su Instituto
de Matemáticas entre 1953 y 1994. Fue Vicedirector de dicho Instituto entre
1978 y 1985 así como entre 1989 y 1992. Sus líneas de investigación están
relacionadas con el álgebra, la dinámica topológica y los cuerpos aleatorios.
También estuvo involucrado en la Olimpiada matemática de Polonia (una de
las más prestigiosas de Europa) entre 1956 y 2013. Pero además Pawel
tenía otras pasiones: era un buen artista gráfico; sus dibujos de paisajes de
los montes Tatra y de los monumentos de la ciudad de Torún son muy
apreciados; un consumado excursionista montañero y un excelente
fotógrafo. Dirigía en Zakopane el campamento matemático de verano para
los ganadores del Canguro en varios países europeos. También le gustaba la
música clásica. Sus colegas del Canguro polaco continúan su incansable
trabajo. Descanse en paz.
Leon van den Broek (Holanda)
Pocas semanas después de la reunión internacional de KSF en Edimburo
(Noviembre 2013) nos llegó la inesperada mala noticia del fallecimiento
repentino de Leon van den Broek, el 11 de diciembre, como consecuencia
de un ataque al corazón.
El equipo holandés del canguro se ha visto así golpeado por la desgracia:
Leon era una persona enormemente activa, creaba cada año un gran
número de problemas para el concurso (de hecho Holanda ganó dos años
consecutivos, desde su creación, el premio al país del que más problemas
se habían elegido; la última vez, precisamente en Edimburgo). Era un
excelente matemático, un gran profesor y un buen polemista. Solía
participar en los grupos de trabajo de KSF de los alumnos más jóvenes para los que resulta, en mi opinión, más difícil encontrar buenos problemas,
con enjundia matemática pero formulación asequible para esos estudiantes;
y en eso, Leon era un maestro.
Pero además, Leon ayudaba a cualquier matemático que se lo pidiera. En
varias ocasiones le he pedido ayuda para encontrar alguna copia de
artículos en holandés del gran matemático holandés Oene Bottema,
publicados en revistas neerlandesas muy difíciles de encontrar. A vuelta de
correo recibía siempre el sobre con la fotocopia de los artículos buscados,
con la cariñosa advertencia: “Warning! Its written in Dutch!”, a lo que yo
solía contestarle: “Lo sé, pero tengo un diccionario” .
Le echaremos mucho de menos.
Marie Hélène Deledicq (Francia)
La esposa de André Deledicq, y cofundadora con él del Concurso Le
Kangourou des Mathématiques, falleció el 15 de abril de 2014 en su casa de
París, donde se fundó el concurso. Dirigió las primeras publicaciones de
ACL-Les éditions du Kangourou, contribuyendo de esta forma a la
popularización de las matemáticas en lengua francesa. Nacida el 11 de
noviembre de 1939, su labor y la de su marido André, Presidente de Honor
de KSF, la continúan sus hijos, Jean-Philippe y Jean-Christophe, tanto en la
Editorial como en la organización en Francia del Concurso.
Descanse en paz.
Valladolid, 11 de mayo de 2014.
Divertimentos matemáticos