Diapositiva 1

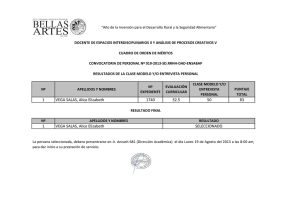
CIBSI’11
TO ARGEN
CI
T
NI
CA
UE
C
E SC
LA
O
IN
EJ É
R
Protocolo de autenticación
ZKP usando grupos no
conmutativos
TÉ
SU P
ERIOR
Juan Pedro Hecht
[email protected]
EST/FCEN/FI/FCE/UBA-Argentina
OBJETIVO
Desarrollar una prueba compacta
de autenticación de la clase ZKP
que pueda ser aplicada en
plataformas computacionales de
bajo porte.
2
SOLUCIÓN
Emplear sistemas algebraicos no
conmutativos (NCAS), en particular el
grupo de matrices de Hill de orden 8
modulo 251.
Como función de una vía se elige la
descomposición simétrica generalizada
(GSDP).
3
GSDP sobre NCAS
Sea G un grupo no conmutativo y S un subgrupo abeliano
dados ( x, y ) G G, S
hallar z
G , (m, n) Z ,
m
S tal que y z x z
n
dados (m,n,x,z) obtener (y)
dados (m,n,x,y) obtener (z)
4
Protocolo de una prueba
interactiva de identidad
Param
P
Alice
Pretendiente
5
Param
Testigo (azar)
Desafío (azar)
Respuesta
V
Bob
Verificador
Repetir r
números
de ciclos
Protocolo ZKP de identidad
• Caso especial de las pruebas interactivas
• Las pruebas de conocimiento cero
ofrecen una vía de probar conocimiento
a cualquier entidad sin transferirle
ningun dato adicional acerca de ese
conocimiento.
Un solo bit del secreto que se
filtre invalida la propiedad ZK
6
ZKP
7
.
ZKP
?
p=½
p=½
Observar que hay p=½ de acertar sin el secreto
y por eso se iteran r-ciclos de intercambio
8
.
OK
El protocolo
9
EL GRUPO MULTIPLICATIVO DE HILL [M8, Z251]
Matrices enteras no singulares módulo 251 de orden 8
Su producto no es conmutativo
Hay 10153.18 matrices en dicho grupo
PARA GENERAR SUBGRUPOS CONMUTATIVOS
TEOREMA: las matrices que comparten todos sus
vectores propios conmutan (dado que las matrices
diagonales poseen esa propiedad).
Basta definir matrices de Hill arbitrarias P como
matrices de autovectores y conjugar matrices diagonales
para obtener un subgrupo conmutativo P8 por cada una.
10
Preparación
PARÁMETROS
Matrices de Hill (M8)
dim=8
p=251
(m,n) εR Z ≥ 32 (m<>n)
Elementos estructurales públicos y compartidos
P εR M8 (matriz de vectores propios de P8)
G εR M8 (matriz base para obtener claves públicas)
Claves privadas de cada entidad
{A, B, …} εR P8 (A=PΔAP-1, B=PΔBP-1 , …) (AB=BA,…)
Claves públicas de cada entidad {GA, GB, …}ε M8 (GA = AmG
An, GB = BmG Bn, ... )
εR : elección aleatoria
11
Las claves privadas
12
Ciclo de intercambios
TESTIGO
k εR Z ≥ 32 (k<>m, k<>n)
S = Ak GB A-m
Alice envia a Bob S como testigo
DESAFÍO
b εR [0, 1]
si b=0  H εR M8 ; Q = Bm H Bn
si b=1  Q = Bm S GA Bn
Bob envia a Alice {b, Q} como desafio
RESPUESTA
si b=0  R = S-m Q S-n
si b=1  R = A-k Q A-n
Alice envia a Bob R como respuesta
13
Verificación del protocolo
VERIFICACIÓN
si b=0  controlar si Sm R Sn = Q
si b=1  controlar si B-mR B-n = GB G
ITERAR
Bob decide iterar el ciclo T-D-R-V r-veces
CONSISTENCIA DE LA VERIFICACIÓN
Si b=0  SmRSn = (SmS-m) Q (S-nSn) = Q
Si b=1  B-mR B-n= B-mA-kQ A-nB-n=B-mA-kBmSGA BnA-nB-n =
= B-m A-k Bm Ak GB A-m Am G An Bn A-n B-n =
= (B-m Bm)( A-k Ak) GB (A-m Am) G (An A-n)( Bn B-n) =
= GB G
14
Un ejemplo numérico
15
0 Se definen los elementos públicos comunes
dim=8, p=251, (m,n) εR Z, {P,G} εR [M8, Z251]
m= 23, n= 20 (m<>n)
60 36 46 213 222 147 178
P 129
71 95 216 84 223 204 66 106
72 27 69
98 34 95
73 114 148
197 196 154
82 77
7
241 142 226
G
16
163 243 133 75 45
182 5 219 160 160
238 0
74 16 143
149 79 240 210 163
67 44 168 61 122
96 146 159 74 183
18 187 1
81 200 172 159 144
48 177 201 138 184 174 22 113
147 207 60 109 77 81 238 149
49 90 67 68 127 8
59 24
163 11 229 82 100 190 239 154
5
10 112 113 170 180 167 243
181 30 244 184 131 90
4 156
129 72 73 140 73 201 141 57
1
Alice define sus claves privada y pública
Privada {A} εR [P8, Z251]
A
17
GA
P
A
*
251
23
251
Diag
G
*
251
251
P
A20
1
Bob define sus claves privada y pública
2
Privada (B) εR GL[P10, Z251]
B
GB
18
P
B
*
251
23
251
Diag
G
*
*
251
251
P
B
1
20
3 Alice calcula y envía el testigo
S
k εR Z = 19 (k<>m, k<>n)
S
19
19
A
*
251
GB
*
251
A
23
4
Bob calcula y envía el desafío
{Q,b}
b εR [0,1] = 1
Q
20
B 23
*
251
S
*
251
GA
*
251
B
20
5
Alice calcula y envía la respuesta
{R }
(b = 1)
R
21
A
19
*
251
Q
*
251
A
20
6
Bob valida la respuesta
(b = 1)
B-23R B-20 = GB G
23
B RB
20
GB G
22
63
122
155
240
20
196
58
170
95
110
152
219
15
112
74
244
121
88
132
55
112
127
150
45
87
197
220
192
31
191
167
80
219
145
191
229
187
13
207
207
192
38
1
233
250
118
230
232
161
139
124
144
209
10
119
245
80
192
238
99
238
182
171
178
63
122
155
240
20
196
58
170
95
110
152
219
15
112
74
244
121
88
132
55
112
127
150
45
87
197
220
192
31
191
167
80
219
145
191
229
187
13
207
207
192
38
1
233
250
118
230
232
161
139
124
144
209
10
119
245
80
192
238
99
238
182
171
178
(?)
Y Bob decide iterar r-veces
Testigo (Alice)
Generar k (entero aleatorio)
Complejidad
y
Velocidad
O(1)
Invertir A (por determinante)
O(2n3)
Generar S (11 productos)
O(11n3)
Desafío (Bob)
Generar b (bit aleatorio)
O(1)
Generar Q (8 productos)
O(8n3)
Respuesta (Alice)
Generar R (9 productos)
O(9n3)
Validación (Bob)
Invertir B (por determinante)
O(2n3)
Generar 8 productos
O(8n3)
Comparar y decidir
O(1)
Con la implementación libro de texto, el número equivalente
de operaciones por ciclo del protocolo es de t ≈ 20500 ops.
La ejecución del protocolo con Z=32, con algoritmos libro de
texto y en lenguaje intérprete Mathematica™ en un equipo
Windows™ XP (sp3)/ Intel™ Core Duo T2060/ 798 MHz/2
Gb RAM insumió 672 µs/fase preparación y 437 µs /ciclo
Testigo-Desafío-Respuesta-Validación.
23
Fraude y propiedad ZKP
24
¿Es posible un fraude?
Supongamos que se presenta Eve queriendo hacerse
pasar por Alice. Obviamente no posee la verdadera clave
privada A y por lo tanto, como no puede resolver GSDP
decide inventar una seudoclave aleatoria *A (pero que
pertenece al mismo subgrupo conmutativo de A).
(caso b = 0)
Lleva adelante un ciclo del protocolo y se autentica
como Alice sin inconvenientes. (Aqui la verificación no
depende del secreto de Alice).
(caso b = 1)
Lleva adelante un ciclo del protocolo y se rechaza su
identidad en forma inexorable. (Sin el secreto no
aprueba)
Veamos porqué…
25
CONSISTENCIA DE UNA
VALIDACIÓN FRAUDULENTA
b=0  *SmR*Sn = (*Sm*S-m) Q (*S-n*Sn) = Q
Cualquier testigo fraguado *S aprueba.
b=1  B-mR B-n= B-m*A-kQ *A-nB-n=B-m*A-kBm*SGA Bn*A-nB-n=
= B-m *A-k Bm *Ak GB *A-m Am G An Bn *A-n B-n =
= (B-m Bm)( *A-k *Ak) GB *A-m Am G An *A-n( Bn B-n)=
= GB *A-m Am G An *A-n <> GB G
La intervención de la clave pública lo impide.
p(fraude)=(1/2)r0
26
PRUEBA DE IDENTIDAD DE
CONOCIMIENTO CERO
•El verificador no puede aprender nada del protocolo
•El pretendiente no puede engañar consistentemente al
verificador
•El verificador no puede engañar consistentemente al
pretendiente
•El verificador no puede fingir ser el pretendiente
•Integridad (completeness).
•Solidez (soundness)
•Conocimiento Cero (ZKP)
27
Prueba de Conocimiento Cero
Propiedad de Integridad
Si el pretendiente y el verificador son honestos,
el protocolo es exitoso (probabilidad éxito = 1).
Supongamos que Alice posee el secreto A.
Entonces puede generar la respuesta correcta
(R=S-m Q S-n o R=A-k Q A-n) para cualquier
desafío Q que le imponga Bob.
Propiedad de Solidez
Si el pretendiente fuese deshonesto y el
verificador honesto, el protocolo falla
aproximadamente la mitad de las rondas de
autenticación (probabilidad éxito ≤ 0.5).
Propiedad de Conocimiento Cero
Una prueba de identidad posee la propiedad de conocimiento cero
(ZKP) si existe un simulador para dicha prueba. Un simulador es un
algoritmo capaz de generar reportes de sesión sin intervención del
pretendiente legítimo y que son indistinguibles de los genuinos.
28
La supuesta
“Alice” genera
el bit aleatorio
1Generar testigo
Generar bit aleatorio b εR [0, 1]
Si b=0  Generar testigo al azar S=*S εR M8
Si b=1  Generar testigo S=GB G GA-1
2Recibir desafío
Si b=0  Generar al azar *Q εR M8
Si b=1Q=BmSGABn=BmGBG(GA-1GA)Bn = BmGBGBn
3Devolver respuesta
Si b=0  *R=*S-m *Q *S-n
Si b=1  R=Q
4Verificar y registrar sesión
Si b=0  *Sm *R * Sn=*Q
Si b=1  B-mRB-n=(B-mBm) GBG(BnB-n)=GBG
Añadir (S, Q, b, R) al registro de sesión.
5Iterar
Repetir a voluntad 1. a 4. r-veces.
Observar que ese bit aleatorio lo debe generar Bob y no
“Alice”, por eso no se puede usar al simulador para
cometer fraude con probabilidad ≥ (½)r (para r-ciclos).
29
Acerca de la seguridad del protocolo:
El grupo de las matrices enteras (módulo 251) y
de orden ocho M8 posee un cardinal 25164 ~
10153.58. El subgrupo de matrices de Hill es de
10153.18, por eso la probabilidad de hallar
matrices Z251 singulares es baja pero no
despreciable (p ~ 0.004).
El tamaño de este grupo no aporta seguridad.
Para quebrar el presente protocolo por fuerza
bruta hay que hallar una clave privada …
30
.
Acerca de la seguridad del protocolo:
En conclusión podemos inferir una seguridad
criptográfica de 64 bits para la presente
instancia del protocolo ZKP.
31
.
NI
CA
UE
C
E SC
LA
O
IN
EJ É
R
TO ARGEN
CI
T
TÉ
SU P
ERIOR
Juan Pedro Hecht
[email protected]
EST/FCEN/FI/FCE/UBA-Argentina