Esfuerzos de estanques - Departamento de Ingeniería Metalúrgica

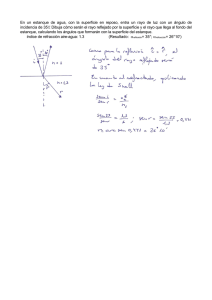
Resistencia de Materiales. Capítulo X. Esfuerzos en estanques.
CAPÍTULO X
ESFUERZOS EN ESTANQUES
En ingeniería es importante conocer los esfuerzos sobre estanques, debido a la
necesidad de diseñar bajo requisitos de seguridad. Usualmente, los estanques
deben resistir presiones internas, ya sea de líquidos o de gases. Esa presión interna
genera esfuerzos en la superficie del estanque, ya sea longitudinales o
transversales, en el caso de estanques cilíndricos. En el caso de estanques esféricos,
dicho esfuerzo es sólo uno. Estos esfuerzos deben compararse con los esfuerzos
admisibles de acuerdo al material de que se trate. A su vez este esfuerzo admisible
está relacionado con el límite elástico y con el factor de seguridad. Este factor de
seguridad se define como:
S
 elástico
 admisible
Así, diseñar con un factor de seguridad 2 (S=2) supone que el máximo esfuerzo
admisible debe ser la mitad del límite elástico.
10.1. Recipientes cilíndricos
L
f

F’
F
F’
Figura 10.1. Estanque cilíndrico.
En la figura 10.1 se muestra la mitad de un estanque cilíndrico. Al balancear las
fuerzas según los ejes x e y queda:
F   f
x
cos   0
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
10-1
Resistencia de Materiales. Capítulo X. Esfuerzos en estanques.
F   f
y
sen   F
pero:
F  P  A
F  PDL
A  DL 
La fuerza ejercida por el fluido interno depende del largo del cilindro.
Además:
F  0

F  2F ` 0
en que F es la fuerza ejercida por el fluido sobre el semicilindro y F’ es la fuerza de
resistencia que oponen las dos paredes del semicilindro.
F `
PDL
2
espesor t
Figura 10.2. Estanque cilíndrico.
El esfuerzo tangencial t se calcula a través de:
t 
F`
A
con lo cual, el esfuerzo transversal t queda:
t 
PD
2t
(1)
Haciendo un análisis similar, se puede determinar el esfuerzo longitudinal a través
del siguiente análisis:
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
10-2
Resistencia de Materiales. Capítulo X. Esfuerzos en estanques.
f
F
Figura 10.3. Esfuerzo longitudinal en un estanque cilíndrico.
La fuerza y el área se pueden calcular a través de:
F  PA
2
A D
4
De aquí, se deduce que:
F
PD 2
4
El esfuerzo longitudinal se calcula a través de:
l 
F
A´
y dado que A’=Dt, el esfuerzo longitudinal queda:
PD 2
PD
  4 
DT
4t
Por lo tanto, el esfuerzo longitudinal l
 
PD
4t
(2)
De (1) y (2) se desprende que
t 
de hecho
 t  2 
de donde se desprende que el esfuerzo limitante en el diseño es t
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
10-3
Resistencia de Materiales. Capítulo X. Esfuerzos en estanques.
10.2 Recipientes esféricos
En este caso, sólo existe un esfuerzo.
f
F
t
Figura 10.4. Esfuerzo en un estanque esférico.
En este caso debe cumplirse que:
f
F
La fuerza se calcula a través de
F=PA
A su vez, el área es:
A D
2
4
la fuerza ejercida por el fluido queda por lo tanto:
F
PD 2
4
El esfuerzo en el estanque esférico se calcula a través de:
 l
F
A'
y dado que el área es:
A'  Dt
entonces el valor del esfuerzo, se calcula a través de :
PD 2
PD
  4 
Dt
4t
con lo cual
 
PD
4t
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
10-4