Lección 4 La conducción en semiconductores. Unión PN.

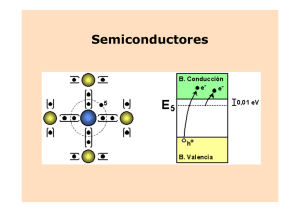
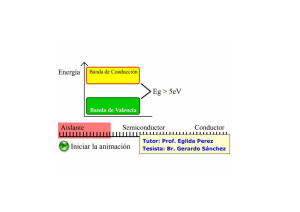
Lección 4
La conducción en semiconductores. Unión PN.
1.
Características generales de los semiconductores.
1
2.
Semiconductores intrínsecos y extrínsecos.
4
3.
La conducción en semiconductores
7
3.1.
Corriente de arrastre. Conductividad.
7
3.2.
Corrientes de difusión
9
3.3.
Generación y recombinación de portadores.
10
3.4.
Ecuación de continuidad.
10
4.
5.
Unión PN.
11
4.1.
Unión PN en equilibrio.
11
4.2.
Unión PN polarizada.
13
4.3.
Característica intensidad-tensión.
15
4.4.
El diodo como elemento de circuito
--
Tipos de diodos.
--
Lección 4. La conducción en semiconductores. Unión PN.
1.-
1
Características generales de los semiconductores.
Además de los elementos pasivos de circuito estudiados hasta ahora
(resistencia, y condensador) en la electrónica actual existen una multitud de
componentes que forman parte de los circuitos y que pueden ser activos pasivos.
Como quiera que la mayor parte de ellos se basan en las propiedades de los
materiales semiconductores, dedicaremos este tema a analizar las características de
estos materiales y su comportamiento eléctrico.
Ya hemos visto en este curso que, desde el punto de vista de la conducción,
las sustancias se clasifican en conductores, aislantes y semiconductores y hemos
estudiado las propiedades eléctricas de los conductores y de los aislantes o
dieléctricos, centraremos nuestro estudio, ahora, en los materiales semiconductores.
Los semiconductores han hecho posible el desarrollo espectacular que ha
experimentado la Electrónica y sus aplicaciones, sobre todo a partir de 1948 cuando
se inventó el transistor y otros dispositivos de estado sólido.
Como ya hemos dicho en lecciones anteriores, la mayor parte de sólidos
presentan una estructura cristalina cuando se observan a través del microscopio. Esta
estructura se manifiesta externamente por la presencia de ciertos ángulos y planos;
así por ejemplo, los cristales de nieve aunque contienen una variedad infinita de
formas geométricas, sólo presentan ángulos de 60°. El cloruro sódico forma cubos;
otros materiales, largas agujas o variantes
de
estructuras
hexagonales
o
rectangulares. Cada elemento (sólido cristalino), por consiguiente, tiene una estructura
característica. La estructura interna de los sólidos se ha investigado mediante los
rayos X; al atravesar un haz de estos un cristal, los rayos son desviados y distribuidos
según la disposición específica de los átomos y moléculas en el cristal. Estos
resultados indican que los átomos se encuentran distribuidos en configuraciones
regulares y específicas, de modo que la estructura se puede generar por la repetición,
en las tres direcciones del espacio, de una unidad estructural básica o celda unidad.
Centraremos nuestro estudio en cómo es la estructura cristalina de los
semiconductores. Los elementos típicamente semiconductores son el germanio y el
silicio; aunque para ciertas aplicaciones se utilizan semiconductores compuestos,
como el arseniuro de Galio (GaAs). Desde 1960, el silicio ha desplazado casi
completamente al germanio en la fabricación de los dispositivos electrónicos, tanto
discretos como integrados.
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
2
El silicio, como el germanio, es un elemento tetravalente. Los cuatro electrones
más periféricos (electrones de valencia) no pueden mover libremente a través del
cristal, es decir no son electrones libres. Forman parte de los enlaces covalentes que
mantienen unidos al conjunto de los átomos del semiconductor, formando su
estructura cristalina.
Esta es la indicada en la figura. Cada
átomo se encuentra en el centro de un
tetraedro regular y tiene cuatro vecinos que
equidistan de él; de forma que cada átomo
comparte sus electrones de valencia con
dichos átomos vecinos. Las barras que en la
figura conectan a los átomos representan la
localización espacial de estos electrones de
valencia.
Para representar, en dos dimensiones, las principales características de la
estructura cristalina, se suele utilizar un modelo bidimensional de enlaces como de de
la figura siguiente. Cada ion o núcleo (núcleo atómico más capas electrónicas
profundas) tiene una carga +4qe. Este incorpora dos de las propiedades más
importantes de la estructura tridimensional:
a) Cada átomo se encuentra rodeado de
+4
Si
+4
Si
+4
Si
+4
Si
+4
Si
+4
Si
+4
Si
+4
Si
+4
Si
cuatro vecinos equidistantes.
b) Los electrones de valencia, cuatro por
átomo,
son
compartidos
por
dichos
vecinos. Cada enlace entre un átomo y uno
de sus vecinos contiene dos electrones.
Cuando todos los electrones de valencia se encuentran en sus respectivos
enlaces covalentes, como ocurre a 0 K, la conducción no es posible ya que no hay
electrones que puedan contribuir a la conducción. Por tanto, el semiconductor se
comporta como un aislante, a esta temperatura. Un elemento que presenta esta
disposición de los electrones, incluso a temperaturas elevadas, es el diamante; que es
un aislante muy bueno.
Para cualquier temperatura por encima de los cero grados, siempre existen
algunos pocos o muchos (dependiendo de aquélla) enlaces covalentes incompletos.
Los electrones que han roto sus enlaces no están confinados en la región donde se
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
3
encontraban éstos, sino que son libres de moverse por todo el cristal. A temperatura
ambiente ( ∼ 300 K), los pocos electrones que han roto sus enlaces lo hacen como
consecuencia de la agitación térmica.
hueco
+4
Si
Electrón de
conducción
Electrón de
valencia
+4
+4
Si
Si
Esta fracción de electrones, que se convierten en libres y, por lo tanto, pueden
cooperar a la conducción, es muy pequeña. Por ejemplo, en el germanio a
temperatura ambiente existen alrededor de 1013 enlaces rotos por centímetro cúbico
(cc); como tiene 1023 átomos/cc, sólo un átomo de cada 1010 ha roto su enlace. No
obstante, aunque la proporción sea tan pequeña, tiene un gran efecto sobre las propiedades eléctricas de un semiconductor; proporciona electrones libres, haciendo, por
tanto, posible la conducción. Por esto, el germanio, se considera un semiconductor
más que un aislante, como es el diamante. En éste el número de enlaces rotos es del
orden de 1 en 1015, es decir, de 108 por cc. En general, el que una sustancia sea
aislante o semiconductora depende de la energía mínima necesaria para hacer que los
electrones de valencia ligados a los enlaces se conviertan en electrones libres que
puedan contribuir a la conducción. A esta energía mínima se le suele denominar Gap
de material (es más correcto decir energía del Gap). Los materiales semiconductores
tienen un Gap del orden del 1 eV frente los 10 eV o más típico de los aislantes. En
concreto, el Germanio, tiene un Gap de 0.7 eV y el silicio, posiblemente el
semiconductor más utilizado, lo tiene de 1.1 eV.
Como consecuencia de los enlaces rotos existen dos grupos de portadores de
carga, distintos e independientes en los semiconductores, que cooperan a la corriente
eléctrica. Unos son los electrones libres, producidos al romperse un enlace, que
pueden moverse a través de todo el cristal y no pertenecen a ningún átomo en
particular. Son los llamados electrones de conducción, que tienen una carga -qe y que
cooperan a la conducción de la misma manera que los electrones libres de un metal.
Los otros portadores de carga están asociados con los electrones de valencia
que permanecen en sus enlaces. Un enlace roto representa una región localizada del
espacio con un exceso de carga positiva. Esta región de carga positiva ( +qe) se
denomina hueco porque aparece como consecuencia de un defecto o una vacante en
la estructura de enlaces. No es evidente que un hueco se pueda mover en el
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
4
semiconductor independientemente de los electrones de conducción. El movimiento de
la carga positiva localizada tiene lugar porque un electrón de valencia, en un enlace
cercano al roto (es decir, al hueco), puede ocupar la vacante, dando lugar a que el
hueco se mueva en sentido opuesto. Los electrones de valencia se pueden mover de
enlace a enlace, sin adquirir la energía necesaria para quedar libres de la estructura
de enlaces. Por lo tanto, los huecos se pueden mover a través del semiconductor sin
interferir con los electrones de conducción.
Aunque esta descripción del movimiento de un hueco, en términos del
movimiento de los electrones de valencia, resulta gráfica y útil, no debe llevarse hasta
los últimas consecuencias, porque da lugar a contradicciones. Sin profundizar en el
tema, insistiremos en que el concepto de hueco, como portador de carga positiva, es
un artificio que nos permite describir, de manera simple y elegante, el movimiento
complejo de los electrones de valencia.
Paralelamente a proceso de generación térmica de pares electrón hueco se
produce el de recombinación; algunos electrones de conducción pueden perder
energía (emitiéndola en forma de radiación luminosa, por ejemplo) y caer en un enlace
vacante, es decir recombinándose con un hueco. Si la temperatura se mantiene
constante los procesos de generación y recombinación están equilibrados de forma
que existirá el mismo número de huecos en la banda de conducción que en la banda
de valencia.
2.- Semiconductores intrínsecos y extrínsecos.
A un semiconductor puro, como el descrito en el apartado anterior, se le
denomina semiconductor intrínseco. En estas condiciones la densidad de
electrones libres (n) será igual que la densidad de huecos (p) de forma que
n = p ≡ ni
ni se denomina concentración intrínseca de portadores y, para un cristal determinado
es función de la temperatura. Nótese que se cumple que: np = ni2 . Esta ecuación se
suele denominar Ley de acción de masas.
La conductividad de un semiconductor intrínseco como el germanio o el silicio
(elementos tetravalentes), se puede mejorar si añade un pequeño porcentaje de
átomos trivalentes o pentavalentes (dopado del semiconductor). A un semiconductor
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
5
de este tipo, se le denomina semiconductor extrínseco y el proceso de adicción de
estas impurezas se suele denominar dopado del semiconductor.
Los semiconductores dopados con
impurezas
pentavalentes
se
denominan
semiconductores tipo N mientras que los que
incorporan
impurezas
trivalentes
+4
Si
+4
Si
+4
Si
+4
Si
+5
Sb
+4
Si
+4
Si
+4
Si
+4
Si
se
denominan de tipo P.
En un semiconductor del tipo N los
átomos de la impureza desplazarán algunos
átomos de silicio (o germanio) del cristal.
Cuatro de los cinco electrones de valencia
ocuparán enlaces covalentes, y el quinto
Semiconductor tipo N de silicio dopado con
impurezas pentavalentes de antimonio (Sb).
quedará inicialmente sin enlace.
Este electrón sobrante del átomo pentavalente no ejerce ninguna función sobre
el enlace covalente, es decir, no contribuye a mantener unido el cristal y estará
débilmente unido al átomo de forma que la energía requerida para liberarlo es mucho
menor que la necesaria para romper un enlace covalente.
A bajas temperaturas el electrón estará ligado a su átomo, pero al aumentar la
temperatura pasará fácilmente a la banda de conducción, posibilitando así, la
conducción eléctrica, sin que se hayan formado pares electrón hueco, ya que no se ha
roto ningún enlace. Estas impurezas que ceden electrones se denominan impurezas
donadoras.
Si se aumenta lo suficiente la temperatura comenzarán a romperse los enlaces
y a formarse, por tanto, pares electrón–hueco de forma que la conducción se llevará a
cabo por ambos tipos de portadores. No obstante, la concentración de electrones de
conducción será mucho mayor que la de huecos de valencia de forma que los
electrones son los portadores mayoritarios y los huecos minoritarios. Dado que las
impurezas están presentes en cantidades siempre muy pequeñas, a temperaturas
elevadas el número de pares de portadores formados puede llegar a ser mucho mayor
que el número de átomos de impurezas y el semiconductor se comportará como
intrínseco. Las impurezas pentavalentes que se suelen emplear son antimonio, fósforo
y arsénico.
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
6
En los semiconductores tipo P las
impurezas son átomos con tres electrones
de valencia que al intercalarse en la red
+4
Si
+4
Si
+4
Si
+4
Si
+3
In
+4
Si
+4
Si
+4
Si
+4
Si
cristalina dejan un enlace por átomo sin
completar. A temperaturas próximas al cero
absoluto, estos enlaces están vacíos, pero al
aumentar la temperatura algunos electrones
de valencia de los enlaces pueden ocupar
estos enlaces desocupados provocando la
aparición de un hueco en enlace que dejan
Semiconductor tipo P de silicio dopado con
impurezas trivalentes de Indio (In)
libre.
Los electrones situados en los en los enlaces de los iones aceptores no
contribuyen a la conducción ya que forman parte de un enlace. Sin embargo, los
huecos que han dejado en la banda de valencia si contribuyen, de forma que aunque
la temperatura sea suficientemente alta para que se produzcan pares electrón –
hueco, la conducción en los semiconductores tipo P se debe fundamentalmente a
huecos. De la misma forma que en el caso de los semiconductores tipo N, a
temperaturas elevadas la concentración intrínseca llega a enmascarar a la extrínseca
y el semiconductor se comporta como si fuese puro.
En el caso de los semiconductores extrínsecos también se cumple la Ley de
acción de masas aunque, a diferencia del caso intrínseco, las concentraciones de
electrones y huecos no son iguales.
Tipo N : n > p 
2
 ⇒ np = ni
Tipo P : p > n 
Además, en un semiconductor que presente impurezas donadoras (de
concentración ND) y aceptoras (de concentración NA), la conservación de la carga
exige que se cumpla que:
ND + p = N A + n
que se conoce con el nombre de ecuación del semiconductor. Hemos considerado, al
escribir esta ecuación que todas las impurezas estaban totalmente ionizadas ya que
esto ocurre a temperaturas muy bajas. Teniendo en cuenta esto, el primer miembro
corresponde a la concentración de cargas positivas en el semiconductor que debe ser
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
7
numéricamente igual a la concentración de cargas negativas (indicada en el segundo
miembro).
3.- La conducción en semiconductores.
3.1.- Corriente de arrastre. Conductividad.
Según todo lo anterior, en semiconductor a temperatura ambiente coexisten
dos tipos de portadores de carga: electrones libres y huecos, cuyas concentraciones
dependen de la temperatura. Aún en ausencia de campo aplicado en un
semiconductor homogéneo y en equilibrio térmico, los iones de la red y los portadores
de carga están siempre en movimiento térmico aleatorio; los iones vibran en torno a
sus posiciones de equilibrio y los portadores de carga se mueven rápidamente en
direcciones aleatorias sufriendo numerosos choque aleatorios entre sí y con las
impurezas y heterogeneidades de la red. Puesto que este movimiento es aleatorio, la
velocidad media de los portadores es nula.
r
Si se aplica un campo eléctrico E , al movimiento aleatorio de las partículas
(agitación térmica) se le superpone un movimiento en la dirección del campo de forma
que la velocidad media de los portadores no es nula.
r r
E=0
r r
E≠0
Si suponemos un modelo de conducción del tipo Drude (lección 3. corriente
eléctrica), la acción del campo eléctrico sobre los portadores estará contrarrestada por
una fuerza disipativa proporcional a la velocidad que representará la interacción de los
portadores de carga con las impurezas y heterogeneidades de la red de forma que la
velocidad media de los portadores de carga será constante y proporcional al campo
aplicado, es decir
r r
r
r
v p = µ p E vn = −µ n E
siendo µp y µn las movilidades de huecos y electrones respectivamente que
dependerán de la temperatura (disminuyen con la temperatura), del tipo de material y
del grado de pureza del mismo. La movilidad de los electrones es mayor de la de los
huecos.
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
8
La densidad de corriente total por esta causa es la suma de la debida a
electrones mas la debida huecos, por tanto
r
r
r
r
J C = − qnv n + qpv p = q (nµ n + pµ p ) E
donde, siguiendo la notación habitual, q es el valor absoluto de la carga del electrón y
n y p las concentraciones de electrones y huecos respectivamente. Comparando esta
expresión con la Ley de Ohm obtenida en el capítulo 3 para conductores, la
conductividad de un semiconductor estará dada por:
σ = q( µ n n + µ p p)
En un semiconductor intrínseco n = p= ni, y por tanto:
σ = q ( µ n + µ p ) ni
Para los semiconductores extrínsecos tendremos las siguientes expresiones
aproximadas.
Tipo N: n >> p ⇒ σ ≈ qµ n n ;
Tipo P: p >> n ⇒ σ ≈ qµ p p
Es importante señalar que ya que la movilidad y la concentración de cada tipo de portadores
son función de la temperatura la conductividad también lo será. En la figura se muestra la
dependencia de la conductividad con la temperatura para semiconductores intrínsecos
Conductividad σ(Ω-1cm-1)
y extrínsecos.
Semiconductor
extrínseco
Semiconductor
intrínseco
273
73
Temperatura (K)
A muy bajas temperaturas, la conductividad es nula en ambos casos, ya que no
hay portadores libres; todos los enlaces están saturados y las impurezas no se han
ionizado. A medida que aumenta la temperatura, se observan grandes diferencias de
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
9
comportamiento entre el material intrínseco y el extrínseco. Un pequeño aumento de
temperatura supone la ionización de la totalidad de las impurezas del material
extrínseco, lo que implica un gran aumento de la concentración de portadores y el
consiguiente aumento de la conductividad. En el material intrínseco, el incremento de
temperatura supone un aumento gradual de la concentración de portadores debido a
la ruptura de enlaces por agitación térmica, siendo este crecimiento mucho mas lento
que en el caso extrínseco.
A partir de ciertos valores de la temperatura, (del orden de 373 K) el número de
pares generados por agitación térmica puede llegar a ser del mismo orden que los
producidos por la ionización de las impurezas. De esta forma, para temperaturas
superiores, la diferencia entre la conductividad intrínseca y extrínseca se reduce
notablemente y el material dopado se comporta como intrínseco.
3.2.- Corriente de difusión.
Hasta ahora hemos considerados semiconductores intrínsecos o con dopado
homogéneo y, por tanto, con una densidad de portadores en equilibrio homogénea. Si
la concentración de portadores en la muestra semiconductora no es uniforme,
aparecerá un gradiente de concentración que da lugar a una difusión de portadores
desde las zonas de mayor concentración a las de menor concentración, con el
correspondiente transporte de cargas. La densidad de corriente de difusión sigue
formalmente la Ley de Fick, siendo proporcional al gradiente de concentraciones, es
decir:
r
r
J nd = qDn ∇n
r
r
J pd = −qD p ∇ p
siendo Dn y Dp las constantes de difusión para electrones y huecos, respectivamente.
Sus dimensiones son: [D]=L2T-1.
Si la variación de concentraciones se produce en una sola dimensión la x, por
ejemplo. Las densidades de corriente de difusión de electrones y huecos,
respectivamente son,
J nd = qDn
∂n
∂p
; J pd = −qD p
∂x
∂x
Hay que señalar que el movimiento de portadores se hace en sentido opuesto al
gradiente de sus concentraciones. En el caso de los huecos, el sentido coincide con el
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)
Lección 4. La conducción en semiconductores. Unión PN.
10
de la corriente, mientras que en le caso de los electrones la densidad de corriente es
opuesta a la velocidad de desplazamiento.
Las constantes de difusión de electrones y de huecos están relacionadas entre
sí y con las movilidades mediante la Relación de Einstein.
Dn
µn
=
Dp
µp
=
kT
= VT
q
donde k es la constante de Boltzmann y T la temperatura absoluta. VT recibe el
nombre de potencial equivalente de temperatura. Su valor a temperatura ambiente
(300 K) es de 26 mV.
En un semiconductor en el que se producen simultáneamente corrientes de
desplazamiento y de difusión, las densidades de corriente totales vendrán dadas por:
r
r
r
J p = qpµ p E − qD p ∇p
r
r
r
J n = qnµ n E + qDn ∇n
que en una dimensión quedan como:
∂p
∂x
∂n
= qnµ n E x + qDn
∂x
J px = qpµ p E x − qD p
J nx
Propiedades eléctricas del silicio y del germanio
Propiedad
Germanio
Silicio
µn a 300 K (cm2/Vs)
3800
1350
µp a 300 K (cm2/Vs)
1829
500
σintrinseca (Ω-1 cm-1)
0.022
4.3×10-6
Dn a 300 K (cm2/s)
100
35
Dp a 300 K (cm2/s)
48
13
εr
16
12
Apuntes de Fundamentos Físicos de la Informática. (© Dr. J. García Rubiano)