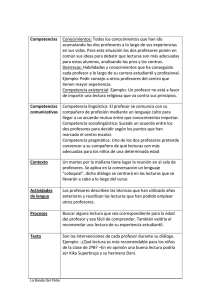
la enseñanza de la geometría y

Antología de lecturas
Matemáticas
¡CÓMO SE DIVERTÍAN!
ISAAC ASIMOV
Margie incluso lo escribió aquella noche en su diario, en la página encabezada con la fecha 17 de
mayo de 2157. «¡Hoy, Tommy ha encontrado un libro auténtico!»
Era un libro muy antiguo. El abuelo de Margie le había dicho una vez que, siendo pequeño, su abuelo
le contó que hubo un tiempo en que todas las historias se imprimían en papel.
Volvieron las páginas, amarillas y rugosas, y se sintieron tremendamente divertidos al leer palabras
que permanecían inmóviles, en vez de moverse como debieran, sobre una pantalla. Y cuando se
volvía a la página anterior, en ella seguían las mismas palabras que se habían leído por primera vez.
-¡Será posible! -comentó Tommy- ¡Vaya despilfarro! Una vez acabado el libro, sólo sirve para tirarlo,
creo yo. Nuestra pantalla de televisión habrá contenido ya un millón de libros, y todavía le queda sitio
para muchos más. Nunca se me ocurriría tirarla.
-Ni a mí la mía -asintió Margie.
Tenía once años y no había visto tantos libros de texto como Tommy, que ya había cumplido los trece.
-¿Dónde lo encontraste? -preguntó la chiquilla.
-En mi casa -respondió él sin mirarla, ocupado en leer-. En el desván.
-¿Y de qué trata?
-De la escuela.
Margie hizo un mohín de disgusto.
-¿De la escuela? ¡Mira que escribir sobre la escuela! Odio la escuela.
Margie siempre había odiado la escuela, pero ahora más que nunca. El profesor mecánico le había
señalado tema tras tema de geografía, y ella había respondido cada vez peor, hasta que su madre,
meneando muy preocupada la cabeza, llamó al inspector.
Se trataba de un hombrecillo rechoncho, con la cara encarnada y armado con una caja de
instrumental, llena de diales y alambres. Sonrió a Margie y le dio una manzana, llevándose luego
aparte al profesor. Margie había esperado que no supiera recomponerlo. Sí que sabía. Al cabo de
una hora poco más o menos, allí estaba de nuevo, grande, negro y feo, con su enorme pantalla, en la
que se inscribían todas las lecciones y se formulaban las preguntas. Pero eso, al fin y al cabo no era
tan malo. Margie detestaba sobre todo la ranura donde tenía que depositar los deberes y los
ejercicios.
Había que transcribirlos siempre al código de perforaciones que la obligaron a aprender cuando tenía
seis años. El profesor mecánico calculaba la nota en menos tiempo que se precisa para respirar.
El inspector sonrió una vez acabada su tarea y luego, dando una palmadita en la cabeza de
Margie, dijo a su madre:
-No es culpa de la niña, señora Jones. Creo que el sector geografía se había programado con
demasiada rapidez. A veces ocurren estas cosas. Lo he puesto más despacio, a la medida de diez
años. Realmente, el nivel general de los progresos de la pequeña resulta satisfactorio por completo...
Y volvió a dar una palmadita en la cabeza de Margie. Ésta se sentía desilusionada. Pensaba que se
llevarían al profesor. Así lo habían hecho con el de Tommy, por espacio de casi un mes, debido a que
el sector de historia se había desajustado.
-¿Por qué iba a escribir alguien sobre la escuela? -preguntó a Tommy.
El chico la miró con aire de superioridad.
-Porque es una clase de escuela muy distinta a la nuestra, estúpida. El tipo de escuela que tenían
hace cientos y cientos de años. -Y añadió campanudamente, recalcando las palabras-: Hace siglos.
Margie se ofendió.
1
Antología de lecturas
Matemáticas
-De acuerdo, no sé qué clase de escuela tenían hace tanto tiempo. -Leyó por un momento el libro por
encima del hombro de Tommy y comentó-: De todos modos, había un profesor.
-¡Pues claro que había un profesor! Pero no se trataba de un maestro normal. Era un hombre.
-¿Un hombre? ¿Cómo podía ser profesor un hombre?
-Bueno... Les contaba cosas a los chicos y a las chicas y les daba deberes para casa y les hacía
preguntas.
-Un hombre no es lo bastante listo para eso.
-Seguro que sí. Mi padre sabe tanto como mi maestro.
-No lo creo. Un hombre no puede saber tanto como un profesor.
-Apuesto a que mi padre sabe casi tanto como él.
Margie no estaba dispuesta a discutir tal asierto. Así que dijo:
-No me gustaría tener en casa a un hombre extraño para enseñarme.
Tommy lanzó una aguda carcajada.
-No tienes ni idea, Margie. Los profesores no vivían en casa de los alumnos. Trabajaban en un
edificio especial, y todos los alumnos iban allí a escucharles.
-¿Y todos los alumnos aprendían lo mismo?
-Claro. Siempre que tuvieran la misma edad...
-Pues mi madre dice que un profesor debe adaptarse a la mente del chico o la chica a quien enseña y
que a cada alumno hay que enseñarle de manera distinta.
-En aquella época no lo hacían así. Pero si no te gusta, no tienes por qué leer el libro.
-Yo no dije que no me gustara -respondió con presteza Margie.
Todo lo contrario. Ansiaba enterarse de más cosas sobre aquellas divertidas escuelas. Apenas
habían llegado a la mitad, cuando la madre de Margie llamó:
-¡Margie! ¡La hora de la escuela!
-Todavía no, mamá -suplicó Margie, alzando la vista.
-¡Ahora mismo! -ordenó la señora Jones-. Probablemente es también la hora de Tommy.
-¿Me dejarás leer un poco más del libro después de la clase? -pidió Margie a Tommy.
-Ya veremos -respondió él con displicencia.
Y se marchó acto seguido, silbando y con su polvoriento libro bajo el brazo. Margie entró en la sala de
clase, próxima al dormitorio. El profesor mecánico ya la estaba esperando. Era la misma hora de
todos los días, excepto el sábado y el domingo, pues su madre decía que las pequeñas aprendían
mejor si lo hacían a horas regulares.
Se iluminó la pantalla y una voz dijo:
-La lección de aritmética de hoy tratará de la suma de fracciones propias. Por favor, coloque los
deberes señalados ayer en la ranura correspondiente.
Margie obedeció con un suspiro. Pensaba en las escuelas antiguas, cuando el abuelo de su abuelo
era un niño, cuando todos los chicos de la vecindad salían riendo y gritando al patio, se sentaban
juntos en clase y regresaban en mutua compañía a casa al final de la jornada. Y como aprendían las
mismas cosas, podían ayudarse mutuamente en los deberes y comentarlos.
Y los maestros eran personas...
El profesor mecánico destelló sobre la pantalla:
-Cuando sumamos las fracciones una mitad y un cuarto.
Margie siguió pensando en lo mucho que tuvo que gustarles la escuela a los chicos en los tiempos
antiguos. Siguió pensando en cómo se divertían.
FIN
Título Original: The Fun They Had © 1951.
2
Antología de lecturas
Matemáticas
EL BRUTO DE LAS MATES
Pedro Pablo Sacristán
Ese año en el colegio del barrio había nuevo profesor de matemáticas, y también unos cuantos niños
nuevos. Y uno de estos niños nuevos era de lo más bruto que había visto nadie. Daba igual lo rápido
o despacio que le explicasen las cosas de números, siempre terminaba diciendo alguna barbaridad:
que si 2 y 2 son cinco, que si 7 por 3 eran 27, que si un triángulo tenía 30 ángulos...
Así que lo que antes era una de las clases más odiadas y aburridas, se terminó convirtiendo en una
de las más divertidas. Animados por el nuevo profesor, los niños descubrían las burradas que decía
el chico nuevo, y con un ejemplo y sin números, debían corregirle. Todos competían por ser los
primeros en encontrar los fallos y pensar la forma más original de explicarlos, y para ello utilizaban
cualquier cosa, ya fueran golosinas, cromos, naranjas o aviones de papel.
Al niño bruto parecía no molestarle nada de aquello, pero el pequeño Luisito estaba seguro de que
tendría que llevar la tristeza por dentro, así que un día decidió seguir al niño bruto a su casa después
del colegio y ver cuándo se ponía a llorar...
A la salida del cole, el niño caminó durante unos minutos, y al llegar a un pequeño parque, se quedó
esperando un rato hasta que apareció... ¡el profesor nuevo! . Se acercó, le dio un beso, y se fueron
caminando de la mano. En la distancia, Luisito podía oir que hablaban de matemáticas... ¡y el niño
bruto se lo sabía todo, y mucho mejor que ninguno en la clase!
Luisito se sintió tan engañado que se dio una buena carrera hasta alcanzarlos, y se plantó delante de
ellos muy enfadado. El niño bruto se puso muy nervioso, pero el maestro, comprendiendo lo que
pasaba, explicó a Luisito que lo del niño bruto sólo era un truco para que todos los niños aprendieran
más y mejor las matemáticas, y que lo hicieran de forma divertida. Su hijo estaba encantado de hacer
de niño bruto, porque para hacerlo bien se lo tenía que aprender todo primero, y así las clases eran
como un juego.
Por supuesto, al día siguiente el profesor explicó la historia al resto de los alumnos, pero éstos
estaban tan encantados con su clase de matemáticas, que lo único que cambió a partir de entonces
fue que todos empezaron a turnarse en el papel de "niño bruto".
Chilanga Banda
Cafe Tacuba
Ya chole chango chilango
Que chafa chamba te chutas
No checa andas de tacuche
Y chale con la charola.
Tan choncho como una chinche
Mas chueco que la fayuca
Con fusca y con cachiporra
Te pasa andar de guarura.
Mejor yo me hecho una chela
Y chance enchufo una chava
Chambiando de chafirete
Me sobra chupe y pachanga.
Si choco saco chipote
La chota no es muy molacha
Chiveando a los que machucan
Se va a morder su talacha.
De noche caigo al congal
No manches dice la changa
Al choro del teporocho
Enchifla pasa la bacha.
Pachucos cholos y chundos,
Chinchinflas y malafachas
Aca los chompiras rifan
Y bailan tibiritabara.
Mejor yo me hecho una chela
Y chance enchufo una chava
Chambeando de chafirete
3
Antología de lecturas
Me sobra chupe y pachanga.
Coro
Mi ñero mata la bacha
Y canta la cucaracha
Su choya vive de chochos
De chemo, chupe y garnachas.
Transando de arriba abajo
Ahi va la chilanga banda
Chinchin si me la recuerdan
Carcacha y se les retacha.
Matemáticas
Circo matemático
Martin Gardner
4
Antología de lecturas
Matemáticas
Capítulo 1
Ilusiones ópticas
Las ilusiones ópticas -figuras, objetos o sucesos que no son lo que aparentan al ser percibidos han
tenido y tienen todavía importante papel en las bellas artes, en matemáticas, en psicología e incluso
en filosofía. Los antiguos griegos deformaron las columnas del Partenón con el fin de que parecieran
perfectamente rectas al ser vistas desde el suelo por la gente. En sus grandes obras murales, los
pintores renacentistas solían distorsionar las figuras con objeto de que, miradas desde abajo,
parecieran ser de proporciones normales. El interés de los matemáticos por las ilusiones ópticas se
debe a que muchas de ellas guardan relación con la perspectiva (una rama de la geometría
proyectiva) y con otras cuestiones geométricas. Los psicólogos estudian las ilusiones para saber
cómo interpreta el cerebro los datos que le llegan a través de los sentidos. Y los filósofos de diversas
escuelas de realismo directo, que mantienen que nosotros percibimos objetos reales externos a
nuestras mentes, tienen el problema de explicar cómo pueden entonces presentarse errores de
percepción.
Consideradas en su aspecto menos serio, las ilusiones visuales son, sencillamente, divertidas.
Disfrutamos sabiéndonos engañados por ellas, por motivos que no se diferencian mucho del placer
de ser confundidos por un ilusionista. Las ilusiones nos recuerdan que el ancho mundo exterior no
siempre es lo que parece. Nos fijaremos en este capítulo en unas cuantas ilusiones ópticas no
demasiado conocidas, que exhalan todas ellas fuerte aroma matemático.
Los procesos de que el cerebro se vale para interpretar los datos visuales son tan complejos y poco
conocidos, que no es milagro que en sus explicaciones los psicólogos mantengan opiniones
divergentes, cuando no contradictorias, incluso para las ilusiones más sencillas. Entre las más
clásicas están el aumento aparente del sol, la luna y las constelaciones cuando están cerca del
horizonte. El difunto Edwin G. Boring, de la Universidad Harvard escribió numerosos artículos
explicando que la «flusión de la luna» se debe fundamentalmente a la acción de alzar la mirada. Una
opinión diferente, que se remonta hasta Ptolomeo, es defendida por Lloyd Kaufman e Irvin Rock en
su artículo «The Moon Illusion», en Scientific American de julio de 1962.
Su teoría, basada en el efecto de «distancia aparente», es a su vez refutada por Frank Restle en un
trabajo publicado en Science del 20 de febrero de 1970. La opinión actual es que casi todas las
ilusiones ópticas se originan en el cerebro, cuando éste va explorando su memoria en busca de lo
que Richard L. Gregory denomina «la apuesta óptima», es decir, la interpretación que mejor explique
los datos visuales a partir de las experiencias acumuladas por el cerebro. Tal punto de vista está
sustentado por el reciente descubrimiento de que muchos animales, entre ellos aves y peces, sufren
ilusiones que podrían ser explicadas de esta forma y también, por trabajos de antropología en
culturas marcadamente diferentes de la nuestra. Los zulúes, por ejemplo, viven inmersos en un
mundo de formas redondeadas. Las cabañas son redondas, y también lo son sus puertas.
Al arar, sus surcos trazan líneas curvas. Raramente tienen ocasión de ver líneas o ángulos rectos, y
su idioma no contiene ningún vocablo que signifique «cuadrado». Así nos lo dice John Updike en la
segunda estrofa de su poema «Zulus Live in Land Without a Square»:
Cuando los zulúes sonreír no pueden, ceñudos fingen enojos,
para siempre tener curvas frente a los ojos.
Y las distancias entre lugares y cosas se calculan «a vuelo de mariposa»...
Diversos estudios recientes han mostrado que ciertas ilusiones relativas a rectas paralelas y esquinas
en ángulo, figuras que con tanta frecuencia observamos en el mundo rectangular de las sociedades
tecnológicamente adelantadas, difícilmente son percibidas por los zulúes. Los filósofos John Locke y
5
Antología de lecturas
Matemáticas
George Berkeley se preguntaron ambos si un ciego de nacimiento que súbitamente recuperase la
vista sabría distinguir, sin tocarlos, cuál de dos objetos era un cubo y cuál una esfera. Locke y
Berkeley respondieron que no. Una obra de Gregory, Eye and Brain, resume estudios recientes en
esta misma dirección, y aunque no se llega a conclusiones tajantes, sí parece dar la razón a aquellos
filósofos, aportando de nuevo pruebas que justifican el enfoque moderno, a saber, que casi todas las
ilusiones ópticas se deben a que el cerebro interpreta erróneamente los datos que recibe.
El descubrimiento de figuras «indecidibles» ha suscitado nuevos y entretenidos desarrollos en la
teoría de las ilusiones visuales. Las figuras indecidibles representan objetos que no pueden existir. La
mente, incapaz de encontrarles pies ni cabeza, queda sumída en un estado de curiosa perplejidad.
(Son figuras que recuerdan proposiciones indecidibles, como «Esta proposición es falsa», o «No te lo
pierdas si puedes».) Entre las figuras indecidibles, la más conocida es el notable «blivet» (que un
americano pronunciaría casi igual que «believe it», «créalo») de tres columnas (¿o sólo dos?) que
vemos en la Figura 1.
Las primeras versiones empezaron a circular entre ingenieros y proyectistas hacia 1964, y la portada
del número de marzo de 1965 de la revista Mad mostraba a un Alfred E. Neuman sonriente y
haciendo equilibrios con el blivet sobre su dedo índice.
Roger Hayward ha publicado un artículo sobre «Blivets: Research and Development» [Investigación y
desarrollo de los blivets] en The Worm Runners Digest (diciembre de 1968), donde presentaba
algunas variantes (véase la Figura l).
Otra conocida figura indecidible es una escalinata cuadrada por la que se puede ascender o
descender indefinidamente sin por ello subir ni bajar. Puede verse en una litografía de Maurits C.
Escher titulada «Ascendiendo y descendiendo», que data de 1960, así como en otra litografía del
6
Antología de lecturas
Matemáticas
mismo artista, de 1961, que representa un salto de agua haciendo funcionar una máquina de
movimiento perpetuo. Esta desconcertante ilusión, creada por el genetista inglés L. S. Penrose y por
su hijo, el físicomatemático Roger Penrose, fue inicialmente publicada en un artículo de ambos,
«Imposible Objects: A Special Type of Visual Illusion» [Un tipo especial de ilusiones visuales: los
objetos imposibles], en The British Journal of Psychology (febrero de 1958, pp. 31-33).
Estos mismos dos autores se sirvieron otra vez de ella en su colección de originales «rompecabezas
navideños» publicada en The New Scientist (25 de diciembre de 1958, pp. 1580-81). Admitiendo
(véase la Figura 2) que hagan falta tres peldaños para ir desde A, en el suelo, hasta lo alto del
escalón B, ¿cómo se puede ir desde A hasta C sin subir más de 10 escalones? La solución sólo es
posible porque la propia estructura dibujada no lo es.
Un tercer objeto imposible también muy conocido es la armazón del cubo sostenido por la figura
sedente de otra famosa litografía de Escher, que puede verse en la página 110 de mi Carnaval
matemático. La sección de «Cartas» de Scientific American reproducía una fotografía de esta
«Canasta de acceso libre» (así fue llamada) en el número de junio de 1966; en realidad aquella
fotografía se obtuvo retocando el negativo. No obstante, sí es posible construir un modelo real que
visto desde un ángulo adecuado nos dé una auténtica fotografía de la «canasta». Su construcción ha
sido explicada por William G. Hyzer en Photo Methods for Industry, enero de 1970.
7
Antología de lecturas
Matemáticas
Vemos en la Figura 3 el modelo de Hyzer. Si lo giramos y ladeamos hasta que, observándolo con un
solo ojo, los huecos coincidan con toda exactitud con dos travesaños traseros del armazón, el cerebro
se convence de que las aristas traseras están delante, produciendo la imagen mental de un cubo
imposible.
Muchas otras curiosas ilusiones son debidas a que poseemos dos ojos. Extienda los brazos ante sí,
manteniendo los dedos índices de ambas manos estirados horizontalmente, con las puntas en
contacto. Mirando más allá de los dedos, enfoque la mirada sobre una pared distante, y separe los
dedos ligeramente. Verá entonces una «salchicha flotante» entre los dedos. Como es obvio, la
salchicha está formada por las imágenes superpuestas de las yemas de los dedos, vistas cada una
por distinto ojo. Otra antigua ilusión, también debida a la visión binocular, se produce acercando un
tubo (es suficiente una hoja arrollada de papel) a un ojo, como si fuera un telescopio. Supongamos
que llevamos el tubo al ojo derecho; la mano izquierda, con la palma vuelta hacia uno mismo, se
coloca verticalmente pegada al borde izquierdo del tubo. Deslizando hacia adelante y hacia atrás la
mano izquierda a lo largo del tubo, con los dos ojos abiertos y mirando algún objeto distante, se
encontrará un punto donde parecerá que estamos mirando a través de un agujero recortado en el
centro de la mano izquierda.
En ciertas circunstancias, también la visión monocular puede crear una ilusión de profundidad.
Mirando una fotografía con un solo ojo a través de un tubo se produce un ligero efecto de
tridimensionalidad. Una de las más llamativas ilusiones de la visión monocular puede verse en la
Figura 4.
8
Antología de lecturas
Matemáticas
Es necesario inclinar el libro hacia atrás, hasta que el plano de la página quede casi enrasado con la
vista. Mirando la figura con un solo ojo desde un punto próximo al borde inferior de la página,
aproximadamente donde convergerían los clavos si fuesen prolongados hacia abajo, durante un
breve instante los clavos parecerán ponerse en pie. William James, en el Capítulo 19 del Volumen 2
de sus famosos Principles of Psychology, tras dar una excelente explicación de esta ilusión, añade
esta sucinta coletilla, que resume las ideas actuales sobre la percepción: «Dicho con otras palabras,
nosotros vemos, como siempre, el objeto más verosímil.»
El llamado «péndulo de Pulfrich» es otra asombrosa ilusión binocular, que recibe su nombre de su
descubridor, Carl Pulfrich, quien la dio a conocer en 1922, en una revista alemana. El péndulo está
formado, sencillamente, por un trozo de hilo, que puede tener desde unos 30 cm hasta más de un
metro. De él pende un objeto pequeño. Pídale a otra persona que sostenga la punta libre del cordel, y
que mantenga el péndulo en oscilación en un plano perpendicular al de su línea de visión.
Sitúese usted en el otro extremo de la habitación, frente al péndulo, que se habrá de observar con
ambos ojos. Con uno se mira directamente; con el otro, a través de uno de los cristales de unas gafas
de sol. Es preciso fijar la mirada en el punto medio de la oscilación; la vista no debe ir siguiendo a la
plomada en su vaivén. ¡Parecerá entonces que el peso describe una órbita elíptica! Trasladando al
otro ojo el cristal oscuro, el peso seguirá describiendo la misma órbita elíptica, pero ahora recorrida
en sentido contrario. Tan fuerte es la ilusión de profundidad, que colocando por detrás del plano de
oscilación un objeto grande parece como si el plomo pasase en realidad a través del objeto, como un
fantasma.
Gregory explica la ilusión de Pulfrich diciendo que el ojo adaptado a la oscuridad envía sus señales al
cerebro más lentamente que el ojo descubierto. Este desfase entre las señales induce al cerebro a
interpretar el movimiento del plomo como si alternativamente fuese pasando por delante y por detrás
de su plano de oscilación.
Pueden experimentarse sensaciones de profundidad parecidas al mirar imágenes de televisión,
cubriendo un ojo con un cristal oscuro o mirando con uno de los ojos a través de un pequeño orificio
perforado en cartulina. Cuando en la pantalla aparece una imagen que se desplaza horizontalmente
9
Antología de lecturas
Matemáticas
con cierta velocidad, el observador tendrá la impresión de que lo hace por delante o por detrás de la
pantalla. Esta ilusión animó a varias compañías a anunciar, en 1966, unas gafas especiales que, de
creer a la publicidad, permitirían al espectador ver en tres dimensiones las imágenes planas de su
televisor. El precio era elevado, pero evidentemente las gafas no eran sino una montura barata
provista de dos lentes de plástico, una transparente y otra oscura.
Otra conocida categoría de figuras ilusorias, muy analizadas por la escuela psicológica de la Gestalt,
está formada por imágenes que pueden ser interpretadas de dos maneras con probabilidades iguales
o casi iguales. La mente fluctúa entre ambas interpretaciones, incapaz de decidir cuál es la apuesta
óptima. Probablemente el ejemplo más conocido sea el apilamiento de cubos que se invierte
repentinamente, haciendo cambiar el número de cubos que parecen formarlo. En estos últimos años
todos hemos tenido dificultades de interpretación al contemplar fotografías de cráteres lunares y no
poderlos ver como montañas, sobre todo si invertimos la fotografía, con lo que los cráteres se ven
iluminados desde abajo por la luz solar, ángulo de iluminación que raramente habremos tenido
ocasión de experimentar.
Hay una figura de un jarrón oscuro cuya silueta puede ser imaginada como los perfiles de dos caras.
Una ilusión parecida saltó inesperadamente a la palestra en la nueva bandera canadiense, adoptada
oficialmente en 1965 tras varios meses de disputas parlamentarias. Fije usted la atención en el fondo
blanco, por encima de la hoja de arce (véase la Figura 5).
Se verán entonces los perfiles de dos hombres malhumorados (¿quizás un liberal y un conservador?)
con las frentes en contacto, zahiriéndose (¿uno en francés y otro en inglés?). En cuanto haya usted
localizado estas dos caras, ya no tendrá dificultad en descifrar el significado de los polígonos de
formas irregulares que en bloques negras podemos ver en la Figura 6.
10
Antología de lecturas
Matemáticas
Otra figura muy estudiada es el cubo de Necker, así llamado en honor del suizo L. A. Necker, quien
escribió acerca de él allá por 1830. El cubo tiene la propiedad de invertirse al observarlo. Los Penrose,
en los acertijos navideños ya mencionados, tuvieron la feliz idea de añadir un escarabajo al «cubo»,
en este caso una caja rectangular. (Véase la Figura 7.) El insecto parece encontrarse en la pared
exterior.
Pero si fijamos la mirada en el ángulo inferior izquierdo de la caja, y con la imaginación nos
esforzamos en pensar que esa es la esquina más cercana, de repente, ¡flip, flop!, el insecto queda
encerrado en su jaula, transportado por la acción del pensamiento.
Con tres monedas podemos poner de manifiesto otra sorprendente ilusión, seguramente relacionada
con la ilusión de Müller-Lyer (dos segmentos de longitudes iguales que parecen ser de tamaños
distintos a causa de las puntas de flecha trazadas en sus extremos: en una de las figuras apuntan
hacia afuera y en la otra hacia adentro). Se colocan las monedas en fila (véase la Figura 8) y se le
11
Antología de lecturas
Matemáticas
pide a otra persona que haga deslizar hacia abajo la moneda central hasta que la distancia AB sea
igual a la distancia CD. Casi nadie separa la moneda lo suficiente; en realidad, cuesta creer que la
solución correcta sea la dada en la ilustración. El truco puede repetirse con monedas mayores,
mesitas circulares, vasos de agua y objetos parecidos.
La ilusión de la «moneda fantasma», que vemos en la Figura 9, es más conocida por los ilusionistas
que por los psicólogos. Sostenga una contra otra dos monedas entre las yemas de los dedos índices
y frótelas rápidamente una contra otra. Aparecerá entonces una tercera moneda, la moneda fantasma.
¿Pero por qué solamente por un extremo y no por el otro?
12
Antología de lecturas
Matemáticas
EL ENTIERRO PREMATURO
Edgar Allan Poe
Hay ciertos temas de interés absorbente, pero demasiado horribles para ser objeto de una obra de
mera ficción. Los simples novelistas deben evitarlos si no quieren ofender o desagradar. Sólo se
tratan con propiedad cuando lo grave y majestuoso de la verdad los santifican y sostienen. Nos
estremecemos, por ejemplo, con el más intenso "dolor agradable" ante los relatos del paso del
Beresina, del terremoto de Lisboa, de la peste de Londres y de la matanza de San Bartolomé o de la
muerte por asfixia de los ciento veintitrés prisioneros en el Agujero Negro de Calcuta. Pero en estos
relatos lo excitante es el hecho, la realidad, la historia. Como ficciones, nos parecerían sencillamente
abominables. He mencionado algunas de las más destacadas y augustas calamidades que registra la
historia, pero en ellas el alcance, no menos que el carácter de la calamidad, es lo que impresiona tan
vivamente la imaginación. No necesito recordar al lector que, del largo y horrible catálogo de miserias
humanas, podría haber escogido muchos ejemplos individuales más llenos de sufrimiento esencial
que cualquiera de esos inmensos desastres generales. La verdadera desdicha, la aflicción última, en
realidad es particular, no difusa. ¡Demos gracias a Dios misericordioso que los horrorosos extremos
de agonía los sufra el hombre individualmente y nunca en masa!
Ser enterrado vivo es, sin ningún género de duda, el más terrorífico extremo que jamás haya caído en
suerte a un simple mortal. Que le ha caído en suerte con frecuencia, con mucha frecuencia, nadie con
capacidad de juicio lo negará. Los límites que separan la vida de la muerte son, en el mejor de los
casos, borrosos e indefinidos... ¿Quién podría decir dónde termina uno y dónde empieza el otro?
Sabemos que hay enfermedades en las que se produce un cese total de las funciones aparentes de
la vida, y, sin embargo, ese cese no es más que una suspensión, para llamarle por su nombre. Hay
sólo pausas temporales en el incomprensible mecanismo. Transcurrido cierto período, algún
misterioso principio oculto pone de nuevo en movimiento los mágicos piñones y las ruedas fantásticas.
La cuerda de plata no quedó suelta para siempre, ni irreparablemente roto el vaso de oro. Pero,
entretanto, ¿dónde estaba el alma? Sin embargo, aparte de la inevitable conclusión a priori de que
tales causas deben producir tales efectos, de que los bien conocidos casos de vida en suspenso, una
y otra vez, provocan inevitablemente entierros prematuros, aparte de esta consideración, tenemos el
testimonio directo de la experiencia médica y del vulgo que prueba que en realidad tienen lugar un
gran número de estos entierros. Yo podría referir ahora mismo, si fuera necesario, cien ejemplos bien
probados. Uno de características muy asombrosas, y cuyas circunstancias igual quedan aún vivas en
la memoria de algunos de mis lectores, ocurrió no hace mucho en la vecina ciudad de Baltimore,
donde causó una conmoción penosa, intensa y muy extendida. La esposa de uno de los más
respetables ciudadanos -abogado eminente y miembro del Congreso- fue atacada por una repentina
e inexplicable enfermedad, que burló el ingenio de los médicos. Después de padecer mucho murió, o
se supone que murió. Nadie sospechó, y en realidad no había motivos para hacerlo, de que no
estaba verdaderamente muerta. Presentaba todas las apariencias comunes de la muerte. El rostro
tenía el habitual contorno contraído y sumido. Los labios mostraban la habitual palidez marmórea. Los
ojos no tenían brillo. Faltaba el calor. Cesaron las pulsaciones. Durante tres días el cuerpo estuvo sin
enterrar, y en ese tiempo adquirió una rigidez pétrea. Resumiendo, se adelantó el funeral por el
rápido avance de lo que se supuso era descomposición.
La dama fue depositada en la cripta familiar, que permaneció cerrada durante los tres años siguientes.
Al expirar ese plazo se abrió para recibir un sarcófago, pero, ¡ay, qué terrible choque esperaba al
marido cuando abrió personalmente la puerta! Al empujar los portones, un objeto vestido de blanco
cayó rechinando en sus brazos. Era el esqueleto de su mujer con la mortaja puesta.
13
Antología de lecturas
Matemáticas
Una cuidadosa investigación mostró la evidencia de que había revivido a los dos días de ser
sepultada, que sus luchas dentro del ataúd habían provocado la caída de éste desde una repisa o
nicho al suelo, y al romperse el féretro pudo salir de él. Apareció vacía una lámpara que
accidentalmente se había dejado llena de aceite, dentro de la tumba; puede, no obstante, haberse
consumido por evaporación. En los peldaños superiores de la escalera que descendía a la espantosa
cripta había un trozo del ataúd, con el cual, al parecer, la mujer había intentado llamar la atención
golpeando la puerta de hierro. Mientras hacía esto, probablemente se desmayó o quizás murió de
puro terror, y al caer, la mortaja se enredó en alguna pieza de hierro que sobresalía hacia dentro. Allí
quedó y así se pudrió, erguida.
En el año 1810 tuvo lugar en Francia un caso de inhumación prematura, en circunstancias que
contribuyen mucho a justificar la afirmación de que la verdad es más extraña que la ficción. La
heroína de la historia era mademoiselle [señorita] Victorine Lafourcade, una joven de ilustre familia,
rica y muy guapa. Entre sus numerosos pretendientes se contaba Julien Bossuet, un pobre littérateur
[literato] o periodista de París. Su talento y su amabilidad habían despertado la atención de la
heredera, que, al parecer, se había enamorado realmente de él, pero el orgullo de casta la llevó por
fin a rechazarlo y a casarse con un tal Monsieur [señor] Rénelle, banquero y diplomático de cierto
renombre. Después del matrimonio, sin embargo, este caballero descuidó a su mujer y quizá llegó a
pegarle. Después de pasar unos años desdichados ella murió; al menos su estado se parecía tanto al
de la muerte que engañó a todos quienes la vieron. Fue enterrada, no en una cripta, sino en una
tumba común, en su aldea natal. Desesperado y aún inflamado por el recuerdo de su cariño profundo,
el enamorado viajó de la capital a la lejana provincia donde se encontraba la aldea, con el romántico
propósito de desenterrar el cadáver y apoderarse de sus preciosos cabellos. Llegó a la tumba. A
medianoche desenterró el ataúd, lo abrió y, cuando iba a cortar los cabellos, se detuvo ante los ojos
de la amada, que se abrieron. La dama había sido enterrada viva. Las pulsaciones vitales no habían
desaparecido del todo, y las caricias de su amado la despertaron de aquel letargo que
equivocadamente había sido confundido con la muerte. Desesperado, el joven la llevó a su
alojamiento en la aldea. Empleó unos poderosos reconstituyentes aconsejados por sus no pocos
conocimientos médicos. En resumen, ella revivió. Reconoció a su salvador. Permaneció con él hasta
que lenta y gradualmente recobró la salud. Su corazón no era tan duro, y esta última lección de amor
bastó para ablandarlo. Lo entregó a Bossuet. No volvió junto a su marido, sino que, ocultando su
resurrección, huyó con su amante a América. Veinte años después, los dos regresaron a Francia,
convencidos de que el paso del tiempo había cambiado tanto la apariencia de la dama, que sus
amigos no podrían reconocerla. Pero se equivocaron, pues al primer encuentro monsieur Rénelle
reconoció a su mujer y la reclamó. Ella rechazó la reclamación y el tribunal la apoyó, resolviendo que
las extrañas circunstancias y el largo período transcurrido habían abolido, no sólo desde un punto de
vista equitativo, sino legalmente la autoridad del marido.
La Revista de Cirugía de Leipzig, publicación de gran autoridad y mérito, que algún editor americano
haría bien en traducir y publicar, relata en uno de los últimos números un acontecimiento muy penoso
que presenta las mismas características.
Un oficial de artillería, hombre de gigantesca estatura y salud excelente, fue derribado por un caballo
indomable y sufrió una contusión muy grave en la cabeza, que le dejó inconsciente. Tenía una ligera
fractura de cráneo pero no se percibió un peligro inmediato. La trepanación se hizo con éxito. Se le
aplicó una sangría y se adoptaron otros muchos remedios comunes. Pero cayó lentamente en un
sopor cada vez más grave y por fin se le dio por muerto.
14
Antología de lecturas
Matemáticas
Hacía calor y lo enterraron con prisa indecorosa en uno de los cementerios públicos. Sus funerales
tuvieron lugar un jueves. Al domingo siguiente, el parque del cementerio, como de costumbre, se
llenó de visitantes, y alrededor del mediodía se produjo un gran revuelo, provocado por las palabras
de un campesino que, habiéndose sentado en la tumba del oficial, había sentido removerse la tierra,
como si alguien estuviera luchando abajo. Al principio nadie prestó demasiada atención a las palabras
de este hombre, pero su evidente terror y la terca insistencia con que repetía su historia produjeron, al
fin, su natural efecto en la muchedumbre. Algunos con rapidez consiguieron unas palas, y la tumba,
vergonzosamente superficial, estuvo en pocos minutos tan abierta que dejó al descubierto la cabeza
de su ocupante. Daba la impresión de que estaba muerto, pero aparecía casi sentado dentro del
ataúd, cuya tapa, en furiosa lucha, había levantado parcialmente. Inmediatamente lo llevaron al
hospital más cercano, donde se le declaró vivo, aunque en estado de asfixia. Después de unas horas
volvió en sí, reconoció a algunas personas conocidas, y con frases inconexas relató sus agonías en la
tumba.
Por lo que dijo, estaba claro que la víctima mantuvo la conciencia de vida durante más de una hora
después de la inhumación, antes de perder los sentidos. Habían rellenado la tumba, sin percatarse,
con una tierra muy porosa, sin aplastar, y por eso le llegó un poco de aire. Oyó los pasos de la
multitud sobre su cabeza y a su vez trató de hacerse oír. El tumulto en el parque del cementerio, dijo,
fue lo que seguramente lo despertó de un profundo sueño, pero al despertarse se dio cuenta del
espantoso horror de su situación. Este paciente, según cuenta la historia, iba mejorando y parecía
encaminado hacia un restablecimiento definitivo, cuando cayó víctima de la charlatanería de los
experimentos médicos. Se le aplicó la batería galvánica y expiró de pronto en uno de esos
paroxismos estáticos que en ocasiones produce.
La mención de la batería galvánica, sin embargo, me trae a la memoria un caso bien conocido y muy
extraordinario, en que su acción resultó ser la manera de devolver la vida a un joven abogado de
Londres que estuvo enterrado dos días. Esto ocurrió en 1831, y entonces causó profunda impresión
en todas partes, donde era tema de conversación.
El paciente, el señor Edward Stapleton, había muerto, aparentemente, de fiebre tifoidea acompañada
de unos síntomas anómalos que despertaron la curiosidad de sus médicos. Después de su aparente
fallecimiento, se pidió a sus amigos la autorización para un examen postmórtem (autopsia), pero
éstos se negaron. Como sucede a menudo ante estas negativas, los médicos decidieron desenterrar
el cuerpo y examinarlo a conciencia, en privado. Fácilmente llegaron a un arreglo con uno de los
numerosos grupos de ladrones de cadáveres que abundan en Londres, y la tercera noche después
del entierro el supuesto cadáver fue desenterrado de una tumba de ocho pies de profundidad y
depositado en el quirófano de un hospital privado.
Al practicársele una incisión de cierta longitud en el abdomen, el aspecto fresco e incorrupto del
sujeto sugirió la idea de aplicar la batería. Hicieron sucesivos experimentos con los efectos
acostumbrados, sin nada de particular en ningún sentido, salvo, en una o dos ocasiones, una
apariencia de vida mayor de la norma en cierta acción convulsiva.
Era ya tarde. Iba a amanecer y se creyó oportuno, al fin, proceder inmediatamente a la disección.
Pero uno de los estudiosos tenía un deseo especial de experimentar una teoría propia e insistió en
aplicar la batería a uno de los músculos pectorales. Tras realizar una tosca incisión, se estableció
apresuradamente un contacto; entonces el paciente, con un movimiento rápido pero nada convulsivo,
se levantó de la mesa, caminó hacia el centro de la habitación, miró intranquilo a su alrededor unos
15
Antología de lecturas
Matemáticas
instantes y entonces habló. Lo que dijo fue ininteligible, pero pronunció algunas palabras, y silabeaba
claramente. Después de hablar, se cayó pesadamente al suelo.
Durante unos momentos todos se quedaron paralizados de espanto, pero la urgencia del caso pronto
les devolvió la presencia de ánimo. Se vio que el señor Stapleton estaba vivo, aunque sin sentido.
Después de administrarle éter volvió en sí y rápidamente recobró la salud, retornando a la sociedad
de sus amigos, a quienes, sin embargo, se les ocultó toda noticia sobre la resurrección hasta que ya
no se temía una recaída. Es de imaginar la maravilla de aquellos y su extasiado asombro.
El dato más espeluznante de este incidente, sin embargo, se encuentra en lo que afirmó el mismo
señor Stapleton. Declaró que en ningún momento perdió todo el sentido, que de un modo borroso y
confuso percibía todo lo que le estaba ocurriendo desde el instante en que fuera declarado muerto
por los médicos hasta cuando cayó desmayado en el piso del hospital. "Estoy vivo", fueron las
incomprendidas palabras que, al reconocer la sala de disección, había intentado pronunciar en aquel
grave instante de peligro.
Sería fácil multiplicar historias como éstas, pero me abstengo, porque en realidad no nos hacen falta
para establecer el hecho de que suceden entierros prematuros. Cuando reflexionamos, en las raras
veces en que, por la naturaleza del caso, tenemos la posibilidad de descubrirlos, debemos admitir
que tal vez ocurren más frecuentemente de lo que pensamos. En realidad, casi nunca se han
removido muchas tumbas de un cementerio, por alguna razón, sin que aparecieran esqueletos en
posturas que sugieren la más espantosa de las sospechas. La sospecha es espantosa, pero es más
espantoso el destino. Puede afirmarse, sin vacilar, que ningún suceso se presta tanto a llevar al
colmo de la angustia física y mental como el enterramiento antes de la muerte. La insoportable
opresión de los pulmones, las emanaciones sofocantes de la tierra húmeda, la mortaja que se adhiere,
el rígido abrazo de la estrecha morada, la oscuridad de la noche absoluta, el silencio como un mar
que abruma, la invisible pero palpable presencia del gusano vencedor; estas cosas, junto con los
deseos del aire y de la hierba que crecen arriba, con el recuerdo de los queridos amigos que volarían
a salvarnos si se enteraran de nuestro destino, y la conciencia de que nunca podrán saberlo, de que
nuestra suerte irremediable es la de los muertos de verdad, estas consideraciones, digo, llevan el
corazón aún palpitante a un grado de espantoso e insoportable horror ante el cual la imaginación más
audaz retrocede. No conocemos nada tan angustioso en la Tierra, no podemos imaginar nada tan
horrible en los dominios del más profundo Infierno. Y por eso todos los relatos sobre este tema
despiertan un interés profundo, interés que, sin embargo, gracias a la temerosa reverencia hacia este
tema, depende justa y específicamente de nuestra creencia en la verdad del asunto narrado. Lo que
voy a contar ahora es mi conocimiento real, mi experiencia efectiva y personal..
Durante varios años sufrí ataques de ese extraño trastorno que los médicos han decidido llamar
catalepsia, a falta de un nombre que mejor lo defina. Aunque tanto las causas inmediatas como las
predisposiciones e incluso el diagnóstico de esta enfermedad siguen siendo misteriosas, su carácter
evidente y manifiesto es bien conocido. Las variaciones parecen serlo, principalmente, de grado. A
veces el paciente se queda un solo día o incluso un período más breve en una especie de exagerado
letargo. Está inconsciente y externamente inmóvil, pero las pulsaciones del corazón aún se perciben
débilmente; quedan unos indicios de calor, una leve coloración persiste en el centro de las mejillas y,
al aplicar un espejo a los labios, podemos detectar una torpe, desigual y vacilante actividad de los
pulmones. Otras veces el trance dura semanas e incluso meses, mientras el examen más minucioso
y las pruebas médicas más rigurosas no logran establecer ninguna diferencia material entre el estado
de la víctima y lo que concebimos como muerte absoluta. Por regla general, lo salvan del entierro
prematuro sus amigos, que saben que sufría anteriormente de catalepsia, y la consiguiente sospecha,
16
Antología de lecturas
Matemáticas
pero sobre todo le salva la ausencia de corrupción. La enfermedad, por fortuna, avanza gradualmente.
Las primeras manifestaciones, aunque marcadas, son inequívocas. Los ataques son cada vez más
característicos y cada uno dura más que el anterior. En esto reside la mayor seguridad, de cara a
evitar la inhumación. El desdichado cuyo primer ataque tuviera la gravedad con que en ocasiones se
presenta, sería casi inevitablemente llevado vivo a la tumba.
Mi propio caso no difería en ningún detalle importante de los mencionados en los textos médicos. A
veces, sin ninguna causa aparente, me hundía poco a poco en un estado de semisíncope, o casi
desmayo, y ese estado, sin dolor, sin capacidad de moverme, o realmente de pensar, pero con una
borrosa y letárgica conciencia de la vida y de la presencia de los que rodeaban mi cama, duraba
hasta que la crisis de la enfermedad me devolvía, de repente, el perfecto conocimiento. Otras veces
el ataque era rápido, fulminante. Me sentía enfermo, aterido, helado, con escalofríos y mareos, y, de
repente, me caía postrado. Entonces, durante semanas, todo estaba vacío, negro, silencioso y la
nada se convertía en el universo. La total aniquilación no podía ser mayor. Despertaba, sin embargo,
de estos últimos ataques lenta y gradualmente, en contra de lo repentino del acceso. Así como
amanece el día para el mendigo que vaga por las calles en la larga y desolada noche de invierno, sin
amigos ni casa, así lenta, cansada, alegre volvía a mí la luz del alma. Pero, aparte de esta tendencia
al síncope, mi salud general parecía buena, y no hubiera podido percibir que sufría esta enfermedad,
a no ser que una peculiaridad de mi sueño pudiera considerarse provocada por ella. Al despertarme,
nunca podía recobrar en seguida el uso completo de mis facultades, y permanecía siempre durante
largo rato en un estado de azoramiento y perplejidad, ya que las facultades mentales en general y la
memoria en particular se encontraban en absoluta suspensión.
En todos mis padecimientos no había sufrimiento físico, sino una infinita angustia moral. Mi
imaginación se volvió macabra. Hablaba de "gusanos, de tumbas, de epitafios". Me perdía en
meditaciones sobre la muerte, y la idea del entierro prematuro se apoderaba de mi mente. El
espeluznante peligro al cual estaba expuesto me obsesionaba día y noche. Durante el primero, la
tortura de la meditación era excesiva; durante la segunda, era suprema, Cuando las tétricas tinieblas
se extendían sobre la tierra, entonces, presa de los más horribles pensamientos, temblaba, temblaba
como las trémulas plumas de un coche fúnebre. Cuando mi naturaleza ya no aguantaba la vigilia, me
sumía en una lucha que al fin me llevaba al sueño, pues me estremecía pensando que, al despertar,
podía encontrarme metido en una tumba. Y cuando, por fin, me hundía en el sueño, lo hacía sólo
para caer de inmediato en un mundo de fantasmas, sobre el cual flotaba con inmensas y tenebrosas
alas negras la única, predominante y sepulcral idea. De las innumerables imágenes melancólicas que
me oprimían en sueños elijo para mi relato una visión solitaria. Soñé que había caído en un trance
cataléptico de más duración y profundidad que lo normal. De repente una mano helada se posó en mi
frente y una voz impaciente, farfullante, susurró en mi oído: "¡Levántate!"
Me incorporé. La oscuridad era total. No podía ver la figura del que me había despertado. No podía
recordar ni la hora en que había caído en trance, ni el lugar en que me encontraba. Mientras seguía
inmóvil, intentando ordenar mis pensamientos, la fría mano me agarró con fuerza por la muñeca,
sacudiéndola con petulancia, mientras la voz farfullante decía de nuevo:
-¡Levántate! ¿No te he dicho que te levantes?
-¿Y tú - pregunté- quién eres?
-No tengo nombre en las regiones donde habito -replicó la voz tristemente-. Fui un hombre y soy un
espectro. Era despiadado, pero soy digno de lástima. Ya ves que tiemblo. Me rechinan los dientes
17
Antología de lecturas
Matemáticas
cuando hablo, pero no es por el frío de la noche, de la noche eterna. Pero este horror es insoportable.
¿Cómo puedes dormir tú tranquilo? No me dejan descansar los gritos de estas largas agonías. Estos
espectáculos son más de lo que puedo soportar. ¡Levántate! Ven conmigo a la noche exterior, y deja
que te muestre las tumbas. ¿No es este un espectáculo de dolor?... ¡Mira!
Miré, y la figura invisible que aún seguía apretándome la muñeca consiguió abrir las tumbas de toda
la humanidad, y de cada una salían las irradiaciones fosfóricas de la descomposición, de forma que
pude ver sus más escondidos rincones y los cuerpos amortajados en su triste y solemne sueño con el
gusano. Pero, ¡ay!, los que realmente dormían, aunque fueran muchos millones, eran menos que los
que no dormían en absoluto, y había una débil lucha, y había un triste y general desasosiego, y de las
profundidades de los innumerables pozos salía el melancólico frotar de las vestiduras de los
enterrados. Y, entre aquellos que parecían descansar tranquilos, vi que muchos habían cambiado, en
mayor o menor grado, la rígida e incómoda postura en que fueron sepultados. Y la voz me habló de
nuevo, mientras contemplaba:
-¿No es esto, ¡ah!, acaso un espectáculo lastimoso?
Pero, antes de que encontrara palabras para contestar, la figura había soltado mi muñeca, las luces
fosfóricas se extinguieron y las tumbas se cerraron con repentina violencia, mientras de ellas salía un
tumulto de gritos desesperados, repitiendo: "¿No es esto, ¡Dios mío!, acaso un espectáculo
lastimoso?"
Fantasías como ésta se presentaban por la noche y extendían su terrorífica influencia incluso en mis
horas de vigilia. Mis nervios quedaron destrozados, y fui presa de un horror continuo. Ya no me
atrevía a montar a caballo, a pasear, ni a practicar ningún ejercicio que me alejara de casa. En
realidad, ya no me atrevía a fiarme de mí lejos de la presencia de los que conocían mi propensión a la
catalepsia, por miedo de que, en uno de esos ataques, me enterraran antes de conocer mi estado
realmente. Dudaba del cuidado y de la lealtad de mis amigos más queridos. Temía que, en un trance
más largo de lo acostumbrado, se convencieran de que ya no había remedio. Incluso llegaba a temer
que, como les causaba muchas molestias, quizá se alegraran de considerar que un ataque
prolongado era la excusa suficiente para librarse definitivamente de mí. En vano trataban de
tranquilizarme con las más solemnes promesas. Les exigía, con los juramentos más sagrados, que
en ninguna circunstancia me enterraran hasta que la descomposición estuviera tan avanzada, que
impidiese la conservación. Y aun así mis terrores mortales no hacían caso de razón alguna, no
aceptaban ningún consuelo. Empecé con una serie de complejas precauciones. Entre otras, mandé
remodelar la cripta familiar de forma que se pudiera abrir fácilmente desde dentro. A la más débil
presión sobre una larga palanca que se extendía hasta muy dentro de la cripta, se abrirían
rápidamente los portones de hierro. También estaba prevista la entrada libre de aire y de luz, y
adecuados recipientes con alimentos y agua, al alcance del ataúd preparado para recibirme. Este
ataúd estaba acolchado con un material suave y cálido y dotado de una tapa elaborada según el
principio de la puerta de la cripta, incluyendo resortes ideados de forma que el más débil movimiento
del cuerpo sería suficiente para que se soltara. Aparte de esto, del techo de la tumba colgaba una
gran campana, cuya soga pasaría (estaba previsto) por un agujero en el ataúd y estaría atada a una
mano del cadáver. Pero, ¡ay!, ¿de qué sirve la precaución contra el destino del hombre? ¡Ni siquiera
estas bien urdidas seguridades bastaban para librar de las angustias más extremas de la inhumación
en vida a un infeliz destinado a ellas!
Llegó una época -como me había ocurrido antes a menudo- en que me encontré emergiendo de un
estado de total inconsciencia a la primera sensación débil e indefinida de la existencia. Lentamente,
18
Antología de lecturas
Matemáticas
con paso de tortuga, se acercaba el pálido amanecer gris del día psíquico. Un desasosiego
aletargado. Una sensación apática de sordo dolor. Ninguna preocupación, ninguna esperanza, ningún
esfuerzo. Entonces, después de un largo intervalo, un zumbido en los oídos. Luego, tras un lapso de
tiempo más largo, una sensación de hormigueo o comezón en las extremidades; después, un período
aparentemente eterno de placentera quietud, durante el cual las sensaciones que se despiertan
luchan por transformarse en pensamientos; más tarde, otra corta zambullida en la nada; luego, un
súbito restablecimiento. Al fin, el ligero estremecerse de un párpado; e inmediatamente después, un
choque eléctrico de terror, mortal e indefinido, que envía la sangre a torrentes desde las sienes al
corazón. Y entonces, el primer esfuerzo por pensar. Y entonces, el primer intento de recordar. Y
entonces, un éxito parcial y evanescente. Y entonces, la memoria ha recobrado tanto su dominio, que,
en cierta medida, tengo conciencia de mi estado. Siento que no me estoy despertando de un sueño
corriente. Recuerdo que he sufrido de catalepsia. Y entonces, por fin, como si fuera la embestida de
un océano, el único peligro horrendo, la única idea espectral y siempre presente abruma mi espíritu
estremecido.
Unos minutos después de que esta fantasía se apoderase de mí, me quedé inmóvil. ¿Y por qué? No
podía reunir valor para moverme. No me atrevía a hacer el esfuerzo que desvelara mi destino, sin
embargo algo en mi corazón me susurraba que era seguro. La desesperación -tal como ninguna otra
clase de desdicha produce-, sólo la desesperación me empujó, después de una profunda duda, a
abrir mis pesados párpados. Los levanté. Estaba oscuro, todo oscuro. Sabía que el ataque había
terminado. Sabía que la situación crítica de mi trastorno había pasado. Sabía que había recuperado
el uso de mis facultades visuales, y, sin embargo, todo estaba oscuro, oscuro, con la intensa y
absoluta falta de luz de la noche que dura para siempre.
Intenté gritar, y mis labios y mi lengua reseca se movieron convulsivamente, pero ninguna voz salió
de los cavernosos pulmones, que, oprimidos como por el peso de una montaña, jadeaban y
palpitaban con el corazón en cada inspiración laboriosa y difícil. El movimiento de las mandíbulas, en
el esfuerzo por gritar, me mostró que estaban atadas, como se hace con los muertos. Sentí también
que yacía sobre una materia dura, y algo parecido me apretaba los costados. Hasta entonces no me
había atrevido a mover ningún miembro, pero al fin levanté con violencia mis brazos, que estaban
estirados, con las muñecas cruzadas. Chocaron con una materia sólida, que se extendía sobre mi
cuerpo a no más de seis pulgadas de mi cara. Ya no dudaba de que reposaba al fin dentro de un
ataúd.
Y entonces, en medio de toda mi infinita desdicha, vino dulcemente la esperanza, como un querubín,
pues pensé en mis precauciones. Me retorcí e hice espasmódicos esfuerzos para abrir la tapa: no se
movía. Me toqué las muñecas buscando la soga: no la encontré. Y entonces mi consuelo huyó para
siempre, y una desesperación aún más inflexible reinó triunfante pues no pude evitar percatarme de
la ausencia de las almohadillas que había preparado con tanto cuidado, y entonces llegó de repente a
mis narices el fuerte y peculiar olor de la tierra húmeda. La conclusión era irresistible. No estaba en la
cripta. Había caído en trance lejos de casa, entre desconocidos, no podía recordar cuándo y cómo, y
ellos me habían enterrado como a un perro, metido en algún ataúd común, cerrado con clavos, y
arrojado bajo tierra, bajo tierra y para siempre, en alguna tumba común y anónima.
Cuando este horrible convencimiento se abrió paso con fuerza hasta lo más íntimo de mi alma, luché
una vez más por gritar. Y este segundo intento tuvo éxito. Un largo, salvaje y continuo grito o alarido
de agonía resonó en los recintos de la noche subterránea.
-Oye, oye, ¿qué es eso? -dijo una áspera voz, como respuesta.
19
Antología de lecturas
Matemáticas
-¿Qué diablos pasa ahora? -dijo un segundo..
-¡Fuera de ahí! -dijo un tercero.
-¿Por qué aúlla de esa manera, como un gato montés? -dijo un cuarto.
Y entonces unos individuos de aspecto rudo me sujetaron y me sacudieron sin ninguna consideración.
No me despertaron del sueño, pues estaba completamente despierto cuando grité, pero me
devolvieron la plena posesión de mi memoria.
Esta aventura ocurrió cerca de Richmond, en Virginia. Acompañado de un amigo, había bajado, en
una expedición de caza, unas millas por las orillas del río James. Se acercaba la noche cuando nos
sorprendió una tormenta. La cabina de una pequeña chalupa anclada en la corriente y cargada de
tierra vegetal nos ofreció el único refugio asequible. Le sacamos el mayor provecho posible y
pasamos la noche a bordo. Me dormí en una de las dos literas; no hace falta describir las literas de
una chalupa de sesenta o setenta toneladas. La que yo ocupaba no tenía ropa de cama. Tenía una
anchura de dieciocho pulgadas. La distancia entre el fondo y la cubierta era exactamente la misma.
Me resultó muy difícil meterme en ella. Sin embargo, dormí profundamente, y toda mi visión -pues no
era ni un sueño ni una pesadilla- surgió naturalmente de las circunstancias de mi postura, de la
tendencia habitual de mis pensamientos, y de la dificultad, que ya he mencionado, de concentrar mis
sentidos y sobre todo de recobrar la memoria durante largo rato después de despertarme. Los
hombres que me sacudieron eran los tripulantes de la chalupa y algunos jornaleros contratados para
descargarla. De la misma carga procedía el olor a tierra. La venda en torno a las mandíbulas era un
pañuelo de seda con el que me había atado la cabeza, a falta de gorro de dormir.
Las torturas que soporté, sin embargo, fueron indudablemente iguales en aquel momento a las de la
verdadera sepultura. Eran de un horror inconcebible, increíblemente espantosas; pero del mal
procede el bien, pues su mismo exceso provocó en mi espíritu una reacción inevitable. Mi alma
adquirió temple, vigor. Salí fuera. Hice ejercicios duros. Respiré aire puro. Pensé en más cosas que
en la muerte. Abandoné mis textos médicos. Quemé el libro de Buchan. No leí más pensamientos
nocturnos, ni grandilocuencias sobre cementerios, ni cuentos de miedo como éste. En muy poco
tiempo me convertí en un hombre nuevo y viví una vida de hombre. Desde aquella noche memorable
descarté para siempre mis aprensiones sepulcrales y con ellas se desvanecieron los achaques
catalépticos, de los cuales quizá fueran menos consecuencia que causa. Hay momentos en que,
incluso para el sereno ojo de la razón, el mundo de nuestra triste humanidad puede parecer el infierno,
pero la imaginación del hombre no es Caratis para explorar con impunidad todas sus cavernas. ¡Ay!,
la torva legión de los terrores sepulcrales no se puede considerar como completamente imaginaria,
pero los demonios, en cuya compañía Afrasiab hizo su viaje por el Oxus, tienen que dormir o nos
devorarán..., hay que permitirles que duerman, o pereceremos.
20
Antología de lecturas
Matemáticas
MANUEL ELARRIERO
Cuentos y Matemáticas
Autor:
José Antonio Martín Corujo
De los muchos oficios que ejerció Manuel en su juventud, quizás sea el de arriero del que guarda un
mejor recuerdo. Se levantaba muy tempranito, a las cinco de la madrugada, y antes de despuntar el
día ya estaba con sus tres mulas en el remate de monte o de carbón, dispuesto a cargarlas y regresar
al pueblo. Hace algún tiempo, me contó que Andrés y Donato eran por aquel entonces en el pueblo
los intermediarios del carbón y de las varas para los tomateros, y siempre le estaban reprochando
que si primero atendía a uno que al otro, cuando la verdad era que él se rompía la cabeza tratando de
satisfacerlos de la mejor manera que podía y sabía. Por esta razón, muchas veces hacía viajes en los
que unas mulas traían varas y otra carbón, o viceversa, con el fin de contentar a ambos.
Una vez se encontró en la situación de tener que acarrear 60 sacos de carbón y 80 fejes de varas, y
se planteó llevar en cada viaje carbón y varas, de modo que en todos los viajes fuera siempre el
mismo número de sacos de carbón y también fuera fijo el número de fejes de varas. Luego de darle
muchas vueltas llegó a la conclusión de que esto era posible, y así podía satisfacer tanto a Donato
como Andrés al comenzar y terminar el mismo día el transporte de ambos productos y, además, cada
día les traería una cantidad fija del respectivo material.
Fue feliz durante los días que duró el trabajo y pudo dedicar mucho de su tiempo a observar la
naturaleza, de la que siempre estuvo enamorado, al no tener que pensar en cada viaje qué cantidad
de cada elemento debía cargar en sus mulas.
Me hizo observar que él nunca cargaba a ninguna con más de 2 fejes de varas o 3 sacos de carbón,
pues éstas constituían su principal medio de trabajo y no quería arriesgarse a que alguna, por exceso
de carga, se le mancase.
¿Podrían ustedes animarse e intentar hallar el número de viajes que tuvo que hacer y los sacos de
carbón y fejes de varas que transportaba en cada viaje?
¿Podría Manuel, respetando las condiciones de carga de sus mulas, haber finalizado en un mismo
viaje el transporte si las cantidades hubieran sido 83 fejes de varas y 60 de carbón? ¿Y cuántos
21
Antología de lecturas
Matemáticas
viajes hubiera tenido que hacer para finalizar conjuntamente el transporte si el carbón hubiera sido 60
sacos y 20 los fejes de varas?
LA CORUJA Y LOS PÁJAROS
Manuel heredó de sus padres una pequeña parcela de terreno, de apenas un par de celemines, con
un pajero, que hoy le sirve de cuarto de aperos y pequeña bodega, al que de vez en cuando me invita
a probar sus buenos vinos con sabor a tea. Estábamos charlando, como casi siempre, de las cosas
de la naturaleza, cuando nos sorprendió el aletear de un gran número de pájaros. No daba crédito a
lo que veía: una bandada de pájaros de distintas especies perseguían amenazadoramente a una
coruja, que pudo escabullirse entre los frondes de grandes helechos que cubrían un risco próximo.
Sonriendo, Manuel me comentó que él creía saber la razón de tales hechos, y sin que yo se lo pidiera,
pero conocedor de mi curiosidad por sus relatos, a veces no exentos de fantasía, comenzó a
contarme lo que sigue:
«Hace algún tiempo, esas aves perseguidoras se reunieron con las rapaces de esta zona con el fin
de establecer algunas normas que pudieran garantizar la supervivencia de todas las especies. Por los
acuerdos alcanzados, se le asignó a cada rapaz los lugares de caza, se fijó la frecuencia de captura y
se puso la condición de que las aves que se podían cazar sólo fueran enfermas o debiluchas, y que
completaran su alimentación con roedores».
Aquí, en mi terreno –prosiguió Manuel–, a esa coruja que acabas de ver le corresponde cazar un
pájaro cada 7 días y un roedor cada 5. Suele ser bastante cumplidora con los acuerdos establecidos,
pero de vez en cuando, el mismo día caza un pájaro y un roedor, lo cual enfurece a los demás
pájaros, y ese es el motivo del enfado y del acoso a la coruja que acabamos de ver. Sin embargo,
dada esa sabiduría que siempre se le ha atribuido a las corujas, yo creo que tiene razón, que ella no
22
Antología de lecturas
Matemáticas
hace otra cosa que cumplir los acuerdos y, ciertos días, tiene derecho a comerse un pájaro y un
roedor. De seguir así las cosas, no le va a quedar otro remedio que acudir ante el Defensor Alado».
De vuelta a mi casa estuve cavilando sobre si la coruja tenía o no razón. Hice cálculos para saber
cuántos días después se volvería a repetir la extraña persecución, con la intención de volver al
terreno de Manuel y contemplarla.
¿Por qué no lo intentan ustedes?
EL FRUTO MARAVILLOSO
Una de las leyendas que más le gustaba contar a Manuel era la de un príncipe guanche del reino de
Galguen, en la isla de La Palma, quien amaba hasta la locura a una bella benahoarita, a quien una
extraña enfermedad mantenía sumida en una gran tristeza y apatía, que aumentaba cada día, sin que
los brujos pudieran hacer nada.
Un día, un viejo sabio le dijo al príncipe que el fruto de un árbol de tronco amarillo-rojizo, existente en
un jardín del reino de Taburiente, curaría a su amada.
23
Antología de lecturas
Matemáticas
Emprendió viaje y después de un largo recorrido, en el que puso de manifiesto su pericia para subir y
descender peligrosos riscos, y en el que la lanza fue su mejor aliada, llegó a Taburiente y se encontró
en un escondido lugar del gran cráter el bello jardín. Luego comenzó para él un verdadero
quebradero de cabeza, pues a la entrada de aquel había un fornido guardián que, después de una
paciente súplica, le permitió entrar, con la condición de que al regresar, le diera la mitad de los frutos
y medio fruto más, sin partir ninguno, quedándose él sólo con uno. Aceptó la propuesta y, cuando se
adentraba por la vereda hacia el jardín, encontró otro guardián que le permitió el paso, con una
condición similar a la del primero: que al volver le diera la mitad de los frutos y medio fruto más, sin
partir ninguno, y él se quedara con el resto.
Cuando ya la emoción le invadía, ante la proximidad del objetivo, se vio ante un tercer guardián, que
le impuso la misma condición que el anterior. Este le indicó que el árbol era el manzano de oro,
situado sobre un pequeño risco, visible desde donde estaban.
El príncipe consiguió volver a Galguen con el fruto codiciado, y su amada, después de comer la
manzana de oro, quedó completamente recuperada.
Bueno, y dicho esto, ¿qué cantidad de frutos cogió el príncipe para que al final se llevase uno sólo?
24
Antología de lecturas
Matemáticas
EL ASESINATO EN EL "MATHEMATICS EXPRESS"
Claudi Alsina
Para hablar de Geometría y de su Enseñanza podría presentar unos bellos axiomas,
mostrarles un nuevo material o intentar evocar un teorema interesante. Sin embargo, quisiera hacer
hoy el experimento de referirme a la Geometría en forma mucho más literaria, de la mano de Agatha
Chiristie,
PRIMERA PARTE
Hércules Poirot pidió una habitación con baño. Luego se aproximó al mostrador del conserje
y preguntó si había llegado alguna correspondencia para él. Había un telegrama esperándole. Sus
cejas se elevaron alegremente a la vista del telegrama. Era algo inesperado: ―Sírvase venir
enseguida‖.
- Si que es una complicación, - murmuró Poirot, consultando su reloj-. Tendré que reanudar el
viaje por el mundo de la Matemática esta misma noche. ¿A qué hora sale el tren?
- Muy pronto, señor.
Un poco más tarde, cuando Poirot llegó a la estación, llamó a los mozos e hizo cargar su
equipaje en el coche cuyas placas proclamaban su destino: LA MATEMÁTICA DEL 2000.
-Tengo entendido que viaja mucha gente esta noche, ¿es cierto?
- Es increíble señor. ¡Todo el mundo ha elegido esta fecha para viajar!
El "Mathematics Express" iniciaba su viaje en aquel momento. Pronto Poirot penetró en su
departamento de indagaciones y se metió en la cama, leyó durante media hora y luego apagó la luz.
Se despertó al cabo de un rato al haber frenado el "Mathematics Express" de forma contundente.
Poirot salió de su departamento y fue a preguntar el motivo de tan brusca parada.
- Un alud de reformas curriculares y cambios, señor. El tren está detenido y Dios sabe
cuanto tiempo estaremos aquí. Recuerdo una vez que estuvimos varias décadas.
- ¿En donde estamos?
- Entre la Matemática algorítmica y la del año 2000, pero aun muy cerca de la Matemática
estructural, señor. Bon soir, monsieur.
- Bon soir, mon ami.
Poirot se acomodó de nuevo en su departamento de indagaciones dispuesto a dormir,
aunque la falta de vaivén no le ayudara a conciliar el sueño. Pronto fueron a despertarle.
- ¡Ah, mi buen amigo! Tenemos necesidad de usted.
25
Antología de lecturas
Matemáticas
- ¿De qué se trata? - preguntó Poirot.
- Cosas muy graves, amigo mío. Primero este alud de reformas,... esta detención. Y ahora,
Hizo una pausa.
- Y ahora la Geometría aparece muerta en este tren...
- ¡Bonita situación! - comentó Poirot- Si que es una situación difícil.
- Y aún puede empeorar. Aquí le presento al doctor del tren, monsieur Poirot... el doctor
opina que la muerte ocurrió hacia la década de los setenta.
- Es difícil puntualizar en estos casos - aclaró el doctor-; pero creo poder decir que la muerte
ocurrió entre la década de los setenta y la de los noventa.
- ¿Cuándo fue descubierto el crimen? - preguntó Poirot.
- Justo en el momento de detenerse el tren. Fue todo muy confuso - aclaró el inspector
ferroviario.
- Y ha sido un crimen tremendo, - añadió el doctor-, han sido por lo menos trece agresiones...
si algo queda claro es que no puede tratarse de un suicidio.
- ¡Por lo visto no ha sido un crimen científico - comentó Poirot.
- Lo más anticientífico que puede imaginarse.
Los golpes fueron descargados al azar.
Algunos causaron apenas daño. Es como si alguien hubiese cerrado los ojos y luego, en loco frenesí,
hubiese golpeado a ciegas una y otra vez.
- Desde el alud de reformas que ha hecho parar el tren - dijo Poirot meditativo-, nadie ni nada
ha podido escaparse. Así pues el asesino continua entre nosotros. ¡He de resolver este caso!
Acompañado del doctor, Poirot se dirigió al lugar del crimen para examinar con detalle
cualquier pista que pudiera aportar un poco de luz al asunto. Algunos elementos desperdigados por
el suelo, constituían posibles pistas: un pañuelo con las iniciales N.B., una regla y un compás, el
tratado de álgebra abstracta y un cubo de Rubik. En la pared una pintada en negro realizada con
spray donde aparecía un diagrama.
Poirot empezó a hablar con repentina nerviosidad.
- ¿Y la víctima? ¿Qué papel desempeña en todo esto? ¿Qué hizo? ¿Gritó? ¿Luchó? ¿Pidió
ayuda? ¿Se defendió?
En este sentido nadie había oído nada... o al menos, nadie dijo haber oído algo.
Lleno de dudas Poirot decidió interrumpir la búsqueda brevemente y se dirigió con el doctor
al vagón restaurante. Entre bocado y bocado Poirot evocó al doctor el recuerdo de un caso muy
antiguo donde la Geometría, ahora víctima, había tenido cierto protagonismo.
26
Antología de lecturas
Matemáticas
- Recuerdo, – empezó a divagar en voz alta Poirot,- que hace muchos años la víctima
protagonizó una serie de sucesos singulares. Ella durante siglos y con la ayuda de Euclídes había
sido la reina de las Matemáticas. Pero con el tiempo empezaron a surgirle alternativas que con su
mismo nombre de pila tuvieron apellido diferente.
La diferencial, la cartesiana, la proyectiva, la
descriptiva, la algebraica, las no-euclídeas, la integral.... hasta Félix Klein intentó salvar la situación a
base de ver en las raíces familiares aquello que quedaba invariante. Pero a pesar de este esfuerzo,
bien es verdad que al llegar al siglo XX nuestra víctima ya no era ni mucho menos lo que fue durante
siglos. Parece que ahora no obstante los acontecimientos se han precipitado y justo cuando estamos
ya en el viaje directo al 2000, ella ha sido la gran víctima. Creo que lo mejor que podemos hacer es
proceder a interrogar a todo el tren.
SEGUNDA PARTE
El tren seguía parado. Aún no se habían podido esclarecer los efectos del alud de reformas.
Mientras tanto Poirot no descansaba, procediendo a interrogar a todos los sospechosos, anotando en
sus fichas aquello que le parecía más sobresaliente o posiblemente relevante. Estas fueron sus
anotaciones:
1.- LA CELESTIAL CORPORATION: Súbdito que vive en el cielo. En su departamento del
tren hay ilustres viajeros que no se hablan entre sí, y si se hablan no se entienden.
Móvil: Intereses inconfesables de protagonismo. Solicitudes de becas y ayudas.
Coartada: La víctima. fue en origen su propia creación.
Pruebas contra ella: Objetos sospechosos en todo el departamento. Sobredosis de
grupos por el suelo. 8e reúnen cada cuatro años para conspirar en el Congreso Internacional de
Matemáticas. Opinan que Euclides nunca hubiese ganado la medalla Fields.
2.- NICOLÁS BOURBAKI: Súbdito francés, litera número 1, primera clase, en el
departamento de Matemática estructural.
Móvil: Posiblemente pudiera derivarse de sus pésimas relaciones con la víctima.
Coartada: Desde la década de los ochenta, no había estado activo ni popular como así lo
atestiguaron muchos pasajeros.
Pruebas contra él: El pañuelo con las iniciales N.B.; la ausencia de dibujos en sus libros
demostrando, por negativa, un singular desprecio hacia la víctima.
3.- FORMALIZACIÓN INC. AND SONS: Súbditos lógicos. Desde que subieron al tren han
pretendido ir en el primer vagón.
Móvil: Celos por falta de protagonismo.
27
Antología de lecturas
Matemáticas
Coartada: Siempre estuvieron en muy buenas relaciones con la víctima.
Pruebas contra ellos: A menudo han pretendido esconder a la víctima.
4.- ―MATHEMÁTIQUE MODERNE": Súbdita universal un tanto pasada de moda.
Móvil: Posible actitud pasional y complejo de inferioridad.
Coartada: Situación decadente.
Pruebas contra ella: Actuación cruel contra la víctima a partir de los años sesenta.
Aparentando ayudarla la mantuvo secuestrada.
5.- EDUCACIÓN MATEMÁTICA: Súbdita obligatoria. Por su departamento han pasado
todos los sospechosos.
Móvil: Posible negligencia.
Coartada: Siempre habían mantenido una buena relación.
Pruebas contra ella: Nerviosismo ante los cambios. Deseos de quedar bien. Incapacidad
para presentar a la víctima de forma atractiva.
6.- COMPUTER COMPANY: Súbdita cibernética. Constituye el departamento más ruidoso
del tren. No han parado de moverse por todos los vagones durante todo el trayecto.
Móvil: Posible oferta de una nueva creación a la cual la víctima podría haber molestado.
Intereses monetarios.
Coartada: Ofrece atractivas visiones de la víctima.
Pruebas contra ella: Incorporación de extraños seres marcianos en sus promociones.
7.- EDITORIALES S.A.: Súbdita práctico. En su departamento han aparecido posesiones
de la víctima.
Móvil: Posible campaña publicitaria de la marca.
Coartada: Incluye bellas fotos de la víctima.
Pruebas contra ella: Aparición del cubo de Rubik, objeto que ha permitido jugar con la
víctima sin entender nada de la misma.
8.- RAIMUNDO CRONOPIO: Súbdito universitario, posee una cátedra con el nombre de la
víctima.
Móvil: Ninguno. Podría darse un deseo de cambiar de silla.
Coartada: Su situación laboral está ligada a la víctima.
Pruebas contra él: Se le ha visto contar cosas insólitas sobre la víctima en grandes
pizarras. Nunca tuvo en sus manos un poliedro.
9.- JOSÉ PÉREZ: Súbdito nacional de enseñanza secundaria.
28
Antología de lecturas
Matemáticas
Móvil: El sospechoso ha dado siempre muestras de nerviosismo e inseguridad ante la
víctima en su apretadísimo programa de acelerada impartición.
Coartada: Sigue los libros de texto aprobados oficialmente.
Pruebas contra él: Aparecen miles de testigos dispuestos a declarar su total ignorancia
sobre la víctima y su posible secuestro por parte del sospechoso.
10.- ANITA CASIOLI: Súbdita en una escuela, maestra de enseñanza primaria.
Móvil: Ninguno
Coartada: Realmente nunca conoció a la víctima.
Pruebas contra ella: El diagrama aparecido en el lugar de los hechos.
11.- AUTORIDADES: Organizadores de los súbditos. De sus departamentos en el tren
acostumbran a salir muchos papeles reformadores pero poco papel moneda.
Móvil: Posible desconocimiento de lo que están haciendo.
Coartada: Ellas sólo organizan. Nunca entran en clase.
Pruebas contra ellas: Confían más en los profesionales de la cola del tren que en los
maquinistas.
12.- FAMILIA S.L.: Súbditos agresivos muy celosos de su departamento.
Móvil: Posible pánico ante el fracaso escolar.
Coartada: Ellos no saben ni han visto nada.
Pruebas contra ella: No colabora en general con las autoridades.
13.-JUANITO GARCÍA: Súbdito escolar. Viaja por obligación. Se apearía a la primera
ocasión posible.
Móvil: Tendencia a la ley del mínimo esfuerzo.
Coartada: No sabe nada, nunca tuvo ni idea de nada sobre la víctima.
Pruebas contra él: Se le ha visto arrancar páginas de textos donde aparecían imágenes
de la víctima. Cuando se pronuncia el nombre de la interfecta acostumbra a bostezar.
La labor de los interrogatorios había dejado muy fatigado a Poirot. Tomó una cena ligera y
se retiró a descansar. Aquella noche no obstante Poirot no podría, como en tantas otras ocasiones,
conciliar el sueño.
TERCERA PARTE
A la mañana siguiente Poirot se levantó de buen humor. Sin pérdida de tiempo mandó
convocar a todos los del tren en el vagón comedor. Todos llegaron y tomaron asiento en torno a las
mesas. Unos más y otros menos tenían la misma expresión: una mezcla de expectación y temor.
Poirot se aclaró la garganta.
29
Antología de lecturas
Matemáticas
- Monsieurs et madames. Estamos aquí para investigar la muerte de la Geometría. Hay dos
posibles soluciones para el crimen. Expondré las dos.
Poirot lanzó una significativa mirada a los presentes y prosiguió.
- Hay una primera posible solución al crimen. Seguramente no ha habido tal crimen y se
trató sólo de una muerte natural, por simple vejez. Eran muchos siglos de vida intensa, fueron
muchos sus enamorados, sus esposos y sus hijos. Seguramente a la geometría le faltó la juventud
necesaria para emprender nuevas aventuras. Así el crimen realmente no lo sería.
Se oyó un cierto respiro entre los presentes a la vez que el doctor movía la cabeza, dudando de
la solución.
- Pero hay otra solución posible, - prosiguió Poirot, - y es la siguiente. La idea me vino al
final de los interrogatorios. Era una coincidencia muy grande que tantos sospechosos de todas las
nacionalidades, clases y edades viajaron hoy, precisamente, en el mismo tren. No podía haber
casualidad, sino designio... el asunto se me apareció con una claridad meridiana. Lo vi como un
mosaico perfecto en el que cada trozo desempeñaba la parte asignada. Cada parte entró por turno
en el mundo de la Geometría y descargó su golpe. Y fueron todos. Los unos con maldad, los otros
por simple ignorancia. Así nadie sabría jamás quien fue en realidad el culpable.... yo creo que esta
segunda solución es la más plausible aunque sugiero que sea la primera solución la que expliquemos
al mundo.
- Entonces, – dijo Poirot -, como ya he expuesto mi solución ante todos ustedes, tengo el
honor de retirarme completamente del caso.
FIN
Agatha Christie gustó siempre acabar sus narraciones con el brillante esclarecimiento de
los hechos en base a la sagacidad de Poirot. Pero para nosotros, gente positiva de la Educación
Matemática, sería triste acabar aquí. Intentemos dictar unos veredictos y unas sentencias en relación
al caso que nos ocupa.
A la vista de los argumentos aportados por Poirot la primera solución queda desestimada
por ingenua. Así pues aceptando la segunda solución como buena queda claro la intervención de
todos los sospechosos en la muerte de la Geometría:
1.- Se considera a la Celestial Corporation culpable de asesinato con la atenuante de
inconsciencia. Se la condena a poner ejemplos concretos de la Geometría en todos sus escritos.
2.- Se considera a Nicolás Bourbaki culpable de asesinato en primer grado. Queda
condenado a reeditar sus libros con dibujos, cómics y chistes.
30
Antología de lecturas
Matemáticas
3.-Se considera a la Formalización Inc. And Sons culpable de homicidio. Deberá durante
un largo periodo no inferior a una década, redactar los escritos en verso, y en el caso de incluir
símbolos, éstos deberían ser en colores variados.
4.- Se considera a la Mathematique Moderne culpable de homicidio. No obstante dada su
avanzada edad y decrepitud se la exime de castigo alguno.
5.- Se considera a la Educación Matemática culpable por negligencia. Deberá incluir
siempre bellos apartados geométricos en cuanta publicación, congreso o clase organice.
6.- Se considera a la Computer Company culpable de homicidio con el agravante de robo.
Por ello queda condenada a no poder vender productos que no contengan, en parte, elementos
geométricos.
7.- Se considera a las Editoriales S.A. culpables de recortes deshonestos. Deberán editar
guías geométricas y regalar con cada ejemplar un poliedro arquimediano cuyo diámetro no será
inferior a 50 cm.
8.- A Raimundo Cronopio se le considera culpable de no hacer una Geometría entendible.
Por ello deberá hacer durante un mes de cada curso clase de geometría en régimen de taller y sin
pizarra.
9.- Se considera a José Pérez culpable de aceleración y olvido. Deberá dedicar dos meses
de cada curso a enseñar Geometría realizando visitas, excursiones y juegos en el patio sin seguir
libro de texto alguno.
10.- Se considera a Anita Casioli culpable en el sentido de que el desconocimiento de la
ley no exime de su cumplimiento. Se la anima a que recupere el tiempo perdido y que se obligue a
explicar cuentos geométricos y hacer construcciones manipulativas.
11.- Se considera a las Autoridades culpables de homicidio involuntario. Deberán financiar
un laboratorio de Geometría en todos los centros bajo su jurisdicción.
12.- A la Familia S.L. se la considera culpable por inhibición con el agravante de
nocturnidad. Queda obligada a decorar su biblioteca con figuras de colores.
13.- A Juanito García, por ser menor de edad, se le exime de toda responsabilidad. Pero
se le anima a que sepa descubrir la belleza geométrica y a que ponga música a cuanto resultado se
le aparezca por delante.
Todo esto parece ya suficiente.
- Ring, Ring, Ring – suena un teléfono.
- ¿Si? ¿Diga? ¿Cómo? ¿Qué no ha muerto?... ¿Pues donde está ahora? Ya, la Geometría
está, espere que lo anoto... en nuestros cuerpos, en el paisaje, en nuestras casas, pero que alegría
31
Antología de lecturas
Matemáticas
me da....¿y se encuentra bien?.... estupendo, mejor que nunca..... Ya ha necesitado varios
trasplantes.... es curioso....y ¿que ha sido?... le han cambiado letras por dibujos, discursos por
talleres.... y le han tenido que administrar unos cuantos axiomas con ternura, unos teoremas felices y
unas cuantas demostraciones emocionantes... ¡Gracias por comunicarlo!
Bien, pueden quedarse tranquilos. La Geometría vive.... ¡Viva la Geometría!
LA SEXTA NOCHE
EL DIABLO DE LOS NÚMEROS
Hans Magnus Enzensberger
—Probablemente crees que soy el único —dijo el diablo de los números cuando volvió a aparecer. En
esta ocasión estaba sentado en una silla plegable, en medio de un enorme campo de patatas.
—¿El único qué? —preguntó Robert.
—El único diablo de los números. Pero no es cierto. Soy sólo uno de muchos. Allá de donde vengo,
en el paraíso de los números hay montones de nosotros. Por desgracia no soy el más importante. Los
verdaderos jefes están sentados en sus habitaciones, pensando. De vez en cuando uno se ríe y dice
algo parecido a: «Rn igual a hn dividido entre función de n por f de n, abre paréntesis, a más theta,
cierra paréntesis», y los otros asienten comprensivos y ríen con él. A veces ni siquiera sé de qué
hablan.
—Pues para ser un pobre diablo eres bastante engreído —objetó Robert—. ¿Qué quieres, que te
compadezca ahora?
—¿Por qué crees que me hacen andar por ahí por las noches? Porque los señores de ahí arriba
tienen cosas más importantes que hacer que visitar a principiantes como tu, mi querido Robert.
—O sea que puedo decir que tengo suerte de poder soñar por lo menos contigo.
—Por favor, no me malinterpretes —dijo el amigo de Robert, porque entre tanto se habían hecho casi
viejos amigos—, lo que cavilan los señores de ahí no es realmente malo. Uno de ellos, al que aprecio
especialmente es Bonatschi. A veces me cuenta lo que va averiguando. Es italiano. Por desgracia
hace mucho que ha muerto, pero eso no significa nada para un diablo de los números. Un tipo
simpático, el viejo Bonatschi. Por otra parte, fue uno de los primeros que entendieron el cero. Desde
luego no lo inventó, pero en cambio se le ocurrió la idea de los números de Bonatschi. ¡Deslumbrante!
Como la mayoría de las buenas ideas, su invento empieza con el uno… ya sabes.
Más exactamente, con dos unos: 1+1=2.
»Luego coge las dos últimas cifras y las suma:
así que... y luego... 1=1
1+1=2
otra vez las dos
1+2=3
últimas...
2+3=5
3+5=8
etcétera.
5+8=13
8+13=21
—Hasta el aburrimiento.
32
Antología de lecturas
Matemáticas
—Naturalmente.
Entonces, el diablo de los números empezó a salmodiar los números de Bonatschi; sentado en su
silla plegable, cayó en una especie de canturreo. Era la más pura ópera de Bonatschi:
— Unounodostrescincoochotreceveintiunotreintaycuatro
cincuentaycincoochentaynuevecientocuarentaycuatro
doscientostreintaytrestrescientossetentaysiete etc...
Robert se tapó los oídos.
—Ya paro —dijo el anciano—. Quizá sea mejor que te los escriba, para que puedas aprendértelos. —
¿Dónde?
—Donde tú quieras. Quizá en un pergamino.
Desatornilló el extremo de su bastón y sacó un fino rollo de papel. Lo tiró al suelo y le dio un
golpecito. ¡Es increíble la cantidad de papel que había dentro del bastón! Una interminable serpiente
que se desenrolló cada vez más y corrió más y más lejos por los surcos del campo, hasta que su
extremo desapareció en la lejanía. Y, naturalmente, en el rollo estaba toda la serie de Bonatschi con
sus números:
1.
1
2.
1
3.
2
4.
3
5.
5
6.
8
7.
13
8.
21
9.
34
10. 11. 12. 12.
55 89 144 233
A partir de ahí, los números estaban tan lejos y eran tan pequeños que Robert ya no pudo leerlos.
—Bueno, ¿y qué? —preguntó Robert.
—Si sumas los cinco primeros y añades uno, te sale el séptimo. Si sumas los seis primeros y añades
uno, te sale el octavo. Etcétera.
—Ya —dijo Robert. No parecía especialmente entusiasmado.
—Pero también funciona si te saltas siempre un número de Bonatschi, sólo tienes que tener siempre
el primer uno —dijo el diablo de los números.
»Mira:
(y ahora te saltas uno)
(y vuelves a saltarte uno)
1+1=2
+3
+8
+ 21
(y te saltas uno más)
sumas esos cuatro, ¿y qué te sale?
—Treinta y cuatro —dijo Robert.
—O sea el número de Bonatschi que sigue al 21.
Si te resulta demasiado trabajoso, también se puede hacer saltando. Por ejemplo, coges el número
de Bonatschi número cuatro y lo haces saltar. El cuarto es el 3, y ¿cuánto es 32?
—Nueve —dijo Robert.
33
Antología de lecturas
Matemáticas
—Luego coges el siguiente número de Bonatschi, es decir, el quinto, y lo haces saltar.
—52 = 25 —dijo Robert sin titubear.
—Bien, y ahora los sumas.
9+25=34
—Otro Bonatschi —exclamó Robert.
—Y además, como cuatro más cinco son nueve, el noveno —dijo el anciano frotándose las manos.
—Comprendo. Todo estupendo, pero dime para qué sirve.
—Oh —dijo el diablo de los números—, no te creas que las Matemáticas son sólo cosa de
matemáticos. Tampoco la Naturaleza sale adelante sin números. Incluso los árboles y los moluscos
saben contar.
—Tonterías —dijo Robert—. ¡Me quieres dar gato por liebre!
—También los gatos, supongo. Todos los animales. Por lo menos, se comportan como si tuvieran los
números de Bonatschi en la cabeza. Es posible que hayan comprendido cómo funcionan.
—No me lo creo.
—O las liebres. Tomemos mejor las liebres, son más espabiladas que los moluscos. ¡En este campo
de patatas tiene que haber liebres!
—Yo no veo ninguna —dijo Robert. —Ahí hay dos.
De hecho, dos diminutas liebres blancas se acercaron dando brincos y se sentaron a los pies de
Robert.
—Creo —dijo el anciano— que son un macho y una hembra. Así que tenemos una pareja. Como
sabes, todo empieza con el uno.
—Quiere convencerme de que sabéis contar —dijo Robert a las liebres—. ¡Esto es demasiado! No le
creo una sola palabra.
—Ah, Robert, qué sabrás tú de liebres —dijeron las dos liebres al unísono—. ¡No tienes ni idea!
Probablemente te has creído que somos liebres de invierno.
—Liebres de invierno, claro —repuso Robert, que quería demostrarles que no era tan ignorante como
parecía—. Solamente en invierno hay liebres de invierno.
—Justo. Nosotras sólo somos blancas mientras somos pequeñas. Pasa un mes hasta que llegamos a
ser adultas. Luego nuestra piel se vuelve parda, y queremos tener hijos. Hasta que vienen al mundo,
chico y chica, pasa cosa de un mes más. ¡Toma nota de esto!
34
Antología de lecturas
Matemáticas
—¿Sólo vais a tener dos? —dijo Robert—. Yo siempre había pensado que las liebres tenían un
montón de hijos.
—Naturalmente que tenemos un montón de hijos —dijeron las liebres—, pero no de un golpe. Cada
mes dos, con eso basta. Y nuestros hijos harán exactamente lo mismo. Ya lo verás.
—No creo que nos quedemos tanto tiempo aquí. Para entonces me habré despertado hace mucho.
Mañana temprano tengo que ir al colegio.
—No hay problema —Intervino el diablo de los números—. En este campo de patatas el tiempo va
mucho más rápido de lo que tú piensas. Un mes dura sólo cinco minutos. Y para que lo creas he
traído un reloj de liebre. iMira!
Y con estas palabras, sacó un reloj de bolsillo considerablemente grande. Tenía dos orejas de liebre,
pero sólo una aguja.
—Además, no marca horas, sino meses. Cada vez que pasa un mes, suena el despertador. Cuando
aprieto el botón de arriba empieza a correr. ¿Lo hago? —Sí —gritaron las liebres.
—Bien.
El diablo de los números apretó, el reloj hizo tic—tac, y la aguja empezó a desplazarse. Cuando hubo
llegado al uno, sonó el timbre. Había pasado un mes, las liebres se habían hecho mucho más
grandes y su piel había cambiado de color… ya no eran blancas, se habían vuelto pardas.
Cuando la aguja llegó al dos, habían pasado tres meses, y la liebre trajo al mundo dos diminutas
liebres blancas.
Ahora había allí dos parejas de liebres, las jóvenes y las viejas. Pero estas últimas aún no estaban, y
cuando la satisfechas. Querían tener más hijos y cuando la aguja llegó al tres volvió a sonar el timbre,
y la liebre vieja trajo otras dos más al mundo.
Robert contó las parejas de liebres. Ahora eran tres: las mayores (pardas), las crías de la primera
camada, que entre tanto también habían crecido (y se habían vuelto pardas), y las más jóvenes, con
su piel blanca.
35
Antología de lecturas
Matemáticas
Entonces la aguja se movió hasta el cuatro, y ocurrió lo siguiente: la liebre mayor trajo al mundo la
siguiente parejita, sus primeros hijos también; los segundos tampoco habían sido perezosos, así que
ahora eran cinco parejas las que brincaban por el sembrado: una pareja de padres, tres parejas de
hijos y una pareja de nietos. Tres parejas eran pardas, y dos blancas.
—Yo en tu lugar —dijo el diablo de los números— ya no intentaría diferenciarlas. ¡Vas a tener
bastante con contarlas!
Cuando el reloj hubo llegado al cinco, Robert ya se las arreglaba bastante bien. Ahora había ocho
pares de liebres.
Cuando sonó por sexta vez, ya había trece… ¡Un barullo increíble, pensó Robert, adónde irá a parar
todo esto!
Pero incluso la séptima vez averiguó la cifra: eran exactamente 21 parejas.
—¿Se te ocurre algo, Robert? —preguntó el diablo de los números.
36
Antología de lecturas
Matemáticas
—Naturalmente —respondió Robert—. Son números de Bonatschi:
1,1,2,3,5,8,13,21…
Pero, mientras lo decía, habían venido al mundo montones de liebres blancas, que caracoleaban
entre las muchas pardas y blancas que brincaban en el campo. No podía verlas y contarlas a todas.
El reloj de liebre avanzaba implacable. Hacia mucho que la aguja había empezado su segunda vuelta.
—¡Socorro! —gritó Robert—. Esto no se acaba. ¡Miles de liebres! ¡Es espantoso!
—Para que veas cómo funciona la cosa, he traído un listado de liebres para ti. En él podrás ver lo que
ha pasado entre las cero y las siete horas.
—Hace mucho que pasaron las siete —exclamó Robert—. Ahora ya deben de ser por lo menos más
de mil.
—Son exactamente 4.181, y ahora mismo, es decir, dentro de cinco minutos, serán 6.765.
—¿Quieres seguir así, hasta que la Tierra entera esté cubierta de liebres? —preguntó Robert.
—Oh, eso no llevaría mucho tiempo —dijo el anciano, sin mover un músculo—. Unas pocas vueltas
más de la aguja y habrá ocurrido.
—¡Por favor, no! —pidió Robert—. ¡Es una pesadilla! ¿Sabes?, no tengo nada contra las liebres, me
gustan incluso, pero lo que es excesivo es excesivo. Tienes que detenerlas.
—Encantado, Robert. Pero sólo si admites que las liebres se comportan como si se hubieran
aprendido los números de Bonatschi.
—Sí, bien, por el amor de Dios, lo admito. Pero date prisa, o acabarán subiéndosenos a la cabeza.
El diablo de los números pulsó dos veces la corona del reloj de liebre, y éste empezó a funcionar,
hacia atrás. Cada vez que sonaba el timbre las liebres disminuían, y al cabo de unas pocas vueltas la
aguja volvía a marcar cero. Había dos liebres en el vacío campo de patatas.
37
Antología de lecturas
Matemáticas
—¿Qué pasa con éstas? —Preguntó el anciano—. ¿Quieres conservarlas?
—Mejor que no. De lo contrario, volverán a empezar desde el principio.
—Sí, eso es lo que pasa con la Naturaleza —dijo el anciano, columpiándose complacido en su silla
plegable.
—Eso es lo que pasa con Bonatschi —replicó Robert—. Con tus números todo va siempre a parar al
infinito. No sé si me gusta.
—Como has visto, a la inversa ocurre exactamente igual. Hemos vuelto a aterrizar donde empezamos,
en el uno.
Y así, se separaron pacíficamente, sin preocuparse de qué ocurriría con la última pareja de liebres. El
diablo de los números se fue con Bonatschi, su viejo conocido del paraíso de los números, y con los
demás, que tramaban allí nuevas diabluras, y Robert siguió durmiendo, sin soñar, hasta que sonó el
despertador. Se alegró de que fuera un despertador corriente, y no un reloj de liebre.
El que aún no se crea que en la Naturaleza las cosas
ocurren como si supiera contar, que mire atentamente el
árbol que viene a continuación. Quizá a alguno de vosotros
le resultó demasiado complicado el asunto de las liebres.
Pero un árbol no brinca de acá para allá se queda quieto y
por eso es más fácil contar sus ramas. Por favor, empieza
por abajo, en la raya roja n.° 1; sólo pasa por el tronco,
igual que la raya n.° 2. Un punto más alto, en la raya n.° 3,
se añade una segunda rama. Y ahora, por favor, sigue
contando. ¿Cuántas ramas hay arriba del todo, en la raya
roja n.° 9?
LA OCTAVA NOCHE
38
Antología de lecturas
Matemáticas
Robert estaba delante del todo, en la pizarra. En el primer banco se sentaban sus dos mejores
amigos de clase: Albert, el futbolista, y Bettina, la de las trenzas. Como siempre, los dos estaban
discutiendo. Esto es lo que me faltaba, pensó Robert. ¡Ahora sueño con el colegio!
Entonces se abrió la puerta, pero no fue el señor Bockel quien entró… fue el diablo de los números.
—Buenos días —dijo—. Según veo, ya estáis discutiendo otra vez. ¿De qué se trata?
— ¡Bettina se ha sentado en mi sitio! —gritó Albert.
—Entonces simplemente cámbialo con ella.
—Pero es que no quiere —dijo Albert.
—Escríbelo en la pizarra, Robert —pidió el anciano.
—¿El qué?
—Escribe A para Albert y B para Bettina. Albert se sienta a la izquierda y Bettina a la derecha.
Robert no veía por qué tenía que escribir eso, pero pensó: Si le gusta, por mí que no quede.
AB
—Bueno, Bettina —dijo el diablo de los números—, ahora siéntate tú a la izquierda y Albert a la
derecha.
¡Es curioso! Bettina no protestó. Se levantó como una niña buena e intercambio su sitio con Albert.
BA
Escribió Robert en la pizarra.
En ese momento se abrió la puerta y entró Charlie, con retraso, como siempre. Se sentó a la
izquierda de Bettina.
CBA
escribió Robert.
Pero eso no le gustó a Bettina.
—¡Si hemos dicho a la izquierda –dijo—, que sea del todo a la izquierda!
—Está bien —bramó Charlie—. ¡Como quieras!
Y ambos intercambiaron sus asientos:
39
Antología de lecturas
Matemáticas
Albert no se quedó conforme con eso.
BCA
—Pero yo prefiero sentarme con Bettina —gritó. Charlie fue tan bondadoso que se levantó sin más y
le dejó su sitió a Albert.
BAC
Si esto sigue así, se dljo Robert, podemos olvidarnos de esta clase de Matemáticas. Pero siguió así
porque ahora era Albert el que quería sentarse del todo a la izquierda.
—Pero entonces tenemos que levantarnos todos —dijo Bettina—. No veo por qué, pero si no hay más
remedio… ¡Ven, Charlie!
Y cuando volvieron a sentarse la cosa estaba así:
ABC
Naturalmente, no duró mucho.
—No aguanto un minuto más al lado de Charlie —afirmó Bettina. Realmente rompía los nervios. Pero,
como no paraba, los otros chicos tuvieron que ceder. Robert escribió:
CAB
—Y ahora basta —dijo.
—¿Tú crees? —preguntó el diablo de los números—. Esos tres aún no han ensayado todas las
posibilidades. ¿Qué os parecería sentaros Albert a la izquierda, Charlie en el centro y Bettina a la
derecha?
—¡Jamás! —gritó Bettina.
—No te pongas así, Bettina —dijo el anciano.
A regañadientes, los tres se levantaron y se sentaron así:
ACB
—¿Te das cuenta Robert? ¡Eh, Robert, te estoy hablando! Seguro que a estos tres no se les ocurre.
Robert alzó la vista hacia la pizarra:
AB
CAB
40
Antología de lecturas
BA
Matemáticas
BCA
BAC
ABC
CAB
ACB
—Creo que hemos probado todas las posibilidades —dijo.
—Eso creo yo también —dijo el diablo de los números—. Pero no puede ser que en vuestra clase
sólo seáis cuatro. Me temo que aún faltan unos cuantos.
Apenas lo había dicho cuando Doris abrió la puerta. Estaba sin aliento.
—¿Qué ocurre aquí? ¿No está el señor Bockel? ¿Quién es usted? —preguntó al diablo de los
números.
—Sólo estoy aquí de manera excepcional —dijo el anciano—. Vuestro señor Bockel se ha tomado el
día libre. Ha dicho que ya no podía más. Que vuestra clase es demasiado movida para él.
—Ya lo puede decir —replicó Doris—: están todos cambiados de sitio. ¿Desde cuándo es ése tu sitio,
Charlie? ¡Ahí me siento yo!
—Entonces propón un orden para sentarse, Dorís —dijo el diablo de los números.
—Yo seguiría simplemente el orden alfabético —dijo ella—. A de Albert, B de Bettina, C de Charlie,
etc. Eso sería lo más sencillo.
—Como quieras. Intentémoslo.
Robert anotó en la pizarra:
ABCD
Pero los demás no estaban en absoluto de acuerdo con el orden propuesto por Doris. En la clase
andaba suelto el Diablo. Bettina era la peor. Mordía y arañaba cuando alguien no quería ceder su sitio.
Todo el mundo empujaba y se daba codazos. Pero, con el tiempo, ese loco juego empezó a gustarles
a los cuatro. El cambio se producía cada vez más deprisa, de tal modo que Robert no daba abasto en
sus anotaciones. Por fin, la banda de los cuatro hubo ensayado todos, los órdenes posibles y en la
pizarra ponía:
ABCD
ABDC
ACBD
ACDB
ADBC
ADCB
BACD
BADC
BCAD
BCDA
BDAC
BDCA
CABD
CADB
CBAD
CBDA
CDAB
CDBA
DABC
DACB
DBAC
DBCA
DCAB
DCBA
Menos mal que hoy no han venido todos, pensó Robert, de lo contrario no acabaríamos nunca.
41
Antología de lecturas
Matemáticas
Entonces se abrió la puerta y Enzio, Felicitas, Gerardo, Heidi, Ivan, Jeannine y Karol se precipitaron a
entrar.
—¡No! —gritó Robert—. ¡Por favor, no! ¡No os sentéis! Voy a volverme loco.
—Está bien —dijo el diablo de los números—, lo dejaremos aquí. Podéis iros a casa. No habrá clase
en las próximas horas.
—¿Y yo? —preguntó Robert.
—Tú puedes quedarte un ratito más.
Los otros habían salido corriendo al patio. Robert miraba lo que ponía en la pizarra.
—Bien, ¿qué opinas? —preguntó el diablo de los números.
—No sé. Sólo hay una cosa clara: que son cada vez más. Cada vez más posibilidades de sentarse.
Mientras sólo había dos alumnos la cosa aún funcionaba. Dos alumnos, dos posibilidades. Tres
alumnos, seis posibilidades. Con cuatro ya son… un momento…: veinticuatro.
—¿Y si sólo hubiera uno?
—¡Qué tontería! Entonces, naturalmente, sólo habría una posibilidad.
—Prueba a multiplicar —dijo el anciano.
Alumnos
1
2
3
4
Posibilidades
1
1x2=2
1x2x3=6
1x2x3x4=24
—Ajá —exclamó Robert—. Qué interesante.
—Si cada vez son más los que participan en el aburrido juego, se vuelve aburrido apuntarlos así.
También se puede hacer más corto. Se escribe el número de participantes y un signo de exclamación
detrás:
4!=24
»Se pronuncia así: ¡cuatro pum!
—Si no hubiéramos mandado a casa a Enzio, Felicitas, Gerardo, Heidi, Ivan, Jeannine y Karol, ¿qué
crees que hubiera ocurrido?
42
Antología de lecturas
Matemáticas
—Una gigantesca confusión —dijo el diablo de los números—. Hubieran estado probando hasta
hartarse todas las posiciones posibles, y puedo asegurarte que hubiera sido algo endemoniadamente
largo. Contando a Albert, Bettina y Charlie hubieran sido once personas, y eso significa ¡once pum!
posibilidades de sentarse. ¿Tienes idea de cuántas posibilidades serían?
—Nadie podría calcular eso de cabeza. Pero en el colegio siempre tengo mi calculadora a mano. En
secreto, claro, porque el señor Bockel no puede soportar que se trabaje con ella.
Y Robert empezó a teclear:
1x2x3x4x5x6x7x8x9x10x11=
—¡Once pum! —dijo— son exactamente 39,916,800. ¡Casi cuarenta millones!
—Ya ves, Robert, si hubiéramos tratado de hacerlo aún estaríamos aquí dentro de ochenta años.
Hace mucho que tus compañeros de clase necesitarían una silla de ruedas, y tendríamos que
contratar a once enfermeras para llevarlos de acá para allá. Pero con un poquito de Matemáticas la
cosa va más rápido. Se me ocurre una cosa más. Mira por la ventana a ver si tus compañeros de
clase aún están ahí.
—Creo que se habrán comprado rápidamente un helado, y ahora irán camino de casa.
—Supongo que se darán la mano al despedirse. —Ni hablar. Como mucho dirán Adiós o Hasta luego.
—Lástima —dijo el diablo de los números—. Me gustaría saber qué ocurre si todo el mundo da la
mano a todo el mundo.
—¡Para ya! Seguro que eso duraría eternamente.
Es probable que haya un número gigantesco de apretones. ¡Puede que once pum! si es que son once
personas.
—¡Error! —dijo el anciano.
Si son dos, reflexionó Robert, sólo se necesita un apretón de manos. Con tres…
—Mejor escríbelo en la pizarra.
Robert escribió:
Personas
A
AB
ABC
ABCD
Apretones de manos:
—
AB
AB
AC
BC
AB
AC
AD
BC
BD
CD
—Entonces, con dos es uno, con tres son tres, y con cuatro son ya seis apretones de manos.
43
Antología de lecturas
Matemáticas
—1, 3, 6… ¿no conocíamos eso?
Robert no conseguía acordarse. Entonces, el diablo de los números pintó unos cuantos puntos
gruesos en la pizarra:
—¡Los cocos! —Gritó Robert—. ¡Números triangulares!
—Y cómo siguen?
—Ya lo sabes:
1+2
3+3
6+4
10+5
15+6
21+7
28+8
36+9
45+10
=3
=6
=10
=15
=21
=28
=36
=45
=
—Son exactamente 55 apretones de manos.
—Eso aún se puede calcular —dijo Robert.
—Si no quieres pasar tanto tiempo calculando, también puedes hacerlo de otra forma. Dibujas unos
círculos en la pizarra, así:
»Luego, pones una letra más en cada nuevo círculo: A para Albert, B para Bettina, C para Charlie,
etcétera.
44
Antología de lecturas
Matemáticas
»Luego unes las letras con líneas:
»No tiene mal aspecto, ¿verdad? Cada raya significa un apretón de manos. Puedes contarlas.
—1, 3, 6, 10, 15… Como antes —dijo Robert—. Sólo hay una cosa que no entiendo: ¿puedes
explicarme por qué contigo siempre cuadra todo?
—Eso es precisamente lo demoníaco de las Matemáticas. Todo cuadra. Bueno, digamos mejor que
casi todo. Porque ya sabes que los números de primera tienen sus pegas. Y también en lo demás hay
que poner una atención enorme, porque de lo contrario es fácil caerse con todo el equipo. Pero, en
líneas generales, en las Matemáticas la cosa discurre con bastante orden. Eso es lo que cierta gente
odia de ellas. Pero yo no puedo soportar a los desordenados y a los chapuceros, y a ellos les pasa al
revés, no soportan los números. A propósito, mira por la ventana: ¡el patio de vuestro colegio es una
auténtica pocilga!
Robert tuvo que admitirlo, porque en el patio había latas de coca cola vacías, tebeos rotos y
envoltorios de bocadillo por todas partes.
—Si tres de vosotros cogierais una escoba, dentro de media hora vuestro patio tendría mucho mejor
aspecto.
—¿Y quiénes serían esos tres? —preguntó Robert.
—Albert, Bettina y Charlie, por ejemplo. O Doris, Enzio y Felicitas. Además, también tenemos a
Gerardo, Heidi, Ivan, Jeannine y Karol.
—Pero tú dices que sólo se necesitan tres.
—Sí —objetó el diablo de los números—, pero ¿qué tres?
—Se les puede combinar a voluntad —dijo Robert.
Robert escribió:
45
Antología de lecturas
Matemáticas
ABC
—Y si entonces llega Doris, ¿qué hacemos?
Vuelve a haber varias posibilidades.
Robert reflexionó. Luego escribió en la pizarra:
ABC
ABD
ACD
BCD
—Cuatro posibilidades —dijo.
—Pero casualmente Enzio pasa por allí. ¿Por qué no va a echar una mano? Ahora tenemos cinco
candidatos. Prueba.
Pero Robert no quiso.
—Mejor dime qué va a salir —dijo desmoralizado.
—Está bien. Con tres personas sólo podemos formar un grupo de tres. Con cuatro personas ya hay
cuatro grupos distintos, y con cinco hay diez. Te lo escribiré:
3 ABC
4 ABC ABD
ACD
BCD
5 ABC ABD ABE ACD ACE ADE BCD BCE BDE CDE
»Hay otra cosa rara en esta lista. La he ordenado conforme al alfabeto, como ves. ¿Y cuántos grupos
empiezan por Albert? Diez. ¿Cuántos por Bettina? Cuatro. Y por Charlie no empieza más que uno. En
este juego aparecen una y otra vez las mismas cifras:
1,4,10…
»¿Adivinas cómo sigue? Quiero decir, si ahora añadimos unos cuantos más, digamos que Felicitas,
Gerardo, Heidi, etc. ¿Cuántos grupos de tres saldrían?
—Ni idea —dijo Robert.
—¿Te acuerdas todavía de cómo discurrimos el asunto de los apretones de manos, cuando todo el
mundo se despedía de todo el mundo?
—Eso fue muy fácil, con ayuda de los números triangulares:
1, 3, 6, 10, 15, 21…
46
Antología de lecturas
Matemáticas
»Pero no sirve para nuestras cuadrillas de limpieza, que trabajan de tres en tres.
—No. Pero ¿qué pasa si sumas los dos primeros números triangulares?
—Sale cuatro.
—¿Y si añades el siguiente? —Diez.
—¿Y otro más?
—10+10=20.
—Ahí lo tienes.
—¿Y tengo que seguir calculando hasta llegar al undécimo? Ésa no es tu forma de hacer las cosas.
—No te preocupes. También se puede hacer sin calcular, sin probar, sin ABCDEFGHIJK.
—¿Cómo?
—Con nuestro viejo triángulo numérico —dijo el anciano.
—¿Vas a pintarlo en la pizarra?
—No. No estoy pensando semejante cosa. Me resultaría demasiado aburrido. Pero tengo mi bastón a
mano.
Tocó la pizarra con su vara, y ahí estaba el triángulo, en todo su esplendor y a cuatro colores.
—Más cómodo imposible —dijo el viejo diablo de los números—. Al estrechar las manos,
simplemente cuentas los cubos verdes de arriba abajo: con dos personas un apretón de manos, con
tres personas tres, con once personas 55.
»Para nuestra cuadrilla de limpieza necesitas los cubos rojos. Vuelves a contar de arriba abajo.
Empiezas con tres personas con ellas no hay más que una posibilidad. Si puedes elegir cuatro
personas dispones de cuatro combinaciones, con cinco personas ya son diez. ¿Y qué pasa cuando
están los once alumnos?
—Entonces son 165 —respondió Robert—. Es realmente sencillo. Este triángulo numérico es casi tan
bueno como una calculadora. Pero ¿para qué sirven los cubos amarillos?
—Oh —dijo el anciano— ya sabes que yo no me doy fácilmente por satisfecho. Nosotros, los diablos
de los números, siempre lo llevamos todo hasta el extremo. ¿Qué harás si las tres personas que
tienes no son suficientes para el trabaIo? Tendrás que coger cuatro. Y la fila amarilla te dirá cuántas
posibilidades hay, por ejemplo, para elegir un cuarteto a partir de ocho personas.
—Setenta —dijo Robert, porque había entendido muy bien lo fácil que era sacar la respuesta del
triángulo.
47
Antología de lecturas
Matemáticas
—Exacto —dijo el diablo de los números—. Por no hablar de los cubos azules.
Probablemente sean los grupos de ocho. Si sólo dispongo de ocho personas, no tengo que pensar
mucho. Sólo hay una posibilidad. Pero con diez candidatos ya puedo formar 45 grupos distintos.
Etcétera, etcétera.
—Veo que lo has comprendido.
—Ahora sólo quisiera saber qué aspecto tiene el patio —dijo Robert.
Miró por la ventana, y he aquí que el patio estaba impecable como nunca.
—Sólo me pregunto qué tres llevarán ahora la escoba.
—En cualquier caso no eres uno de ellos, mi querido Robert —dijo el diablo de los números.
—¡Cómo voy a barrer el patio del colegio si tengo que pasarme toda la noche peleando con números
y cubos!
—Admite —dijo el anciano— que te has divertido haciéndolo.
—¿Y ahora? ¿Volverás pronto?
—Antes me tomaré unas vacaciones —dijo el diablo de los números—. Entre tanto, puedes
entretenerte con el señor Bockel.
48
Antología de lecturas
Matemáticas
Eso era algo que a Robert le apetecía bastante poco, pero ¿qué remedio le quedaba? A la mañana
siguiente tenía que volver al colegio. Cuando llegó al aula, Albert, Bettina y los otros estaban ya
sentados en sus sitios. Nadie estaba deseando cambiar su sitio con los otros.
—Ahí viene nuestro genio de las Matemáticas —exclamó Charlie.
—El bueno de Robert estudia incluso en sueños —le pinchó Bettina.
—¿Creéis que le va a servir de algo? —preguntó Doris.
—Yo creo que no —gritó Karol—. De todos modos el señor Bockel no le soporta.
—Y viceversa —repuso Robert—. ¡Por mí que no vuelva!
Antes de que llegara el señor Bockel, Robert echó una rápida mirada por la ventana.
Como siempre, pensó al ver el patio. ¡Un verdadero montón de basura! Uno no puede fiarse de las
cosas que sueña. Solamente de los números. En ellos sí se puede confiar.
Luego entró el inevitable señor Bockel, con su maletín lleno de trenzas.
FERMAT.
Berardo Castiñeira de Aragón
―Para todos los que amamos las matemáticas.‖
Paul se sentó incómodo en su butaca de piel. La edad no dejaba de marcar su rostro con profundas
líneas en la piel cuyo comienzo y final eran indecisos. Sus ojos, que en otro tiempo habían sido de un
vivo color azul, ahora buscaban desesperadamente la luz que desprendieron tiempo atrás. Se miró
las manos vacías y observó decaído que habían perdido la fuerza y el vigor de antaño. Aunque su
cuerpo no había superado los cincuenta
años su alma vagaba indecisa entre los noventa y los cien años y cada día que superaba era un
penoso viaje hacia algún lugar que, sea cual fuese, le causaba profundo dolor.
Se echó las manos a la cabeza e indagó en sí mismo en busca de un único motivo que le impulsase a
levantarse de aquel sofá. Apretó fuertemente sus sienes. Pronto comenzó a sudar y aquellas gotas
de sudor que resbalaban por su piel se mezclaron con las lágrimas que florecían marchitas por sus
ojos. Se tapó la cara con las manos para evitar que los fantasmas de toda su existencia le
descubrieran llorando como un simple niño que no quería admitir que todos sus juguetes se habían
roto y se volvían despreciables. Entonces gimió. Era un gemido profundo y vasto que llegaba al
exterior como la sombra de un grito que, encadenado por el peso de los años, no es capaz de
liberarse.
Lo encontró. Encontró el motivo para levantarse. Se incorporó empapado de sudor y lágrimas y se
acercó a su escritorio. Abrió el cajón y sacó de él un pequeño revólver que guardaba para su propia
seguridad. No dejaba de ser irónico –pensaba él- que el objeto que garantizaba su propia seguridad
fuese el que iba a terminar con los fantasmas que le atormentaban. Lo colocó encima de la mesa, se
sentó, cogió un papel y una pluma y mientras puso en el tocadiscos la sonata ―claro de luna‖ de
Beethoven se dispuso a escribir su testamento.
49
Antología de lecturas
Matemáticas
Paul había sido un brillante matemático durante toda su vida. Al comienzo de su carrera profesional,
varios éxitos deslumbraron a toda la comunidad científica y su nombre era conocido por todas partes.
Pronto consiguió una plaza en una prestigiosa universidad y en ella desarrolló su labor docente
acompañada de su incansable tarea investigadora. Su campo era la teoría de números por la que se
sintió atraído desde que conoció, casualmente, la existencia de los números que Pitágoras llamaba
―perfectos‖, aquellos que son la suma de todos sus divisores. Con el tiempo su genialidad se tornó en
mediocridad y, aunque seguía escribiendo con periodicidad en las revistas científicas y estaba en
contacto con la comunidad, su nombre desapareció de los congresos más importantes y nadie
contaba con él a la hora de verificar un resultado o a la hora de pedirle consejo. Nadie está muy
seguro de si la muerte de la genialidad que despuntó al inicio de su carrera fue causa o consecuencia
de su casi total pérdida de ilusión por el mundo de las matemáticas. Éstas le insidiaban
constantemente en su trabajo y en su vida y no podía separarse de ellas produciendo en él una
insaciable sensación de hastío de todo.
Un día llegó al despacho una nueva profesora, Judith. La primera impresión que tuvo de ella le
descolocó momentáneamente. Era una mujer hermosa. Aparentaba tener la misma edad que él y no
podía dejar de observar admirado aquella sonrisa sincera que regalaba a todo el que se acercaba.
Con el paso de los meses y el trabajo conjunto que les unía, Paul se enamoró profundamente de ella.
Era una mujer especial y llena de virtudes. Paul, que creía que el sentimiento era recíproco, decidió
un día manifestarle todos sus sentimientos y explicarle cómo en seis meses había conseguido que se
volviese a emocionar con su vida, con su trabajo, con las matemáticas y, especialmente, con ella.
Pero antes de que él dijese nada ella le habló de su amor por otro hombre. En aquel momento un
oscuro telón cubrió el entendimiento y el alma de Paul. Nunca supo qué ocurrió en los instantes
posteriores ni lo que dijo. Pareciera que todo el ánimo recobrado en el último medio año desde la
llegada de Judith le hubiese golpeado violentamente. Tras dos días de intensa agonía, una tarde,
sentado en su butaca de piel decidió quitarse la vida.
Como siempre hacía con todo, decidió organizar de forma meticulosa y ordenada su muerte. Después
de meditarlo, consideraba que aquello no respondía a un momento de frustración nefasta si no, más
bien, a la resolución adecuada y elegante de una ecuación en la que finalmente la solución, que
existía y era única, era el suicidio. Escribió su testamento. Escribió también una carta en la que
explicaba su situación para que la leyesen cuando encontrasen su cuerpo. Lo cierto es que dudaba
que a nadie le importase mucho los motivos pero, le parecía lo más apropiado dadas las
circunstancias. Y, finalmente, preparó cómo sería la noche de su muerte. Claramente –pensaba éldebía ser por la noche, que es el momento más preciso para las acciones sobrecogedoras. Es más,
sería exactamente a media noche envuelto entre las notas del Réquiem de Mozart que comenzaría
puntualmente a las 23:00 de forma que su cuerpo yaciese en el suelo atravesado por una bala
mientras la magnífica Misa de muertos tocaba a su fin. Así quedaría patente que, en definitiva, todo
acaba.
Por fin llegó la noche elegida. Era una noche abierta en la que las estrellas brillaban poderosamente
queriendo ser testigos directos del suceso que iba a tener lugar. Paul lo había dejado todo preparado
y aún le quedaban algunas horas hasta la media noche. Se sentó una vez más, la última, sobre su
butaca de piel en medio del despacho de su casa. Contempló todo lo que le rodeaba. Un magnífico
despacho acabado en madera cuyas paredes quedaban ocultas por una espléndida biblioteca
atestada de libros, unos de contenido matemático, otros de literatura y una última sección llena de
autores de filosofía. En su esquema inicial no había previsto que le sobrase tanto tiempo antes de la
media noche así que para matar el tiempo – le pareció irónico tener que matar el tiempo antes de
50
Antología de lecturas
Matemáticas
matarse a sí mismo- cogió un libro. Eran los dos artículos de Andrew Wiles en los que se recogía la
demostración del Teorema de Fermat.
Lo abrió por una parte que conocía muy bien y había estudiado en varias ocasiones. Era una de las
partes fundamentales en las que se demostraba la conjetura de Taniyama-Shimura. Aquellas
fórmulas y números eran una sinfonía maravillosa orquestada por un magnífico director y a la vez
autor. Todo parecía tener sentido y cerrarse en sí mismo. Contemplaba la maravilla de las
matemáticas que, con su estructura perfecta, definen de manera exacta su propia esencia. El orden,
la pulcritud, la puntualidad, la exactitud, la coherencia, la ausencia de sinsentidos, la lógica, todas las
virtudes a las que aspira el hombre quedan embebidas en las matemáticas y es por esto que, al igual
que un músico se deleita con la armonía, aquellos que saben entender las matemáticas se deleitan y
disfrutan con el reto que éstas suponen. De pronto, las notas del Réquiem comenzaron a sonar.
Aquellas notas llegaron a la mente de Paul como un bálsamo reconfortante. ―Ya llega el momento de
terminar con esto‖.
Continuó observando la demostración. Entonces vio algo extraño en ella. Era una nota discordante en
medio de la inmensa jerarquía de notas bien organizadas que la acompañaban. No podía detectar si
se trataba de un fallo del músico o, más bien, una nota que el autor no había puesto en el lugar
correcto. Era un paso probablemente baladí en la demostración pero no estaba del todo detallado.
Andrew Wiles había supuesto que la solución de una ecuación trivial era una constante real, lo cual
tenía sentido, pero después hacía uso de ella considerando que era un número positivo y esto no
quedaba reflejado en ningún paso previo. Esto le inquietó. Aquella demostración había sido revisada
por cientos de matemáticos y no podía contener un fallo tan trivial pero… ¿Y si la estructura formal de
la demostración había sido bien revisada pero un detalle tan nimio había pasado desapercibido?
Rápidamente Paul tomó un lápiz y garabateó los pasos previos y siguientes al punto dudoso sobre el
margen del libro. Parecía tener sentido que aquella constante fuese positiva pero… ¿Por qué? La
intuición dejaba claro que tenía que ser así pero la intuición, tan válida para físicos e ingenieros, no es
suficiente para un matemático. Tras un rato trabajando decidió usar un cuaderno pues todos los
márgenes estaban ya repletos de números.
El silencio, agazapado durante el Réquiem, reinaba ahora triunfante en el despacho mientras Paul
seguía concentrado y preocupado por aquella cuestión tan aparentemente sencilla pero a la par
enrevesada. Maldito Fermat –pensó-. Las horas pasaban mientras Paul continuaba absorbido por
aquel paso. Parecía que había avanzado bastante y, desde luego, no era algo tan absolutamente
trivial como para no detallarlo en la demostración. Tenía buen aspecto el rumbo que había tomado
Paul en sus notas y llevaba tres folios rellenos. Ya comenzaba a ver la luz al final del túnel. En unos
pocos pasos más habría, por fin, terminado. En su mente tenía perfectamente clara la estructura de
los últimos pasos y ya veía que, en efecto, aquella constante debía ser positiva. Finalmente, terminó.
La última línea que escribió contenía sencillamente ―por tanto, a es una constante real positiva‖.
Respiró tranquilo y se recostó en la butaca con la satisfacción de quien ha completado un duro
trabajo con un acabado brillante.
Entonces un fogonazo le cegó instantáneamente. Al recuperar la vista miró hacia la fuente de la luz.
Era el primer rayo de sol que se asomaba por la ventana. La luz del sol iluminaba completamente su
rostro. De pronto se dio cuenta… No se había suicidado. Contempló el libro, sus notas en los papeles,
el revolver sobre la mesa. Todo tal y como lo había dejado al inicio de la noche. Entonces sonrió, era
una sonrisa sincera y profunda como hacía mucho tiempo que no disfrutaba. Volvió a mirar al cielo.
Parecía que Dios, a través de las matemáticas, le había regalado una vez más la vida. Se sintió
descansado y sintió asimismo el rebrotar de la vida en su interior con una fuerza desconocida para él.
51
Antología de lecturas
Matemáticas
Una vez más las lágrimas florecieron de sus ojos pero esta vez radiantes como el sol que las cubría
con su luz. Oró como hacía muchos años que no había hecho. Sentado en su butaca de piel
contempló sus manos y, aunque envejecidas, se dio cuenta de que aún tenían la fuerza y el ánimo
para seguir trabajando y luchando. Es la maravilla de la vida – pensó de repente- que es un torrente
de esperanza y fuerza que dura incluso después de la muerte, un paso más en la vida. Se levantó,
arregló sus cosas, cogió su cartera llena de apuntes y se fue a la universidad.
Desde entonces no desperdició ni un solo segundo de su vida. Sus clases se convirtieron en
auténticas lecciones vibrantes y emocionantes en las que sus alumnos disfrutaban y gozaban con sus
maestras palabras. En la comunidad científica volvió a despuntar ilusionado como lo había hecho en
su juventud y nunca dejó de hablar a todos del don inmenso recibido con la vida, escenario perfecto
donde enamorarse, sufrir y amar son preciosas oportunidades para disfrutar aún más de ella.
Finalmente, Paul murió felizmente una dulce tarde de otoño treinta años más tarde de ―la noche de su
verdadero nacimiento‖, como él la llamó siempre, con una sonrisa en los labios. La misma sonrisa
que dedicó siempre al mundo en su paso por él.
EL HOMBRE QUE CALCULABA
Malba Tahan
Capítulo XXIII: De lo que sucedió durante una honrosa visita que recibimos. Palabras del
príncipe Cluzir Schá. Una invitación principesca. Beremiz resuelve un nuevo problema. Las
perlas del rajá. Un número cabalístico. Queda determinada nuestra partida para la India.
El barrio humilde en que vivíamos conoció hoy su primer día glorioso en la Historia.
Beremiz, por la mañana, recibió inesperadamente la visita del príncipe Cluzír Schá.
Cuando la aparatosa comitiva irrumpió por la calle, azoteas y miradores se llenaron de curiosos.
Mujeres, viejos y niños admiraban, mudos y sorprendidos, el maravilloso espectáculo.
Venían delante cerca de treinta jinetes montados en soberbios corceles árabes con arreos adornados
de oro y gualdrapas de terciopelo bordado en plata. Llevaban turbantes blancos con yelmos
metálicos reluciendo al sol, mantos y túnicas de seda y largas cimitarras pendientes de cinturones de
cuero labrado. Les precedían los estandartes con el escudo del Príncipe: un elefante blanco sobre
fondo azul. Seguían varios arqueros y batidores, todos a caballo.
Cerrando el cortejo iba el poderoso maharajá acompañado por dos secretarios, tres médicos y diez
pajes. El Príncipe llevaba una túnica escarlata, adornada con hilos de perlas. En el turbante, de
una riqueza inaudita, centelleaban zafiros y rubíes.
Cuando el viejo Salim vio en su hostería aquella majestuosa comitiva, se puso como loco. Se tiró al
suelo y empezó a gritar:
-¿Men ein?
52
Antología de lecturas
Matemáticas
Mandé que un aguador que allí se hallaba arrastrara al alucinado amigo al fondo del patio hasta que
volviera la calma a su conturbado espíritu.
La sala de la hostelería era pequeña para contener a los ilustres visitantes. Beremiz, maravillado con
la honrosa visita, bajó al patio a fin de recibirlos.
El príncipe Cluzir, al llegar con su porte señorial, saludó al Calculador con un amistoso salam, y
le dijo:
-- El peor sabio es aquel que frecuenta a los ricos; el mayor de los ricos es aquel que frecuenta
a los sabios.
-¡Bien sé, señor, respondió Beremiz, que vuestras palabras están inspiradas en el más arraigado
sentimiento de bondad. La pequeña e insignificante parte de ciencia que conseguí adquirir,
desaparece ante la infinita generosidad de vuestro corazón.
-Mi visita, ¡oh Calculador!, empezó el Príncipe, viene dictada más por el egoísmo que por el amor a la
ciencia. Desde que tuve el honor de oírte en casa del poeta lezid, pensé en ofrecerte algún cargo de
prestigio en mi corte. Deseo nombrarte mi secretario o bien director del Observatorio de Delhi.
¿Aceptas? Partiremos dentro de pocas semanas para La Meca y desde allí, sin mayor dilación
regresaremos directamente a la India.
-Desgraciadamente, ¡oh Príncipe generoso!, respondió Beremiz, no puedo salir ahora de Bagdad. Me
liga a esta ciudad un serio compromiso. Sólo podré ausentarme de aquí cuando la hija del ilustre lezid
haya aprendido las bellezas de la Geometría.
Sonrió el maharajá y replicó:
-Si el motivo de tu negativa se apoya en ese compromiso, creo que pronto llegaremos a un acuerdo.
El jeque lezid me dijo que la joven Telassim, dados los progresos realizados, estará dentro de pocos
meses en condiciones de enseñar a los ulemas el famoso problema de ""las perlas del rajá"
Tuve la impresión de que las palabras de nuestro noble visitante sorprendían a Beremiz. El calculador
parecía muy confuso.
-Mucho me holgaría, siguió diciendo el Príncipe, conocer este complicado problema que desafía
la sagacidad de los algebristas y que se remonta sin duda a uno de mis gloriosos antepasados.
Beremiz, para cumplir el deseo del maharajá, tomó la palabra y habló sobre el problema que
interesaba al Príncipe. Y con su hablar lento y seguro, dijo lo siguiente:
-Se trata menos de un problema que de una mera curiosidad aritmética. Su enunciado es el
siguiente:
"Un rajá dejó a sus hijas cierto número de perlas y determinó que la división se hiciera del
siguiente modo: la hija mayor se quedaría con una perla y un séptimo de lo que quedara. La segunda
hija recibiría dos perlas y un séptimo de lo restante, la tercera joven recibiría 3 perlas y un séptimo de lo
que quedara. Y así sucesivamente".
53
Antología de lecturas
Matemáticas
Las hijas más jóvenes presentaron demanda ante el juez alegando que por ese complicado sistema de
división resultaban fatalmente perjudicadas.
El juez, que, según reza la tradición, era hábil en la resolución de problemas, respondió prestamente que las
reclamantes estaban engañadas y que la división propuesta por el viejo rajá era justa y perfecta.
Y tenía razón. Hecha la división, cada una de las hermanas recibió el mismo número de perlas.
Se pregunta:
¿Cuántas perlas había? ¿Cuántas eran las hijas del rajá?
La solución de ese problema no ofrece la menor dificultad. Veamos:
Las perlas eran 36 y tenían que ser divididas entre 6 personas.
La primera recibió una perla y un séptimo de 35; cinco: Es decir recibió realmente 6 perlas y quedaban
30.
La segunda, de las 30 que encontró recibió 2 y un séptimo de 28, que es 4. Luego recibió 6 y dejó 24.
La tercera, de las 24 que encontró recibió 3 y un séptimo de 21; es decir 3. Se quedó pues con 6 y dejó
un resto de 18.
La cuarta, de las 18 que encontró, se quedó 4 más un séptimo de 14. Y un séptimo de 14 es 2.
Recibió también 6 perlas.
La quinta encontró 12 perlas. De ellas recibió 5 y un séptimo de 7, es decir 1. Luego recibió 6.
La hija menor recibió 6 perlas que quedaban.
Y Beremiz concluyó:
-Como veis, el problema, realmente ingenioso, nada tiene de difícil. Se llega a la solución sin artificios
ni sutilezas de raciocinio.
En aquel momento la atención del príncipe Cluzir Schá fue atraída por un número que se hallaba escrito
cinco veces en las paredes del cuarto:
142.857
-¿Qué significado tiene ese número?, preguntó.
-Se trata, respondió el calculador, de uno de los más curiosos números de las Matemáticas. Este
número presenta, en relación con sus múltiplos, coincidencias verdaderamente interesantes:
Multipliquémoslo por 2. El producto será:
54
Antología de lecturas
Matemáticas
142.857 x 2 = 285.714
Vemos que las cifras que constituyen el producto son los mismos del número dado, pero en distinto
orden. El 14 que se hallaba a la izquierda se ha trasladado a la derecha.
Multipliquemos el número 142.857 por 3:
142.857 x 3 = 428.571
Otra vez observamos la misma singularidad: las cifras del producto son precisamente las mismas del
número pero con el orden alterado. El 1, que se halla a la izquierda pasó a la derecha; las otras
cifras quedan donde estaban.
Lo mismo ocurre cuando el número se multiplica por 4:
142.857 x 4 = 571.428
Veamos ahora lo que ocurre en caso de que la multiplicación sea 5:
142.857 x 5 = 714.285
La cifra 7 pasó de la derecha a la izquierda. Las restantes permanecieron en su sitio. Veamos la
multiplicación por 6:
142.857 x 6 = 857.142
Realizada la multiplicación resulta que el grupo 142 cambió de lugar con relación al 857.
En efecto, el grupo 142 que antes se hallaba a la derecha del grupo 857, ha pasado a la izquierda de
éste y viceversa.
Una vez llegados al factor 7 nos impresiona otra particularidad. El número 142.857 multiplicado
por 7 da como producto:
999.999
número formado con seis nueves.
Multipliquemos ahora el número 142.857 por 8. El producto será:
142.857 x 8 = 1.142.856
55
Antología de lecturas
Matemáticas
Todas las cifras del número aparecen aún en el producto con excepción del 7. El 7 del número
primitivo fue descompuesto en dos partes: 6 y 1. La cifra 6 quedó a la derecha y el 1 fue a la
izquierda completando el producto.
Veamos ahora qué acontece cuando multiplicamos el número 142.857 por 9:
142.857 x 9 = 1.285.713
Observemos con atención este resultado. La única cifra del multiplicando que no figura en el producto
es 4. ¿Qué ha pasado con ella? Aparece descompuesta en dos partes: 3 y 1, colocadas en los
extremos del producto.
Del mismo modo podríamos comprobar las singularidades que presenta el número 142.857 cuando se
multiplica por 11, 12, 13, 14, 15, 17, 18 etc.
Por eso el número 142.857 se incluye entre los números cabalísticos de la Matemática. Me lo
enseñó el derviche No-Elin...
-¿No-Elin?, repitió asombrado y jubiloso el príncipe Cluzir Schá. ¿Es posible que hayas conocido a
ese sabio?
-Lo conocí muy bien, ¡oh Príncipe!, respondió Beremiz. Con él aprendí todos los principios que hoy
aplico a mis investigaciones matemáticas.
- Pues el grande No-Elin, explicó el hindú era amigo de mi padre. Cierta vez después de haber perdido a un
hijo en una guerra injusta y cruel, se apartó de la vida ciudadana y nunca más volvió a verlo. Hice
muchas pesquisas para encontrarlo, pero no conseguí obtener la menor indicación sobre su paradero.
Llegué incluso a admitir que quizá había muerto en el desierto, devorado por las panteras. ¿Puedes
acaso decirme dónde se halla No-Elin?
Respondió Beremiz:
-Cuando salí para Bagdad lo dejé en Khoi, en Persia, junto con tres amigos.
- Pues en cuanto regrese de la Meca iremos a la ciudad de Khoi a buscar a ese gran ulema,
respondió el Príncipe. Quiero llevarlo a mi palacio. ¿Podrás, ¡oh Calculador!, ayudarnos en esa
grandiosa empresa?
-Señor, respondió Beremiz. Si es para prestar auxilio y hacer justicia a quien fue mi guía y maestro,
estoy dispuesto a acompañaros si preciso fuera hasta la India.
Y así, a causa del número 142.857, quedó resuelto nuestro viaje a la India, a la tierra de los rajás.
Y tal número es realmente cabalístico...
56
Antología de lecturas
Matemáticas
Capítulo XXIV: Sobre el rencoroso Tara-Tir. El epitafio de Diofanto. El problema de Hierón.
Beremiz se libra de un enemigo peligroso. Una carta del capitán H a s s a n . Los cubos de 8
y 27. La pasión por el cálculo. La muerte de Arquímedes.
La amenazadora presencia de Tara-Tir causó en mi espíritu una desagradable impresión. El rencoroso
jeque, que había pasado fuera de Bagdad algún tiempo, fue visto al anochecer, rodeado de sicarios,
rondando por nuestra calle.
Sin duda preparaba alguna celada contra el incauto Beremiz.
Preocupado con sus estudios y problemas, el Calculador no se daba cuenta del peligro que le
seguía como una sombra negra.
Le hablé de la presencia siniestra de Tara-Tir y le recordé las advertencias cautelosas del jeque lezid.
-Todo ese recelo es infundado, me respondió Beremiz sin ponderar detenidamente mi aviso. No
puedo creer en esas amenazas. Lo que me interesa de momento es la solución completa de un
problema que constituye el epitafio del célebre geómetra griego Diofanto:
He aquí el túmulo de Diofanto -maravilla para quien lo contempla con artificio aritmético la piedra enseña
su edad.
"Dios le concedió pasar la sexta parte de su vida en la juventud; un duodécimo en la adolescencia; un
séptimo en un estéril matrimonio. Pasaron cinco años más y le nació un hijo. Pero apenas este hijo había
alcanzado la mitad de la edad del padre, cuando murió. Durante cuatro años más, mitigando su dolor con
el estudio de la ciencia de los números, vivió Diofanto, antes de llegar al fin de su existencia".
Es posible que Diofanto, preocupado en resolver los problemas indeterminados de la Aritmética, no hubiera
pensado en obtener la solución perfecta del problema del rey Hierón, que no aparece en su obra.
-¿Qué problema es ese?, pregunté.
Beremiz me contó lo siguiente:
-Hierón, rey de Siracusa, mandó a sus orfebres cierta cantidad de oro para que hicieran una corona
que deseaba ofrecer a Júpiter. Cuando el rey recibió la obra acabada, comprobó que la corona tenía
el peso del oro entregado, pero el color del oro le inspiró cierta desconfianza pensando que pudieran
haber mezclado plata con el oro. Para aclarar sus dudas consultó a Arquímedes, el geómetra.
Arquímedes, habiendo comprobado que el oro pierde en el agua 52 milésimas de su peso, y la plata
99 milésimas, determinó el peso de la corona sumergida en el agua y halló que la pérdida de peso
era en parte debida a cierta porción de plata adicionada al oro.
Se cuenta que Arquímedes pasó mucho tiempo sin poder resolver el problema propuesto por
Hierón. Un día, estando en el baño, descubrió el modo de solucionarlo, y, entusiasmado, salió de
él corriendo por el palacio del monarca, gritando:
¡Eureka! ¡Eureka!
57
Antología de lecturas
Matemáticas
Que quiere decir: ¡Lo he encontrado! ¡ Lo he encontrado!
Mientras estábamos conversando así, llegó a visitarnos el capitán Hassan Maurique, jefe de la
guardia del Sultán. Era un hombre corpulento, muy expedito y servicial. Había oído hablar del caso
de los treinta y cinco camellos y desde entonces no cesaba de exaltar el talento del Hombre que
Calculaba. Todos los viernes, después de pasar por la mezquita, iba a visitarnos.
-Nunca imaginé, declaró después de expresar su profunda admiración, que la Matemática fuera
tan prodigiosa. La solución del problema de los camellos me dejó encantado.
Al ver el entusiasmo del turco, le llevé hasta el mirador de la sala que daba a la calle, mientras
Beremiz buscaba nueva solución al problema de Diofanto, y le hablé del peligro que corríamos bajo
la amenaza del odioso Tara-Tir.
-Allí está, indiqué, junto a la fuente. Los que lo acompañan son peligrosos asesinos. Al menor
descuido esos asesinos nos apuñalarán.
Tara-Tir está resentido contra Beremiz por cierta cuestión ya pasada pero es hombre violento y
rencoroso y mucho me temo que ahora intente vengarse. He observado varias veces que nos viene
espiando.
- ¡Por el honor de Amina! ¿Qué me dices?, exclamó Hassan. No podía ni imaginar que ocurriera una
cosa semejante. ¿Cómo puede un bandido perturbar la vida de un sabio geómetra? ¡Por la gloria
del Profeta! Voy a resolver ese caso inmediatamente...
Volví al cuarto y me acosté. Estuve un rato fumando tranquilamente.
Por violento que fuera Tara-Tir, el capitán Hassan era también hombre expeditivo y decidido y
actuaría en nuestro favor.
Una hora más tarde recibí el siguiente aviso de Hassan:
'Todo resuelto. Los tres asesinos han sido ejecutados hoy sumariamente. Tara-Tir recibió 8
bastonazos y pagó una multa de 27 cequíes de oro y fue advertido de que tiene que dejar
inmediatamente la ciudad. Lo mandé a Damasco bajo guardia-.
Mostré la carta del capitán turco a Beremiz. Gracias a mi eficiente intervención podríamos ahora vivir
tranquilos en Bagdad.
-Es interesante, sentenció Beremiz. ¡Es realmente curioso! Esas líneas me hacen recordar una
curiosidad numérica relativa a los números 8 y 27.
Y como mostrarse cierta sorpresa al oír aquella observación, él concluyó:
-Excluida la unidad, 8 y 27 son los únicos números cubos e iguales también a la suma de las cifras
de sus respectivos cubos. Así:
83 =
512
58
Antología de lecturas
Matemáticas
3
27 = 19.683
La suma de las cifras 19.683 es 27. La suma de las cifras de 512 es 8.
-¡Es increíble, amigo mío!, exclamé. Preocupado con los cubos y los cuadrados, te olvidaste de
que estabas amenazado por el puñal de un peligroso asesino.
-La matemática, ¡oh bagdalí!, respondió tranquilo el Calculador, prende de tal modo nuestra
atención que a veces nos ensimismamos y olvidamos los peligros que nos rodean. ¿Recuerdas
cómo murió Arquímedes, el gran geómetra?
Y sin esperar la respuesta, me contó el siguiente episodio histórico:
-Cuando la ciudad de Siracusa fue tomada al asalto por las fuerzas de Marcelo, general romano, se
hallaba el geómetra absorto en el estudio de un problema, para cuya solución había trazado una figura
geométrica en la arena. Allí se hallaba el geómetra enteramente olvidado de- las luchas, de las guerras y de la
muerte. Sólo le interesaba la investigación de la verdad. Un legionario romano lo encontró y le ordenó que
se presentara ante Marcelo. El sabio le pidió que esperara un momento hasta que acabara la
demostración que estaba haciendo. El soldado insistió y le cogió del brazo: -Cuidado. i Mira donde
pisas! -le dijo el geómetra-. ¡No me borres la figura! Irritado al ver que no le obedecía inmediatamente,
el sanguinario romano, de una puñalada, postró sin vida al mayor sabio de aquel tiempo.
Marcelo, que había dado órdenes de que se respetara la vida de Arquímedes, no ocultó el pesar que
le causaba la muerte del genial adversario. Sobre la lápida de la tumba que mandó erigirle, hizo grabar
una circunferencia inscrita en un triángulo, figura que recordaba uno de los teoremas del célebre
geómetra.
Y Beremiz concluyó, acercándose a mí y poniéndome la mano en el hombro:
-¿No crees, ¡oh bagdalíl, que sería justo incluir al sabio siracusano entre los mártires de la
Geometría?
¿Qué podía responderle yo?
El fin trágico de Arquímedes me trajo de nuevo al recuerdo la figura indeseable y rencorosa de Tara-Tir,
el pérfido envidioso.
¿Estaríamos realmente libres de aquel sanguinario vendedor de sal? ¿No volvería más tarde de su
destierro en Damasco para buscarnos nuevas dificultades?
Junto a la ventana, con los brazos cruzados sobre el pecho, Beremiz, con cierto aire de tristeza, observaba
descuidado a los hombres que pasaban apresurados en dirección al mercado.
Me pareció interesante interferirme en sus meditaciones, arrancándolo de su nostalgia, y le pregunté:
-¿Qué es eso? ¿Estás triste? ¿Sientes añoranza por tu país o es que estás planeando nuevos
cálculos?
E insistí en tono divertido:
59
Antología de lecturas
Matemáticas
-¿Cálculos o añoranza?
-Amigo bagdalí: la añoranza y el cálculo andan entrelazados. Ya lo dijo uno de nuestros más
inspirados poetas:
La añoranza es calculada
mediante cifras también.
Distancia multiplicada
por el factor Amor.
No creo sin embargo que la nostalgia, una vez reducida a fórmulas, sea calculable en cifras. ¡Por
Allah! Cuando yo era niño oí muchas veces a mi madre, encerrada en el harem de nuestra casa,
cantando:
Nostalgia, vieja canción
Nostalgia, sombra de alguien
Que solo se llevara el tiempo
Cuando a mi también me lleve
Capítulo XXV: Beremiz es llamado nuevamente a palacio. Una extraña sorpresa. Difícil torneo
de uno contra siete. La restitución del misterioso anillo. Beremiz es obsequiado con una
alfombra de color azul. Versos que conmueven a un corazón apasionado.
La primera noche después del Ramadán tras llegar al palacio del Califa, fuimos informados por un
viejo escriba, compañero nuestro de trabajo, que el soberano preparaba una extraña sorpresa a
nuestro amigo Beremiz.
Nos esperaba un grave acontecimiento. El Calculador iba a tener que competir, en audiencia
pública, con siete matemáticos, tres de los cuales habían llegado días antes de El Cairo.
¿Qué hacer? ¡Allah Akbar! Ante aquella amenaza procuré animar a Beremiz diciéndole que debía
tener confianza absoluta en su capacidad tantas veces comprobada.
El calculador me recordó un proverbio de su maestro No-Elin:
"Quien no desconfía de sí mismo no merece la confianza de los otros".
Con pesada sombra de aprensiones y tristeza entramos en el palacio.
El enorme y rutilante salón, profusamente iluminado, aparecía repleto de cortesanos y jeques de
renombre.
A la derecha del Califa se hallaba el joven príncipe Cluzir Schá, invitado de honor, acompañado
de ocho doctores hindúes que ostentaban vistosos ropajes de oro y terciopelo, y exhibían
curiosos turbantes de Cachemira. A la izquierda del trono se sentaban los visires, los poetas,
los cadíes y los elementos de mayor prestigio de la alta sociedad de Bagdad. Sobre un estrado,
donde se veían varios cojines de seda, se hallaban los siete sabios que iban a interrogar al
60
Antología de lecturas
Matemáticas
Calculador. A un gesto del Califa, el jeque Nurendim Barur tomó a Beremiz del brazo y lo condujo
con toda solemnidad hasta una especie de tribuna alzada en el centro del rico salón.
La expectación era visible en el rostro de los allí reunidos si bien los deseos eran dispares pues
no todos deseaban que el éxito acompañara al Calculador.
Un esclavo negro gigantesco hizo sonar por tres veces consecutivas un pesado gong de plata.
Todos los turbantes se inclinaron. Iba a iniciarse la singular ceremonia. Por mi imaginación, lo
confieso, volaban alucinados mis pensamientos.
Un imán tomó el Libro Santo y leyó con cadencia invariable, pronunciando lentamente las palabras,
las preces del Corán:
En nombre de Allah Clemente y Misericordioso Alabado sea el Omnipotente, Creador de todos los
mundos. La misericordia es en Dios el atributo supremo. Nosotros te adoramos, Señor, e imploramos
tu divina asistencia.
Llévanos por el camino cierto. Por el camino de aquellos esclarecidos y benditos por Ti.
Cuando la última palabra se perdió con su cortejo de ecos por las galerías del palacio, el rey
avanzó dos pasos, se detuvo y dijo:
-¡Allah! Nuestro amigo y aliado, el príncipe Cluzir-ehdin-Mubarec-Schá, señor de Lahore y Delhi,
me pidió que proporcionara a los doctores de su comitiva la posibilidad de admirar la cultura y la
habilidad del geómetra persa, secretario del visir Ibrahim Maluf. Sería un desaire dejar de
atender a esa solicitud de nuestro ilustre huésped. Y así, siete de los más sabios y famosos
ulemas del Islam van a plantear el calculador Beremiz una serie de preguntas relativas a la ciencia de'
los números. Si Beremiz responde a estas preguntas, recibirá, -así lo prometo-, recompensa tal, que
hará de él uno de los hombres más envidiados de Bagdad.
Vimos en este momento que el poeta lezid se acercaba al Califa.
-¡Comendador de los Creyentes!, dijo el jeque. Tengo en mi poder un objeto que pertenece al
calculador Beremiz. Se trata de un anillo encontrado en nuestra casa por una de las esclavas del
harem. Quiero devolvérselo al calculador antes de que se inicie la importantísima prueba a que va a
ser sometido. Es posible que se trate de un talismán y no deseo privar al calculador del auxilio de los
recursos sobrenaturales.
Y tras breve pausa, el noble lezid añadió:
-Mi encantadora hija Telassim, verdadero tesoro entre los tesoros de mi vida, me pidió que le permitiera
ofrecer al geómetra persa, su maestro en la Ciencia de los Números, esta alfombra por ella bordada.
Esta alfombra, si lo permite el Emir de los Creyentes, será colocada bajo el cojín destinado al
calculador que va a ser sometido hoy a prueba por los siete sabios más famosos del Islam.
Permitió el Califa que el anillo y 1a alfombra fueran entregados inmediatamente al calculador.
61
Antología de lecturas
Matemáticas
El propio jeque lezid, siempre amable y lleno de cordialidad, hizo entrega de la caja. Luego, a una
señal del jeque, un mabid adolescente apareció trayendo en las manos una pequeña alfombra
azul claro que fue colocada bajo el cojín verde de Beremiz.
-Todo esto es un hechizo; es bar aka, insinuó en voz baja un viejo risueño, flaco, vestido con una
túnica azul, que se hallaba detrás de mí. Ese joven calculador persa es un buen conocedor de la
barak a. Hace sortilegios. Esa alfombra azul me parece un tanto misteriosa.
¿Cómo podía creer la mayoría de los asistentes que la gran disposición de Beremiz para el cálculo
fuera fruto de la inteligencia?
El inculto, cuando algo escapa a su comprensión, busca siempre una razón en lo desconocido y lo
atribuye a poderes mágicos y a sortilegios. Sin embargo, el nivel cultural de los jefes que
provocaron y presidían la reunión era suficientemente elevado para comprender que lo que allí se
dilucidaba era exclusivamente un juego de la inteligencia.
Beremiz iba a ser puesto, pues, a prueba por los hombres más capaces y precisamente en una
materia en que los árabes hemos sido siempre adelantados.
¿Podría superarla el calculador Beremiz?
Se mostró Beremiz profundamente emocionado al recibir la joya y la alfombra. A pesar de la distancia
a que me hallaba pude notar que algo muy grave estaba ocurriendo en aquel momento. Al abrir la
pequeña caja, sus ojos brillantes se humedecieron. Supe después que juntamente con el anillo la
piadosa Telassim había colocado un papel en el que Beremiz leyó emocionado:
"Animo. Confía en Dios. Rezo por ti."
¿Y la alfombra azul claro?
¿Habría allí realmente algo de baraka, como insinuaba el viejecito alegre de la túnica azul? Nada de
sortilegios.
Aquella pequeña alfombra que a los ojos de los jeques y los ulemas era sólo un pequeño presente,
llevaba, escrito en caracteres, cúficos -que sólo Beremiz sabría interpretar y leer- algunos versos
que conmovieron el corazón de nuestro amigo. Aquellos versos, que yo más tarde pude traducir, habían
sido bordados por Telassim como si fueran arabescos en los bordes de la pequeña alfombra:
Te amo, querido. Perdona mi amor.
Fui consolada como un pájaro que se extravió en el camino.
Cuando mi corazón fue tocado, perdió el velo y quedó a la intemperie. Cúbrelo con piedad, querido, y
perdona mi amor. Si no me puedes amar, querido, perdona mi dolor.
Y volveré a mi canto, y quedaré sentada en la oscuridad.
62
Antología de lecturas
Matemáticas
Y cubriré con las manos la desnudez de mi recato.
¿Estaría el jeque lezid enterado de aquel doble mensaje de amor?
No había motivo para que tal idea me preocupara ahora demasiado. Sólo más tarde, como he dicho ya,
me confió Beremiz el secreto.
¡Sólo Allah sabe la verdad!
Se hizo un profundo silencio en el suntuoso recinto.
Iba a iniciarse, en el rico salón del palacio del Califa, el torneo cultural más notable que hasta ahora
había tenido lugar bajo los cielos del Islam.
¡Allah!
Capítulo XXVI: De nuestro encuentro con un teólogo famoso. El problema de la vida futura.
Todo musulmán debe conocer el Libro Sagrado. ¿Cuántas palabras hay en el Corán? ¿Cuántas
letras? El nombre de Jesús es citado 19 veces. Un engaño de Beremiz.
El sabio designado para iniciar las preguntas se levantó con austera solemnidad. Era un hombre
respetable, octogenario, que me inspiraba un medroso respeto., Las largas barbas blancas, proféticas,
le caían abundantes sobre el amplio pecho.
-¿Quién es ese noble anciano? pregunté en voz baja a un haquim ojo-len de rostro flaco y atezado
que se hallaba junto a mí.
-Es el célebre ulema Mohadeb lbhageAbner-Rama,-me respondió. Dicen que conoce más de
quince mil sentencias sobre el Corán. Enseña Teología y Retórica.
Las palabras del sabio Mohadeb eran pronunciadas con un tono extraño y sorprendente, sílaba a
sílaba, como si el orador pusiera empeño en medir el sonido de su propia voz.
-Voy a interrogarte, ¡oh Calculador!, sobre un tema de importancia indiscutible para un musulmán.
Antes de estudiar la ciencia de un Euclides o de un Pitágoras, el buen islamita debe conocer
profundamente el problema religioso, pues la vida no se concibe si se proyecta divorciada de la Verdad
y de la Fe. El que no se preocupa del problema de sus existencia futura, de la salvación, de su alma, y
desconoce los preceptos de Dios; los, mandamientos, no merece el calificativo de sabio. Quiero pues que
nos presentes, en este momento, sin la menor vacilación, quince indicaciones numéricas y citas notables
sobre el Corán, el libro de Allah.
Entre esas quince indicaciones deberán figurar:
1.° - El número de. suras del Corán.
2. 0- El número exacto de versículos
3.° - El número de palabras.
4.° - EI número de letras del Libro Increado.
5.º- El número exacto de los profetas citados en la página
del Libro Eterno.
63
Antología de lecturas
Matemáticas
Y el sabio teólogo insistió, haciendo sonar fuerte su voz:
-Quiero en fin, que aparte de las cinco indicaciones que te he dado, nos des otras diez relaciones
numéricas ciertas y notables sobre el Libro Increado.
¡Uassalam!
Siguió un profundo silencio. Se esperaba con ansiedad la palabra de Beremiz. Con tranquilidad asombrosa,
el joven calculador respondió:
-El Corán ¡oh sabio y venerable mufti!, consta de 114 suras, de las cuales 70 fueron dictadas en
La Meca y 44 en Medina. Se divide en 611 ashrs y contiene 6.236 versículos, de los cuales 7 son del
primer capítulo Fatihat y 8 del último, Los Hombres. La sura mayores la segunda, que encierra 280
versículos. El Corán contiene 46.439 palabras y 323.670 letras, cada una de las cuales contiene
diez virtudes especiales. Nuestro Libro Santo cita el nombre de 25 profetas. Issa, hijo de María, es
citado 19 veces. Hay cinco animales cuyos nombres fueron tomados como epígrafes de cinco
capítulos: la vaca, la abeja, la hormiga, la araña y el elefante. La sura 102 se titula: "La contestación
de los números". Es notable ese capítulo del Libro Increado por la advertencia que dirige en sus cinco
versículos, a quienes se preocupan de disputas estériles sobre números que no tienen importancia
alguna para el progreso espiritual de los hombres.
Al llegar a este punto, Beremiz hizo una ligera pausa y añadió luego:
-Estas son, atendiendo a vuestra petición, las indicaciones numéricas sobre el Libro de Allah. En la
respuesta que acabo de formular hay un error que me apresuro a confesar. En vez de quince
relaciones cité dieciséis.
-¡Por Allah ¡ murmuró tras de mí el viejo de la túnica azul. ¿Cómo puede un hombre saber de memoria
tantos números y tantas cosas? ¿Es fantástico? ¡Sabe hasta las letras que tiene el Corán!
-Estudia mucho, replicó casi en secreto el vecino, gordo y con una cicatriz en la barbilla. Estudia
mucho y lo recuerda todo. Ya oí algunos rumores al respecto.
-Recordar no sirve de nada, cuchicheó aún el viejecito de la cara chupada. No sirve de nada. Yo por
ejemplo no me preocupo de recordar ni la edad de la hija de mi tío.
Me molestaban enormemente todos aquellos secreteos, aquellas palabras cuchicheadas a media voz.
Pero el hecho es que Mohadeb confirmó todas aquellas indicaciones, que había dado Beremiz. Hasta
el número de letras del Libro de Allah había sido enunciado sin error de una unidad.
Me dijeron que este docto teólogo Mohadeb era un hombre que vivía en la pobreza. Y debía ser
verdad. A muchos sabios Allah les priva de riquezas, pues raramente aparecen juntas la sabiduría y la
riqueza.
Beremiz había superado con brillantez la primera prueba que le habían planteado en aquel terrible debate,
pero le faltaban aún otras seis.
64
Antología de lecturas
Matemáticas
-¡Allah quiera! -pensé- ¡Allah quiera que todo pueda seguir así, y terminar bien!
Capítulo XXVII: Cómo un sabio Historiador interroga a Beremiz. El geómetra que no podía
mirar al cielo. La Matemática de Grecia. Elogio de Eratóstenes.
Solucionado el primer caso con todas sus minucias, el segundo sabio inició el interrogatorio de
Beremiz. Este ulema era un historiador famoso que había dado lecciones durante veinte años en
Córdoba y más tarde, por cuestiones políticas, se trasladó a El Cairo, donde pasó a residir bajo la
protección del Califa. Era un hombre bajo, cuyo rostro bronceado aparecía enmarcado en una barba
elíptica. Tenía los ojos mortecinos, sin brillo.
He aquí las preguntas que el sabio historiador dirigió a Beremiz:
-¡En nombre de Allah, Clemente y Misericordioso! ¡Se engañan quienes aprecian el valor de un
matemático por la mayor o menor habilidad con que efectúa las operaciones o aplica las reglas
banales del cálculo! A mi ver, el verdadero geómetra es el que conoce con absoluta seguridad el
desarrollo y el progreso de la Matemática a través de los siglos. Estudiar la Historia de la
Matemática es rendir homenaje a los ingenios maravillosos que enaltecieron y dignificaron a las
antiguas civilizaciones que por su esfuerzo e ingenio pudieron desvelar algunos de los misterios más
profundos de la inmensa Naturaleza, consiguiendo, por la ciencia, elevar y mejorar la miserable condición
humana. Logramos además, por medio de las páginas de la Historia, honrar a los gloriosos
antepasados que trabajaron en la formación de la Matemática, y conservamos el nombre de las obras
que dejaron. Quiero, pues, interrogar al Calculador sobre un hecho interesante de la Historia de la
Matemática: "¿Cuál fue el geómetra célebre que se suicidó al no poder mirar al cielo?
Beremiz meditó unos instantes y exclamó:
- Fue Eratóstenes, matemático de Cirenaica y educado al principio en Alejandría y más tarde en la
Escuela de Atenas, donde aprendió las doctrinas de Platón.
Y completando la respuesta, prosiguió:
- Eratóstenes fue elegido para dirigir la gran Biblioteca de la Universidad de Alejandría, cargo que ejerció
hasta el fin de sus días. Además de poseer envidiables conocimientos científicos y literarios que lo
distinguieron entre los mayores sabios de su tiempo, era Eratóstenes poeta, orador, filósofo y -aún másun completo atleta. Basta decir que conquistó el título excepcional de vencedor del pentatlón, las cinco
pruebas máximas de los Juegos Olímpicos. Grecia se hallaba entonces en el período áureo de su
desarrollo científico y literario. Era la patria de los aedos, poetas que declamaban, con
acompañamiento musical, en los banquetes y en las reuniones de los reyes y de los grandes
jerarcas.
Conviene aclarar que entre los griegos de mayor cultura y valor, el sabio Eratóstenes era considerado
como un hombre extraordinario que tiraba la jabalina, escribía poemas, vencía a los grandes
corredores y resolvía problemas astronómicos. Eratóstenes legó a la posteridad varias obras.
Al rey Ptolomeo lll de Egipto le presentó una tabla de números primos hechos sobre una plancha
metálica en la que los números múltiplos estaban marcados con un pequeño agujero. Se dio por eso
el nombre de "Criba de Eratóstenes" al proceso de que se servía el sabio astrónomo para formar su
tabla.
65
Antología de lecturas
Matemáticas
A consecuencia de una enfermedad en los ojos, adquirida a orillas del Nilo durante un viaje,
Eratóstenes quedó ciego. Él, que cultivaba con pasión la Astronomía, se hallaba impedido de mirar al
cielo y de admirar la belleza incomparable del firmamento en las noches estrelladas.
La luz azulada de Al-Schira jamás podría vencer aquella nube negra que le cubría los ojos. Abrumado
por tan gran desgracia, y no pudiendo resistir el pesar que le causaba la ceguera, el sabio y atleta se
suicidó dejándose morir de hambre, encerrado en su biblioteca.
El sabio historiador de ojos mortecinos; se volvió hacia el Califa y declaró, tras breve silencio:
-Me considero plenamente satisfecho con la brillante exposición histórica hecha por el sabio calculador
persa. El único geómetra célebre que se suicidó fue realmente el griego Eratóstenes, poeta, astrónomo y
atleta, amigo fraternal del famosísimo Arquímedes de Siracusa. ¡Allah!
-¡Por la belleza de Selsebit! exclamó el Califa entusiasmado. ¡Cuántas cosas acabo de aprender!
¡Cuántas cosas ignoramos! Ese griego notable que estudiaba los astros, escribía poemas y cultivaba el
atletismo, merece nuestra sincera admiración. De hoy en adelante, siempre, al mirar al cielo, en la noche
estrellada, hacia la incomparable Al-Schira, pensaré en el fin trágico de aquel sabio geómetra que
escribió el poema de su muerte entre un tesoro de libros que ya no podía leer.
Y posando con estrema cortesía su mano en el hombro del príncipe, añadió con cautivadora naturalidad:
¡Vamos a ver ahora si el tercer ulema conseguirá vencer a nuestro Calculador!
Capítulo XXVIII: Prosigue el memorable torneo. El tercer sabio interroga a Beremiz. La
falsa inducción. Beremiz demuestra que un principio falso puede ser sugerido por
ejemplos verdaderos.
El tercer sabio que debía interrogar a, Beremiz era el célebre astrónomo Abul Hassan Ali de Alcalá,
llegado a Bagdad por especial-invitación de Al -Motacén. Era alto, huesudo, y tenía el rostro, surcado
de arrugas. Su pelo era rubio y ondulado. Exhibía en la muñeca derecha un ancho brazalete de oro.
Dicen que en ese brazalete llevaba señaladas las doce constelaciones del Zodíaco.
El astrónomo Abul Hassan, después de saludar al rey y a los nobles, se dirigió a Beremiz. Su voz,
profunda y hueca, parecía rodar pesadamente.
- Las dos respuestas que acabas de formular demuestran ¡oh Beremiz Samir! que tienes una
sólida cultura. Hablas de la ciencia griega con la misma facilidad con que cuentas las Letras del Libro
Sagrado. Sin embargo, en el desarrollo de la ciencia matemática, la parte más interesante es la que indica
la forma de raciocinio que lleva a la verdad. Una colección de hechos está tan lejos de ser una ciencia
como un montón de piedras de ser una casa. Puedo afirmar igualmente que las sabias combinaciones
de hechos inexactos o de hechos que no fueron comprobados al menos en sus consecuencias, se
encuentran tan lejos de formar una ciencia como se encuentra el espejismo de sustituir en el desierto a
la presencia real: del oasis. La ciencia debe observar los hechos y deducir de ellos leyes. Con auxilio
de esas leyes se pueden prever otros hechos o mejorar las condiciones materiales de la vida. Sí, todo
eso es cierto. ¿Pero cómo deducir la verdad? Se presenta pues la siguiente duda:
66
Antología de lecturas
Matemáticas
¿Es posible extraer en Matemática una regla falsa de una propiedad verdadera? Quiero oír tu
respuesta, ¡oh Calculador!, ilustrada con un ejemplo sencillo y perfecto.
Beremiz calló, durante un rato, reflexivamente. Luego salió del recogimiento y dijo:
-Admitamos que un algebrista curioso deseara determinar la raíz cuadrada de un número de cuatro
cifras. Sabemos que la raíz cuadrada de un número es otro número que, multiplicado por sí mismo, da
un producto igual al número dado. Es un axioma en matemáticas.
Vamos a suponer aún que el algebrista, tomando libremente tres números a su gusto, destacase
los siguientes números: 2.025, 3.025 y 9.801.
Iniciemos la resolución del problema por el número 2.025. Hechos los cálculos para dicho
número, el investigador hallaría que la raíz cuadrada es igual a 45. En efecto: 45 veces 45 es
igual a 2.025. Pero se puede comprobar que 45 se obtiene de la suma de 20 + 25, que son partes
del número 2.025 descompuesto mediante un punto, de esta manera: 20. 25.
Lo mismo podría comprobar el matemático con relación al número 3.025, cuya raíz cuadrada
es 55 y conviene notar que 55 es la suma de 30 + 25, partes ambas del número 3.025.
Idéntica propiedad se destaca con relación al número 9.801, cuya raíz cuadrada es 99, es decir 98
+ 01.
Ante estos tres casos, el inadvertido algebrista podría sentirse inclinado a enunciar la siguiente
regla:
"Para calcular la raíz cuadrada de un número de cuatro cifras, se divide el número por medio de un
punto en dos partes de dos cifras cada una, y se suman las partes así formadas. La suma
obtenida será la raíz cuadrada del número dado".
Esa regla, visiblemente errónea, fue deducida de tres ejemplos verdaderos. Es posible en
Matemática, llegar a la verdad por simple observación; no obstante hay que poner cui dado
especial en evitar la "falsa inducción".
El astrónomo Abul Hassan, sinceramente satisfecho con la respuesta de Beremiz, declaró que jamás
había oído una explicación tan sencilla e interesante de la cuestión de la "falsa inducción
matemática".
Seguidamente, a una señal del Califa, se levantó el cuarto ulema y se dispuso a formular su pregunta.
Su nombre era Jalal lbn-Wafrid. Era poeta, filósofo y astrólogo. En Toledo, su ciudad natal, se
había hecho muy popular como narrador de historias.
Jamás olvidaré su venerable y singular figura. Nunca se borrará en mí el recuerdo de su mirada
serena y bondadosa. Se adelantó hacia el extremo del estrado, y, dirigiéndose al Califa, habló así:
- Para que mi pregunta pueda ser bien comprendida, he de aclararla contando una antigua
leyenda persa...
67
Antología de lecturas
Matemáticas
-¡Apresúrate a contarla, oh elocuente ulema! respondió el Califa. Estamos ansiosos de oír tus
sabias palabras, que son, para nuestros oídos, como pendientes de oro.
El sabio toledano, con voz firme y sonora como el andar de una caravana, narró lo siguiente:
Capítulo XXIX: En el que escuchamos una antigua leyenda persa. Lo material y lo espiritual.
Los problemas humanos y trascendentes. La multiplicación más famosa. El Sultán
reprime con energía la intolerancia de los jeques islamitas.
-"Un poderoso rey que gobernaba Persia y las grandes llanuras del Irán, oyó a cierto derviche decir que el
verdadero sabio debía conocer, con absoluta perfección, la parte espiritual y la parte material de la vida.
Se llamaba Astor ese monarca, y su sobrenombre era "El Sereno".
¿Qué hizo Astor? Vale la pena recordar la forma en que procedió el poderoso monarca.
Mandó llamar a los tres mayores sabios de Persia, y entregó a cada uno de ellos dos dinares de plata,
diciéndoles:
- En este palacio hay tres salas iguales, completamente vacías. Cada uno de vosotros quedará
encargado de llenar una de ellas, pero para esta tarea no podrá gastar suma mayor que la que acaba de
recibir.
El problema era realmente difícil. Cada sabio debía llenar una sala vacía gastando sólo la
insignificante cantidad de dos dinares.
Partieron los sabios a fin de cumplir la misión que les había confiado el caprichoso rey Astor.
Horas después regresaron a la sala del trono. El monarca, interesado por la solución del problema, les
interrogó.
El primero en ser interrogado habló así:
-Señor: gasté los dos dinares, pero la sala quedó completamente llena. Mi solución fue muy práctica.
Compré varios sacos de heno y con ellos llené el aposento desde el suelo hasta el techo.
-¡Muy bien!, exclamó el rey Astor, el Sereno. Tu solución estuvo realmente bien imaginada. Conoces,
en mi opinión, la parte material de la vida, y desde este punto de vista habrás de enfrentarte con
los problemas que la vida te presente.
Seguidamente, el segundo sabio, después de saludar al monarca, dijo con cierto énfasis:
-En el desempeño de mi tarea, gasté sólo medio dinar. Voy a explicar cómo lo hice: Compré una vela
y la encendí en la sala vacía. Ahora ¡oh rey! podrás observarla. Está llena, enteramente llena de luz...
-¡Bravo!, exclamó el monarca. ¡Descubriste una solución brillante para el caso! La luz simboliza la
parte espiritual de la vida. Tu espíritu se halla, por lo que puedo deducir, dispuesto a enfrentarse con todos
los problemas de la existencia desde el punto de vista espiritual.
68
Antología de lecturas
Matemáticas
Llegó al fin el tercer sabio, y dijo
-Pensé en principio, ¡oh Rey de los Cuatro Rincones del Mundo!, en dejar la sala confiada a mi
cuidado exactamente cómo se hallaba. Era fácil ver que la sala no estaba vacía. Evidentemente, estaba
llena de aire y de oscuridad. No quise, sin embargo, colocarme en la cómoda postura de indolencia y
picardía. Resolví pues actuar también, como mis compañeros. En consecuencia tomé un puñado
de heno de la primera sala y lo quemé con la vela de la segunda, y con la humareda que se
desprendía llené enteramente la tercera sala. Como es de suponer esto no me costó nada, y conservo
íntegra la cantidad que se me dio. La sala está pues llena: llena de humo.
-¡Admirable!, exclamó el rey Astor. Eres el mayor sabio de Persia y tal vez del mundo. Sabes unir con
justiciosa habilidad lo material y lo espiritual para alcanzar la perfección".
El sabio toledano, terminó su narración. Luego, volviéndose hacia Beremiz, habló sonriente y con aire de
extremada amabilidad.
-Mi deseo es, ¡oh Calculador!, comprobar si, a semejanza del tercer sabio de esta historia, eres
capaz de unir lo material a lo espiritual, y si puedes resolver, no sólo problemas humanos, sino
también cuestiones trascendentales. Mi pregunta es pues la siguiente: ¿Cuál es la multiplicación
famosa, de que hablan las historias, multiplicación que todos los hombres cultos conocen, y en la que
sólo figura un factor?
Esta inesperada pregunta sorprendió con sobrada razón a los ilustres musulmanes. Algunos no
disfrazaron sus contenidas manifestaciones de desagrado o impaciencia. Un cadí a mi lado, rezongó
irritado, con gesto desabrido:
-Eso es una insensatez, un disparate...
Beremiz se quedó un momento pensativo. Después, coordinadas sus ideas, dijo:
- La única multiplicación famosa con un solo factor, citada por todos los historiadores y que conocen
todos los hombres cultos, es la multiplicación de los panes, hecha por Jesús, hijo de María. En
aquella multiplicación sólo figuraba un factor: el poder milagroso de la voluntad de Dios.
- Excelente respuesta, declaró el toledano. ¡Ciertísimo! Es la respuesta más perfecta y completa que
he oído hasta hoy. Este Calculador resolvió de manera irrefutable el problema que le planteé. ¡Allah!
Algunos musulmanes, inspirados por la intolerancia, se miraron espantados. Hubo susurros. El Califa
exigió enérgicamente:
-¡Silencio! Veneremos a Jesús, hijo de María, cuyo nombre es citado diecinueve veces en el Libro
de Allah.
Y seguidamente se dirigió al quinto ulema y añadió con voz amable:
-Esperamos vuestra pregunta, ¡oh jeque Nascif Rahal! Seréis el quinto en intervenir en este
maravilloso torneo de ciencia y fantasía...
69
Antología de lecturas
Matemáticas
Oída esta orden del rey, el quinto sabio se levantó prestamente. Era un hombre bajo, gordo, de blanca
cabellera. En vez de turbante llevaba un pequeño gorro verde. Era muy conocido en Bagdad, pues
enseñaba en la mezquita y aclaraba a los estudiosos los puntos oscuros de los hadiths del Profeta.
Yo lo había visto ya dos veces cuando salía del haman. Hablaba nerviosamente, de modo
arrebatado y un poco agresivo.
-El valor de un sabio, empezó a decir con grave entonación, sólo puede ser medido por el poder
de su imaginación. Los números tomados al azar, los hechos históricos. recordados con
precisión y oportunidad, pueden tener un interés momentáneo, pero al cabo de algún tiempo
caen en el olvido. ¿Quién de vosotros recuerda aún el número de letras del Corán? Hay números,
nombres, palabras y obras que están, por su propia naturaleza y finalidad, condenados al
irremediable olvido. El saber que no sirve al sabio, es vano. Voy en consecuencia a asegurarme de la
capacidad y del valer del Calculador aquí presente, haciéndole una pregunta que no se relaciona con
ningún problema que pueda exigir memoria ni habilidad de cálculo. Quiero que el matemático
Beremiz Samir nos cuente una leyenda, o una simple fábula, en la que aparezca una división de 3
por 3,indicada, pero no efectuada, y otra de 3 por 2 indicada y efectuada sin dejar resto.
¡Buena idea!, susurro el anciano de la túnica azul. Buena idea la de este ulema de blanca
cabellera. Vamos a dejarnos de cálculos que nadie entiende y oigamos una leyenda. ¡Qué maravilla!
¡Al fin vamos a oír una leyenda!
-Pero esa leyenda tendrá números y cuentas, seguro, rezongó por lo bajo el haquím llevándose la
mano a la boca. Ya lo verá, amigo mío: todo acaba en cálculos, números y problemas. ¡Mala suerte la
nuestra!
- Dios quiera que eso no ocurra, dijo el anciano. Quiéralo Dios ¡Al-uahhad!
Quedé bastante desconcertado y sorprendido ante la imprevista exigencia del quinto ulema.
¿Cómo iba Beremiz a inventar en aquel angustioso momento una leyenda en la que apareciera
una división planteada pero no efectuada, y más aún, una división de 3 por 2 sin resto?
¡Es lógico que quien divide tres entre dos ha de dejar un resto de 1!
Dejé de lado mis inquietudes y confié en la imaginación de mi amigo. En la imaginación de Beremiz
y en la bondad de Allah...
El Calculador, tras hacer por unos instantes una ferviente rebusca en su memoria, empezó a relatar
el siguiente caso.
Capitulo XXX: El Hombre que Calculaba narra una leyenda. El tigre sugiere la división de
"tres" entre "tres". El chacal indica la división de "tres" entre "dos". Cómo se calcula el
cociente en la Matemática del más fuerte. El jeque del gorro verde elogia a Beremiz.
"¡En nombre de Allah, Clemente y Misericordioso!
El león, el tigre y el chacal abandonaron cierta vez la cueva sombría en que vivían y salieron en
peregrinación amistosa a vagabundear por el mundo, a la busca de alguna región rica en rebaños
de tiernas ovejas.
70
Antología de lecturas
Matemáticas
En medio de la gran selva, el temible león que dirigía, como es lógico el grupo, se sentó
fatigado sobre las patas traseras y alzando la enorme cabeza soltó un rugido tan fuerte que hizo
temblar los árboles más próximos.
El tigre y el chacal se miraron asustados. Aquel rugido amenazador con que el peligroso monarca
turbaba el silencio del bosque, quería decir, traducido lacónicamente, en un lenguaje al alcance de
los otros animales, lo siguiente:
Tengo hambre.
-¡Tu impaciencia es perfectamente justificable! observó el chacal dirigiéndose humildemente al
león. Te aseguro, sin embargo, que en esta selva hay un atajo misterioso que ninguna fiera conoce
y por el que podremos llegar fácilmente a un pequeño poblado, casi en ruinas, donde hay caza
abundante al alcance de las garras y sin el menor peligro...
-¡Vamos, chacal!, ordenó el león. ¡Quiero conocer ese adorable rincón del mundo!
Al anochecer, guiados por el chacal, llegaron los viajeros a lo alto de un monte, no muy alto, desde
cuya cima se divisaba una amplia planicie verdeante.
En medio de la llanura se hallaban descuidados, ajenos al peligro que los amenazaba, tres pacíficos
animales: una oveja, un cerdo y un conejo.
Al ver la presa fácil y segura, el león sacudió su abundante melena con un movimiento de patente
satisfacción, y con ojos brillantes de gula se volvió hacia el tigre y dijo en tono aparentemente
amistoso:
-¡Oh tigre admirable! Veo allí tres bellos y sabrosos bocados: una oveja, un cerdo y un conejo. Tú,
que eres listo y experto, has de dividirlos entre tres. Haz, pues, esa operación con justicia y equidad:
divide fraternalmente las tres presas entre tres cazadores...
Lisonjeado por semejante invitación, el vanidoso tigre, después de expresar con aullidos de falsa
modestia su incompetencia y su humildad, respondió:
-La división que generosamente acabas de proponer ¡oh rey! es muy sencilla y se puede hacer con
relativa facilidad. La oveja, que es el bocado mayor, y el más sabroso también, es capaz de saciar el
hambre de una banda entera de leones del desierto. Pues bien: té corresponde, ¡oh rey! Es tuya,
absolutamente tuya. Y aquel cerdito flaco, sucio y triste que no vale una pata de oveja bien cebada,
quedará para mí, que soy modesto y con bien poco me contento. Y finalmente, aquel minúsculo y
despreciable conejo de reducidas carnes, indigno del paladar mimado de un rey, le corresponderá a
nuestro compañero el chacal, como recompensa por la valiosa indicación que nos proporcionó hace poco.
-¡Estúpido! ¡Egoísta!, rugió el pavoroso león con furia indescriptible. ¿Quién te ha enseñado a hacer
divisiones como ésta? ¡ Eres un imbécil! ¿Dónde se ha visto una división de tres entre tres resuelta de
este modo?
Y levantando su zarpa la descargó en la cabeza del inadvertido tigre que cayó muerto a pocos pasos
de distancia.
71
Antología de lecturas
Matemáticas
Luego, volviéndose hacia el chacal, que había asistido horrorizado a aquella trágica división de tres entre
tres, habló así:
-¡Querido chacal! Siempre he tenido el más elevado concepto de tu inteligencia. Sé que eres el
más ingenioso y hábil animal de la selva y no conozco otro que sepa resolver con tanta habilidad los
más difíciles problemas. Te encargo pues de hacer esta división, tan sencilla y trivial, que el estúpido
tigre, como acabas de ver, no supo hacer satisfactoriamente. Viendo, amigo chacal, esos tres apetitosos
animales: la oveja, el cerdo y el conejo. Nosotros somos dos, y los bocados a repartir son tres. Pues
bien: vas a dividir tres entre dos. Vamos: ¡ Haz los cálculos, pues quiero saber lo que me corresponde
exactamente... !
-¡No paso de humilde y rudo siervo de Su Majestad!, gimió el chacal en tono de humildísimo respeto.
Tengo, pues, que obedecer ciegamente la orden que acabo de recibir. Como si fuera un sabio
geómetra, voy a dividir por dos aquellos tres animales. ¡Se trata de una sencilla división de tres entre
dos!
La división matemáticamente justa y cierta es la siguiente: La admirable oveja, manjar digno de un soberano,
corresponde a tus reales caninos, pues es indiscutible que eres el rey de los animales. El hermoso
cerdito, cuyos armoniosos gruñidos se oyen desde aquí, corresponde también a tu real paladar, pues
dicen los entendidos que la carne de cerdo da más fuerza y energía a los leones. Y el saltarín conejo,
con sus largas orejas, debe ser también para ti, que lo saborearás como postre, ya que a los reyes, por ley
tradicional entre los pueblos, les corresponde siempre, como complemento de los opíparos banquetes,
los manjares más finos y delicados.
-¡Oh incomparable chacal!, exclamó el león encantado con la división que acababa de oír. ¡Qué
armoniosas y sabias son siempre tus palabras! ¿Quién te enseñó ese artificio maravilloso de dividir con
tanta perfección y acierto tres entre dos?
-Lo que tu justicia acaba de hacerle al tigre hace un momento por no haber sabido dividir con habilidad
tres entre dos cuando uno de esos dos es un león y el otro un chacal. En la Matemática del más
fuerte, digo yo, el cociente es siempre exacto y al más débil, después de la división, sólo le debe
quedar el resto.
Y desde aquel día, sugiriendo siempre divisiones de aquel tipo, inspiradas en la más torpe bajeza,
juzgó el ambicioso chacal que podría vivir tranquilo su vida de parásito, regalándose con las sobras
que dejaba el sanguinario león.
Pero se equivocó.
Pasadas dos o tres semanas, el león, irritado, hambriento, desconfió del servilismo del chacal y
acabó matándolo como al tigre.
Y la moraleja es que siempre la verdad debe ser dicha, una y mil veces:
"¡El castigo de Dios está más cerca del pecador de lo que están los párpados de los ojos!'"
He aquí, ¡oh justicioso ulemal, concluyó Beremiz, narrada con la mayor sencillez, una fábula en la
que hay dos divisiones. La primera fue una división de tres entre tres, planteada, pero no efectuada.
La segunda fue una división de tres entre dos, efectuada sin resto.
72
Antología de lecturas
Matemáticas
Oídas estas palabras del calculista se hizo un profundo silencio. Aguardaban todos con vivo
interés la apreciación, o mejor, la sentencia del severo ulema.
El jeque Hacíf Rahal, después de ajustarse nerviosamente su gorro verde y pasarse la mano por la
barba, pronunció con cierta amargura su sentencia:
-La fábula narrada se ajustó perfectamente a las exigencias por mí formuladas. Confieso que no la
conocía y, a mi ver, es de las más felices. El famoso Esopo, el griego, no la haría mejor. Y ese es mí
parecer. Allah es sin embargo más sabio y más justo.
La narración de Beremiz, aprobada por el jeque del gorro verde, agradó a todos los visires y nobles
musulmanes. El príncipe Cluzir Schá, huésped del rey, declaró en voz alta dirigiéndose a todos los
presentes:
-La fábula que acabamos de oír encierra una lección moral. Los viles aduladores que se arrastran
en las cortes, en la alfombra de los poderosos, pueden, al principio, lograr algún provecho de su
servilismo, pero al fin son siempre castigados, pues el castigo de Dios está siempre muy cerca del
pecador. La contaré a mis amigos y colaboradores cuando vuelva a mis tierras de Lahore.
El soberano árabe calificó de maravillosa la narración de Beremiz. Y dijo, además, que aquella singular
división de tres entre tres debería ser conservada en los archivos del Califato, pues la narración
de Beremiz, por su elevada finalidad moral, merecía ser escrita con letras de oro en las alas
transparentes de una mariposa blanca del Cáucaso.
Seguidamento tomó la palabra el sexto ulema.
Era éste cordobés. Había vívido quince años en España y había huido de allá al caer en desgracia
ante su soberano. Era hombre de mediana edad, rostro redondo, fisonomía franca y risueña. Decían
sus admiradores que era muy hábil en escribir versos humorísticos y sátiras contra los tiranos. Durante
seis años había trabajado en el Yemen como simple mutavif.
-¡Emir del Mundo!, comenzó el cordobés dirigiéndose al Califa. Acabo de oír con verdadera
satisfacción la admirable fábula denominada la división de tres entre dos. Esta narración encierra a mi
ver grandes enseñanzas y profundas verdades. Verdades claras como la luz del sol en la hora del
adduhhr. Me veo forzado a confesar que los preceptos maravillosos toman forma viva cuando son
presentados en forma de historias o de fábulas. Conozco una leyenda que no contiene divisiones,
cuadrados ni fracciones, pero que encierra un problema de Lógica cuya solución sólo es posible
mediante el raciocinio puramente matemático. Narrada en forma de leyenda, veremos cómo resolverá
el eximio Calculador el problema en ella contenido.
Y el sabio cordobés contó lo siguiente:
Capítulo XXXI: El sabio -cordobés narra una leyenda. Los tres novios de Dahizé. El
problema de "los cinco discos". Cómo Beremiz reprodujo el raciocinio de un novio
inteligente.
Macudó, el famoso historiador árabe, en los veintidós volúmenes de su obra, habla de los siete mares,
de los grandes ríos, de los elefantes célebres, de los astros, de las montañas, de los diferentes reyes de
73
Antología de lecturas
Matemáticas
la China y de otras mil cosas, y no hace la menor referencia al nombre de Dahizé, hija única del rey
Cassim "el Indeciso". No importa. A pesar de todo, Dahizé no quedará olvidada, pues en los
manuscritos árabes se encuentran más de cuatrocientos mil versos en los, que centenares de poetas
alaban y exaltan los encantos de la famosa princesa. La tinta gastada para describir la belleza de los
ojos de Dahizé, daría, transformada en aceite, el suficiente para iluminar la ciudad de El Cairo
durante medio siglo sin interrupción.
¡Qué exagerado, diréis.¡
¡No admito eso de exagerado, hermanos árabes! ¡La exageración es una forma de mentira!
Pasemos sin embargo al caso que narraba.
Cuando Dahizé cumplió dieciocho años y veintisiete días, fue pedida en matrimonio por tres príncipes
cuyos nombres ha perpetuado la tradición: Aradin, Benefir y Comozán.
El rey Cassim estaba indeciso. ¿Cómo elegir entre los tres ricos pretendientes aquél que debería ser el
novio de su hija? Hecha la elección, se presentaría la siguiente consecuencia fatal: El rey, ganaría un
yerno, pero en cambio los otros dos pretendientes despechados se convertirían en rencorosos
enemigos. ¡Pésimo negocio para un monarca sensato y cauteloso, que solo deseaba vivir en paz con
su pueblo y sus vecinos!
La princesa Dahizé, consultada, declaró que se casaría con el más inteligente de sus tres
pretendientes.
La decisión de la joven fue recibida con gran contento por el rey Cassim. El caso, que parecía tan
delicado, presentaba una solución muy simple. El soberano árabe mandó llamar a los cinco sabios más
sabios de la corte y les dijo que sometieran a los tres príncipes a un riguroso examen.
¿Cuál de los tres sería el más inteligente?
Terminadas las pruebas, los sabios presentaron al soberano un minucioso informe. Los tres príncipes eran
inteligentísimos. Conocían además profundamente las Matemáticas, la Literatura, la Astronomía y la
Física. Resolvían complicados problemas de ajedrez, cuestiones sutilísimas de Geometría, enigmas
enrevesados y escritos cifrados.
-No vemos manera, declaraban los sabios, de llegar a un resultado definitivo en favor de uno u otro...
Ante el lamentable fracaso de la ciencia, resolvió el rey consultar a un derviche que tenía fama de conocer
la magia y los secretos del ocultismo.
El sabio derviche se dirigió al rey:
-Sólo conozco un medio que nos permita determinar quién es el más inteligente de los tres: ¡La
prueba de los cinco discos!
-Hagamos, pues, esa prueba, exclamó el rey.
74
Antología de lecturas
Matemáticas
Los tres príncipes fueron conducidos al palacio. El derviche, mostrándoles cinco discos de madera
muy fina, les dijo:
-Aquí hay cinco discos. Dos de ellos son negros y tres blancos. Todos son del mismo tamaño y de
idéntico peso, y sólo se distinguen por el color.
Acto seguido, un paje vendó cuidadosamente los ojos de los tres príncipes, de modo que no podían
ver ni la menor sombra.
El viejo derviche tomó entonces al azar tres de los cinco discos y colgó uno a la espalda de cada uno
de los pretendientes.
Dijo luego el derviche:
-Cada uno de vosotros lleva colgado a su espalda un disco cuyo color ignora. Seréis interrogados uno
tras otro. El que descubra el color del disco que le cayó en suerte, será declarado vencedor y se casará
con la bella Dahizé. El primer interrogado podrá ver los discos de los otros dos competidores. El
segundo podrá ver el disco del último. Y éste tendrá que formular su respuesta sin ver nada. El que dé la
respuesta cierta, para probar que no fue favorecido por el azar, tendrá que justificarla por medio de un
razonamiento riguroso, metódico y simple. ¿Quién desea ser el primero?
Respondió prontamente el príncipe Comozán:
-¡Yo quiero ser el primero!
El paje le quitó la venda de los ojos, y el príncipe Comozán pudo ver el color de los discos que pendían de
la espalda de sus rivales.
Interrogado en secreto por el derviche, su respuesta fue errada. Declarado vencido tuvo que retirarse del
salón. Comozán había visto los dos discos de sus rivales y había errado al decir de qué color era el suyo.
El rey anunció en voz alta para que se enteraran los otros dos:
-i El príncipe Comozán ha fracasado!
-¡Quiero ser el segundo!, declaró el príncipe Benefir.
Descubiertos sus ojos, el segundo príncipe vio el color del disco que llevaba a cuestas su competidor.
Se acercó al derviche y formuló en secreto su respuesta.
El derviche sacudió negativamente su cabeza. El segundo príncipe se había equivocado, y fue invitado a
abandonar inmediatamente el salón.
Sólo quedaba el tercer competidor, el príncipe Aradín.
Este, cuando el rey anunció la derrota del segundo pretendiente, se acercó al trono con los ojos
aún vendados y dijo en voz alta cuál era el color exacto de su disco.
Concluida la narración, el sabio cordobés se volvió hacia Beremiz y le dijo:
75
Antología de lecturas
Matemáticas
- El príncipe Aradín, para formular la respuesta, realizó un razonamiento riguroso y perfecto que le
llevó a resolver con absoluta seguridad el problema de los cinco discos y conquistar la mano de
la hermosa Dahizé.
Deseo pues saber:
1.°-¿Cuál fue la respuesta de Aradín?
2.°-¿Cómo descubrió con la precisión de un geómetra el color de su disco?
Beremiz, con la cabeza baja, reflexionó unos instantes. Luego, alzando el rostro, discurrió sobre
el caso con seguridad y desembarazo. Y dijo:
- El príncipe Aradín, héroe de la curiosa leyenda que acabamos de oír, respondió al rey Cassim
padre de su amada:
i El disco es blanco!
Y al proferir tal afirmación, tenía la certeza lógica de que estaba diciendo la verdad. ¡El disco es
blanco!
¿Cuál fue, pues, el razonamiento que le hizo llegar a esta conclusión?
El razonamiento del príncipe Aradín fue el siguiente:
El primer pretendiente, Comozán, antes de responder vio los dos discos de sus dos rivales. Vio
los "dos" discos, y equivocó la respuesta.
Conviene insistir: De los cinco discos - "tres" blancos y "dos" negros- Comozán vio dos y, al
responder, se equivocó.
¿Por qué se equivocó?
Se equivocó porque respondió en la inseguridad.
Pero si hubiera visto en sus rivales "dos discos negros" no se habría equivocado, no hubiese
dudado, y habría dicho al rey:
Veo que mis dos rivales llevan discos negros, y como sólo hay dos discos, negros, el mío forzosamente
ha de ser blanco.
Y con esta respuesta hubiera sido declarado vencedor.
Pero Comozán, el primer enamorado, se equivocó. Luego los discos que vio "no eran ambos
negros".
Pero si esos dos discos vistos por Comozán no eran ambos negros, cabían dos posibilidades:
76
Antología de lecturas
Matemáticas
Primera: Comozán vio que los dos discos eran blancos.
Segunda: Comozán vio un disco negro y otro blanco.
De acuerdo con la primera hipótesis -reflexionó Aradin- mi disco "era blanco".
Queda por analizar la segunda hipótesis:
Vamos a suponer que Comozán vio un disco negro y otro blanco.
¿Quién tendría el disco negro?
Si el disco negro lo tuviera yo - razonó Aradín- el segundo pretendiente habría acertado.
En efecto: el segundo pretendiente de la princesa habría razonado así:
Veo que el tercer competidor lleva un disco negro; si el mío fuera también negro, el primer candidato Comozán--, al ver los dos discos negros no se habría equivocado. Luego, si se equivocó concluiría el segundo candidato-, mi disco "es blanco".
¿Pero qué ocurrió?
El segundo pretendiente también se equivocó. Quedó en la duda. Y quedó en la duda por haber visto
en mí -reflexionó Aradín- no un disco negro, sino un disco blanco.
Conclusión de Aradín:
-De acuerdo con la segunda hipótesis, mi disco también es blanco.
Ese fue concluyó Beremiz, el razonamiento de Aradín, para resolver con toda seguridad el problema de
los cinco discos, y por eso pudo afirmar: "Mi disco es blanco".
El sabio cordobés tomó entonces la palabra y se dirigió al Califa con expresión admirada diciendo que
la solución dada por Beremiz al problema de los cinco discos había sido com pleta y brillantísima.
El razonamiento, formulado con sencillez y claridad, era impecable para el más exigente geómetra.
Aseguró aún el cordobés que las personas allí -presentes habían sin duda comprendido en su totalidad el
problema de los cinco discos y que serían capaces de repetirlo más tarde en cualquier albergue de
caravanas del desierto.
Un jeque yemenita que se hallaba frente a mí sentado en un cojín rojo, hombre moreno, malcarado,
cubierto de joyas, murmuró a un amigo, oficial de la corte, que se hallaba a su lado:
-¿Oyes, capitán, Sayeg? Afirma ese cordobés que todos hemos entendido esa historia del disco blanco
y del disco negro. Mucho lo dudo. Por mi parte confieso que no entendí palabra...
Y añadió: -Sólo a un derviche cretino se le ocurriría colocar discos blancos y negros en las espaldas de
los tres pretendientes ¿No crees? ¿No sería más práctico promover una carrera de camellos en el
77
Antología de lecturas
Matemáticas
desierto? El vencedor sería escogido entonces y todo acabaría perfectamente sin complicaciones ¿no
crees?
El capitán Sayeg no respondió. Parecía no prestar la menor atención a aquel yemenita de pocas luces que
quería resolver un problema sentimental con una carrera de camellos por el desierto.
El Califa, con aire afable y distinguido, declaró a Beremiz vencedor de la sexta y penúltima prueba del
concurso.
¿Tendría nuestro amigo el calculador el éxito que esperábamos en la prueba séptima y final? ¿La
coronaría con la misma brillantez?
¡Sólo Allah sabe la verdad!
Pero al fin, las cosas parecían correr a medida de nuestros deseos.
Capítulo XXXII: En el que Beremiz es interrogado por un astrónomo libanés. El problema de
"la perla más ligera". El astrónomo cita un poema en alabanza a Beremiz.
Su nombre era Mohildín lhaia Banabixacar, geómetra y astrónomo, una de las figuras más
extraordinarias del Islam, el séptimo y último sabio que debía interrogar a Beremiz. Había
nacido en el Líbano, su nombre estaba escrito en cinco mezquitas, y sus libros eran leídos hasta
por los rumís. Sería imposible encontrar bajo el cielo del Islam inteligencia más segura ni cultura
más sólida y amplia.
El erudito Banabixacar, el libanés, con su hablar claro e impecable, dijo:
-Me siento realmente encantado con lo que llevo oído hasta ahora. El ilustre matemático persa
acaba de demostrar repetidamente el poder indiscutible de su talento. Me gustaría también,
colaborando en este brillante torneo, ofrecer al calculador Beremiz Samir un interesante
problema que aprendí, siendo aún joven, de un sacerdote budista que cultivaba la Ciencia de los
Números.
Exclamó el Califa, vivamente interesado:
-¡Oigamos, hermano de los árabes! Escucharemos con el mayor placer vuestra argumentación.
Espero que el joven persa, que hasta ahora se ha mantenido incólume en los dominios del Cálculo,
sepa resolver la cuestión formulada por el viejo budista ¡Allah se compadezca de ese idólatra!-.
Viendo el sabio libanés que su inesperada propuesta había despertado la atención del rey, de los
visires y de los nobles musulmanes, habló así, dirigiéndose serenamente al Hombre que
Calculaba:
-Este problema podría denominarse "Problema de la perla más ligera". Y se enuncia así:
-Un mercader de Benarés, en la India, disponía de ocho perlas iguales por su forma, tamaño
y color. De estas ocho perlas, siete tenían el mismo peso; la octava era sin embargo un poquito
más ligera que las otras. ¿Cómo podría el mercader descubrir la perla más ligera e indicarla con
78
Antología de lecturas
Matemáticas
toda seguridad utilizando la balanza y efectuando dos pesadas, sin disponer de pesa alguna?
¡Este es el problema! -Que Allah te inspire, ¡oh Calculador! la solución más sencilla y más
perfecta-.
Al oír el enunciado del problema de las perlas un jeque de cabello blanco, con largo collar de oro, que
se hallaba al lado del capitán Sayeg, murmuró en voz baja.
-¡Que problema tan hermoso! ¡Ese sabio libanés es admirable! i Gloria al Líbano, el País de los
Cedros!
Beremiz Samir, después de reflexionar durante breves momentos, habló con pausada y firme voz:
-No me parece difícil el oscuro problema budista de la perla más leve. Un razonamiento bien
encaminado puede revelarnos desde luego la solución.
Veamos: "Tengo ocho perlas iguales. Iguales en la forma, en el color, en el brillo y en el tamaño.
Rigurosamente iguales. Alguien nos aseguró que entre esas ocho perlas destacaba una por ser un
poquito más leve que las otras y que las otras siete presentaban el mismo peso. Para descubrir la
más ligera sólo hay un medio: usar una balanza. Y para pesar perlas debe ser una balanza delicada y
fina, de brazos largos y platillos muy ligeros. La balanza debe ser sensible. Y aún más: la balanza
deber ser exacta. Tomando las perlas de dos en dos y colocándolas en la balanza -una en cada
platillo-, se podría descubrir, naturalmente, la perla más ligera. Pero si la perla más ligera fuera una
de las dos últimas, me vería obligado a efectuar cuatro pesadas. Y el problema exige que la perla más
ligera sea descubierta y determinada sólo en dos pesadas, cualquiera que sea la posición que ocupe.
La solución que me parece más sencilla es la siguiente:
Dividamos las perlas en tres grupos, y llamemos a cada uno de estos grupos A, B y C.
El grupo A tendrá tres perlas; el grupo B, tendrá también tres perlas; el grupo C estará formado por las
dos restantes. Con sólo dos pesadas descubriré así cual es la perla más ligera, sabiendo que siete
pesan exactamente lo mismo.
Pongamos los grupos A y B en la balanza y coloquemos un grupo en cada platillo efectuaremos así
la primera pesada-. Pueden ocurrir dos cosas:
1.° Que los grupos A y B presenten pesos iguales.
2.° Que presenten pesos desiguales al ser uno de ellos-A por ejemplo- más ligero.
En la primera hipótesis -A y B con el mismo peso- podemos asegurar queda perla más ligera no
pertenece al grupo A ni figura en el grupo B. La perla más ligera habrá que buscarla entre las que forman
el grupo C.
Tomemos, pues, esas dos perlas que forman el grupo C y pongámoslas en los platillos de la balanza segunda pesada Esta indicará cual es la más ligera y el caso quedará así resuelto.
En la segunda hipótesis -A más ligero que B-. queda claro que la perla más ligera está en el grupo A,
es decir: es una de las tres perlas del grupo menos pesado. Tomemos entonces dos perlas
cualesquiera del grupo A y dejemos la 'otra de lado. Pesemos esas dos perlas -segunda pesada-. Si
79
Antología de lecturas
Matemáticas
la balanza queda en equilibrio, la tercera perla -la que dejamos de lado es la más ligera. Si hubiera
desequilibrio, la perla más ligera está en el platillo que se alza."
Así queda, ¡oh príncipe de los Creyentes!, resuelto el "problema de la perla más ligera" formulado por
el ilustre sacerdote budista y presentado aquí por nuestro huésped el geómetra libanés, terminó
Beremiz.
El astrónomo Banabixacar el libanés, clasificó de impecable la solución presentada por Beremiz, y remató
su sentencia en los siguientes términos:
-Sólo un verdadero geómetra podría razonar con tanta perfección. La solución que acabo de oír en
relación con el "problema de la perla más ligera" es un verdadero poema de belleza y sencillez.
Y rindiendo homenaje al Calculador, el viejo astrónomo del País de los Cedros, recitó los siguientes
versos de Omar Khayyam, poeta muy delicado y gran geómetra de Persia:
Si una rosa de amor tú has guardado bien en tu corazón...
Sí a un Dios supremo y justo dirigiste tu humilde oración. Si con la copa alzada Cantas un día tu alabanza
a la vida. No has vivido en vano...
Beremiz agradeció emocionado este homenaje inclinando levemente la cabeza y llevándose la mano
derecha a la altura del corazón.
¡Qué bello era el poema de Omar Khayyam! Sí, realmente: ¡No has vivido en vano, oh Omar Khayyam!
ÉRASE UNA VEZ UN PROBLEMA.
Carolina Ocaña Castillo
Había una vez, en un lugar remoto detrás de una montaña, un pueblecito que era conocido como el lugar
más culto del planeta. Esto era, quizás, por sus dos grandes ―Centros del Conocimiento‖: ―El Mundo de
las Letras‖ y ―El Universo de los Números‖.
Pero todo lugar tiene sus ventajas y sus inconvenientes. Estos dos ―Centros del Conocimiento‖ siempre
estaban discutiendo sobre cuál de ellos impartía más cultura y, por tanto, era el mejor. Cada trimestre se
celebraban competiciones para ver cuál había enseñado mejor, el centro cuyos alumnos hubiesen sacado
mejores notas era el ganador.
Un día llegó a ese pueblo un señor llamado Aristoquímedes, que tenía un gran problema. Había oído
hablar de sus dos grandes escuelas y pensaba que en una de ellas encontraría su respuesta.
Primero fue a preguntar a ―El Universo de los Números‖.
- Hola, me llamo Aristoquímedes y he oído hablar muy bien de este pueblo. Me dijeron que aquí podría
hallar cualquier respuesta.
- Sí, así es. Los números son capaces de todo y esta es su casa así que usted dirá.
80
Antología de lecturas
Matemáticas
- Verá…resulta que soy el encargado de suministrar y llevar los cálculos del agua en mi edificio. El otro
día tenía que hacer un recado muy urgente y le pedí a uno de mis criados que se encargase de los
cálculos en mi lugar. Cuando volví me dijo que al principio se gastó la mitad del agua, y que 2 horas más
tarde se había usado 1/5 de lo que quedaba. En el depósito quedaban 600 litros pero necesito saber
cuánto había al principio.
- Eh…pues…esto es muy fácil…sólo hay que… no, hay que… ¿le importaría esperar un momento? Iré a
preguntar al jefe.
- Claro.
- Lo siento no se cómo es posible pero no existe ninguna solución matemática que resuelva su
problema…Lamento decirle que tendrá que ir a ―El Mundo de las Letras‖ a ver si allí saben qué hacer.
- Está bien. Muchas gracias.
Se dirigió al edificio de al lado, su próximo destino. Una vez dentro se dirigió al mostrador y le dijo al
responsable:
- Hola, me llamo Aristoquímedes y he oído hablar muy bien de este pueblo. Me dijeron que aquí podría
hallar cualquier respuesta…aunque no tuviese mucho que ver con la literatura.
- ¡Claro que sí! Verá la lengua está relacionada con todo en esta vida y a través de ella y con un poco de
lógica podemos responderle a cualquier cosa.
- Bien pues verá, es que en mi edificio yo me encargo de suministrar el agua y llevar todos los gastos. El
problema es que el otro día tuve que hacer un recado muy urgente que me requeriría todo el día.
Entonces dejé a mi criado a cargo del agua. Cuando terminé y volvía a casa el criado me dijo que primero
utilizaron la mitad del depósito y que poco después se gastó 1/5 de lo que quedaba. Miré en el depósito y
aún habían 600 litros de agua. Pero para hacer las facturas necesito saber qué cantidad de agua había al
principio. Sé que esto es un problema más bien matemático pero acabo de ir al otro edificio y no han
sabido resolverlo…
- Eso es obvio. No se preocupe: como ya le dije antes con un poco de lógica las letras pueden hacer
milagros. Verá: si al principio se gastó eso y luego esto y quedan tantos pues yo diría que al principio
había… que había…me sorprende que vaya a decir esto pero… ¡no sé lo que había!
- No me diga que he venido hasta aquí para nada…
- Lo siento, pero no podemos hacer nada por usted.
- Bueno, sí hay algo que puedan hacer…pero no les va a gustar.
- ¡Por favor! Cualquier cosa por el saber.
- Si ustedes no saben resolver mi problema y los números tampoco tal vez si uniesen sus conocimientos
podrían.
- ¡No siga! Eso que dice es una locura. Nunca y digo nunca haríamos tal cosa.
- Entonces significa que no harían cualquier cosa por el saber.
- No es eso. El problema son los de la escuela de matemáticas. Ellos nunca accederían, no son buenos
profesionales como nosotros.
- Muy bien si ustedes están dispuestos iré a preguntárselo a ellos. Gracias y hasta luego.
Aristoquímedes se dirigió de nuevo a ―El Universo de los Números‖.
Allí se dirigió directamente al presidente y le dijo:
- Hola de nuevo. Quería proponerle una cosa.
- Dígame, ¿de qué se trata?
- Bueno como antes no supieron resolver mi problema pues he encontrado una solución.
- ¡¿De verdad?! ¿Y cuál es?
81
Antología de lecturas
Matemáticas
- Pues verá he estado pensando que tal vez si su organización se uniese a la de las letras pues tal vez
resolverían mi problema.
- No, no y no. Y no es que nosotros no queramos ayudarle sino que la otra organización nunca accedería
y…
- Ya lo ha hecho.
- Y… ¿qué? Bueno pues siendo así…nosotros no vamos a ser menos. Le ayudaremos accediendo a lo
que nos pide.
- Genial. Nos veremos mañana a las seis de la tarde en la biblioteca.
Aristoquímedes fue a avisar del encuentro a la otra organización. Al día siguiente llegada la hora los dos
centros se reunieron uno frente a otro. Se pusieron a discutir sobre cuál había sido más puntual.
Aristoquímedes les separó y empezó a decirles:
- Bien, os recuerdo que hemos venido aquí para encontrar un modo de resolver mi problema. Tenéis
todos los materiales que vayáis a necesitar. Hemos encontrado un método para que no os peleéis: Al
primero que discuta se le restarán puntos de honor que se le irán sumando al otro centro. Ahora sólo me
queda deciros que buena suerte y a trabajar.
Tardaron varios días en encontrar métodos pero ninguno resultaba exacto.
Pero un buen día, todos gritaron a la vez:
- ¡¡ÁLGEBRA!!
- ¿Qué?- preguntó Aristoquímedes
- ÁLGEBRA
Algunos números primos
Los signos son importantes
Gran cantidad de letras
Ecuaciones que
Buscan soluciones
Raras de entender y por eso
A las letras has de atender
- ¡Ah!… ¿y eso cómo me va a ayudar?
- Verás, dentro de esto que hemos llamado Álgebra hay unas operaciones que combinan letras y
números a las que denominamos ecuaciones. Así que según la fórmula en tu depósito habría al
principio… ¡1500 litros!
- ¡Genial! Lo habéis conseguido y todo porque habéis trabajado juntos.
- Sí, y todo gracias a ti. Te condecoraremos con el título de Padre del Álgebra.
Con nuestras imprentas y la rapidez matemática de la otra escuela publicaremos libros para enviarlos al
resto del mundo.
Pasaron muchos años hasta que el Álgebra se distribuyó por todo el planeta.
Actualmente hay muchas operaciones creadas a partir del Álgebra.
82
Antología de lecturas
Matemáticas
MAGIA MATEMÁTICA
La mirada de Yaiza era algo inquietante. Sus ojos, oscuros y pequeños, despedían un brillo intenso y,
a la vez, profundo y enigmático. En cambio su sonrisa, amplia, franca, transparente y generosa,
invitaba a la confidencia y a la amistad.
Estas dos vertientes tan diferentes de su personalidad hacían de Yaiza una compañera especial.
Todos la queríamos y nos gustaba estar con ella, pero al mismo tiempo sentíamos una admiración y
un respeto reservados sólo para algunas personas adultas.
A Yaiza le encantaba el mundo de los números y descubrir sus secretos. Un día me dijo: -Si en el
mundo existiera sólo el número 1, operando con él podríamos obtener todos los demás números.- Yo
me quedé con la boca abierta, pero ella enseguida me aclaró: - Multiplica 1 x 1 y tendrás el 1. Ahora
multiplica 11 x 11 y te aparecerá el 2, multiplica el 111 x 111 y te aparecerá el 3...Actividad 1: ¿Hasta cuánto tendríais que multiplicar para obtener los 10 dígitos diferentes, desde el 0
hasta el 9?
Tuve que reconocer que a mí lo que me fallaba era el cálculo mental. - Tienes que conseguir ver cada
uno de los números con su complemento hasta el 10, – me explicó – si oyes el 8, tú ya tienes que ver
el 2, que es lo que falta para llegar al 10. Si te nombran el 6, tú ya lo asocias al 4, que es lo que falta
para completar 10.Hablaba de los números como si fueran criaturas suyas y, al hacerlo, los ojos se le volvían más
pequeños y su sonrisa se agrandaba hasta transmitir una emoción casi mágica.
-Te voy a conseguir algo para que puedas mejorar tu cálculo mental – me prometió.
Al día siguiente, a primera hora, se me acercó y me dijo: - Te he traído la primera y la última
generación de instrumentos de cálculo – y sacó de su mochila un ábaco y un papel con una dirección
de internet.
-Este ábaco me lo trajo mi padre de Rusia. Desde siempre la Humanidad se ha ayudado de ábacos
para llevar sus cuentas. En muchas partes de Europa y Asia los ábacos se hacían insertando bolas,
piedras o cuentas en varillas. En cambio en Perú, durante el Imperio Inca, los ábacos estaban hechos
con una cuerda gruesa de la que pendían otras más finas con distintos tipos de nudos a diferentes
alturas. Estos ábacos se llamaban Quipus.
Ese día la profesora explicó en clase la raíz cuadrada. Cuando faltaban 5 minutos para que sonara el
timbre, la profesora concluyó: - Así pues, la raíz cuadrada de 36 es 6, porque 6 x 6 son 36. Mañana
hablaremos de la raíz cuadrada de 2025 -, sonrió pícaramente. Yaiza levantó la mano y contestó: - 45
-. -¿Y de 5625? – sonrió la profe. - 75 –, respondió Yaiza. -¿Y de 4225? - , - 65 – afirmó Yaiza. Toda la
clase quedó petrificada. La profe asintió con la cabeza y levantó el pulgar con el puño cerrado,
felicitando a Yaiza. Yaiza se echó a reír. Sonó el timbre y todos corrimos a su lado. Aquello era magia
y queríamos saber el truco.
-La única magia que hay es la de los números – aclaró Yaiza. Si hacéis una lista de los cuadrados de
números acabados en 5 y miráis los resultados, también vosotros sabréis hacerlo – dijo – y sobre un
banco del patio escribió en un papel:
15 x 15 = 225
25 x 25 = 625
35 x 35 = 1225
45 x 45 = 2025
........................
85 x 85 = 7225
83
Antología de lecturas
Matemáticas
Actividad 2: Investigad y descubrid qué regla se cumple en estos casos.
Poco a poco me fui aficionando a los números. Yaiza me descubrió los triángulos y los cuadrados
mágicos, en donde había que colocar los números del 1 al 9, sin repetir ninguno, de forma que en
todas las direcciones tuvieran que sumar un número determinado.
-Existe una leyenda china – me aseguró Yaiza – que explica el origen del cuadrado mágico en el
caparazón de una tortuga.
-¿Nunca has pensado en dedicarte a la magia? - le pregunté. -Sí, muchas veces, porque lo que parece
magia, en realidad son propiedades de los números y yo, con ellos, estoy como pescado en el agua.- Se dice, como pez en el agua corregí, y se rió conmigo.
-Me sé un truco muy bueno con cartas.- -Tráetelas mañana y lo haces – le pedí. -Mañana no puedo,
tengo que ir con mis padres al consulado para tratar de arreglar unos papeles. Las traeré pasado
mañana.El jueves en el recreo Yaiza se colocó en un banco del patio y toda la clase la rodeamos. Hizo ademán
de concentrarse, barajó 15 cartas que había traído, cogió aire, lo expulsó y, con gestos ceremoniosos,
me pidió a mí que me fijara en una las cartas y dijera luego en qué montón había caído. Fue colocando
las cartas boca arriba de una en una en 3 montoncitos. Después de señalar yo el montón en el que
estaba mi carta, ella recogió las cartas, colocando el montón en el que estaba mi carta entre los otros
dos. Yaiza repitió la operación por segunda y tercera vez. Después fue depositando las cartas en un
solo montón, una encima de otra y cuando llegó a la octava carta me dijo: - ésta es tu carta.- ¡Había
acertado! Todos aplaudimos y el patio se inundó de ―ahora a mí‖, ―ahora a mí‖, ahora a mí‖...
Entramos en clase de Música y mientras preparábamos las flautas yo le cuchicheé: -Me he fijado en
los gestos ceremoniosos que hiciste antes de empezar el truco de las cartas.- -Eso es parte de la
magia, – sonrió – es importante hacer creer que algo extraordinario y sobrenatural va a ocurrir. Lo
demás lo harán nuestros números – y volvió a sonreír.
¡No me lo podía creer! Había dicho ―nuestros números‖. ¡Me consideraba su cómplice! ¡Su amigo!
Sentí algo nuevo, además de admiración. Sentí que el corazón me latía con fuerza y que por dentro
me crecía una felicidad que casi me ahogaba. ¿Qué me estaba pasando?
El profesor reclamó nuestra atención y empezamos a ensayar, pero ese día no me enteré de nada.
Tenía la cabeza embotada y no podía pensar, sólo podía mirar a Yaiza.
Al acabar la clase ella volvió a acercarse a mí y me dijo: - También la música tiene que ver con los
números. - Creí que estaba bromeando. Pero ella me propuso construir una flauta con pajitas de
refresco porque, según me explicó, las notas guardan entre sí relaciones numéricas.
-Mira, - dijo -si nosotros soplamos por un tubo fino, se producirá un sonido, por ejemplo, un DO grave.
Si ahora soplamos por un tubito con la mitad de longitud que antes, sonará un DO agudo. Esto quiere
decir que entre un DO grave y un DO agudo la relación es 1 a ½. Y si soplamos por un tubo con los
2/3 de la longitud primera, la del DO grave, sonará un SOL. Y con ¾ de la longitud sonará un FA. Yo te
voy a decir todas las relaciones, es decir, todas las fracciones con las que se corresponden todas las
notas y construiremos una flauta, ¿vale?. -
84
Antología de lecturas
Matemáticas
-¡Pues claro que vale! - pensé yo, que para entonces me parecía que no tocaba el suelo, que
caminaba levitando. Algo raro me había sucedido y no acertaba a saber qué era.
Yaiza trajo al día siguiente un paquete de pajitas de refrescos de colores y muchos compañeros de la
clase se apuntaron al experimento.
-Fijaos, - dijo – ésta es la relación que existe entre un DO grave, que será nuestra unidad, o sea,
nuestra referencia, y las demás notas de la escala:
DO grave = 1; RE = 9/10; MI = 4/5; FA = ¾; SOL = 2/3; LA = 3/5; SI = 11/20; DO agudo = ½
Cogeremos para el DO grave una longitud de 10 centímetros. - Y todos nos afanamos en cortar una de
las pajillas exactamente con 10 cm de longitud.
-Ahora calcularemos lo que tienen que medir las pajitas para cada una de las notas.
Para el RE sería 9/10 de 10 cm, o sea, 9 cm.
Para el MI sería 4/5 de 10 cm, o sea, 8 cm.
Para el FA sería ¾ de 10 cm, o sea, 7,5 cm
Cortamos las pajitas con esas longitudes y las unimos de mayor a menor con cinta adhesiva.
¡Habíamos construido nuestras propias flautas!
-¡Es maravilloso!- pensé - ¡Pero, no, la maravillosa era ella! - Allí estábamos la mitad de la clase
intentando tocar lo aprendido en clase de música con nuestras propias flautas. Nos sentíamos
auténticos luthiers. Eso era una verdadera magia. Otra era que me había enamorado. Yaiza saltaba y
reía entre las risas y saltos de todos nosotros. Pero hubo un momento en que nuestras miradas se
cruzaron y, como por encanto, los dos nos quedamos inmóviles, como electrocutados por alguna
chispa sobrenatural.
Ese día la acompañé a casa. Durante el camino no pudimos articular palabra. De vez en cuando nos
mirábamos y sonreíamos. Al despedirnos Yaiza me pasó una dirección de internet. -A ver si sabes
cuál es el truco – me dijo – y, si no, mañana te lo explico. Sus ojos brillaron profundos y pequeños y su
boca desplegó una sonrisa amplia y sincera antes de que saliera corriendo para su portal.
Me quedé un rato sin reaccionar y con la sonrisa puesta. Cuando llegué a casa busqué la dirección.
¡Funcionaba! ¡La bola mágica adivinaba mi número! Pero no sabía por qué.
Yaiza no ha vuelto al colegio. Los profesores nos dicen algo sobre dificultades para conseguir unos
documentos y que la familia se ha tenido que volver a su país.
He llorado muchos días. Ahora confío en la magia de que algún día consigan arreglar esos dichosos
papeles para que todos podamos tener otra vez a Yaiza con nosotros.
85
Antología de lecturas
Matemáticas
Algebra Recreativa
Yakov Perelman.
1. La vida de Diofanto
Problema
La historia ha conservado pocos rasgos biográficos de Diofanto, notable matemático de la
antigüedad. Todo lo que se conoce acerca de él ha sido tomado de la dedicatoria que figura en su
sepulcro, inscripción compuesta en forma de ejercicio matemático. Reproducimos esta inscripción:
En la lengua vernácula:
En el idioma del álgebra
¡Caminante! Aquí fueron sepultados los restos de
Diofanto. Y los números pueden mostrar, ¡Oh milagro!,
cuan larga fue su vida,
Cuya sexta parte constituyó su hermosa infancia.
x
x/6
Había transcurrido además una duodécima parte de su
vida, cuando de vello cubrióse su barbilla
x/12
Y la séptima parte de su existencia transcurrió en un
matrimonio estéril.
x/7
Pasó un quinquenio más y le hizo dichoso el
nacimiento de su precioso primogénito,
Que entregó su cuerpo, su hermosa existencia, a la
tierra, que duró tan solo la mitad de la de su padre
5
x/2
Y con profunda pena bajó a la sepultura, habiendo
sobrevivido cuatro años al deceso de su hijo
Dime cuantos años había vivido Diofanto cuando le llegó la muerte.
Solución
Al resolver la ecuación y hallar el valor de la incógnita, 84, conocemos los siguientes datos
biográficos de Diofanto: se casó a los 21 años, fue padre a los 38, perdió a su hijo a los 80 y murió a
los 84.
86
Antología de lecturas
Matemáticas
2. El caballo y el mulo
Problema
He aquí un antiguo ejercicio muy sencillo y fácil de traducir al idioma del álgebra.
―Un caballo y un mulo caminaban juntos llevando sobre sus lomos pesados sacos.
Lamentábase el jamelgo de su enojosa carga, a lo que el mulo le dijo: ―¿De qué te quejas?
Si yo te tomara un saco, mi carga sería el doble que la tuya. En cambio, si te doy un saco, tu carga
se igualará a la mía‖. ¿Decidme, doctos matemáticos, cuántos sacos llevaba el caballo, y cuántos el
mulo?‖.
Una vez resuelto el sistema vemos que x = 5, y = 7. El caballo llevaba 5 sacos, y el mulo, 7.
3. El paseo
Problema
- Pase usted mañana por mi casa - dijo el viejo doctor a un conocido.
- Muy agradecido. Saldré mañana a las tres. Quizá desee usted dar también un paseo. En este caso
salga a la misma hora y nos encontraremos a la mitad del camino.
- Usted olvida que soy ya viejo y ando tan sólo tres kilómetros por hora, en tanto que usted,
jovenzuelo, cuando más despacio va, hace 4 kilómetros por hora. No sería ningún delito que me
concediera alguna ventaja.
- Tiene razón - contestó el joven -. Comoquiera que yo recorro un kilómetro a la hora más que usted,
le doy este kilómetro de ventaja, es decir, saldré de casa un cuarto de hora antes ¿le será suficiente?
- Es usted muy amable - aprobó al instante el anciano. El joven cumplió lo prometido y salió de su
casa a las tres menos cuarto, marchando a 4 kilómetros por hora. El doctor salió a la calle a las tres
en punto y anduvo a tres kilómetros por hora. Cuando se encontraron, el anciano dio la vuelta, yendo
juntos a su domicilio.
Tan sólo cuando el joven regresó a su casa comprendió que debido a la ventaja concedida tuvo que
caminar, no el doble, sino el cuádruplo de lo que anduvo el doctor.
¿A qué distancia de la casa del doctor estaba la de su joven conocido?
Solución
Expresemos la distancia que separa las casas con la x (km). El joven anduvo en total 2x, y el doctor,
la cuarta parte, es decir x/2. Desde que salió de casa hasta que se encontraron, el doctor recorrió la
mitad de cuanto anduvo en total, es decir, x/4, y el joven hizo el resto, es decir, 3x/4. El anciano
caminó x/12 y el joven 3x/16 horas; además, sabemos que éste caminó ¼ de hora más que el doctor.
Establezcamos la siguiente ecuación
87
Antología de lecturas
Matemáticas
de donde x=2,4 km.
Entre las dos casas mediaba una distancia de 2,4 km.
4. El arte de adivinar números
Cada uno de ustedes se encontraba indudablemente con ―prestidigitadores‖ que pueden adivinar
números. Como regla un prestidigitador propone realizar operaciones del siguiente carácter: pensar
un número cualquiera, adicionar 2, multiplicar el resultado por 3, restar 5, restar el número pensado
etc., en total cinco a una decena de operaciones. Luego el prestidigitador pide que le comuniquen el
resultado y, al obtener la respuesta, en seguida comunica el número pensado.
Claro está que el secreto de la ―prestidigitación‖ es muy fácil y se basa en las mismas ecuaciones.
Supongamos que el prestidigitador le haya propuesto a usted realizar un programa de operaciones
indicado en la columna izquierda de la tabla siguiente:
piense un número
x
adicione 2
x+2
el resultado multiplíquelo por 3
3x+6
reste 7
3x-1
reste el número pensado
2x+1
multiplique por 2
4x+2
reste 1
4x+1
Luego el prestidigitador pide que le comuniquen el resultado final y, al obtenerlo, dice al instante el
número pensado. ¿Cómo lo hace?
Para comprender esto, hay que mirar la columna derecha de la tabla, donde las indicaciones del
prestidigitador están traducidas al idioma del álgebra. Mirando esta columna se puede comprender,
que si usted ha pensado cualquier número x, entonces realizadas todas las operaciones se obtendrá
4x + 1. Conociendo este resultado no es difícil ―adivinar‖ el número.
Supongamos, por ejemplo, que usted haya dicho al prestidigitador que el resultado es 33.
Entonces el prestidigitador resuelve mentalmente muy rápido la ecuación 4x + 1 = 33 y obtiene la
respuesta: x = 8. Es decir, hace falta restar 1 del resultado final (33 - 1 = 32) y luego el número
obtenido se divide entre 4 (32: 4 = 8), El resultado de esta división es el número pensado (8). Si el
resultado final es 25, entonces el prestidigitador hace mentalmente las siguientes operaciones 25 – 1
= 24, 24 / 4 = 6 y le comunica que usted ha pensado el número 6.
Como se ve todo es muy fácil. El prestidigitador sabe de antemano qué hace falta hacer con el
resultado para obtener el número pensado.
Después de comprender esto usted puede asombrar y desconcertar aún más a sus amigos
proponiéndoles a ellos mismos escoger según su propio parecer, el carácter de operaciones sobre
un número pensado. Usted propone a su amigo pensar un número y realizar en cualquier orden
operaciones del carácter siguiente: sumar o restar un número conocido (por ejemplo: sumar 2, restar
88
Antología de lecturas
Matemáticas
5, etc.), multiplicar ([1]) por un número conocido (por 2, por 3, etc.), sumar o restar el número
pensado. Su amigo, para embrollarle, va a amontonar una serie de operaciones. Por ejemplo, él ha
pensado el número 5 (el número pensado no se le comunica a usted) y realizando operaciones le
dice:
- he pensado un número, lo he multiplicado por 2, al resultado he sumado 3, luego he sumado el
número pensado, al resultado he sumado 1, todo lo he multiplicado por 2, he restado el número
pensado, luego he restado 3, una vez más he restado el número pensado, he restado 2. Por fin, el
resultado lo he multiplicado por 2 y he sumado 3.
Al decidir que él le ha embrollado por completo él comunica a usted con el aspecto triunfante:
- el resultado final es 49.
Para su asombro usted le comunica inmediatamente que él ha pensado el número 5.
¿Cómo lo hace usted? Ahora todo eso es bastante claro. Cuando su amigo le comunica las
operaciones que él está realizando con el número pensado, usted a la vez actúa mentalmente con la
incógnita x. El le dice: ―He pensado un número...‖, usted repite mentalmente:
―entonces tenemos x‖. El dice: ―...lo he multiplicado por 2...‖ (él de veras realiza la multiplicación de
números), usted prosigue mentalmente; ―...ahora tenemos 2x‖. El dice: ―...al resultado he sumado
3...‖, usted le sigue inmediatamente: 2x+3 etc. Cuando él le ―ha embrollado‖ completamente y ha
realizado todas las operaciones mencionadas arriba, usted ha llegado al resultado indicado en la
tabla siguiente (en la columna izquierda está escrito todo lo dicho en voz alta por su amigo y en la
derecha - las operaciones que usted ha hecho mentalmente):
He pensado un número
x
lo he multiplicado por 2
2x
al resultado he sumado 3
2x+3
luego he sumado el número pensado
3x+3
ahora he sumado 1
3x+4
el resultado lo he multiplicado por 2
6x+8
he restado el número pensado
5x+8
he restado 3
5x+5
más he restado el número pensado
4x+5
he restado 2
4x+3
por fin, el resultado lo he multiplicado por 2
8x+6
y he sumado 3
8x+9
Usted ha pensado por último: el resultado final es 8x + 9. Ahora él dice: ―El resultado final es 49‖.
Usted tiene ya la ecuación hecha: 8x + 9 = 49. Resolverla es una futilidad y usted le comunica en el
acto que él ha pensado el número 5. Esta prestidigitación es particularmente impresionante porque
las operaciones que hace falta realizar con el número pensado no las propone usted, sino su amigo
las ―inventa‖.
Sin embargo, hay un caso cuando la prestidigitación no tiene éxito. Si usted después de realizar
(contando mentalmente) una serie de operaciones ha obtenido, por ejemplo, x + 14, y su amigo dice
luego: ―...ahora he restado el número pensado y el resultado final es 14‖.
Usted le sigue (x + 14) – x = 14, de verdad resulta 14, pero no hay ninguna ecuación y por eso usted
no puede adivinar el número pensado. ¿Qué es necesario hacer en este caso? Obre así: tan pronto
usted tenga el resultado que no contiene la incógnita x, interrumpa a su amigo, diciéndole: ―¡Para!
Ahora puedo sin preguntar nada comunicarte el resultado que tienes. Es 14‖. Esto de veras va a
desconcertar a su amigo, pues él no le ha dicho completamente nada. A pesar de que usted no supo
adivinar el número pensado, la prestidigitación ha resultado espléndida.
89
Antología de lecturas
Matemáticas
LECTURA SECUNDARIA
EL HOMBRE QUE FUE JUEVES
CAPÍTULO PRIMERO
LOS DOS POETAS DE SAFRON PARK
El barrio de Saffron Park —Parque de Azafrán— se extendía al poniente de Londres, rojo
y desgarrado como una nube del crepúsculo. Todo él era de un ladrillo brillante; se destacaba sobre
el cielo fantásticamente, y aun su pavimento resultaba de lo más caprichoso: obra de un constructor
especulativo y algo artista, que daba a aquella arquitectura unas veces el nombre de "estilo Isabel" y
otras el de "estilo reina Ana", acaso por figurarse que ambas reinas eran una misma.
No sin razón se hablaba de este barrio como de una colonia artística, aunque no se sabe qué tendría
precisamente de artístico. Pero si sus pretensiones de centro intelectual parecían algo infundadas, sus
pretensiones de lugar agradable eran justificadísimas. El extranjero que contemplaba por vez
primera aquel curioso montón de casas, no podía menos de preguntarse qué clase de gente vivía allí.
Y si tenía la suerte de encontrarse con uno de los vecinos del barrio, su curiosidad no quedaba
defraudada.
El sitio no sólo era agradable, sino perfecto, siempre que se le considerase como un sueño, y no como
una superchería. Y si sus moradores no eran "artistas", no por eso dejaba de ser artístico el conjunto.
Aquel joven —los cabellos largos y castaños, la cara insolente— si no era un poeta, era ya un
poema. Aquel anciano, aquel venerable charlatán de la barba blanca y enmarañada, del sombrero
blanco y desgarbado, no sería un filósofo ciertamente, pero era todo un asunto de filosofía. Aquel
científico sujeto —calva de cascarón de huevo, y el pescuezo muy flaco y largo— claro es que no
tenía derecho a los muchos humos que gastaba: no había logrado, por ejemplo, ningún
descubrimiento biológico; pero ¿qué hallazgo biológico más singular que el de su interesante
persona? Así y sólo así había que considerar aquel barrio: no taller de artistas, sino obra de arte, y
obra delicada y perfecta. Entrar en aquel ambiente era como entrar en una comedia. Y sobre todo, al
anochecer; cuando, acrecentado el encanto ideal, los techos extravagantes resaltaban sobre el
crepúsculo, y el barrio quimérico aparecía aislado como una nube flotante. Y todavía más en las
frecuentes fiestas nocturnas del lugar —iluminados los jardines, y encendidos los farolillos
venecianos, que colgaban, como frutos monstruosos, en las ramas de aquellas miniaturas de árboles.
395 PALABRAS
Nombre:
Fecha:
Palabras
minuto.
por
90
Antología de lecturas
Matemáticas
BESTIARIO
El Rinoceronte
Hagamos entonces homenaje a la bestia endurecida y abstrusa porque ha dado lugar a una leyenda hermosa.
Aunque parezca imposible, este atleta rudimentario es el padre espiritual de la criatura poética que desarrolla en
los tapices de la Dama, el tema del Unicornio caballeroso y galante.
Vencido por una virgen prudente, el rinoceronte carnal se transfigura, abandona su empuje y se agacela, se
acierva y se arrodilla. Y el cuerno obtuso de agresión masculina se vuelve ante la doncella una esbelta endecha
de marfil.
Aves de Rapiña
Todos, halcones, águilas o buitres, repasan como frailes silenciosos su libro de horas aburridas, mientras la
rutina de cada día miserable les puebla el escenario de deyecciones y de vísceras blandas: triste manjar para
sus picos desgarradores.
El Bisonte
Sin dejarse arrebatar por esa ola de cuernos, de pezuñas y de belfos, el hombre emboscado arrojó flecha tras
flecha y cayeron uno por uno los bisontes. Un día se vieron pocos y se refugiaron en el último redil cuaternario.
La Hiena
Antes de abandonar a este cerbero abominable del reino feroz, al necrófilo entusiasmado y cobarde, debemos
hacer una aclaración necesaria: la hiena tiene admiradores y su apostolado no ha sido vano. Es tal vez el animal
que más prosélitos ha logrado entre los hombres.
Las Focas
Veloces lanzaderas, las focas tejen y destejen la tela interminable de sus juegos eróticos. Se abrazan sin brazos
y resbalan de una en otra improvisando sus rondas ad libitum. Baten el agua con duras palmadas; se aplauden
ellas mismas en ovaciones viscosas. La alberca parece de gelatina. El agua está llena de labios y de lenguas y
las focas entran y salen relamiéndose.
El Elefante
En vez de calcular, vámonos todos al circo y juguemos a ser los nietos del elefante, ese abuelo pueril que ahora
se bambolea al compás de una polka.
No. Mejor hablemos del marfil. Esa noble sustancia, dura y uniforme, que los paquidermos empujan
secretamente con todo el peso de su cuerpo, como una material expresión de pensamiento.
El Búho
Antes de devorarlas, el búho digiere mentalmente a sus presas. Nunca se hace cargo de una rata entera si no se
ha formado un previo concepto de cada una de sus partes. La actualidad del manjar que palpita en sus garras va
haciéndose pasado en la conciencia y preludia la operación analítica de un lento devenir intestinal.
La Cebra
Golosas, las cebras devoran llanuras de pasto africano, a sabiendas de que ni el corcel árabe ni el pura sangre
pueden llegar a semejante redondez de las ancas ni a igual finura de cabos.
El Hipopótamo
Ya muchos milenios antes (¿cuántos?), los monos decidieron acerca de su destino oponiéndose a la tentación
de ser hombres. No cayeron en la empresa racional y siguen todavía en el paraíso: caricaturales, obscenos y
libres a su manera. Los vemos ahora en el zoológico, como un espejo depresivo: nos miran con sarcasmo y con
pena, porque
Jubilado por la naturaleza y a falta de pantano a su medida, el hipopótamo se sumerge en el hastío.
Potentado biológico, ya no tiene qué hacer junto al pájaro, la flor y la gacela. Se aburre enormemente y se queda
dormido a la orilla de su charco, como un borracho junto a la copa vacía, envuelto en su capote colosal.
La Boa
La absorción se inicia fácilmente y el conejo se entrega en una asfixia sin pataleo. Desaparecen la cabeza y las
patas delanteras. Pero a medio bocado sobrevienen las angustias de un taponamiento definitivo. En ayuda de la
boa transcurren los últimos instantes de vida del conejo, que avanza y desaparece propulsado en el túnel costillar
por cada vez más tenues estertores.
615 PALABRAS.
Nombre:
Fecha:
Palabras por minuto.
91
Antología de lecturas
Matemáticas
LA MUERTE TIENE PERMISO
Sobre el estrado, los ingenieros conversan, ríen. Se golpean unos a otros con bromas incisivas.
Sueltan chistes gruesos cuyo clímax es siempre áspero. Poco a poco su atención se concentra en el
auditorio. Dejan de recordar la última juerga, las intimidades de la muchacha que debutó en la casa de
recreo a la que son asiduos. El tema de su charla son ahora esos hombres, ejidatarios congregados
en una asamblea y que están ahí abajo, frente a ellos.
-Sí, debemos redimirlos. Hay que incorporarlos a nuestra civilización, limpiándolos por fuera y
enseñándolos a ser sucios por dentro...
-Es usted un escéptico, ingeniero. Además, pone usted en tela de juicio nuestros esfuerzos, los de la
Revolución.
-¡Bah! Todo es inútil. Estos jijos son irredimibles. Están podridos en alcohol, en ignorancia. De nada ha
servido repartirles tierras.
-Usted es un superficial, un derrotista, compañero. Nosotros tenemos la culpa. Les hemos dado las
tierras, ¿y qué? Estamos ya muy satisfechos. Y el crédito, los abonos, una nueva técnica agrícola,
maquinaria, ¿van a inventar ellos todo eso?
El presidente, mientras se atusa los enhiestos bigotes, acariciada asta por la que iza sus dedos con
fruición, observa tras sus gafas, inmune al floreteo de los ingenieros. Cuando el olor animal, terrestre,
picante, de quienes se acomodan en las bancas, cosquillea su olfato, saca un paliacate y se suena las
narices ruidosamente. Él también fue hombre del campo. Pero hace ya mucho tiempo. Ahora, de
aquello, la ciudad y su posición sólo le han dejado el pañuelo y la rugosidad de sus manos.
Los de abajo se sientan con solemnidad, con el recogimiento del hombre campesino que penetra en
un recinto cerrado: la asamblea o el templo. Hablan parcamente y las palabras que cambian dicen de
cosechas, de lluvias, de animales, de créditos. Muchos llevan sus itacates al hombro, cartucheras para
combatir el hambre. Algunos fuman, sosegadamente, sin prisa, con los cigarrillos como si les hubieran
crecido en la propia mano.
329 PALABRAS
Nombre:
Fecha:
Palabras
minuto.
por
92
Antología de lecturas
Matemáticas
EL ALBUM
ANTÓN CHEJOV
El consejero administrativo Craterov, delgado y seco como la flecha del Almirantazgo, avanzó algunos pasos y,
dirigiéndose a Serlavis, le dijo:
-Excelencia: Constantemente alentados y conmovidos hasta el fondo del corazón por vuestra gran autoridad y
paternal solicitud...
-Durante más de diez años-le sopló Zacoucine.
-Durante más de diez años... ¡Hum!... en este día memorable, nosotros, vuestros subordinados, ofrecemos a su
excelencia, como prueba de respeto y de profunda gratitud, este álbum con nuestros retratos, haciendo votos
porque vuestra noble vida se prolongue muchos años y que por largo tiempo aún, hasta la hora de la muerte, nos
honréis con...
-Vuestras paternales enseñanzas en el camino de la verdad y del progreso-añadió Zacoucine, enjugándose las
gotas de sudor que de pronto le habían invadido la frente-. Se veía que ardía en deseos de tomar la palabra para
colocar el discurso que seguramente traía preparado.
-Y que-concluyó-vuestro estandarte siga flotando mucho tiempo aún en la carrera del genio, del trabajo y de la
conciencia social.
Por la mejilla izquierda de Serlavis, llena de arrugas, se deslizó una lágrima.
-Señores-dijo con voz temblorosa-, no esperaba yo esto, no podía imaginar que celebraseis mi modesto jubileo.
Estoy emocionado, profundamente emocionado y conservaré el recuerdo de estos instantes hasta la muerte.
Creedme, amigos míos, os aseguro que nadie os desea como yo tantas felicidades... Si alguna vez ha habido
pequeñas dificultades... ha sido siempre en bien de todos vosotros...
Serlavis, actual consejero de Estado, dio un abrazo a Craterov, consejero de estado administrativo, que no
esperaba semejante honor y que palideció de satisfacción. Luego, con el rostro bañado en lágrimas como si le
hubiesen arrebatado el precioso álbum en vez de ofrecérselo, hizo un gesto con la mano para indicar que la
emoción le impedía hablar. Después, calmándose un poco, dijo unas cuantas palabras más muy afectuosas,
estrechó a todos la mano y, en medio del entusiasmo y de sonoras aclamaciones, se instaló en su coche
abrumado de bendiciones. Durante el trayecto sintió su pecho invadido de un júbilo desconocido hasta entonces
y de nuevo se le saltaron las lágrimas.
En su casa le esperaban nuevas satisfacciones. Su familia, sus amigos y conocidos, le hicieron tal ovación que
hubo un momento en que creyó sinceramente haber efectuado grandes servicios a la patria y que hubiese sido
una gran desgracia para ella que él no hubiese existido. Durante la comida del jubileo no cesaron los brindis, los
discursos, los abrazos y las lágrimas. En fin, que Serlavis no esperaba que sus méritos fuesen premiados tan
calurosamente.
-Señores-dijo en el momento de los postres-, hace dos horas he sido indemnizado por todos los sufrimientos que
esperan al hombre que se ha puesto al servicio, no ya de la forma ni de la letra, si se me permite expresarlo así,
sino del deber. Durante toda mi carrera he sido siempre fiel al principio de que no es el público el que se ha
hecho para nosotros, sino nosotros los que estamos hechos para él. Y hoy he recibido la más alta recompensa.
Mis subordinados me han ofrecido este álbum que me ha llenado de emoción.
Todos los rostros se inclinaron sobre el álbum para verlo.
-¡Qué bonito es!-dijo Olga, la hija de Serlavis-. Estoy segura de que no cuesta menos de cincuenta rublos. ¡Oh,
es magnífico! ¿Me lo das, papá? Tendré mucho cuidado con él... ¡Es tan bonito!
Después de la comida, Olga se llevó el álbum a su habitación y lo guardó en su secreter. Al día siguiente arrancó
los retratos de los funcionarios tirándolos al suelo y colocó en su lugar los de sus compañeras de pensión. Los
uniformes cedieron el sitio a las esclavinas blancas. Colás, el hijo pequeño de su excelencia, recortó los retratos
de los funcionarios y pintó sus trajes de rojo. Colocó bigotes en los labios afeitados y barbas oscuras en los
mentones imberbes. Cuando no tuvo más que colorear recortó siluetas y les atravesó los ojos con una aguja,
para jugar con ellas a los soldados. Al consejero Craterov lo pegó de pie en una caja de cerillas y lo llevó
colocado así al despacho de su padre
-Papá, mira un monumento.
Serlavis se echó a reír, movió la cabeza y, enternecido, dio un sonoro beso en la mejilla a Nicolás.
-Anda, pilluelo, enséñaselo a mamá para que lo vea ella también.
726 PALABRAS.
Nombre:
Fecha:
Palabras por minuto.
93
Antología de lecturas
Matemáticas
EL CAPITÁN ALATRISTE
No era el hombre más honesto ni el más piadoso, pero era un hombre valiente. Se llamaba Diego
Alatriste y Tenorio, y había luchado como soldado de los tercios viejos en las guerras de Flandes.
Cuando lo conocí malvivía en Madrid, alquilándose por cuatro maravedís en trabajos de poco lustre, a
menudo en calidad de espadachín por cuenta de otros que no tenían la destreza o los arrestos para
solventar sus propias querellas. Ya saben: un marido cornudo por aquí, un pleito o una herencia
dudosa por allá, deudas de juego pagadas a medias y algunos etcéteras más. Ahora es fácil criticar
eso; pero en aquellos tiempos la capital de las Españas era un lugar donde la vida había que
buscársela a salto de mata, en una esquina, entre el brillo de dos aceros.
En todo esto Diego Alatriste se desempeñaba con holgura. Tenía mucha destreza a la hora de tirar de
espada, y manejaba mejor, con el disimulo de la zurda, esa daga estrecha y larga llamada por algunos
vizcaína, con que los reñidores profesionales se ayudaban a menudo. Una de cal y otra de vizcaína,
solía decirse. El adversario estaba ocupado largando y parando estocadas con fina esgrima, y de
pronto le venía por abajo, a las tripas, una cuchillada corta como un relámpago que no daba tiempo ni
a pedir confesión. Sí. Ya he dicho a vuestras mercedes que eran años duros.
El capitán Alatriste, por lo tanto, vivía de su espada. Hasta donde yo alcanzo, lo de capitán era más un
apodo que un grado efectivo. El mote venía de antiguo: cuando, desempeñándose de soldado en las
guerras del rey, tuvo que cruzar una noche con otros veintinueve compañeros y un capitán de verdad
cierto río helado, imagínense, viva España y todo eso, con la espada entre los dientes y en camisa
para confundirse con la nieve, a fin de sorprender a un destacamento holandés. Que era el enemigo
de entonces porque pretendían proclamarse independientes, y si te he visto no me acuerdo. El caso es
que al final lo fueron, pero entre tanto los fastidiamos bien. Volviendo al capitán, la idea era sostenerse
allí, en la orilla de un río, o un dique, o lo que diablos fuera, hasta que al alba las tropas del rey nuestro
señor lanzasen un ataque para reunirse con ellos. Total: que los herejes fueron debidamente
acuchillados sin darles tiempo a decir esta boca es mía. Estaban durmiendo como marmotas, y en
ésas salieron del agua los nuestros con ganas de calentarse y se quitaron el frío enviando herejes al
infierno, o a donde vayan los malditos luteranos. Lo malo es que luego vino el alba, y se adentró la
mañana, y el otro ataque español no se produjo. Cosas, contaron después, de celos entre maestres de
campo y generales.
Arturo Pérez-Reverte
475 PALABRAS
Nombre:
Fecha:
Palabras
minuto.
por
94
Antología de lecturas
Matemáticas
MACARIO (fragmento)
JUAN RULFO
Estoy sentado junto a la alcantarilla aguardando a que salgan las ranas. Anoche, mientras estábamos
cenando, comenzaron a armar el gran alboroto y no pararon de cantar hasta que amaneció. Mi
madrina también dice eso: que la gritería de las ranas le espantó el sueño. Y ahora ella bien quisiera
dormir. Por eso me mandó a que me sentara aquí, junto a la alcantarilla, y me pusiera con una tabla en
la mano para que cuanta rana saliera a pegar de brincos afuera, la apalcuachara a tablazos... Las
ranas son verdes de todo a todo, menos en la panza. Los sapos son negros. También los ojos de mi
madrina son negros. Las ranas son buenas para hacer de comer con ellas. Los sapos no se comen;
pero yo me los he comido también, aunque no se coman, y saben igual que las ranas. Felipa es la que
dice que es malo comer sapos. Felipa tiene los ojos verdes como los ojos de los gatos. Ella es la que
me da de comer en la cocina cada vez que me toca comer. Ella no quiere que yo perjudique a las
ranas. Pero a todo esto, es mi madrina la que me manda a hacer las cosas... Yo quiero más a Felipa
que a mi madrina. Pero es mi madrina la que saca el dinero de su bolsa para que Felipa compre todo
lo de la comedera. Felipa sólo se está en la cocina arreglando la comida de los tres. No hace otra cosa
desde que yo la conozco. Lo de lavar los trastes a mí me toca. Lo de acarrear leña para prender el
fogón también a mí me toca. Luego es mi madrina la que nos reparte la comida. Después de comer
ella, hace con sus manos dos montoncitos, uno para Felipa y otro para mí. Pero a veces Felipa no
tiene ganas de comer y entonces son para mí los dos montoncitos. Por eso quiero yo a Felipa, porque
yo siempre tengo hambre y no me lleno nunca, ni aun comiéndome la comida de ella. Aunque digan
que uno se llena comiendo, yo sé bien que no me lleno por más que coma todo lo que me den. Y
Felipa también sabe eso... Dicen en la calle que yo estoy loco porque jamás se me acaba el hambre.
Mi madrina ha oído que eso dicen. Yo no lo he oído. Mi madrina no me deja salir solo a la calle.
Cuando me saca a dar la vuelta es para llevarme a la iglesia a oír misa. Allí me acomoda cerquita de
ella y me amarra las manos con las barbas de su rebozo. Yo no sé por qué me amarra mis manos;
pero dice que porque dizque luego hago locuras. Un día inventaron que yo andaba ahorcando a
alguien; que le apreté el pescuezo a una señora nada más por nomás. Yo no me acuerdo. Pero, a todo
esto, es mi madrina la que dice lo que yo hago y ella nunca anda con mentiras. Cuando me llama a
comer, es para darme mi parte de comida, y no como otra gente que me invitaba a comer con ellos y
luego que me les acercaba me apedreaban hasta hacerme correr sin comida ni nada. No, mi madrina
me trata bien. Por eso estoy contento en su casa.
562 PALABRAS
Nombre:
Fecha:
Palabras
minuto.
por
95
Antología de lecturas
Matemáticas
EL RASTRO DE TU SANGRE EN LA NIEVE (fragmento)
GABRIEL GARCÍA MÁRQUEZ
Al anochecer, cuando llegaron a la frontera, Nena Daconte se dio cuenta de que el dedo con el anillo de bodas le
seguía sangrando. El guardia civil con una manta de lana cruda sobre el tricornio de charol examinó los
pasaportes a la luz de una linterna de carburo, haciendo un grande esfuerzo para que no lo derribara la presión
del viento que soplaba de los Pirineos. Aunque eran dos pasaportes diplomáticos en regla, el guardia levantó la
linterna para compro bar que los retratos se parecían a las caras.
Nena Daconte era casi una niña, con unos ojos de pájaro feliz y una piel de melaza que todavía irradiaba la
resolana del Caribe en el lúgubre anochecer de enero, y estaba arropada hasta el cuello con un abrigo de nucas
de visón que no podía comprarse con el sueldo de un año de toda la guarnición fronteriza. Billy Sánchez de Avila,
su marido, que conducía el coche, era un año menor que ella y casi tan bello y llevaba una chaqueta de cuadros
escoceses y una gorra de pelotero. Al contrario de su esposa, era alto y atlético y tenía las mandíbulas de hierro
de los matones tímidos. Pero lo que revelaba mejor la condición de ambos era el automóvil platinado, cuyo
interior exhalaba un aliento de bestia viva, como no se había visto otro por aquella frontera de pobres. Los
asientos posteriores iban atiborrados de maletas demasiado nuevas y muchas cajas de regalos todavía sin abrir.
Ahí estaba, además el saxofón tenor que había sido la pasión dominante en la vida de Nena Daconte antes de
que sucumbiera al amor contrariado de su tierno pandillero de balneario.
Cuando el guardia le devolvió los pasaportes sellados, Billy Sánchez le preguntó dónde podía encontrar una
farmacia para hacerle una cura en el dedo a su mujer, y el guardia le gritó contra e1 viento que preguntaran en
Indaya, del lado francés. Pero los guardias s de Hendaya estaban sentados a la mesa en mangas de camisa,
jugando barajas mientras comían pan mojado en tazones de vino dentro de una garita de cristal cálida y bien
alumbrada, y les bastó con ver el tamaño y la clase del coche para indicarles por señas que se internaran en
Francia. Billy Sánchez hizo sonar varias veces la vocina, pero los guardias no entendieron que los llamaban, sino
que uno de ellos abrió el cristal y les gritó con más rabia que el viento: Merde! Allez-, es pece de con!
Entonces Nena Daconte salió del automóvil envuelta con el abrigo hasta las orejas, y le preguntó al guardia en
un francés perfecto dónde había una farmacia. El guardia contestó por costumbre con la boca llena de pan que
eso no era asunto suyo. Y menos con semejante borrasca, y cerró la ventanilla. Pero luego se fijó con atención
en la muchacha que se chupaba el dedo herido envuelta en el destello de los visones naturales, y debió
confundirla con una aparición mágica en aquella noche de espantos, porque al instante cambió de humor.
Explicó que la ciudad más cercana era Biarritz, pero que en pleno invierno y con aquel viento de lobos, tal vez no
hubiera una farmacia abierta hasta Bayona, un poco más adelante.
-¿Es algo grave? -preguntó.
-Nada -sonrió Nena Daconte, mostrándole el dedo con la sortija de diamantes en cuya yema era apenas
perceptible la herida de la rosa-. Es sólo un pinchazo.
584 PALABRAS
Nombre:
Fecha:
Palabras por minuto.
96
Antología de lecturas
Matemáticas
EL HUNDIMIENTO DE LA CASA USHER (fragmento)
Edgar Allan Poe
Durante un día entero de otoño, oscuro, sombrío, silencioso, en que las nubes se cernían pesadas y opresoras
en los cielos, había yo cruzado solo, a caballo, a través de una extensión singularmente monótona de campiña, y
al final me encontré, cuando las sombras de la noche se extendían, a la vista de la melancólica Casa de Usher.
No sé cómo sucedió; pero, a la primera ojeada sobre el edificio, una sensación de insufrible tristeza penetró en
mi espíritu. Digo insufrible, pues aquel sentimiento no estaba mitigado por esa emoción semiagradable, por ser
poético, con que acoge en general el ánimo hasta la severidad de las naturales imágenes de la desolación o del
terror. Contemplaba yo la escena ante mí la simple casa, el simple paisaje característico de la posesión, los
helados muros, las ventanas parecidas a ojos vacíos, algunos juncos alineados y unos cuantos troncos blancos y
enfermizos - con una completa depresión de alma que no puede compararse apropiadamente, entre las
sensaciones terrestres, más que con ese ensueño posterior del opiómano, con esa amarga vuelta a la vida diaria,
a la atroz caída del velo. Era una sensación glacial, un abatimiento, una náusea en el corazón, una irremediable
tristeza de pensamiento que ningún estímulo de la imaginación podía impulsar a lo sublime. ¿Qué era aquello me detuve a pensarlo -, qué era aquello que me desalentaba así al contemplar la Casa de Usher? Era un
misterio de todo punto insoluble; no podía luchar contra las sombrías visiones que se amontonaban sobre mí
mientras reflexionaba en ello. Me vi forzado a recurrir a la conclusión insatisfactoria de que existen, sin lugar a
dudas, combinaciones de objetos naturales muy simples que tienen el poder de afectamos de este modo,
aunque el análisis de ese poder se base sobre consideraciones en que perderíamos pie. Era posible, pensé, que
una simple diferencia en la disposición de los detalles de la decoración, de los pormenores del cuadro, sea
suficiente para modificar, para aniquilar quizá, esa capacidad de impresión dolorosa. Obrando conforme a esa
idea, guié mi caballo hacia la orilla escarpada de un negro y lúgubre estanque que se extendía con tranquilo brillo
ante la casa, y miré con fijeza hacia abajo - pero con un estremecimiento más aterrador aún que antes - las
imágenes recompuestas e invertidas de los juncos grisáceos, de los lívidos troncos y de las ventanas parecidas a
ojos vacíos.
Sin embargo, en aquella mansión lóbrega me proponía residir unas semanas. Su propietario, Roderick Usher, fue
uno de mis joviales compañeros de infancia; pero habían transcurrido muchos años desde nuestro último
encuentro. Una carta, empero, habíame llegado recientemente a una alejada parte de la comarca -una carta de
él-, cuyo carácter de vehemente apremio no admitía otra respuesta que mi presencia. La letra mostraba una
evidente agitación nerviosa. El autor de la carta me hablaba de una dolencia física aguda -de un trastorno mental
que le oprimía- y de un ardiente deseo de verme, como a su mejor y en realidad su único amigo, pensando hallar
en el gozo de mi compañía algún alivio a su mal. Era la manera como decía todas estas cosas y muchas más,
era la forma suplicante de abrirme su pecho, lo que no me permitía vacilación, y, por tanto, obedecí desde luego,
lo que consideraba yo, pese a todo, como un requerimiento muy extraño.
Aunque los niños hubiéramos sido camaradas íntimos, bien mirado, sabía yo muy poco de mi amigo. Su reserva
fue siempre excesiva y habitual. Sabía, no obstante, que pertenecía a una familia muy antañona que se había
distinguido desde tiempo inmemorial por una peculiar sensibilidad de temperamento, desplegada a través de los
siglos en muchas obras de un arte elevado, y que se manifestaba desde antiguo en actos repetidos de una
generosa aunque recatada caridad, así como por una apasionada devoción a las dificultades, quizá más bien
que a las bellezas ortodoxas y sin esfuerzo reconocibles de la ciencia musical. Tuve también noticia del hecho
muy notable de que del tronco de la estirpe de los Usher, por gloriosamente antiguo que fuese, no había brotado
nunca, en ninguna época, rama duradera; en otras palabras: que la familia entera se había perpetuado siempre
en línea directa, salvo muy insignificantes y pasajeras excepciones. Semejante deficiencia, pensé - mientras
revisaba en mi imaginación la perfecta concordancia de aquellas aserciones con el carácter proverbial de la raza,
y mientras reflexionaba en la posible influencia que una de ellas podía haber ejercido, en una larga serie de
siglos, sobre la otra -, era acaso aquella ausencia de rama colateral y de consiguiente transmisión directa, de
padre a hijo, del patrimonio del nombre, lo que había, a la larga, identificado tan bien a los dos, uniendo el título
originario de la posesión a la arcaica y equívoca denominación de «Casa de Usher», denominación empleada
por los lugareños, y que parecía juntar en su espíritu la familia y la casa solariega.
835 PALABRAS
Nombre:
Fecha:
Palabras por minuto.
97
Antología de lecturas
Matemáticas
EL HUEVO DE CRISTAL (fragmento)
HERBERT GEORGE WELLS
Todavía el año pasado existía no lejos de "Los Siete Cuadrantes" una tiendecita de aspecto mísero, sobre cuya
puerta, en borrosas letras amarillas, campeaba este letrero: "C. Cave. Taxidermista y Anticuario". Entre la
diversidad confusa de objetos veíanse en el escaparate varios colmillos de elefante, un juego de ajedrez
incompleto, diversos cacharros de vidrio, algunas armas, un muestrario de ojos de animales, dos cabezas de
tigre disecadas, una calavera, varios monos, uno de los cuales servía de soporte a un quinqué, un huevo de
avestruz punteado de negro por las moscas, aparejos de pesca, una pecera vacía empolvadísima, y un esferoide
de cristal maravillosamente traslúcido. Al empezar la acción de esta historia dos personas estaban estacionadas
ante el escaparate, contemplando el esferoide de cristal. Una de esas personas era alta, enjuta, de aspecto
eclesiástico; -la otra mucho más joven-, baja y magra, de cobriza tez y cabellera y barba negras. Hablaban con
vivacidad, y el joven parecía empezado en decidir a su compañero a comprar el objeto antedicho. Mientras se
desarrollaba en la calle esta escena, salió de la trastienda el propietario mascujando aún la última tonada del
desayuno, y al advertir la presencia de los presuntos compradores y darse cuenta de que el huevo de cristal
había suscitado su interés, no pudo reprimir un gesto de inquietud, y luego de lanzar miradas furtivas hacia los
importunos, acercóse a la puerta, y en vez de abrirla para que entraran, la cerró. Era el señor Cave un viejecillo
de amojamado rostro y palidez casi verdosa; sus rasgos salientes constituíanlos los claros ojos azules, siempre
intranquilos, y la melena de un pardo gris, que caía sobre el grasiento cuello de una levita pasada de moda.
Añadid a estos detalles un bonete de forma caprichosa y unas pantuflas de orillo, dignas por su antigüedad de
figurar en el escaparate, y con un poquito de imaginación ya podréis figuramos al viejo anticuario.
Al ver que no acababan de irse los tenaces observadores, acentuóse su nerviosidad. El que parecía clérigo sacó
de su bolsillo del pantalón un puñado de dinero y, mostrándolo a su amigo, sonrió complacido. Este gesto
aumentó la zozobra del anticuario que los espiaba, y su intranquilidad convirtióse en pavor al verlos apartarse del
escaparate y penetrar resueltamente en la tienda. El clérigo, llamémosle así, preguntó sin detenerse en
ceremoniosos preámbulos el precio del esferoide de cristal; y el señor Cave, luego de dirigir una inquieta mirada
hacia la trastienda, contestó con voz trémula y queda:
-Vale cinco libras, señor.
El clérigo objetó que era un precio inverosímil se dispuso a entrar en regateos, como si no comprendiese que
pedir tal suma equivalga a negarse a venderlo. El anticuario entonces avanzó hacia la puerta como si quisiera
despedirlos, y dijo con voz más firme ya:
-Cinco libras, ni un penique menos.
En este instante apareció tras la mampara de la trastienda una cara femenina, que al través de las gafas púsose
a observar con curiosidad ceñuda el incidente; y el señor Cave, fingiendo no verla y deseoso de concluir, volvió a
decirles:
-Nada, señores, ya lo saben. no puedo rebajar ni un penique. El comprador más joven, que hasta entonces había
permanecido silencioso, clavó su mirada en el señor Cave, y dirigiéndose a su acompañante le dijo en tono
decisivo:
-Está bien. Déle usted las cinco libras. El clérigo, en vez de obedecer, se volvió hacia él, para comprobar si la
orden era dada en broma, y cuando se convenció de su seriedad, y tornó a mirar al anticuario, vio que se había
puesto pálido como un cadáver.
-Es un precio exorbitante -dijo, mientras rebuscaba en sus bolsillos.
614 PALABRAS
Nombre:
Fecha:
Palabras por minuto.
98
Antología de lecturas
Matemáticas
LAS MUERTES CONCÉNTRICAS (Fragmento)
JACK LONDON
Oficina de los Sicarios de Midas, 17 de agosto, 1899.
Señor Eben Hale, plutócrata.
Muy señor nuestro:
Queremos obtener al contado, en la forma que usted decida, veinte millones de dólares. Le requerimos que nos
pague esta suma, a nosotros o a nuestros agentes; usted notará que no especificamos tiempo, pues no
deseamos apresurarlo en este detalle. Hasta puede pagarnos, si le es más fácil, en diez, quince o veinte cuotas;
pero no aceptamos cuotas inferiores a un millón.
Créanos, querido señor Hale, cuando decimos que emprendemos esta acción desprovistos de toda animosidad.
Somos miembros del proletariado intelectual, cuyo número en creciente aumento marca con letras rojas los
últimos días del siglo XIX; hemos decidido entrar en este negocio después de un completo estudio de la
economía social. Nuestro plan no nos permite lanzarnos a vastas y lucrativas operaciones sin disponer de capital
inicial. Hasta ahora hemos tenido bastante éxito, y esperamos que nuestras gestiones con usted resulten gratas
y satisfactorias. Le rogamos que nos siga con atención mientras le explicamos nuestros puntos de vista. En la
base del presente sistema social se halla el derecho de propiedad. Este derecho del individuo a detentar
propiedad se funda única y enteramente, en última instancia, en la fuerza. Los caballeros de Guillermo el
Conquistador dividieron y se repartieron Inglaterra con la espada desnuda. Esto es verdad para todas las
potencias feudales. Con la invención del vapor y la revolución industrial vino al mundo la clase capitalista, en el
sentido moderno de la palabra. Estos capitalistas o capitanes de la industria virtualmente despojaron a los
descendientes de los capitanes de la guerra. La mente, y no el músculo, prima hoy en la lucha por la vida: pero
esta situación también está basada en la fuerza. El cambio ha sido cualitativo. Los magnates feudales
saqueaban el mundo a sangre y fuego; los magnates financieros explotan al mundo, aplicando las fuerzas
económicas. La mente y no el músculo es lo que perdura, y los intelectual y comercialmente poderosos son los
más aptos para sobrevivir.
Nosotros, los Sicarios de Midas, no nos resignamos a ser esclavos a sueldo. Los grandes trusts y combinaciones
de negocios (entre los que sobresale el que usted dirige) nos impiden levantarnos al lugar que nuestra
inteligencia reclama. ¿Por qué? Porque no tenemos capital. Pertenecemos al bajo pueblo, pero con esta
diferencia: nuestras mentes están entre las mejores, Y no nos traban escrúpulos éticos o sociales. Como
esclavos a sueldo, trabajando de sol a sol, con vida sobria y avara no podríamos ahorrar en sesenta años —ni en
veinte veces sesenta años— una suma de dinero capaz de competir con las grandes masas de capital existentes
ahora. Sin embargo, entramos en la lucha. Arrojamos el guante al capital del mundo. Si éste acepta el desafío o
no, igual tendrá que luchar.
Señor Hale, nuestros intereses nos dictan exigir de usted veinte millones de dólares.
Ya que nosotros somos considerados y le otorgamos un plazo razonable para que lleve a cabo su parte de la
transacción, le rogamos que no se demore demasiado. Cuando usted se haya conformado con nuestras
condiciones, inserte un anuncio conveniente en el Morning Blazer. Entonces le comunicaremos nuestro plan para
transferir el capital.
Es mejor que usted lo haga antes del lº de octubre. Si no es así, para demostrarle que hablamos en serio,
mataremos a un hombre en esa fecha, en la calle Treinta y Nueve Este. Se tratará de un obrero, a quien ni usted
ni nosotros conoceremos. Usted representa una fuerza en la sociedad moderna y nosotros otra —una nueva
fuerza—. Sin odio entramos en combate. Usted es la muela superior en el molino, nosotros la inferior. La vida de
ese hombre será molida por las dos, pero podrá salvarse si usted acepta nuestras condiciones a tiempo.
Hubo una vez un rey maldito por el oro: su nombre está en nuestro sello oficial. Algún día, para protegernos de
competidores, lo haremos registrar.
Quedamos Ss. Ss. Ss.
Los Sicarios de Midas.
672 PALABRAS
Nombre:
Fecha:
Palabras por minuto.
99