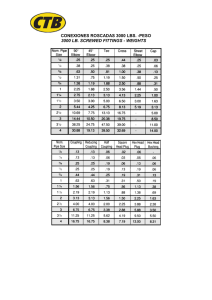
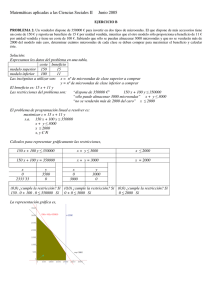
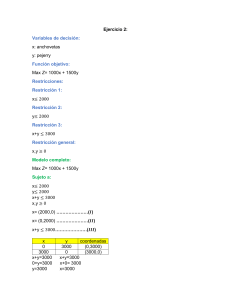
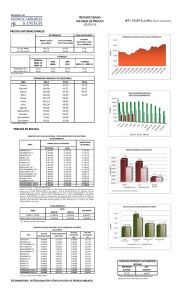
LOS INTERESES

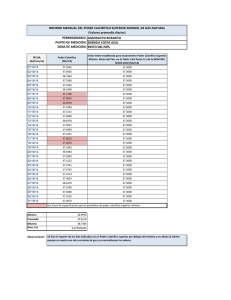
LOS INTERESES.
Interés simple e Interés compuesto
Situación problema -Los ahorros y las deudasEn la vida cotidiana las transacciones de dinero como cuentas de ahorro,
certificados de depósito a término, préstamos, compras a crédito, entre otras,
exige que las personas conozcan temáticas como interés, tasas de interés,
intereses, plazos, cuotas, para que cuando se requiera una de esas
transacciones, de acuerdo con las condiciones deseadas, la elección que se
haga sea la más favorable, y, en caso de asumir responsabilidades, éstas sean
perfectamente conocidas.
Con tu grupo de trabajo, busca dar respuestas a la siguiente situación.
María coloca en una cuenta de ahorros $100 000. La entidad bancaria ofrece
una tasa de interés del 3% mensual, que quiere decir que por cada $100
ahorrados se reciben $3 de interés. María acuerda retirar cada mes los
intereses obtenidos y dejará su dinero durante 6 meses, en la entidad.
a) ¿Cuánto dinero recibe María mensualmente?
b) ¿Cuánto recibe por este concepto durante los 6 meses?
c) María quiere, al final de los 6 meses, calcular en cuánto dinero se ha
convertido su capital ahorrado. ¿Cómo puede hacer este cálculo?
a) La tasa de interés que ofrece la entidad es 3%. Así $100 producen en un
mes:
$100 x 3% = 100 x 3 = $3
100
¿Cuánto recibe María de intereses por sus $100 000 en el primer mes?
¿Cómo procedes para hacer este cálculo?
b) Ya calculaste cuánto recibe María por concepto de intereses en un mes.
¿Cómo calculas el dinero que recibirá María en 6 meses?
c) ¿En cuánto estima María que se ha convertido su capital ahorrado? ¿Cómo
lo calculará?
Recuerda: María tenía inicialmente $100 000 y recibe intereses producidos en
los 6 meses que ha dejado su dinero en la entidad.
Compara tus respuestas con las obtenidas por tus compañeros(as).
Con tus compañeros(as) lee y analiza el siguiente texto:
INTERÉS SIMPLE E INTERÉS COMPUESTO
Las actividades comerciales se basan en el pago adicional de una cierta
cantidad de dinero por periodo o unidad de duración a la cual llamamos interés
por el uso del dinero, en algunos casos prestado, en otros depositado. La
mayor parte de los ingresos de bancos y entidades financieras provienen de los
intereses sobre préstamos, como los de vivienda, de compra de artículos, etc.
También las entidades como bancos o corporaciones reciben dinero de los
usuarios y por su uso pagan intereses, como en cuentas de ahorro o
certificados a término.
INTERÉS SIMPLE
Cuando el capital dado en préstamo o en ahorro es el único que gana interés,
se habla de interés simple. Es el caso del ahorro de María del problema que
resolviste inicialmente.
Al retirar los intereses mensuales esta suma no aumenta el capital inicial para
que, como un nuevo capital, produjera intereses también mayores.
Analicemos el desarrollo de la operación financiera de María, la cual nos dará
pistas para encontrar expresiones generales que puedan ser usadas en la
solución de problemas similares.
No. de periodos
(meses)
Capital al comienzo
de cada periodo
(capital que gana
intereses)
Intereses
producidos en cada
periodo (cada mes)
Capital al final de
cada periodo
100 000 = Co
100 000 × 0.03 =
3000 = I
100 000 = Co
100 000 × 0.03 =
3000 = I
100 000 = Co
100 000 × 0.03 =
3000 = I
100 000 = Co
100 000 × 0.03 =
3000 = I
100 000 = Co
100 000 × 0.03 =
3000 = I
100 000 = Co
100 000 × 0.03 =
3000 = I
C1 = 100 000 + 3 000
= 103 000
= Co + I
C1 = 103 000 + 3 000
= 106 000
= Co + I
C1 = 106 000 + 3 000
= 109 000
= Co + I
C1 = 109 000 + 3 000
= 112 000
= Co + I
C1 = 112 000 + 3 000
= 115 000
= Co + I
C1 = 115 000 + 3 000
= 118 000
= Co + I
1
2
3
4
5
6
Este análisis nos permite encontrar una expresión para el capital al final de un
número fijo de periodos n, que gana un interés I para ese periodo.
Cn = Co + n i
Pero debemos explicitar cómo calcular i, interés producido en cada periodo,
cuando conocemos Co y la tasa de interés ofrecida por periodo.
In = Co i
Cn = Co + n Co I = Co (1 + ni)
Comprueba si la expresión obtenida nos ayuda a calcular en cuánto se
convirtió el ahorro de María después de 6 meses.
C6 = Co (1 + 6 x3 )
100
C6 = 100 000 (1 + 6 x0.03)
= 100 000 (1 + 0.18)
= 100 000 (1.18) = 118 000
Compara con el valor de C6 , en la tabla y con el valor que obtuviste en c) del
problema inicial.
INTERÉS COMPUESTO
¿Qué ocurre si los intereses producidos en cada periodo no se retiran, sino que
éstos van aumentando el capital inicial y sobre éste se calculan los intereses en
el siguiente periodo de tiempo?
En este caso se dice que los intereses se capitalizan, y que la operación
financiera es a
Interés compuesto.
Veamos, en nuestro ejemplo, cuando María decide capitalizar los intereses, es
decir no los retira durante los meses en que va a ahorrar.
No. de
meses
Capital al comienzo
de cada mes
Intereses producidos
en cada mes
Capital al final de cada mes
100 000
Co
103 000
C 1 = Co (1 + i)
106 050
C2 = Co (1 + i)2
100 000 0.03 = 3 000
I1 = Co i
103 000 0.03 = 3 090
I2 = Co (1 + i) i
106 090 0.03 = 3 182.70
I3 = Co (1 + i)2 i
109 272.70 0.03 = 3
278.18
I4 = Co (1 + i)3 i
112 550.88 0.03 = 3
376.52
I5 = Co (1 + i)4 i
115 927.40 0.03 = 3
477.82
I 6=Co (1 + i)5 i
100 000 + 3 000 = 103 000
C1 = Co (1 + i)
103 000 + 3 090 = 106 090
C2 = Co (1 + i)2
106 090 + 3 182.70 = 109 272.70
C3 = Co (1 + i)3
109 272.70 + 3 278.18 = 112 550.88
C4 = Co (1 + i)4
109 272.70
C3 = Co (1 + i)3
112 550.88
C4 = Co (1 + i)4
115 927.40
C5 = Co (1 + i)5
112 550.88 + 3 376.52 = 115 927.40
C5 = Co (1 + i)5
115 927.40 + 3 477.82 = 119 415.22
C6 = Co (1 + i)6
Las expresiones que permiten calcular los intereses y el capital en un periodo
cualquiera n son:
In = Co (1 + i)n – 1. I
Cn = Co (1 + i)n
Compara, para el ejemplo que hemos desarrollado, los intereses simples y los
intereses compuestos que produjera el dinero de María colocado en una u otra
opción de ahorro.
¿Qué opinas? Discútelo con tus compañeros(as) y el profesor.
Con tu equipo, resuelve el siguiente problema:
Una persona solicita a una entidad un préstamo de $500 000, por tres meses.
Ofrece una tasa de 3.5% mensual.
¿Cuánto dinero cancelará la persona por el préstamo si:
a) Le cobran interés simple durante los tres meses?
b) Le cobran interés compuesto, durante los tres meses?
Compara tus respuestas con las que encuentren tus compañeros(as).
Trabaja individualmente, en tu cuaderno.
Un certificado a término ofrece una tasa de 2.4% mensual.
¿En cuánto se convierte un capital de $2 000 000 colocados por tres meses si
no se retiran los intereses cada mes?