Álgebra de Boole Automatismos cableados Introducción

Automatización Industrial
Algebra de Boole/Automatismos cableados
Álgebra de Boole
Automatismos cableados
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 1
Automatización Industrial
Algebra de Boole/Automatismos cableados
Introducción
•
•
•
•
•
Se ha modelado la realidad como 0’s y 1’s
La salida es una función de las entradas
¿Cómo se forma la función?
– Álgebra de Boole
¿Cómo se simplifica?
– Álgebra de Boole
¿Cómo se implanta?
– Depende de la tecnología elegida
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 2
1
Automatización Industrial
Algebra de Boole/Automatismos cableados
Algebra de Boole
•
•
Un álgebra está definida por:
– Un conjunto de elementos Κ
– Un conjunto de operaciones Φ que actúan sobre los miembros de
Κ y que cumplen unas ciertas propiedades
El Algebra de Boole (caso más simple) se define por:
– Un conjunto B con sólo dos elementos {0,1}
– Un conjunto de operaciones (lógicas) {+,·,’} definidas sobre B
• 2 operaciones binarias (f(x,y)):
– (+) función suma, función O, función OR
– (·) función multiplicación, función Y, función AND
• 1 operación monaria (f(x)):
– (‘ ó ¯) función negación, función NO, función NOT
– tales que para x,y,z ∈ B se cumplen las siguientes propiedades:
• Postulados de Huntington
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 3
Automatización Industrial
Algebra de Boole/Automatismos cableados
Postulados (axiomas) de Huntington
•
•
•
•
•
•
Conjunto cerrado:
– x·y ∈ B, x+y ∈ B, x’ ∈ B
Ley conmutativa:
– x+y=y+x
– x·y=y·x
Ley asociativa:
– (x+y)+z=x+(y+z)
– (x·y)·z=x·(y·z)
Ley distributiva:
– (x+y)·z=x·z+y·z
– x+y·z=(x+y)·(x+z)
Complemento
– x+x’=1
– x·x’=0
•
En la siguiente transparencia
se definen las operaciones
básicas. Todas ellas cumplen
los postulados de
Huntington. Puede haber otra
definición que también los
cumpla.
Identidad:
– x+0=x
– x·1=x
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 4
2
Automatización Industrial
Algebra de Boole/Automatismos cableados
Definición operaciones básicas/tablas de verdad
•
Función suma lógica, O o OR
a
b
•
c = a+b
b
0
1
0
1
a+b
0
1
1
1
a
0
0
1
1
b
0
1
0
1
a·b
0
0
0
1
a
0
1
a’
1
0
¡¡ 1 + 1 = 1 !!
– Para activar la salida, a o b
tienen que estar activas
Función producto lógico, Y o
AND
a
b
•
a
0
0
1
1
c = a·b
– Para activar la salida, a y b
tienen que estar activas
Función complemento, NO o
NOT
a
b = a’
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 5
Automatización Industrial
Algebra de Boole/Automatismos cableados
Variables, expresiones lógicas, tablas de verdad
•
•
Variable lógica (booleana)
– Variable perteneciente a B
– Por tanto, sólo puede tener dos
valores: 0 y 1
Expresión (función) lógica
(booleana)
– Combinación de variables lógicas
pertenecientes a B y de operaciones
lógicas (+ paréntesis):
•
• f = xy+xy’z+x’yz (· implícito)
• Tabla de verdad equivalente a la
anterior.
• Formas estándar de representación:
– Producto de sumas
– Suma de productos
Tabla de verdad (con todas las
posibilidades) y expresión lógica
son equivalentes entre sí.
Prof. José A. Rodríguez Mondéjar
x
y
z
f
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
A una misma tabla de la verdad
le corresponden varias expresiones
lógicas
UPCO ICAI Departamento de Electrónica y Automática 6
3
Automatización Industrial
Algebra de Boole/Automatismos cableados
Equivalencia entre expresiones
•
Dos expresiones son equivalentes si sus tablas de verdad
son iguales
a
b
c
a+b·c
(a+b)(a+c)
– f1 = a+bc
– f2 = (a+b)(a+c)
•
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
1
1
1
0
0
1
1
1
0
1
1
1
1
1
0
1
1
1
1
1
1
1
O si se puede llegar de la una a la otra (ambas direcciones)
– f2=(a+b)(a+c)=aa+ac+ba+bc=a+ac+ba+bc=a(1+c+b)+bc=a+bc
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 7
Automatización Industrial
Algebra de Boole/Automatismos cableados
Convertir tabla de verdad en expresión lógica I
x
y
z
f
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
f=x’yz’+x’yz+xy’z+xyz’+xyz
Prof. José A. Rodríguez Mondéjar
•
•
•
•
•
Forma canónica con minterm:
1. Tómese cada combinación
que dé 1 a la salida y fórmese
un producto de variables, de
forma que si una variable vale
0 en aquella fila se coloca su
complemento y si vale 1 se
coloca la variable sin
complementar.
2. Escríbase la función que
resulta de sumar todos los
productos.
f=x’yz’+x’yz+xy’z+xyz’+xyz
Hay muchas expresiones
equivalentes f=x’y+xy’z+xy
UPCO ICAI Departamento de Electrónica y Automática 8
4
Automatización Industrial
Algebra de Boole/Automatismos cableados
Convertir tabla de verdad en expresión lógica II
•
x
y
z
f
0
0
0
0
0
0
1
0
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
•
•
•
1. Tómese cada combinación
que dé 0 a la salida y fórmese
un producto de variables, de
forma que si una variable vale
0 en aquella fila se coloca su
complemento y si vale 1 se
coloca la variable sin
complementar.
2. Escríbase la función que
resulta de sumar todos los
productos, negando el valor
de la función.
f’=x’y’z’+x’y’z+xy’z’
Simplificada: f=(x’y’+xy’z’)’
f=(x’y’z’+x’y’z+xy’z’)’
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 9
Automatización Industrial
Algebra de Boole/Automatismos cableados
Más puertas
•
AND de tres o más entradas
f=abc
c
a
•
f=a+b+c+d
c = (a·b)’
OR exclusiva - XOR
(diferentes)
a
b
NOR
•
a
b
b
c=a’+b’
OR de tres o más entradas
b
c
d
•
NAND
a
a
b
•
•
c = (a+b)’
XNOR (coincidentes)
a
b
Prof. José A. Rodríguez Mondéjar
c=a⊕b
c = a’b + ab’
c = (a ⊕ b)’
c = ab + a’b’
UPCO ICAI Departamento de Electrónica y Automática 10
5
Automatización Industrial
Algebra de Boole/Automatismos cableados
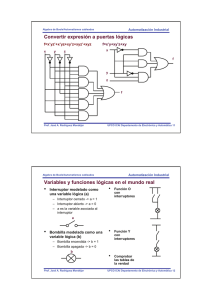
Convertir expresión a puertas lógicas
f=x’yz’+x’yz+xy’z+xyz’+xyz
x
y
f=x’y+xy’z+xy
x
z
f
y
z
f
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 11
Automatización Industrial
Algebra de Boole/Automatismos cableados
Variables y funciones lógicas en el mundo real
• Función O
• Interruptor modelado como
con
interruptores
una variable lógica (a)
– Interruptor cerrado -> a = 1
– Interruptor abierto -> a = 0
– a es la variable asociada al
interruptor
a
•
Bombilla modelada como una
variable lógica (b)
•
Función Y
con
interruptores
•
Comprobar
las tablas de
la verdad
– Bombilla encendida -> b = 1
– Bombilla apagada -> b = 0
b
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 12
6
Automatización Industrial
Algebra de Boole/Automatismos cableados
Función complemento
•
•
Se puede realizar la función
complemento de forma
mecánica: se dispone de la
variable complementada y sin
complementar
mecánicamente( contacto
abierto, contacto cerrado).
En muchos casos resulta
difícil con interruptores y sin
provocar cortocircuitos
realizar la función
complemento: manejar f1 y
f1’ en el mismo circuito,
donde f1’ se ha construido a
partir de f1. En estos casos
se necesitan relés (caso de
circuito eléctrico).
Prof. José A. Rodríguez Mondéjar
Físicamente es el mismo
pulsador: 2 contactos (NO y NC)
b
b
f2=b
a
f1=ab’
UPCO ICAI Departamento de Electrónica y Automática 13
Automatización Industrial
Algebra de Boole/Automatismos cableados
Lógica positiva/Lógica negativa
•
•
Si una variable lógica está a 1 significa que la acción o
estado asociado a dicha variable se está cumpliendo. Si es
0 indica que no se cumple.
– En electrónica 1 significa tensión positiva ( típico 5V) y 0 significa
tensión cero o tensión negativa.
– Interruptor abierto igual a 0.
– Interruptor cerrado igual a 1.
Lo anterior es una convención. Se puede cambiar 0 por 1.
– Lógica negativa: 1 - 0 voltios, 0 - 5 voltios.
– 1 - Interruptor abierto 0 - Interruptor cerrado. Típico para detectar
fallos de alimentación.
Alimentación
Planta
Prof. José A. Rodríguez Mondéjar
Unidad de
control
Bombilla alarma
UPCO ICAI Departamento de Electrónica y Automática 14
7
Automatización Industrial
Algebra de Boole/Automatismos cableados
Simplificación
•
•
•
Problema: Juan quiere
instalar 2 interruptores en su
habitación (a y b) para
encender una bombilla (f) de
tal forma que sólo se
encienda cuando:
a
a
a
b
– a y b están simultáneamente
cerrados.
– a está cerrado
Juan que es un lanzado hace
la instalación
Juan está muy contento
porque la instalación
funciona perfectamente hasta
que llega su amigo Antonio y
le pregunta para qué sirve el
interruptor b
Prof. José A. Rodríguez Mondéjar
a
b
f
0
0
0
0
1
0
1
0
1
1
1
1
f = ab + a = a(b+1) = a·1 = a
UPCO ICAI Departamento de Electrónica y Automática 15
Automatización Industrial
Algebra de Boole/Automatismos cableados
Propiedades útiles del Algebra de Boole
•
•
Idempotencia
•
– a+a=a
– a·a=a
Maximalidad del 1
– a+1=1
•
Minimalidad del 0
•
Involución
•
Leyes de Morgan
– a+ab=a
– a(a+b)=a
•
– a+0=a
– a’’=a
–
–
–
–
(a+b)’=a’b’
(ab)’=a’+b’
(a+b+c+...)’=a’b’c’...
(abc...)’=a’+b’+c’+...
Prof. José A. Rodríguez Mondéjar
Absorción
•
Todas estas propiedades se
comprueban mediante la
aplicación de las propiedades
del Algebra de Boole
(postulados de Hungtinton) o
recurriendo a las tablas de la
verdad (en todos los casos
posibles se cumple la
igualdad).
Permiten simplificar
fácilmente.
UPCO ICAI Departamento de Electrónica y Automática 16
8
Automatización Industrial
Algebra de Boole/Automatismos cableados
Simplificando
•
•
f=x’yz’+x’yz+xy’z+xyz’+xyz
–
–
–
–
Asociativa y distributiva: f=x’y(z’+z)+xy’z+xy(z’+z)
Complemento: f=x’y+xy’z+xy
Complemento: f=y(x’+x)+xy’z
f=y+xy’z
f=(x’y’z’+x’y’z+xy’z’)’
–
–
–
–
Asociativa y distributiva: f=(x’y’(z’+z)+xy’z’)’
Complemento: f=(x’y’+xy’z’)’
Leyes de Morgan: f=(x’y’)’(xy’z’)’
Leyes de Morgan: f=(x+y)(x’+y+z)
–
–
–
–
f=xx’+xy+xz+yx’+yy+yz
f=xz+y+xy+yx’+yz
f=xz+y(1+x+x’+z)
f=xz+y Es equivalente a la de arriba (ver tabla de la verdad)
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 17
Automatización Industrial
Algebra de Boole/Automatismos cableados
Implantaciones alternativas de f
A
F = A' B C + A B' C' + A B' C + A B C' + A B C
B
F1
C
Suma de productos canónica
F2
Prof. José A. Rodríguez Mondéjar
Suma de productos minimizada
F3
Producto de sumas canónica
F4
Producto de sumas minimizado
UPCO ICAI Departamento de Electrónica y Automática 18
9
Automatización Industrial
Algebra de Boole/Automatismos cableados
Simplificación mediante el método de Karnaugh
•
Hay muchos métodos para simplificar (aplicando
directamente los postulados del Algebra)
Programas de simplificación automática
El método de Karnaugh es un método gráfico muy útil para
funciones de 2 a 4 variables lógicas.
•
•
– Se basa en buscar términos adyacentes en la tabla de la verdad.
– Los términos adyacentes son aquellos que tienen las mismas
variables con el mismo estado de complemento, excepto una.
• xyz’ y xyz son adyacentes
– Los términos adyacentes se pueden simplificar fácilmente
• xyz’+xyz = xy(z’+z) = xy
– Para buscar fácilmente los términos adyacentes se dispone la tabla
de la verdad de tal forma que los valores de las variables de
entrada vecinos resulten adyacentes. Esta tabla recibe el nombre
de tabla o mapa de Karnaugh.
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 19
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplos de simplificación por Karnaugh I
•
•
•
•
•
Construir el mapa de Karnaugh.
Colocar los ceros y unos de la tabla
de verdad sobre el mapa de
Karnaugh.
Formar grupos (paralelogramos)
con las casillas que tienen 1, de tal
forma que contengan el máximo
número de elementos y éste sea
potencia de 2.
Casillas de un grupo pueden formar
parte de otro.
Cada grupo representa un producto.
Éste está formado por las variables
que no cambian de valor en dicho
grupo. Si está a 1 la variable se
escribe tal cual, y si está a 0, se
complementa.
Prof. José A. Rodríguez Mondéjar
b
0
1
0
0
1
1
0
1
a
f=b
adyacente
yz
00
01
11
10
0
0
0
1
1
1
0
1
1
1
x
f = y + xz
UPCO ICAI Departamento de Electrónica y Automática 20
10
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplos de simplificación por Karnaugh II
AB
00
CD
01
11
10
00
1
0
0
1
01
0
1
0
0
11
1
1
1
1
10
1
1
1
1
f = c + d’b’ + a’bd
Adyacentes
f = a’b’cd + a’bcd+ab’cd+
AB
00
CD
01
11
10
00
0
0
1
0
01
0
0
1
0
11
1
1
0
1
10
0
0
1
0
+abc’d’+abc’d+abcd’
f =abc’+abd’+cda’+cdb’
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 21
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplos de simplificación por Karnaugh III
•
•
Don’t care: combinación de
entradas que nunca se dan.
Pueden ser utilizadas para
simplificar las funciones
lógicas: se toma su valor como
1 o como 0, en función de lo
que más interese.
AB
00
CD
01
11
10
00
1
0
1
1
01
0
1
1
1
11
X
X
X
X
10
1
1
X
X
f = a + c + b’d’ + bd
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 22
11
Automatización Industrial
Algebra de Boole/Automatismos cableados
Funciones lógicas y tiempo
•
•
•
Si las entradas de la función lógica varían en el tiempo, la
función lógica también varía.
Al variar la entrada, la salida tardará un cierto tiempo en
cambiar, dependiendo de la tecnología.
Retardo de la función lógica: tiempo que media entre el
cambio en la entrada de la función y el cambio en el valor
de dicha función. Dependerá del tipo de cambio.
a
b
a
f=a+b
b
f = a+b
t
retardo1
Prof. José A. Rodríguez Mondéjar
retardo2
UPCO ICAI Departamento de Electrónica y Automática 23
Automatización Industrial
Algebra de Boole/Automatismos cableados
Relés y contactos
• Relé: todo dispositivo que utilizando,
•
•
I
R
S
T
ya sea un impulso eléctrico que le es
Esquema de
enviado a distancia, o la acción de
conexión
otros fenómenos ajenos (como
presión, temperatura, etc) actúa de
modo automático como interruptor,
accionando o desconectando un
Ecuación
M=I
M
circuito.
lógica
De modo manual o automático retorna
a su posición inicial, una vez
terminada la acción del impulso del
Esquema
Variable
accionador; a esta operación se le
eléctrico /
I
de
entrada
llama rearme o desbloqueo.
Esquema de
relés
Clasificación:
Variable
M
– Relés:gobiernan circuitos de baja
de salida
potencia.
Esquema
M
– Contactores: circuitos de alta
I
de contactos
potencia.
(PLC)
Contacto
Bobina
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 24
12
Automatización Industrial
Algebra de Boole/Automatismos cableados
Relé con más detalle
R
S
A
I
Ecuación Lógica
24VDC
T
P
24VDC
M=I
A=I
P = I’
Esquema de
Contactos (PLC)
I
Esquema
General de
conexiones
M
I
M
Esquema Eléctrico (Esquema de relés)
Esquema R S T
Esquema
de
de Mando
I
Potencia
A
KM
P
KM
P
Prof. José A. Rodríguez Mondéjar
A
M
UPCO ICAI Departamento de Electrónica y Automática 25
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplo de circuito de mando y de potencia real
Relé de
máxima
corriente
Contacto
temporizado.
Evita que el pico
de intensidad en
el arranque abra
el circuito
Relé de
protección
térmica
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 26
13
Automatización Industrial
Algebra de Boole/Automatismos cableados
Tipos de relés y estructura
•
•
•
Clasificación según
tecnología:
–
–
–
–
Electromagnéticos
Neumáticos
Térmicos
Electrónicos
Clasificación según misión:
– Instantáneos
– Temporizados
•
Partes de un relé (contactor)
– Contactos principales
• Cierre o apertura del circuito
principal.
– Contactos auxiliares
• Gobierno del contactor y su
señalización.
– Circuito electromagnético
– Sistema de soplado
• Apaga el arco al abrir el
circuito. Aunque se separen los
contactos, la corriente sigue
pasando a través del aire
ionizado, cuando la carga es
inductiva. Esto aumenta la
resistencia y por tanto el calor
originado, que puede dañar los
contactos.
En automatismos industriales
tienen dos funciones:
– Separación galvánica.
– Elemento de memoria (se
contará más adelante)
– Soporte o estructura del
aparato.
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 27
Automatización Industrial
Algebra de Boole/Automatismos cableados
Circuito electromagnético de un relé
•
•
Puede trabajar en continua o
en alterna.
Estructura:
BOBINA
Contactos
moviles
– Núcleo
• Chapa magnética aislada
– Armadura
• Chapa magnética aislada
NUCLEO
– Bobina
•
• En alterna se coloca una
espira de sombra para evitar la
vibración por los pasos por 0
de la corriente alterna.
Los contactos pueden estar
normalmente abiertos o
normalmente cerrados.
Permite realizar la operación
complemento fácilmente.
Prof. José A. Rodríguez Mondéjar
ARMADURA Contactos
fijos
UPCO ICAI Departamento de Electrónica y Automática 28
14
Automatización Industrial
Algebra de Boole/Automatismos cableados
Usos del relé
•
Aislamiento galvánico
– Circuito de bobina y circuito de los contactos son independientes
•
• Suficiente rigidez eléctrica
Amplificador
– Señal en potencia: Contactor
• Ejemplo: Con 24V manejar 380 voltios trifásicos
– Repetidor lógico
•
• Utilizar la misma variable lógica en diferentes circuitos eléctricos.
Memoria de 1 bit
– Muy utilizado en el pasado
– Relegado actualmente a esquemas sencillos de marcha/paro.
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 29
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplo combinacional con contactos y bobinas
f = a + bc
Esquema eléctrico
Esquema de contactos
a
b
f
a
b
K
c
c
K
Prof. José A. Rodríguez Mondéjar
f
UPCO ICAI Departamento de Electrónica y Automática 30
15
Automatización Industrial
Algebra de Boole/Automatismos cableados
Pulsadores, interruptores y contactos.
•
•
•
Pulsadores sólo se mantiene
la acción mientras se pulsa.
Interruptores: la acción se
mantiene después de
conmutar.
Contactos: mecánicamente
acoplado al pulsador/
interruptor se pueden colocar
contactos que cambian al
cambiar el estado del
pulsador/interruptor.
– Normalmente abierto.
– Normalmente cerrado
IEC 1082
Pulsador
Contacto normalmente
abierto NO
Contacto normalmente
cerrado NC
Muelle
IEC 1082
Interruptor
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 31
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplo combinacional con contactos y bobinas II
f = ab + a’c+b’d
Esquema de contactos
a
b
a
c
b
d
Esquema de eléctrico
Esquema de Conexiones
f
a
a
a
b
b
c
d
d
c
f
Prof. José A. Rodríguez Mondéjar
f
b
f
UPCO ICAI Departamento de Electrónica y Automática 32
16
Automatización Industrial
Algebra de Boole/Automatismos cableados
Variables negadas con interruptores
•
Una variable asociada a un interruptor no puede ser 0 y 1
simultáneamente, si no es un doble interruptor con un
contacto normalmente abierto y otro normalmente cerrado
a
Conmutador
Esquema
eléctrico
a’
a
y
y
x
z
f=yx+y’z
f
a
a’
a
y
x
y
z
Esquema de contactos
f
a’
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 33
Automatización Industrial
Algebra de Boole/Automatismos cableados
Funciones lógicas y la práctica
•
Una función lógica de más de 4 variables es común en la práctica
– Ir por la tabla de la verdad y obtener la función lógica es inviable.
•
• Imposible de aplicar Karnaugh.
• Hay programas para simplificar (orientados al diseño digital).
Solución práctica
– Obtener directamente desde la especificación del problema una función
lógica representativa que, por supuesto, no será la óptima
– Refleja directamente el funcionamiento del sistema
•
• A veces, aplicando Karnaugh aparecen expresiones que son difíciles de
interpretar desde el punto vista del sistema a controlar
Problema de escribir la función lógica directamente
– ¿Habré contemplado todos los casos?
• Ejemplo: Poner en marcha un motor cuando no se debe
– Muy grave si hay un obrero manipulándolo
•
– Con la tabla no había problemas porque se contemplaban todos los
posibles valores de las entradas
Solución:
– Intentar prevenir que la función tome valor 1 en casos indeseados.
– ¿Cómo? Analizando y separando las condiciones de parada
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 34
17
Automatización Industrial
Algebra de Boole/Automatismos cableados
Escribir funciones lógicas de control en la práctica
•
Primero: Analizar las condiciones bajo las cuales no debe
funcionar el sistema (variable a controlar)
– Si ninguna de estas condiciones se cumple entonces es posible arrancar el
sistema
– Ejemplo:
•
• No arrancar el motor si está activado su relé térmico de temperatura
• No poner en marcha una bomba si no hay agua en su depósito
Segundo: Analizar las condiciones que hacen que el sistema
funcione (1 lógico) cuando no hay ninguna condición de parada
activa.
– Ejemplo:
•
• Interruptor de arranque
• Pieza en la posición correcta
Formato de la función lógica final:
f = CondiciónParada1’*CondiciónParada2’*...*(Condición Arranque1 +
+ CondiciónArranque2 + ...)
– Si no se cumple ninguna de las condiciones de parada y se cumple alguna de las
condiciones de arranque se pone en marcha el sistema
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 35
Automatización Industrial
Algebra de Boole/Automatismos cableados
Ejemplo
•
•
Una cinta trasportadora que
se pone en marcha al cerrar
el interruptor de arranque o
cuando recibe una orden de
arranque remota
– IA: Interruptor de arranque
– RA: señal remota de arranque
– M: señal arranque motor
La cinta no debe funcionar si
el motor tiene
sobrecalentamiento
– TM: contacto relé térmico
motor. Se abre el contacto
cuando hay sobrecalentamiento
Prof. José A. Rodríguez Mondéjar
M
M = TM(IA+RA)
UPCO ICAI Departamento de Electrónica y Automática 36
18
Automatización Industrial
Algebra de Boole/Automatismos cableados
Resumen automatismos combinacionales
•
•
•
•
Primero: Identificar las entradas de la planta:
– Variables a controlar: bomba, motor, piloto, etc.
– Salidas del control
Segundo: Identificar las salidas de la planta:
– Variables a partir de las cuales se construyen las funciones lógicas
que rigen las salidas
– Entradas del control
Tercero: Construir las funciones lógicas que rigen las
salidas del control a partir de las entradas del control
– Primero: las condiciones que hacen que la salida no se active.
(PRIMERO ASEGURAR LA PARADA)
– Segundo: las condiciones que hacen que la salida se active.
– Simplificarlas si es posible y no se pierde la legibilidad del control.
Cuarto: Implementar
– Lógica de relés, sistema digital, PLC
Prof. José A. Rodríguez Mondéjar
Algebra de Boole/Automatismos cableados
UPCO ICAI Departamento de Electrónica y Automática 37
Automatización Industrial
Más información
•
•
•
Telesquemario de Schneiderelectric: página web de la
asignatura: capítulos 6 y 7.
Automatismos y Cuadros eléctricos. Roldán Viloria.
Paraninfo 2001.
– Módulo 1: Aparellaje, esquemas de automatismos, esquemas de
alimentación.
– Módulo 3: Ejemplo completo.
Página web muy completa sobre automatismos:
– http://www.cnice.mecd.es/recursos/fp/cacel/CACEL1/menu_1.htm
Prof. José A. Rodríguez Mondéjar
UPCO ICAI Departamento de Electrónica y Automática 38
19