Modelos continuos: Características:

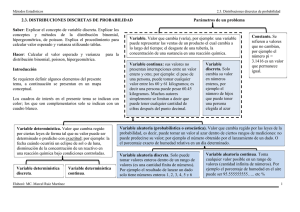
Modelos continuos:
Características:
X® Es una variable que puede tomar tanto valores enteros como fraccionarios.
X® 1.0, 3.7, 4.0, 4.6, 7.9, 8.0, 8.3, 11.5,....., ¥
Es generada por una variable continua (x).
La sumatoria de las probabilidades asociadas a cada uno de los valores que
toma x debe ser igual a 1. El área definida bajo la función de densidad de
probabilidad deberá ser de 1.
Modelos Discretos:
Características:
X toma solo valores enteros, X toma valores x1.........xk con probabilidad 1/k.
Se dice que X sigue una distribución uniforme discreta de parámetro k.
El suceso de eventos es independiente.
Modelo binomial:
Se utiliza cuando En cada prueba del experimento sólo son posibles dos
El resultado obtenido en cada prueba es independiente de los resultados
obtenidos anteriormente.
La probabilidad del suceso A es constante, la representamos por p, y no varía
es 1- p y la representamos por
q.
El experimento consta de un número n de pruebas.
Ejemplos de binomial:
1. En una sucesión de 30 años interesa la ocurrencia o no de un caudal mayor
que la capacidad de un vertedero, si las magnitudes del caudal son
independientes año tras año y la probabilidad de una ocurrencia no cambia a
través de los 30 años, suponiendo p = 0.02.
Solución
X: Número de años en los cuales ocurren grandes inundaciones, en la sucesión
de 30 años.
X = 0, 1, 2,.....30
Durante un año cualquiera pueden ocurrir ó no, grandes inundaciones
independientemente una de la otra, con probabilidad fija de 0.02.
Por lo tanto, X ~ B (n=30, P =0.02)
a. ¿Cuál es la probabilidad de que ocurra al menos una gran inundación
durante los 30 años, de un sistema propuesto de control de inundaciones?
b. Si se considera, muy grande el riesgo de tener al menos una gran
inundación, el ingeniero debe incrementar la capacidad de diseño, de modo
que la magnitud de la inundación crítica sea sólo excedida con la probabilidad
0,01 en un año cualquiera.
2. La probabilidad de éxito de una determinada vacuna es 0,72. Calcula la
probabilidad de a que una vez administrada a 15 pacientes:
a) Ninguno sufra la enfermedad
b) Todos sufran la enfermedad
c) Dos de ellos contraigan la enfermedad
Modelo de Poisson:
Características:
Características:
En este tipo de experimentos los éxitos buscados son expresados por unidad
de área, tiempo, pieza, etc., etc.,:
- # de defectos de una tela por m2
- # de aviones que aterrizan en un aeropuerto por día, hora, minuto, etc., etc.
- # de llamadas telefónicas a un conmutador por hora, minuto, etc., etc.
p( x , ) 
x 
x!
Donde:
p(x,) = probabilidad de que ocurran x éxitos, cuando el número promedio de
ocurrencia de ellos es 
 = media o promedio de éxitos por unidad de tiempo, área o producto
 = 2.718
x = variable que nos denota el número de éxitos que se desea que ocurra
Hay que hacer notar que en esta distribución el número de éxitos que ocurren
por unidad de tiempo, área o producto es totalmente al azar y que cada
intervalo de tiempo es independiente de otro intervalo dado, así como cada
área es independiente de otra área dada y cada producto es independiente de
otro producto dado.
Ejemplos de Poisson:
1.El número de clientes que llega a un banco es una variable aleatoria de
Poisson. Si el número promedio es de 120 por hora, ¿cuál es la probabilidad de
que en un minuto lleguen por lo menos tres clientes? ¿Puede esperarse que la
frecuencia de llegada de los clientes al banco sea constante en un día
cualquiera?
1. Una compañía compra cantidades muy grandes de componentes
electrónicos. La decisión para aceptar o rechazar un lote de componentes se
toma con base en una muestra aleatoria de 100 unidades. Si el lote se rechaza
al encontrar tres o más unidades defectuosas en la muestra, ¿cuál es la
probabilidad de rechazar un lote si éste contiene un 1 % de componentes
defectuosos? ¿Cuál es la probabilidad de rechazar un lote que contenga un 8%
de unidades defectuosas?