2.3. DISTRIBUCIONES DISCRETAS DE

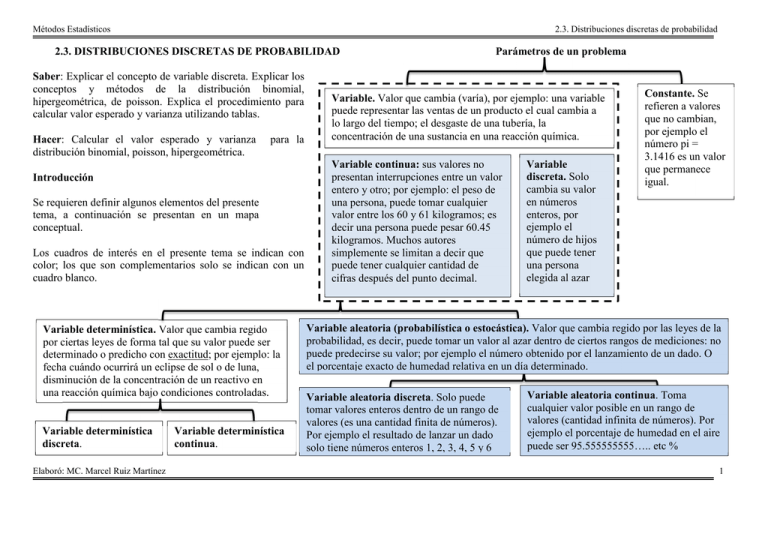
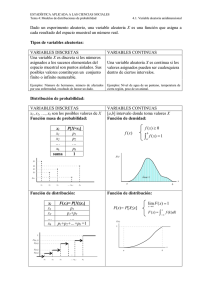
Métodos Estadísticos
2.3. Distribuciones discretas de probabilidad
2.3. DISTRIBUCIONES DISCRETAS DE PROBABILIDAD
Saber: Explicar el concepto de variable discreta. Explicar los
conceptos y métodos de la distribución binomial,
hipergeométrica, de poisson. Explica el procedimiento para
calcular valor esperado y varianza utilizando tablas.
Hacer: Calcular el valor esperado y varianza
distribución binomial, poisson, hipergeométrica.
para la
Introducción
Se requieren definir algunos elementos del presente
tema, a continuación se presentan en un mapa
conceptual.
Los cuadros de interés en el presente tema se indican con
color; los que son complementarios solo se indican con un
cuadro blanco.
Variable determinística. Valor que cambia regido
por ciertas leyes de forma tal que su valor puede ser
determinado o predicho con exactitud; por ejemplo: la
fecha cuándo ocurrirá un eclipse de sol o de luna,
disminución de la concentración de un reactivo en
una reacción química bajo condiciones controladas.
Variable determinística
discreta.
Elaboró: MC. Marcel Ruiz Martínez
Variable determinística
continua.
Parámetros de un problema
Variable. Valor que cambia (varía), por ejemplo: una variable
puede representar las ventas de un producto el cual cambia a
lo largo del tiempo; el desgaste de una tubería, la
concentración de una sustancia en una reacción química.
Variable continua: sus valores no
presentan interrupciones entre un valor
entero y otro; por ejemplo: el peso de
una persona, puede tomar cualquier
valor entre los 60 y 61 kilogramos; es
decir una persona puede pesar 60.45
kilogramos. Muchos autores
simplemente se limitan a decir que
puede tener cualquier cantidad de
cifras después del punto decimal.
Variable
discreta. Solo
cambia su valor
en números
enteros, por
ejemplo el
número de hijos
que puede tener
una persona
elegida al azar
Constante. Se
refieren a valores
que no cambian,
por ejemplo el
número pi =
3.1416 es un valor
que permanece
igual.
Variable aleatoria (probabilística o estocástica). Valor que cambia regido por las leyes de la
probabilidad, es decir, puede tomar un valor al azar dentro de ciertos rangos de mediciones: no
puede predecirse su valor; por ejemplo el número obtenido por el lanzamiento de un dado. O
el porcentaje exacto de humedad relativa en un día determinado.
Variable aleatoria discreta. Solo puede
tomar valores enteros dentro de un rango de
valores (es una cantidad finita de números).
Por ejemplo el resultado de lanzar un dado
solo tiene números enteros 1, 2, 3, 4, 5 y 6
Variable aleatoria continua. Toma
cualquier valor posible en un rango de
valores (cantidad infinita de números). Por
ejemplo el porcentaje de humedad en el aire
puede ser 95.555555555….. etc %
1
Métodos Estadísticos
La distribución binomial
Binomial indica solo dos resultados posibles de múltiples ensayos: éxito o
fracaso. El número total de ensayos se conoce como la población “n”. y se
debe conocer una probabilidad de éxito y de fracaso al realizar cada
ensayo.
Extraer un solo componente de una población y determinar si está o no
defectuoso es ejemplo de un ensayo de Bernoulli. En la práctica, es posible
extraer varios componentes de una gran población y contar el número de
elementos defectuosos. Esto implica realizar diversos ensayos de Bernoulli
independientes y contar el número de éxitos. El número de éxitos es una
variable aleatoria, que tiene una distribución binomial.
Es decir, para una población donde se extraen muestras con dos resultados
posibles, se puede aplicar la distribución de binomial bajo las condiciones
siguientes
•
Los ensayos son independientes
•
Cada ensayo tiene la misma probabilidad de éxito p
•
X es el número de éxitos en los n ensayos
La función de probabilidad binomial está dada por la siguiente función de
densidad:
Donde:
n = Número total de elementos de la población
x = Número de éxitos.
p = Probabilidad de éxito
A continuación se describe un ejemplo para la aplicación de la ecuación
descrita.
Elaboró: MC. Marcel Ruiz Martínez
2.3. Distribuciones discretas de probabilidad
Ejemplo 1. Se lanza al aire ocho veces un dado. Determine la probabilidad
de que el número 6 salga:
a) Cero veces.
b) Una vez
c) Dos veces
d) Menos de tres veces
Solución: Los datos para todos los incisos incluyen:
n = 8 (número total de veces que se lanza el dado)
p = 1/6 (probabilidad de que al realizar un lanzamiento se obtenga el
número 6, es decir el éxito).
Para el inciso a) Se usa la siguiente sustitución con x = 0 (no se obtiene
nunca el número 6 después de 8 lanzamientos).
n!
n -x
p(x) =
p x (1 - p )
x!(n − x )!
x
8!  1   1 
p(x = 0) =
  1 - 
0!(8 − 0 )!  6   6 
Datos:
x=
0
n=
8
p = 1/6
8 -0
= 0.2326
Usando EXCEL:
Usando la ecuación de la función BINOMIAL
0.232568039 RESULTADO INCISO A)
FORMULA
=(FACT(B3)/(FACT(B2)*FACT(B3-B2)))*(B4^B2)*(1-B4)^(B3-B2)
Usando la función BINOMIAL de EXCEL
0.232568039 RESULTADO INCISO A)
FORMULA:
=DISTR.BINOM(B2,B3,B4,FALSO)
El resto de los incisos serán resueltos por los alumnos. Puede
usar el siguiente archivo de EXCEL como apoyo
http://marcelrzmut.comxa.com/MetodosEstadisticos/23DistribucionesProbabilidadDiscretas.xls
2
Métodos Estadísticos
El siguiente problema será resuelto por los alumnos en clase.
Ejercicio. La probabilidad de que un basquetbolista anote un tiro de tres
puntos es 0.4. Si el jugador fue invitado a un concurso de tiros de tres
puntos en donde se hacen 15 lanzamientos. Determine la probabilidad de
encestar:
a) Cero veces.
b) Una vez
c) Dos veces
d) Menos de tres veces
e) Al menos 10 tiros
Problemas de probabilidad binomial:
1. Se toma una muestra de cinco elementos de una población grande
en la cual 10% de los elementos está defectuoso. Determine la
probabilidad de que:
a) Ninguno de los elementos de la muestra esté defectuoso.
b) Sólo uno de ellos tenga defectos.
c) Uno o más de los elementos estén defectuosos.
d) Menos de dos elementos de la muestra tenga defectos.
2. Se lanza al aire una moneda diez veces. ¿Cuál es la probabilidad de
obtener exactamente tres veces “cara”?
3. En un cargamento grande de llantas de automóvil, 5% tiene cierta
imperfección. Se eligen aleatoriamente cuatro llantas para
instalarlas en el automóvil. ¿ Cuál es la probabilidad de que:
a) Ninguna de las llantas tenga imperfección?
b) Sólo una de las llantas tenga imperfección?
c) Una o más de las llantas tenga imperfección?
Elaboró: MC. Marcel Ruiz Martínez
2.3. Distribuciones discretas de probabilidad
4. En un patrón aleatorio de ocho bits utilizado para probar un
microcircuito, cada bit tiene la misma probabilidad de ser 0 o 1.
Suponga que los valores de los bits son independientes.
a) ¿Cuál es la probabilidad de que todos los bits sean 1?
b) ¿Cuál es la probabilidad de que exactamente tres de los bits
sean 1?
c) ¿Cuál es la probabilidad de que al menos seis de los bits
sean 1?
d) ¿Cuál es la probabilidad de que al menos dos de los bits
sean 1?
5. Un ingeniero que supervisa el control de calidad de un proceso de
producción y sabe que el 92% de las varillas fabricadas satisfacen
las especificaciones. Al seleccionar 15 varillas del proceso de
producción determine la probabilidad de obtener:
a) 15 varillas que cumplen con las especificaciones.
b) 14 varillas que cumplen con las especificaciones
c) 13 varillas que cumplen con las especificaciones
d) Que más de 12 varillas cumplan las especificaciones.
Actividad 2.3. Probabilidad Binomial. De la lista de problemas
anteriores realice los ejercicios: 1 y 4.
Elabore una PRÁCTICA DE EJERCICIOS de este trabajo (INDIVIDUAL), las
rúbricas se indican en la liga siguiente:
http://marcelrzm.comxa.com/Rubricas/Rubricas.htm
Enviar el documento final por correo electrónico a las siguientes direcciones:
[email protected]; [email protected]; [email protected]
y [email protected]
Colocar en ASUNTO: Actividad 2.3. Probabilidad Binomial.
No olvide enviarse copia a sí mismo del correo que envía, si usa Outlook solicite
confirmación de entrega y de lectura.
3
Métodos Estadísticos
2.3. Distribuciones discretas de probabilidad
La distribución hipergeométrica
Para una combinación se usa la fórmula:
Cuando una población finita contiene dos tipos de unidades, que pueden
ser denominados como éxitos y fracasos, y se extrae una muestra aleatoria
simple de la población, cada unidad representa un ensayo de Bernoulli. A
medida que se selecciona cada unidad, la proporción de éxitos en la
población restante disminuye o aumenta, dependiendo si la unidad extraída
es un éxito o fracaso. Por esta razón, los ensayos no son independientes, de
ahí que el número de éxitos en la muestra no siga una distribución
binomial. En su lugar, la distribución que describe adecuadamente el
número de éxitos en esta situación se llama distribución hipergeométrica.
Suponga una población finita que contiene N unidades, de ellas R son
clasificadas como éxitos y N − R como fracasos. Suponga que se extrae n
unidades de esta población, y sea X el número de éxitos en la muestra.
Entonces X sigue la distribución hipergeométrica con los parámetros N, R
y n, que se puede denotar como X ∼ H(N, R, n).
La función de masa de probabilidad de X es:
Donde (el alumno debe rellenar el significado de las variables):
R=
N=
n=
x=
Elaboró: MC. Marcel Ruiz Martínez
Ejemplo 1. De 50 edificios en un parque industrial, 12 no cumplen el
código eléctrico. Si se seleccionan aleatoriamente diez edificios para
inspeccionarlos, Determine la probabilidad de que:
a) Tres no cumplan el código
b) Cuatro no cumplan el código
c) Menos de cinco no cumplan el código
Datos: Los siguientes datos son genéricos para todos los incisos, ya que
sus valores se encuentran en el texto del problema:
N = 50 Número de elementos en la población total
n = 10 Número de elementos en la muestra tomada
R = 12 Dado que estamos interesados en la cantidad de elementos que no
cumplen el código, se denomina éxito encontrar elementos que no
cumplan el código.
Solución inciso A: x = 3 (tres no cumplan el código, es el valor indicado
solo para el inciso A)
 R  N − R 
 

x  n − x 

p(x) =
 N
 
n
12  50 − 12   12!  

(50 - 12)!
 
 


3  10 − 3   3!(12 - 3)!  (10 - 3)!(50 - 12 - (10 - 3) )!

p(x = 3) =
=
 50 


50!
 


10!(50 - 10 )!
 10 
p(x = 3) = 0.2703 o 27.03%
4
Métodos Estadísticos
Usando EXCEL:
Datos
N = 50
n = 10
R = 12
x=
3
Población total
Muestra tomada
Número de éxitos en la población
Número de éxitos en la muestra
RESPUESTA INCISO A) USANDO LA FUNCIÓN
DE DISTRIBUCIÓN HIPERGEOMÉTRICA DE EXCEL
0.27028633
2.3. Distribuciones discretas de probabilidad
El siguiente ejercicio deberá ser resuelto por los alumnos en clase:
Ejercicio: Lotes de 40 componentes cada uno se denominan aceptables si
no contienen más de tres defectuosos. El procedimiento para muestrear el
lote es la selección de cinco componentes al azar y rechazar el lote si se
encuentra un componente defectuoso. ¿Cuál es la probabilidad de que se
encuentre exactamente un defectuoso en la muestra si hay tres defectuosos
en todo el lote?
A continuación se reporta la ayuda de EXCEL para dicha función:
Elaboró: MC. Marcel Ruiz Martínez
5
Métodos Estadísticos
La distribución de Poisson
La distribución de Poisson se utiliza con frecuencia en el trabajo científico.
Una manera de considerarla es como una aproximación de la distribución
binomial cuando n es grande y p es pequeña. Esto último se muestra con
un ejemplo.
Una masa contiene 10 000 átomos de una sustancia radiactiva. La
probabilidad de que cierto átomo decaiga en un periodo de un minuto es de
0.0002. Sea X el número de átomos que decae en un minuto. Se puede
considerar a cada átomo como un ensayo de Bernoulli, en los que el éxito
ocurre si el átomo decae. Por tanto, X es el número de éxitos en 10 000
ensayos de Bernoulli independientes, cada uno con probabilidad de éxito
de 0.0002, de tal forma que la distribución de X es Bin(10 000, 0.0002).
La media de X es µX = (10 000)(0.0002) = 2.
Si X ∼ Poisson(λ), entonces
• X es una variable aleatoria discreta, cuyos posibles valores son
enteros no negativos.
• El parámetro λ es una constante positiva.
• La función de masa de probabilidad de X es
2.3. Distribuciones discretas de probabilidad
Ejemplo 1. Unas partículas están suspendidas en un medio líquido con
concentración de seis partículas por mL. Se agita por completo un
volumen grande de la suspensión, y después se extrae 3 mL. ¿Cuál es la
probabilidad de que sólo se retiren 15 partículas?
Solución: Los datos son los siguientes:
λ = (6 particulas / mL) * (3 mL) = 18 particulas
x = 15 partículas
λx
p(x) = e −λ
x!
15
−18 18
p(x = 15) = e
= 0.0786
15!
Ahora usando EXCEL:
Lamda 18 particulas
x=
15 particulas
p ( x = 15 ) = 0.07857552 RESPUESTA
=POISSON(C3,C2,FALSO)
Como puede notarse lo único que debe cuidarse es identificar el promedio
LAMDA y la cantidad “x” a estudiar. El valor de “x” debe estar en
números enteros dado que es una variable aleatoria discreta.
A continuación se muestra la información de ayuda de EXCEL sobre dicha
función:
Elaboró: MC. Marcel Ruiz Martínez
6
Métodos Estadísticos
2.3. Distribuciones discretas de probabilidad
Ejemplo 2. La abuela hornea galletas de chispas de chocolates en grupos
de 100. Ella agrega 300 chispas en la masa. Cuando las galletas están
hechas, le ofrece una. Determine:
a) ¿Cuál es la probabilidad de que su galleta no tenga chispas de
chocolate?
b) ¿Cuál es la probabilidad de que la galleta tenga 1 chispa?
c) ¿Cuál es la probablidad de que la galleta tenga mas de 2 chispas?
d) ¿Cuál es la probabilidad de que la galleta tenga menos de 3
chispas?
λ=
El alumno debe identificar el promedio de chispas de
chocolate esperado para una galleta.
x = ________
El alumno debe identificar cual es el número de chispas
de chocolate para el cual se desea identificar la probabilidad.
Usando la distribución poisson se debe llegar a la respuesta (para el inciso
A es: 0.0498)
λx
p(x) = e − λ
x!
EL SIGUIENTE EJEMPLO TAMBIEN DEBE SER RESUELTO
POR EL ALUMNO.
Ejemplo 3. Suponga que el número de visitas a cierto sitio web durante un
intervalo fijo sigue una distribución de Poisson. Suponga que la media de
la razón de visitas es de cinco en cada minuto. Determine la probabilidad
de que haya sólo:
a) 17 visitas en los siguientes tres minutos.
b) Menos de 15 visitas
c) Más de 5 visitas.
d) Igual o más de 5 visitas
Elaboró: MC. Marcel Ruiz Martínez
7
Métodos Estadísticos
Problemas de la distribución poisson:
1. La concentración de partículas en una suspensión es 2 mL. Se agita
por completo la concentración, y posteriormente se extraen 3 mL.
Sea X el número de partículas que son retiradas. Determine
a) P(X =5)
b) P(X ≤2)
c) P(X >1)
d) P(X<3)
2. Suponga que 0.03% de los contenedores plásticos producidos en
cierto proceso tiene pequeños agujeros que los dejan inservibles. X
representa el número de contenedores en una muestra aleatoria de
10 000 que tienen este defecto. Determine
a) P(X = 3)
b) P(X ≤ 2)
c) P(1 ≤ X <4)
d) P(2 ≤ X <4)
3. El número de mensajes recibidos por el tablero computado de
anuncios es una variable aleatoria de Poisson con una razón media
de ocho mensajes por hora. Determine la probabilidad de que se
reciban:
a) cinco mensajes en una hora
b) diez mensajes en 1.5 horas
c) menos de tres mensajes en 112 horas
TIP: Debe pasarse la media de 8 mensajes/hora a el promedio
de mensajes recibidos en 1.5 horas y en 112 horas; para usarlos
en la ecuación de la distribución poisson.
Elaboró: MC. Marcel Ruiz Martínez
2.3. Distribuciones discretas de probabilidad
4. Cierto tipo de tablero de circuitos contiene 300 diodos. Cada uno
tiene una probabilidad p = 0.002 de fallar.
a) ¿Cuál es la media del número de diodos que falla?
b) ¿Cuál es la probabilidad de que fallen exactamente dos diodos?
c) Un tablero funciona si ninguno de sus diodos falla. ¿Cuál es la
probabilidad de que funcione un tablero?
d) Se envían cinco tableros a un cliente. ¿Cuál es la probabilidad
de que cuatro o más de ellos funcione?
Actividad 2.4. Probabilidad Poisson. De la lista de problemas anteriores
realice los ejercicios: 1 y 2.
Elabore una PRÁCTICA DE EJERCICIOS de este trabajo (INDIVIDUAL), las
rúbricas se indican en la liga siguiente:
http://marcelrzm.comxa.com/Rubricas/Rubricas.htm
Enviar el documento final por correo electrónico a las siguientes direcciones:
[email protected]; [email protected]; [email protected]
y [email protected]
Colocar en ASUNTO: Actividad 2.4. Probabilidad Poisson.
No olvide enviarse copia a sí mismo del correo que envía, si usa Outlook solicite
confirmación de entrega y de lectura.
8