Capítulo 12 - Departamento de Ingeniería Metalúrgica

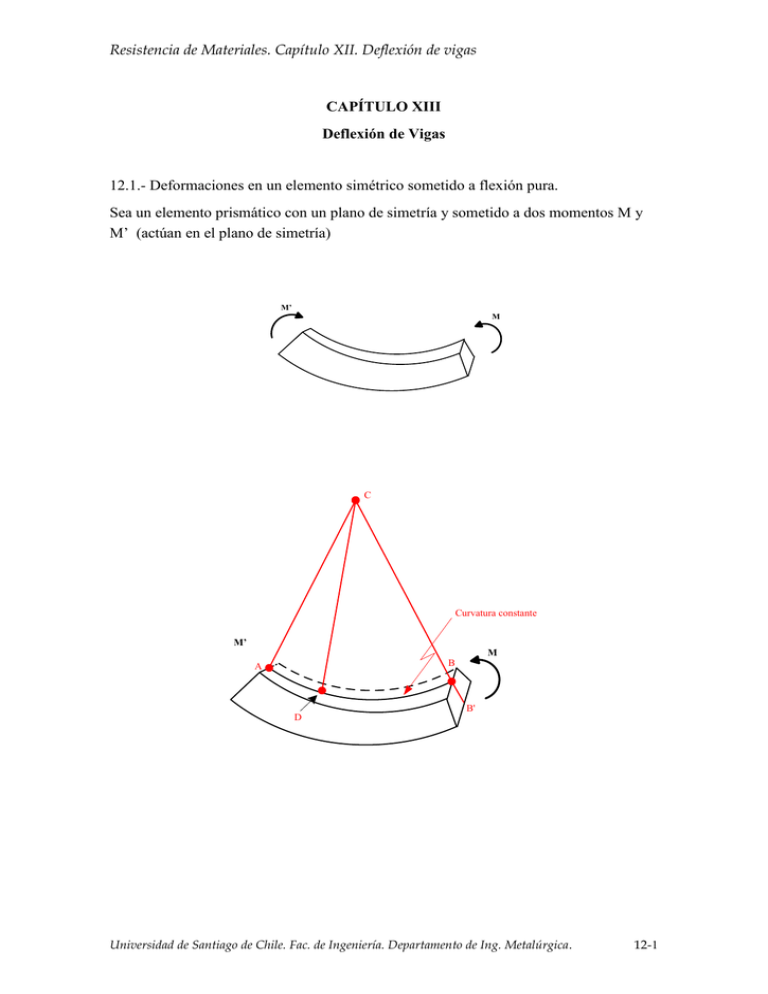
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
CAPÍTULO XIII
Deflexión de Vigas
12.1.- Deformaciones en un elemento simétrico sometido a flexión pura.
Sea un elemento prismático con un plano de simetría y sometido a dos momentos M y
M’ (actúan en el plano de simetría)
M’
M
C
Curvatura constante
M’
M
B
A
B'
D
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-1
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
C
Θ
y

y
B
A
D
x
A’
DE  L
JK  L'
y
K
J
E
B’
L  
L'     
  Deformación de JK
  L'L    y      y
x 
Definición Máximo
m 

L
c


 




L



 x  

c
m
c
m
  x   m

c
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-2
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
y
C
m
x
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-3
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
12.2.- Esfuerzos en un elemento simétrico sometido a flexión pura en el rango elástico.
 x  E x
Pero
 x   m

 x  E
y
c
m y
c
y
c
 m  EsfuerzoMáximo
x   m
y
C
m
x
Para hallar la superficie neutra se hace

x

y
dA     m dA   m
c
c
El momento de cualquier área
F
x
 ydA  0
0
  ydA  0
dA respecto del eje neutro es:
 y   x dA  dM
EI momento total será:
  y
x
dA  M
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-4
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
y
  y   c
m
c
y
2
dA  M
dA  M
m
m 
Mc
I
Ecuación de flexión elástica
I
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-5
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
y
c
x   m
Pero:

m 
A demás
1

1

Pero

x 
1


c

My
I

Ecuación de flexión elástica
1



Mc M

EIc EI

M
EI
d2y
dx 2
  dy  2 
1    
  dx  
d2y M

dx 2 EI
1
m
c
m


2

EI
E
c
1


d2y
dx 2
d2y
M
dx 2
Ejemplo 1 . Hallar la ecuación de la curva elástica de la viga.
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-6
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
P
M
R
L
PR
PL  M
PL=M
V
P
M
x
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-7
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
P V  0
V P
PL  Vx  M  0
M  Vx  PL
EI
d2y
 Vx  PL
dx 2
EI
dy Vx 2

 PLx  C1
dx
2
En x  0
EI
;
y' 0
;
0  C1
dy Vx 2
Px 2

 PLx 
 PLx
dx
2
2
 x3
x2 

EI y  P  L   C2
2
6
x0
En
Por tanto:
y  0  C2  0
P  x3
x2 
  L 
y
EI  6
2
Ejemplo 2. Hallar la ecuación de la curva elástica de la viga.
W
A
B
L
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-8
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
WX
A
V
M
X
wL
2
M A  0
x
 wx  Vx  M  0
2
x
M  Vx  w
2
2
x
wL
wx 2 wx
L

L  x 
M  w  x  x  w 
x

2
2
2
2
2

2
d2y
EI
 M x 
dx 2
EI
dy
wx
  L  x dx
dx
2
dy wx 2
wx 4

L
 C1 x  C 2
dx
12
24
EI y 
en
EI
wx3
wx 4
L
 C1 x  C2
12
24
x0
xL y0
C1   w
y0

C2  0
wL4 wL4

 C1 L  0
12
24
L3
L3
wL3
wL3
w 

12
24
24
24
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-9
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
y
1  wx 3
wx 4 wL3

L

EI  12
24
24

x 

Determinación del punto mínimo (flecha)
w  x3 L x 4 xL3 


y


EI  12 24 24 
y,  0 
3x 2 L 4 x 3 L3


0
12
24 24
6 x 2 L  4 x3  L3  0
x  L / 2 es solución
w  L3  L
L4
L4  wL4  1 1 1 

y L / 2  

 
   
EI  8  12 16  24 48  24 EI  4 16 2 

 5WL4
384 EI
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-10
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
12.3. Vigas Estáticamente Indeterminadas
Viga estáticamente indeterminada de primer grado contiene una reacción resultante.
Ejemplo:
A
M
B
A
y
B
A
x
Hay tres ecuaciones
EI
F
x
d2y
 M ( x)
dx 2
0
y
permite calcular
Hay dos condiciones de contorno
Hay una condición de contorno para
Total : 6 ecuaciones
F
0
M  0
y = f(x)
y0
en
x0
y0
en
xL
y ' en x  0
Incógnitas:
y' 0
Ax , Ay , M , C1 , C2
Esto significa que las seis incógnitas pueden ser obtenidas a partir de las condiciones
planteadas.
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-11
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
Ejemplo: Hallar las reacciones
w
MA
0
Ax  0
F
0
Ay  B  wL  0
x
B
Ax
F
y
Ay
M  0
MA  BLw
MA  w
M
Ax
MA
L2
0
2
L2
 BL
2
V
Ay
Ay  wx  V  0
x
M
M A  M  Vx  w
A
V  Ay  wx
0
x2
0
2
M  Vx  w
x2
MA
2
M  Ay x  wx 2  w
EI
d2y
1
 Ay x  wx 2  M A
2
2
dx
EI
dy
x2 1 3
 Ay
 wx  M A x  C1
dx
2 6
en
x0 ;
y' 0
x2
MA
2
 C1  0
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-12
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
EI y  Ay
en
x3 1
x2
 wx 4  M A  C2
6 24
2
x0 ;
y0
 C2  0
xL ;
y0
 0  Ay
L3 wL4
L2

MA
6
24
2
A L wL2
 L wL2 
  M A  y 
 M A  2 Ay 
3
12
 6 24 
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-13
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
B  wL  Ay
Ay  B  wL
L2
M A  BL  w
0
2
MA 
Ay L
3
w
L2
0
12
M A  wL2  Ay L  w
MA 
Ay L
3
 Ay L  Ay
 w
L2
2
L2
12
L wL2
wL2

 wL2 
3
2
12
1
1 
1
 6  12  1 
Ay   1  wL  1    wL

12 
3 
2
 12 

2
 2
Ay  wL  
3
 12 
Ay  wL
5 3

12 2
5 

 Ay  8 wL 


5
3 
 5 
B  wL  Ay  wL  wL  wL1     B  wL
8
8 
 8 
wL2
wL 2 3 2
3  wL2
2 1
MA 
 BL 
 wL  wL    
2
2
8
8
 2 8
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-14
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
12.2.- Relación entre carga, momento flector y fuerza cortante
a) Carga y fuerza cortante
Sea una viga sometida a una distribución de carga
A
C
C’
B
Al considerar un segmento de viga, se tiene:
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-15
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
Wx
V  V
M
M  M
V
 Fy  0
V  V  V   wx  0
V  V   V
x
 w 
dV
 w
dx
dV  wdx
Al integrar entre C y D se obtiene

D
C
xD
dV  VD  VC   wdx
xC
VD  VC  Área bajo la curva de carga entre C y D
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-16
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
b) Fuerza cortante y momento flector
 MC,  0
 M  M  M   V  x  wx 
M  Vx 
x
0
2
w
x 2
2
O bien
M  M   M  Vx  w x 2
2
M  M  M
w
 V  x
x
2
Si x  0
dM
V
dx
Al integrar entre C y D

D
C
D
dM   Vdx
C
xD
M D  M C   Vdx
xC
= área bajo la curva de fuerza cortante entre C y D
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-17
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
Determinación directa de la curva elástica a partir de la distribución de
carga.
d 2 y M x 

dx 2
EI
Dado que  w 
dV
dx
y V
dM
dx
Se tiene
d3y
1 dM
d3y w
x 



dx 3 EI dx
dx 3 EI
d 4 y 1 dV
d4y
w

 4   x 
4
dx
EI dx
dx
EI
EI
d3y
V
dx 3
EI
d4y
 w
dx 4
Ejemplo
W
Hallar
A
EI
y  f x 
B
d4y
 w
dx 4
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-18
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
EI
dey
  wx  C1  V x 
dx 3
d 2 y  wx 2
EI 2 
 C1 x  C2  M x 
dx
2
EI
dy  wx 3
x2

 C1
 C 2 X  C3
dx
6
2
EI y 
wx 4
x3
x2
 C1  C2  C3 x  C4
24
6
2
En
x0
M 0
xL
M 0
 C2  0


En
wL2
wL
 C1  L  0  C1 
2
2
yx  

1   wx 4 wL 3


x  C3 x  C4 
EI  24 12

x0
y0
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-19
Resistencia de Materiales. Capítulo XII. Deflexión de vigas
xL

y0
wL3 wL3  wL3


24
12
24
1
Y
EI
y
w
EI
  wx 4 wL 3 wL3


x 
12
24
 24

x 

  x 4 Lx 3 L3 x 




24 
 24 12
Universidad de Santiago de Chile. Fac. de Ingeniería. Departamento de Ing. Metalúrgica.
12-20