ETS DEVELOPMENT CHALLENGE

ETS DEVELOPMENT CHALLENGE
¿Te apetece un reto?
Nosotros te proponemos 3 entretenidos retos con los que seguro te divertirás poniendo a
trabajar tus neuronas. Si eres de los que además de “darle a la tecla” te gusta “darle al coco”,
te desafiamos a que nos sorprendas con las líneas de código que salen de tus dedos.
RETO 1
Para ir abriendo boca te presentamos este primer problema tipo. Un pequeño programa muy académico
con el que desentumecer nuestros dedos y la mente.
¿Sabes lo que es un palíndromo? Seguro que sí, pero a lo mejor no sabías que ese era
su nombre. Descubre con nosotros su significado y de paso resuelve la algoritmia escondida en la construcción de estas curiosas palabras.
Detrás del término de palíndromo se esconde un concepto muy sencillo pero a la vez único: un palíndromo no es más que una palabra o cadena de caracteres que se lee igual de izquierda a derecha que
de derecha a izquierda.
Otro concepto que viene a cuento para este problema es el de PalMeasure de una cadena. Este término
hace referencia a la suma de las longitudes de sus subcadenas, que son palíndromos a su vez.
El reto consiste en que implementes una solución que devuelva el PalMeasure de la concatenación de
todas las cadenas de caracteres contenidas en el array de cadenas de texto pasado por parámetro al
programa.
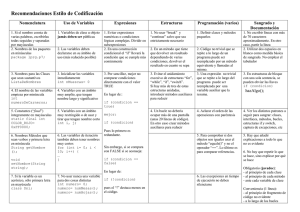
DEFINICIÓN
Clase: Método: Parámetros: Devuelve: Cabecera del Método: PalindromeAnalyzer
SummaryLength
String []
long
long SummaryLength (String [] text)
(Asegúrate de que tu método es público)
NOTAS
•
•
•
Una subcadena es una secuencia de caracteres consecutivos de una cadena.
Una cadena completa cuenta como una subcadena de sí misma.
Ten en cuenta que aunque las subcadenas tengan el mismo texto, si estas se encuentran en posiciones distintas también contarán para el cálculo del PalMeasure. Por ejemplo, si el parámetro de
entrada es {“AAA”}, el resultado sería 10.
RESTRICCIONES
•
•
•
text contendrá entre 1 y 50 elementos, ambos inclusive.
Cada elemento de text contendrá únicamente letras mayúsculas (“A” - “Z”).
Cada elemento de text contendrá entre 1 y 50 caracteres, ambos inclusive.
EJEMPLOS
1){“AAA”}
Returns: 10
2){“AB”}
Returns: 2
3){“AB”, “BA”}
Returns: 10
4){“AB”, “AAA”}
Returns: 15
5){“AZ”, “ZZ”, “A”}
Returns: 17
RETO 2
Si has llegado hasta aquí es que has aceptado nuestro desafío y tienes ganas de seguir devanándote los
sesos. Vamos pues con un problema con algo más de complejidad, con el que vamos a intentar transmitirte, a grandes rasgos, qué tipo de información manejamos en nuestro día a día. Como podrás imaginar,
los complejos algoritmos que desarrollamos en nuestras oficinas vienen respaldados por una ingente
cantidad de información que en la mayoría de los casos toma la forma de series de precios o matrices.
Es por esto que el siguiente reto quiere medir cómo te manejas con estas estructuras de datos complejas y tu habilidad a la hora de recorrerlas de forma eficiente. Vayamos entonces al problema concreto.
Llamamos a una matriz rectangular monótona si en todas las filas y en todas las columnas cada elemento es mayor que el anterior (ai,j < ai + 1,j y ai,j < ai,j + 1). Se tienen cuatro números enteros, n, m, row y col.
Se debe devolver una matriz rectangular monótona con n filas y m columnas que contenga todos los
números enteros entre 0 y (n*m - 1), de tal forma que el elemento que ocupa la posición (row, col) sea
el más pequeño posible. Todos los índices empiezan de 0. Si hay varias soluciones, se debe devolver la
más pequeña según el orden lexicográfico (ver nota).
Por ejemplo, si n = 4, m = 5, row = 3 and col = 3, la matriz que se debe devolver es:
0 1 2 3 16
4 5 6 7 17
8 9 10 11 18
12 13 14 15 19
La matriz debe devolverse como un tipo string[] donde el i-ésimo elemento representa la i-ésima fila.
Cada fila debe representarse como una lista de los valores de la fila separados por un solo espacio.
DEFINICIÓN
Namespace: Clase: Método: Parámeteros:
Devuelve: Cabecera del método: ETS.Pruebas
ConstructorMatriz
Construir
int, int, int, int
string[]
string[] construir(int n, int m, int row, int col)
(el método debe ser público)
NOTAS
•
La matriz rectangular A nxm es menor según el orden lexicográfico que la matriz Bsi y solo si el
vector (A0,0, A0,1, ..., A0,m-1, A1,0, A1,1, ..., A1,m-1, ..., An-1,0, An-1,1, ..., An-1,m-1) es menor según el orden lexicográfico
que el vector (B0,0, B0,1, ..., B0,m-1, B1,0, B1,1, ..., B1,m- 1, ..., Bn-1,0, Bn-1,1, ..., Bn-1,m-1).
RESTRICCIONES
•
•
•
•
n debe tener un valor entre 1 y 10, ambos inclusive.
m debe tener un valor entre 1 y 10, ambos inclusive.
row debe tener un valor entre 0 y n-1, ambos inclusive.
col debe tener un valor entre 0 y m-1, ambos inclusive.
EJEMPLOS
1)
4
5
3
3
Devuelve: {“0 1 2 3 16”, “4 5 6 7 17”, “8 9 10 11 18”, “12 13 14 15 19” }
2)
4
5
2
1
Devuelve: {“0 1 6 7 8”, “2 3 9 10 11”, “4 5 12 13 14”, “15 16 17 18 19” }
3)
1
1
0
0 Devuelve: {“0” }
4)
10
10
9
9
Devuelve:
{“0 1 2
“10 11
“20 21
“30 31
“40 41
“50 51
“60 61
“70 71
“80 81
“90 91
3 4 5
12 13
22 23
32 33
42 43
52 53
62 63
72 73
82 83
92 93
6 7 8
14 15
24 25
34 35
44 45
54 55
64 65
74 75
84 85
94 95
9”,
16 17
26 27
36 37
46 47
56 57
66 67
76 77
86 87
96 97
18
28
38
48
58
68
78
88
98
19”,
29”,
39”,
49”,
59”,
69”,
79”,
89”,
99” }
RETO 3
Por último vayamos con un problema algo más distendido, porque en ETS no todo es trabajar y también
disfrutamos de divertidas propuestas con las que relajarnos y desconectar de las presiones del día a día.
La fiebre de los drones ha llegado a nuestra compañía y se quiere organizar una carrera con estas divertidas aeronaves dentro de nuestra sede. Para esta carrera se ha querido definir una serie de puntos de
control dentro de nuestras instalaciones.
Si superas todos los retos que te proponemos probablemente tendrás oportunidad de conocer nuestras
oficinas de primera mano, pero a modo de presentación te diremos que nuestras oficinas están situadas en la zona norte de Madrid. Disponemos de tres edificios que designamos con las letras A, M y F
(siglas de Asset Management Factory), una zona de parking para empleados y en el medio de todo ello
una pequeña casita rodeada de jardines que hace las veces de punto de reunión en el que comemos y
socializamos.
Dicho esto, parece lógico definir los siguientes puntos de control o checkpoints para la I carrera oficial de
drones de ETS:
•
•
•
•
•
Edificio A (código A)
Edificio M (código M)
Edificio F (código F)
“La casita” (código C)
Parking (código P)
Partiendo de estas localizaciones se pide que se diseñe un programa que calcule todos los itinerarios
posibles entre un punto de origen y uno de destino teniendo en cuenta un tiempo máximo marcado
por la autonomía de los drones.
Para proceder al cálculo de las trayectorias posibles y después de un “riguroso” estudio sobre el terreno
se debe facilitar un grafo dirigido en el cual un vértice representa un punto de control y un arco representa una ruta entre dos puntos. El peso del arco representa el tiempo de vuelo en minutos entre dos
puntos. Un itinerario entre dos localizaciones (de A a M) con un tiempo de 5 minutos es representado
con AM5 (códigoSalida + códigoLlegada + tiempoVuelo).
Un ejemplo de grafo dirigido sería: AM5, MF4, FC8, CF8, CP6, AC5, FP2, PM3, AP7
DEFINICIÓN
Namespace: Clase: Método: Parámeteros: Devuelve: Cabecera del método: ETS.Drones
ItinerariosDrones
obtenerItinerarios
string, string, int, string[]
string[]
string[] obtenerItinerarios (string origen, string destino, int
tiempoMax, string[] grafo)
(el método debe ser público)
NOTAS
Debido a la orografía de la zona en la que se encuentran nuestras oficinas se tienen en cuenta las siguientes consideraciones:
•
Que exista la ruta entre A y M no implica que exista también la ruta entre M y A, ya que si el espacio
disponible es muy reducido se podrían producir cuellos de botella con drones volando en direcciones opuestas.
•
En el caso de haber rutas bidireccionales no necesariamente tienen que tomar el mismo tiempo
en ambos sentidos. Por ejemplo, para llegar del punto A al C se puede tardar 2 minutos y en cambio de C a A la duración sería de 3 minutos, debido a que los trayectos definidos son distintos y el
segundo implica salvar unos setos de por medio.
NOTAS
En lo referente al grafo dirigido que se pasa por parámetro, dado un itinerario, cada ruta que lo compone
no puede aparecer más de una vez, y para cada ruta, el punto de salida y el de llegada no pueden ser
nunca el mismo.
EJEMPLOS
origen : “F”
destino : “F”
tiempoMax : 30
grafo : [“AM5”,“MF4”,“FC8”,“CF8”,“CP6”,“AC5”,“FP2”,“PM3”,“AP7”]
Devuelve: {“FCF”, “FPMF”, “FPMFCF”, “FCFPMF”, “FCPMF”, “FPMFPMF”, “FPMFPMFPMF” }