Traslacion_en_el_plano_Cartesiano

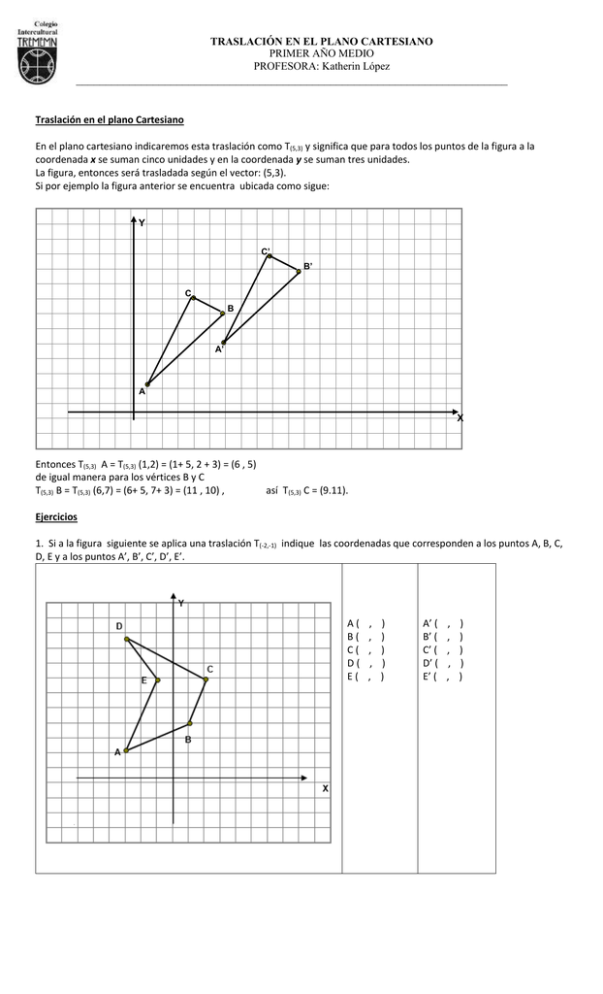
TRASLACIÓN EN EL PLANO CARTESIANO
PRIMER AÑO MEDIO
PROFESORA: Katherin López
_________________________________________________________________________
Traslación en el plano Cartesiano
En el plano cartesiano indicaremos esta traslación como T(5,3) y significa que para todos los puntos de la figura a la
coordenada x se suman cinco unidades y en la coordenada y se suman tres unidades.
La figura, entonces será trasladada según el vector: (5,3).
Si por ejemplo la figura anterior se encuentra ubicada como sigue:
Y
C’
B’
C
B
A’
A
X
Entonces T(5,3) A = T(5,3) (1,2) = (1+ 5, 2 + 3) = (6 , 5)
de igual manera para los vértices B y C
T(5,3) B = T(5,3) (6,7) = (6+ 5, 7+ 3) = (11 , 10) ,
así T(5,3) C = (9.11).
Ejercicios
1. Si a la figura siguiente se aplica una traslación T(-2,-1) indique las coordenadas que corresponden a los puntos A, B, C,
D, E y a los puntos A’, B’, C’, D’, E’.
A(
B(
C(
D(
E(
,
,
,
,
,
)
)
)
)
)
A’ (
B’ (
C’ (
D’ (
E’ (
,
,
,
,
,
)
)
)
)
)
TRASLACIÓN EN EL PLANO CARTESIANO
PRIMER AÑO MEDIO
PROFESORA: Katherin López
_________________________________________________________________________
2. Un desafío.
¿Dónde se encuentra el tesoro del pirata?
Siguiendo los pasos del pirata que partió desde su escondite ubicado
en A (1,-1), encuentre la posición F donde finalmente escondió su
tesoro, sabiendo que:
T (4,2) A
T (-5,3) B
T (-2,2) C
T (0,-6) D
T (8,-2) E
=B
=C
=D
=E
=F
A) Marque los ejes coordenados y dibuja su trayectoria
B) ¿Es único el camino que debe seguir para llegar al escondite? Explique
C) ¿Cuál es el camino mas corto y directo para llegar del punto A al punto F?
D) Si existe un número finito de trayectorias a seguir. ¿Cuántas son?
Traslación de un triángulo dado un vector
I. Si trasladamos una figura mediante una traslación T(a,b), diremos que
Ejemplo:
1.- trace en su cuaderno los ejes de coordenadas.
v  (a,b) corresponde al vector traslación.
2.- Dado un triángulo ABC y con vértice A(-2, -5); B(4, -2) y C(2, 3) y su vector de traslación es v (4, 3). Grafíquelo.
3.- Determinar los vértices homólogos del triángulo ABC. (es decir A’, B’ y C’)
Luego los triángulos ABC y A’B’C’ tienen sus lados homólogos respectivamente congruentes y paralelos, por lo tanto,
estos triángulos son congruentes.
II. Los vértices de un cuadrilátero ABCD son los puntos A(-6, -2), B(-2, -5), C(6, -1) y D(2, 4). Trasládelo de modo que el
vector de traslación sea respectivamente.
a) v(4,2)
b) v(0,5)
c) v(2,4)
Los dibujos correspondientes a cada traslación deben estar en un mismo plano cartesiano.
III. Determine y dibuje la preimagen del un triángulo A’B’C’ de vértices A’(-4, -4), B’(2,0) y C’(0, 5), siendo v(2,3) , el
vector de traslación.
IV. Si el centro de una circunferencia C es O(-1, -3) y el centro de la circunferencia trasladada es O’(-1, 5). ¿Cuál es el
vector de traslación de la circunferencia C?
Como se habrá dado cuenta una traslación es una función, donde todos los puntos de la figura original conforman la
preimagen y la figura resultante es la imagen, luego de aplicar el vector traslación.