Marzo - Aprende Matemáticas
Anuncio
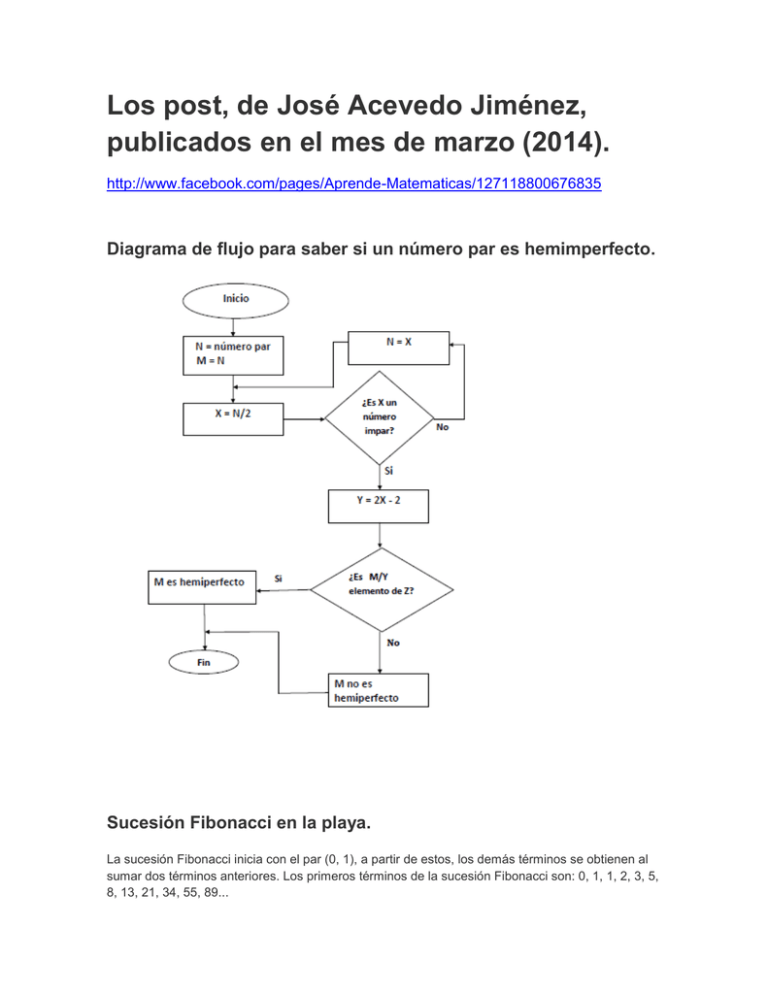
Los post, de José Acevedo Jiménez, publicados en el mes de marzo (2014). http://www.facebook.com/pages/Aprende-Matematicas/127118800676835 Diagrama de flujo para saber si un número par es hemimperfecto. Sucesión Fibonacci en la playa. La sucesión Fibonacci inicia con el par (0, 1), a partir de estos, los demás términos se obtienen al sumar dos términos anteriores. Los primeros términos de la sucesión Fibonacci son: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... La sucesión Fibonacci por lo general se llama serie Fibonacci, pero, esta última forma de llamarla no es correcta, pues, una serie es la suma de todos los términos de una sucesión. La sucesión Fibonacci tiene muchas propiedades interesantes. Entre tantas se encuentra la siguiente: Sea un número de Fibonacci y el siguiente número, entonces, el límite cuando n tiende al infinito de se aproxima al número áureo o fi. Natalicio de Descartes. "Pero en seguida advertí que mientras de este modo quería pensar que todo era falso, era necesario que yo, que lo pensaba, fuese algo. Y notando que esta verdad: yo pienso, por lo tanto soy era tan firme y cierta, que no podían quebrantarla ni las más extravagantes suposiciones de los escépticos, juzgué que podía admitirla, sin escrúpulo, como el primer principio de la filosofía que estaba buscando." René Descartes. El matemático y filósofo francés René Descartes nació en La Haye, Francia, el 31 de marzo de 1596. Descartes estableció los cimientos de la geometría analítica y de la filosofía moderna. En el 1637 apareció su muy conocida obra: Discurso del método. Hoy, 31 de marzo en www.aprendematematicas.org.mx/ celebramos el natalicio de René Descartes. Fuente de la imagen: stamps.postbit.com Jugando con números. Un número es hemimperfecto si se puede expresar mediante la fórmula que se muestra en la imagen del post. Entre sus divisores, existe un número impar ( de la forma , donde es una potencia de dos (ver imagen del post). Características de los números hemimperfectos. Los números hemimperfectos son números semiperfectos. Eso significa que tales números se pueden expresar como la suma de algunos de sus divisores propios. Ejemplo: Los divisores propios del 40 son: 20, 10, 8, 5, 4, 2, 1. 40 = 20 + 10 + 8 + 2 = 20 + 5 + 4 + 1 +8 + 2. Como se puede observar, entre los divisores propios del 40 se encuentran dos números pares consecutivos (10, 8). Esta característica es distintiva de los números hemimperfectos. Los divisores propios que sumados nos dan el número hemimperfecto son fáciles de encontrar. Ejemplo: Dado el número hemimperfecto 544, encontrar los divisores que sumados sean iguales al número dado. Para encontrar tales divisores, hacemos lo siguiente: Dividimos entre dos el número dado. El resultado también lo dividimos entre dos y repetimos el proceso hasta que el resultado sea un número impar (primo). Al último resultado le restamos dos, este número también es un divisor propio del número dado; finalmente sumamos todos los divisores encontrados y a dicha suma le agregamos dos. Los divisores propios encontrados del 544 son: (272,136,68,34,32). Suma de los divisores propios encontrados (SDPE). Todo número hemimperfecto tiene una cantidad par de divisores (incluido el propio número). Del total de divisores, solo basta tomar la mitad (ni más ni menos) para que al ser sumados nos den el número hemimperfecto dado. De ahí el nombre hemimperfecto (hemi- prefijo griego que significa mitad). Nota: El nombre hemimperfecto ha sido dado por el autor del post. ¿Sabías que…? El genetista británico Karl Pearson (1857 - 1936) nació en Londres, Inglaterra, el 27 de marzo de 1857. Pearson fundó la bioestadística, disciplina que combina la biología con la estadística. Fuente de la imagen: Wikipedia.org ¿Sabías que…? El matemático húngaro Paul Erdős (1913 - 1996) fue uno de los matemáticos más prolíficos de todos los tiempos, superado sólo por Leonhard Euler que publicó más páginas . Erdős nació el 26 de marzo de 1913 en Budapest, Hungría. En www.aprendematematicas.org.mx/ le recordamos en su día. Fuente de la imagen: cunymath.cuny.edu ¿Sabías que…? El matemático francés Joseph Liouville (1809 - 1882) fue el primero en demostrar la existencia de los números trascendentes o trascendentales (números irracionales que no pueden ser expresados como raíces polinómicas de coeficientes enteros). Los números (pi) y (e) son trascendentales. Liouville nació el 24 de marzo de 1809, por tal motivo en www.aprendematematicas.org.mx/ celebramos su día. Fuente de la imagen: www.ecured.cu Laplace grabado en la arena. Pierre-Simon Marqués de Laplace (23 de marzo de 1749 - 5 de marzo de 1827). ¿Sabías que…? La matemática Amalie Emmy Noether (1882 - 1935) nació en Alemania el 23 de marzo del 1882. Noether realizó importantes contribuciones en el campo del álgebra abstracta. Fuente de la imagen:search.credoreference.com Natalicio de Laplace. Un día como hoy, pero del 1749, nació en Beaumont-en-Auge, Francia, el matemático y astrónomo Pierre-Simon Laplace (1749 - 1827). Laplace desarrolló la transformada que lleva su nombre (transformada de Laplace). Hoy, 23 de marzo, en www.aprendematematicas.org.mx/ recordamos a Laplace en su día. Fuente de la imagen: mimosa.pntic.mec.es ¿Quieres saber si eres curioso/a? Si eres curioso/a no podrás contenerte… ¿qué número se muestra en la imagen del post? ¿Sabías que…? El matemático francés Jean-Baptiste Joseph Fourier (1768 - 1830) nació en Auxerre, Francia, el 21 de marzo de 1768. Fourier desarrolló las muy conocidas series que llevan su apellido . Las series de Fourier son de gran utilidad en diversas ramas de la ingeniería. Fuente de la imagen: loshackersmatematicos.blogspot.com ¿Sabías que…? El matemático Christian Goldbach (1690 - 1764) nació en Königsberg, Prusia (actual Kaliningrado, Rusia) el 18 de marzo del 1690. Goldbach se conoce, principalmente, por la conjetura matemática que lleva su apellido. Dicha conjetura afirma que todo número par mayor que 2 puede ser expresado como la suma de dos números primos. Fuente de la imagen: www.sansimera.gr No hay matemáticas baratas, sólo matemáticas. Alguna vez han escuchado la expresión: “sólo es matemática barata”. El enunciado hace referencia a ciertas ramas de las matemáticas que, para dominarlas, sólo requieren de un conocimiento básico. Entre las mal llamadas “matemáticas baratas” se encuentra el algebra tradicional. Aunque es sólo una expresión, lo cierto es que, no existen las matemáticas baratas. Es mejor hablar de matemáticas: básicas, medias y avanzadas. Razón para no llamarlas “matemáticas baratas”. El conocimiento matemático ha evolucionado con el paso de los años. Muchos de los enunciados, métodos y procedimientos, empleados en matemáticas, que consideramos sencillos no aparecieron de la nada o simplemente porque sí. A los matemáticos les tomó tiempo y esfuerzo desarrollar algunos de los conceptos que hoy consideramos "simples"; pienso que es una falta de respeto, a la memoria de muchos matemáticos, decir que: “sólo son matemáticas baratas”. ¿Sabías que…? El matemático Gösta Mittag-Leffler (1846 - 1927) nació en Estocolmo, Suecia, el 16 de marzo del 1846. Mittag-Leffler y el Nobel nunca concedido a las matemáticas Según una leyenda, cuando Alfred Nobel pidió consejo a especialistas sobre quién podría merecer el premio “Nobel de matemáticas” le advirtieron que el matemático sueco Mittag-Leffler, era el más indicado para recibirlo. El problema es que Nobel no se llevaba bien con él, así que Nobel decidió no instaurar dicho premio para las matemáticas, de esta manera evitaría tener que dárselo al destacado matemático. Otra leyenda, menos creíble, asevera que la mujer de Alfred Nobel y Mittag-Leffler tenían un romance, siendo ésta la razón por la cual Alfred Nobel declinó a instaurar el premio para las matemáticas; es fácil refutar esta última leyenda ya que Alfred Nobel nunca estuvo casado. En cuanto a la primera leyenda, es poco probable que sucediera ya que Nobel apenas conocía a Mittag-Leffler por lo que no se podía llevar mal con él. Fuente de la imagen: owpdb.mfo.de Fuente del mito: Hablemos de números y matemáticos. El número (pi) Vemos tu semblante en el Sol al amanecer y en la Luna llena cuando oscurece. Número trascendental de eternos dígitos, que dibuja su silueta en una simple flor o en la suave curva plasmada en la arena del cálido desierto. Y es que eres casi omnipresente; número divino, revelado a los mortales en la redondez de las cosas. Triángulo de Sierpiński. Es un fractal construido a partir de un triángulo dado. Fuente de la imagen: alfredo-barrera-cuevas.blogspot.com ¿Sabías que…? El matemático Wacław Sierpiński (1882 - 1969) nació en Varsovia, Polonia, el 14 de marzo del 1882. En su honor tres fractales llevan su apellido, estos son: el triángulo de Sierpiński, la alfombra de Sierpiński y la curva de Sierpiński. Hoy, 14 de marzo, en www.aprendematematicas.org.mx/ recordamos a: Wacław Sierpiński. Fuente de la imagen: m.ztopics.com ¿Sabías que…? El físico Albert Einstein (1879 - 1955) nació en Ulm, Alemania, el 14 de marzo de 1879. Einstein, entre otras cosas, es muy conocido por haber desarrollado las teorías de la relatividad especial y general. Dato curioso: Eistein nació el 14 de marzo que en notación anglo se expresa: 3/14. Dicha fecha nos recuerda el número (pi) y es por esa razón que el natalicio de Eistein coincide con el día de (pi). Fuente de la imagen: marthasialer-2.blogspot.com Dato matemático: Números Complejos. Los números complejos son aquellos que poseen una parte real y otra imaginaria. Si la componente imaginaria es igual a cero el número es un real puro, pero, si es la parte real la que es igual a cero entonces el número se denomina imaginario puro. Los números complejos tienen muchas aplicaciones en campos tan útiles como la ingeniería y la física. ¿Sabías que…? El matemático Ernesto Cesàro (1859 - 1906) nació en Nápoles, Italia, el 12 de marzo. Cesàro fue profesor en la Universidad de Palermo. En el campo del análisis matemático la sumación de Cesàro se nombra en su honor. Hoy 12 de marzo, en www.aprendematematicas.org.mx/ recordamos a Ernesto Cesàro en su día. Fuente de la imagen: www.geocities.ws ¿Sabías que…? El matemático francés Joseph Louis François Bertrand (1822 - 1900) nació en parís el 11 de marzo de 1822. En 1845, Bertrand conjeturó que existe por lo menos un número primo (p) entre (n) y (2n -2) para todo (n) > 3. Este resultado, demostrado por el matemático ruso Pafnuti Chebyshov, se conoce como: postulado de Bertrand o postulado de Bertrand-Chebyshov. Hoy 11 de marzo, en www.aprendematematicas.org.mx/ recordamos a Joseph Bertrand. Fuente de la imagen:www.apprendre-math.info Mujer Ni el cálculo ni la aritmética pueden describir tu sublime belleza. Hermosa Atenea, el ser más divino de toda la Tierra. Eres amor, entrega y fortaleza. Todo lo bueno en una sola palabra: MUJER. Fuente de la imagen: www.nobelprize.org Porque no sólo tienes un día… ¿Sabías que…? El símbolo cuantificador universal (A de cabeza) que aparece en la imagen del post se lee: para todo. ¿Saben quién es la chica en la imagen del post? Es Danica McKellar, la actriz estadounidense que representó a la tierna Winnie Cooper en la serie televisiva: “Los años maravillosos”. ¿La recuerdan? De seguro se preguntan: ¿qué hace una actriz en un post de matemáticas? Pues resulta que McKellar además de ser actriz, muy hermosa por cierto, también es matemática. Así es, McKellar es matemática e incluso tiene un teorema: Teorema de Chayes-McKellar-Winn (coautora), el mismo fue publicado con la colaboración de otros matemáticos. McKellar estudió matemáticas en la UCLA (se graduó con honores). Es autora del libro: Math Doesn't Suck: How to Survive Middle-School Math Without Losing Your Mind or Breaking a Nail. Como pueden ver las chicas no solo pueden saber de matemáticas, también, tienen la ventaja de ser muy guapas (inteligencia no quita belleza y viceversa)… las féminas, por naturaleza, tienen una inteligencia prodigiosa; ¡claro! es lógico que sean listas pues nuestra civilización depende de sus genes, nacemos de una mujer. Mujer, el ser más perfecto de este mundo…muchas felicidades en su día. Fuente de la imagen:www.picstopincom La culpa la tienen las inversas. El término número, en matemáticas, es un concepto que está muy bien definido. Hoy en día aceptamos, de forma muy natural, conceptos tales como: números negativos, números fraccionarios, números imaginarios entre otras abstracciones. Aunque nos parezca algo extraño, algunos números como los enteros negativos o los números imaginarios no fueron reconocidos o aceptados por los matemáticos desde el momento que surgió la necesidad de contar en los humanos. En un principio, sólo tuvimos la capacidad de reconocer el conjunto de números más simples, el de los números naturales; un concepto que, a diferencia del resto de los números, surgió con la necesidad misma de contar. Algo obvio si tomamos en cuenta que los naturales son los únicos números que usamos para tal propósito. A medida que el concepto de número evolucionaba iban surgiendo, casi a la par, algunos problemas. En algún punto de la historia, nuestros ancestros notaron que no todos los números eran naturales, así pues, una manzana, por tomar un ejemplo, se podía dividir en partes más pequeñas o fracciones; habían nacido los números racionales. En un principio, hubo algunos inconvenientes; los antiguos egipcios se aferraban a la idea de que el numerador siempre debía ser igual a 1. Los numeradores diferentes a la unidad se expresaban sumando las primeras. Ejemplo: . Los números negativos surgieron con la necesidad de representar deudas. Un concepto que los banqueros y en general las personas que se dedican a los negocios entienden a la perfección. Sin embargo, los números negativos, en occidente, fueron aceptados muy tardíamente por los matemáticos. Si los números negativos y los fraccionarios fueron difíciles de reconocer por los matemáticos, entonces imaginen el trauma que le debieron causar los números imaginarios. En efecto, reconocer los números imaginarios fue todo un reto para los matemáticos. Resultado de las operaciones. Como ya dijimos, los naturales fueron los primeros números desarrollados por los humanos. Al efectuar las operaciones de: suma, multiplicación y potenciación, con los números naturales, el resultado obtenido es siempre otro número natural. Esto significa que al efectuar, con los números naturales, las operaciones mencionadas no surgieron nuevas inquietudes respecto a la existencia de otros conjuntos numéricos. El problema surgió con las operaciones inversas de las mencionadas. La resta es la operación inversa a la suma. Al restar dos números naturales con los siguientes casos: . Si no tenemos ningún problema al efectuar la operación seguirá siendo un número natural. El inconveniente surge cuando tales casos surgen los números negativos y el cero. nos encontramos puesto que el resultado es mayor o igual a En La división es la operación inversa a la multiplicación. Con la división aparecieron los números fraccionarios, una idea que iba más allá del concepto de número natural. Con las fracciones surgió la necesidad de crear un nuevo conjunto de números, los llamados racionales. Con la radicación surgen los números imaginarios, que junto con los reales dan paso a un nuevo conjunto de números, los complejos. Los números imaginarios nacieron de la necesidad de dar solución a ecuaciones tales como: . Sin las operaciones inversas sólo tendríamos el conjunto de los números naturales. Aunque nadie duda lo útiles que son, no fue tarea fácil reconocer el resto de los números. Durante siglos, los matemáticos tuvieron que devanarse los sesos para poder identificar los diferentes conjuntos numéricos; todo por culpa de las operaciones inversas. ¿Sabías que…? En matemáticas, el conjunto de los números enteros es representado por la letra Z. Dicha Z es la inicial de la palabra Zahlen que en alemán significa números. Nacimiento de grandes matemáticos (3 de marzo). Un día como hoy, pero del 1845, nació en San Petersburgo, el matemático alemán (de origen ruso) Georg Cantor (1845 - 1918). Cantor fue uno de los fundadores de la teoría de conjuntos. En la mencionada teoría, introdujo el término de número transfinito para referirse a los ordinales infinitos. Fuente de la imagen:nmalbert.hubpages.com ¡Menos que cero a la izquierda! Fuente de la imagen: custodiapaterna.blogspot.com. Alguna vez han escuchado la expresión: “vale menos que cero a la izquierda”. Pues bien, como sabemos, el cero es un número neutro que no tiene ningún valor. A diferencia del resto de los números, el cero no posee un elemento opuesto con relación a la suma. En otras palabras, al ser neutro, el cero no es ni negativo ni positivo. Entonces, es prudente preguntarse: ¿tiene algún sentido la expresión vale menos que cero a la izquierda? Para dar respuesta a la pregunta, la analizaremos desde dos puntos de vistas diferentes. El cero como número. El cero es un número neutro y siempre ocupa el mismo lugar en la recta numérica, a la derecha de los números negativos y a la izquierda de los positivos, justo en el centro de la recta, ni más a la izquierda ni más a la derecha, neutral en su lugar. El cero como dígito. Dado un número entero, de dos o más cifras, mientras más a la derecha se encuentren más peso tienen sus dígitos. En el caso del cero existe un límite; si de todos los dígitos, de un número dado, el cero es el que se encuentra más a la izquierda, entonces, no tiene ningún valor o peso (es por tal razón que decimos que tiene un límite). Ejemplo: 011 = 0011 = 00011 = 11. Sin importar la cantidad de ceros que se agreguen, a la izquierda del número 11, el valor se mantendrá inalterable. Es decir que un cero a la izquierda de un número dado es lo mismo que mil o más ceros a la izquierda de dicho número. En otras palabras, dado que es lo mismo, un cero a la izquierda de otro cero que se encuentra a la izquierda de un número dado no vale menos. Mayor que los números negativos. En la recta numérica, mientras más a la izquierda se encuentra un número, respecto a otro, menor es su valor. Como los números negativos se encuentran a la izquierda del cero, tales enteros, poseen un valor menor que el número en cuestión. Matemáticamente hablando, la expresión “menos que cero a la izquierda” no tiene ningún sentido si hablamos del cero como un número (no existe el cero a la izquierda del cero). Por otro lado, si lo vemos como un dígito de un número (cosa que no se especifica en la expresión) no tiene ningún valor si se encuentra como primer dígito a la izquierda del número dado, pero, a la derecha sería algo totalmente diferente, tendría un peso que le agregaría valor al número; aunque claro, en tal caso ya no sería cero, solo sería el dígito de un número. Ejemplo: 0203, el cero a la izquierda del 2, como dígito, tiene menos peso que el cero a la derecha del 2. Cosas del lenguaje. Si asumimos que: “vale menos que cero a la izquierda” es una expresión válida coloquialmente hablando, sería lo mismo que decir: vale menos que cero (expresión matemáticamente correcta, hace referencia a los números negativos). Eso sí, hay que reconocer que la primera expresión es mucho más dramática que la segunda. ¿Sabías que…? Dos o más números son primos relativos si el único divisor que tienen en común es el 1. Ejemplos: (9, 25); (9, 8, 25); (8, 21). Dos número naturales consecutivos siempre son primos relativos, o coprimos o primos entre sí.



![[Escribir texto] Grupo kínder 1 Semana del 7 al 11 de octubre Lunes](http://s2.studylib.es/store/data/000780850_1-1fa5892f95679b5fc141cf6c4da220a3-300x300.png)



