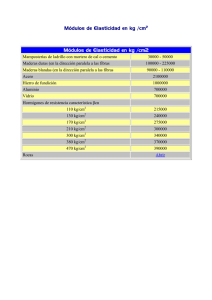
Soluciones

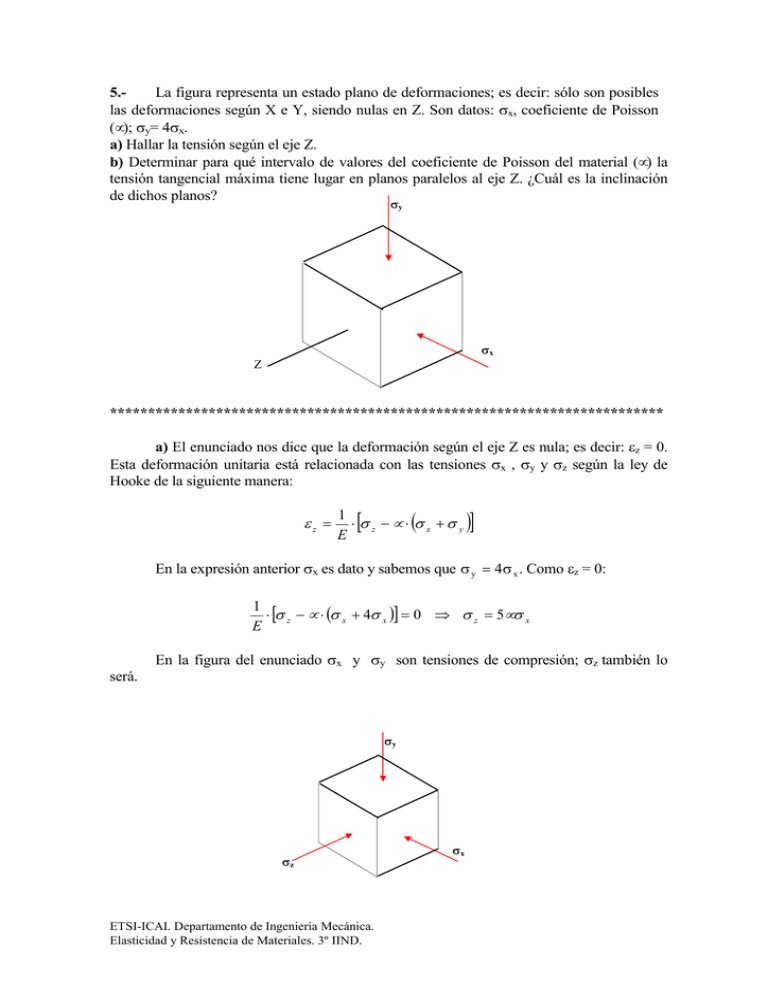
5.La figura representa un estado plano de deformaciones; es decir: sólo son posibles
las deformaciones según X e Y, siendo nulas en Z. Son datos: σx, coeficiente de Poisson
(µ); σy= 4σx.
a) Hallar la tensión según el eje Z.
b) Determinar para qué intervalo de valores del coeficiente de Poisson del material (µ) la
tensión tangencial máxima tiene lugar en planos paralelos al eje Z. ¿Cuál es la inclinación
de dichos planos?
σy
σx
Z
*************************************************************************
a) El enunciado nos dice que la deformación según el eje Z es nula; es decir: εz = 0.
Esta deformación unitaria está relacionada con las tensiones σx , σy y σz según la ley de
Hooke de la siguiente manera:
εz =
[
]
1
⋅ σ z − µ ⋅ (σ x + σ y )
E
En la expresión anterior σx es dato y sabemos que σ y = 4σ x . Como εz = 0:
1
⋅ [σ z − µ ⋅ (σ x + 4σ x )] = 0 Þ σ z = 5µσ x
E
será.
En la figura del enunciado σx y σy son tensiones de compresión; σz también lo
σy
σz
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
σx
b) σx , σy y σz son tensiones principales y las direcciones en que actúan direcciones
principales. Del apartado a) sabemos que sus valores son:
σx = σx
σ y = 4σ x
σ z = 5νσ x
Para que la tensión tangencial máxima tenga lugar en planos paralelos al eje Z es
necesario que ésta quede determinada por σx y σy . Expresemos esto a través de los
círculos de Mohr:
τ
τmax
σy
σz
σ
σx
Por lo tanto debe cumplirse que:
1º) σ z > σ x
Þ 5⋅ µ ⋅ σ x > σ x
Þ µ > 0 .2
2º) σ z < σ y
Þ 5⋅ µ ⋅ σ x < 4⋅ σ x
Þ µ < 0 .8
De los cálculos anteriores parece desprenderse que 0.2 < µ < 0.8 . Sin embargo,
se sabe que el coeficiente de Poisson está siempre comprendido en el intervalo
0 < µ < 0.5 . Por lo tanto la solución es:
0 .2 < µ < 0 .5
En los círculos de Mohr puede verse además que los planos de tensión tangencial
máxima forman un ángulo de 45º con los planos cuyos vectores normales son los ejes X e
Y.
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
6.Una columna de hormigón armado de 20x20
2
cm con 4∅20 (cuatro redondos de acero de 20 mm de
diámetro), se carga con P = 30.000 kg (centrada).
Hallar la tensión a que queda sometido cada material
(hormigón y acero), y el acortamiento unitario de la
columna.
Datos: módulos de elasticidad:
- acero Ea = 2,1·106 kg/cm2.
- hormigón Eh = 2,1·105 kg/cm2.
P=30000kg
4 ∅20
SECCION
**********************************************************************
La columna de hormigón armado se encuentra sometida a compresión. Por ser el
acero y el hormigón materiales diferentes, la tensión en cada uno de ellos, σa y σh
respectivamente, también lo serán. Para que exista equilibrio la carga P = - 30000 kg debe
ser absorbida entre el hormigón y los cuatro redondos de acero (esta carga P es negativa
por ser fuerza de compresión).
En secciones de hormigón armado no es habitual descontarle al hormigón la
sección de acero, debido a que supone un error pequeño en comparación con las
tolerancias en las dimensiones de la sección de hormigón. Se obtiene así una primera
ecuación:
P = 4 ⋅ S redondo ⋅ σ a + S columna ⋅ σ h Þ
−30000 = 4π ⋅ σ a + 400 ⋅ σ h
(1)
Además, para que las deformaciones en los redondos y en el hormigón sean
compatibles, ambas, εa y εh , deben ser iguales. Esto nos dará la segunda ecuación:
σa ü
E a ïï
σa
σh
=
ý Þ
6
σ
2 ⋅ 10
2 ⋅ 105
εh = h ï
E h ïþ
εa =
Þ σ a = 10 ⋅ σ h
(2)
Introduciendo (2) en (1):
−30000 = (125.6 + 400) ⋅ σ h Þ σ h = −57 kg/cm2.
Por lo tanto, a través de (2):
σ a = 10 ⋅ σ h = −570 kg/cm2.
Calculamos ahora el acortamiento unitario de la columna:
ε columna = ε a = ε h Þ ε columna =
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
σa σh
=
= −2.71 ⋅ 10 −4
Ea Eh
El número anterior significa que la columna se acorta 2.71·10-4 cm. por cada cm.
que tenga de longitud. El signo menos nos indica que se trata de un acortamiento.
ETSI-ICAI. Departamento de Ingeniería Mecánica.
Elasticidad y Resistencia de Materiales. 3º IIND.
7.- La barra de la figura tiene los extremos fijos. Sabemos que se ha producido un error de
construcción de + 0.2mm. , por lo que para su montaje será necesario someterla a una
fuerza de compresión. Son datos:
Dimensiones (mm.):
a=200
b=125
c=400
r1=50
r2=65
Material 1
Material 2
Material 3
1.2x106
1.4x10-5
0.75x106
2.4x10-50
Sección circular.
Características de los materiales:
2.0x106
1.2x10-5
Modulo de elasticidad
Coeficiente de dilatación
kg/cm2
C -1
a) Definir la ley de variación de las tensiones normales a lo largo de la barra.
b) Hallar la variación de temperatura que debe producirse para que se anulen dichas
tensiones.
r1
r1
r2
1
2
a
3
2
b
b
c
**********************************************************************
a) La barra de la figura tiene un exceso de longitud igual a +0.2 mm. Esto significa
que cuando se efectúe el montaje quedará sometida a una fuerza de compresión P, que será
la reacción en los extremos.
P
P
1
2
2
3
Esta fuerza P originará unas tensiones de compresión a lo largo de la barra, tales
que provoquen un acortamiento total de la barra también de 0.2 mm. Si no fuese así, el
montaje de la pieza no sería posible.
En los tramos 1 y 3, la sección es constante, luego la tensión también lo será en
cualquier sección perpendicular al eje. Sin embargo, en el tramo 2, la tensión dependerá de
la sección en que nos encontremos, por ser ésta variable.
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND
La ecuación de compatibilidad de deformaciones será por tanto:
δT = - 0.2 mm. = δ1 + δ2 + δ3
donde δT es la variación total de longitud en la barra, y δ1 , δ2 y δ3 son las variaciones de
longitud en los tramos 1, 2 y 3 respectivamente. El signo menos en - 0.2 mm. se debe a
que se trata de un acortamiento.
• TRAMO 1.
P
P
P
=
=
kg/cm2 .
2
2
A 1 π ⋅ r1
π ⋅5
σ1 =
(1)
Por la ley de Hooke:
ε1 =
σ1
P
=
2
E 1 π ⋅ 5 ⋅ 2 ⋅ 10 6
Puesto que σ1 es constante en todo el tramo, ε1 también lo es.
δ1 = ε1 ⋅ a =
P
⋅ 200 mm.
π ⋅ 5 ⋅ 2 ⋅ 10 6
2
• TRAMO 2.
En este caso, la tensión dependerá de la sección en que nos encontremos. La
geometría del tramo es simétrica respecto a su sección media, luego bastará encontrar cuál
es el acortamiento de una de las mitades ( δb ), y multiplicarlo por dos para saber el
acortamiento del tramo 2 completo ( δ2 ).
α
r
r1
r2
tg α =
r2 − r1 65 − 50
=
= 012
.
b
125
r = r1 + tg α ⋅ x* = 50 + 012
. ⋅x
x*
b
El área de cada sección será:
A sec ción − 2 = π ⋅ r 2 = π ⋅ (50 + 0.12 ⋅ x*) 2
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND
mm2 .
mm.
Y la tensión en cada una de ellas debido a la fuerza de compresión P:
σ 2 ( x*) =
P
A sec ción _ 2
=
P
100 ⋅ P
=
2
π ⋅ (50 + 012
π ⋅ (50 + 012
. ⋅ x*)
. ⋅ x*) 2
100
kg/cm2 . (2)
Por la ley de Hooke:
ε 2 ( x*) =
σ 2 ( x*)
100 ⋅ P
=
E2
π ⋅ (50 + 012
. ⋅ x*) 2 ⋅ 12
. ⋅ 10 6
Puesto que ε2 depende de x* , la variación total de longitud de este tramo de
longitud b será la integral de ε2(x*) a lo largo de dicho tramo.
b
δ b = ò ε 2 ( x*) ⋅ dx =
125
100 ⋅ P
ò π ⋅ (50 + 012
. ⋅ x*)
0
0
2
⋅ 1.2 ⋅ 10
6
⋅ dx* =
100 ⋅ P
1ù
é 1
⋅ ê − + ú mm.
6
π ⋅ 12
. ⋅ 10 ⋅ 0.12 ë 65 50 û
Por lo tanto:
δ2 = 2 ⋅ δb =
200 ⋅ P
1ù
é 1
⋅ ê − + ú mm.
6
π ⋅ 1.2 ⋅ 10 ⋅ 0.12 ë 65 50 û
• TRAMO 3.
Procediendo del mismo modo que en el tramo 1:
σ3 =
P
P
P
kg/cm2 .
=
=
2
2
A 3 π ⋅ r1
π ⋅5
ε3 =
σ3
P
=
2
E 3 π ⋅ 5 ⋅ 0.75 ⋅ 106
(3)
Se observa que la tensión σ3 coincide con σ1 . No ocurre así con las deformaciones
unitarias en la dirección del eje, ε1 y ε3 , ya que el módulo de elasticidad es diferente para
los tramos 1 y 3.
δ3 = ε3 ⋅ c =
P
⋅ 400 mm.
π ⋅ 5 ⋅ 0.75 ⋅ 10 6
2
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND
La ecuación de compatibilidad de deformaciones queda finalmente:
−0.2 =
200 ⋅ P
200 ⋅ P
1ù
400 ⋅ P
é 1
⋅ ê− + ú +
+
2
6
6
2
π ⋅ 5 ⋅ 2 ⋅ 10
π ⋅ 1.2 ⋅ 10 ⋅ 0.12 ë 65 50 û π ⋅ 5 ⋅ 0.75 ⋅ 10 6
Resolviéndola se obtiene:
P = - 19794 kg.
El signo menos indica que es compresión. Conocido el valor de P, a través de las
expresiones (1) , (2) y (3) , la ley de variación de las tensiones normales a lo largo de la
barra está definida de la siguiente manera:
P
P
1
2
3
2
x
0 ≤ x ≤ 200 mm.
σ( x) = −252 kg/cm2.
200 ≤ x ≤ 325 mm.
σ ( x) =
325 ≤ x ≤ 450 mm.
σ ( x) =
450 ≤ x ≤ 850 mm.
σ( x) = −252 kg/cm2.
−630063
. ⋅ ( x − 200)]
[50 + 012
−630063
. ( x − 325)]
[65 − 012
2
2
kg/cm2.
kg/cm2.
Se muestra a continuación la representación gráfica de esta ley de variación:
x
-149 kg/cm2
-252 kg/cm2
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND
b) Para que se anulen las tensiones que se producen por el error de construcción
de +0.2 mm. , se necesitaría una disminución de temperatura que provoque una
disminución de longitud igual a este error.
Suponiendo la misma variación de temperatura en todos los tramos:
∆l =
3
3
i =1
i =1
å ∆T ⋅ α i ⋅ l i = ∆ T ⋅ å α i ⋅ l i
[
]
−0.2 = ∆T ⋅ 12
. ⋅ 10 −5 ⋅ 200 + 14
. ⋅ 10 −5 ⋅ (125 + 125) + 2.4 ⋅ 10 −5 ⋅ 400
Resultando:
∆T = −12.9 ºC
El signo menos indica que se trata de un descenso de temperatura.
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND
8. Una barra de directriz rectilínea y de sección constante, fija en sus extremos a dos
cuerpos rígidos separados una distancia L, está sometida a una ley de carga axial p=p(x)
y a una ley de variación de temperatura ∆T=∆T(x), tal como se indica en la figura. Se
sabe, por otra parte, que dicha barra tiene un error de construcción, de forma que, en
ausencia de carga y de variación de temperatura, resulta 0’5 mm más larga que la
referida distancia L. Se pide:
a) Reacciones en los extremos de la barra.
L
b) Expresión analítica y representación gráfica
aproximada de la ley de variación de la fuerza
normal, indicando el valor del máximo.
Datos:
p (kg/m)
Coeficiente de dilatación lineal: 1’2.10-5 ºC-1.
6
2
Módulo de elasticidad: 2’1.10 kg/cm .
4000
Sección de la barra: 5 cm2.
Longitud L=2’000 m.
1000
x
∆T (ºC)
40
20
******************************************************
Suprimiendo la ligadura de la izquierda (se podría hacer también con la de la derecha)
se puede definir un sistema isostático equivalente, con una fuerza desconocida X en la
ligadura suprimida, y la condición de deformación ∆L = 0.
p = p(x)
X
El esfuerzo normal en una rebanada elemental de abscisa x viene dado por:
X
p = p(x)
p1
p2
x
N ( x) = X −
x
ò p( x )dx = X − ò
0
x
0
p 2 − p1
p 2 − p1 x 2
x )dx = X − p 1 x −
( p1 +
L
L
2
De donde, la deformación debida a las cargas en la rebanada elemental es:
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND.
p 2 − p1 x 2
N ( x )dx
1
=
( X − p1 x −
)dx
d ( ∆L p ) =
EA
EA
L
2
Integrando:
∆L p =
1
L2 p 2 − p 1 L3
−
( XL − p 1
)
EA
2
L
3
Para considerar el efecto de la variación de temperatura se puede seguir un proceso
análogo con T = T(x), o bien, considerando que la ley de variación de temperaturas es
lineal, calcular la deformación con la temperatura media:
∆LT = αL
∆T1 + ∆T2
2
Considerando, además, el error de construcción, ∆L0, la deformación total, que ha de ser
igual a cero, viene dada por:
∆L = ∆L p + ∆LT + ∆L0
Sustituyendo las expresiones anteriores y despejando X, resulta:
X = p1
∆T1 + ∆T2
EA
L
L
EA − ∆L0
+ p2 − α
2
L
3
6
Con los valores numéricos:
p1=1000kg/m
p2=4000kg/m
∆T1=40ºC
∆T2=20ºC
∆L0=0,5×10-3 m
α=1,2×10-5 ºC-1 m
E=2,1×1010 kg/m2
A=5×10-4 m2
L=2 m
resulta:
X = − 4405 kg (el signo menos indica que la reacción va en sentido contrario al
supuesto, es decir, hacia la derecha).
N(x)= − 4405 − 1000 x − 750 x2 (con N en Kg y x en m.; signo +:tracción; signo − :
compresión).
Para el cálculo de la reacción en el extremo de la derecha, consideramos ΣFx=0:
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND.
L
p = p(x)
X
X + X'=
X’
L
ò0 p( x )dx
de donde:
X ' = − X + p1 L + ( p 2 − p 1 )
L
2
con: X = − 4405 kg, y sustituyendo los demás valores numéricos, resulta:
X’ = 9405 kg (el signo positivo expresa que el sentido supuesto, hacia la izquierda, es
correcto).
Nótese la concordancia de los resultados de X y X’ con los valores de la expresión de
N(x) para x=0 y para x=L.
Para proceder a la representación gráfica de N(x), así como para obtener los valores más
característicos, bastaría con introducir su ecuación en la calculadora. No obstante,
observemos que, del equilibrio de la rebanada elemental:
N
p
N+dN
dx
p dx + dN = 0 ; p = −
Es decir, la ley de carga p(x) es la derivada de
N(x) con el signo cambiado. Así, al ser p(x)
positiva (hacia la derecha) y creciente en toda la
barra, su primitiva N(x) tiene signo negativo
(compresión), y es creciente, y con derivada
creciente, en valor absoluto, en todo el
intervalo.
dN
dx
N
9405
4405
L=2
ETSI-ICAI. Departamento de Ingeniería Mecánica
Elasticidad y Resistencia de Materiales. 3º IIND.
x