to get the file
Anuncio

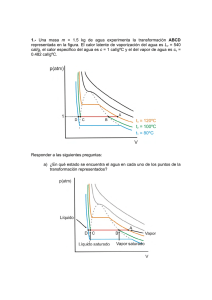
1. Cinco moles de un gas perfecto cuyo coeficiente adiabático es γ = 7 están a 5 una temperatura TA=300K, y experimentan dos procesos reversibles A→B: Calentamiento isóbaro hasta duplicar su temperatura B→C: Enfriamiento isócoro hasta hacerse la mitad su temperatura. a) Representar los dos procesos en los diagramas P-V, T-V y P-T. b) Calcular el calor total, expresado en calorías, indicando si es realizado por el gas o sobre él. c) Calcular el trabajo total, expresado en calorías, indicando si es realizado por el gas o sobre él. d) Calcular la variación de la energía interna del gas e) Calcular la variación de entropía del gas. Considerar Ln2=0.7 Resolución P El diagrama P-V de Clapeyron es A B C V T P=Cte V=Cte B 2TA TA P A B A C C V 7 C b) Con el valor del coeficiente adiabático γ = = p y la relación de Mayer T 5 Cv TA 2TA R = C p − Cv se deduce que C p = 7R 5R y Cv = . 2 2 La etapa A-B es isóbara, por lo que el calor es cal 7 (600 − 300) K = 10500 cal absorbido QA→ B = nCP (TB − TA ) = 5mol ⋅ 2 2 mol ⋅ K y en la etapa B-C se mantiene constante el volumen, por tanto cal 5 QB →C = nCv (TC − TB ) = 5mol ⋅ 2 (300 − 600) K = −7500 cal cedido por el gas 2 mol ⋅ K El calor neto es Qneto = QA→ B + QB →C = 10500 cal − 7500cal = 3000 cal c) En la etapa B-C, no hay variación del volumen y por tanto no se realiza trabajo; así, el trabajo total es el trabajo realizado en la primera etapa B WA→ B = ∫ PdV = PA (VB − VA ) = nR(TB − TA ) = 5 mol ⋅ 2 A cal (600 − 300) K = 3000 cal = Wneto mol ⋅ K Por ser positivo, es un trabajo realizado sobre el gas. d) La variación de energía interna cal 5 ∆U A→ B = nCv (TB − TA ) = 5mol ⋅ 2 (600 − 300) K = 7500 cal 2 mol ⋅ K 5 cal ∆U B →C = nCv (TC − TB ) = 5mol ⋅ 2 (300 − 600) K = −7500 cal 2 mol ⋅ K de forma que la variación total de energía interna es nula. e) La variación total de entropía es la suma de las variaciones de entropía de cada etapa ∆S = ∆S A→ B + ∆S B →C = TB ∫ TA nC p T dT + TC nCv T T dT = nC p Ln B + nCv Ln C = T TA TB TB ∫ cal cal cal 5 7 = 5 mol ⋅ ⋅ 2 Ln 2 + 5 mol ⋅ ⋅ 2 Ln0,5 = 35 Ln 2 − 25Ln 2 = 10Ln 2 = 7 K 2 mol ⋅ K 2 mol ⋅ K