GUÍA DE ACTIVIDADES – LEYES DE KEPLER – PARTE 3 1) La 3ª
Anuncio
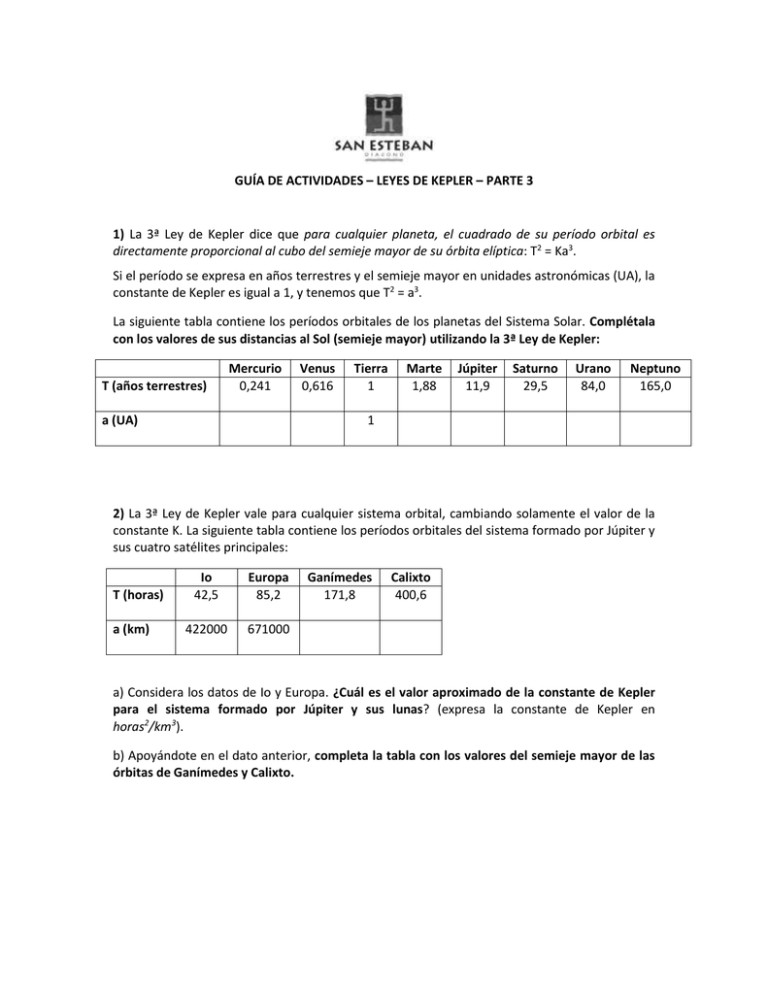
GUÍA DE ACTIVIDADES – LEYES DE KEPLER – PARTE 3 1) La 3ª Ley de Kepler dice que para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo del semieje mayor de su órbita elíptica: T2 = Ka3. Si el período se expresa en años terrestres y el semieje mayor en unidades astronómicas (UA), la constante de Kepler es igual a 1, y tenemos que T2 = a3. La siguiente tabla contiene los períodos orbitales de los planetas del Sistema Solar. Complétala con los valores de sus distancias al Sol (semieje mayor) utilizando la 3ª Ley de Kepler: T (años terrestres) Mercurio 0,241 a (UA) Venus 0,616 Tierra 1 Marte 1,88 Júpiter 11,9 Saturno 29,5 Urano 84,0 Neptuno 165,0 1 2) La 3ª Ley de Kepler vale para cualquier sistema orbital, cambiando solamente el valor de la constante K. La siguiente tabla contiene los períodos orbitales del sistema formado por Júpiter y sus cuatro satélites principales: T (horas) a (km) Io 42,5 Europa 85,2 422000 671000 Ganímedes 171,8 Calixto 400,6 a) Considera los datos de Io y Europa. ¿Cuál es el valor aproximado de la constante de Kepler para el sistema formado por Júpiter y sus lunas? (expresa la constante de Kepler en horas2/km3). b) Apoyándote en el dato anterior, completa la tabla con los valores del semieje mayor de las órbitas de Ganímedes y Calixto.