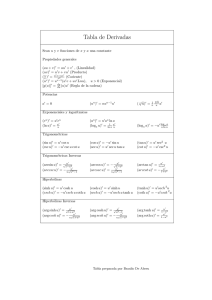
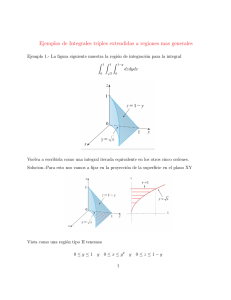
Tablas o fórmulas de integración

Tablas o fórmulas de integración
Efraı́n Martı́nez M.
19 de abril de 2016
Resumen
Integrales de funciones
elementales f (x) tales que F ′ (x) = f (x) que se pueden invertir y
Z
escribir de la forma
f (x) dx = F (x) + C, se conocen como integrales inmediatas o simplemente
de inversión directa, las siguientes propiedades y fórmulas se utilizan como tablas de integración
inmediata.
0.1.
Propiedades
(i)
Z
dF (x) = F (x),
(ii)
Z
kf (x)dx = k
(iii)
Z
[f (x) ± g(x)]dx =
(iv)
Z
0.2.
n
X
Z
y
Z
f (x) dx = f (x) dx,
esto es:
Z
d=d
Z
=I
f (x)dx
Z
!
ki fi (x) dx =
i=1
d
f (x)dx ±
Z
g(x)dx
n Z
X
ki fi (x)dx
suma de n funciones
i=1
Fórmulas de integración inmediata
En las siguientes fórmulas u = u(x), v = v(x) son funciones de variable x, mientras que a, k, n
constantes y C constante de integración.
Z
un+1
1.
un dx =
+ C n 6= −1
n+1
Z
du
2.
= ln |u| + C
u
Z
3.
eu du = eu + C
4.
Z
au du =
Z
5.
Z
u dv = uv −
eu ln a du =
Z
v du,
eu ln a
au
=
+C
ln a
lna
integración por partes.
1
6.
Z
f (n) g dx = f (n−1) g − f (n−2) g ′ + f (n−3) g ′′ − · · · (−1)n
7.
Z
sin u du = − cos u + C
8.
Z
cos u du = sin u + C
9.
Z
sec2 u du = tan u + C
10.
Z
csc2 u du = − cot u + C
11.
Z
sec u tan u du = sec u + C
12.
Z
csc u cot u du = − csc u + C
13.
Z
√
14.
Z
a2
15.
Z
du
u
1
u
1
√
= arcsec + C = − arccsc + C
a
a
a
a
u u 2 − a2
16.
Z
sinh u du = cosh u + C
17.
Z
cosh u du = sinh u + C
18.
Z
sech2 u du = tanh u + C
19.
Z
csch2 u du = − coth u + C
20.
Z
sech u tanh u du = − sech u + C
21.
Z
csch u coth u du = − csch u + C
Z
√
f g (n) dx
forma general
u
u
du
= arcsin + C = − arc cos + C
2
a
a
−u
a2
du
1
u
1
u
= arctan + C = − arccot + C
2
+u
a
a
a
a
p
du
u
= argsinh + C = ln(u + u2 + a2 ) + C,
a
u 2 + a2
Z
p
du
√
23.
= argcosh u + C = ln u + u2 − a2 + C
u 2 − a2
22.
Z
2
a>0
u>a>0
E.MARTÍNEZ M.
u+a
24.
+ C,
a2 > u 2
u−a
Z
du
1
u
1
u−a
25.
=
−
argcoth
+
C
=
ln
+ C,
u 2 > a2
u 2 − a2
a
a
2a
u+a
Z
du
1
u
√
√
26.
= argsech u + C = ln
+ C,
a>u>0
a
u a2 − u 2
a + a2 − u 2
Z
du
1
u
√
√
27.
= argcsch u + C = ln
+ C,
u 6= 0
a
u u 2 + a2
a + u 2 + a2
Z
du
1
u
1
= argtanh + C =
ln
a2 − u 2
a
a
2a
Fórmulas sujetas a demostración, las mismas que serán deducidas en el desarrollo de los diferentes
métodos de integración.
Cualquier error es responsabilidad del autor1 , sugerencias a la dirección que aparece en pie de
página, gracias.
1 Email:
[email protected];
SitioWeb: http://www.eframath.com
3
E.MARTÍNEZ M.