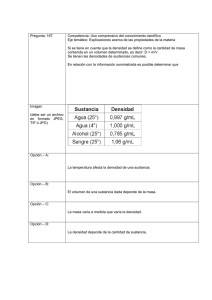
tema2 - WordPress.com

“Sapere Aude”
Ronda de los molinos s/n. Écija. e-­‐mail: [email protected] Departamento de Física y
Química
Tercero de Secundaria. Profesor: Rafael González
Farfán.
La materia y sus propiedades.
Modelo Cinético
http://www.iesnicolascopernico.org/fisica.htm
Física y Química para 3º de ESO 2 La Materia y sus Propiedades. Estados de Agregación. Teoría Cinética. “[…] consiste, pues, toda naturaleza en dos principios: cuerpos y vacío en donde aquéllos nadan y se mueven. Que existen cuerpos lo demuestra el sentido común. […] Si no existiera, pues, aquel espacio que llamamos vacío, no estarían los cuerpos asentados, ni moverse podrían, como acabo de decirte. Además de los cuerpos y el vacío, no conocemos en la naturaleza una tercera clase independiente de los principios dichos: lo que existe es necesariamente de pequeña o gran extensión, si lo sintiera el tacto, aunque ligera y levemente, debemos colocarlo entre los cuerpos”. De rerum natura, Tito Lucrecio Caro. (siglo I a. C.) [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 3 LA MATERIA Y SUS PROPIEDADES.
ESTADOS DE AGREGACIÓN. TEORÍA CINÉTICA
Al igual que ocurre con muchos conceptos en Ciencia, no es fácil dar una definición de materia. Aquí
daremos una definición que veremos enriquecida cuando estudiemos algunas de sus propiedades, como
la masa, el volumen, la temperatura, la densidad, el punto de fusión y el punto de ebullición entre otras.
Durante el desarrollo del tema intentaremos eliminar algunas ideas que podamos tener sobre la
materia, como por ejemplo que es continua, que en la materia no existe, el vacío, que es estática, etc.
La materia está formada por sustancias. El agua, el cobre, el dioxígeno o la sal común son sustancias y
las podemos encontrar en diferentes estados de agregación: sólido, líquido y gaseoso. Las sustancias
tienen unas propiedades generales, comunes a todas ellas, independiente del estado de agregación
en el que se presenten, y otras propiedades, características de cada una, que pueden servir para
identificarlas. Todas las sustancias, ya se presenten en estado sólido, líquido o gaseoso, tienen masa
(pesan) y ocupan un lugar en el espacio (tienen volumen). En estado sólido y líquido el comportamiento
de las distintas sustancias difiere mucho presentando una gran variedad en los valores de sus
propiedades, mientras que las sustancias en estado gaseoso, aunque sean distintas, se comportan de
forma parecida. Llegar a un conocimiento de la estructura interna de la materia es más sencillo si
estudiamos el comportamiento de los gases, fijando nuestra atención tanto en sus propiedades
generales (pues son materia), como en el hecho de que es el estado de agregación en el que la
materia presenta un comportamiento más simple.
Para poder explicar el comportamiento de la materia surge la necesidad de proponer un modelo
discontinuo de la materia, el modelo cinético; pero debemos tener claro que este modelo, (hoy totalmente
probado por los científicos, por lo que se llama teoría), es una ‘herramienta’ para explicar lo observable,
que es distinto al hecho observable en sí.
Indicar por último, que la materia está en continuo cambio. Y en cualquier cambio que sufre la
materia interviene algo que los científicos ha denominado energía, que no es más que una propiedad de
la materia relacionada con la capacidad de producir cambios en ella misma o en otros sistema
materiales. Aunque a lo largo del curso se hace uso de este concepto, será en cursos posteriores de Física
y Química cuando estudies con detalle las manifestaciones de esta importante magnitud.
I. LA MATERIA Y SUS PROPIEDADES.
La idea de materia está íntimamente relacionada con lo que percibimos con nuestros sentidos, como ya
indicó el poeta Tito Lucrecio Caro hace más de dos milenios. En Ciencia es muy frecuente que la
definición de un concepto no sea fácil, por lo que muchas veces se recurre a su descripción a partir de
sus propiedades. Este es el caso de la materia. Resulta más sencillo definir lo que es la materia a
partir de las propiedades que presenta. Entre esas propiedades podemos destacar a la masa y el
volumen. En una primera instancia, podemos definir la materia como todo aquello que tiene masa (se
puede pesar) y ocupa un volumen (un lugar en el espacio). En realidad, esto no es más que una primera
aproximación a la definición que andamos buscando, pues una definición más precisa al concepto de
‘materia’ es algo más profunda y escapa a los objetivos que ahora buscamos. Así, es materia una pizarra,
un vaso de agua o el aire que respiramos y no es materia la belleza, el amor o la inteligencia.
Para proceder al estudio de la materia hacemos uso de fracciones limitadas de la misma. Se
denomina sistema material a la porción de materia que se considera de forma aislada para ser
objeto de estudio. Si además tiene una forma determina se llama cuerpo. El agua contenida en un
vaso o el aire de una habitación son ejemplos de sistemas materiales, mientras que una roca o un florero
de cristal son sistemas materiales o cuerpos. Por otro lado, no toda la materia es igual. A cada una de
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 4 las diversas clases de materia que existen en la Naturaleza se le denomina sustancia. Son sustancias el
agua, el hierro, el oxígeno y el butano. Todo lo que es materia está formado por sustancias o mezclas de
sustancias.
A continuación se presenta una clasificación de los sistemas materiales, que iremos estudiando poco a
poco en los temas siguientes, pero que es conveniente que te vayas familiarizando:
Una sustancia pura
es aquella que no
puede descomponerse
en otras más
elementales por
métodos físicos
sencillos y que
presenta una
composición y
propiedades fijas en
toda su masa.
Sistemas Materiales Una mezcla es un
sistema material
formado por dos o
más sustancias.
Simple Una sustancia
simple es una
sustancia pura que
no se puede
descomponer en
otras más sencillas
por ningún método.
Mezcla Sustancia Pura Compuesto Un compuesto es una
sustancia pura,
constituida por diferentes
elementos, que se puede
descomponer en otras más
sencillas por
procedimientos químicos
Homogéneas Una mezcla homogénea o
disolución es una mezcla
cuyos componentes no se
distinguen ni con un
microscopio ordinario y
presenta propiedades y
composición Heterogénea Una mezcla heterogénea es
aquella cuyos componentes se
distinguen a simple vista o con
ayuda de un microscopio
ordinario y su composición y
propiedades varían en
distintas porciones de la
misma La mayoría de las sustancias que conocemos son sustancias compuesto, como el agua, el butano, el
amoniaco, etc. Las sustancias compuesto están constituidas por moléculas (o iones) iguales, formadas
por dos o más átomos de distinta clase. Sólo existen en la Naturaleza unos 88 tipos de átomos o
elementos (sodio, Na, azufre, S, oxígeno, O, …). Cuando una sustancia está formada por un solo tipo de
átomo se denomina sustancia simple. Así, el O2 (oxígeno que se encuentra en el aire) y el O3 (ozono) son
sustancias simples constituidas por el mismo elemento, el oxígeno. Puede ser conveniente aclarar esto
un poco más. Una sustancia simple es algo observable, como por ejemplo el plomo, que encontramos en
estado sólido, pero que si lo calentamos suficientemente, puede pasar a estado líquido e, incluso, a
estado gaseoso. Sin embargo, el elemento químico plomo ni es sólido, ni tiene punto de fusión, etc., ya
que a él no se le pueden aplicar las propiedades observables, pues se trata de un concepto que
representa a un átomo de una determinada clase.
Por último, comentar que los métodos físicos a los que nos referimos en el esquema son la filtración, la
decantación, la destilación, etc. Con respecto a los métodos químicos, destacamos la electrólisis, o
reacción química provocada por el paso de la corriente eléctrica, y la descomposición térmica, o reacción
química que ocurre cuando aumentamos la temperatura de una sustancia, para desaparecer y obtener
nuevas sustancias. Como ya se ha comentado anteriormente, todo esto se tratará con detalle en temas
próximos.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 5 I.1. Propiedades de la materia.
Son muchas y muy diversas las propiedades que podemos encontrar en la materia. Todas estas
propiedades podemos clasificarlas en dos grandes grupos: propiedades generales y propiedades
características. Las propiedades generales de la materia son aquéllas que NO permiten
identificar las sustancias, como la masa, el volumen y la temperatura, que estudiaremos en este
tema. Así, por ejemplo, dos sistemas completamente diferentes pueden tener la misma masa (un kg de
garbanzos y un kg de oro), volumen (un litro de agua y un litro de mercurio) o temperatura (la pizarra
de una clase y una mesa de la misma). Las propiedades características de la materia son
aquéllas que SÍ permiten identificar las sustancias, como el sabor, la elasticidad, la dureza, o la
densidad. Es importante destacar que hablamos de sustancias puras y no de mezclas.
A1. Contesta a estas cuestiones: (a) ¿Qué pesará más 100 gramos de aceite o 100 gramos de hierro?; (b) ¿qué ocupará mayor 3
3
volumen 25 cm de agua o 25 cm de plomo?; (c) En el interior de una esfera de cristal introducimos un trozo de papel y la cerramos. Todo el conjunto tiene una masa de 75 gramos. Con una lupa hacemos que arda el papel interior. Al final, ¿la masa será mayor, menor o igual a 75 gramos? Explicación. A2. Cuando se calienta un objeto, éste aumenta de tamaño. Por ello, habrás visto que, por ejemplo, se deja una pequeña separación entre los tramos de raíl del tren. Disponemos de una pieza metálica de 150 gramos. La calentamos y la volvemos a pesar. La balanza indicará una masa: (a) mayor de 150 gramos; (b) menos de 150 gramos; (c) igual que 150 gramos; (d) no podemos saberlo. A3. Si en una jeringa tapamos la salida, podemos comprimir el aire contiene. En qué casos habrá más aire: (a) antes de comprimir; (b) después de comprimir; (c) en los dos casos el mismo; (d) no puede saberse. A4. La medida de la masa de un objeto con una balanza es 36.4 g, ¿crees que lo mismo que decir 36.40 g? Veamos a continuación algunas de estas propiedades más detalladamente:
La Masa:
Es una propiedad general de la materia que se define (en una aproximación válida para nuestros
propósitos) como la cantidad de materia que contiene un cuerpo, y se mide con un instrumento
denominado balanza. En los laboratorios podemos encontrarnos dos tipos de balanzas: la balanza de
platillos, en la que la masa de un cuerpo se mide por comparación con otras masas que se presentan en
pesas de distintas cantidades, y la balanza digital, una balanza electrónica que es muy precisa y
cómoda. Su unidad en el SI es el kilogramo, y en el sistema cegesimal, el gramo. Conviene destacar
que la cantidad de materia que tienen los cuerpos es independiente del estado de agregación en que se
encuentren, es decir, dada una cierta masa de sustancia, ésta sigue siendo la misma si su estado es
sólido, líquido o gaseoso. Tras la realización de muchas experiencias, los científicos han formulado el
principio de conservación de la masa, que dice que en cualquier proceso, la masa total del sistema
se conserva, siempre que no entre o salga materia del mismo.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 6 El Volumen:
Se trata de otra propiedad general de la materia que se define como el
espacio que ocupa un sistema material. Medir el volumen es una
operación fácil, pero debemos tener en cuenta el estado en que se encuentra.
Así, para medir un líquido aprovechamos la propiedad que tienen de adoptar
la forma del recipiente que los contiene, con lo que se emplea una probeta,
una pipeta, una bureta, o cualquier aparato específicamente diseñado para
ello.
Si lo que queremos medir es un sólido con forma geométrica regular, su
volumen se calcula directamente, mediante el uso de la fórmula adecuada (V
Instrumentos de medida de
volúmenes de líquidos: pipeta
= l3 para un cubo, V = a· b· c para un ortoedro, V = π· r2 · h para un cilindro,
(izada.) y probeta (dcha.)
3
V = (4/3)· π· r para una esfera, etc.). Si el sólido no tiene forma regular,
podemos determinar su volumen aplicando el método de inmersión, que
consiste en sumergir el sólido en agua contenida en un recipiente graduado, como una probeta. El nivel
del líquido se elevará tanto como el sitio que ocupe el sólido, esto es, tanto como el volumen que tenga.
Medir el volumen de los gases no es tan directo. Es preciso tener en cuenta unos factores que afectan al
espacio que ocupan. Tales factores son la presión y la temperatura, de los que hablaremos más adelante.
Aunque los gases ocupan siempre el volumen del recipiente que los contiene, una misma masa de gas
puede ocupar distintos volúmenes según a la presión y temperatura a la que se encuentre. Esto no sucede
de modo apreciable ni con los sólidos ni con los líquidos, para los valores usuales de presión y
temperatura.
La unidad de volumen en el SI es el m3 y en el sistema CGS es el cm3. Un concepto relacionado con el
volumen es la capacidad de un sólido hueco, que es el espacio que queda en su interior. Normalmente se
utiliza como unidad de capacidad al litro y, como ya sabemos, un litro equivale a un decímetro cúbico.
A5. ¿Cuántos litros de agua caben en un cubo hueco de 2 cm de lado? ¿Y cuántos de leche? ¿Y cuántos de mercurio? ¿Cómo se denomina es espacio que queda en el interior de un sólido hueco? A6. Una piscina tiene 25 m de longitud, 10 m de anchura y 2 m de profundidad. Se pide: (a) su capacidad, en litros; (b) el tiempo que tardaría en llenarla un grifo con un caudal de 4 L/s. A7. ¿Por qué no se puede medir el volumen de un trozo de tiza irregular o de un poco de sal por inmersión? A8. ¿Cómo podríamos medir el volumen de sólidos que flotan en el agua? A9. Supón que tenemos dos esferas exactamente iguales, una de plomo y otra de plastilina. Las sumergimos en sendos recipientes con agua que inicialmente tienen el mismo nivel. ¿En qué caso elevará más el agua después de haber sumergido cada cuerpo? En un segundo experimento, sacamos la plastilina del recipiente anterior, y la moldeamos como un gusano. Ahora la volvemos a introducir. ¿Se elevará el agua hasta el mismo nivel que antes? Explicación. A10. Si nos dan una botella de refresco vacía, indica cómo se podría medir: (a) el volumen total ocupado por la botella; (b) su capacidad; (c) el volumen del vidrio. [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 7 La Temperatura:
Supongamos que dejamos una chapa metálica al Sol. Al cabo de un tiempo, la chapa ha absorbido una
cierta cantidad de energía, que podemos detectar porque al tocarla nos quemamos. Decimos entonces
que la chapa ‘se ha calentado’. Cuando por el contrario la chapa pierde energía notamos justo lo
contrario: decimos que ‘se ha enfriado’. Si colocamos un cuerpo caliente en contacto con un cuerpo frío,
se produce una transferencia de energía del cuerpo caliente al cuerpo frío. Esta transferencia de
energía se denomina calor. Como consecuencia de este tránsito energético, el cuerpo ‘caliente’ se
enfría y el cuerpo frío se calienta hasta que ambos cuerpos llegan a tener algo en común. Los físicos han
inventado una nueva magnitud para denominar a ese algo común: la temperatura. Por tanto, cuando
dos cuerpos a distinta temperatura se ponen en contacto, tiene lugar un tránsito de energía del cuerpo
de mayor temperatura al cuerpo de menor temperatura hasta que los cuerpos adquieren la misma
temperatura.
Es importante que se reflexione esto detenidamente. El calor es una manera de transferir energía,
por lo que los cuerpos no tienen calor. Los cuerpos poseen energía, de manera que cuando dos cuerpos a
distinta temperatura se ponen en contacto, se produce una transferencia de energía que llamamos
calor. Por tanto, no existe el calor como algo ‘dentro de los cuerpos’. Hay materia y energía. De igual
manera, tampoco existe el frío. Un cuerpo frío es un cuerpo con una temperatura menor que otro (al que
llamamos cuerpo caliente). Así pues, cuando dos cuerpos se ponen en contacto, tienden a alcanzar la
misma temperatura.
Un fenómeno que se aprecia en los cuerpos cuando aumenta su temperatura es que se dilatan, es
decir, aumenta su tamaño. Ésta es la propiedad que se aprovecha para medir la temperatura, mediante
el uso de los termómetros de líquidos (normalmente de mercurio o de alcohol teñido con algún
colorante). Estos termómetros disponen de un tubo muy fino, cerrado por la parte inferior y con un
abultamiento llamado bulbo, que sirve como depósito de líquido (en el dibujo se ha exagerado la anchura
del tubo, ya que el volumen total del tubo no excede el 2% del volumen del bulbo). Al aumentar la
temperatura del líquido, aumenta su volumen y asciende por el tubo. Al disminuir la temperatura, el
volumen del líquido desciende.
Un termómetro se gradúa señalando dos puntos. El primero
corresponde a la altura que alcanza el líquido cuando el
termómetro se sumerge en una mezcla de hielo y agua líquida. El
segundo punto corresponde a la altura que alcanza el líquido
cuando se sumerge en agua hirviendo. Pues bien, la graduación
del termómetro dependerá de los valores que le demos a estos
puntos:
- El físico alemán Daniel Gabriel Fahrenheit asignó, en
1724, el valor de 32 al punto de la mezcla de hielo y agua
líquida y el valor de 212 al punto del agua hirviendo. Cada
una de las 180 partes en que se puede dividir el intervalo (valor que se obtiene
de 212 - 32) se llama grado Fahrenheit (ºF).
- El físico y astrónomo sueco Anders Celsius asignó, en 1742, el valor 0 al
primer punto y el valor 100 al segundo. Cada una de las 100 partes se
denomina grado Celsius (anteriormente denominado grado centígrado,
nomenclatura vigente entre 1750 y 1967). Ambas escalas son relativas, porque
los valores dados a los dos puntos es arbitrario.
Anders CELSIUS
(1701-1744)
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 8 Independientemente de la escala utilizada, la
proporción entre el segmento (TC - 0) en ºC y el
segmento total (100 - 0) en ºC ha de ser la misma
en las dos escalas. Es decir:
T f − 32 Tx − x1
Tc − 0
=
=
100 − 0 212 − 32 x 2 − x1
donde Tx es la temperatura en cualquier escala y
x1 y x2 son los valores asignados a los puntos de
referencia correspondiente a la mezcla de
agua/hielo y al agua hirviendo.
- El científico inglés William Thomson demostró teóricamente que la
temperatura más baja posible sería, aproximadamente, 273 ºC bajo cero
(es decir, -273 ºC). Este valor se tomó como cero absoluto, dando lugar a la
escala absoluta de temperatura o escala Kelvin. En esta escala, al punto
de la mezcla agua/hielo se le asigna el valor de 273 K (no se pone ºK) y a
al punto de ebullición, 373 K. La escala Kelvin queda divida también en
100 partes (373-273), con lo que un grado Celsius equivale a un Kelvin. Al
final del tema trataremos de nuevo este asunto.
Las relaciones entre estas escalas se indican a continuación:
William THOMSON
TK = TC + 273; TF = 1.8 ⋅ TC + 32; 1K = 1º C; 1K = 1.8º F
primer baron de Kelvin (18241907)
La temperatura es una propiedad general y más adelante la
definiremos en función de la velocidad de las partículas que constituyen la materia.
A11. Supón que tienes dos termómetros, uno graduado en la escala Celsius y otro en la escala Fahrenheit, que se encuentran en el mismo lugar. Se pide: (a) ¿En cuál de los dos alcanzará el mercurio mayor altura? Explicación; (b) ¿qué valor numérico será mayor, Tc o Tf? A12. Un líquido se encuentra a una temperatura de 50 ºC y otro a 120 ºF. ¿Qué liquido se encuentra a mayor temperatura? A13. Un cuerpo experimenta una disminución de temperatura de 20 ºC. Expresa dicha variación en K. A14. Si leemos en la prensa que Nueva York está a 82 ºF, ¿cuál será la temperatura en ºC? A15. Un alumno decide inventar su propia escala de temperaturas. Para ello asigna el valor de 30 ºP (grado Pepe) a la mezcla agua/hielo y el valor de 90 ºP al agua hirviendo. ¿Cuál es la temperatura corporal habitual del ser humano expresada en dicha escala? Si el hierro funde a 1538 ºC, ¿qué valor le corresponde en la escala Pepe? A16. Un líquido hierve a 373 K y otro a 100 ºC. ¿Cuál de los dos hierve a una temperatura mayor? [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 9 La Densidad: Se trata de una propiedad característica de la materia, puesto que el valor de la
densidad es propio de cada sustancia pura en unas condiciones dadas; es decir, depende de la
naturaleza de cada sustancia. Esto significa que no hay dos sustancias puras que en las mismas
condiciones tengan la misma densidad, por lo que podemos utilizar esta magnitud para identificarlas.
Llamamos densidad de una sustancia al cociente entre su masa y el volumen que ocupa. Este
cociente significa la masa que tiene la unidad de volumen de la sustancia. Este concepto se hace
extensible a cualquier sistema material, porque las mezclas también tienen densidad, pero en este caso
NO se puede considerar una propiedad característica, porque depende de la composición de dicha
mezcla:
d=
m
V
La unidad en el SI es el kg/m3, aunque frecuentemente se utiliza la unidad del sistema cegesimal, el
g/cm3. En la tabla siguiente se muestran las masas de distintos cubos de hierro:
3
Arista (cm) Volumen (cm ) 1 1 2 8 3 27 4 64 3
Masa (g) Densidad (g/cm ) 7.9 7.9 63.2 7.9 213.3 7.9 505.6 7.9 Puede
observarse
que
la
relación
masa/volumen permanece constante,
independientemente del tamaño del cubo
elegido.
Este hecho es fundamental: la densidad de una sustancia no depende de la cantidad de materia que se
escoja, aunque sí depende de otros factores como la temperatura y el estado físico.
En la siguiente tabla se indican las densidades de algunas sustancias en g/cm3:
La determinación de la densidad de cualquier sustancia sólida es relativamente fácil.
Primero, con una balanza se mide la masa. Segundo, con una probeta y por el método
indirecto de inmersión se mide el volumen del cuerpo. Y en tercer lugar, el cociente
entre la masa y el volumen del objeto es su densidad.
Densímetro En el caso de un líquido, la densidad se determina con un densímetro, que es un flotador graduado de
vidrio que lleva en la parte inferior un lastre de perdigones para que flote verticalmente.
ACTIVIDAD RESUELTA como Ejemplo.
Se tienen 100 gramos de tres sustancias diferentes (A, B y C), cuyas densidades respectivas son: dA = 1,2
g/mL; dB = 2,8 kg/L; dC = 1,7 g/cm3. Se pide: a) ¿qué sustancia tendrá mayor masa?; b) ¿qué sustancia
tendrá más volumen?; c) ¿es cierto que 5 g de la sustancia B pesan más que 10 g de la sustancia A?; d) si
ponemos en el platillo de una balanza 10 g de la sustancia B, ¿qué volumen de la sustancia A habrá que
poner en el otro platillo para equilibrar la balanza?
Antes de resolver las cuestiones, transformamos las unidades de las densidades al sistema cegesimal, más práctico
en este ejercicio que el SI:
d A = 1.2
g 1ml
g
kg 10 3 g
1l
1dm3
g
g
⋅
= 1.2
; dB = 2.8
⋅
⋅
⋅
= 2.8
; dC = 1.7
.
3
3
3
3
3
3
ml 1cm
l 1kg 1dm 10 cm
cm
cm
cm3
(a) Esta cuestión sólo requiere una lectura atenta del enunciado. No se debe confundir masa con densidad. Como
partimos de 100 gramos de tres sustancias, todas tienen la misma masa.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 10 (b) Conocida la masa y la densidad de cada sustancia, determinar el volumen no es ningún problema:
VA =
m
mA
m
100 g
100 g
100 g
=
= 83.3 cm3 ; V B = B =
= 35.7 cm3 ; VC = C =
= 58.8 cm3 .
g
g
g
dA
dB
dC
1.2
2.8
1.7
cm3
cm3
cm3
(c) De nuevo hay que leer atentamente el enunciado. Podemos pensar que como la sustancia B es más densa que la
sustancia A, la respuesta es afirmativa. Paro debemos tener claro, que estamos comparando masas, no densidades.
Por tanto, no es cierto que 5 g de B pesen más que 10 g de A, puesto que 5 g es menor que 10 g.
(d) Obviamente debemos poner en el otro platillo 10 g de A para que la balanza se equilibre. Y estos 10 g de A
ocupan un volumen de:
VA =
mA
=
dA
10 g
= 8.3 cm3 .
g
1.2
cm3
Puede ocurrir que nos encontremos con dos sustancias cuyas densidades sean muy parecidas, y que al
determinar experimentalmente nos den el mismo valor. El valor de una sola propiedad no puede
hacernos decir que dos sistemas son de la misma sustancia. De ahí que sea necesario el estudio de más
propiedades características. Sin embargo, cuando el valor de una propiedad es diferente, sí podemos
afirmar que corresponde a sustancias distintas.
A17. En el laboratorio se mide la masa y el volumen y el volumen de diferentes cantidades de sal común obteniéndose los siguientes datos: Volumen (mL) Masa (g) 20.0 44.00 30.0 66.00 50.0 110.00 70.0 150.00 80.0 172.00 Se pide: (a) la densidad de la sal común; (b) el volumen que ocuparán 500 g de sal común; (c) ¿El volumen ocupado por un paquete de 1000 g de sal será igual, mayor o menor que el volumen ocupado por un paquete de 500 g?; (d) La densidad de la sal en un paquete de 1000 g de sal será igual, mayor o menor que la densidad de la sal en el paquete de 500 g?; (e) ¿La densidad del azúcar será igual o diferente a la densidad de la sal común? ¿Cómo podríamos comprobarlo? A18. ¿Qué quiere 3
decir que la densidad del mercurio, a 20 ºC, es 13.6 g/cm ? Determina la masa en kilogramos de 1 L de mercurio y compárala con la de 1L de agua, también a 20 ºC. ¿Qué volumen ocupan 272 g de mercurio? A18.Una bola de aluminio de 8 cm de diámetro, ¿qué masa tendrá? A19. Tenemos bloque de aluminio cuyas dimensiones son 2 dm x 4 dm x 1 dm. Se pide: (a) determina su masa; (b) cortamos un trozo del bloque y, al ponerlo en la balanza, marca 0.125 kg. ¿Qué volumen ocupa ese trozo? ¿Cuál será su densidad? A20. ¿Qué volumen de gasolina hay que poner en el plato de una balanza para equilibrar 100 g de harina? [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 11 Otras propiedades características de la materia son:
Punto de fusión:
Es la temperatura a la cual una sustancia pasa del estado sólido al estado líquido. En
las sustancias puras, el proceso de fusión ocurre a una sola temperatura y el aumento
de temperatura por la adición de energía se detiene hasta que la fusión es completa.
Punto de ebullición:
Es la temperatura a la cual una sustancia pasa del estado líquido al gaseoso. Al igual
que el punto de fusión, mientras dura el proceso, la temperatura permanece constante.
La densidad, el punto de fusión y el punto de ebullición son las propiedades características más
utilizadas para identificar sustancias puras.
Dureza:
Es la propiedad que mide la resistencia de un sólido a ser rayado por otro sólido.
Ductilidad:
Propiedad de los metales por la cual se puede deformar y estirar en forma de cables o
hilos finos.
Maleabilidad:
Propiedad de los metales de deformarse mediante golpes en forma de láminas.
Compresibilidad:
Propiedad de los gases de reducir su volumen por aumento de una presión.
Viscosidad:
Propiedad que mide el grado de fluidez de un líquido. No tiene que ver con la
densidad: el agua es más densa que el aceite, pero es menos viscosa.
Conductividad, capilaridad, fragilidad, elasticidad, …
Por último, recordar de nuevo que en la práctica, una sola propiedad característica no puede
asegurarnos cuál sustancia es la que estamos estudiando, sino que tendremos que recurrir al estudio de
varias de ellas.
II.
ESTADOS DE AGREGACIÓN DE LA MATERIA.
Si analizamos con detalle cualquier sistema material que tengamos a nuestro alrededor, podemos llegar
a la conclusión de que pueden encontrarse de tres maneras diferentes, que denominamos estados físicos
o de agregación. Estos tres estados físicos son el estado sólido, el estado líquido y el estado
gaseoso. Las propiedades características de la materia (aun del mismo tipo de materia) son diferentes
en cada estado. Así, el hielo es menos denso que el agua líquida.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 12 Las propiedades que corresponden a los estados de agregación se indican en la tabla:
Sólidos
Líquidos
Gases
Tienen una forma definida.
No se comprimen. Su volumen es fijo.
No fluyen ni se difunden.
Toman la forma del recipiente que los contiene.
Prácticamente no se comprimen. Su volumen es fijo.
Fluyen con facilidad, aunque no se difunden.
Se adaptan a la forma del recipiente que los contiene.
Se comprimen y se expanden con facilidad.
Se dilatan y contraen con facilidad.
Fluyen fácilmente y se difunden
La experiencia nos demuestra que es posible encontrar una misma sustancia en los tres estados de
agregación, y el paso de un estado a otro depende de la temperatura fundamentalmente (y también de
la presión). Los cambios de estado nos informan sobre el nivel energético de la materia. El estado de
menor nivel energético es el sólido; el estado líquido presenta un mayor nivel energético y el gaseoso es
el de mayor nivel energético. Cuando los cambios de estado van en el sentido sólido " líquido " gas, se
dicen que son endotérmicos, pues se necesita un aporte de energía para que tenga lugar.
Cuando los cambios de estado van en el
sentido gas " líquido " sólido, se dicen que
son exotérmicos, pues en ellos se desprende
energía. En la figura se detallan los
nombres de los distintos procesos. Así, para
fundir el hielo es necesario aportar energía
(proceso endotérmico), mientras que la
solidificación requiere retirar energía del
sistema material (proceso exotérmico).
Es importante aclarar tres aspectos. En
primer lugar, el cambio de estado es un proceso físico, ya que al terminar, la sustancia sigue siendo la
misma. Sólo varían las características relacionada a la forma que adopta y al volumen que ocupa, pero
sigue siendo la misma sustancia. En segundo lugar, la palabra gas se emplea cuando se habla de una
sustancia que se encuentra normalmente en estado gaseoso (dioxígeno, dinitrógeno,…), mientras que el
término vapor se utiliza cuando la sustancia gaseosa procede de la evaporación de una sustancia
sólida o líquida. Y en tercer lugar, hablamos de vaporación, evaporación y ebullición como si fueran
sinónimos. Y no es exactamente así. La vaporización es el término genérico que se da al paso de líquido
a gas. Cuando la vaporización ocurre en la superficie del líquido a cualquier temperatura, se denomina
evaporización, cuya velocidad aumentará con el incremento de la temperatura. Si la vaporización se da
en toda la masa del líquido y a una temperatura determinada, se denomina ebullición, y llamamos a esa
temperatura, temperatura de ebullición.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 13 Cuando se calienta una sustancia pura sólida, su temperatura comienza a subir hasta que se alcanza el
punto de fusión, que es la temperatura a la
que se produce la fusión. Mientras el
sólido
se
está
fundiendo,
la
T (ºC) temperatura de la sustancia permanece
constante (por eso la temperatura de la
mezcla de hielo y agua no varía). Una vez
Ebullición Teb que se ha fundido todo el sólido, si se sigue
suministrando energía, la temperatura del
líquido comienza a subir hasta alcanzar el
Fusión Tfus punto de ebullición, o temperatura en que se
produce
la
situación
de
máxima
vaporización. Mientras el líquido puro
hierve se mantiene constante la
temperatura
(la
temperatura
de
Energía aportada ebullición). Cuando todo el líquido se haya
transformado en vapor, y si se sigue
aportando energía, la temperatura vuelve a subir. Este proceso se muestra en la gráfica.
Otro aspecto importante a destacar es la influencia de la presión en la temperatura de ebullición. Supón
que el matraz del dibujo del margen contiene agua destilada y ha estado hirviendo unos cinco minutos,
tiempo suficiente para que el vapor de agua desaloje el aire que había sobre el líquido. Apartamos el
matraz de la fuente de calor, lo cerramos y adaptamos en el tapón un manómetro que puede medir la
presión hasta 1 atm. El manómetro mide la presión de vapor del agua en el interior del matraz, que va
disminuyendo a medida que baja la temperatura, ya que parte se condensa pasando al estado líquido. A
cada temperatura le corresponde una presión de vapor.
Con un experimento análogo, disponiendo de un Presión de vapor del agua a distintas temperaturas Pv (mmHg) T (ºC) manómetro de precisión se obtiene una tabla de presión
0 4.5 de vapor del agua como la que se muestra a la derecha.
20 17.3 Lo mismo podría hacerse con otro líquido. Cuando
40 55.1 hemos puesto a calentar el matraz para que hierva el
60 149.3 agua destilada, la temperatura ha ido subiendo y
80 355.0 también la presión de vapor, tal como nos informa la
100 760.0 tabla. En un momento dado, el agua ha comenzado a
hervir y durante la ebullición la temperatura no ha variado. Pues
bien, cuando el agua, o cualquier líquido, entra en ebullición, la
presión de vapor es igual a la presión atmosférica que soporta la
superficie del líquido.
Por ejemplo, el punto de ebullición del agua es 100 °C, porque
hierve a esta temperatura cuando la presión atmosférica es de 1
atm. Pero puede hervir a otra temperatura si se modifica la
presión. Esto tiene consecuencias interesantes:
En una montaña muy alta, el agua hierve por debajo de
los 100 °C, porque allí la presión de la atmósfera es
inferior a la normal.
Por el contrario, en un recinto cerrado, la presión del vapor generado impide la
ebullición. Por ejemplo, en las ollas a presión, aumenta la presión de vapor hasta
cierto valor (superior a 1 atm), y entonces se abre una válvula que da salida al
exceso de vapor, controlando la presión interior. El agua hierve en la olla por
encima de los 100 °C a la presión de control regulada por la válvula.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 14 A21. Con una balanza determinamos la masa de una probeta que contiene 100 mL de agua, resultando ser de 350 g. Después 3
introducimos un cuerpo en el agua, con lo que el nivel sube hasta 150 cm , y volvemos a determinar la masa del conjunto, que resulta ser de 725 g. Determina la densidad de dicho cuerpo. 3
A22. Una moneda de cobre tiene un volumen de 0.5 mL. Sabiendo que la densidad del cobre es aproximadamente 9 g/cm , halla el número de monedas que necesitaremos para tener una masa de 0.054 kg? A23. Para determinar la densidad del agua, un alumno congela una botella con agua. Pesa el hielo formado y mide el volumen del agua que se forma al derretirse ese hielo. Luego divide la masa primera entre el volumen, expresando el resultado en el SI. ¿Es correcto hacer esto? Explicación. 3
3
A24. Una determinada sustancia A tiene una densidad dA = 1245 kg/m y otra sustancia B tiene una densidad dB = 1319 kg/m . Se pide: (a) si disponemos de 1/2 kg de cada sustancia, ¿cuál pesará más?; (b) si disponemos de 1/2 L de cada sustancia, ¿cuál pesará menos?; (c) si ponemos 100g de la sustancia A en el platillo de una balanza, ¿qué masa de B habrá que poner en el otro platillo para que el conjunto quede equilibrado; (d) si ponemos 100 mL de la sustancia B en el platillo de una balanza, ¿qué masa de A habrá que poner en el otro platillo para que el conjunto quede equilibrado?; (e) siguiendo con el apartado anterior, ¿y qué volumen de A? A25. En el platillo de una balanza ponemos 750 g de gasolina. Si se ponen 750 mL de aceite en el otro platillo, ¿hacia dónde se inclinará la balanza? ¿Cuál debería ser el radio de la esfera de oro que habría que poner para restablecer el equilibrio? A26. ¿Qué interesa más: comprar litros de aceite o kilos de aceite por el mismo precio? A27. Un depósito contiene 1500 kg de aceite. ¿En cuánto aumenta su volumen si añadimos 200 kg de aceite? 3
A28. Un bote que contiene 2 cm de alcohol líquido se encuentra encima de una balanza que marca una masa de 56 g. Si logramos que el alcohol se evapore, manteniendo cerrado el bote, entonces: (elige la(s) opción(es) correcta(s)) (a) el vapor de alcohol ocupa la parte superior del bote; (b) la balanza señalará un peso inferior; (c) la densidad del alcohol sigue siendo la misma; (d) al abrir el bote, lo marcado por la balanza varía. A29. ¿Por qué la nieve de una montaña tarda varios meses en hacerse líquida a pesar de que la temperatura ambiente es mayor de 0 ºC, que es la temperatura de fusión del hielo? [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 15 A30. Las siguientes gráficas representan la variación de la temperatura de 100 g de agua y de 100 g de alcohol en función del tiempo, cuando los calentamos con dos placas calefactoras iguales hasta que pasan completamente a estado gaseoso. Se pide: (a) Describe qué le sucede a la temperatura del agua en el tramo A y en el tramo B. ¿Qué está sucediendo en el tramo B?; (b) Describe qué le sucede a la temperatura del alcohol en el tramo A y en el tramo B. ¿Qué está sucediendo en el tramo B?; (c) ¿Cuál es la temperatura de ebullición de ambas sustancias?; (d) Las placas calefactoras suministran a cada líquido 8000 calorías en cada minuto. ¿Qué cantidad de energía hay que darle a los 100 g de agua para que hiervan totalmente?, ¿y al alcohol?
A31. La gráfica temperatura-­‐tiempo siguiente, se ha obtenido anotando la temperatura del agua de una botella en el interior del congelador cada 30 minutos. Se pide: (a) Interpreta la gráfica, indicando lo que ocurre en cada tramo; (b) Indica si el agua está sólida o líquida cuando han transcurrido: 20 min, 150 min y 330 min. A32. La siguiente tabla de datos representa el proceso al se sometió una sustancia pura. Se pide: (a) Realiza una representación gráfica temperatura-­‐tiempo; (b) Expresa la temperatura final alcanzada en este experimento en la escala Kelvin y Fahrenheit; (c) Explica que le sucede a la sustancia Tiempo (min) Temperatura (ºC) 0 98 entre los 8 y 16 minutos; (d) Sabemos que la temperatura de fusión de esta sustancia 4 77 es -­‐15 ºC y su temperatura de ebullición, de 51 ºC. ¿En qué estado se hallaba la 8 51 sustancia al comienzo de la experiencia? ¿Y al final de los 32 minutos? 12 51 16 51 A33. Dada la siguiente tabla de valores: (a) clasifica estos materiales en tres grupos: 20 33 sólidos, líquidos y gaseosos, a temperatura ambiente; (b) si estuvieran a 900 ºC; (c) si 24 18 estuvieran a -­‐100 ºC. 28 4 32 -­‐8 Sustancia Tª fusión (ºC) Tª ebullición (ºC) Agua 0 100 Etanol -­‐114 78 Azufre 119 444 Dioxígeno -­‐219 -­‐183 Dinitrógeno -­‐210 -­‐196 Estaño 232 2270 Plata 961 2212 A34. ¿Dónde se cuece antes un huevo en agua hirviendo, en el Teide o en Santa Cruz de Tenerife? A36. En una visita a un templo budista en el Tíbet, observamos como un monje está tomando un té hirviendo. ¿Por qué no se quema? ¿Acaso tiene un extraordinario control del dolor fuera de lo común? Es hora de explicar cómo los científicos interpretan los cambios de estado de la materia.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 16 III. LA TEORÍA CINÉTICA-MOLECULAR: UN MODELO PARA EXPLICAR LOS ESTADOS DE LA
MATERIA.
Vamos a suponer que tenemos una jeringa y en su interior hay un gas. Una de las propiedades más
características de los gases es su facilidad para comprimirse. ¿Cuál podrá ser la explicación de que esto
sea así? Aunque podríamos dar muchas explicaciones, trabajaremos con estas tres:
Cualquiera de las tres interpretaciones constituye un modelo científico. Es decir, nos hemos servido de
algo familiar para tratar de explicar un fenómeno. Conviene aclarar que un modelo no es la realidad,
sino que es algo que nos ayuda a describirla e interpretarla. Los científicos intentan explicar las cosas
de dos formas diferentes. Una de ellas consiste en describir las cosas que observan. A eso le llamamos
descripción de las observaciones. También explican por qué las cosas suceden tal como ellos la observan,
es lo que llamamos interpretación teórica.
Un modelo consta de una serie de puntos básicos (postulados) que se suponen. Con ayuda de estos
postulados intentamos explicar los fenómenos que se dan en la Naturaleza. Si los postulados sirven
para predecir el comportamiento del sistema físico que se estudia, el modelo es útil y se acepta. Basta
con encontrar un fallo entre las previsiones que efectúa el modelo y la realidad para hacer inútil el
modelo: es necesario ampliar dicho modelo, cambiando algunos de sus postulados o, en caso necesario,
desechar el modelo completamente. Ésta es la forma de trabajar en la Ciencia: a medida que el modelo
se perfecciona se acerca a la realidad.
A partir del modelo que hayas elegido para explicar la facilidad para comprimirse que tienen los gases,
intenta explicar estas otras propiedades que también se manifiesta en este estado de la materia; a
saber, ocupan todo el recipiente que los contiene, tienen baja densidad y se difunden fácilmente.
Después de una reflexión podemos llegar a las siguientes conclusiones:
- El modelo A, aunque puede explicar la facilidad de compresión de un gas, no nos sirve para explicar
la propiedad de ocupar todo el recipiente que los contiene. Así, por ejemplo, si abrimos un poco un
tarro de perfume, las pocas partículas olorosas de gas que salgan se difundirán por toda la
habitación, y para ello las partículas tendrían que crecer tanto su tamaño que podrían ser visibles a
simple vista, hecho que no ocurre.
- El modelo B tampoco es correcto. Una esponja puede comprimirse y desde un estado, puede
expandirse. Se podría suponer que la estructura de la masa gaseosa es parecida a una esponja y este
modelo podría explicar perfectamente la compresibilidad y la difusión de los gases. Pero no explicaría
la tendencia que tiene los gases a ocupar todo el recipiente que lo contiene. Además, ¿cómo explicar
la diferencia entre gases y líquido? ¿Y entre líquidos y sólidos?
- El modelo C es el que más se acerca a la opinión de los científicos actuales. Veamos esto
detenidamente.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 17 A37. Los gases se difunden hasta ocupar todo el volumen disponible. En la foto de la derecha se muestra un Erlenmeyer que contiene un gas rojo. La foto de la derecha muestra lo que ocurre cuando se le une a este matraz otro vacío: el gas rojo se encuentra ahora en ambos recipientes ocupando todo el volumen disponible. Se pide: (a) ¿Había aire en los matraces antes de que hubiera gas rojo? ¿Le resulta fácil o difícil al gas rojo pasar a través del aire?; (b) Si en una esquina de la clase se abre una lata de gasolina (o una botella de perfuma), al cabo de un rato huele a Actualmente explicamos el comportamiento de los
gasolina (o a perfume) en otra esquina de la clase. gases con el llamado modelo cinético molecular
(más simplemente llamado modelo de partículas). El
Explicación. desarrollo de este modelo tiene unas fechas claves:
1808:
El británico John Dalton publicó su modelo atómico según el cual la materia estaría constituida por
unas partículas indivisibles llamadas átomos. Los átomos de una sustancia son diferentes a los de otra
(tendrían unas determinadas masas atómicas).
En esta época ya se sabía que el aire es una mezcla de gases (nitrógeno, oxígeno, dióxido de carbono,
vapor de agua, argón, etc.). Incluso se conocía la masa relativa de estas partículas, de forma que se
sabía que unas son más pesadas que otras. Se podría suponer que las zonas bajas de la atmósfera serían
más ricas en partículas pesadas y las zonas altas más ricas en partículas ligeras. Dalton efectuó
medidas con aire cogido a diferentes alturas y encontró que la composición del aire es la misma. ¿Por
qué la composición del aire era independiente de la altura? Dalton postuló que las partículas no
estarían en reposo sino en continuo movimiento, de forma que chocarían entre ellas y contra
todos los objetos, rebotando y ocupando, de esa forma, todo el espacio disponible (modelo
cinético). Por supuesto, la velocidad de las partículas es variable debido a los continuos choques entre
ellas. Actualmente se sabe que, por ejemplo, a la temperatura de 0 ºC, la velocidad de una molécula de
dihidrógeno (H2) es de 1600 m/s; a 25 ºC, esa velocidad aumenta a 1930 m/s. Para que nos hagamos una
idea, la velocidad de un avión a reacción es aproximadamente de 700 m/s.
1857:
El físico-ingeniero alemán Rudolf J. E. Clausius desarrolla el modelo
cinético de forma matemática (basándose en un modelo primitivo
desarrollado en 1738 por Daniel Bernoulli) y establece que el choque de las
partículas gaseosas se manifiesta en la magnitud conocida como
presión. La presión que ejerce un gas es un empuje de fácil medida y
resulta ser consecuencia de los choques de las partículas con las paredes del
recipiente (o con los cuerpos sumergidos dentro del gas). La presión ejercida
por un gas depende de la cantidad que haya (a mayor cantidad de gas, mayor
presión), de la temperatura (a mayor temperatura, mayor energía cinética de
las partículas, mayor número de choques) y del volumen (a mayor volumen,
disminuye el número de choques y menor presión). La unidad de la
presión en SI es el pascal, Pa; también se utilizan otras unidades como la
atmósfera (atm), los milibares (mmb) y los milímetros de mercurio (mmHg).
Rudolf J. E. CLAUSIUS (1822-­‐1888) [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 18 Las relaciones son: 1 atm = 101300 Pa = 1013 mb = 760 mmHg
1860:
En el primer Congreso Internacional de Química un joven químico italiano
llamado Stanislao Cannizzaro presentó la obra de un genial químico que había
muerto en 1856: Amedeo Avogadro. Una de las claves de la Química fue
postular que las partículas que constituyen los gases no son átomos
aislados, sino agrupaciones de átomos unidos entre sí llamadas moléculas.
1870:
El físico inglés James Clerk Maxwell y el austríaco Ludwig Boltzmann
encuentran el significado físico de la temperatura. Las moléculas de un gas se
encuentran en movimiento, con velocidades variables debido a los múltiples
Amedeo AVOGADRO choques que se producen; la energía de una partícula en movimiento se
denomina energía cinética. Por tanto cada partícula posee una energía
(1776-­‐1856) cinética. La temperatura determina el valor de la energía cinética media de las
partículas. En otras palabras, las partículas de un gas a alta temperatura tienen una energía cinética
media mayor que las moléculas de un gas a una temperatura menor. Es importante hacer notar que se
trata de la energía cinética media: en el gas hay moléculas que se mueven con velocidades diferentes.
Como resultado de todas estas aportaciones se elaboró el modelo cinético molecular (modelo muy
aproximado a la realidad). Los aspectos fundamentales de este modelo, que intenta explicar el
comportamiento de los gases, son:
I.
Un gas está formado por partículas llamadas moléculas. Las moléculas de un gas son iguales
entre sí y diferentes a las de otro. Entre partícula y partícula no hay nada, solo espacio vacío (la
materia es discontinua).
II. Son partículas muy pequeñas (imposible verlas en un microscopio) por lo que el número de
moléculas es muy grande: en un litro de aire hay del orden de 2,6 · 1022 moléculas.
III. Las moléculas están en continuo movimiento al azar: se mueven en todas las direcciones y
chocan entre sí y contra las paredes del recipiente. La temperatura está relacionada con la
energía cinética media de las moléculas (y por tanto con la velocidad media de las moléculas).
IV. No existen fuerzas entre las moléculas. Sólo existen interacciones cuando chocan y esto ocurre
en un intervalo de tiempo muy pequeño.
V. La presión de un gas es el resultado de los choques entre las moléculas del gas y las paredes del
recipiente que las contiene (o con los objetos que se encuentran sumergidos en el gas). Por ello,
la presión depende del número de choques (y de la intensidad de cada uno) que den las
moléculas por unidad de tiempo y superficie.
Este modelo también es aplicable a líquidos y sólidos, con una simple adaptación de las características
1
de cada estado. Así, en el estado sólido, en los sólidos cristalinos, se suponen que las moléculas están
ordenadas, las distancias entre ellas son del orden del diámetro molecular y tienen un movimiento
vibratorio, que aumenta con la temperatura. En el estado líquido se supone que las moléculas están
1
En estos apuntes y siempre que hagamos uso de la TCM, utilizaremos el término molécula para referirnos a las unidades elementales que constituyen la materia, sin distinguir entre átomos, iones o molécula en sentido estricto. [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 19 desordenadas, las distancias son aproximadamente las mismas que en el estado sólido y pueden
moverse, tanto más cuanto mayor sea la temperatura, desplazándose de un lugar a otro, pero ligadas
entre sí, sin poder independizarse unas de otras.
A38. (a) Dibuja cómo te imaginas las moléculas de una sustancia en estado gaseoso cuando la sustancia está «normal», cuando está comprimida y cuando está expandida. ¿Ha cambiado el tamaño de cada molécula?, ¿ha cambiado la distancia entre moléculas?; (b) Explica con la TCM la propiedad que tienen las sustancias en estado gaseoso de difundirse fácilmente; (c) Dibuja cómo te imaginas las moléculas de una sustancia en estado gaseoso cuando la sustancia está «normal», cuando está dilatada y cuando está contraída. ¿Ha cambiado el tamaño de cada molécula?, ¿ha cambiado la distancia entre moléculas?, ¿ha cambiado la velocidad de las moléculas? A39. Utiliza la TCM para explicar las siguientes propiedades de las sustancias en estado gaseoso: (a) Ejercen presión sobre las paredes del recipiente que las contiene; (b) Se pueden comprimir y expandir mucho; (c) Cuando se encuentran encerradas en un recipiente de paredes flexibles se dilatan o se contraen al aumentar o disminuir la temperatura. A40. Si un gas está encerrado en u recipiente de paredes rígidas, al variar la temperatura, ¿cómo cambiará la presión que ejerce sobre las paredes del recipiente? Utiliza la TCM para justificar tu respuesta. A41. Si mezclamos dos gases de diferente densidad en un recipiente, ¿es posible que permanezcan separados? Justifica tu respuesta aplicando la TCM. A42. En el laboratorio hemos medido la temperatura de ebullición del agua, resultando ser 97 ºC. Para ello hemos calentado agua hasta que ha comenzado a hervir, observando además que mientras permanece la ebullición esa temperatura se mantenido constante. Explica razonadamente estos hechos. A43. ¿Qué ocurre con un gas a una temperatura de 0 K? En el siguiente esquema, se explican brevemente las propiedades de la materia según el estado en que
se encuentren:
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 20 Actualmente este modelo está totalmente aceptado y corroborado por la comunidad científica, por lo que
se denomina Teoría Cinético-Molecular (TCM).
III.1. Explicación de los cambios de estado.
La TCM puede explicarnos por qué tienen lugar los cambios de estado de una sustancia. El que una
sustancia se encuentre en un estado u otro depende fundamentalmente de la fortaleza de las uniones de
entre sus partículas constituyentes. Así, para convertir una sustancia líquida en gas, por ejemplo,
bastará con romper esas uniones, lo cual se consigue incrementando la temperatura de ese líquido para
que la velocidad de sus partículas sea mayor y, de este modo, se liberen de las mutuas atracciones,
pasando al estado gaseoso. El aumento de temperatura también es necesario para el cambio de estado
sólido a líquido y de sólido a gas. El proceso inverso, la disminución de temperatura, se aplicará en los
cambios de estado regresivos (de gas a líquido o sólido y de líquido a sólido).
A la temperatura que sucede un cambio de estado se la denomina temperatura de cambio de estado.
Así, se habla de temperatura de fusión (o solidificación) y de ebullición (licuación). Mientras que se
produce el cambio de estado de una sustancia pura, la temperatura permanece constante, ya que toda la
energía que se aporta se invierte en la ruptura de las uniones que existen entre las partículas. Sólo
cuando ya no quedan uniones por romper y si se sigue aportando energía, la temperatura volverá a
subir.
A44. Contesta a la siguientes cuestiones teniendo en cuenta la TCM: (a) ¿Crees que las sustancias en estado líquido se comprimen y se expanden? ¿Cómo podríamos comprobarlo?; (b) ¿Crees que las sustancias en estado sólido se comprimen y expanden? A45. Las densidades de los sólidos son, en general, parecidas a la del los líquidos, aunque un poco más elevadas. Sin embargo, las densidades de los gases suelen ser unas mil veces inferiores a la de los líquidos. Explicación. A46. Completa en tu cuaderno el esquema de la figura, dibujando cómo te imaginas la distribución o agrupación de moléculas de agua en cada estado de agregación. Escribe sobre cada flecha el nombre del cambio de estado correspondiente. Indica qué cambia de las moléculas cuando pasa el agua de un estado de agregación a otro. A47. Interpreta los siguientes fenómenos aplicando la TCM: (a) la fusión; (b) la condensación; (c) la evaporación; (d) ¿De qué formas podríamos aumentar la velocidad de evaporación de un líquido? A48. El rocío es la formación de gotas de agua a ras del suelo. Ocurre al caer la noche y es más intenso de madrugada. Es más frecuente en zonas costeras y en noches despejadas. Explica este fenómeno a la luz de la TCM. [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 21 III.2. Algo más sobre la presión de los gases.
Como sabemos, la presión es una magnitud que está relacionada con los choques de las partículas del
gas con las paredes del recipiente que los contiene. Las primeras experiencias con gases se realizaron
con el aire. Nuestro planeta está rodeado por la atmósfera, que es una capa gaseosa constituida por una
mezcla de gases. Éstos presionan a nuestro alrededor y sobre nosotros mismos de igual manera que el
agua del mar presiona sobre el casco de un submarino. Pues bien, a la presión que ejerce el aire sobre la
superficie de los cuerpos se denomina presión atmosférica.
Los efectos de la presión atmosférica son conocidos desde el siglo XVII. Fue Galileo
Galilei (1564-1642) el que demostró que el aire pesa. Un discípulo suyo,
Evangelista Torricelli, determinó el modo de medir la presión atmosférica
mediante un instrumento denominado barómetro. Para ello, llenó de mercurio un
tubo de vidrio de 1 metro de longitud, aproximadamente, cerrado por uno de sus
extremos. Tapó el extremo abierto y lo introdujo invertido en una cubeta con
mercurio. Al destapar el extremo libre del tubo, observó que el nivel del tubo
descendió hasta quedar a la altura de 760 mm por encima de la superficie libre del
mercurio de la cubeta. Ante esta situación, surge irremediablemente la siguiente
cuestión: ¿por qué no descendía todo el mercurio del tubo a la cubeta? La respuesta
está en la presión atmosférica. Ésta actúa sobre la superficie de mercurio de la cubeta y presiona al
mercurio contenido en el tubo impidiendo que baje. La presión atmosférica normal (a 0 ºC) es la presión
ejercida por una columna de mercurio de 760 mm de mercurio. A este valor se le denomina 1 atmósfera,
y así 1 atm = 760 mmHg
A49. ¿Por qué se seca antes la ropa los días ventosos? ¿Por qué no se seca bien los días de lluvia, aunque esté cubierto? A50. ¿Por qué los médicos advierten sobre el riesgo que corren los fumadores pasivos? A51. ¿Por qué cuando echas unas gotas de agua sobre una placa muy caliente se mueve de un lado para otro antes de desaparecer? A52. ¿Por qué si calientas una lata vacía y luego la tapas, las paredes de la lata se aplastan a medida que se enfría? A53. ¿Cómo funciona una olla a presión? ¿Para qué sirve la válvula de la olla a presión? IV. LAS LEYES DE LOS GASES.
El hecho de que los gases se compriman y expandan fácilmente ha permitido estudiar las relaciones
entre la presión, el volumen y la temperatura a la que se encuentra una determinada cantidad de gas y
expresarlas mediante fórmulas matemáticas. Este estudio comenzó en el siglo XVII, cuando se observó
que el aire y otros gases obtenidos en diversos procesos químicos eran materia.
Muchos científicos de diversas nacionalidades, durante dos siglos, dedicaron parte de sus esfuerzos a
aclarar el comportamiento de materia en estado gaseoso. Intentaremos resumir este proceso, siguiendo
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 22 un orden cronológico y constataremos cómo la vaguedad histórica se hace presente también en Ciencia,
como actividad humana que es.
IV.1. Ley de Boyle y Mariotte.
Imagina que tenemos una determinada masa de gas encerrada en un recipiente, calibrado para medir
volúmenes, como el que se indica en la figura.
Si empujamos el émbolo móvil, hacemos disminuir el volumen que ocupa el
gas y, como consecuencia, la presión aumenta, tal y como se constata en el
manómetro. Los resultados que se pueden obtener se detallan en la tabla.
Experiencia Volumen (l) 1 2.80 2 1.40 3 0.93 4 0.70 Presión (atm) 0.25 0.50 0.75 1.00 Puede observarse que el producto de la presión por el volumen que ocupa el gas tiene siempre el mismo
valor. Dicho de otro modo, el producto de ambas variables se mantiene constante. Si traducimos esta
idea al lenguaje matemático, podemos escribir:
P ⋅V = k
El origen de esta ley es algo confuso y generalmente no se indica en los libros de textos. Sin embargo, en
estos apuntes iremos un poco más allá, para que obtengas la idea de que los científicos no son
personajes aislados en sus laboratorios que descubren hechos sin ningún esfuerzo, de que su trabajo
suele basarse en el trabajo de otros científicos, y de que es necesario la comunicación con la comunidad
científica para hacer conocer sus resultados.
Esta ley recibe el nombre de ley de Boyle, en honor al químico irlandés que en 1662 realizó experimentos
similares al que comentamos anteriormente. Más tarde, en 1676, el francés Edmé Mariotte puntualizó
que el producto P· V es constante siempre que la temperatura no varíe durante la experiencia. Por eso
se denomina ley de Boyle y Mariotte:
Para una determinada cantidad de gas, el producto de la presión y el
volumen que ocupa un gas permanece constante, siempre que la
temperatura no varíe.
Sin embargo, los historiadores han descubierto recientemente que la ley fue propuesta primeramente
por dos científicos británicos, Henry Power y Richard Towneley, sobre la base de unos experimentos que
realizaron en 1653. No publicaron sus resultados inmediatamente, sino después de que los primeros
experimentos de Boyle sobre la presión del aire hubieran sido publicados en 1660. Power envió un
artículo describiendo los resultados de su trabajo a su amigo William Croone, en Londres. El título del
artículo era “Experimentos adicionales realizados en Towneley Hall durante los años 1660 y 1661 con la
ayuda y el consejo del heroico y valioso caballero Richard Towneley”. Pero Power no quiso poner su
nombre en el artículo. Croone envió el artículo a Boyle olvidando mencionar que Power era el autor.
Boyle fue muy cauteloso antes de dar crédito a la información recibida y en su monografía de 1662
replicando a Linus, estableció que él no había comprobado que la simple relación P· V = constante se
aplicaba a sus propios datos, hasta que Richard Towneley se lo insinuó. Científicos posteriores, que
leyeron los trabajos de Boyle sin mucha atención, supusieron que Boyle había hecho el descubrimiento
por sí mismo.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 23 Esta ley se puede expresar de otra forma.
Supongamos que tenemos un cierto volumen de gas, V0, que se encuentra a una presión P0, al comienzo
del experimento. Si variamos el volumen de gas hasta un nuevo valor V1, entonces la presión cambiará a
P1 y se cumple experimentalmente que:
P0 ⋅ V0 = P1 ⋅ V1 = k
lo que supone que a temperatura constante, el volumen que ocupa un gas es inversamente
proporcional a la presión que ejerce dicho gas sobre las paredes del recipiente que lo contiene.
Por último, indicar que si se trabaja con valores elevados de presión, la ley de Boyle y Mariotte deja de
ser válida, pues las moléculas que forman los gases se acercan y su interacción recíproca empieza a
influir en el comportamiento del gas. Por tanto, esta ley nos permite describir el comportamiento de un
gas si trabajamos con valores de presión normales.
ACTIVIDAD RESUELTA como Ejemplo
En una experiencia se han medido las presiones y los volúmenes de un gas encerrado en un
recipiente en el que la temperatura permanece constante:
Volumen (ml)
Presión (mb)
100
1000
90
1111
80
1250
70
1430
60
1666
50
2000
40
2500
Presión (mb)
Se pide: a) representa los datos en una gráfica en la que en ordenadas esté la presión y en
abcisas el volumen; b) ¿cómo varía la presión del gas cuando aumentamos o disminuimos el
volumen?; c) para cada pareja de valores de la tabla calcula el producto P.V. ¿Qué
conclusiones se pueden obtener?; d) haz un dibujo que represente cómo crees que están las
moléculas cuando el volumen ocupado por el
3000
gas sea de 100 ml y otro dibujo para cuando el
volumen ocupado sea de 50 ml; e) explica los
2500
resultados obtenidos teniendo en cuenta la
2000
TCM.
1500
1000
(a) La gráfica que se obtiene con estos datos se
muestra a la derecha. Está realizada con un
500
programa de tratamiento de datos. A la hora de
0
elegir las escalas hemos de tener en cuenta que NO
0
20
40
60
80
100
120
tienen que ser iguales. Así, para el volumen hemos
Volumen (ml)
elegido una escala de 20 ml en 20 ml y para la
presión, de 500 mb en 500 mb. Si deseamos hacer la
gráfica MANUALMENTE en papel milimetrado, podemos escoger para el volumen la escala de 10
ml/1 cm y para la presión 200 mb/1cm.
(b) Se observa que a medida que se disminuye el volumen la presión aumenta y viceversa; al
aumentar el volumen disminuye la presión. Son pues, magnitudes inversamente proporcionales.
(c) El producto PV es igual a: 100000; 99999; 100000; 100100; 99960; 100000; 100000. Podemos
admitir que el valor del producto es prácticamente idéntico en todos los casos.
(d) En ambos casos, las moléculas tienen el mismo tamaño y la misma rapidez (recuérdese que la
experiencia se realiza a temperatura constante). Sólo cambia la distancia entre ellas, siendo menor
cuando el volumen que ocupa el gas es menor.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 24 (e) Al disminuir el volumen aumenta el número de golpes de las moléculas (en cada unidad de tiempo)
con las moléculas de las paredes del recipiente, aunque se mantiene igual la intensidad de cada golpe.
Al producirse más golpes, la presión será mayor.
IV.2. Ley de Charles y Gay-Lussac.
En 1787, el francés Charles sugirió que distintos gases experimentan la
misma dilatación, con un mismo incremento de temperatura, siempre que la
presión se mantuviera constante. Sin embargo, no llegó a publicar sus
resultados. Un poco más tarde, en 1802, otro francés, Gay-Lussac repitió los
experimentos de Charles y publicó las conclusiones.
Supongamos que tenemos una masa de un gas
encerrada en un matraz redondo como el de la
figura. El matraz está cerrado por un tapón de
Jacques A. CHARLES corcho, con un orificio por donde se introduce un
termómetro y del cuello del matraz sale un tubo
fino y graduado, cerrado con una gota móvil de
mercurio que aísla el gas, que se encuentra a una atmósfera de presión.
Cuando calentamos, el gas se dilata y empuja la gota hacia fuera. Se va
midiendo el aumento de temperatura (absoluta) y el correspondiente
incremento de volumen de gas. Los resultados de una posible experiencia
se detallan en la tabla:
Puede observarse que el cociente entre el volumen que
ocupa el gas a cada temperatura absoluta es siempre el
mismo; es decir, el cociente de ambas variables es
constante. Matemáticamente podemos escribir:
Experiencia Temperatura (K) Volumen (l) 1 200 1.0 2 250 1.2 3 300 1.5 4 350 1.7 5 400 2.0 V
=k
T
Podemos enunciar la ley de Charles y Gay-Lussac como sigue:
Para una determinada cantidad de gas, el cociente entre el volumen que
ocupa un gas y la temperatura absoluta a la que se encuentra es constante,
siempre que la presión no varíe.
Esta ley se puede expresar de otra forma.
Supongamos que tenemos un cierto volumen de gas, V0, que se encuentra a una temperatura T0, al
comienzo del experimento. Si aumentamos la temperatura del gas hasta un nuevo valor T1 (sin variar la
presión), entonces el gas se dilatará hasta un nuevo volumen V1 y se cumple experimentalmente que:
V0 V1
=
=k
T0 T1
lo que supone que a presión constante, el volumen que ocupa una determinada cantidad de gas es
directamente proporcional a la temperatura absoluta.
Es importante destacar que estas expresiones sólo son válidas si las temperaturas se expresan en
Kelvin, nunca en grados Celsius.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 25 ACTIVIDAD RESUELTA como Ejemplo
En una experiencia parecida a las realizadas por Charles y Gay-Lussac, se obtuvieron los
siguientes datos:
Volumen (ml)
Temperat. (ºC)
50.0
20
51.7
30
53.4
40
55.1
50
56.8
60
58.5
70
60.2
80
61.9
90
63.7
100
Se pide: a) ¿Cuál es la variable dependiente y la independiente? Representa los datos en una
gráfica en la que la variable independiente esté en abcisas y la dependiente en ordenadas; b)
Según la gráfica, ¿qué relación existe entre los valores de volumen y temperatura del gas?; c)
Si la presión del gas se mantiene constante, ¿qué cambios le ocurren a las moléculas del gas
cuando aumenta la temperatura? (i) aumenta la masa y el volumen de cada molécula, (ii)
aumenta la distancia entre las moléculas, (iii) aumenta la velocidad de las moléculas; (d)
¿Cómo podríamos explicar con ayuda de la TCM que el volumen aumente cuando aumenta
la temperatura del gas?
(a) La variable independiente es aquella cuyo valor controlamos y podemos modificar directamente,
en este caso es la temperatura. La variable dependiente, en este caso el volumen, es aquella en la que
los cambios son causados por los cambios de la variable independiente. La gráfica se muestra a
continuación.
(b) La gráfica pone de manifiesto que
volumen varía en el mismo sentido que
hace la temperatura. Al aumentar
temperatura aumenta el volumen, y
disminuir la temperatura disminuye
volumen.
el
lo
la
al
el
(c) Al aumentar la temperatura aumenta
la velocidad de las moléculas lo que
produce un aumento de la presión interior
respecto a la exterior que no cambia, por lo
que se producirá un aumento del volumen
hasta que se restablece el equilibrio entre
las presiones interior y exterior. Así pues, aumenta la velocidad de las moléculas y la distancia entre
ellas: (ii) y (iii).
(d) Un aumento de temperatura supone un aumento de velocidad de las moléculas, lo que provoca un
aumento del número de golpes y de la intensidad de cada golpe, lo que es la causa del aumento de la
presión, y al ser las paredes flexibles, aumenta el volumen hasta que la presión interior vuelve a ser
igual a la presión exterior.
IV.3. Ley de Gay-Lussac.
En 1805, el propio Gay-Lussac estudió experimentalmente la variación que
sufría la presión de un gas cuando se modificaba la temperatura,
manteniendo invariable el volumen (y la cantidad de gas, claro está). Para
ello, encerró una masa de un determinado gas en un matraz como el que
aparece en la figura siguiente y fue midiendo la temperatura y la presión,
mientras comunicaba calor al interior.
Experiencia Temperatura (K) Presión (atm) 1 200 0.65 2 250 0.85 3 300 1.00 4 350 1.15 5 400 1.35 Joseph Louis GAY-­‐LUSSAC [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 26 Puede observarse con ayuda de la tabla anterior, que el cociente entre la
presión del gas y la temperatura absoluta a la que se encuentra es
constante. Matemáticamente podemos escribir:
P
=k
T
Podemos enunciar la ley de Gay-Lussac (muchos textos hablan de segunda
ley de Gay-Lussac) como sigue:
Para una determinada cantidad de gas, el cociente entre la presión de un
gas y la temperatura absoluta a la que se encuentra es constante, siempre
que el volumen no varíe.
Se puede expresar esta ley de otra forma.
Supongamos que una cierta cantidad que se encuentra a una determina presión P0 y temperatura T0. Si
aumentamos la temperatura del gas (sin variar el volumen) hasta el valor T1, entonces la presión del
gas aumentará hasta P1 y se cumple experimentalmente que:
P0 P1
=
=k
T0 T1
lo que supone que a volumen constante, la presión de una determinada cantidad de gas es directamente
proporcional su temperatura absoluta.
Al igual que ocurría con la ley de Charles y Gay-Lussac, la temperatura debe expresarse en Kelvin.
Los gases que cumplen perfectamente estas leyes (Boyle y Mariotte, Charles y Gay-Lussac) se
denominan gases ideales. En realidad no existe ningún gas que cumpla perfectamente estas leyes,
pero su comportamiento se acerca bastante si se trabaja a bajas presiones.
IV.4. Ecuación general de los gases.
De las leyes de los gases que hemos estudiado se deduce otra ley más amplia, que nos permite predecir
el comportamiento gaseoso, para una cantidad de gas constante. En ella se relacionan la presión, el
volumen y la temperatura absoluta. Supongamos que tenemos un gas encerrado en un recipiente (como
en el esquema) y, en primer lugar se aumenta la temperatura hasta que se alcance el equilibrio y
posteriormente se aumenta la presión, tal y como se indica en el esquema:
P0
P0
temperat.
V0 , T0
presión
V´ , T1
(I)
P1
V1 , T1
(II)
Aplicando la ley de Charles y Gay-Lussac (a presión constante) al primer proceso, se tiene:
V0/T0 = V’/T1.
Y si hacemos uso de la ley de Boyle-Mariotte (a temperatura constante) en el segundo proceso,
obtenemos:
P0· V’ = P1· V1.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 27 Si despejamos de ambas ecuaciones V´, igualando y reordenando, se obtiene:
P0 ⋅ V0 P1 ⋅ V1
=
=k
T0
T1
Esta expresión recibe el nombre de ecuación general de los gases y nos informa que para una cierta
cantidad de gas, el producto de la presión por su volumen, dividido por la temperatura absoluta es
constante.
Si en la ecuación anterior hacemos que la presión, el volumen o la temperatura sean constantes,
obtenemos la ley de Charles y Gay-Lussac, la ley de Gay-Lussac y la ley de Boyle-Mariotte,
respectivamente.
En un próximo curso estudiaremos una variación en la forma de presentar esta ecuación.
ACTIVIDAD RESUELTA como Ejemplo
Tenemos una bombona de 40 L en cuyo interior hay gas helio a 15 ºC y 990 mmHg.
Calcular: a) ¿qué volumen ocuparía ese gas en condiciones normales?; b) ¿hasta qué
temperatura habría que llevar al gas en el interior de esa misma bombona para que la
presión fuese de 3.5 atm?; c) si dejásemos escapar cierta cantidad de gas de la bombona,
¿cómo se modificaría la presión? Ofrece una explicación en base a la TCM.
(a)Un gas se encuentra en condiciones normales (c.n.) cuando está a 1 atm de presión y 0 ºC.
Aplicando la ecuación general de los gases, con la temperatura (obligatoriamente) en Kelvin y presión
en las mismas unidades (por ejemplo mmHg), tenemos:
P0 ⋅ V0 P1 ⋅ V1 990mmHg ⋅ 40l 760mmHg ⋅ V1
=
;
=
⇒ V1 = 49.4l
T0
T1
(15 + 273)K
273K
(b) En este caso, al no variar el volumen de la bombona, se aplica la ley de Gay-Lussac:
P0 P1 990mmHg
=
;
=
T0 T1
288K
3.5atm ⋅
760mmHg
1atm
⇒ T1 = 773.8 K = 500.8º C
T1
(c) Al disminuir la cantidad de gas, el número de moléculas que chocan contra las paredes de la
bombona es menor con lo que la presión disminuirá. Lógicamente, hemos supuesto que la
temperatura se mantiene constante en el proceso.
IV.5. El cero absoluto de temperatura.
Si se disminuye la temperatura del un gas manteniendo invariable la presión, el volumen ocupado
también disminuye. Si se sigue el proceso, suponiendo que el gas no cambie de estado, llegará un
momento en que el volumen ocupado por el gas sea nulo. Ahora bien, es imposible concebir que el
volumen ocupado por una masa sea nulo.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 28 El valor de la temperatura a la que el volumen tomaría ese hipotético valor de cero puede obtenerse a
partir de la gráfica volumen-temperatura que se deduce de los siguientes datos experimentales:
300 97.8 100
75
V (ml)
Temperatura (ºC) Volumen (l) 0 46.6 50 55.1 100 63.7 150 72.2 200 80.7 250 89.2 50
25
0
-400 -300 -200 -100
0
100
200
300
400
t (ºC)
Si se prolonga la línea recta hasta que corte con el eje de abscisas (donde se representa la temperatura),
2
vemos que -273 ºC se alcanzaría el volumen nulo.
W. Thomson propuso una escala de temperaturas, conocida como escala absoluta, que da el valor 0 a
la temperatura de -273 ºC. La unidad de temperatura en esa escala absoluta es el Kelvin (K). Aunque en
principio se llegó a esa idea mediante un razonamiento a partir de las experiencias realizadas con gases,
debemos saber que nunca se ha conseguido experimentalmente una temperatura inferior o igual al cero
absoluto (como mínimo 0.002 K).
A54. Una jeringa a 20 ºC contiene 20 mL de aire. Si la introducimos verticalmente en agua caliente, el émbolo se desplaza hacia arriba y el aire interior ocupa un volumen de 23 mL. Se pide: (a) La temperatura alcanzada por el aire; (b) ¿En qué ley te basas para realizar el cálculo?; (c) ¿Qué nombre recibe el proceso que le ha ocurrido al aire?; (d) Explica el proceso con la TCM; (e) Dibuja cómo te imaginas el aire a la temperatura inicial y final. A55.Determina, en ºC, la temperatura de un gas que en c.n. ocupa un volumen de 150 L y que a 10 atm de presión solo ocupa un volumen de 20 L. A56. Cuando la presión de cierta masa de gas es de 30 cmHg y su temperatura de 25 ºC, ocupa un volumen de 200 L. ¿cuál será entonces la presión necesaria para que el gas ocupe un volumen de 150 L si la temperatura aumenta hasta 50 ºC? A57. La densidad del dihidrógeno en c.n. es 0.089 g/L. Calcula su densidad a 1.5 atm y -­‐10 ºC. 2
El valor exacto es -­‐273.15 ºC. [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 29 3
A58. Una burbuja de aire de 3 cm de volumen está a una presión de 1 atm y a una temperatura de 20 ºC. ¿Cuál será su volumen si asciende hasta un lugar donde la presión es de 0.95 atm y la temperatura no varía? A59. A temperatura constante, si disminuimos a la cuarta parte el volumen de un gas, ¿qué le ocurre a la presión? A60. En un matraz cerrado hay dioxígeno a 47 ºC y 1 atm. Si se calienta hasta 407 ºC y el volumen aumenta un 5%, ¿cuál será la presión final? A61. Tenemos un gas a 50 ºC en un recipiente de paredes flexibles (presión constante). Si se caliente el gas hasta 100 ºC, ¿se duplica su volumen? A62. Dos recipientes de igual volumen contienen dos gases diferentes A y B que se encuentran a la misma temperatura y a la misma presión. La masa de una molécula de A es mayor que la masa de una molécula de B. ¿Qué recipiente contiene mayor número de moléculas? ¿Qué recipiente pesa más? A63. Un recipiente A tiene doble volumen que otro recipiente B. El recipiente A contiene gas dihidrógeno y el recipiente B gas dioxígeno, ambos gases a la misma presión y temperatura. ¿En cuál de ellos hay más moléculas? A64. Una determinada masa gaseosa ocupa un volumen de 20 L cuando su presión es 2 atm y su temperatura es 25 ºC. Se pide: (a) ¿Cuánto vale la constante K para esta masa gaseosa a esta temperatura? Expresa el valor de la constante en 𝑚𝑚 𝐻𝑔 ∙ 𝑐𝑚! ; (b) ¿Qué presión tendrá si se aumenta el volumen hasta 30 L sin modificar la temperatura?; (c) ¿Qué volumen ocuparía dicho gas a una presión de 900 mm Hg, sin variar la temperatura? 3
A65. Dos gramos de cierto gas ocupan un volumen de 60 cm cuando su temperatura es de35 ºC. ¿A qué temperatura ocupará 3
un volumen de 30 cm ? Determina el volumen ocupado por dicho gas a la temperatura de 600 K (se supone que la presión del gas no varía). A66. En un recipiente de 5 L de capacidad tenemos 10 g de un gas A. En otro recipiente, también de 5 L, tenemos 10 g de un gas B a la misma temperatura del gas A. Sabemos que una molécula del gas A pesa más que una molécula del gas B. Comenta las siguientes afirmaciones: (a) el gas A pesará más que el gas B, ya que sus moléculas pesan más; (b) los gases A y B tendrán igual número de moléculas pues están en recipientes de igual volumen; (c) las densidades de ambos gases serán las mismas; (d) si el gas A estaba en el recipiente de 5 L a 20 ºC y 0.89 atm de presión, ¿qué volumen ocuparía en c.n.? A67. Dos recipientes cerrados, iguales, de 25 L cada uno, tiene gas en su interior. En uno de ellos, hay 2 g de dihidrógeno y en el otro hay 32 g de dioxígeno. Se sabe que la masa de una molécula de dioxígeno es 16 veces superior a la de una molécula de dihidrógeno. Responde a estas cuestiones: (a) ¿En cuál habrá mayor número de moléculas?; (b) ¿Qué recipiente pesará más?; (c) ¿Qué gas tendrá mayor densidad?; (d) Si la temperatura es la misma en ambos recipientes, ¿cuál de ellos tiene mayor presión?; (e) Si el hidrógeno en su recipiente estaba inicialmente a 20 ºC y 1 atm, ¿a qué temperatura habría que someterlo para que manteniendo el mismo volumen, su presión pasara a ser de 790 mm Hg?; (f) Si mezclamos los dos gases en un único recipiente de 30 L, ¿qué densidad tendrá cada gas entonces? [Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 30 Actividades finales
AF1. Indica si las siguientes propiedades de la materia son generales o características: (a) masa; (b)
forma geométrica; (c) solubilidad; (d) olor; (e) color; (f) temperatura; (g) fluidez; (h) densidad.
AF2. Una balanza admite una carga máxima de 200 g y tiene una precisión de 1 cg. ¿Cuáles de las
siguientes medidas no pueden ser correctas: (a) 15.32 g; (b) 43.8 cg; (c) 123.456 g; (d) 41 mg; (e) 285.42 g;
(f) 25.0 dg.
AF3. Explica cuáles de los siguientes enunciados son verdaderos y cuáles no: (a) el termómetro con el
mercurio en 0 ºC pesa menos que con el mercurio en 90 ºC; (b) el agua a 32 ºF está más fría que a 20 ºC;
(c) un cuerpo a 290 K está más caliente que a 45 ºF; (d) hace un día agradable en Nueva York, pues su
temperatura es de 78 ºF.
AF4. ¿Es el volumen una propiedad característica? ¿Y la masa? ¿Por qué?
AF5. ¿Qué diferencia hay entre el volumen de un cuerpo y su capacidad? ¿Qué unidad se utiliza
normalmente para expresar la capacidad?
AF6. Determina los volúmenes de los siguientes cuerpos geométricos, dando el resultado en cm3 y en
notación científica: (a) un cubo de 12 m de lado; (b) una piscina de 8 m de largo, 4 m de ancho y 2 m de
profundidad; (c) un bote de tomate con una base de 6 cm de diámetro y 15 cm de altura; (d) una pelota
de 1.5 dm de radio
AF7. Una alumna dispone de dos recipientes iguales que contienen la misma cantidad de agua. En el
primero de ellos sumerge una esfera de aluminio de radio 20 cm y en el segundo una esfera de acero del
mismo radio. ¿En cuál de los dos recipientes alcanzará el agua una altura mayor?
AF8. Un bloque de forma cúbica de aluminio tiene una masa de 780 g. Determina el volumen que ocupa.
Si partimos justo por la mitad este bloque, ¿qué masa, qué volumen y qué densidad tendrá cada trozo?
AF9. Explica si las siguientes cuestiones son verdaderas o falsas: (a) medio litro de aceite no cabe en un
recipiente de 400 mL; (b) tres kilogramos de hierro caben en un depósito de 12 L; (c) un litro de aceite
pesa menos que un litro de acetona; (d) un kilogramo de mercurio pesa más que 5 litros de aceite.
(Busca los datos que necesites)
AF10. Una determinada sustancia A tiene de densidad 1200 kg/m3 y otra sustancia diferente B tiene de
densidad 10.5 g/mL. Se pide: (a) si se dispone de medio kilogramo de cada sustancia, ¿cuál pesará más?;
(b) si se dispone de medio litro de cada sustancia, ¿cuál pesará menos?; (c) si ponemos 100 mL de la
sustancia A en el platillo de una balanza, ¿qué volumen de B habrá que poner en el otro platillo para
que el conjunto quede equilibrado?
AF11. Un recipiente, de 250 mL de capacidad y 100 g de masa, está herméticamente
cerrado y contiene en su interior aire y una bola de hierro de 75 cm3 y de 585 g. Se pide:
(a) el espacio que ocupa la bola; (b) el espacio que ocupa el aire; (c) la densidad del
hierro, a través de la experiencia; (d) la densidad del aire, sabiendo que todo el sistema
tiene una masa total de 685.227 g.
AF12. Tenemos en un recipiente tapado, 5 litros de una mezcla de agua y alcohol a la
temperatura de 20 ºC. Si hacemos hervir por completo toda la mezcla, ¿qué sustancia habrá hervido
antes? Una vez en estado gaseoso, ¿qué volumen ocupará el vapor de agua? ¿Y el vapor de alcohol?
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO 31 AF13. En la figura se representa una jeringa con cierta cantidad de gas y con el
émbolo en dos posiciones diferentes (A y B). Explica cuál de las siguientes
magnitudes varían al pasar de la situación A a la situación B: (a) la masa del gas;
(b) el volumen ocupado por el gas; (c) la densidad del gas; (d) la temperatura del
gas; (e) la presión del gas.
AF14. Dada la siguiente tabla de valores: (a) clasifica estos
materiales en tres grupos: sólidos, líquidos y gaseosos a
temperatura ambiente. Razona tu clasificación; b) ídem si
estuvieran a 1000ºC; c) ídem a –100ºC.
AF15. Explica que se entiende por condiciones normales de un
gas.
AF16. Indica razonadamente cuál de las siguientes frases es
correcta: (i) la temperatura de ebullición del agua es 100 ºC; (ii) la
temperatura de ebullición del agua es 100 ºC a la presión
atmosférica; (iii) la temperatura de ebullición del agua aumenta si
seguimos calentando.
Material T fusión (ºC) T ebullición (ºC) Calcio 810 1200 Cobre 1083 2310 Criptón -­‐169 -­‐152 Bromo -­‐7.3 63 Amoniaco -­‐78 -­‐33.5 Oro 1063 2500 AF17. Sabiendo que la ciudad de Soria se halla a 1080 m de altitud sobre el nivel del mar, ¿dónde hierve
más fácilmente el agua, en Soria o en Málaga? ¿Y dónde se
cocería antes un huevo?
AF18. Observa la gráfica adjunta, que corresponde al
calentamiento de dos sustancias (A y B) inicialmente sólidas.
Se pide: (a) la temperatura de partida de cada sustancia; (b)
¿qué sucede en cada tramo horizontal de las gráficas? ¿a qué
situación física corresponde?; (c) el estado físico de cada
sustancia a la temperatura de 35 ºC. Explicaciones.
AF19. CUESTIONES:
a) Un recipiente contiene agua en estado vapor. ¿Qué hay
entre las partículas de vapor?
b) ¿Por qué aumenta la presión de los neumáticos de un coche
en días calurosos? Responde utilizando la teoría cinética.
c) Teniendo en cuenta la gráfica adjunta ¿a qué temperatura, en
grados Celsius, es nulo el volumen de un gas? ¿Se puede llegar a
esa temperatura? Explicaciones.
d) Explica por qué al abrir un frasco de perfume se esparce el olor
por toda la habitación. ¿Cuándo lo hará antes, en verano o en
invierno? Explicación.
e) Dispones de un recipiente con cierta cantidad de gas. Explica qué
le ocurre a la presión del gas cuando: (i) se aumenta la
temperatura; (ii) se disminuye el volumen; (iii) se añade más gas;
(iv) se aumenta la temperatura y el volumen; (v) se disminuye el
volumen y se aumenta la temperatura.
AF20. ¿Por qué la evaporación de cualquier líquido puro sucede a cualquier temperatura a la que se
halle el líquido, mientras que la ebullición tiene lugar a una temperatura fija?
AF21. Dentro de las cubiertas de un coche el aire está a 15 ºC y a 2 atm de presión. Determina la
presión que ejercerá ese aire si la temperatura, debido al rozamiento, sube hasta los 65 ºC.
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán Física y Química para 3º de ESO AF22. Una vasija A de 200 cm3 está separada de otra B de 600 cm3 mediante una
tubería de capacidad despreciable, provista de una llave de paso. La vasija A
contiene un gas a 750 mmHg y en la B se ha hecho el vacío. Calcula la presión en los
dos recipientes después de abrir la llave de paso, si no varía la temperatura.
AF23. Una cierta masa de gas es sometida a distintas presiones,
manteniendo constante la temperatura. A partir de los datos de la
tabla, se pide: (a) la representación P-V; (b) ¿cumple alguna ley?; (c)
¿cuál es su expresión matemática?
32 B A P(atm) 0.10 0.25 0.50 0.75 1.00 V(L) 5.00 2.00 1.00 0.67 0.50 AF24. Una muestra de gas ocupa un volumen de 500 mL a -10 ºC. ¿A qué temperatura, expresada en
grados Celsius y en Kelvin, ocupará 1.5 L si la presión se duplica en el proceso?
AF25. Manteniendo constante el volumen, calentamos un gas hasta duplicar su presión. Si la
temperatura inicial era de 22 ºC, ¿cuál será la nueva temperatura expresada en grados Celsius?
AF26. A presión constante, ¿se duplica el volumen de un gas al calentarlo de 2 ºC a 4 ºC?
[Materia y Modelo Cinético] | Departamento de Física y Química IES NICOLÁS
COPÉRNICO. Prof.: Rafael Glez. Farfán