Los problemas de este número abarcan dos áreas de las

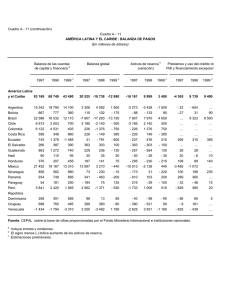
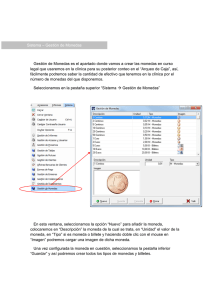
el espejo no diferencia entre derecha-izquierda
y arriba-abajo, la aparente discriminación en
las direcciones de que trata este problema se
debe sólo a la interpretación de la mente.
Carlos Montenegro
Profesor asociado del
Departamento de Matemáticas
Los problemas de este número abarcan dos
áreas de las matemáticas. Los primeros dos
son de geometría –relacionan puntos, segmentos, longitud y área–, aunque los objetos físicos son listones y monedas; el tercero
podría decirse que es de lógica. Al final encontrarán las respuestas a los problemas de la edición pasada. Como siempre, pueden hacernos
llegar sus soluciones o enviar otros problemas
a la dirección: [email protected].
Problema 1
Listones y cuadrados. Tome ocho listones,
cuatro de 15 cm y cuatro de 30 cm. Colóquelos
sobre un plano de manera que delimiten tres
cuadrados que tengan la misma área.
Problema 2
Más monedas. Ponga cinco monedas sobre una mesa de tal forma que todas estén a
la misma distancia de cada una de las demás.
Problema 3
El día menos esperado. A un prisionero le
dicen: “Lo liberaremos la próxima semana, el día
menos esperado”. ¿Qué día lo deben liberar?
Nota: desconozco la fuente de estos problemas, pues los copié hace mucho tiempo.
Problema 1
Cuando miramos a través de un espejo, lo que
está a la izquierda aparece a la derecha, y lo que
está a la derecha, a la izquierda; lo de arriba,
arriba, y lo de abajo, abajo. ¿Por qué el espejo invierte el sentido derecha-izquierda y no el
sentido arriba-abajo?
>Solución.
La óptica del espejo hace que los objetos se
vean con la orientación contraria. Por ejemplo:
sin importar cómo se coloque frente al espejo,
un guante derecho se ve como si fuera zurdo.
Si el espejo invirtiera tanto derecha-izquierda
como arriba-abajo, la doble inversión no cambiaría la orientación de las cosas; por esa razón sólo vemos una inversión. Además, como
Realmente el espejo intercambia el dorso por
el frente, pero pensamos que la inversión es
de derecha-izquierda porque comparamos
nuestro encuentro con uno mismo ante el espejo con el encuentro frontal con otra persona.
Para ver lo que está detrás, giramos sobre el
eje vertical, por lo que la orientación vertical
(arriba-abajo) no cambia mientras se invierte
la orientación horizontal (izquierda-derecha).
Si giráramos sobre el eje horizontal (mirando
entre las piernas) se conservaría la orientación
horizontal y cambiaría la vertical. En otras palabras, imaginémonos unos seres extraterrestres
que viven en completa ingravidez y suelen encontrarse frontalmente entre ellos, de manera
que los pies de uno queden frente a la cara del
otro. Al verse en el espejo, estos seres pensarían que éste invierte el sentido arriba-abajo y
no el sentido derecha-izquierda [1 y 2].
Problema 2
Hay doce monedas idénticas en apariencia,
pero una es falsa y tiene un peso distinto a las
otras. Encuentre la moneda falsa usando una
balanza sólo tres veces. Se trata de una balanza
antigua con dos platones en los que se pueden
poner las monedas para comparar su peso.
>Solución.
Para este problema hay muchas variaciones y
generalizaciones. Invitamos al lector a consultarlas en internet. La solución para el problema
clásico se explica a continuación. Se colocan
ocho monedas en la balanza, cuatro en cada
plato. Hay dos posibles resultados:
1. Si la balanza no queda en equilibrio, se tiene
un grupo liviano de cuatro monedas, que podemos llamar A, B, C, D, y un grupo pesado
de cuatro monedas: E, F, G, H, y se puede
concluir que las cuatro monedas restantes
–I, J, K, L– son buenas. Ahora se pesan los
siguientes dos grupos: E, I, J, K y A, F, G, H;
en otras palabras, se intercambia una moneda del grupo liviano con una del pesado y se
cambian las demás monedas del grupo liviano
por tres buenas. Si la balanza se invierte, la
moneda falsa está entre las dos monedas de la
balanza que fueron intercambiadas; es decir,
A y E. Si la balanza no cambia su posición, la
falsa está entre las tres del grupo pesado que
permanecieron en la balanza: F, G, H, y podemos concluir que es más pesada que las otras.
8 | Hipótesis | Apuntes científicos uniandinos | no. 8 | diciembre 2006
Si la balanza queda en equilibrio, la moneda
falsa está entre las tres del grupo liviano que se
sacaron y es más liviana que las demás. Para
terminar, en el primer caso se pesa una moneda buena junto a la moneda A. Si la balanza
queda en equilibrio, la falsa es E, y si no, la
falsa es A. En los otros dos casos, pesando
dos de las tres monedas resultantes se puede
decidir, pues se sabe si la moneda falsa es más
liviana o más pesada.
2. Si en la primera pesada la balanza queda en
equilibrio, el problema se reduce a encontrar
una moneda falsa entre cuatro. Esto se puede
hacer con dos usos más de la balanza. Le dejamos al lector la posibilidad de descifrar cómo
hacerlo [3].
Problema 3
Cuatro señoras están en una sala esperando
una entrevista. Dos de ellas tienen la cara sucia. Todas las señoras pueden percatarse de
que alguna o algunas de las otras tienen la cara
sucia, pero no dicen nada. Se asoma el entrevistador y dice: “¡Aquí hay personas con la cara
sucia!”, y cierra la puerta. Minutos después, sin
pronunciar palabra alguna, las dos señoras con
la cara sucia se paran y van al baño a lavársela.
Las cuatro mujeres escucharon lo que dijo el
entrevistador, pero, ¿cómo lograron descifrar
que se dirigía explícitamente a ellas o no?
>Solución.
Si sólo una señora tuviera la cara sucia, ella se
habría puesto de pie inmediatamente cuando el
entrevistador hizo su comentario. Al ver que las
demás la tenían limpia, la suya tendría que ser
la sucia. Como son dos señoras las que tienen
la cara sucia, cada una de ellas verá a otra con
la cara sucia, y al ver que la otra no se levanta
enseguida, caerá en cuenta que es ella porque
está viendo una cara sucia que tiene que ser la
suya. Por último, al ver que estas dos señoras
se levantan, las otras seguirán tranquilas, porque si las que se pusieron de pie hubieran visto
dos caras sucias, no se habrían levantado.
[1] Navon D. 2001.The puzzle of mirror reversal:
A view from Clockland. Psycolocuy: 13(11).
Disponible en http://psycprints.ecs.soton.ac.uk/archive/00000146/.
[2] Corballis MC. 2001. Why mirrors reverse left
and right. Psycolocuy: 12 (32). Disponible en http://
psycprints.ecs.soton.ac.uk/archive/00000161/.
[3] Michon G. 2000-2006. The counterfeit penny
problem. En Numericana.com. Disponible en
http://home.att.net/~numericana/answer/weighing.htm.