Presentación de PowerPoint
Anuncio

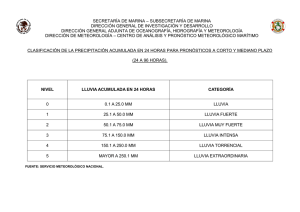
Lecciones aprendidas de estudios hidrológicos en las cuencas de los ríos Coyolate y Villalobos. Algunos conceptos básicos Evento extremo Probabilidad de excedencia “p” P(X > xo) P( T° > 40°C) Probabilidad de no excedencia “q” P(X ≤ xo) Período de retorno “Intervalo de recurrencia” P(T° ≤ 40°C) (Tr = 1/p) Las probabilidades son complementarias y positivas p+q=1 p=1–q q=1–p A > p < q < Tr A < p > q > Tr La inundación de 2 años se produce en promedio 25 veces durante un periodo de 50 años. Así como la inundación de 25 años se producirá en promedio una vez cada 25 años, la tormenta de 25 años también se producen en promedio una vez cada 25 años. Un error común es que una tormenta de 25 años siempre producirá una inundación de 25 años. Concepto de serie de tiempo Conjunto de datos correspondientes a una variable continua o discreta medidos cuantitativa o cualitativamente en el tiempo. Ejemplo: Pp, T, P°, HR, V, Q,,, Serie diaria Serie mensual Serie anual Serie anual Antecedentes Posee una red de estaciones hidrométricas y meteorológicas que data a partir de la década de los años 60´. La red llegó a estar conformada por más de 300 estaciones, de la cuales actualmente están en operación 70, siendo 40 meteorológicas y 30 hidrométricas. Estaciones hidrométricas Estaciones meteorológicas Estaciones meteorológicas Instrumentación hidrológica Instrumentación satelital Análisis red meteorológica subcuenca río Villalobos Características de las redes de monitoreo meteorológico e hidrométrico Densidad Características Instrumentación Análisis red meteorológica subcuenca Río Villalobos Metodología propuesta por Fattorelli & Fernández, 2011 Se basa en el comportamiento espacial de la lluvia, considerando la variabilidad y el error asociado a las estimaciones. Se estima que la cantidad total de estaciones debe ser de 6 con un error del 10%, lo que te tendría 1 estación por cada 52 km2. Propiedades de las series Longitud Homogeneidad Independencia Tendencia Longitud (l) La longitud l ≥ 30 años Datos faltantes n ≤ 5% Longitud (l) No. 1 2 Estación Compuertas Amatitlán Guatemala Sur Tipo Inicio Longitud (años) Datos faltantes (%) INDE B 1977 38 1.97 INDE B 1980 35 1.63 Institución 3 La Pampa INDE B 1983 32 0.00 4 Observatorio INSIVUMEH A 1970 45 0.58 5 Suiza Contenta INSIVUMEH B 1973 42 3.43 Homogeneidad Pruebas t Student, Cramer, Helmert, t est < t teor α = 90, 95 % Independencia Prueba de Anderson (correlograma) y corridas de Wald-Wolfowitz Al menos el 90% de los puntos debe quedar en el intervalo de confianza. Independientes & Homogéneas Independientes y Heterogéneas Dependientes & Homogéneas Dependientes & Heterogéneas Las series de tiempo de eventos hidrometeorológicos deben de ser independientes y homogéneas. Tendencia Test de Spearman Rank Order Correlation, recomendado por OMM. La tendencia posee dos componentes: 1. Sentido (+, - o nulo) 2. Significancia (presencia o ausencia) Como se clasifican las series de tiempo? Normales Lluvia anual, temperatura media anual, Extremas Máximas Crecidas “avenidas”, vientos huracanados, olas de calor, Mínimas Sequías, heladas, Parámetros estadísticos Media µ Desviación estándar S Coeficiente de variación Cv Coeficiente de sesgo ~ asimetría σ Kurtosis δ Estimación de los parámetros Momentos convencionales “Mc” Momentos lineales “Ml” Comportamiento del coeficiente de Pearson “asimetría ~ sesgo” Cs < 0 Min Cs = 0 Normal Cs > 0 Max Escalas Aritmética Logarítmica (log) Probabilístic a Normal Gumbel Papel a escala probabilística Normal Papel a escala probabilística Gumbel Como se clasifican las series extremas? Mínimas Q1D, Q2D, Q3D, Q5D, Q7D, Q10D, Q15D, Q30D Máximas De excedencia anual 1 dato/año Caudal máximo anual De excedencia parcial ≥ 1 dato/año Distribución teórica de frecuencia ~ Función de probabilidad Modelo estadístico de aplicabilidad en el análisis de eventos extremos para la estimación de la magnitud y período de retorno. Funciones de probabilidad Normal~ Gauss Normal Galton Serie Máxima Extrema Mínima Series extremas Mínimas Weibull (Tipo III) Máximas Gumbel (Tipo I), Fréchet (Tipo II), Pearson, Gama, Pareto, Wakeby, VEG, Objetivos en el análisis de series de tiempo de eventos extremos hidrometeorológicos Predecir la magnitud de un evento posible durante un cierto período de tiempo Objetivo Estimar la frecuencia con que un evento de cierta magnitud pueda producirse Principio de Parsimonía Proyecciones no más de 2 a 3 veces la longitud del registro de las series analizadas. Aplicación a la cuenca del río Coyolate 1. Enfoque estadístico ~ estocástico: Análisis clásico de frecuencia a series de crecidas 1. Seleccionar y verificar serie 2. Parámetros estadísticos 3. Análisis de frecuencia 4. Seleccionar función de probabilidad 5. Eventos de diseño Qmax = µ + KT S Homogeneidad & Independencia Estadística Homogeneidad Hidrológica Condiciones Estadística Independencia Hidrológica Independencia hidrológica Serie de caudales máximos anuales Homogeneidad estadística Prueba t Student Cramer t (95%) Estimado Teórico 2.53 2.76 1.84 2.78 Conclusión Homogénea Homogénea Independencia estadística Ajuste estadístico Función de probabilidad de mayor ajuste Eventos de diseño 2. Enfoque estadístico ~ estocástico: Análisis regional de crecidas 1. Seleccionar y verificar series 2. Parámetros estadísticos 3. Análisis regional de frecuencia 4. Seleccionar función de probabilidad 5. Eventos de diseño Qmax = µ + KT S Región hidrológica Región geográfica en donde el régimen de lluvias y los factores que inciden son similares. Regiones hidrológicas Series utilizadas Elevación Área msnm 360 Km2 395 Naranjo 291 501 10 Meléndrez Naranjo 20 149 12 Nahuatán Naranjo 40 185 23 Ocosito Ocosito 48 462 32 Sis Sis-Icán 28 156 25 Sn. Miguel Moca Nahualate Nahualate 176 620 30 San Mauricio Nahualate Nahualate 30 1191 10 Montecristo Cutzán Nahualate 229 129 31 Puente Coyolate Coyolate Coyolate 213 512 31 Cerro Color. Coyolate Coyolate 42 1154 6 Barriles Siguacán Nahualate 67 154 6 Estación Río Cuenca Malacatán Suchiate Naranjo Meléndrez II Pajapita Cabúz Coatepeque Caballo Blanco La Máquina Longitud 30 Caudal específico (Qe) vrs área (A) Ajuste estadístico regional Eventos de diseño Período de retorno (años) 2 5 10 25 50 100 200 3 Q máximo (m /s) Clásico Regional 147 199 313 395 482 594 784 949 1,088 1,310 1,476 1,777 1,965 2,375 Diferencia Q % 52 36 82 26 112 23 165 21 222 20 301 20 409 21 3. Estimación de lluvias de diseño y su transformación a hidrogramas (enfoque estadístico-determinístico) 1. Estimar lluvias de diseño 2. Transformar las lluvias de diseño 3. Estimar los componentes de los hidrogramas generados Lluvia de diseño (lámina) Lluvia diaria máxima anual Lluvia de diseño Lluvia en 24 horas máxima anual Lluvia de diseño (lámina) Lluvia efectiva (Pe = PB – pérdidas) Ingenieril ~ Hidrológica Fracción de la lluvia que escurre Agronómica ~ Ambiental Fracción de la lluvia que infiltra Lluvia efectiva Hietograma de diseño Sintético Hietograma Histórico ~ observado Hietograma de diseño Curva masa La cuenca como un sistema, Ven Te Chow (1998) Efecto de la humedad del suelo Modelación determinística Modelación determinística Componentes de los hidrogramas Consideraciones finales “La modelación hidrológica es más un arte que una ciencia y es probable que siga siendo así. La utilidad de los resultados depende en gran medida del talento y la experiencia del hidrólogo, del entendimiento de los matices matemáticos del modelo en particular y de los matices hidrológicos de la cuenca en particular”. Loague & Freeze (1985)