construcción geométrica de las cónicas

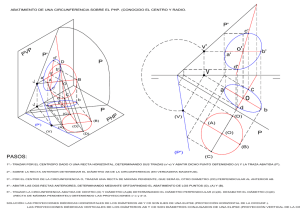
CONSTRUCCIÓN GEOMÉTRICA
DE LAS CÓNICAS
Yuli Andrea Rodríguez Rodríguez1
Benjamin R. Sarmiento Lugo2
Universidad Pedagógica Nacional
[email protected]
Universidad Pedagógica Nacional
[email protected]
RESUMEN
En este artículo se presentan diversos métodos para construir geométrica las cónicas.
Para lograr cada curva mediante los pasos que aquí se presentan se sugiere usar el
software de geometría dinámica Cabri II Plus. Para la elipse se presentan dos métodos
de construcción y para la hipérbola se presentan cuatro métodos
1. CONSTRUCCIÓN DE LA ELIPSE
Ecuación cartesiana:
x2
y2
+
=1
a2
b2
Ecuación polar: ρ =
ab
2
2
b Cos θ + a 2 Sen 2 θ
Ecuaciones paramétricas: x = a Cost , y = b Sent
1.1 PRIMER MÉTODO
1. Mostrar ejes coordenados. Sea O el origen de coordenadas.
2. Sean A y B puntos sobre el eje OX positivo, tales que O – A – B.
3. Trazar la circunferencia CO con centro O y radio OA.
4. Trazar la circunferencia CO1 con centro O y radio OB.
5. Sea C un punto sobre la circunferencia CO.
6. Trazar la semirrecta OC.
7. Sea D la intersección entre la semirrecta OC y la circunferencia CO1.
8. Trazar la recta h perpendicular al eje Y que pase por C.
9. Trazar la recta v perpendicular al eje X que pase por D.
10. Sea E la intersección entre las rectas h y v.
11. El lugar geométrico generado por E cuando se mueve C sobre la circunferencia CO
es la Elipse.
Nota: Al mover los puntos A y B se modifican los semiejes de la elipse.
1
2
Licenciada en Matemáticas – Universidad Pedagógica Nacional
Magíster en Educación Matemática – Universidad Pedagógica Nacional
-1-
Figura 1
1.2 SEGUNDO MÉTODO
Del paso 1 al paso 4, se describen objetos iniciales que permitirán controlar vértices y
focos de la elipse.
Trazar una semirrecta PQ.
Sea A un punto sobre la semirrecta PQ.
Trazar la semirrecta AQ.
Sea B un punto sobre la semirrecta AQ.
Trazar dos rectas h y v, perpendiculares entre si, que se crucen en O (h = horizontal,
v = vertical).
6. Trazar la circunferencia CO con centro O y radio PA.
7. Sean F1 y F2 las intersecciones de la recta h con la circunferencia CO.
8. Trazar la circunferencia CO1 con centro O y radio PB.
9. Sean V1 y V2 las intersecciones de la recta h con la circunferencia CO1.
10. Trazar el segmento V1V2.
11. Sea X un punto sobre el segmento V1V2.
12. Trazar la circunferencia CF1 con centro F1 y radio XF1.
13. Trazar la circunferencia CV2 con centro V2 y radio XF1.
14. Sean S y R las intersecciones de la circunferencia CV2 con la recta h, tales que
S – V2 – R.
15. Trazar la circunferencia CF2 con centro F2 y radio V1S.
1.
2.
3.
4.
5.
Nota: En los pasos del 11 al 16 se está haciendo uso de la condición d(F1,X) + d(F2,X)
= d(V1,V2) = 2a de la definición de elipse.
16. Sean M y N los puntos de intersección entre las circunferencias CF1 y CF2.
17. El lugar geométrico generado por los puntos M y N cuando se mueve X sobre el
segmento V1V2 es la Elipse.
-2-
Nota: Las intersecciones de la recta v con el lugar geométrico se usan para determinar
la longitud del semieje vertical de la elipse.
Figura 2
2. CONSTRUCCIÓN DE LA HIPÉRBOLA
x 2 y2
Ecuación cartesiana: 2 - 2 = 1 ;
a
b
Ecuación polar: ρ =
ab
b 2 Cos 2 θ - a 2 Sen 2 θ
Ecuaciones paramétricas: {x = a Sect ; y = b Tant
2.1 PRIMER MÉTODO
1. Mostrar ejes coordenados. Sea O el origen de coordenadas.
2. Sean F1 y F2 puntos sobre el eje X, tales que F1 sea el simétrico de F2 con respecto
al eje Y. (F1 y F2 son los focos de la hipérbola).
3. Sea A un punto sobre el eje X, entre F1 y F2.
4. Trazar una circunferencia CF1 con centro F1 y radio AF1.
5. Sea B un punto sobre la circunferencia CF1.
6. Trazar el segmento BF2.
7. Trazar la recta BF1.
8. Trazar la mediatriz m del segmento BF2.
9. Sea P la intersección entre la recta BF1 y la mediatriz m.
-3-
10. El lugar geométrico generado por el punto P cuando se mueve B sobre la
circunferencia CF1 es la Hipérbola.
Nota: Al mover los puntos F1 y A se modifica la hipérbola. Si A es un punto sobre el
eje X tal que F1 – F2 – A, se obtiene una elipse.
Figura 3
2.2 SEGUNDO MÉTODO
Del paso 1 al paso 4, se describen objetos iniciales que permitirán controlar vértices y
focos de la hipérbola.
1.
2.
3.
4.
5.
Trazar una semirrecta PQ.
Sea A un punto sobre la semirrecta PQ.
Trazar la semirrecta AQ.
Sea B un punto sobre la semirrecta AQ.
Trazar dos rectas h y v, perpendiculares entre si, que se crucen en O, (h = horizontal,
v = vertical).
6. Trazar circunferencia CO con centro O y radio BA.
7. Sean V1 y V2 las intersecciones de la recta h con la circunferencia CO.
8. Trazar la circunferencia CO1 con centro O y radio PB.
9. Sean F1 y F2 las intersecciones de la recta h con la circunferencia CO1.
10. Sea X un punto sobre la recta h a la derecha de V2 (que no quede entre V1 y V2).
11. Trazar la circunferencia CF1 con centro F1 y radio XF1.
12. Trazar la circunferencia CX con centro X y radio V1V2.
13. Sea K el punto de intersección de la circunferencia CX con la recta h (a la derecha
de X).
14. Trazar la circunferencia CF2 con centro F2 y radio KF1.
Nota: En los pasos del 10 al 14 se está haciendo uso de la condición d(F1,X) – d(F2,X)
= d(V1,V2) = 2a de la definición de hipérbola.
-4-
15. Sean M y N las intersecciones entre las circunferencias CF1 y F2.
16. El lugar geométrico generado por los puntos M y N cuando se mueve X sobre la
recta h es la Hipérbola.
Nota: La recta vertical v se usa para construir las asíntotas de la hipérbola.
Figura 4
2.3 TERCER MÉTODO (HIPÉRBOLA EQUILÁTERA)
1. Mostrar los ejes coordenados. Sea O el origen de coordenadas.
2. Sea A un punto sobre el eje Y.
3. Sean V1 y V2 puntos sobre el eje X, simétricos entre si con respecto al eje Y (V1 y
V2 son los vértices de la hipérbola).
4. Trazar la circunferencia CA con centro A y radio AV1.
5. Trazar la recta p perpendicular al eje Y y que pase por A.
6. Sean P y Q las intersecciones entre la recta p y la circunferencia CA.
7. El lugar geométrico generado por los puntos P y Q cuando se mueve A sobre el eje
Y es la Hipérbola Equilátera.
-5-
Figura 5
2.4 CUARTO MÉTODO (HIPÉRBOLA EQUILÁTERA)
1. Trazar dos rectas h y v, perpendiculares entre si, que se corten en O (h = horizontal,
v = vertical).
2. Sean V1 y V2 puntos sobre la recta h, simétricos entre si con respecto a la recta v.
3. Sea X un punto sobre h, (que no este entre V1 y V2).
4. Trazar circunferencia CO con centro O y radio OX.
5. Trazar la recta l perpendicular a la recta h y que pase por V2.
6. Trazar la recta m perpendicular a la recta h y que pase por X.
7. Sea C la intersección entre la recta l y la circunferencia CO.
8. Trazar recta n perpendicular a la recta v y que pase por C.
9. Sea P la intersección entre las rectas m y n.
10. El lugar geométrico generado por P cuando se mueve X sobre la recta h es la
Hipérbola Equilátera.
Nota: Para construir las asíntotas se trazan las rectas oblicuas que pasan por los vértices
del cuadrado con centro en O con lados paralelos a las rectas h y v, y longitud de los
lados iguales a la distancia entre V1 y V2.
Figura 6
-6-
3. CONSTRUCCIÓN DE LA PARÁBOLA
Ecuación cartesiana: y = ax 2 + bx + c
Ecuación polar: ρ = 2p
Cosθ
Sen 2 θ
p
⎧
Ecuaciones paramétricas: ⎨ x = t 2 ; y = pt
2
⎩
3.1 PRIMER MÉTODO
1. Trazar una recta horizontal h.
2. Sea X un punto sobre la recta horizontal h.
3. Sea F un punto exterior a la recta h.
4. Trazar el segmento XF.
5. Sea m la mediatriz del segmento XF.
6. Trazar la recta l perpendicular a la recta h que pase por el punto X.
7. Sea P la intersección de las rectas l y m.
8. El lugar geométrico generado por P cuando se mueve X sobre la recta h es la
parábola.
Figura 3.30
REFERENCIAS BIBLIOGRÁFICAS
Álvarez, J. (2006), Curvas en la historia. España. Nivola Libros Ediciones.
Boyer, Carl. Historia de las matemáticas, Madrid editorial,1996
Cordero, F. y Suárez. L. Modelación en matemática educativa. (Clame 2005).
-7-
Fuller, G. y Tarwater, D. Geometria Analítica. Eddison Wesley. Iberoamericana.
Wilmington, 1995.
Kline, Morris. El pensamiento matemático de la antigüedad a nuestros días. Madrid,
Editorial Alianza. Tomos I , II y III.
Lehmann, Charles. Geometría Analítica. Editorial Limusa. Máxico, 1994.
Pérez, Antonio. Curvas con historia: De las cónicas a las ecuaciones de las flores.
En http://platea.cnice.mecd.es/~aperez4
http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Curves.html
http://xahlee.org/SpecialPlaneCurves_dir/specialPlaneCurves.html
http://www.mathcurve.com/courbes2d/courbes2d.shtml
-8-